Intro to Quantum Mechanics - part II
The wavefunction
Intro to Quantum Mechanics - part II
The wavefunction
Background
Introduction to Quantum Mechanics II
The Wavefunction
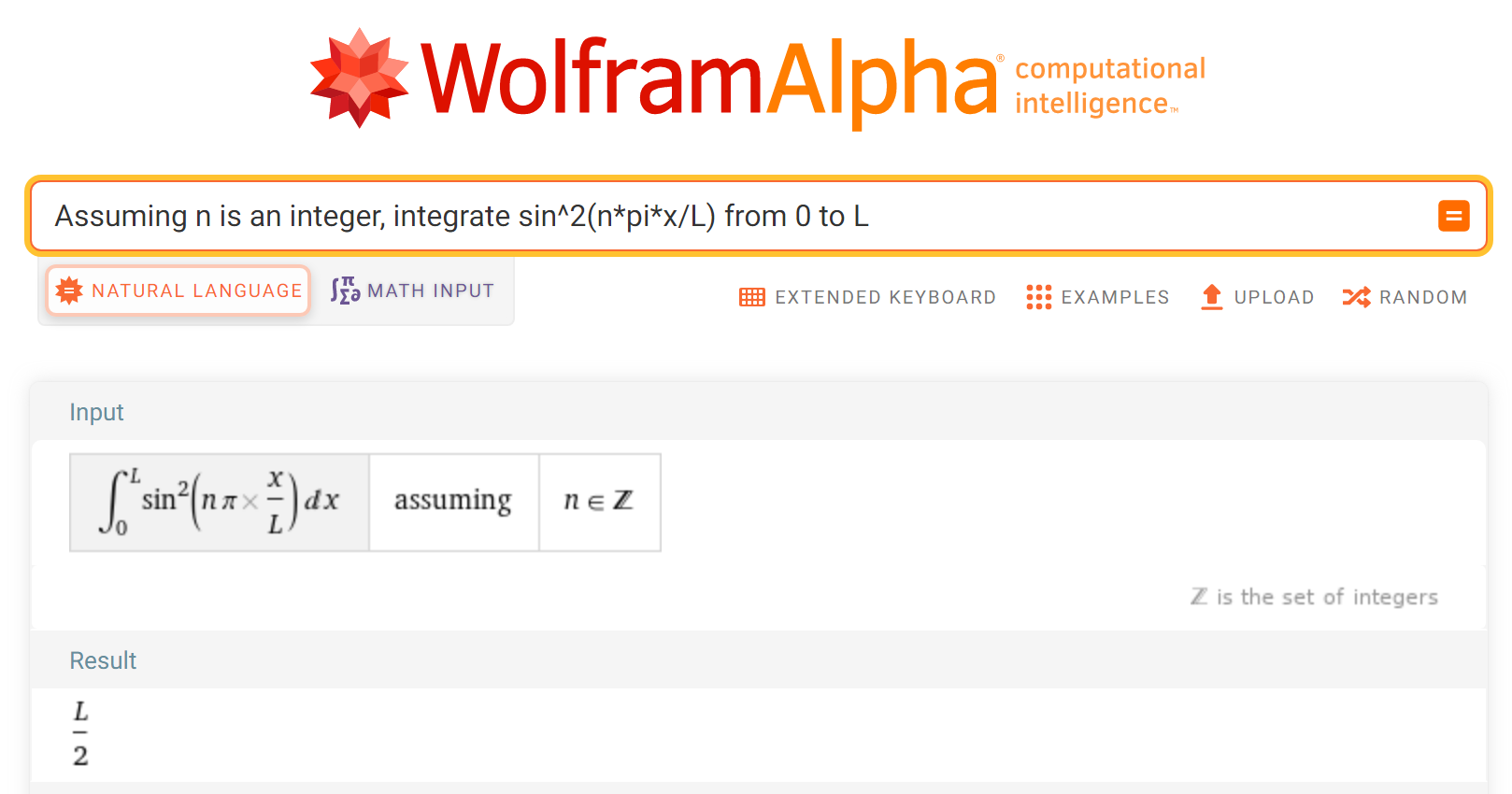
Complex numbers
Intro to Quantum Mechanics - part II
The wavefunction
Schrodinger's Wave Equation
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-dependent Schrodinger equation (1932)
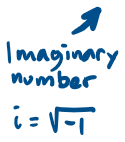


Starring
A complex-valued wave function, whose
nature is still under investigation to this day, but whose
norm evidently provides the correct probability density
&
Born's Rule
Normalization condition
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-dependent Schrodinger equation (1932)
A complex-valued wave function, whose
nature is still under investigation to this day, but whose
norm evidently provides the correct probability density
A proper must satisfy the following conditions
All first-order derivatives must be continuous.
for a given pair of x and t, the wave function must have a unique value. This is typically satisfied for most mathematical functions anyway.
Since the norm of the wave function corresponds to the probability density, it must not be infinite over any range.
Essentially, there should be no jumps in the wave function. This is to guarantee that the momentum (which is the gradient of the wave function) is not infinite at any point.
Essentially, the wave function should be smooth. This is to guarantee that the energy is not infinite at any point.
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-dependent Schrodinger equation (1932)
Show that any wave function of the form
satisfies the TDSWE for any potential energy function V.
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-dependent Schrodinger equation
For a wave function of the form
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-dependent Schrodinger equation
Recall: the classical expression for the kinetic energy in terms of momentum is:
where m is the rest mass of the particle.
The total energy of the particle is
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-dependent Schrodinger equation
One of the most important features of TDSWE is ...

i.e. The linear sum of solutions is also a solution!
Superposition
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-dependent Schrodinger equation
satisfies
since
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-dependent Schrodinger equation
One of the most important features of TDSWE is ...

i.e. The linear sum of solutions is also a solution!
Superposition
Intro to Quantum Mechanics - part II
The wavefunction
Time-dependence
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Separating the time and position dependence
If the potential energy function does not explicitly depend on time, then the position and time dependence of the wave function can be separated:
where is only position dependent
and is only time dependent
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Separating the time and position dependence

Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time dependence
The time dependent part of the wavefunction satisfies the differential equation:
whose solution is
for
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time evolution of quantum states is in the form of a time dependent phase.
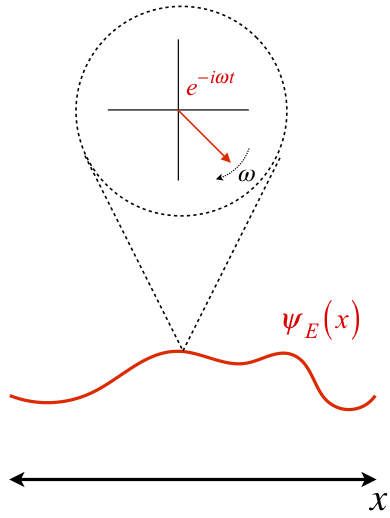
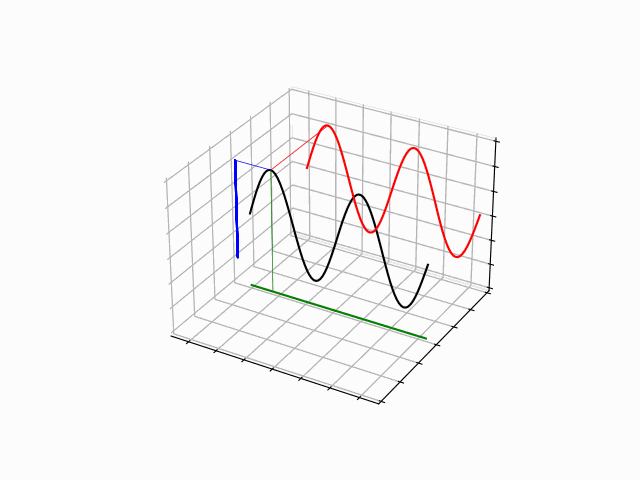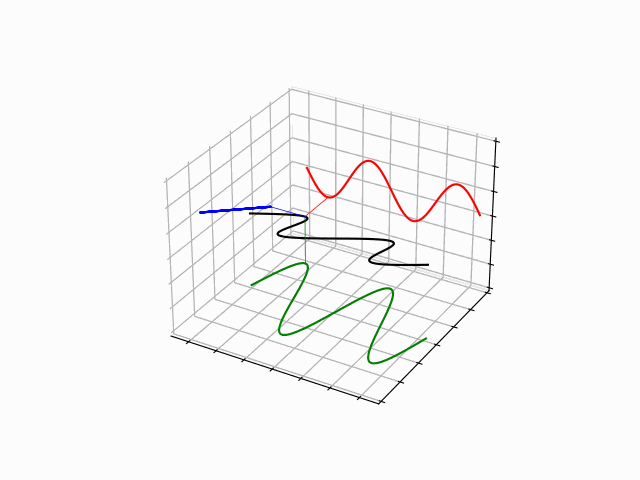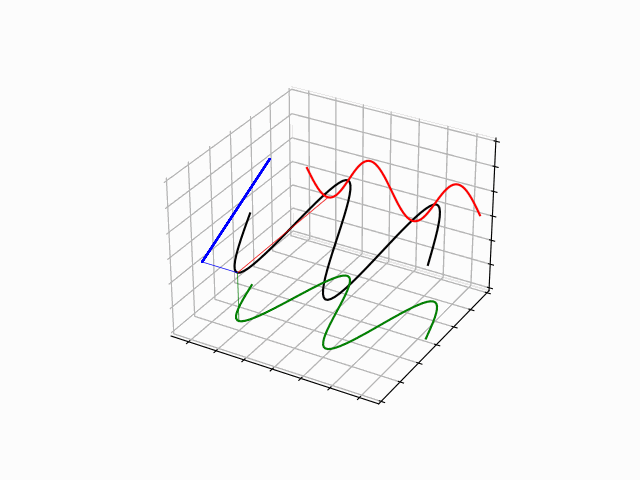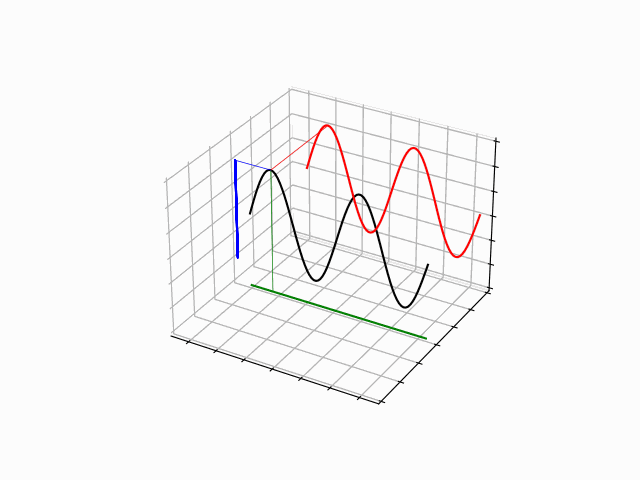
The time dependence
Intro to Quantum Mechanics - part II
The wavefunction
The time-independent Schrodinger equation
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-independent Schrodinger equation
The time-independent part of the wave function satisfies the time-independent Schrodinger wave equation
whose solution depends on
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-independent Schrodinger equation for constant potential
In a region where the potential is 0 (free particle)
Rearranging,
with the general solution:
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
The time-independent Schrodinger equation for constant potential
In a region where the potential is constant:
Rearranging,
case:
with the general solution:
case:
with the general solution:
Intro to Quantum Mechanics - part II
The wavefunction
Detailed Example: The infinite potential well in 1-D
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.

Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.

The wavefunction, , has to satisfy
Region I:
Region II:
Region III:
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.

The wavefunction, , has to also be single- valued, continuous everywhere, and normalized.
Normalization :
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.

Region I:
Region III:
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.

Region II:
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.

Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.

Normalization :
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.

... satisfies TDSWE:
... is single-valued & continuous
... is square-integrable
... is normalized
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.

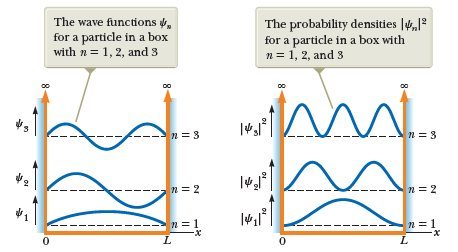
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.

Recall
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.



Intro to Quantum Mechanics - part II
The wavefunction
Example: The finite potential well in 1-D
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
finite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in a finite square-well potential, and their energies.

Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Finite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in a finite square-well potential, and their energies.

The wavefunction, , has to satisfy
Region I:
Region II:
Region III:
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Finite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in a finite square-well potential, and their energies.

The wavefunction, , has to also be single- valued, continuous everywhere, and normalized.
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Finite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in a finite square-well potential, and their energies.

Region I:
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Finite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in a finite square-well potential, and their energies.

Region III:
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Finite square-well potential

Region I:
Region III:
&
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in a finite square-well potential, and their energies.
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Finite square-well potential

Region II:
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in a finite square-well potential, and their energies.
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Finite square-well potential

There are 5 unknowns:
and
Need 5 equations:
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in a finite square-well potential, and their energies.
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Finite square-well potential

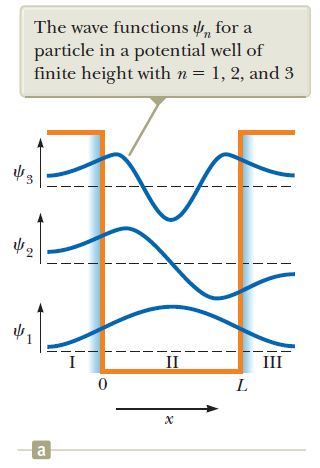
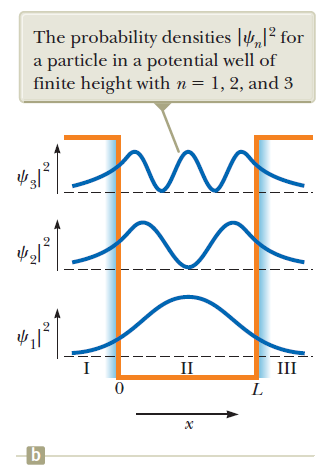
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in a finite square-well potential, and their energies.
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Finite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle in a finite square-well potential, and their energies.

Penetration depth
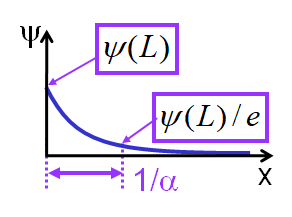
Intro to Quantum Mechanics - part II
The wavefunction
Example: The harmonic potential well in 1-D
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Simple harmonic oscillator
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle experiencing a simple harmonic potential
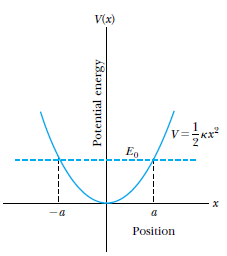
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Simple harmonic oscillator
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle experiencing a simple harmonic potential

or, simply
where
&
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Simple harmonic oscillator
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle experiencing a simple harmonic potential

Solving
with the conditions
as
we find
Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Simple harmonic oscillator
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle experiencing a simple harmonic potential
we find

Introduction to Quantum Mechanics II
The Schrodinger Wave Equation
Simple harmonic oscillator
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle experiencing a simple harmonic potential



Intro to Quantum Mechanics - part II
The wavefunction
Expectation Values
Introduction to Quantum Mechanics II
Expectation values
Definition
For any physical observable,
, the expectation value of repeated measurements of this observable is given by
where
is a mathematical operator corresponding to the physical observable, and
is the wavefunction of the system.
Introduction to Quantum Mechanics II
Expectation values
example
Determine the expectation values
for a particle in the first excited state in an infinite square well.
Introduction to Quantum Mechanics II
Expectation values
example
Determine the expectation values
for a particle in the first excited state in an infinite square well.

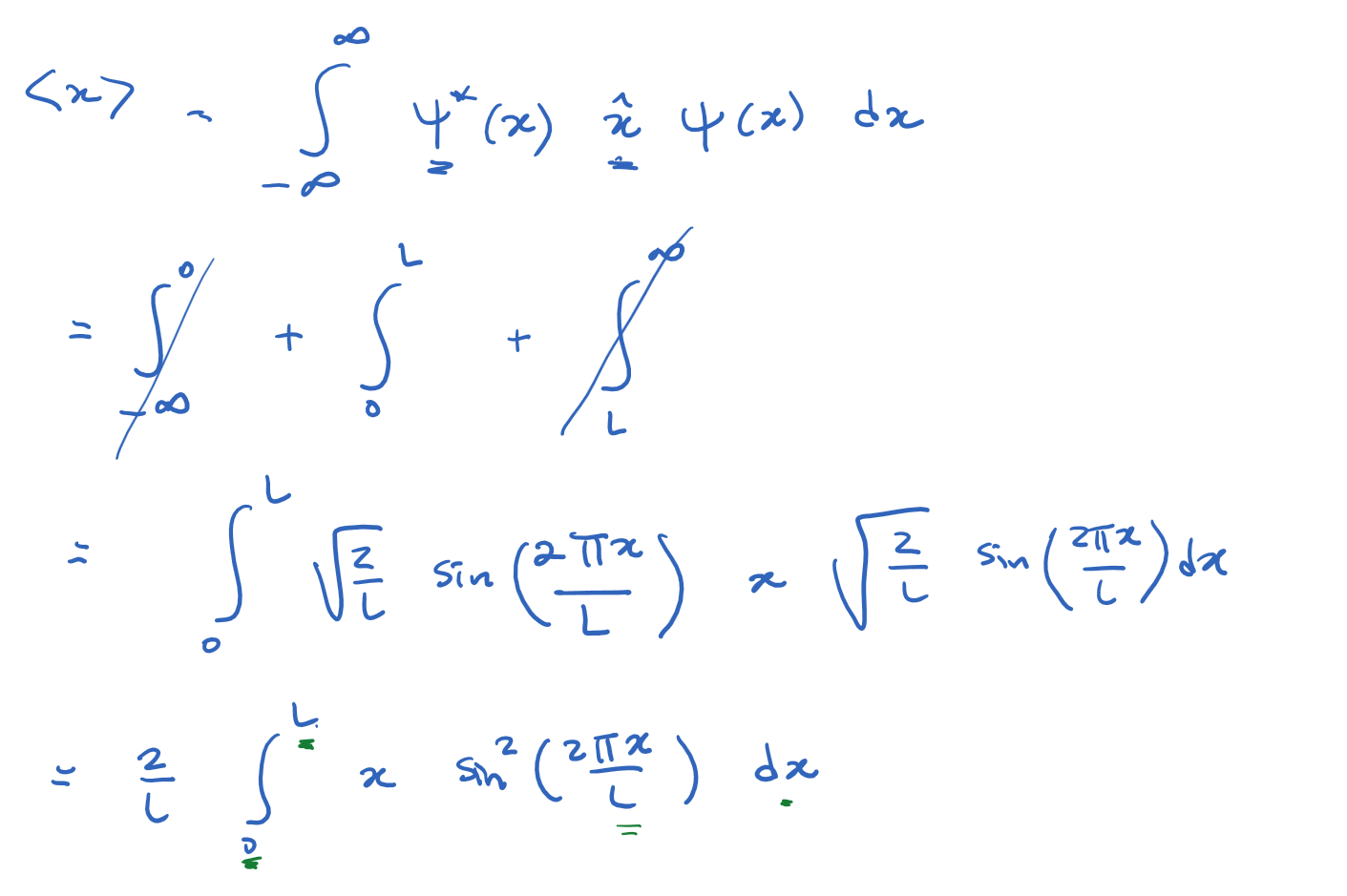
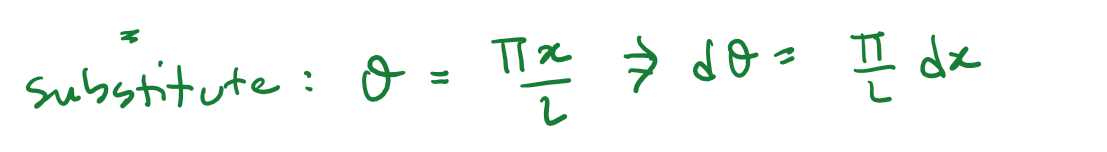
Introduction to Quantum Mechanics II
Expectation values
example
Determine the expectation values
for a particle in the first excited state in an infinite square well.

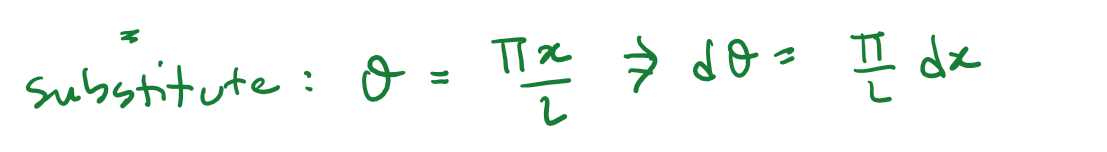
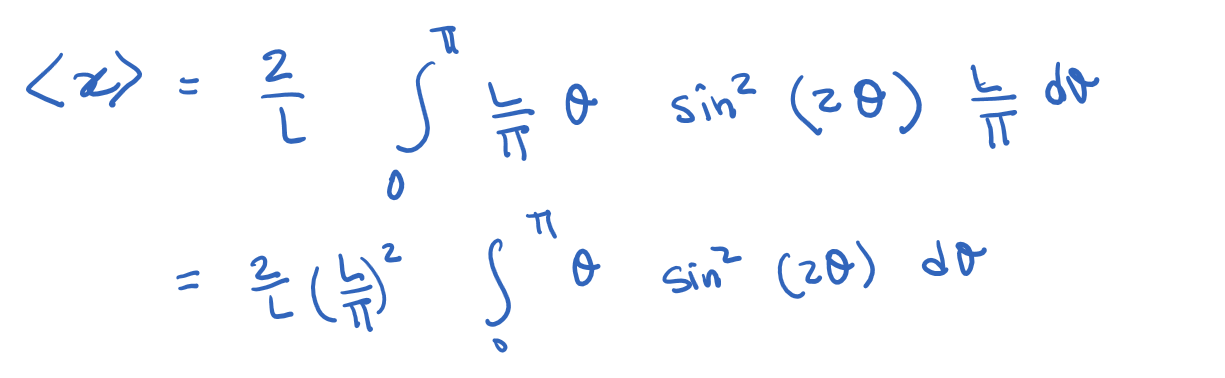
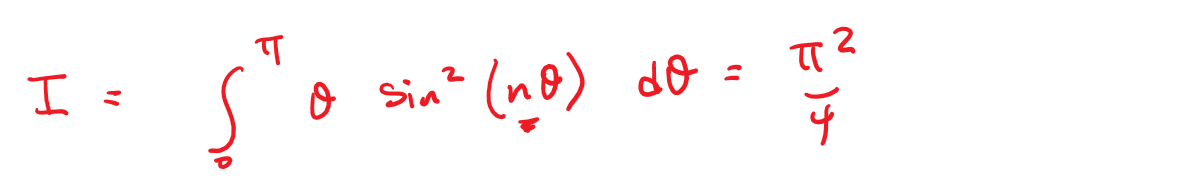
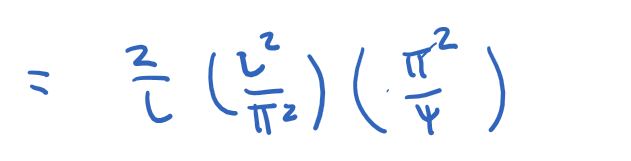
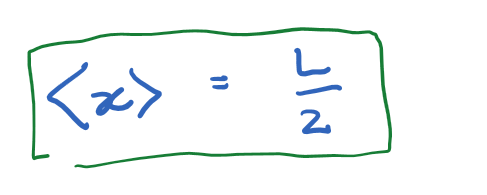
Introduction to Quantum Mechanics II
Expectation values
example
Determine the expectation values
for a particle in the first excited state in an infinite square well.
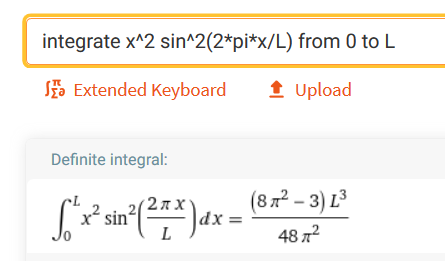
Introduction to Quantum Mechanics II
Expectation values
example
Determine the expectation values
for a particle in the first excited state in an infinite square well.
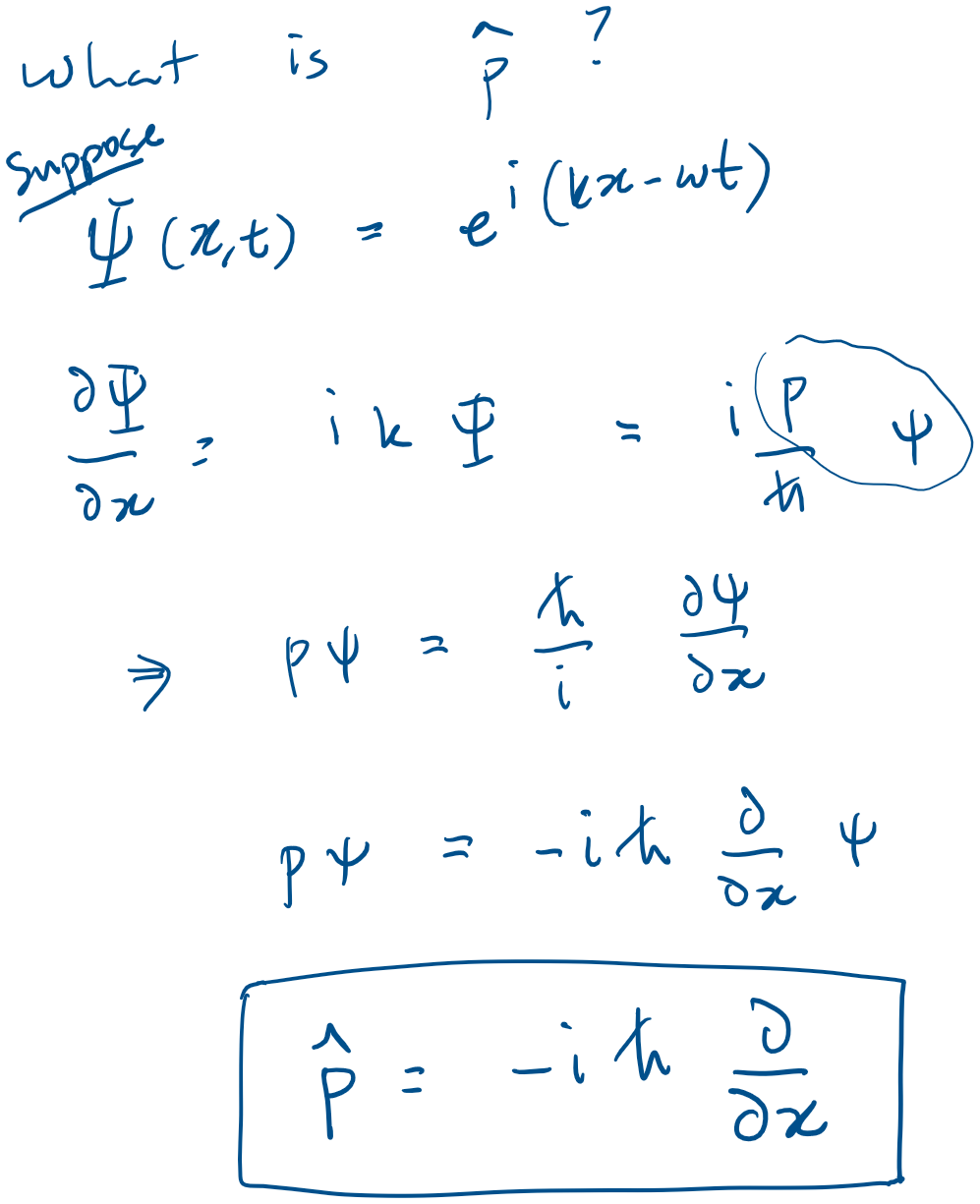
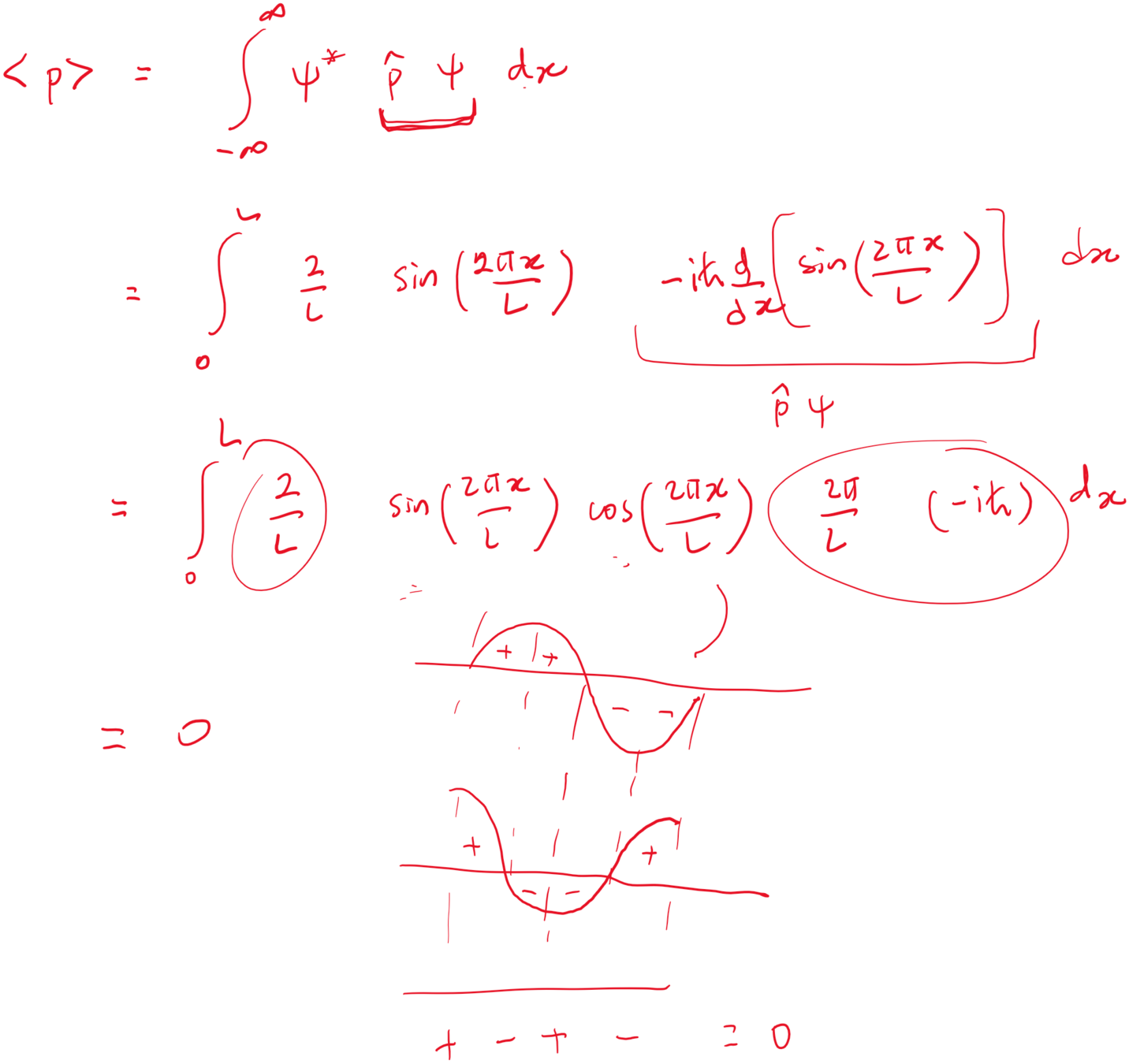
Introduction to Quantum Mechanics II
Expectation values
example
Determine the expectation values
for a particle in the first excited state in an infinite square well.
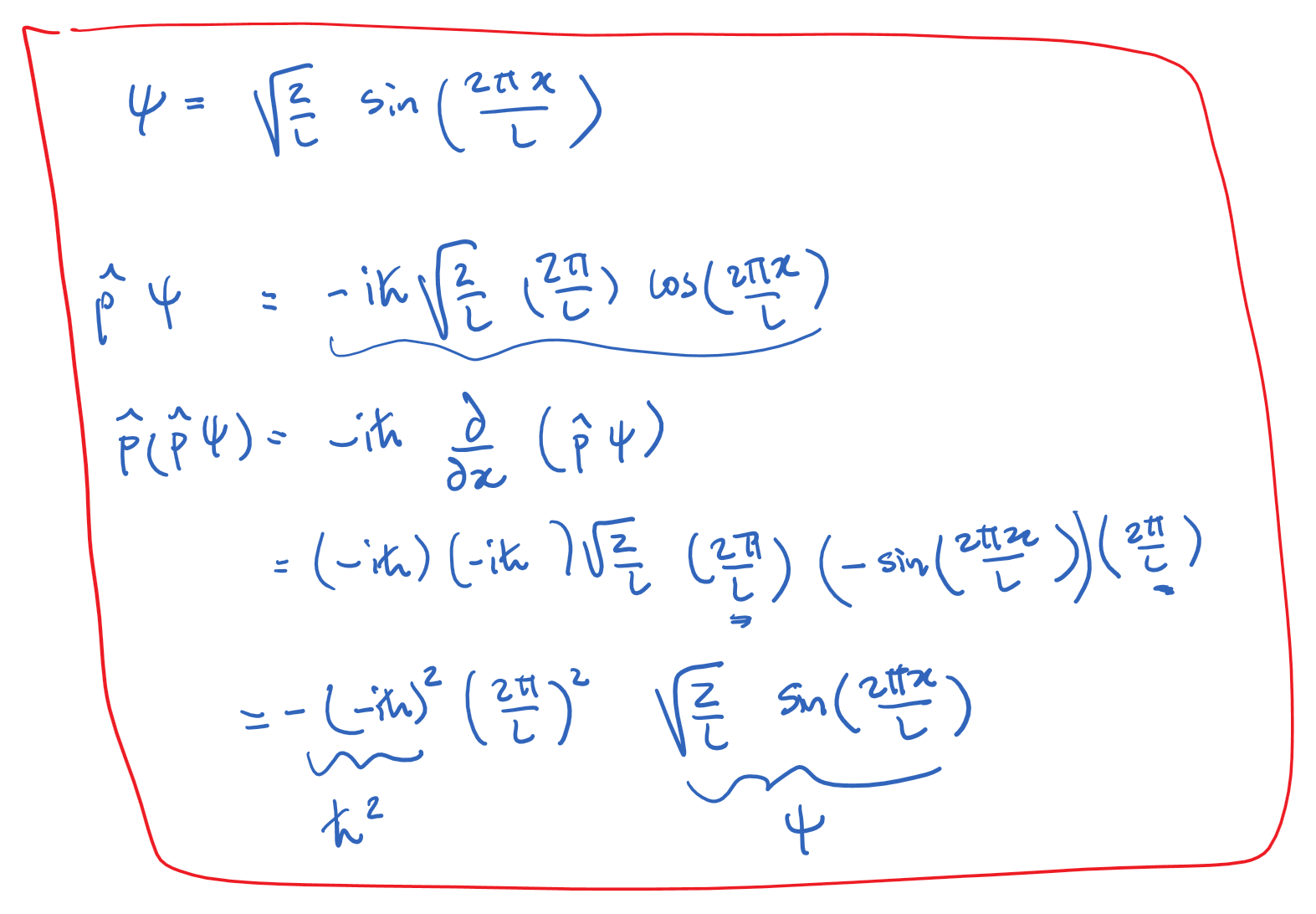
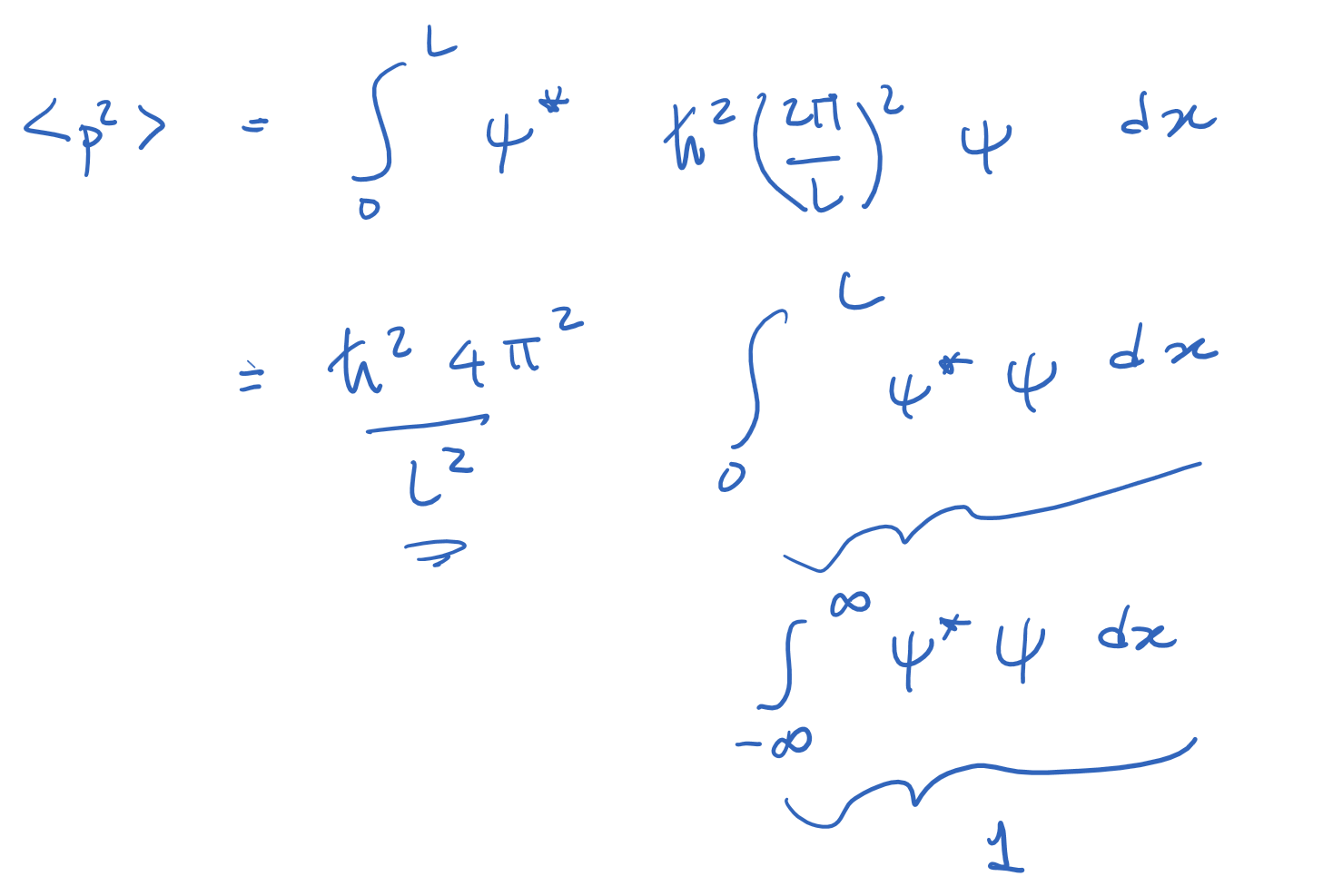
Introduction to Quantum Mechanics II
Expectation values
example
Determine the expectation values
for a particle in the first excited state in an infinite square well.
Introduction to Quantum Mechanics II
Expectation values
example
Determine the expectation values
for a particle in the first excited state in an infinite square well.
Alternatively,
since the energy of the first excited state in an infinite square potential well is definite (i.e. not uncertain)
repeated measurement of the energy will always yield the same outcome
then
the average of those outcomes will always come out to be the known energy of that state
thus
Introduction to Quantum Mechanics II
Expectation values
example
Determine the expectation values
for a particle in the first excited state in an infinite square well.
Introduction to Quantum Mechanics II
Uncertainties from Expectation values
Definition


Introduction to Quantum Mechanics II
Uncertainties from Expectation values
Example
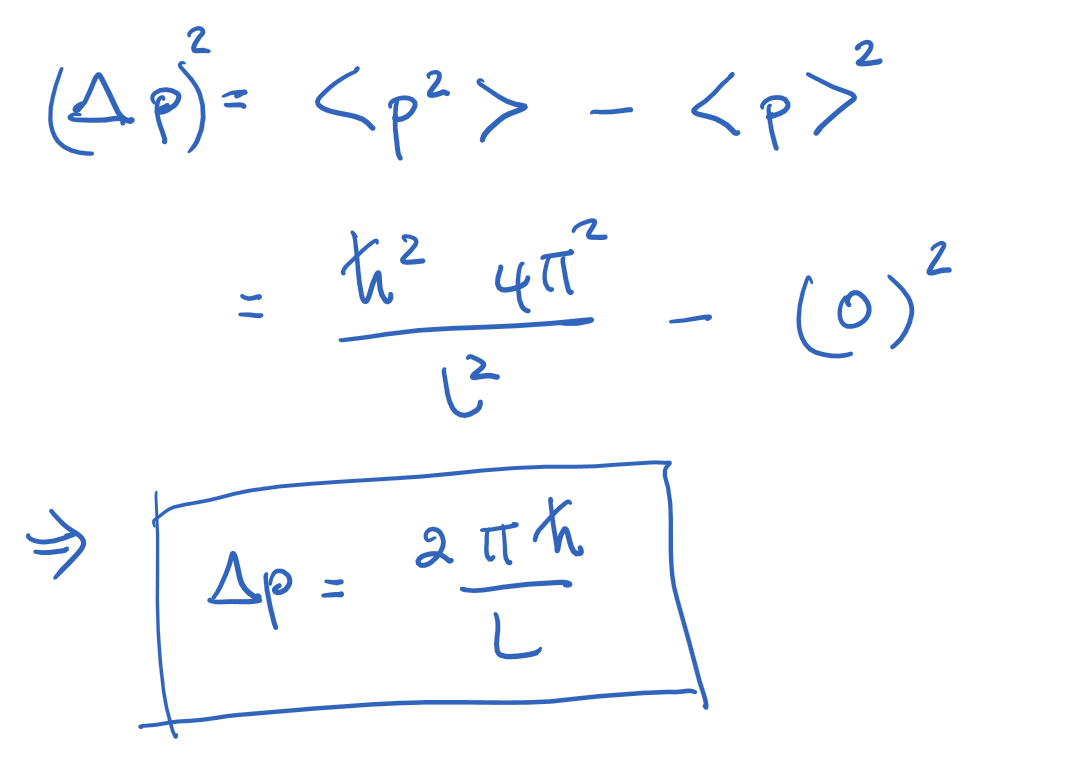

Determine the momentum uncertainty for a particle in the first excited state in an infinite square well, and use Heisenberg's uncertainty principle to bound the uncertainty in position.
Introduction to Quantum Mechanics II
Summary
The time-dependent Schrodinger equation (1932)

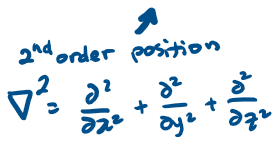

Starring
A complex-valued wave function, whose
nature is still under investigation to this day, but whose
norm evidently provides the correct probability density
&
Born's Rule
Normalization condition
Introduction to Quantum Mechanics II
Summary
Separating the time and position dependence
If the potential energy function does not explicitly depend on time, then the position and time dependence of the wave function can be separated:
(known as stationary states) are solutions of the time-independent SWE, each with a corresponding definite energy
Introduction to Quantum Mechanics II
Summary
Expectation values and uncertainties
The expectation value of any observable can be calculated for a given wave function via:
The variance of any physical quantity can be estimated from the expectation values:
Introduction to Quantum Mechanics II
Summary
Infinite square-well potential
Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in an infinite square-well potential, and their energies.



Introduction to Quantum Mechanics II
Summary
Finite square-well potential



Find an expression for the wave functions that satisfy the time-independent Schrodinger wave equation for a particle "trapped" in a finite square-well potential, and their energies.
Introduction to Quantum Mechanics II
Summary
Example
Suppose the wavefunction describing the position of a particle is given by a gaussian wavefunction of the form:
What is the probability of finding the particle in the range
Does this wavefunction satisfy Heisenberg's uncertainty principle?
Introduction to Quantum Mechanics II
By omoussa
Introduction to Quantum Mechanics II
- 949