Special Relativity
Description of motion from a special set of perspectives.
The Special Theory of Relativity
What is relativity?
Intro
The Special Theory of Relativity
What is relativity?
intro
How to change perspectives?
Relativity is concerned with the description of physical phenomena from different perspectives.
What physical quantities/laws are perspective dependent?
What physical quantities/laws are perspective independent?
The Special Theory of Relativity
What is relativity?
Relative and absolute quantities from a stationary perspective
Position is relative
Time is absolute
yet
Velocity is absolute
Acceleration is absolute
Displacement is absolute
= ((\red{x_2}\purple{-\Delta x})-(\red{x_1}\purple{-\Delta x}),...)
\vec{r}_1 = (x_1,y_1)
\vec{r}_2 = (x_2,y_2)
\vec{r}_1' = (x_1',y_1')
\vec{r}_2' = (x_2',y_2')
= (\red{x_1}\purple{-\Delta x},\red{y_1}\purple{-\Delta y})
= (\red{x_2}\purple{-\Delta x},\red{y_2}\purple{-\Delta y})
\Delta \vec{r} = \vec{r}_2 - \vec{r}_1
= (x_2-x_1,y_2-y_1)
\Delta \vec{r}' = \vec{r}_2' - \vec{r}_1'
= (x_2'-x_1',y_2'-y_1')
= (\red{x_2-x_1},\red{y_2-y_1})
\red{\vec{r}}\purple{\ne} \vec{r'}
\red{\Delta \vec{r}}\purple{=} \Delta \vec{r'}
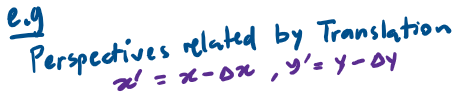
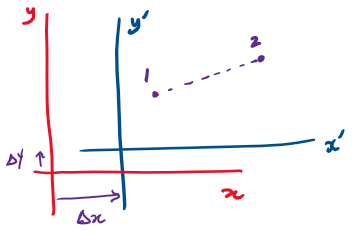
The Special Theory of Relativity
What is relativity?
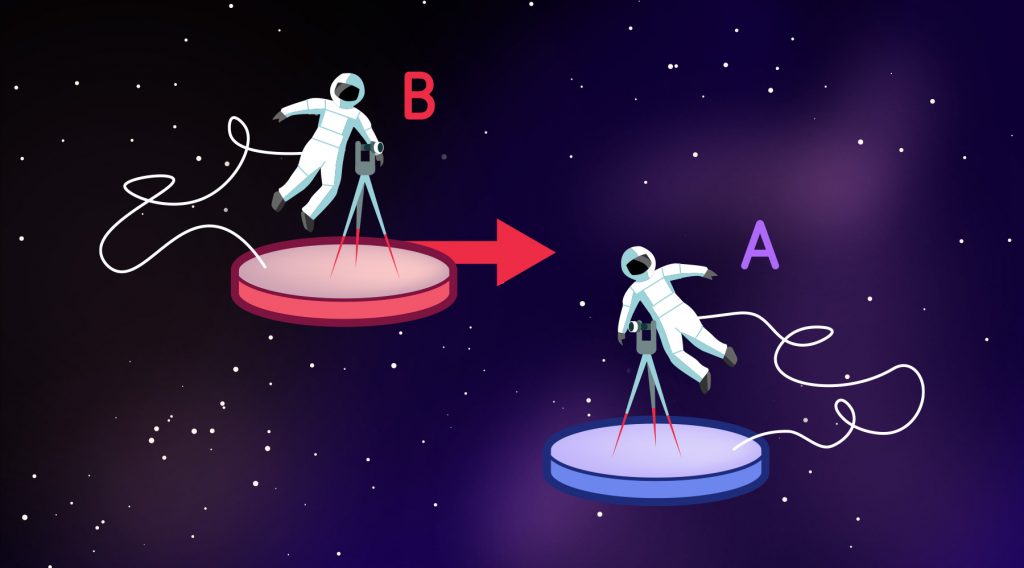
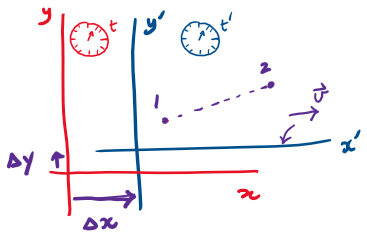
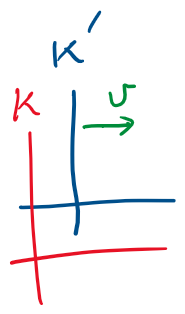
Relative and absolute quantities from an inertial perspective
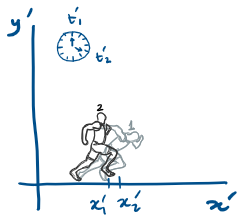
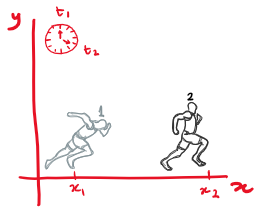
K: spectator view
1: how it started
2: how it's going
K': TV view
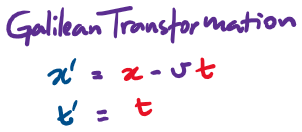
Eg
The Special Theory of Relativity
What is relativity?
Relative and absolute quantities from an inertial perspective
Velocity is relative
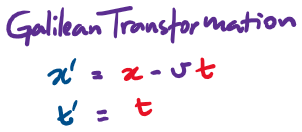
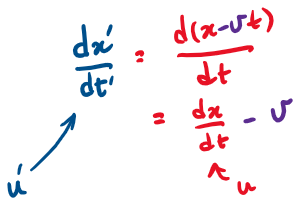
Acceleration is absolute
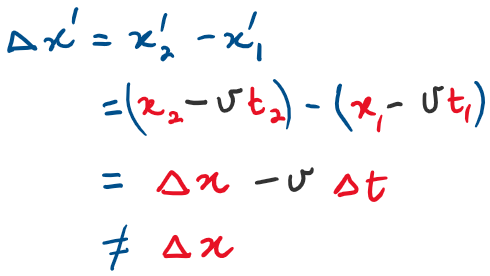
Position is relative
Displacement is relative
The Special Theory of Relativity
What is relativity?
Relative and absolute quantities from an inertial perspective
\ \text{or is}\ c' = c-v\ ?\
\ \text{is}\ c' = c =\frac{1}{\sqrt{{\epsilon_0}{\mu_0}}} ?\
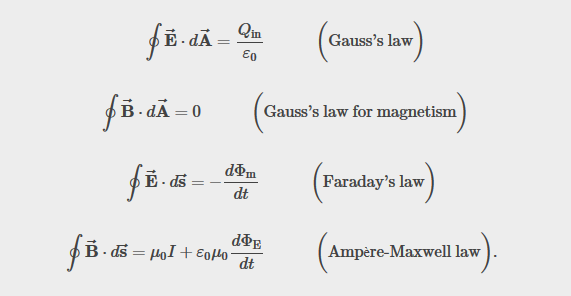
The Special Theory of Relativity
Meanwhile
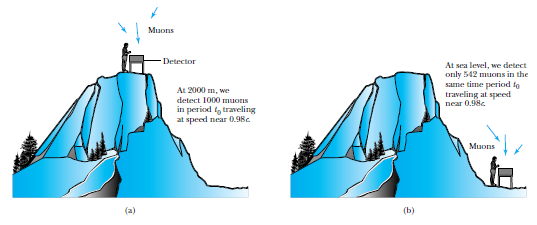
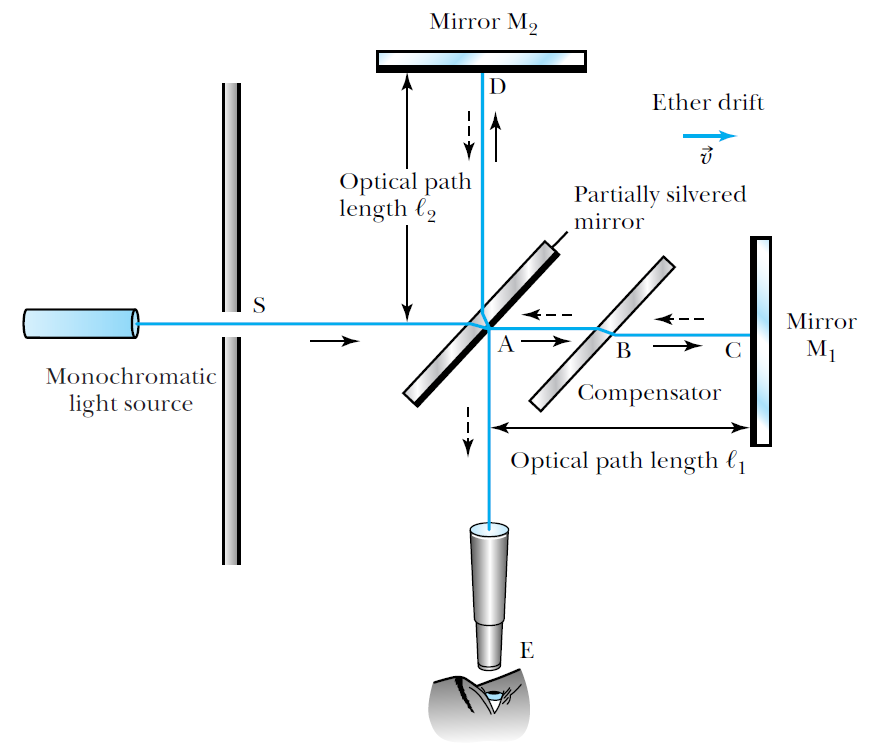
Michelson (&Morley) 's Experiment to measure Ether drift
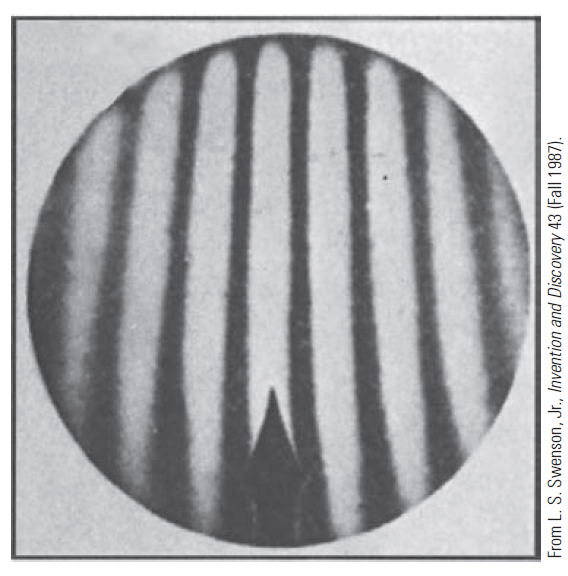
The Special Theory of Relativity
Meanwhile
Michelson's Experiment to measure Ether drift
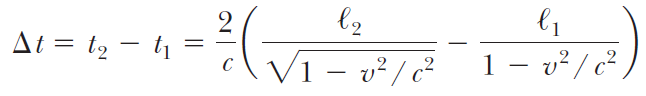
Assuming ether drift as indicated on figure, and relative velocity given by Galilean transformation,
If you rotate the apparatus by 90 degrees, the presumed drift is now along the other arm of the interferometer.
implying a different value of the delay (corresponding to switching l1 and l2 in the above expression)
Michelson cleverly designed an interferometer, where the interference pattern depends on that time delay.
And he saw none!
we find that there will be a time difference between light traveling A-D-A and A-C-A given by:
i.e. there will be a shift in the interference pattern...
The Special Theory of Relativity
Meanwhile
Michelson's Experiment
Lorentz and FitzGerald, in an attempt to explain the null result, pointed out,
(in an ad-hoc way)
that it is possible to get
=0
l_1 \rightarrow \ l_1 \sqrt{1-v^2/c^2}
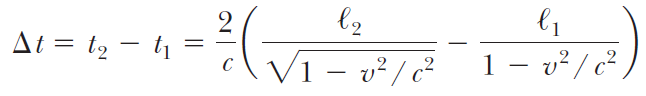
That is to say, the null result would be justified if the length in the direction of the drift somehow contracted by a factor of
\sqrt{1-v^2/c^2}
The Special Theory of Relativity
Einstein's postulates
The laws of physics are the same in all intertial systems. There is no way to detect absolute motion, and no preferred intertial system exits.
Observers in all intertial systems measure the same value for the speed of light in vacuum.
1
2
Encompassing Electrodynamics
Einstein's Special Relativity
\blue{x'} = \frac{\red{x}-\green{v}\red{t}}{\sqrt{1-\frac{\green{v^2}}{c^2}}}
\blue{y'} = \red{y}
\blue{z'} = \red{z}
\blue{t'} = \frac{\red{t}-\frac{\green{v}\red{x}}{c^2}}{\sqrt{1-\frac{\green{v^2}}{c^2}}}
\blue{u'} = \frac{\red{u}-\green{v}\red{t}}{{1-\frac{\red{u}\green{v}}{c^2}}}
Lorentz Transformation
The Special Theory of Relativity
Lorentz Transform
Einstein's Special Relativity
\blue{x'} = \frac{\red{x}-\green{v}\red{t}}{\sqrt{1-\frac{\green{v^2}}{c^2}}}
\blue{x'} = \green{\gamma} (\red{x}-\green{v}\red{t})
\blue{x'} = \green{\gamma} (\red{x}-\green{\beta}\ c\red{t})
Expressing the relative speed of the perspectives as a fraction of the speed of light:
\green{\beta}=\frac{\green{v}}{c}\;,
and defining the relativistic factor:
\green{\gamma}=\frac{1}{\sqrt{1-\green{\beta^2}}}
\blue{t'} = \frac{\red{t}-\frac{\green{v}\red{x}}{c^2}}{\sqrt{1-\frac{\green{v^2}}{c^2}}}
c \blue{t'} = \frac{c \red{t}-\frac{\green{v}\red{x}}{c}}{\sqrt{1-\frac{\green{v^2}}{c^2}}}
c \blue{t'} = \green{\gamma} (c \red{t}-\green{\beta}\red{x})
Then the Lorentz Transformation can be written as:
The Special Theory of Relativity
Lorentz Transform - note 1
Einstein's Special Relativity
\blue{x'} = \green{\gamma} (\red{x}-\green{\beta}\ \red{ct})
\green{\beta}=\frac{\green{v}}{c}\;,
\green{\gamma}=\frac{1}{\sqrt{1-\green{\beta^2}}}
\blue{ct'} = \green{\gamma} (\red{ct}-\green{\beta}\ \red{x})
The Lorentz Transformation
\red{(x,ct)} \rightarrow \blue{(x',ct')}
In our universe, motion
mixes
space and time!
\blue{\left(\begin{matrix}x'\\ ct'\end{matrix}\right)} = \green{\gamma} {\left(\begin{matrix}1&-\green{\beta}\\ -\green{\beta}&1\end{matrix}\right)}
\red{\left(\begin{matrix}x\\ ct\end{matrix}\right)}
The Special Theory of Relativity
Lorentz Transform - note 2
Einstein's Special Relativity
\blue{x'} = \green{\gamma} (\red{x}-\green{\beta}\ \red{ct})
\green{\beta}=\frac{\green{v}}{c}\;,
\green{\gamma}=\frac{1}{\sqrt{1-\green{\beta^2}}}
\blue{ct'} = \green{\gamma} (\red{ct}-\green{\beta}\ \red{x})
The Lorentz Transformation
\red{(x,ct)} \rightarrow \blue{(x',ct')}
\red{x} = \green{\gamma} (\blue{x'}+\green{\beta}\ \blue{ct'})
\green{\beta}=\frac{\green{v}}{c}\;,
\green{\gamma}=\frac{1}{\sqrt{1-\green{\beta^2}}}
\red{ct} = \green{\gamma} ( \blue{ct'}+\green{\beta}\ \blue{x'})
The inverse Lorentz Transformation
\red{(x,ct)} \leftarrow \blue{(x',ct')}
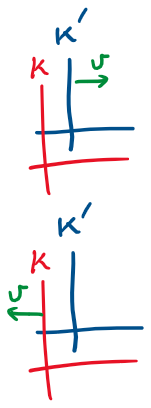
The Special Theory of Relativity
Lorentz Transform - note 3
Einstein's Special Relativity
\blue{x'} = \green{\gamma} (\red{x}-\green{\beta}\ \red{ct})
\green{\beta}=\frac{\green{v}}{c}\;,
\green{\gamma}=\frac{1}{\sqrt{1-\green{\beta^2}}}
\blue{ct'} = \green{\gamma} (\red{ct}-\green{\beta}\ \red{x})
The Lorentz Transformation
\red{(x,ct)} \rightarrow \blue{(x',ct')}
Taylor expansion of the relativistic factor at small relative velocities
The Special Theory of Relativity
Lorentz Transform - note 3
Einstein's Special Relativity
\blue{x'} = \green{\gamma} (\red{x}-\green{\beta}\ \red{ct})
\green{\beta}=\frac{\green{v}}{c}\;,
\green{\gamma}=\frac{1}{\sqrt{1-\green{\beta^2}}}
\blue{ct'} = \green{\gamma} (\red{ct}-\green{\beta}\ \red{x})
The Lorentz Transformation
\red{(x,ct)} \rightarrow \blue{(x',ct')}
At small velocities:
\green{\beta}={\green{v}}/{c} \approx 0
\green{\gamma}=\frac{1}{\sqrt{1-\green{\beta^2}}} \approx 1
\blue{x'} = \green{\gamma} (\red{x}-\green{\beta}\ \red{ct}) \approx \red{x}-\green{v}\ \red{t}
\blue{ct'} = \green{\gamma} (\red{ct}-\green{\beta}\ \red{x}) \approx \red{ct}
The Lorentz Transformation
reduces to
the Galilean Transformation.
The Special Theory of Relativity
Lorentz Transform - summary of the story so far
Einstein's Special Relativity
\blue{x'} = \green{\gamma} (\red{x}-\green{\beta}\ \red{ct})
\green{\beta}=\frac{\green{v}}{c}\;,
\green{\gamma}=\frac{1}{\sqrt{1-\green{\beta^2}}}
\blue{ct'} = \green{\gamma} (\red{ct}-\green{\beta}\ \red{x})
The Lorentz Transformation
\red{(x,ct)} \rightarrow \blue{(x',ct')}
Different inertial perspectives
\red{K}, \blue{K'}, \gray{K''}, ...
will assign to the same event
a different set of Spacetime coordinates
\red{e_1=(x_1, y_1 , z_1,ct_1)},
\text{event 1}
\blue{e_1'=(x_1',y_1',z_1',ct_1')},
\gray{e_1''=(x_1'',y_1'',z_1'',ct_1'')}, ...
To transform between these sets, you need to know the relative velocity of the frames.
The Special Theory of Relativity
Einstein's Special Relativity
Example 1
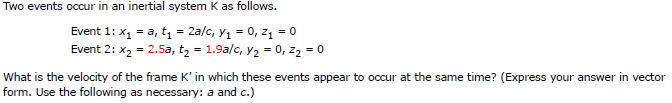
What are the spacetime coordinates of these events in an inertial system K' that is moving at 25% the speed of light in the +x direction relative to K.
The Special Theory of Relativity
Einstein's Special Relativity
Example 1 - solution
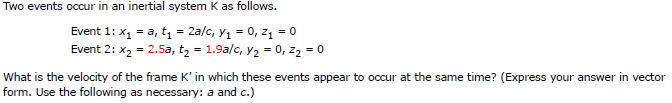
What are the spacetime coordinates of these events in an inertial system K' that is moving at 25% the speed of light in the +x direction relative to K.
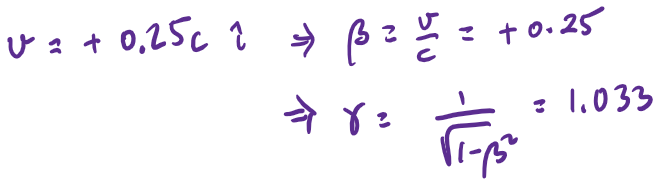
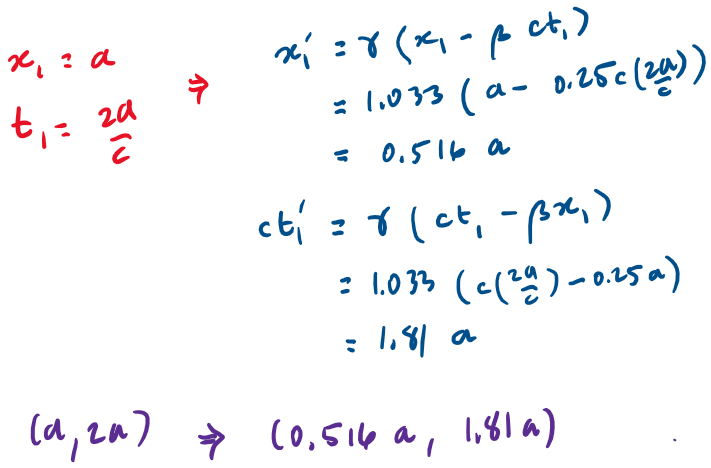
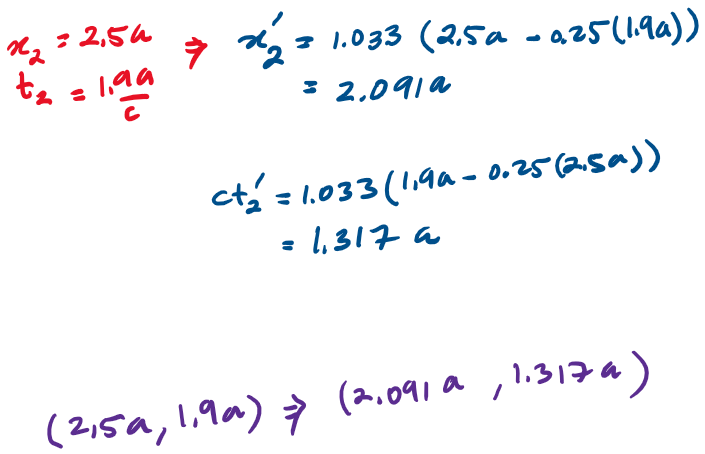
The Special Theory of Relativity
Einstein's Special Relativity
The relativity of simultaneity
Suppose that you would assign the same time to two distinct events happening at different places from your perspective.
According to a perspective moving relative to yours, would the two events be assigned the same time as well?
t_1 = t_2
x_1 \ne x_2
Suppose that you would assign the same time to two distinct events happening at different places from your perspective.
Suppose that you would assign the same time to two distinct events happening at different places from your perspective.
t_1' = t_2' ?
According to a perspective moving relative to yours, would the two events be assigned the same time as well?
The Special Theory of Relativity
Einstein's Special Relativity
Example - 2
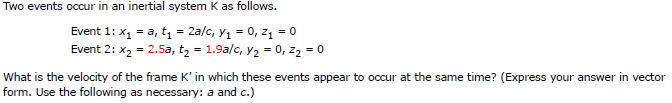
The Special Theory of Relativity
Einstein's Special Relativity
Example 2 - Solution
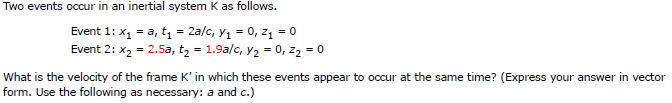
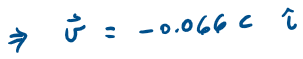
The Special Theory of Relativity
Einstein's Special Relativity
Example 3
The Special Theory of Relativity
Einstein's Special Relativity
Example 3 - Solution
The Special Theory of Relativity
Einstein's Special Relativity
Invariant quantities
If space is relative and time is relative, is there any spacetime quantity that is invariant under the Lorentz transformation?
The spacetime interval
\Delta s^2 = \Delta x^2 - c^2\Delta t^2
Lightlike separation
Space-like
separation
timelike
separation
\Delta s^2 = 0
\Delta s^2 < 0
\Delta s^2 > 0
No causal connection!
The Special Theory of Relativity
Einstein's Special Relativity
Example - Invariant quantities
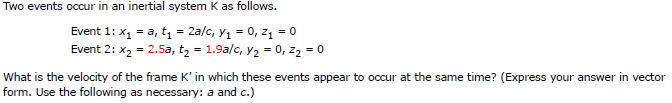
What are the spacetime coordinates of these events in an inertial system K' that is moving at 25% the speed of light in the +x direction relative to K.
Calculate the spacetime intervals between events 1 and 2 in K and K'
Is it possible that event 2 caused event 1 ?
The Special Theory of Relativity
Einstein's Special Relativity
Example - Invariant quantities
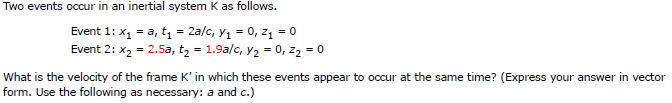
What are the spacetime coordinates of these events in an inertial system K' that is moving at 25% the speed of light in the +x direction relative to K.
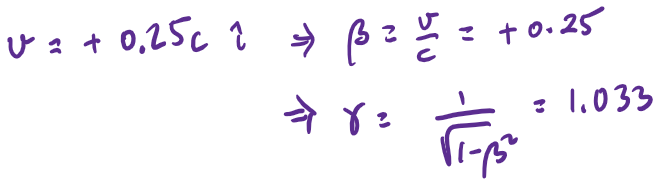
Calculate the spacetime intervals between events 1 and 2 in K and K'
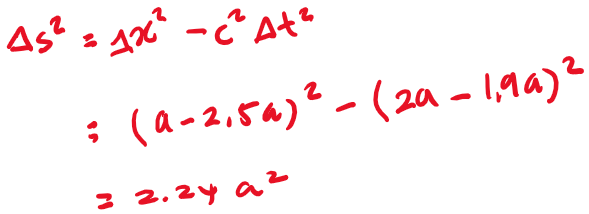
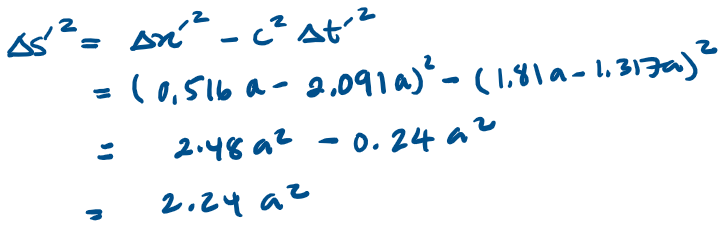
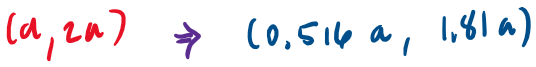
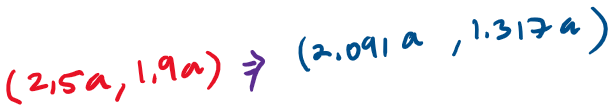
Is it possible that event 2 caused event 1 ?
No Way! Since the space time interval is positive, the two events are spacelike separated, which implies that for the signal to travel between the two events it would have had to travel faster than light!
The Special Theory of Relativity
Visual representation of spacetime
Spacetime as a map
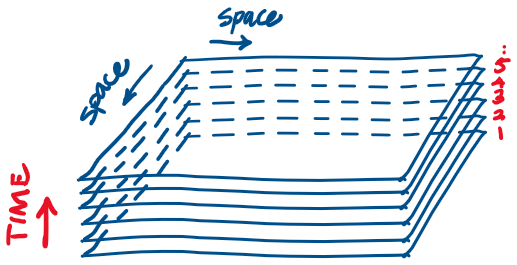
From any given perspective, events unfold in a 4-D spacetime, where a new version of 3-D space manifests at every point in time -- like a 4-D flip book.
Spacetime is a description of relationships between entities and events, constructed from sensory (and extended-sensory) data mainly communicated via electromagnetic waves (i.e. photons) and travelling vibrations (i.e. phonons.)
Only perspectives that are at rest w.r.t. each other share a common spacetime.
The Special Theory of Relativity
Visual representation of spacetime
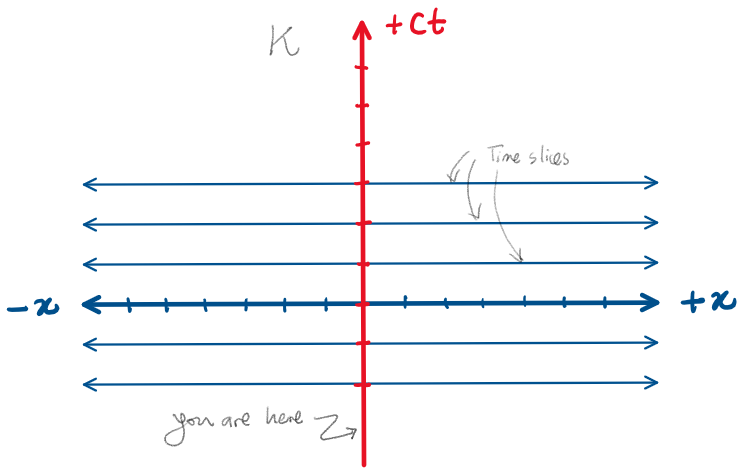
Minkowski spacetime diagrams
Minkowski diagrams are two-dimensional graphs that depict events as happening in a universe consisting of one space dimension and one time dimension.
The "time" axis has units of length (to match the space units.)
The world line of an entity travelling with a constant velocity is a straight line.
The scale is typically taken such that the motion of light is represented by worldlines that are at
\pm 45^\circ
Events are represented by points in the spacetime diagram e=(x,ct).
The trajectories of entities in a spacetime diagram are called world lines.
From your perspective, you are always at x=0. i.e. your world line in your own frame is the time axis.
The Special Theory of Relativity
Visual representation of spacetime
Minkowski spacetime diagrams
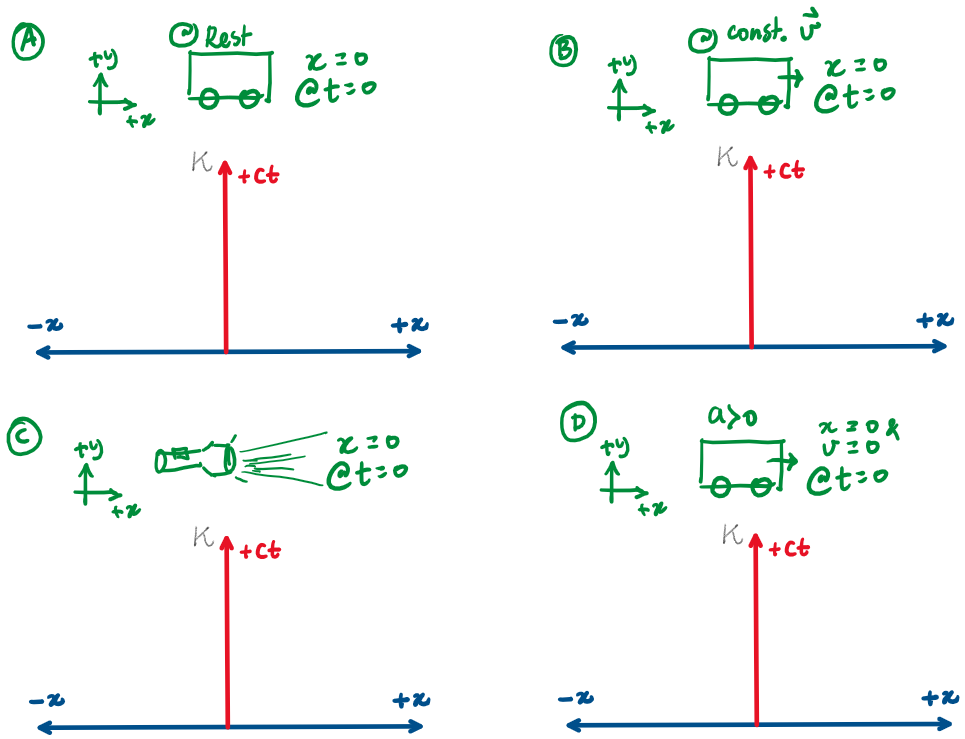
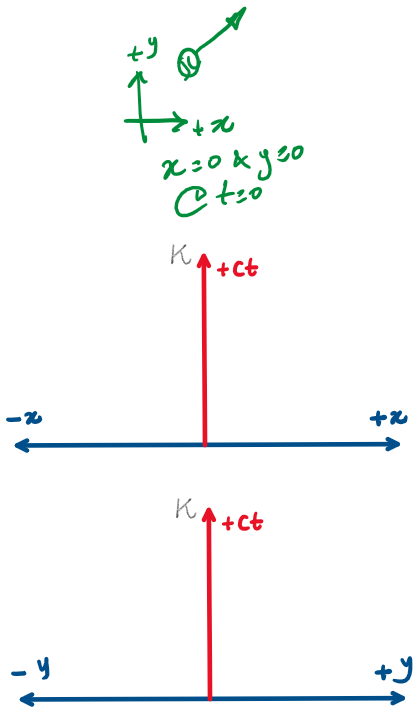
Draw the world lines representing the shown scenarios.
The Special Theory of Relativity
What stories are told by the world lines illustrated in the spacetime diagrams ?
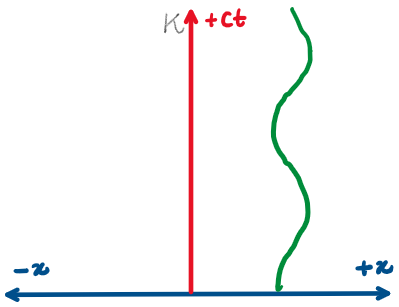
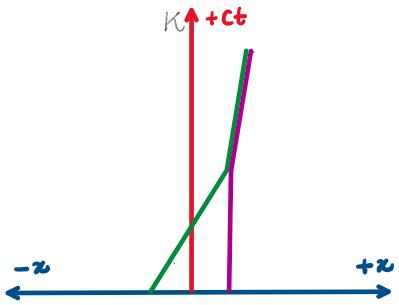
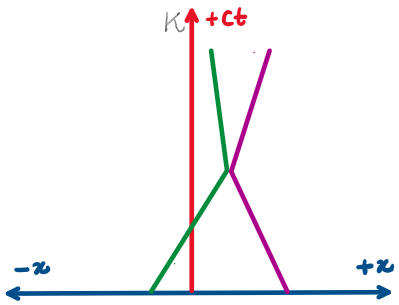
A
B
C
Visual representation of spacetime
Minkowski spacetime diagrams
The Special Theory of Relativity
Visual representation of spacetime
What is the composition of the "present"?
The Special Theory of Relativity
Visual representation of spacetime
What is the composition of the "present"?
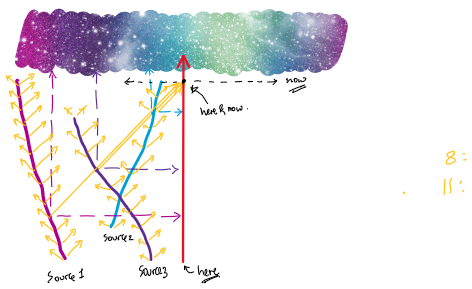
The Special Theory of Relativity
Only events within the light cone have the potential to influence your present or be influenced by it.
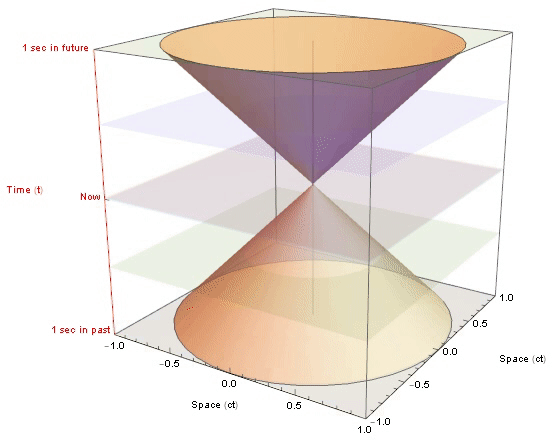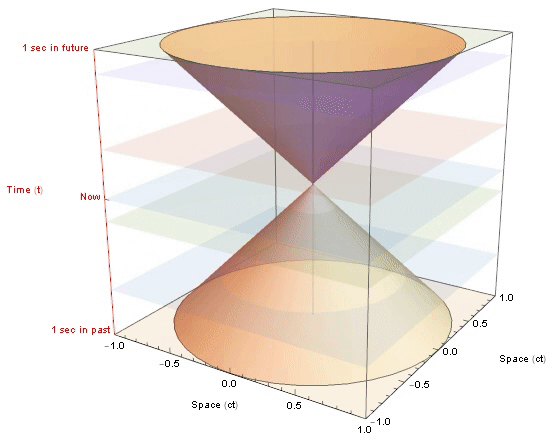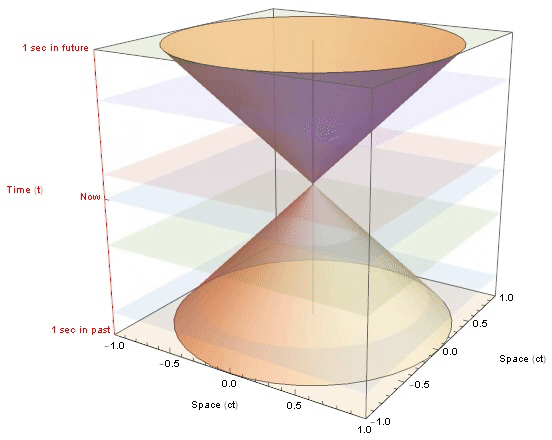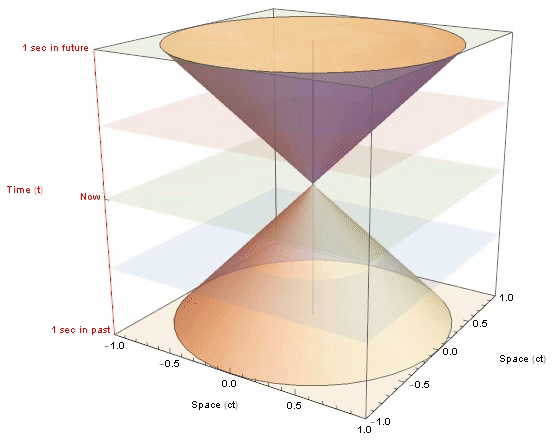
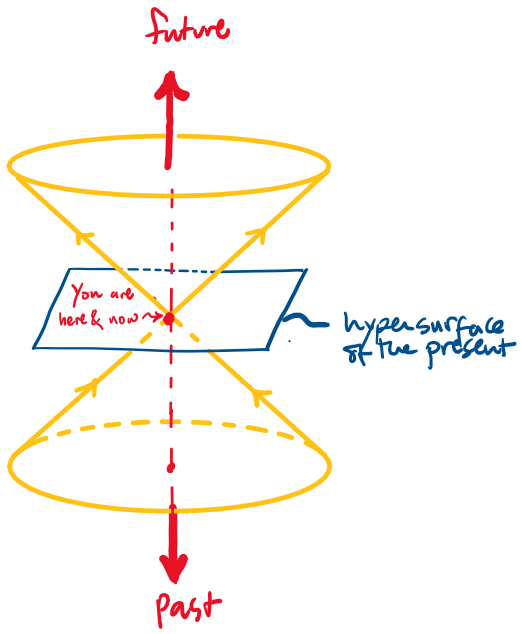
The Light-cones
Visual representation of spacetime
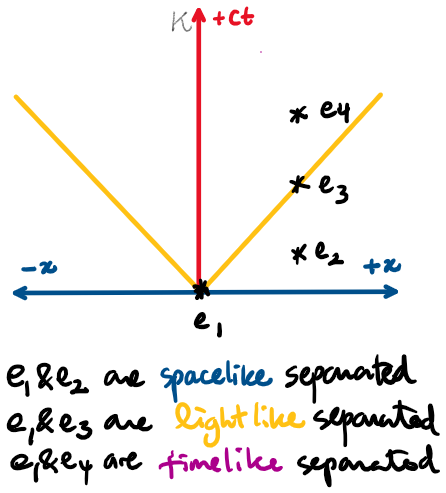
The Special Theory of Relativity
more on Spacetime diagrams
Visual representation of spacetime
The Special Theory of Relativity
Einstein's Special Relativity
Visualizing the Lorentz Transformation
K-frame
K'-frame
\vec{v}= +0.25 c\ \hat{i}
\blue{x'} = \green{\gamma} (\red{x}-\green{\beta}\ \red{ct})
\green{\beta}=\frac{\green{v}}{c}\;,
\green{\gamma}=\frac{1}{\sqrt{1-\green{\beta^2}}}
\blue{ct'} = \green{\gamma} (\red{ct}-\green{\beta}\ \red{x})
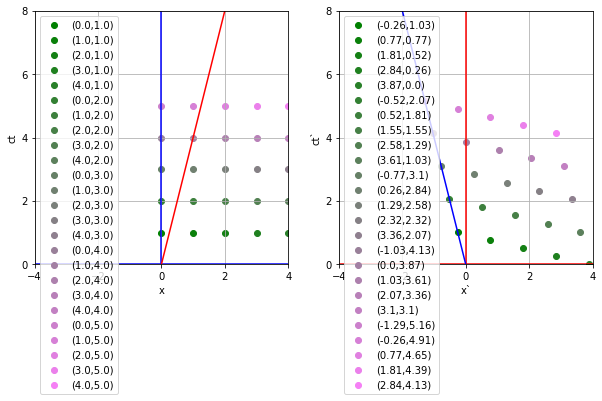
The Lorentz Transformation
\red{(x,ct)} \rightarrow \blue{(x',ct')}
The Special Theory of Relativity
Einstein's Special Relativity
Visualizing the Lorentz Transformation
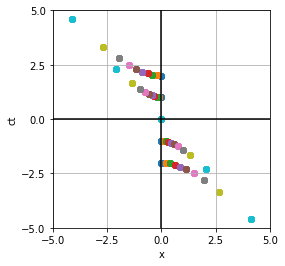
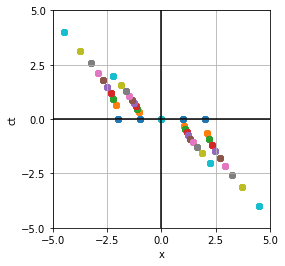
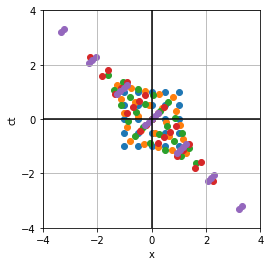
In all of the examples on this slide, shown are the events in K and all the K'(s) overlaid on the same spacetime diagram.
\beta = 0:0.1:0.9
Example 3:
Combining
examples 1 & 2
Example 1:
What happens to simultaneous events in K as increases?
\beta
Example 2:
What happens to events at the same location in K as increases?
\beta
The Special Theory of Relativity
Einstein's Special Relativity
Visualizing the Lorentz Transformation
The Special Theory of Relativity
Einstein's Special Relativity
Time Dilation
Suppose that there are two events (a and b), which from the K-perspective happen at the same position, but are separated by a time interval T0. Question is, what time, T', separates the same two events from a moving perspective K'?
cT'
= ct_b'-ct_a'
= \gamma \left(ct_b- \beta x_b\right)- \gamma \left(ct_a- \beta x_a \right)
= \gamma \left(ct_b- ct_a \right)
= \gamma\ cT_0
\ge cT_0
i.e. The shortest observed time between any two events is the "Proper Time," which is measured in a frame where they happen at the same location!
The Special Theory of Relativity
Einstein's Special Relativity
Length Contraction
The Special Theory of Relativity
Einstein's Special Relativity
Time Dilation & Length Contraction
The Special Theory of Relativity
Einstein's Special Relativity
Relativity of relative velocity
The Special Theory of Relativity
Einstein's Special Relativity
Transformation of velocities
What does motion look like from the different perspectives?
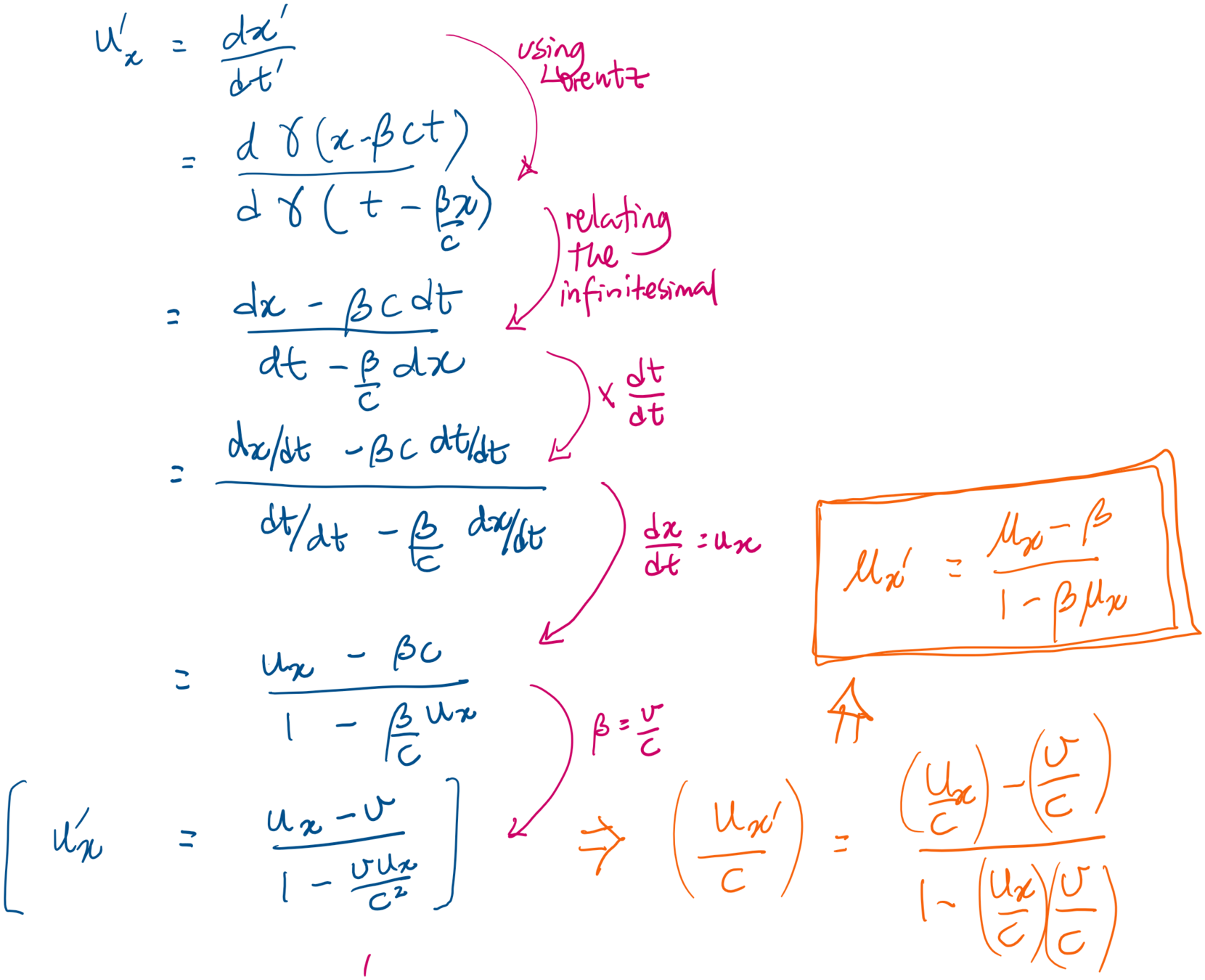
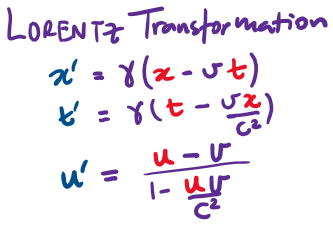
The Special Theory of Relativity
Einstein's Special Relativity
Transformation of velocities
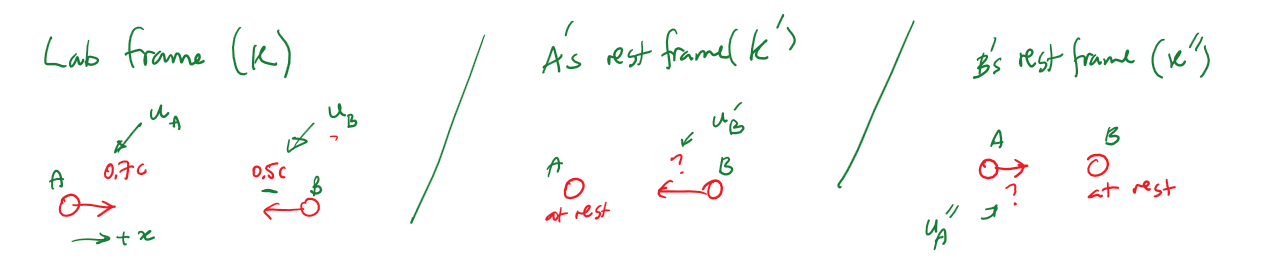
Suppose that we are colliding two particles, A and B, whose speeds in the lab frame are 70% and 50% the speed of light, respectively. Describe the motion of the two particles from their respective perspectives. (i.e. calculate their speeds from A's perspective, and then from B's perspective.)
The Special Theory of Relativity
Einstein's Special Relativity
Transformation of velocities
Suppose that we are colliding two particles, A and B, whose speeds in the lab frame are 70% and 50% the speed of light, respectively. Describe the motion of the two particles from their respective perspectives. (i.e. calculate their speeds from A's perspective, and then from B's perspective.)
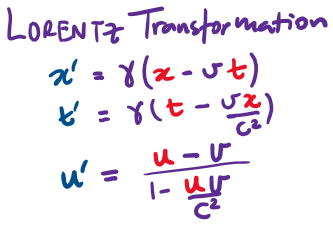
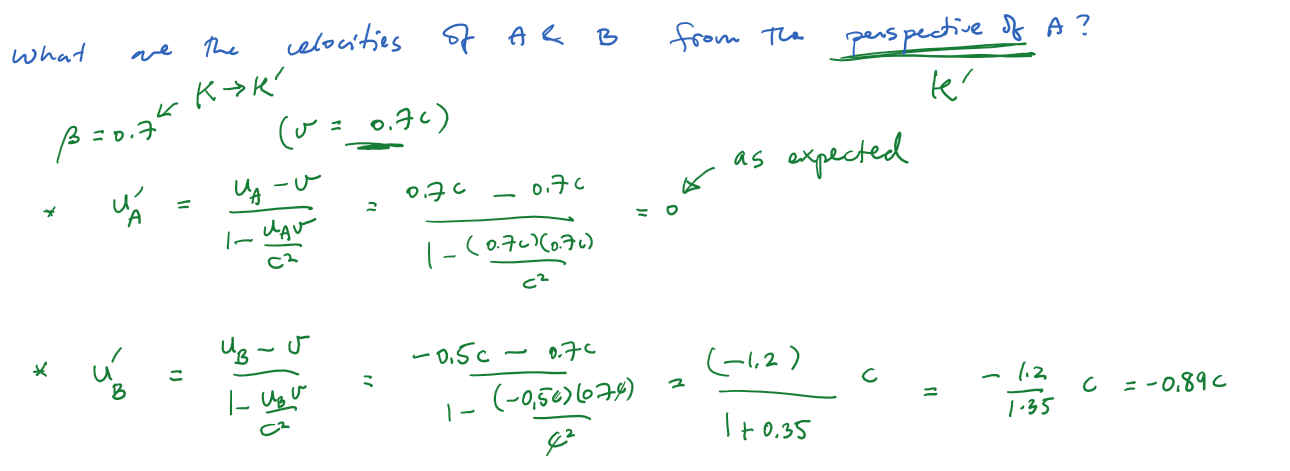
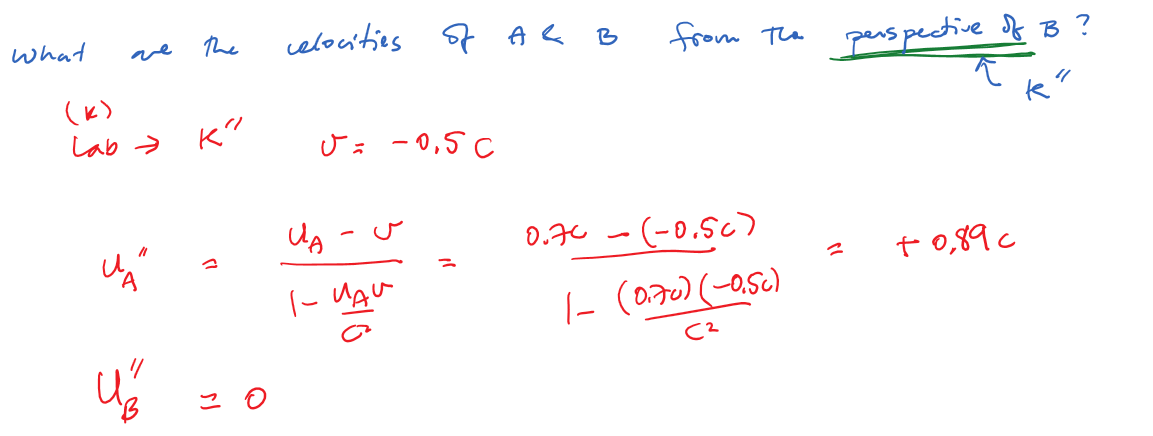
The Special Theory of Relativity
Einstein's Special Relativity
Transformation of velocities
How does (perpendicular) motion look like from the different perspectives?
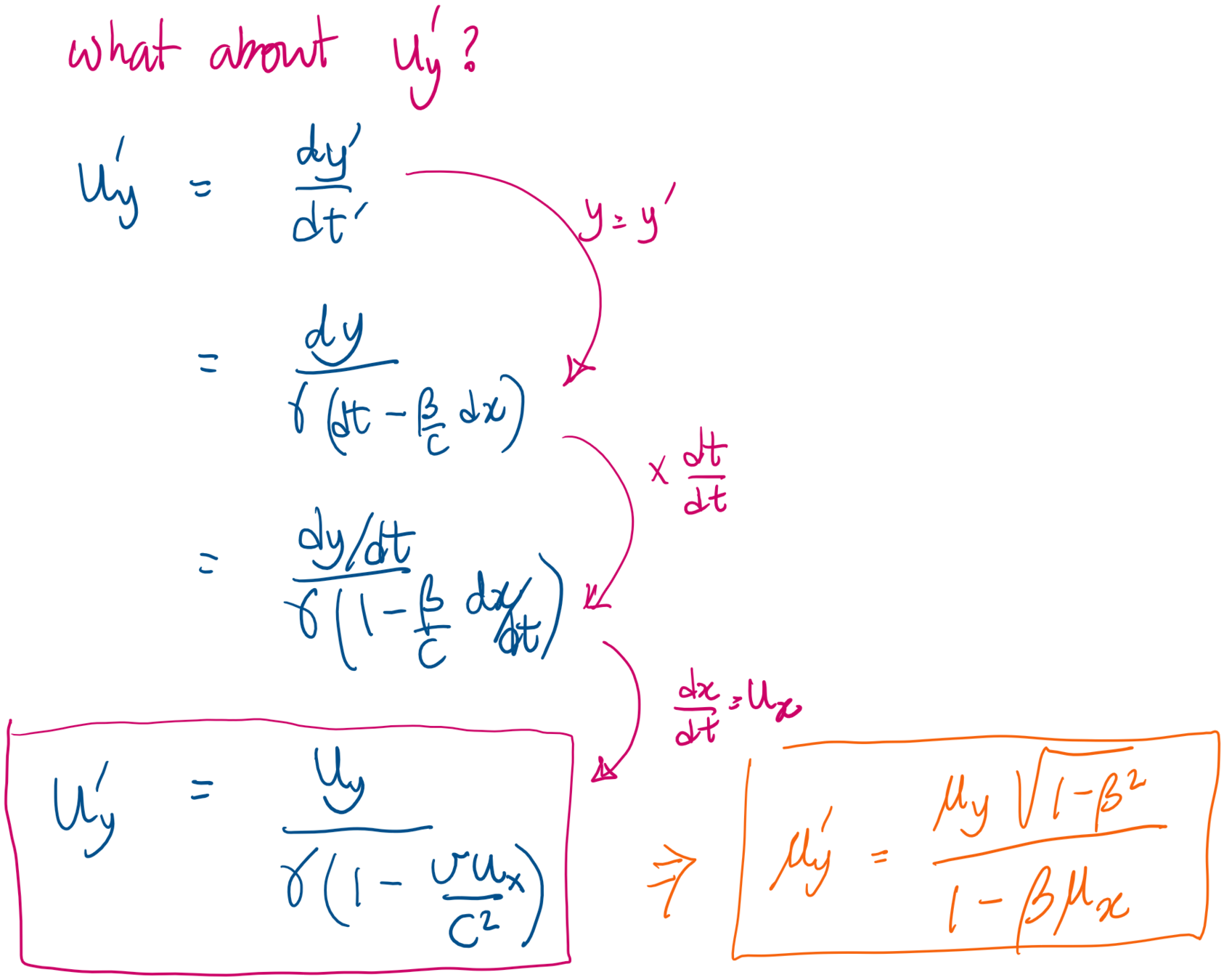
The Special Theory of Relativity
Einstein's Special Relativity
Transformation of velocities
How does motion look like from the different perspectives?
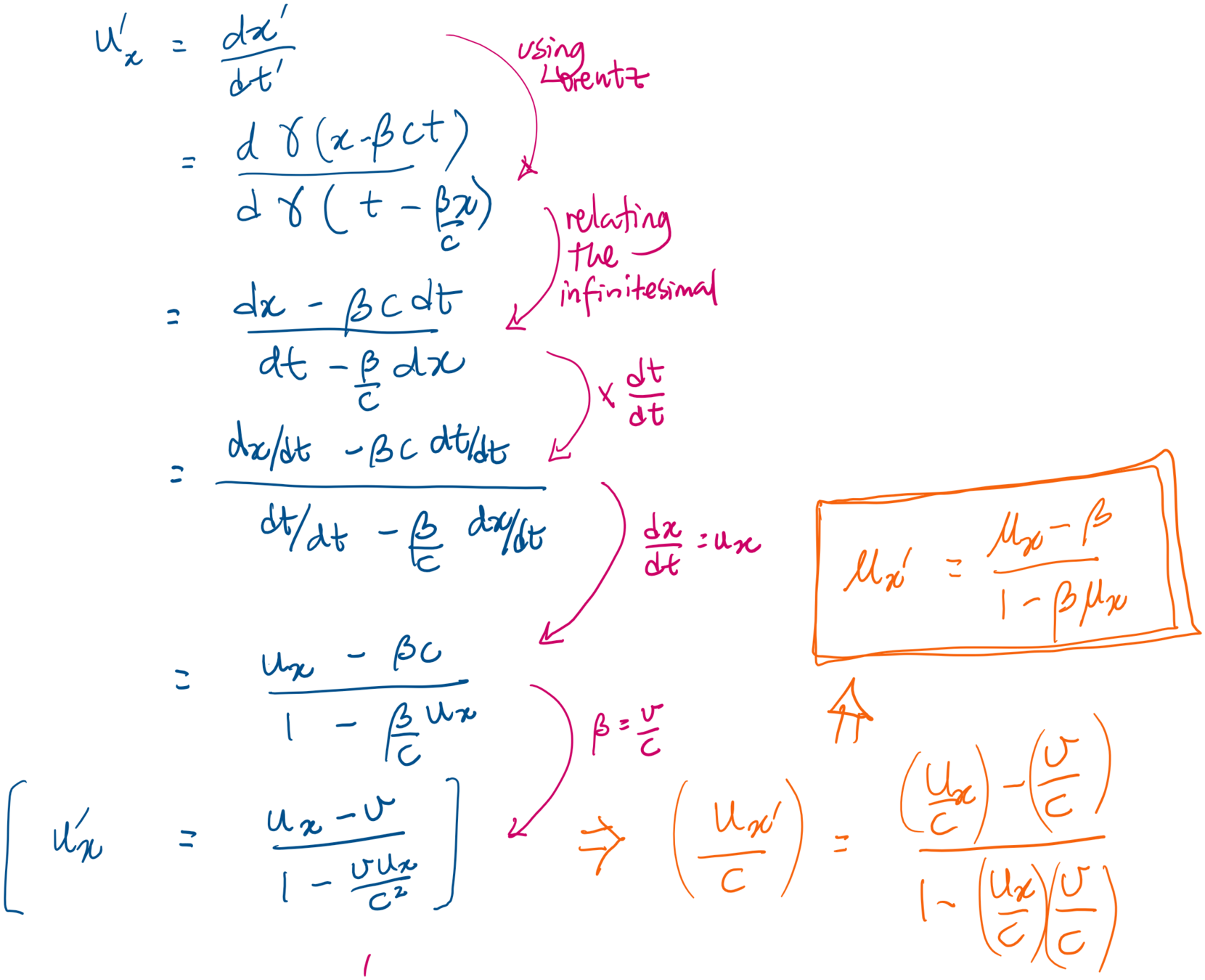
The Special Theory of Relativity
Einstein's Special Relativity
Relativistic momentum and energy
The Special Theory of Relativity
Einstein's Special Relativity
Relativistic momentum
\vec{p} \ne m \vec{u}
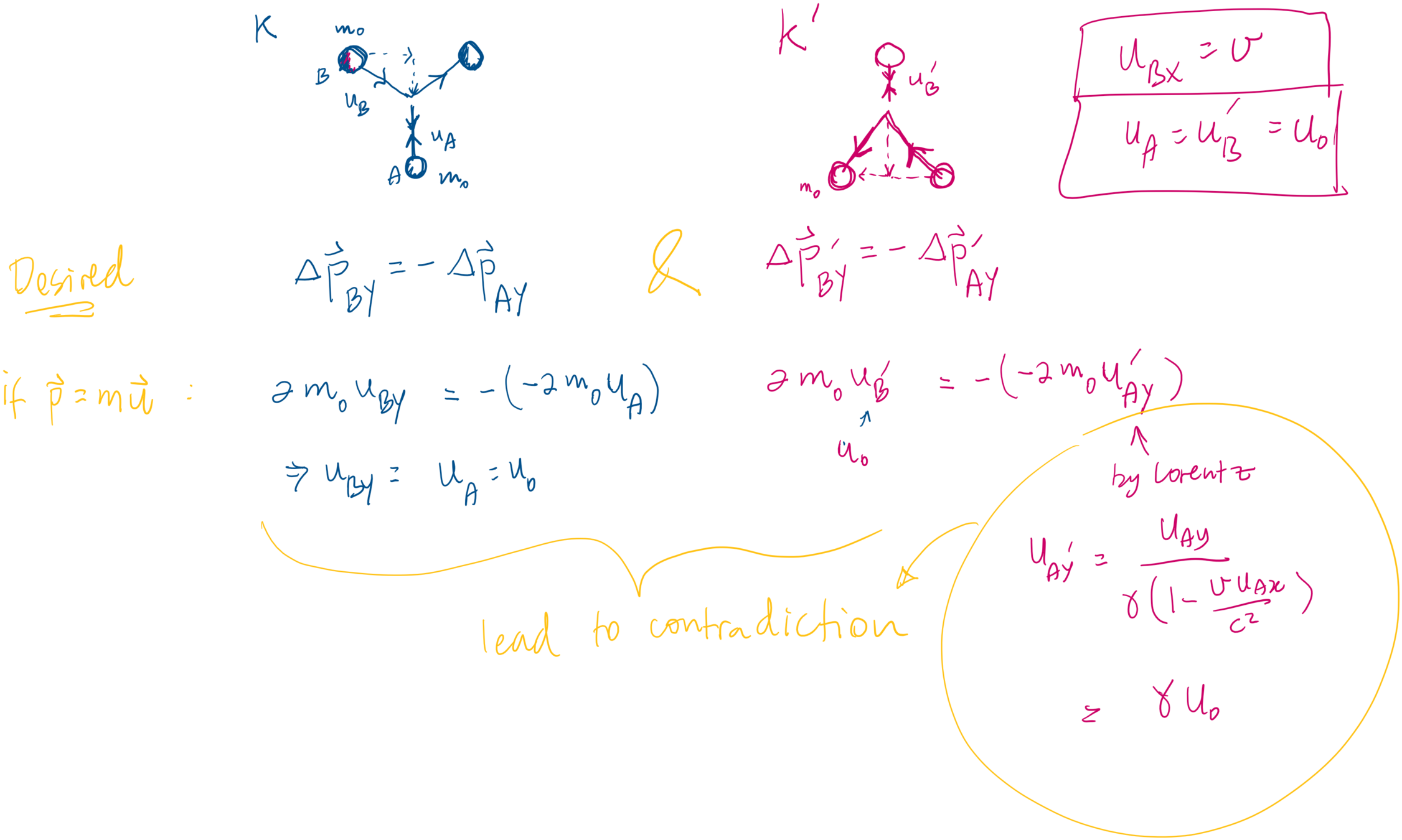
With this thought experiment, you can show that, for objects traveling with speeds comparable to c,
We need a relativistic expression for momentum that is conserved at high speeds.
The Special Theory of Relativity
Einstein's Special Relativity
Relativistic momentum
\vec{p} = \gamma_u m \vec{u}
\gamma_u=\frac{1}{\sqrt{1-u^2/c^2}}
u^2=u_x^2+u_y^2+u_z^2
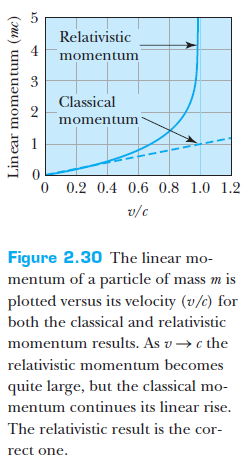
where
The relativistic momentum takes the form:
The Special Theory of Relativity
Einstein's Special Relativity
Relativistic Kinetic Energy
K = (\gamma_u-1) m c^2
\gamma_u=\frac{1}{\sqrt{1-u^2/c^2}}
u^2=u_x^2+u_y^2+u_z^2
where
The Special Theory of Relativity
Einstein's Special Relativity
Relativistic Energy
Example
Suppose you want to accelerate an electron from rest on a metal plate to strike another metal plate at 9E7 m/s.
What potential difference should you place across the plates?
(compare the classical and relativistic results)
The Special Theory of Relativity
Einstein's Special Relativity
Relativistic Energy
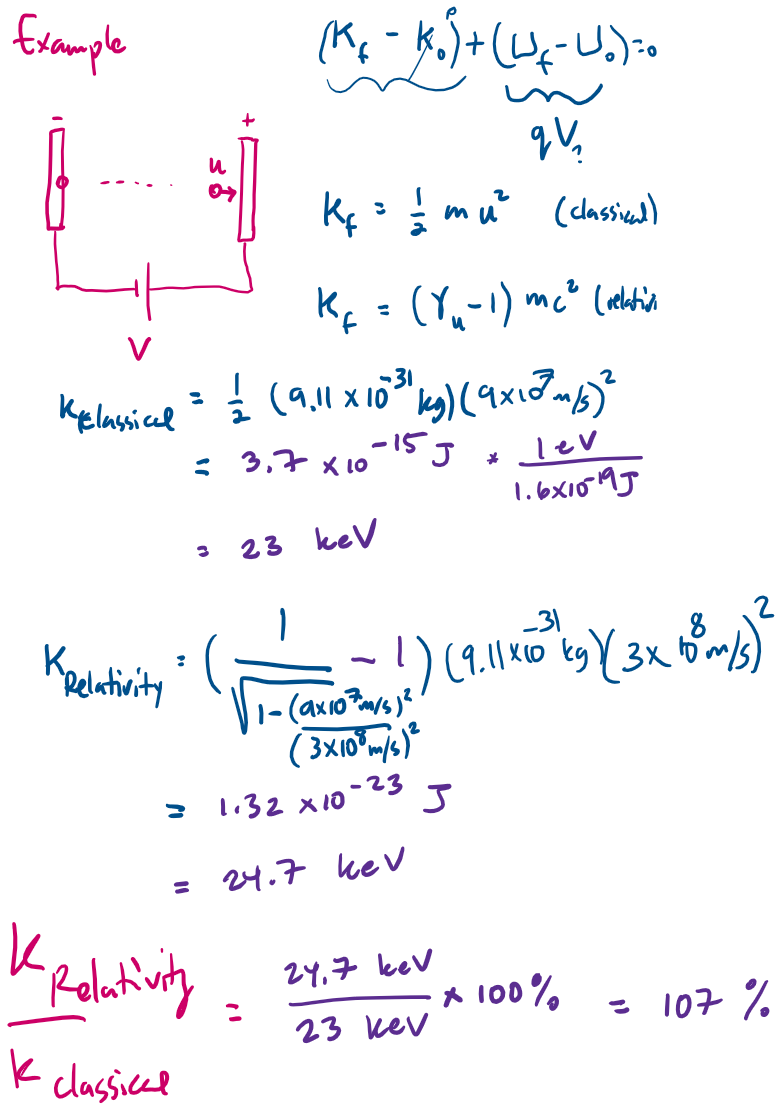
Example
Suppose you want to accelerate an electron from rest on a metal plate to strike another metal plate at 9E7 m/s.
What potential difference should you place across the plates?
(compare the classical and relativistic results)
The Special Theory of Relativity
Einstein's Special Relativity
Relativistic Energy
K = \gamma_u m c^2 - m c^2
K = (\gamma_u-1) m c^2
Total
Energy
\gamma_u m c^2 = K + m c^2
Kinetic
Energy
Rest
Energy
=
+
E\quad = K\quad + E_0
The Special Theory of Relativity
Einstein's Special Relativity
Relativistic Energy
Example
Suppose an electron is traveling at 0.5C in the lab frame. In units of eV, what is its rest energy, kinetic energy, and total energy, (a) in the lab frame, and (b) in its own frame?
The Special Theory of Relativity
Einstein's Special Relativity
Relativistic Energy
Example
Suppose an electron is traveling at 0.5C in the lab frame. In units of eV, what is its rest energy, kinetic energy, and total energy, (a) in the lab frame, and (b) in its own frame?
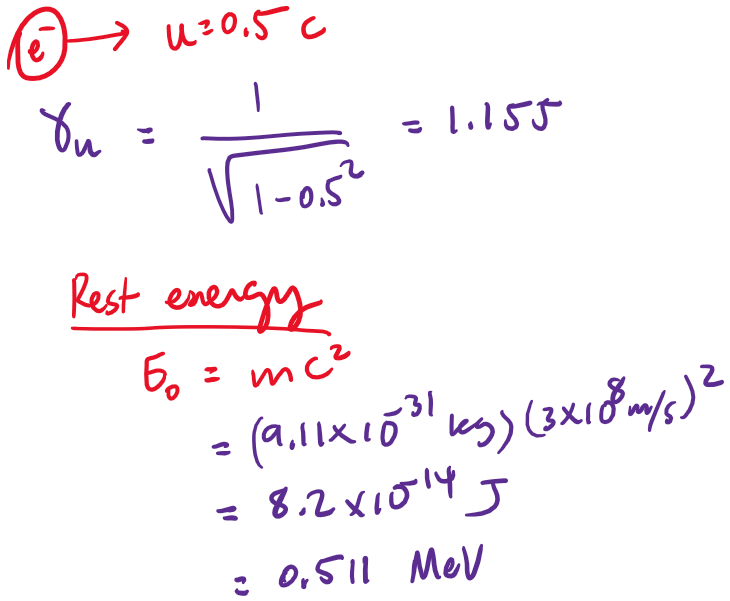
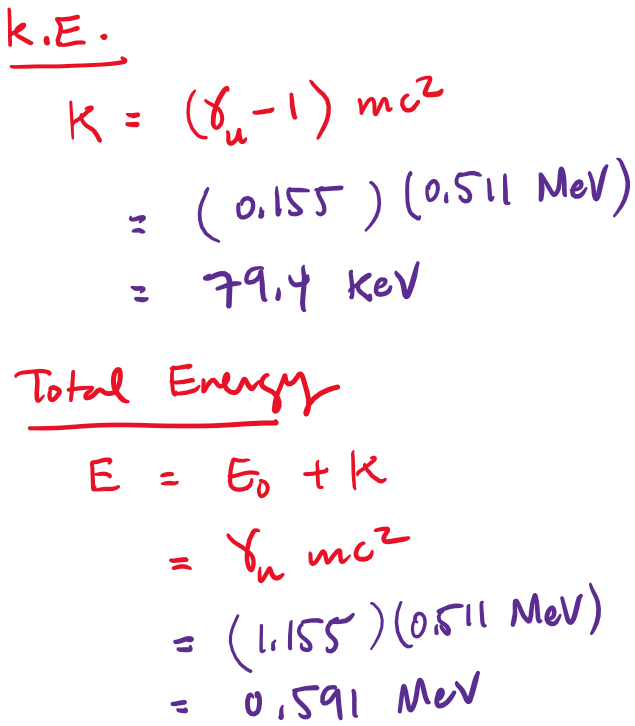
The Special Theory of Relativity
Einstein's Special Relativity
Energy and momentum
What is the relationship between the relativistic momentum and energy?
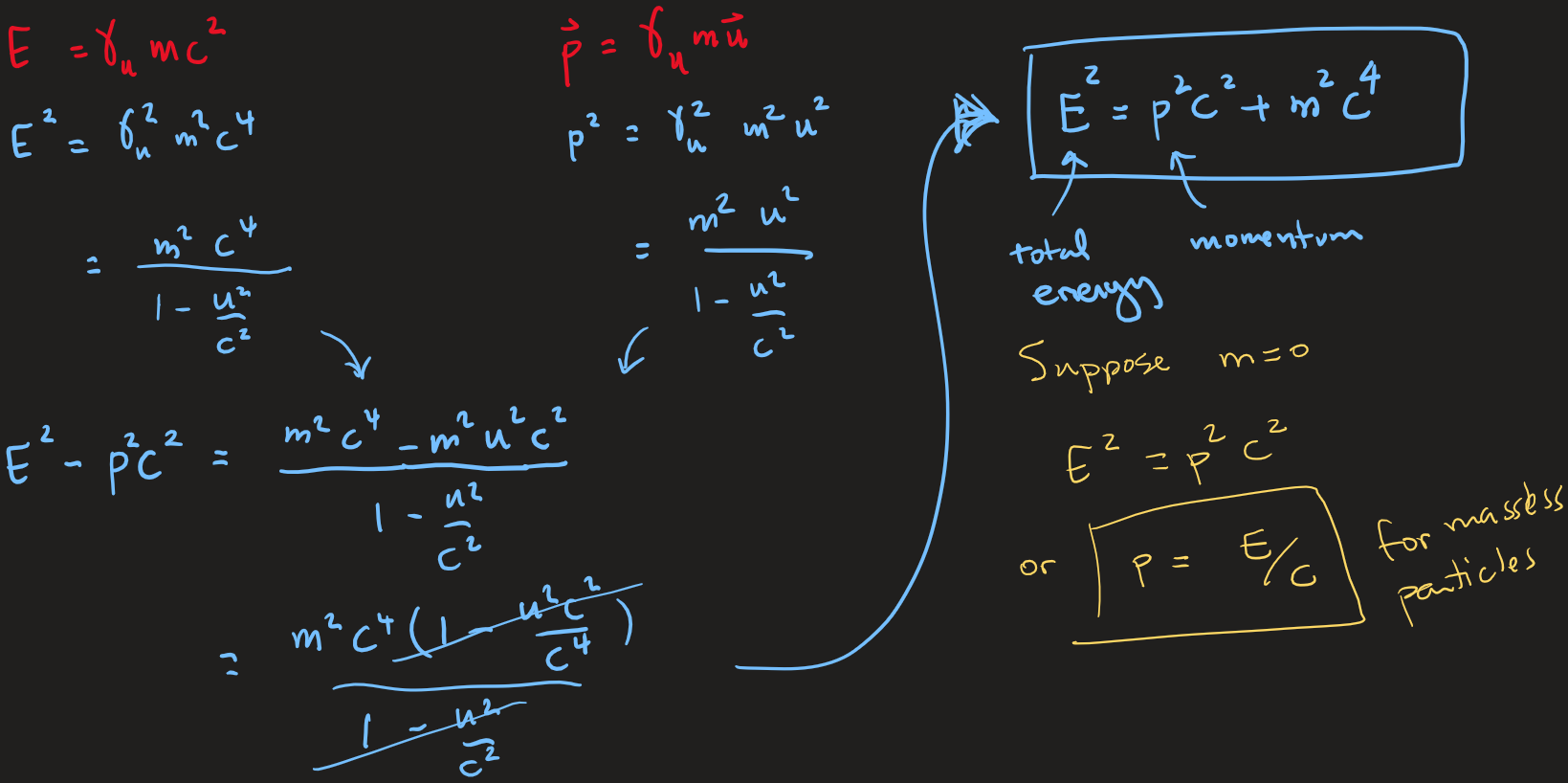
The Special Theory of Relativity
Einstein's Special Relativity
Relativistic momentum and energy
The Special Theory of Relativity
Einstein's Special Relativity
Energy and momentum
For a massless particle, its momentum and energy are related by:
p=\frac{E}{c}
The Special Theory of Relativity
Einstein's Special Relativity
Energy and momentum
Example
Suppose a particle accelerator accelerates a proton to the point that its total relativistic energy in the lab frame is 3 times its rest energy. Determine the following for the proton:
a) Its rest energy.
b) Its relativistic energy in the lab frame (in MeV)
c) Its relativistic Kinetic energy.
d) Its speed (as a fraction of the speed of light.)
e) The magnitude of its relativistic momentum in the lab frame.
f) Verify that, in the lab frame,
E^2=p^2c^2+m^2c^4
The Special Theory of Relativity
Einstein's Special Relativity
Energy and momentum
Example
Suppose a particle accelerator accelerates a proton to the point that its total relativistic energy in the lab frame is 3 times its rest energy. Determine the following for the proton:
a) Its rest energy.
b) Its relativistic energy in the lab frame (in MeV)
c) Its relativistic Kinetic energy.
d) Its speed (as a fraction of the speed of light.)
e) The magnitude of its relativistic momentum in the lab frame.
f) Verify that, in the lab frame,
E^2=p^2c^2+m^2c^4
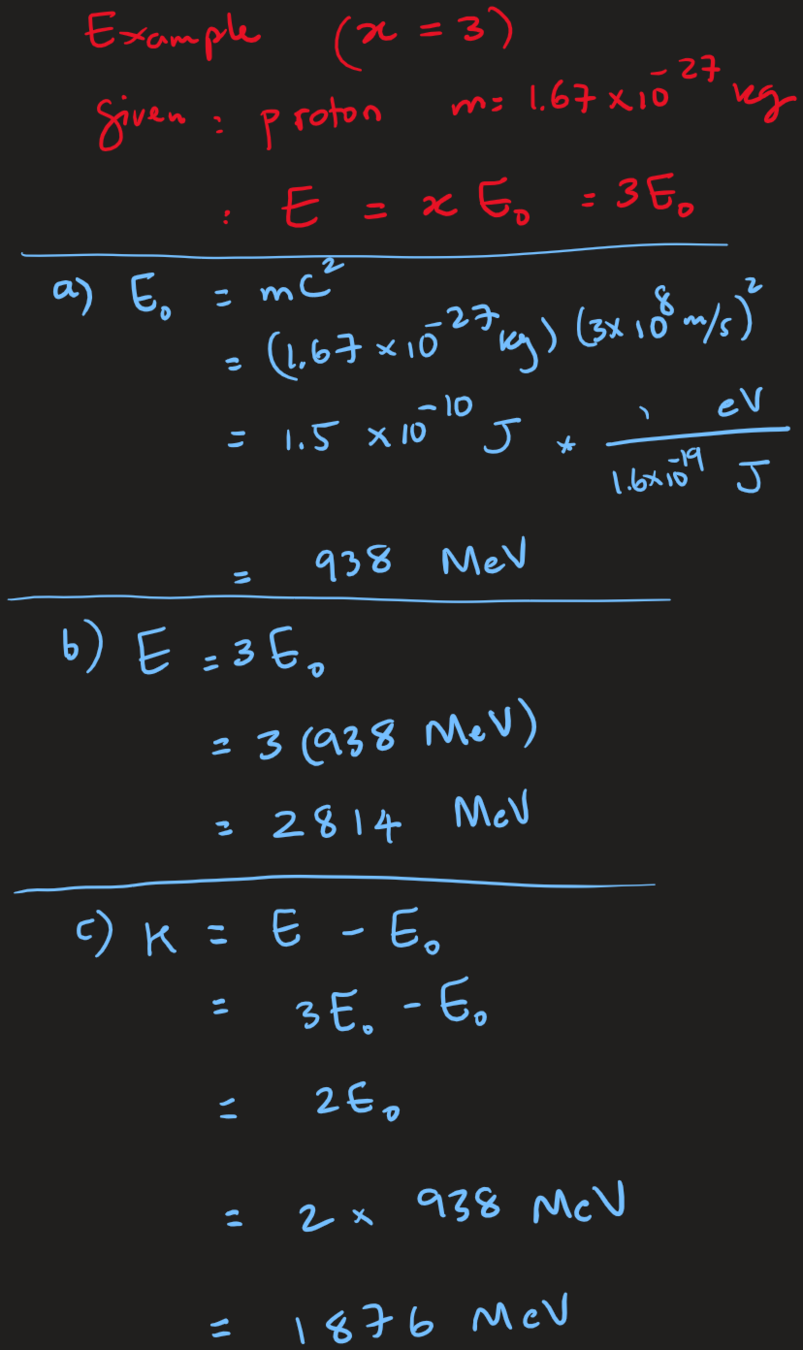
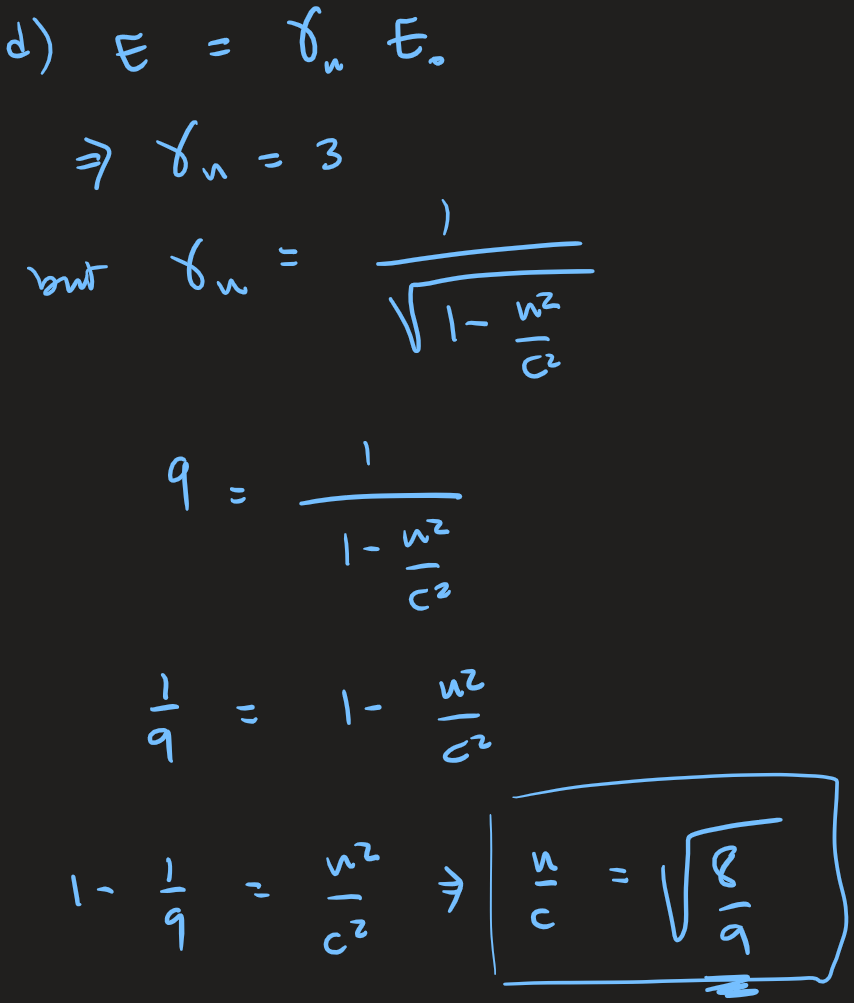
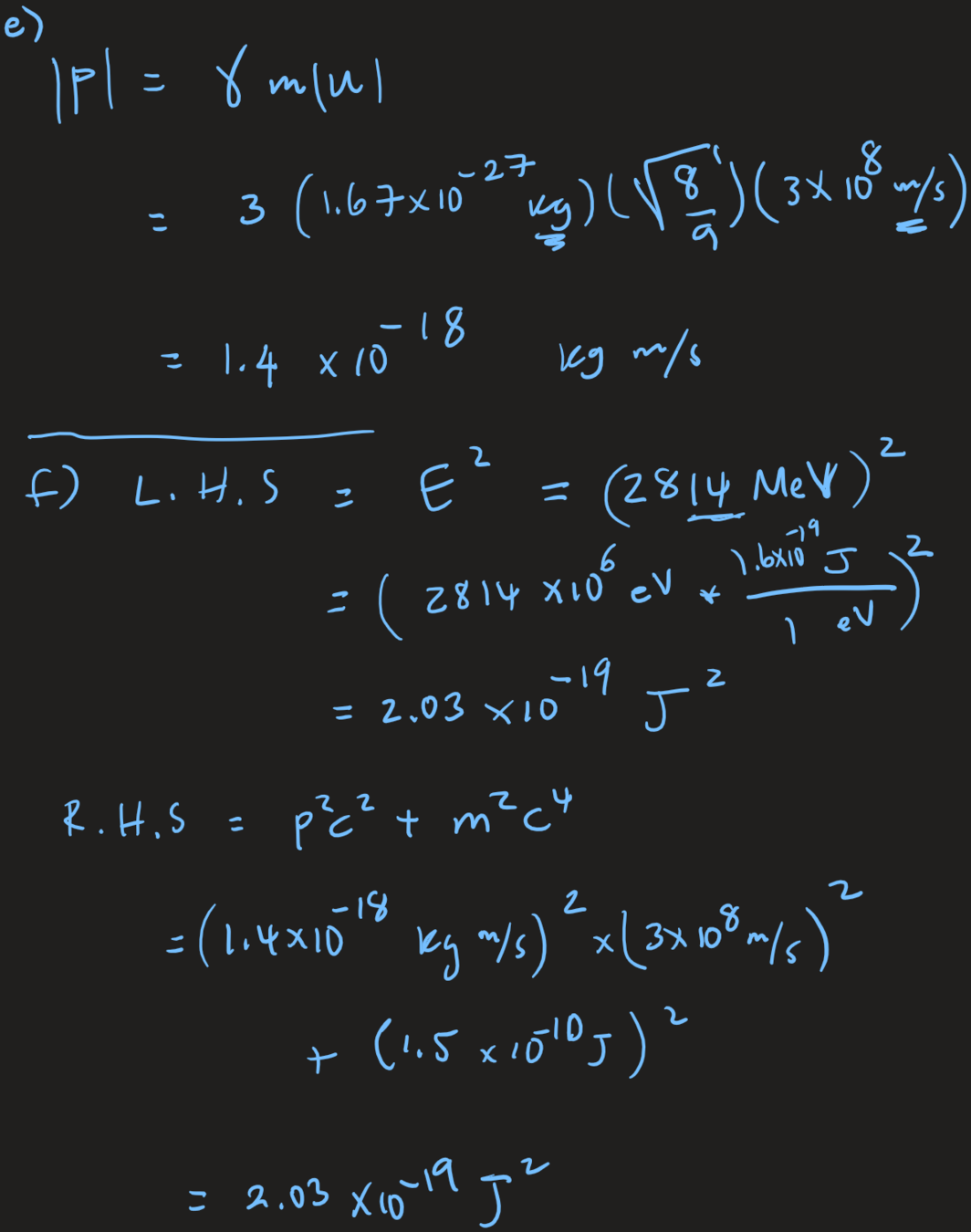
Special Relativity
By omoussa
