¿Cuál es el número mas grande que podés imaginar?
bit.ly/pablokbs-2
Condiciones
- Tiene que ser útil
- No puede ser arbitrario
- No vale número +1
- No puede ser infinito
∞
La paradoja del Grand Hotel de Hilbert
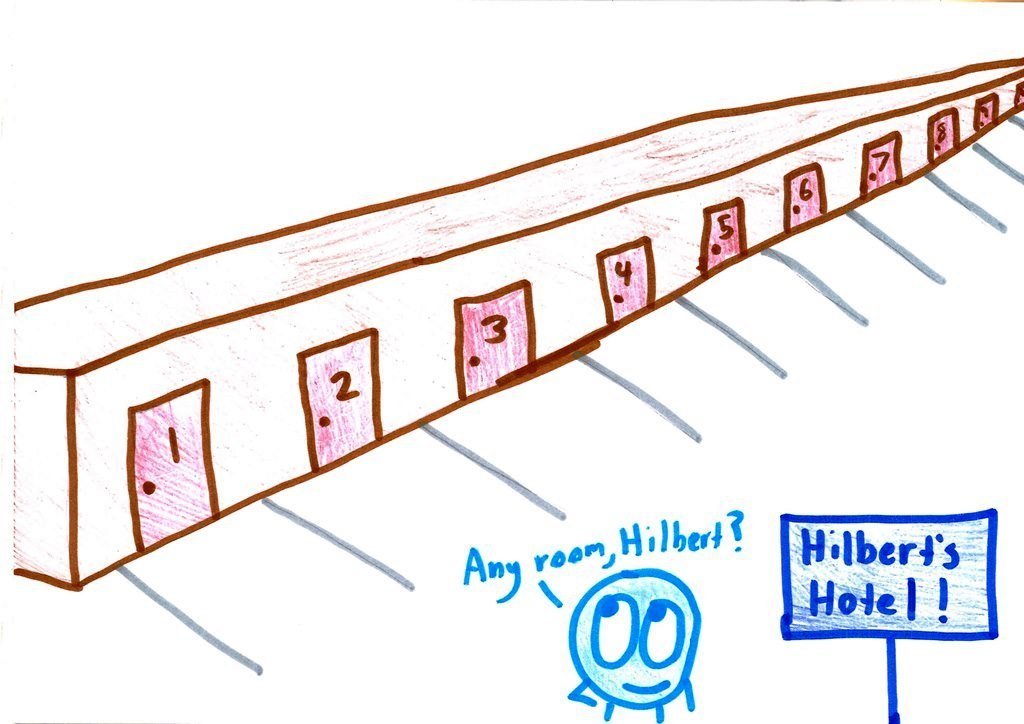
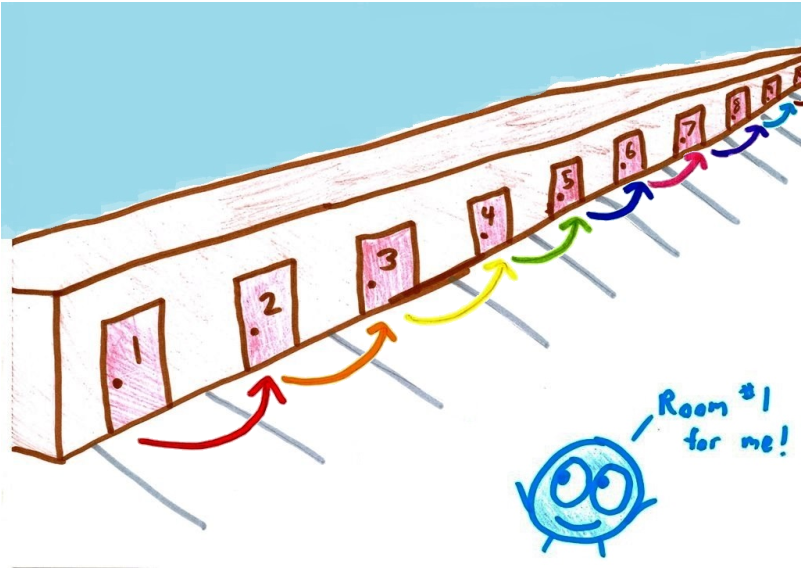
∞ = ∞ + 1
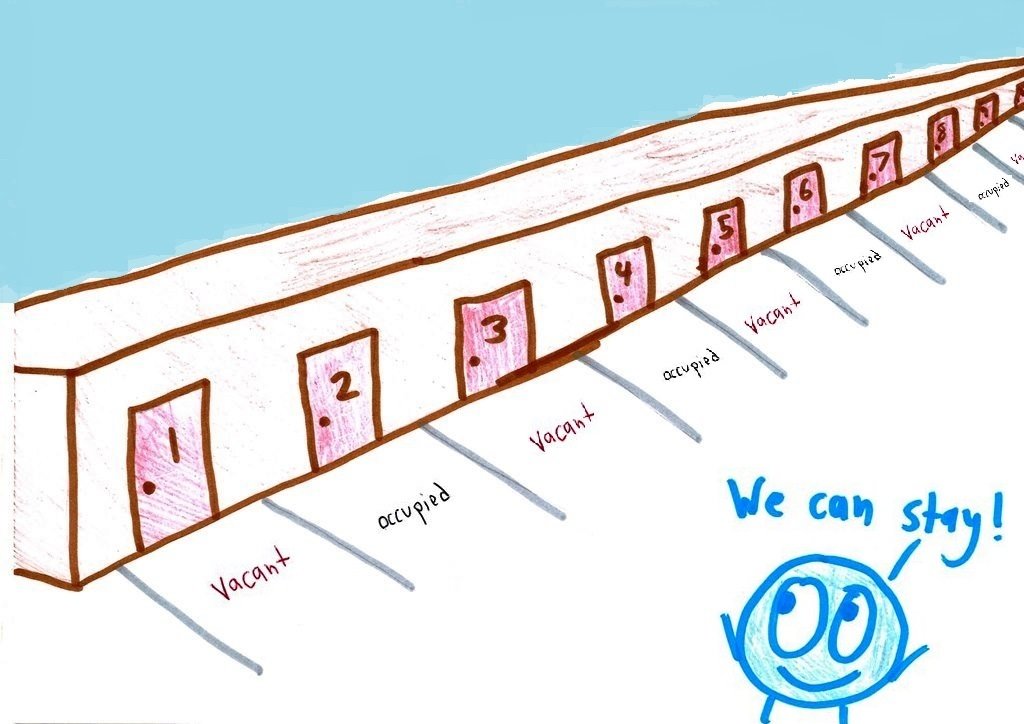

∞ = ∞ + ∞
Googol
10^{100}
Googol
Átomos en el cuerpo humano
Átomos en la Tierra
Átomos en el universo observable
= 10^{100}
= 7\times10^{27}
= 1,33\times10^{50}
= 10^{80}
Cubo de Rubik 7x7
= 1,95\times10^{160}

Googolplex
10^{10^{100}}
Googolplex
Número de posibles universos
= 10^{10^{100}}
=10^{10^{10^{7}}}
Googolplexian
10^{10^{10^{100}}}
Matemáticas
Teoría de Ramsey
¿Cuántos elementos debe contener una estructura para garantizar la existencia de una propiedad particular?
El desorden completo es imposible.
Theodore S. Motzkin
Número de Graham
Hay tres "4"
Multiplicación (x)
4 \times 3
= 4 + 4 + 4
Hay tres "4"
Flechita para arriba (↑)
= 4 \times 4 \times 4
4 \uparrow 3
= 4^3
* Inventada por Donald Knuth
Hay tres "4"
Flechita para arriba (↑↑)
= 4 \uparrow 4 \uparrow 4
4 \uparrow \uparrow 3
= 4^{4^4}
¿Cómo vamos?
= 3^3
3 \uparrow \uparrow 2
=27
= 3^{3^3}
3 \uparrow \uparrow 3
=7.625.597.484.987
Casi números grandes
=7.625.597.484.987
3 \uparrow \uparrow 3
= 3^{3^{3^3}}
3 \uparrow \uparrow 4
=3^{7.625.597.484.987}
=
?
¡Sigamos!
=4 \uparrow \uparrow 4 \uparrow \uparrow 4
4 \uparrow \uparrow \uparrow 3
Hay tres "4"
Ya casi
3 \uparrow \uparrow \uparrow \uparrow 3
g_{1} =
Posta que ya casi
3 \uparrow ...\uparrow 3
g_{2} =
g_{1}
Posta que posta que ya casi
3 \uparrow ...\uparrow 3
g_{7} =
g_{6}
Número de Graham
G =
g_{64}
Orden sucede entre
6 <
< G

3,141592...
\pi =
...195387
G=
Fuentes
¿Cuál es el número mas grande que podés imaginar?
By Pablo Fredrikson
¿Cuál es el número mas grande que podés imaginar?
Charla para nerdear.la 2016
- 1,015



