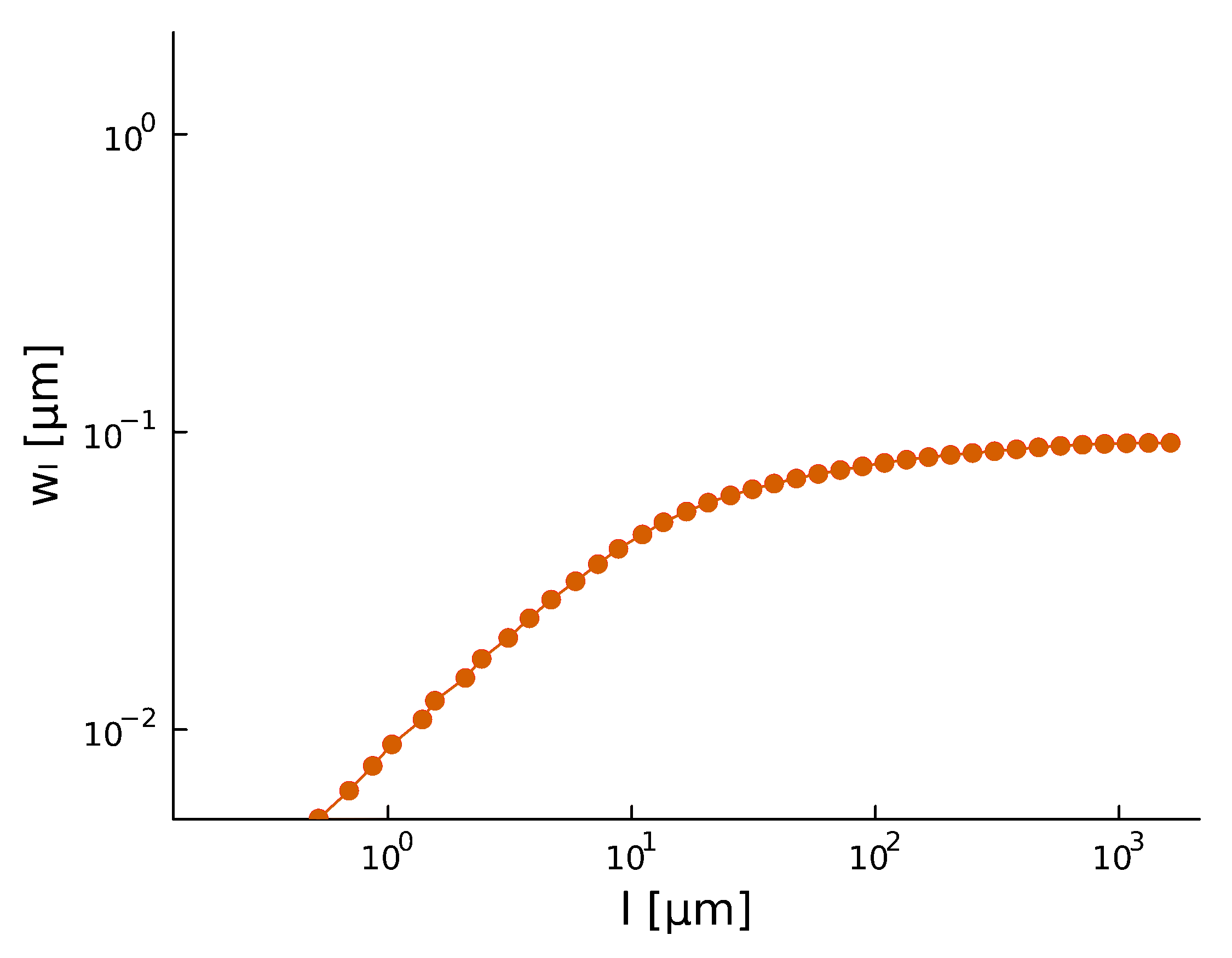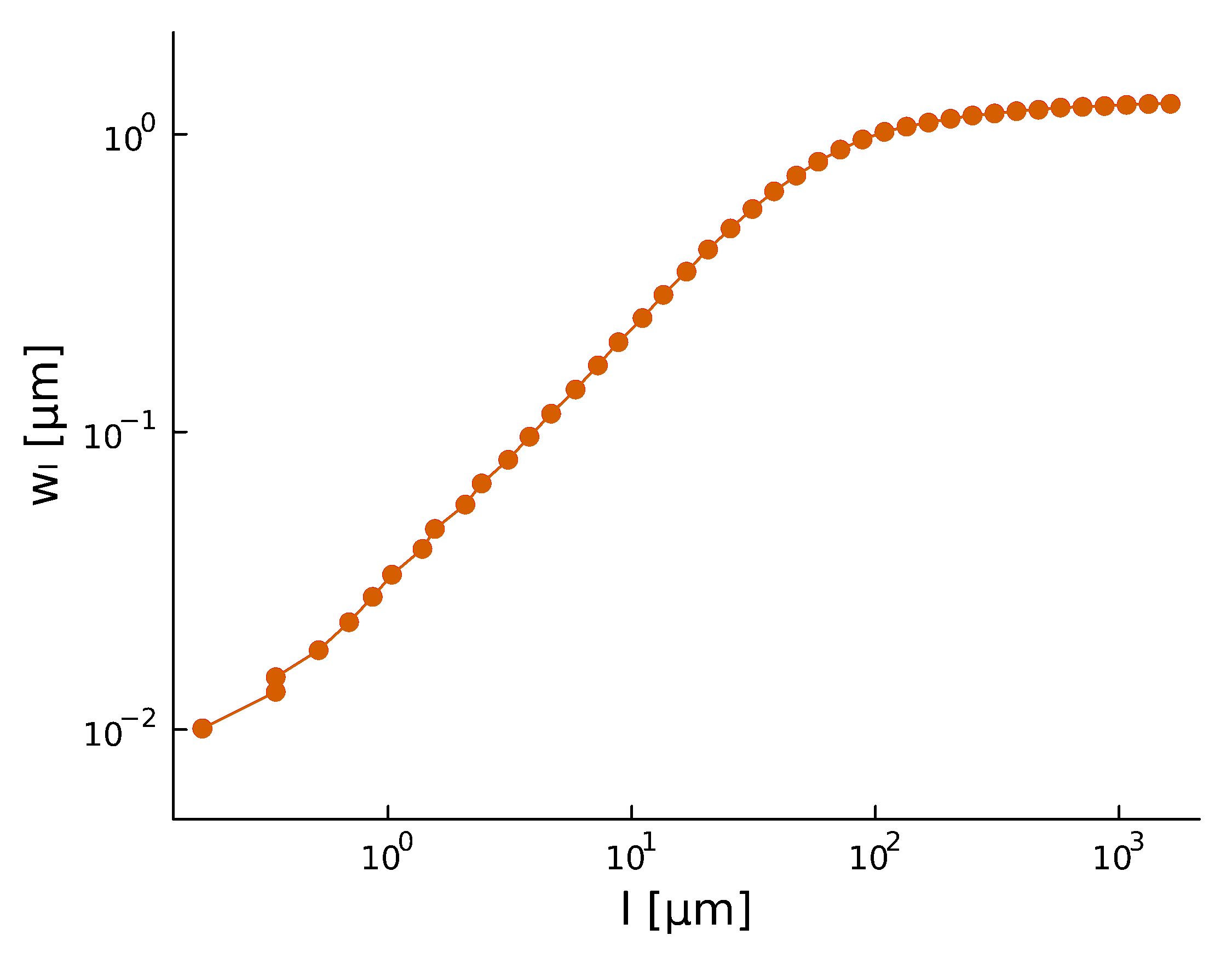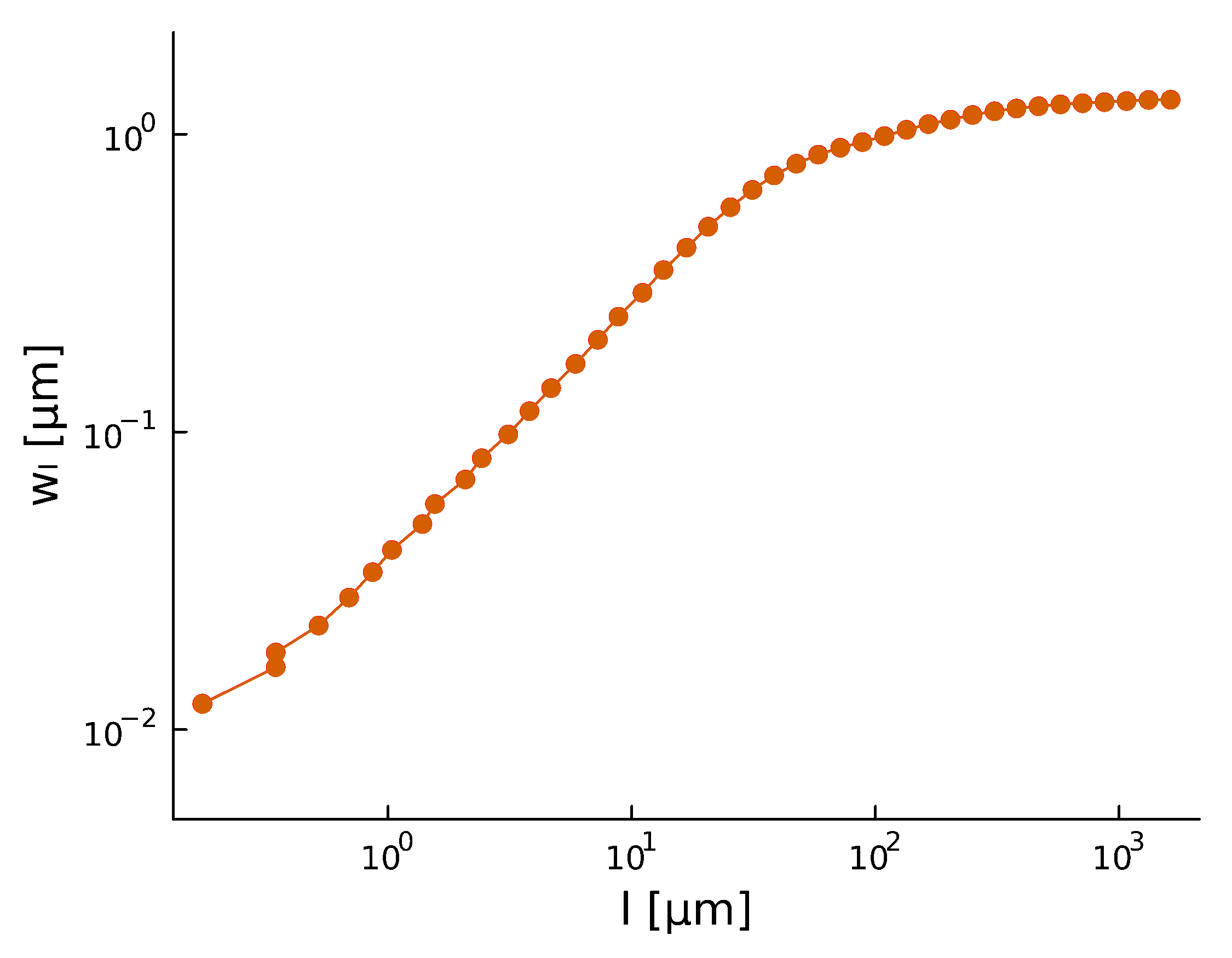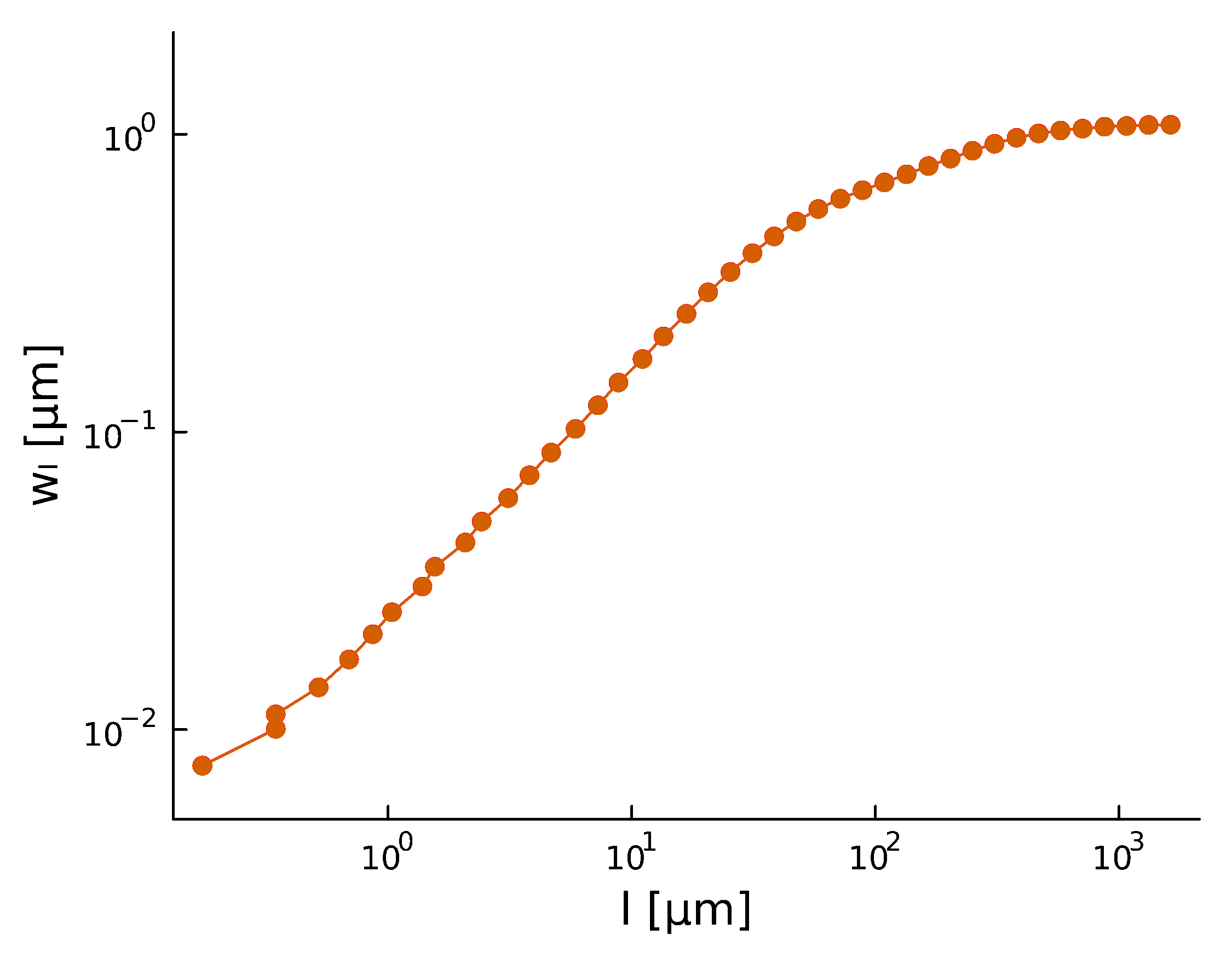
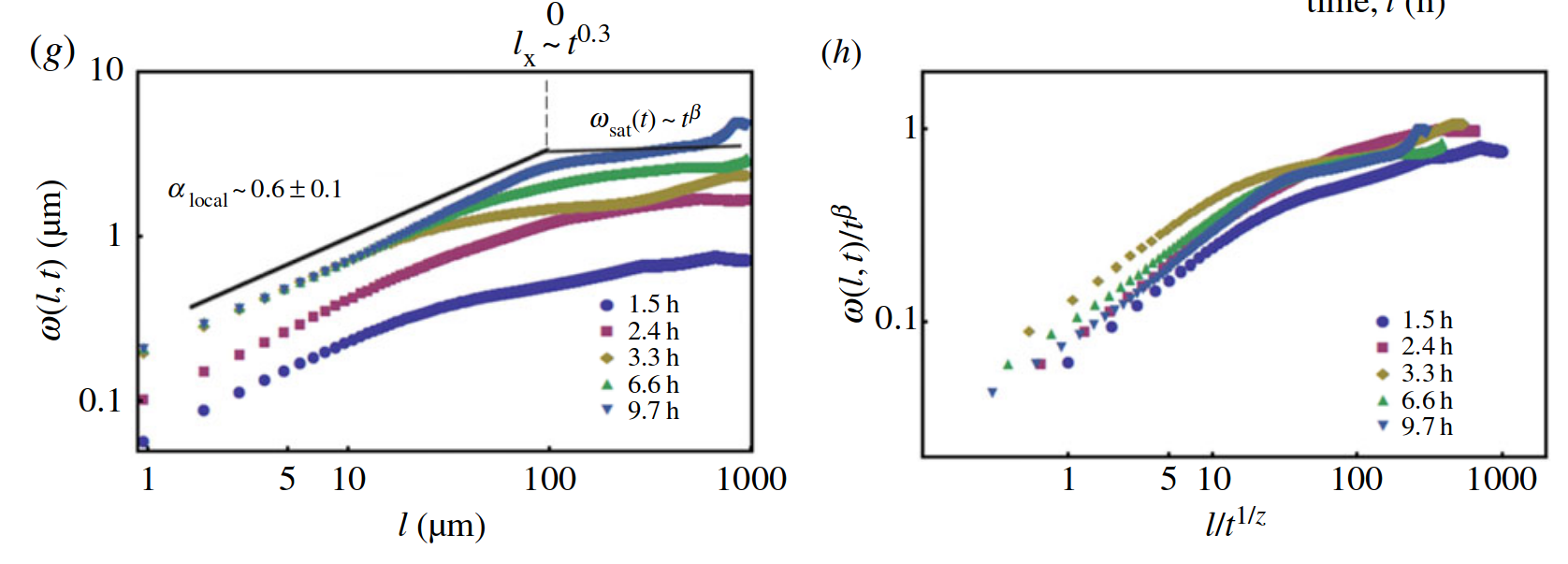
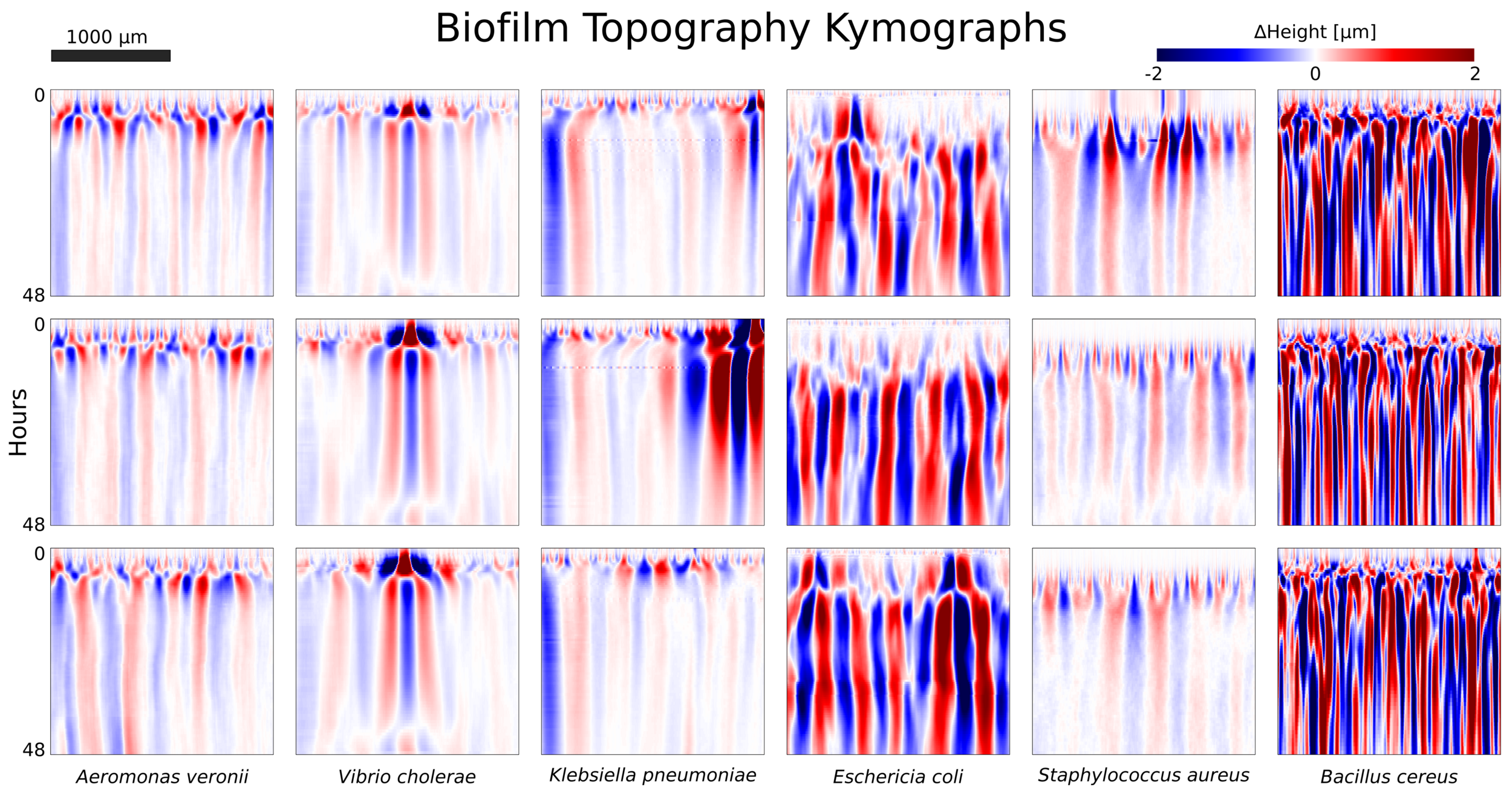
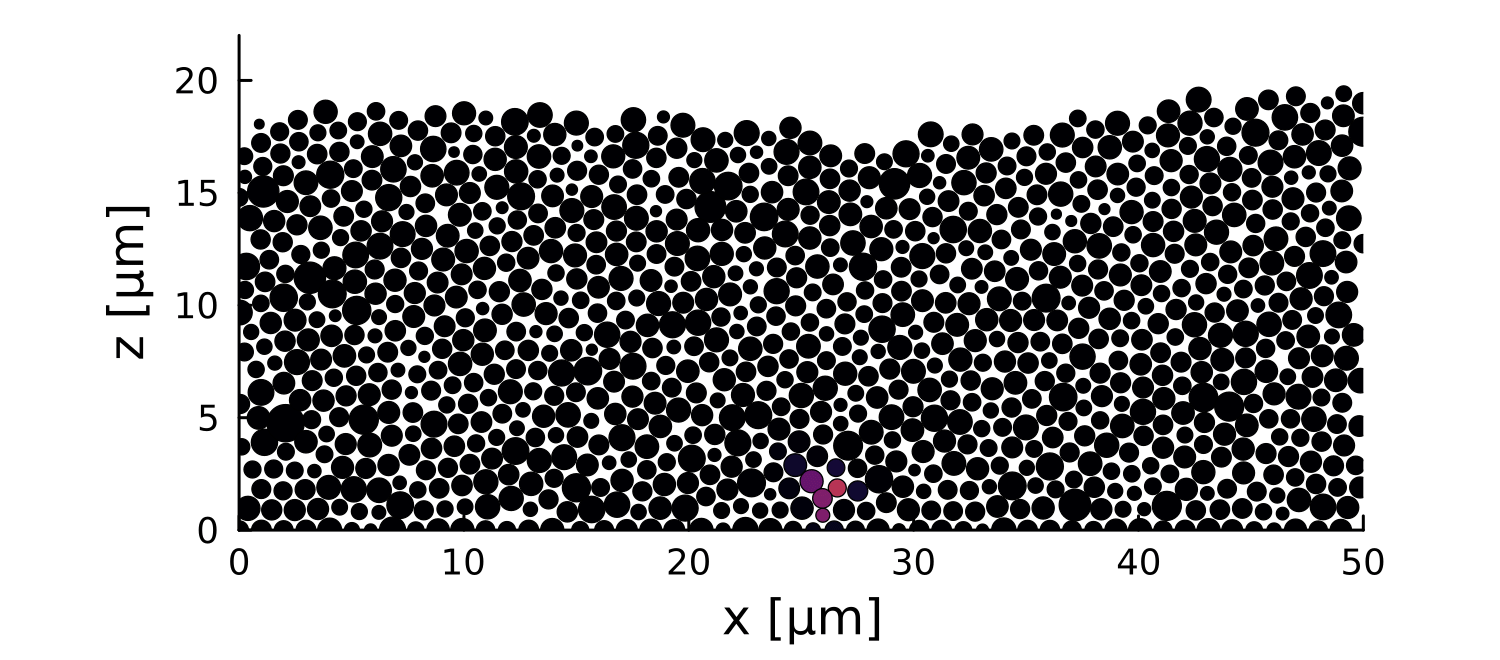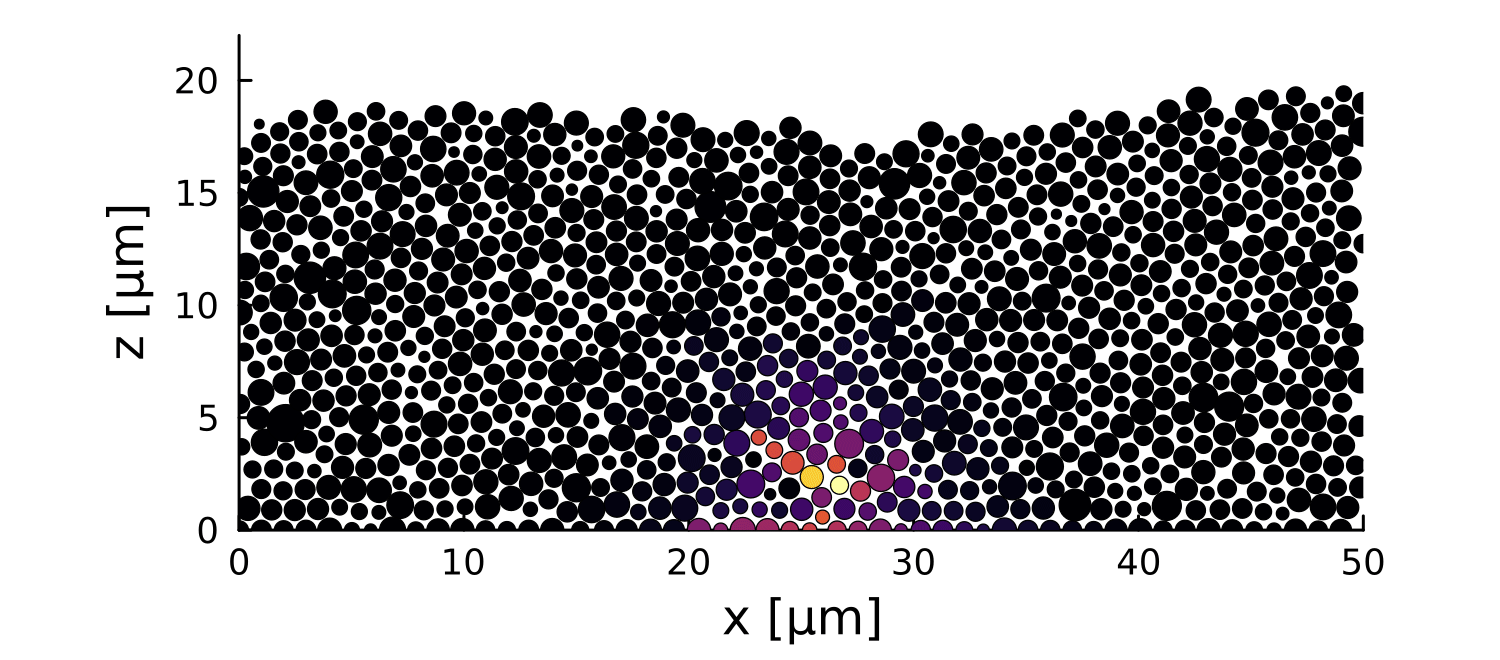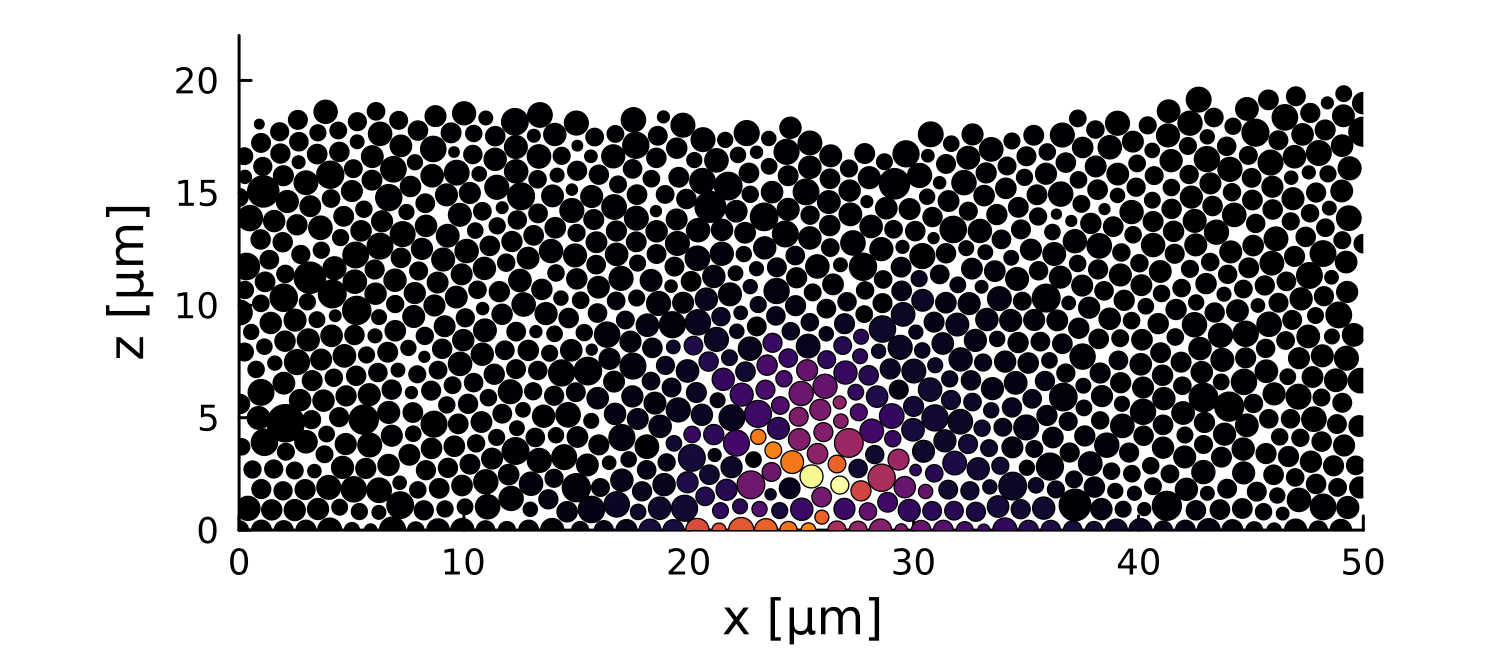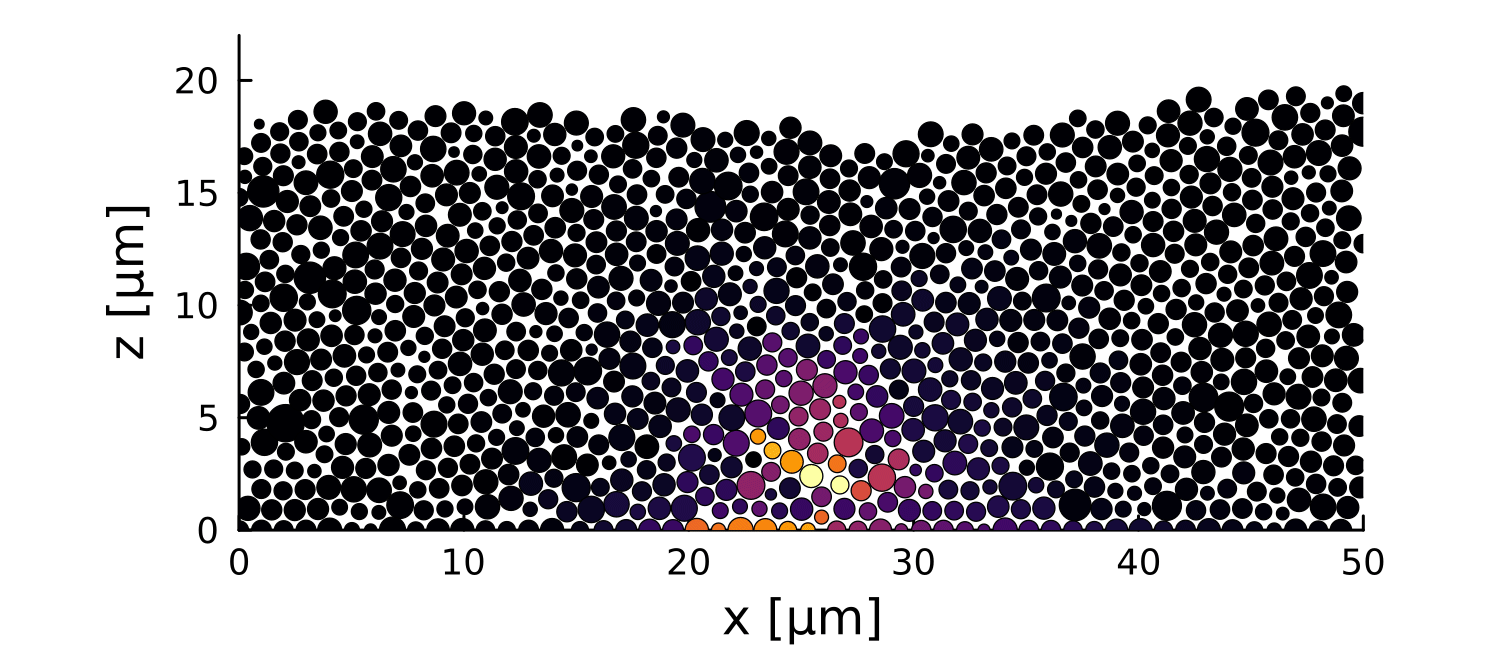
Pablo Bravo
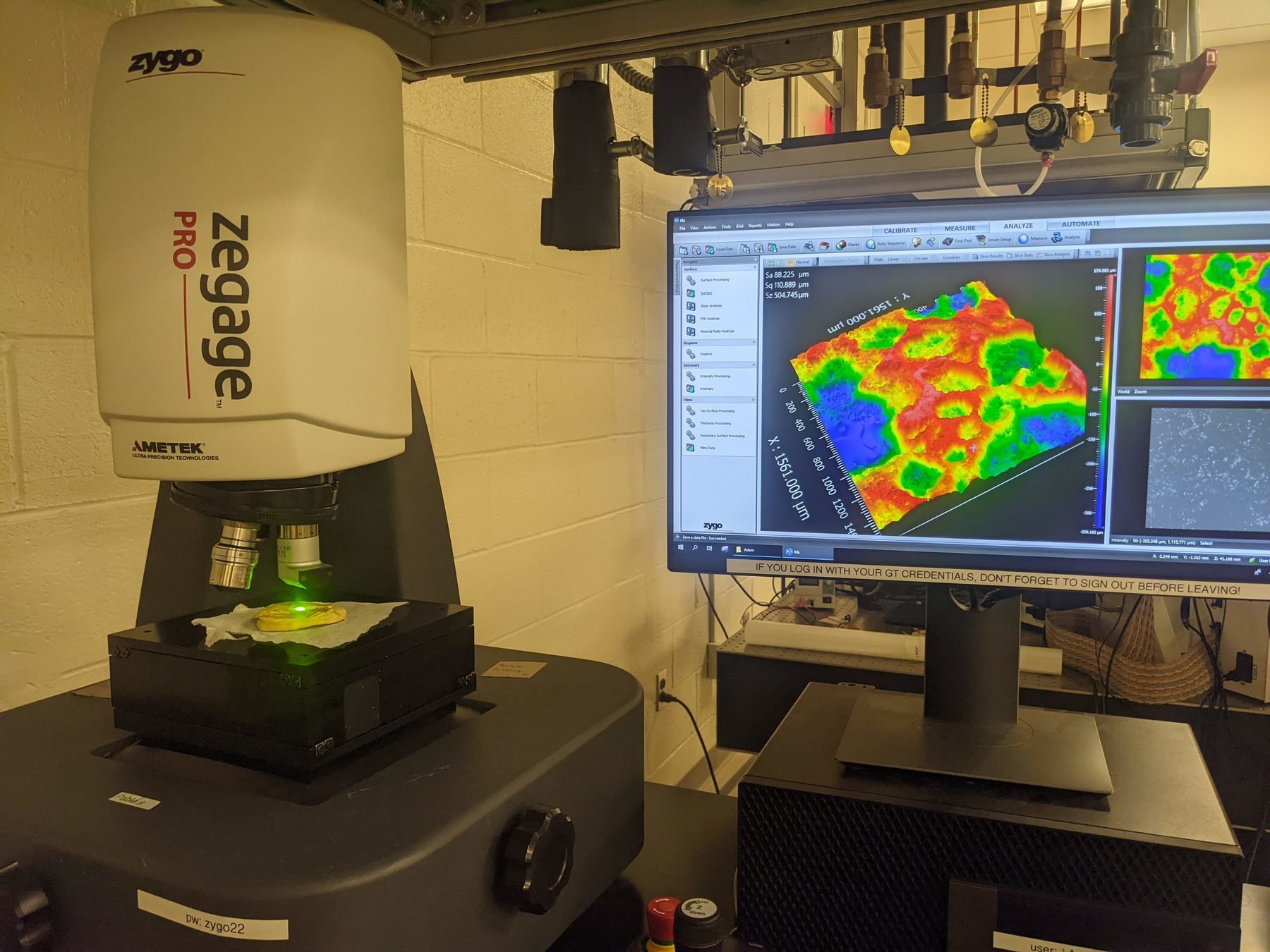
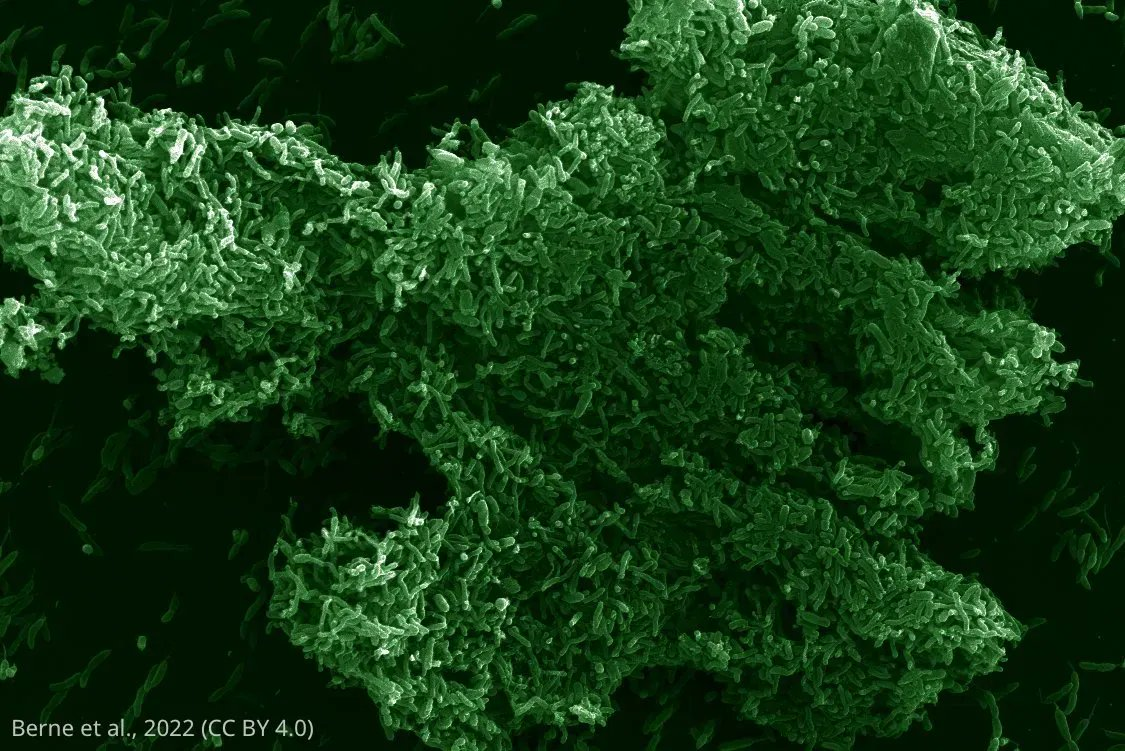
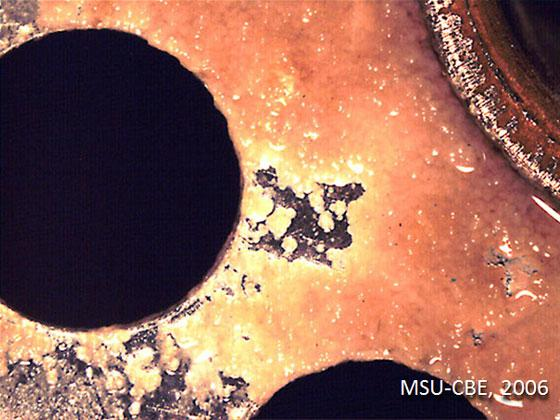
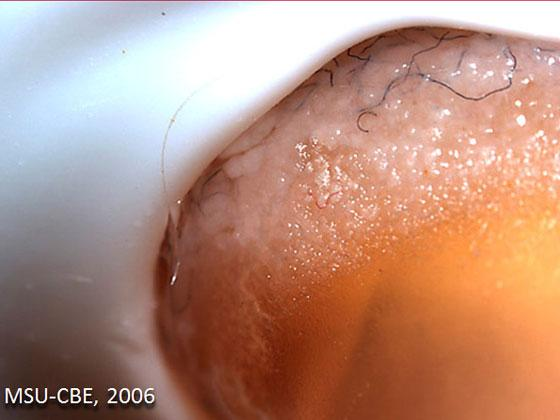
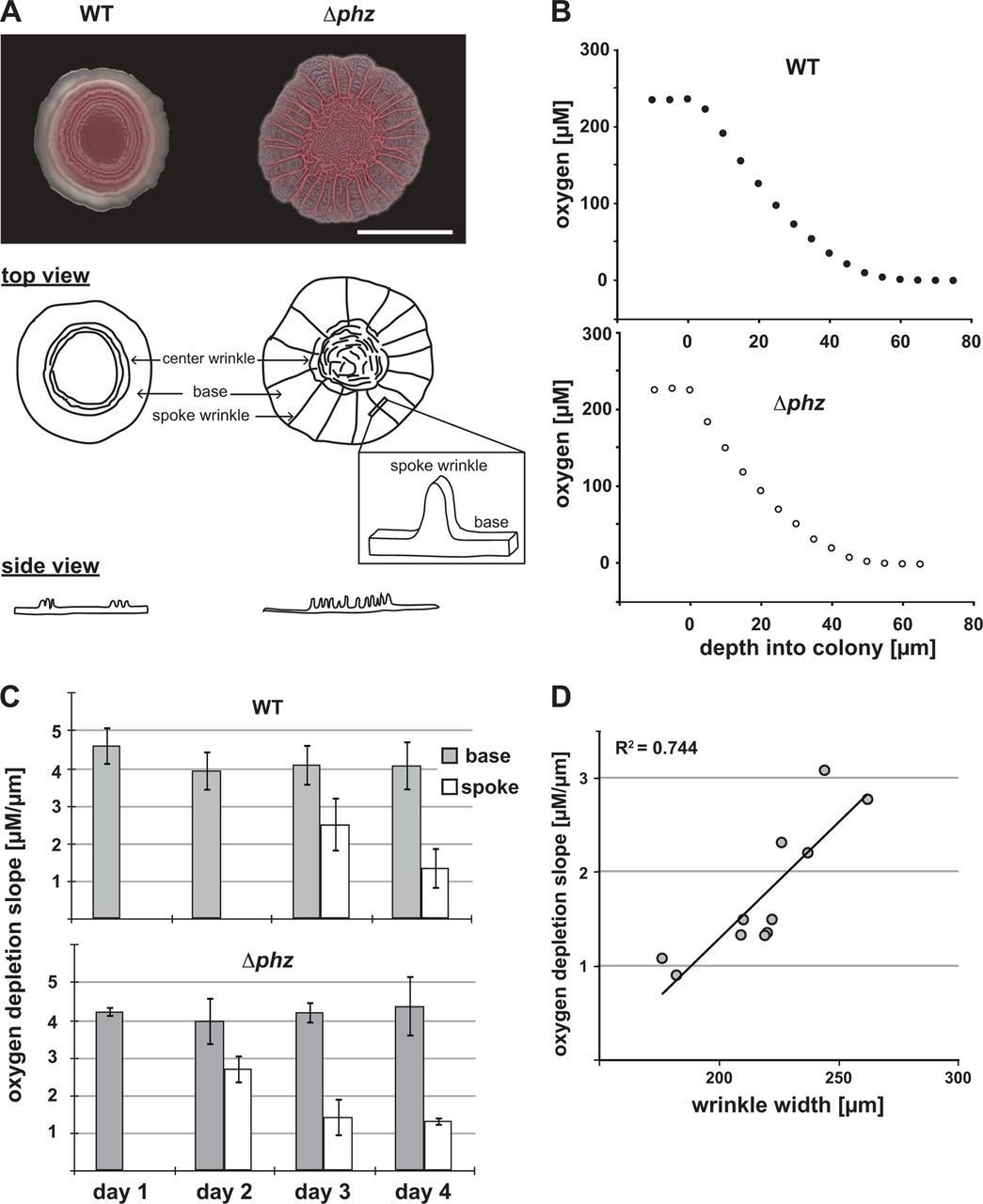
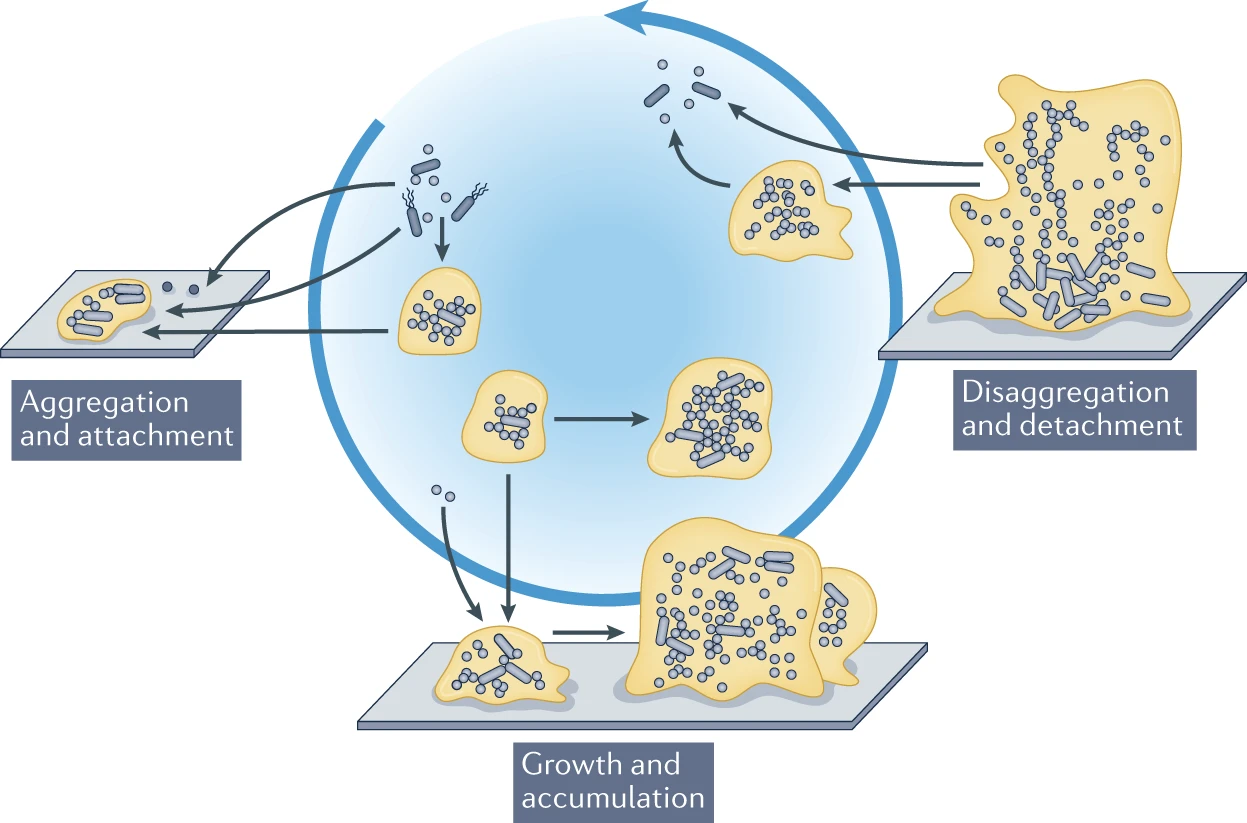
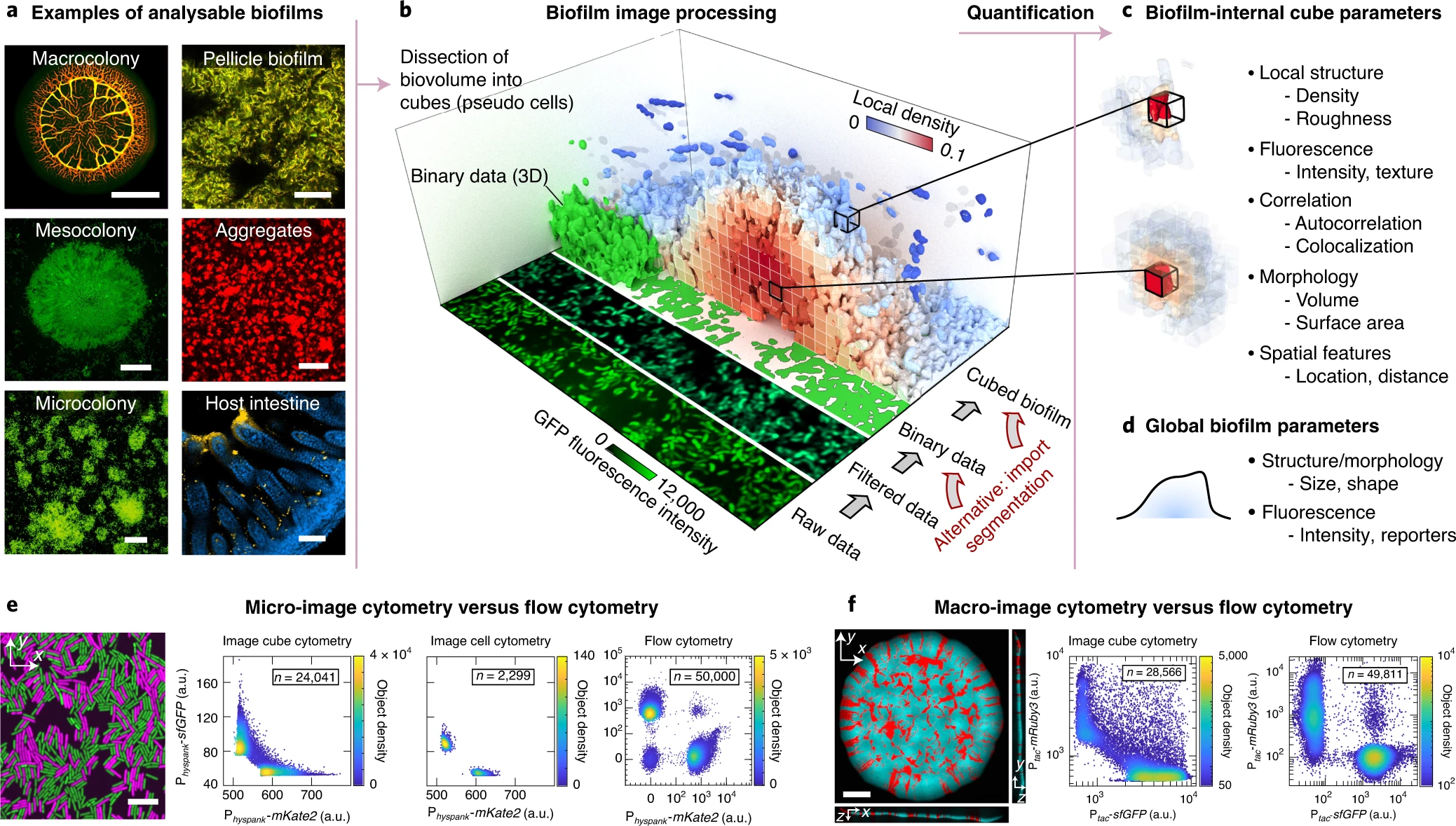
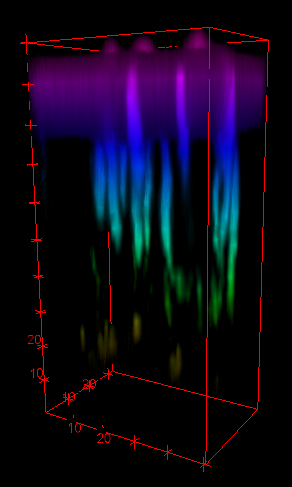
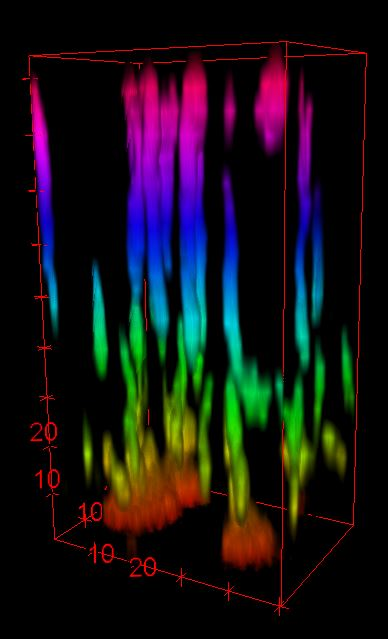
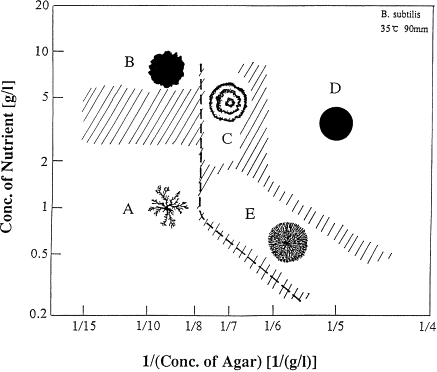
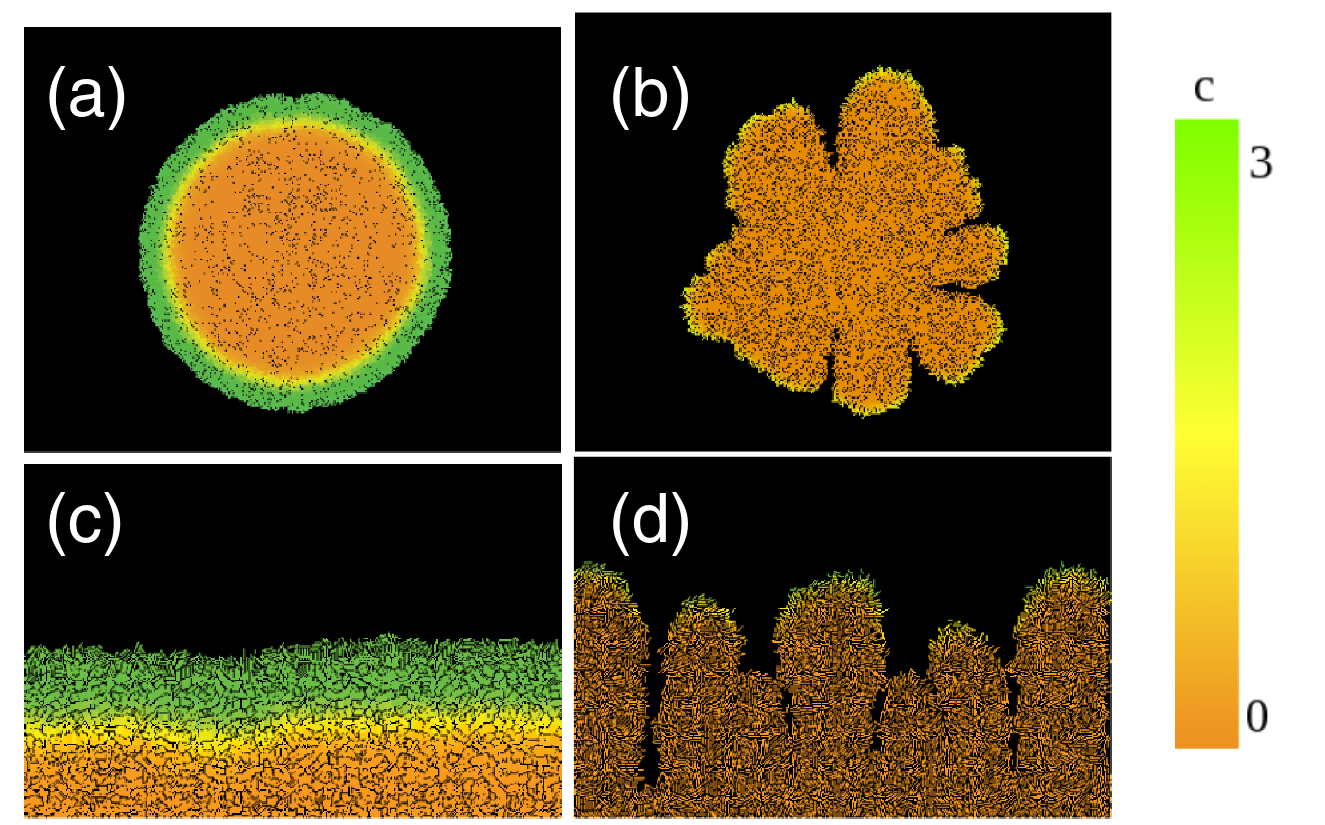
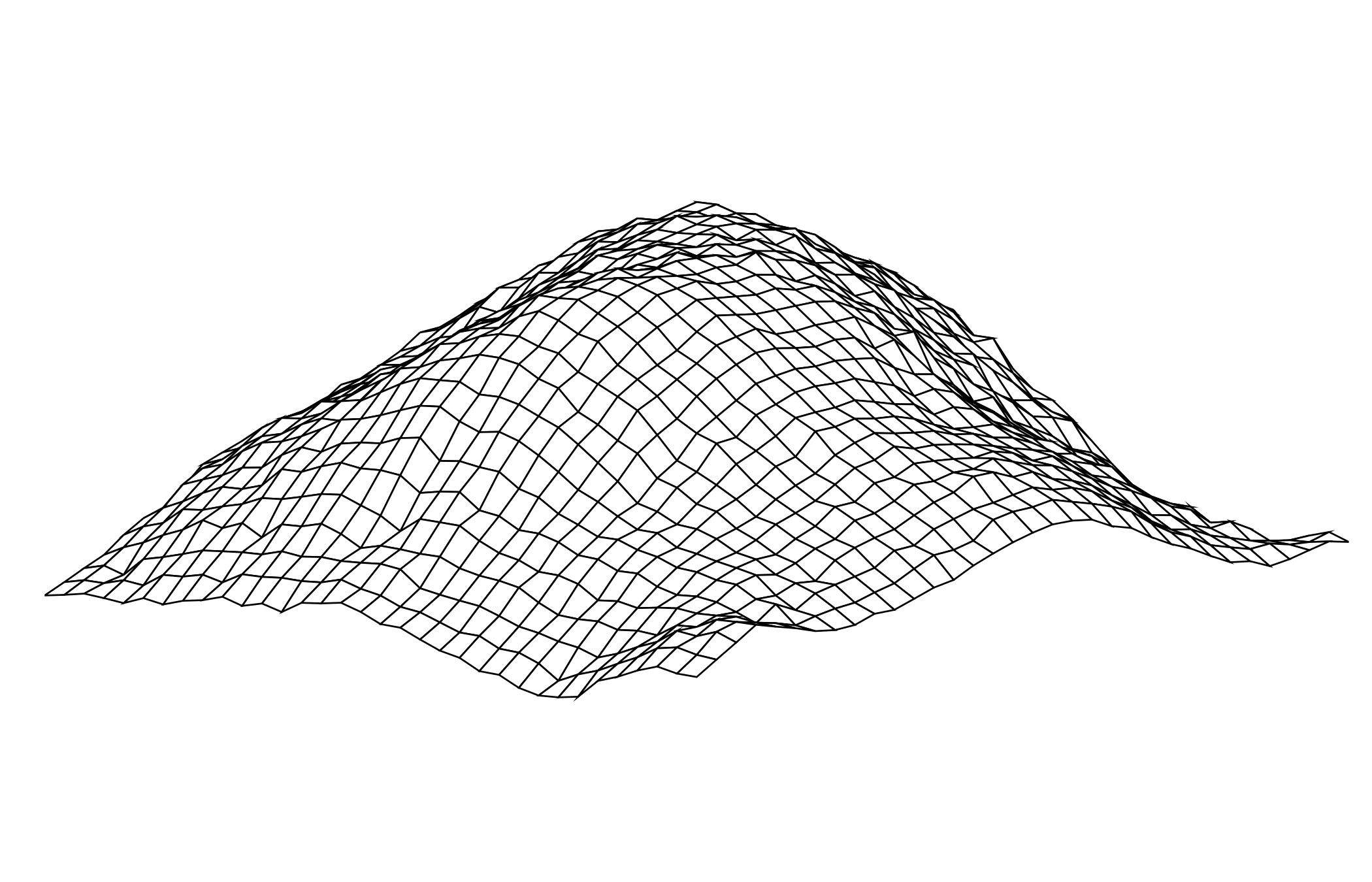
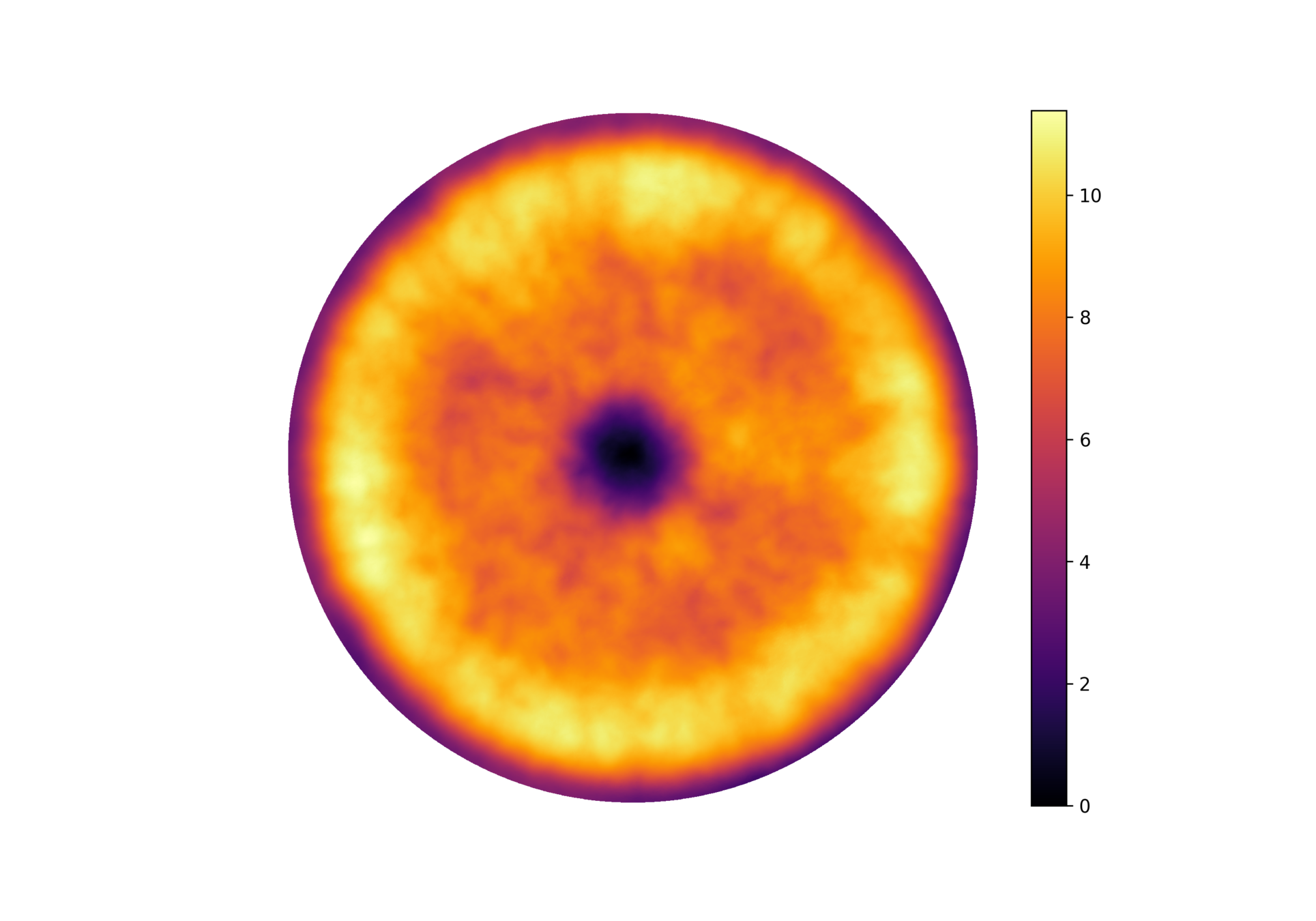
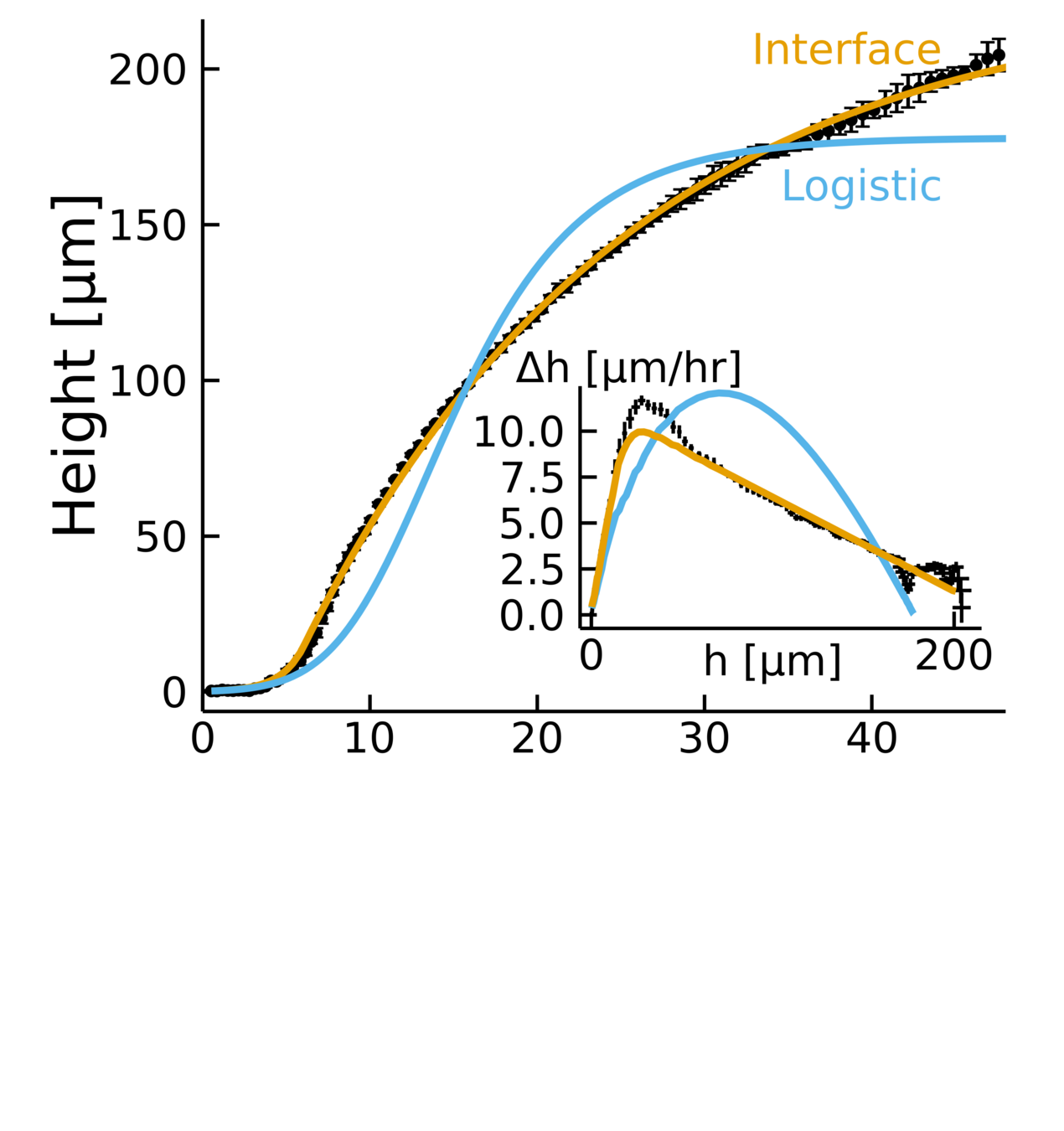
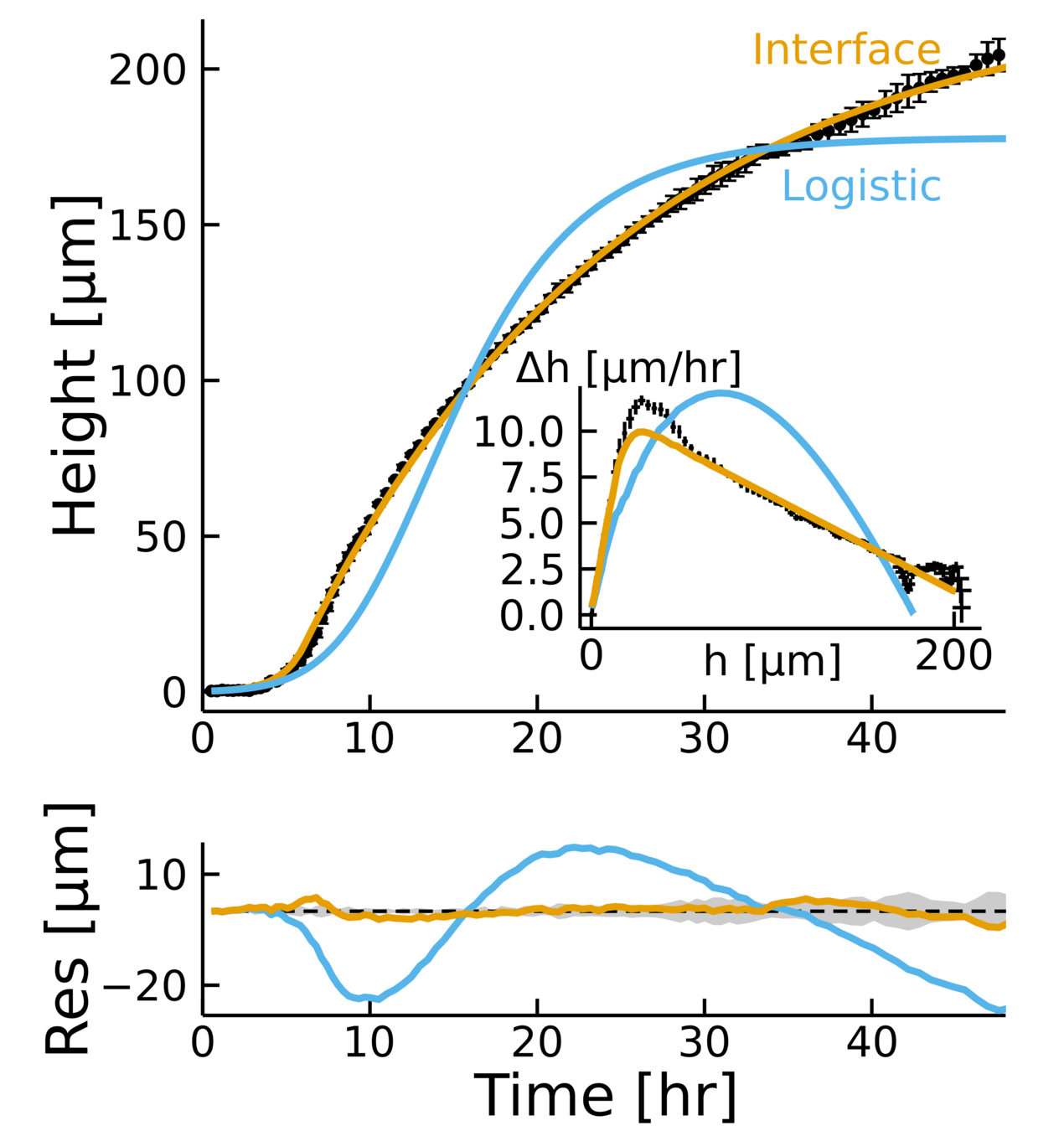
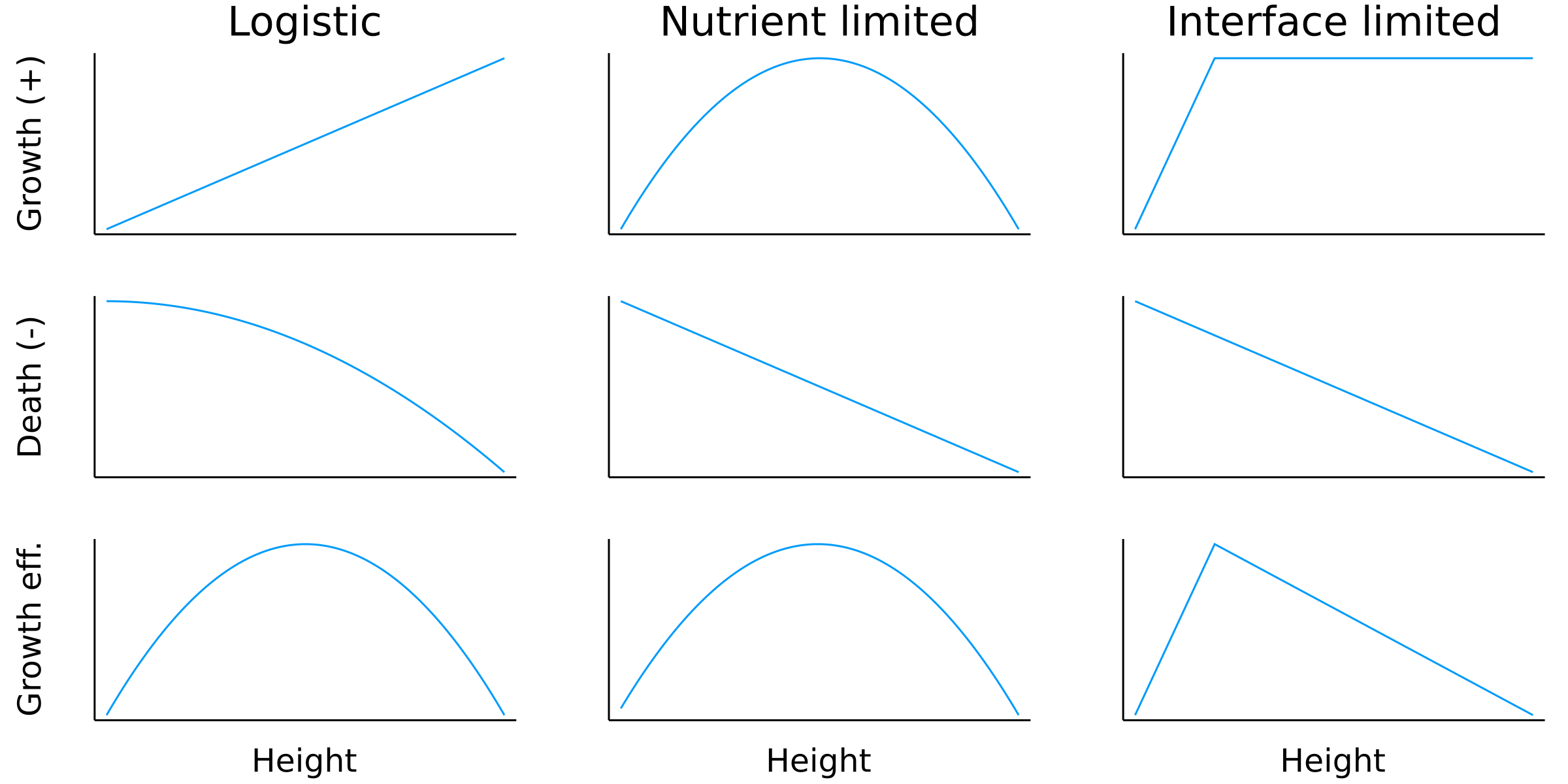
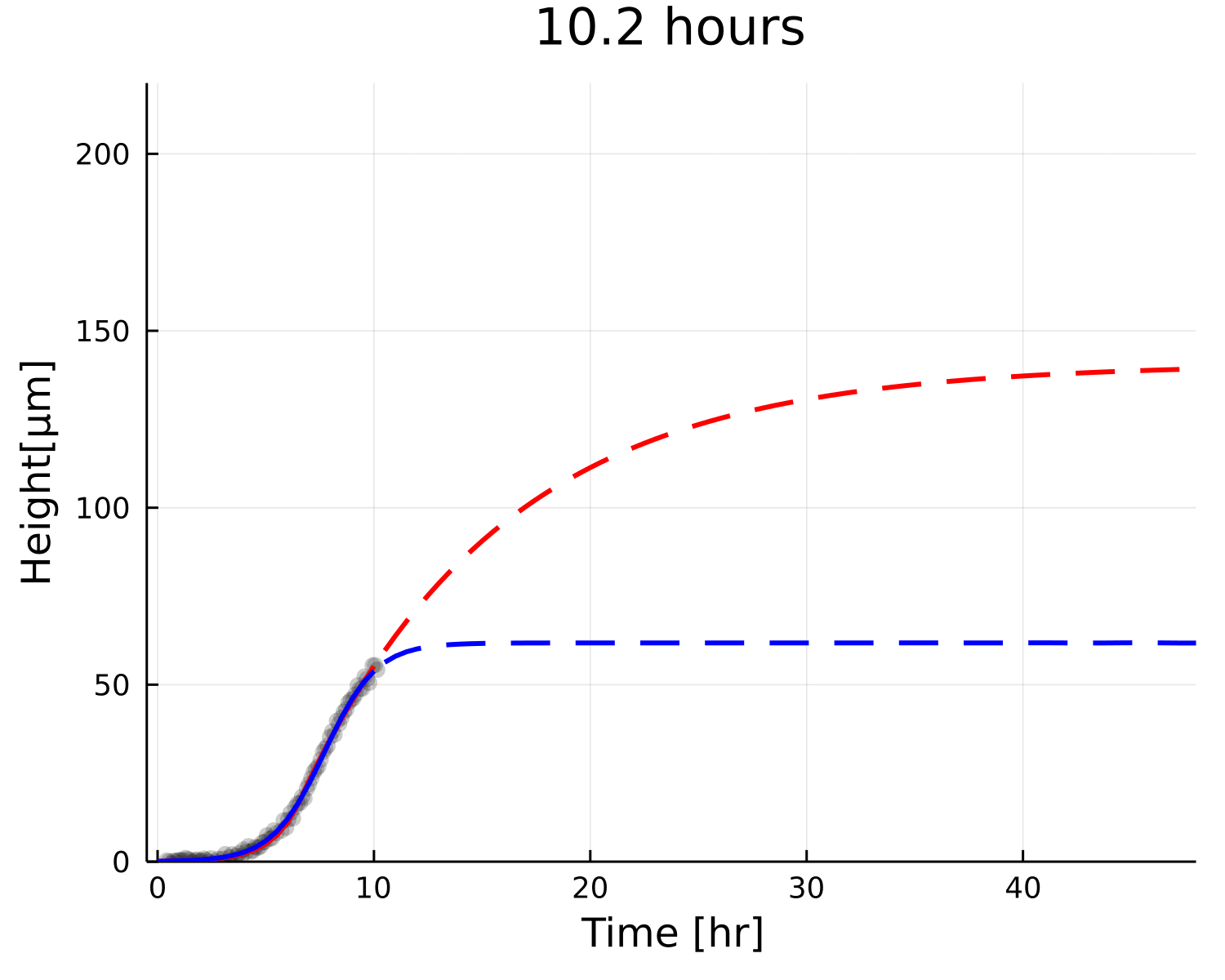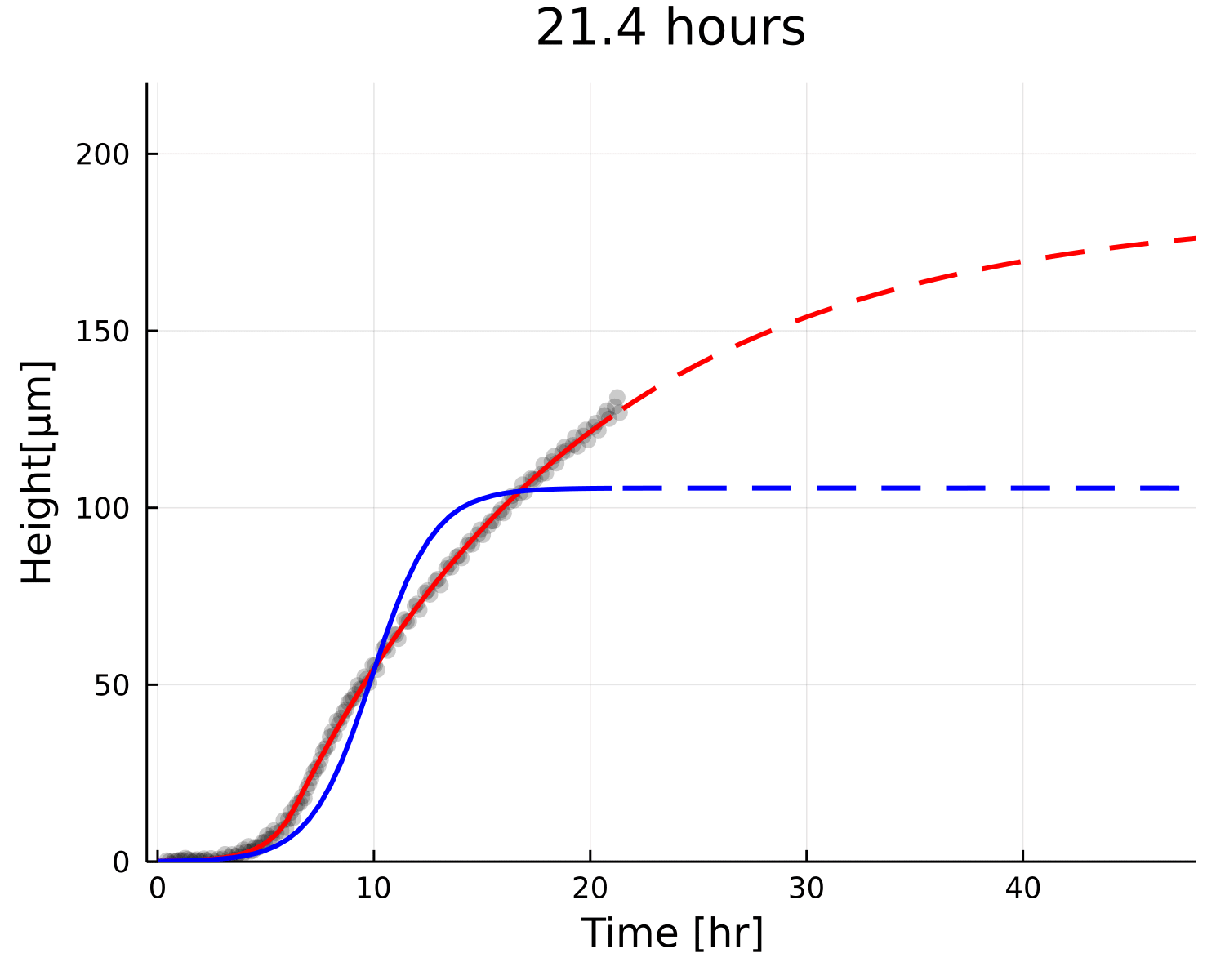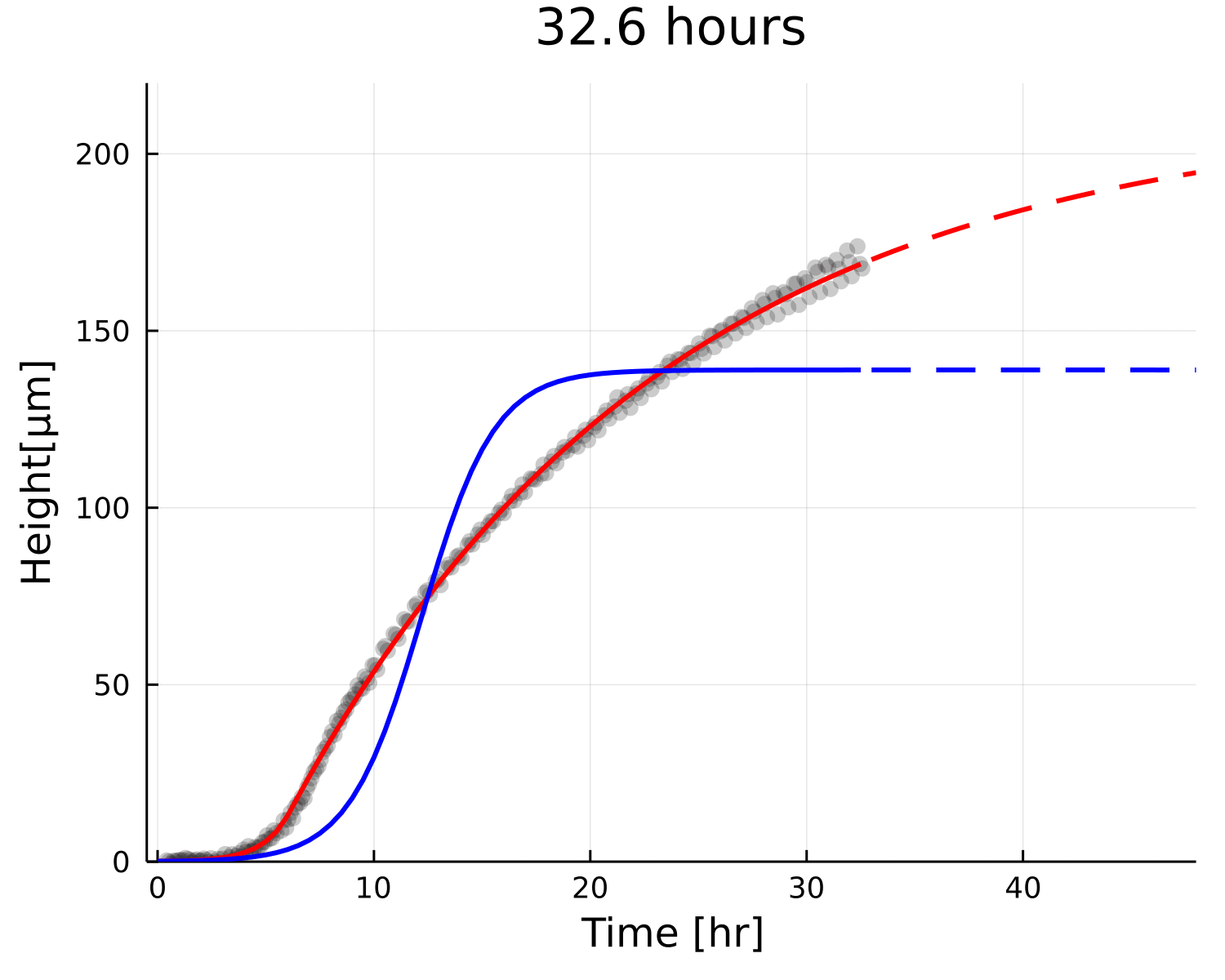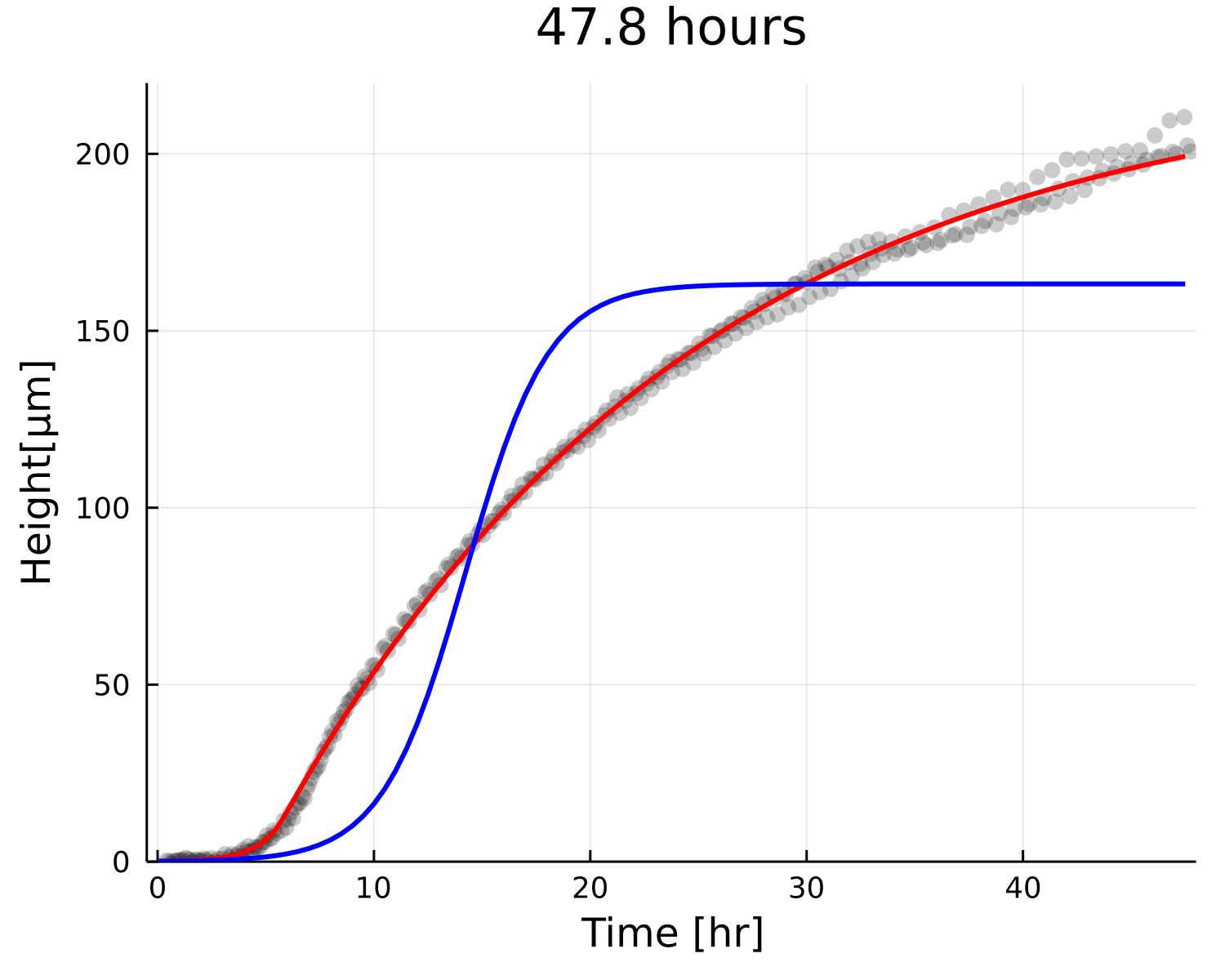
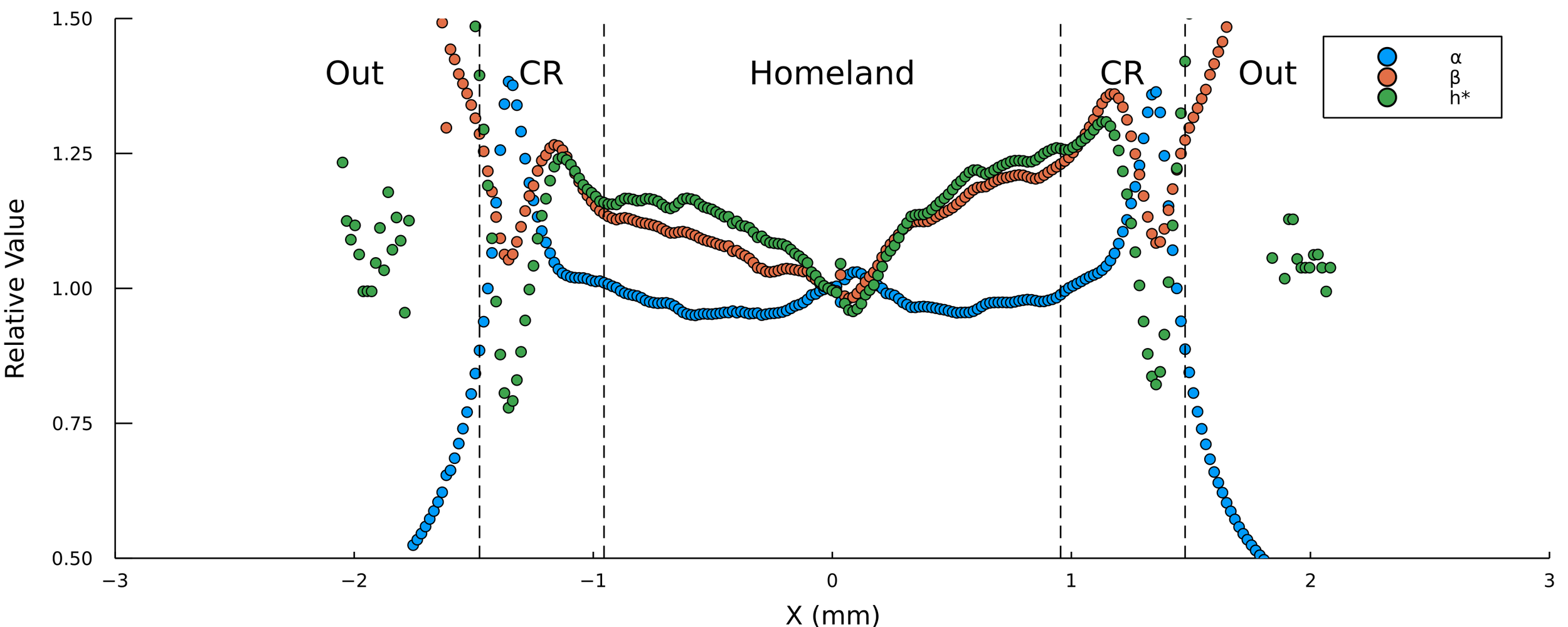
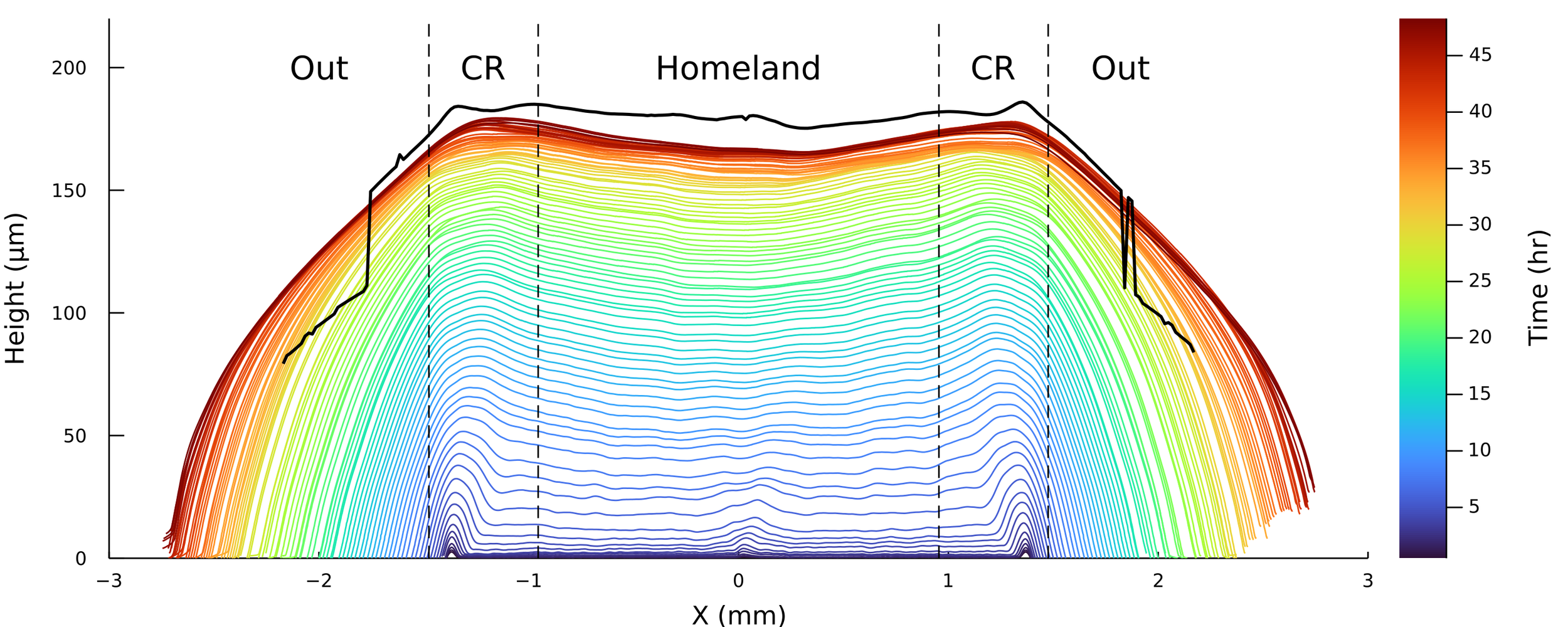
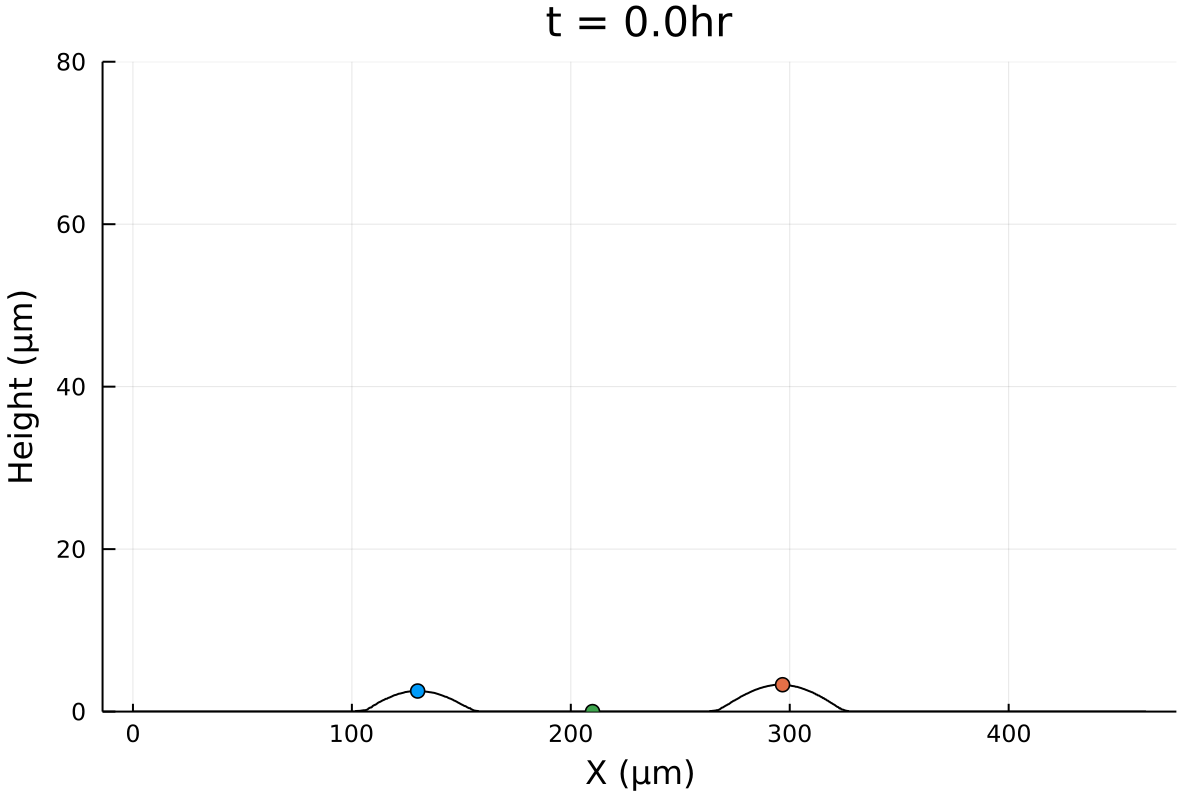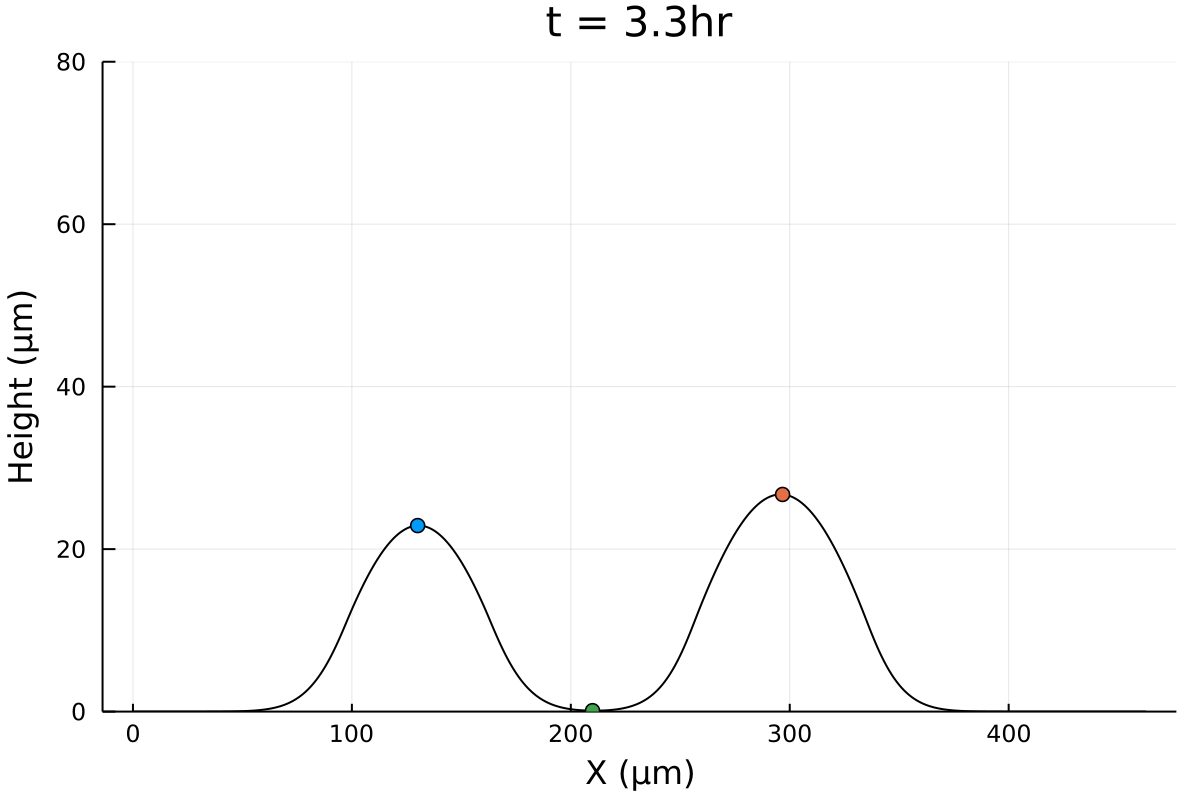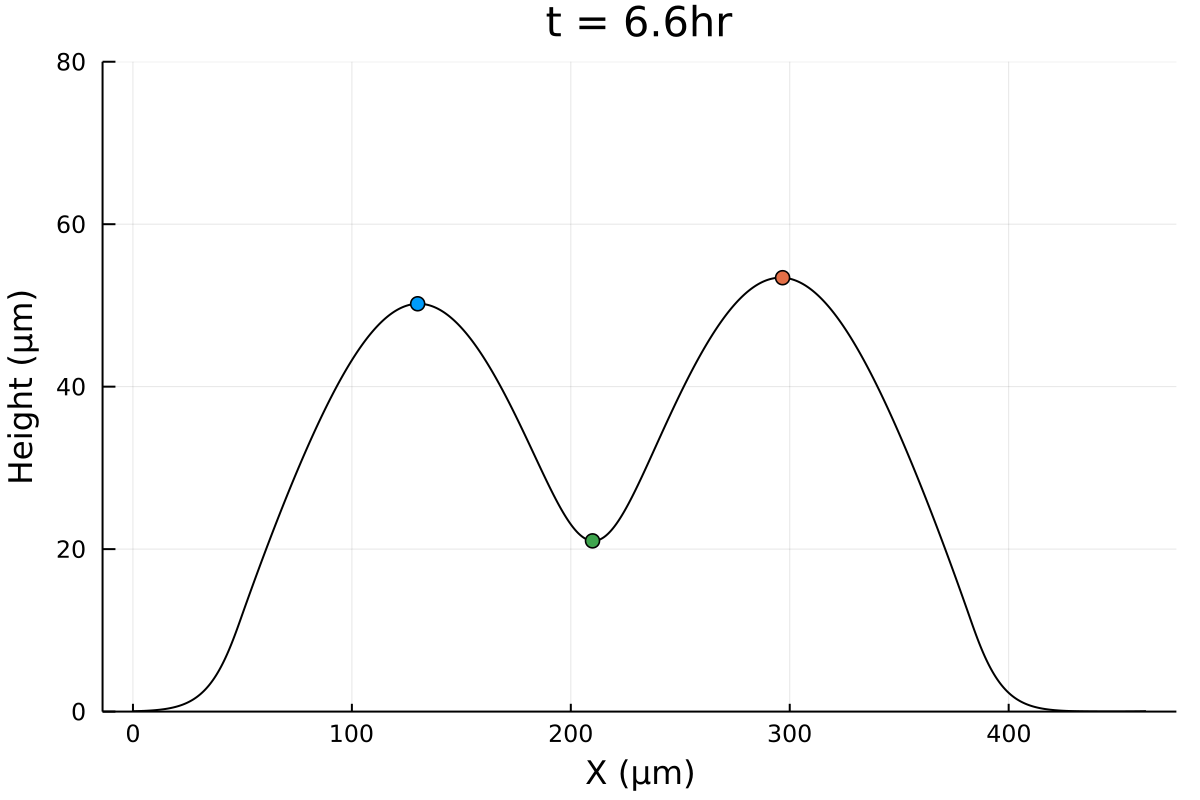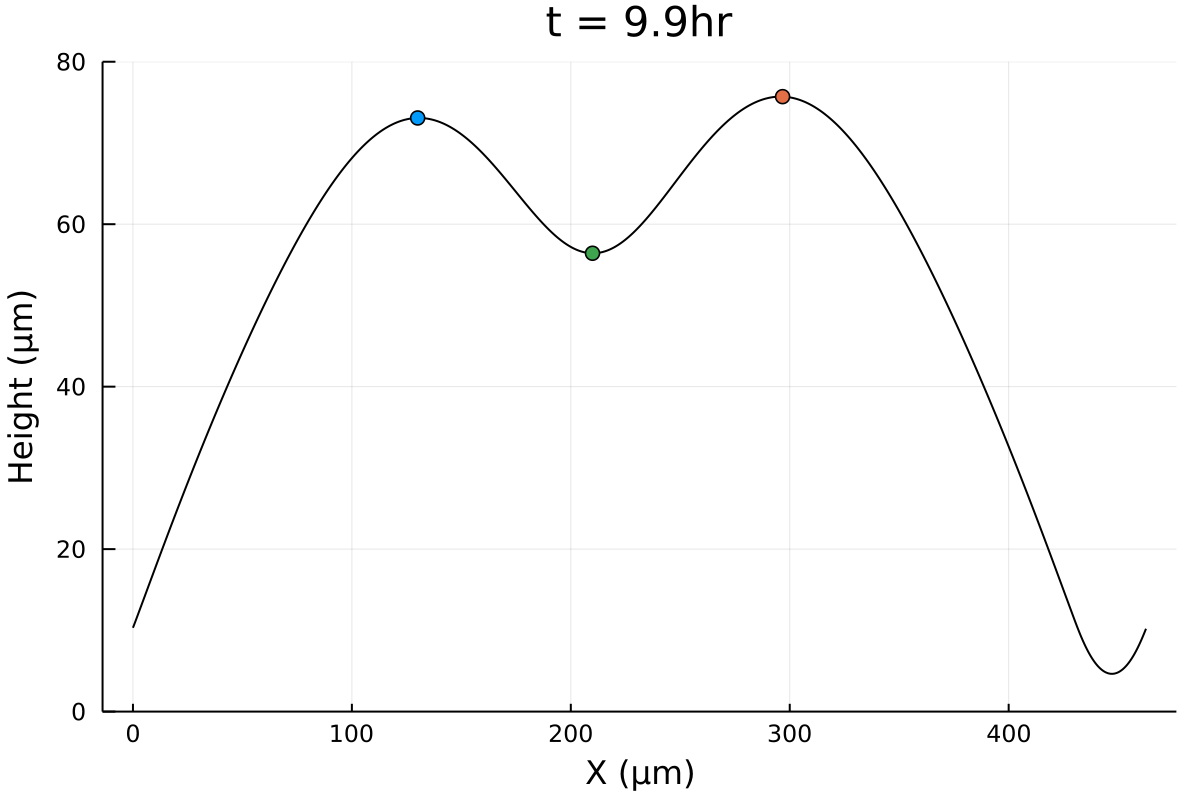
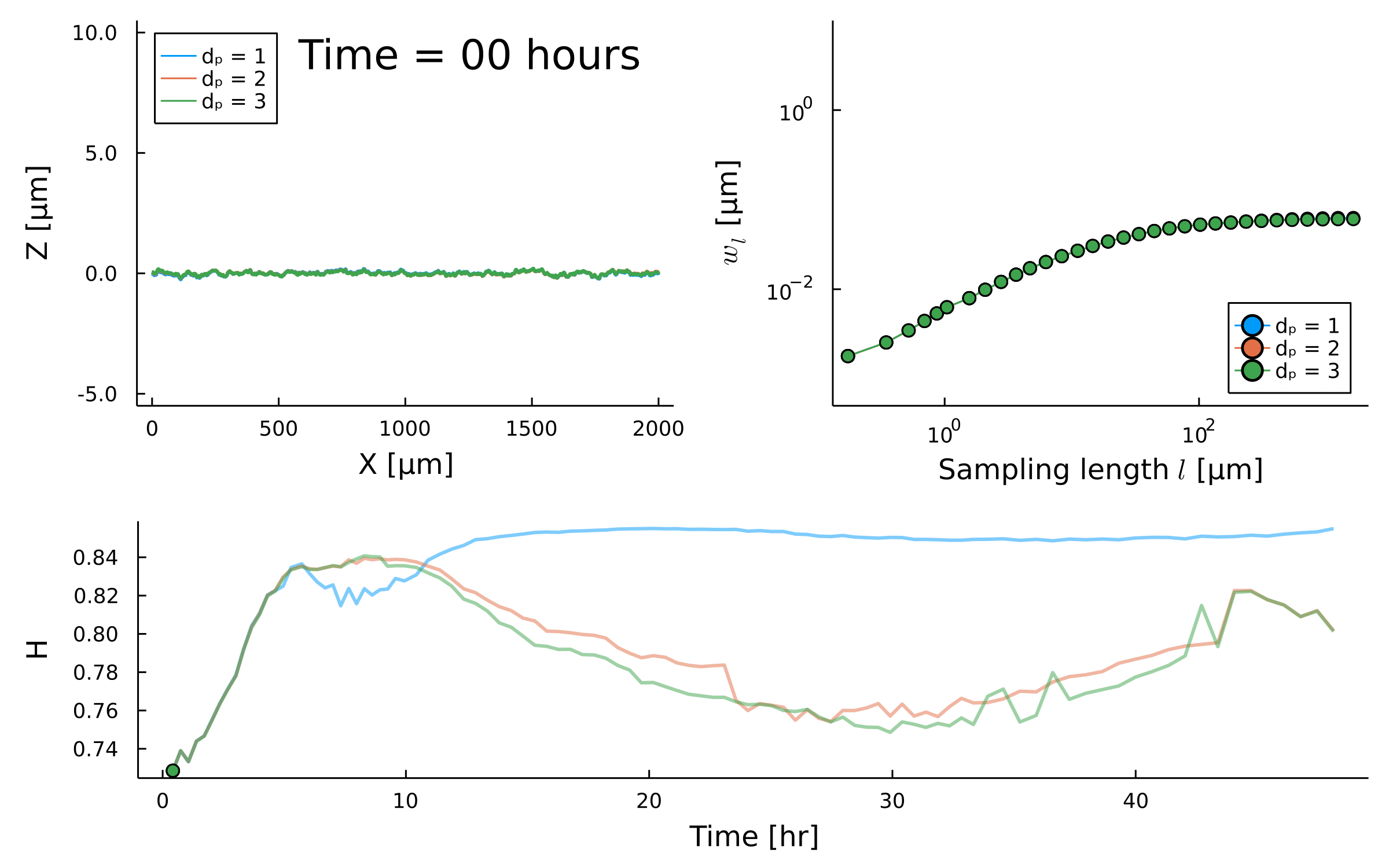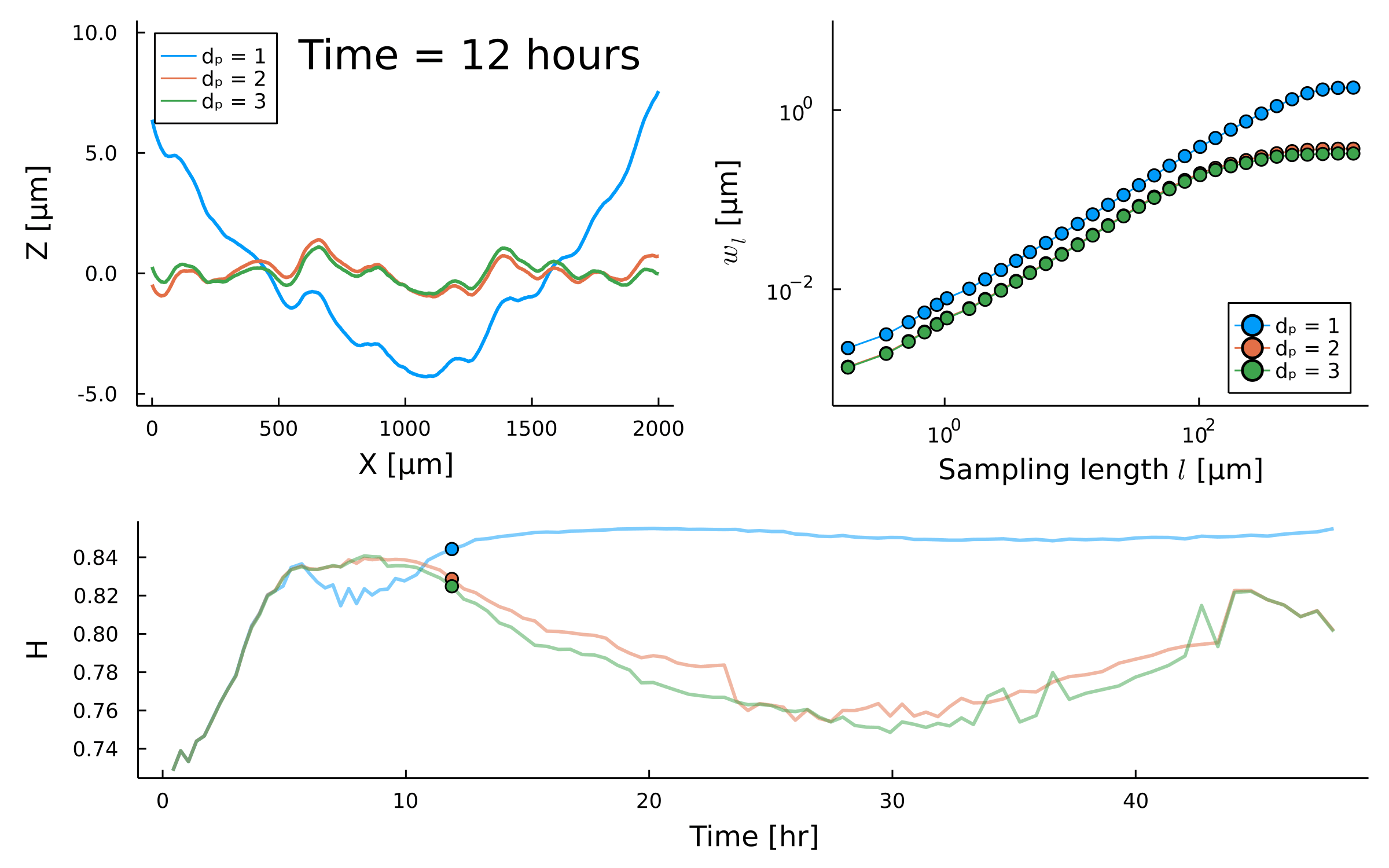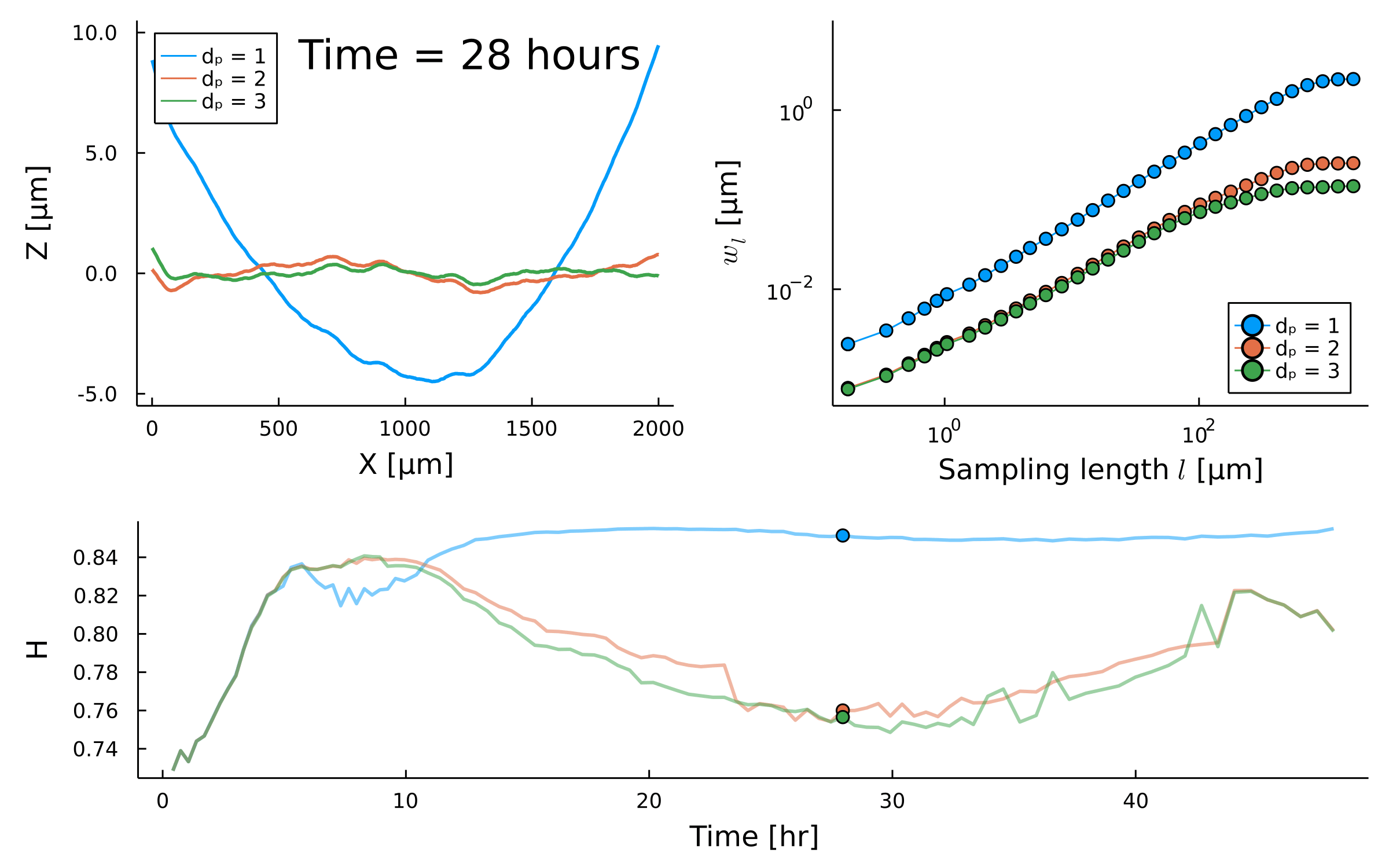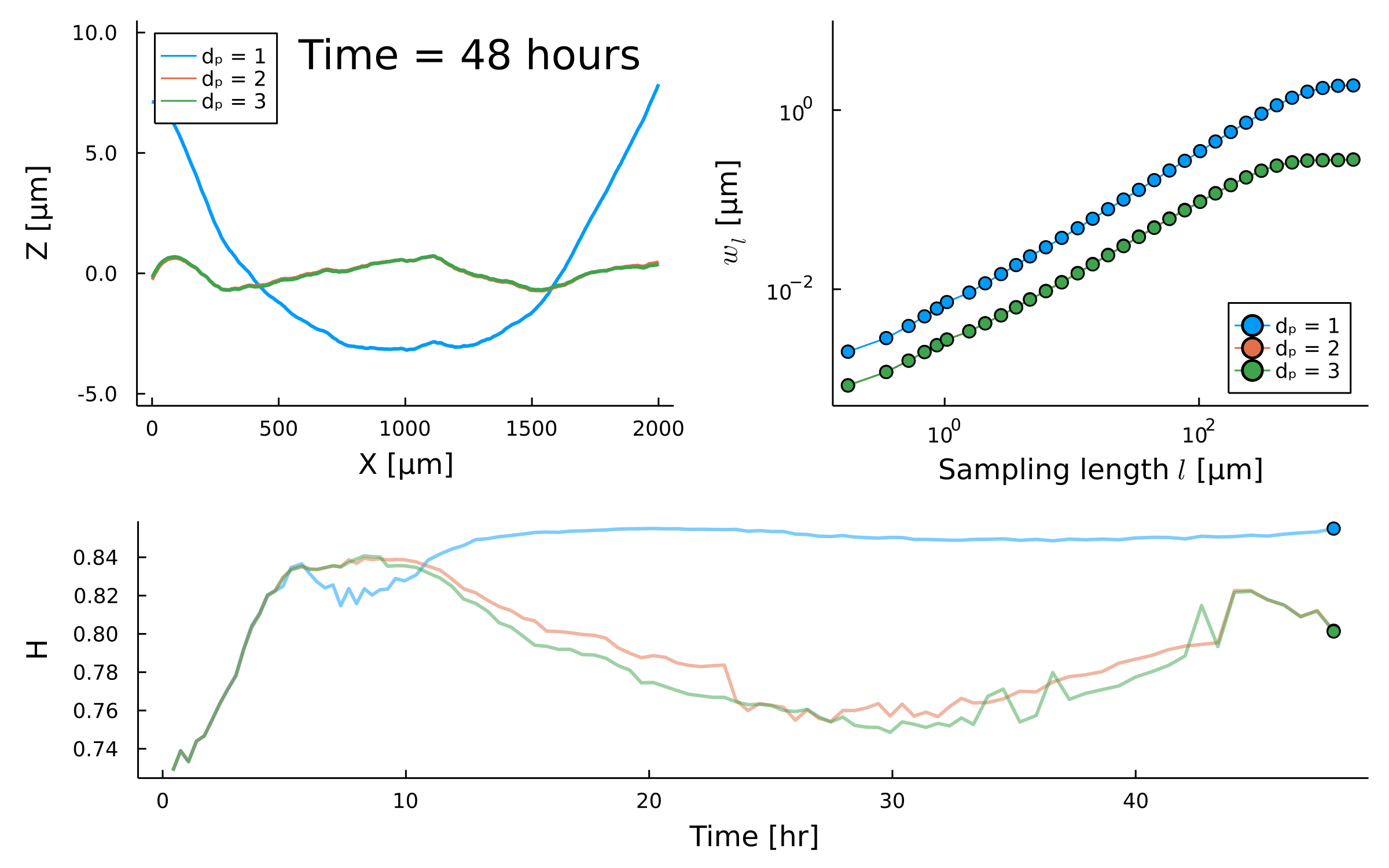
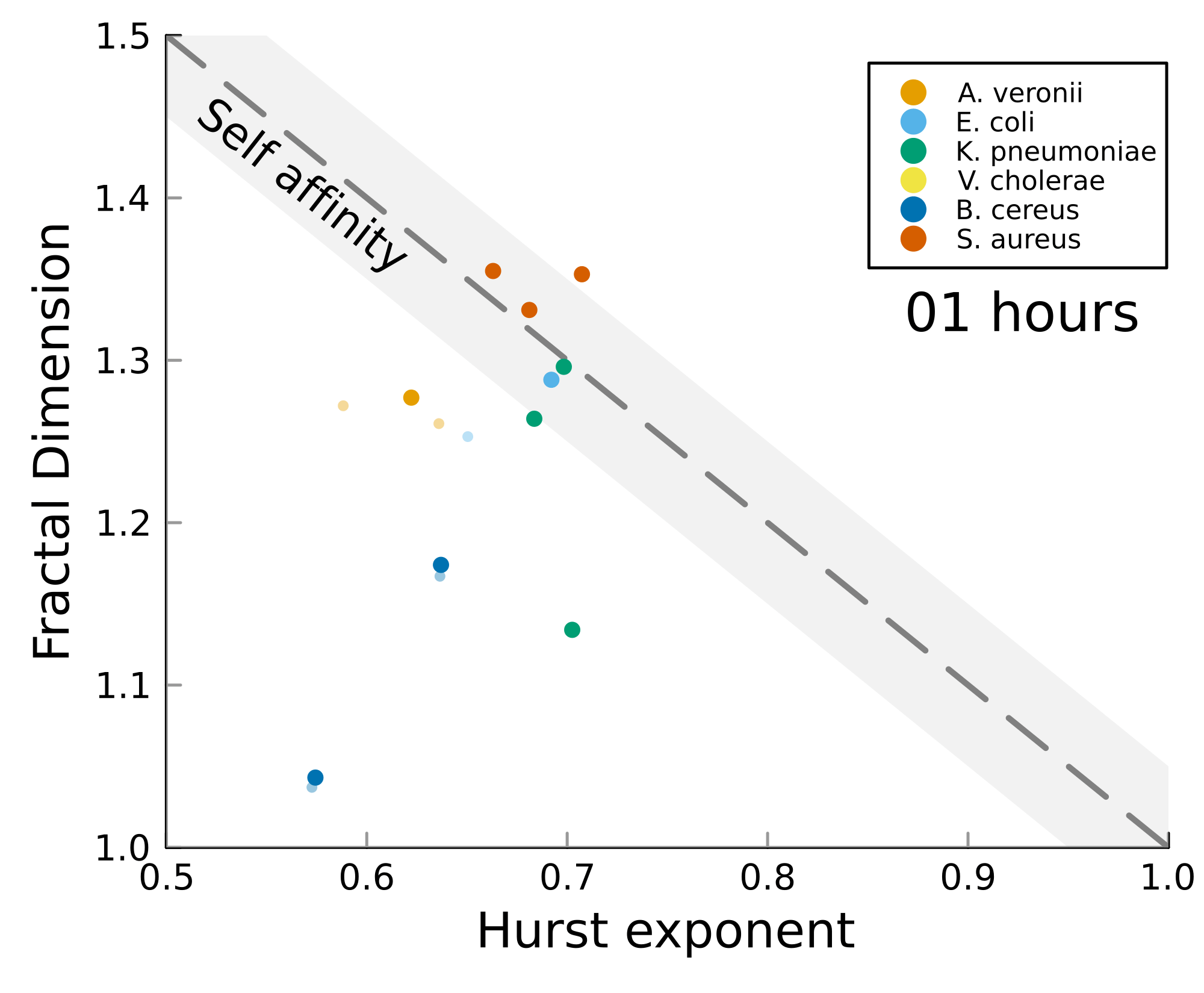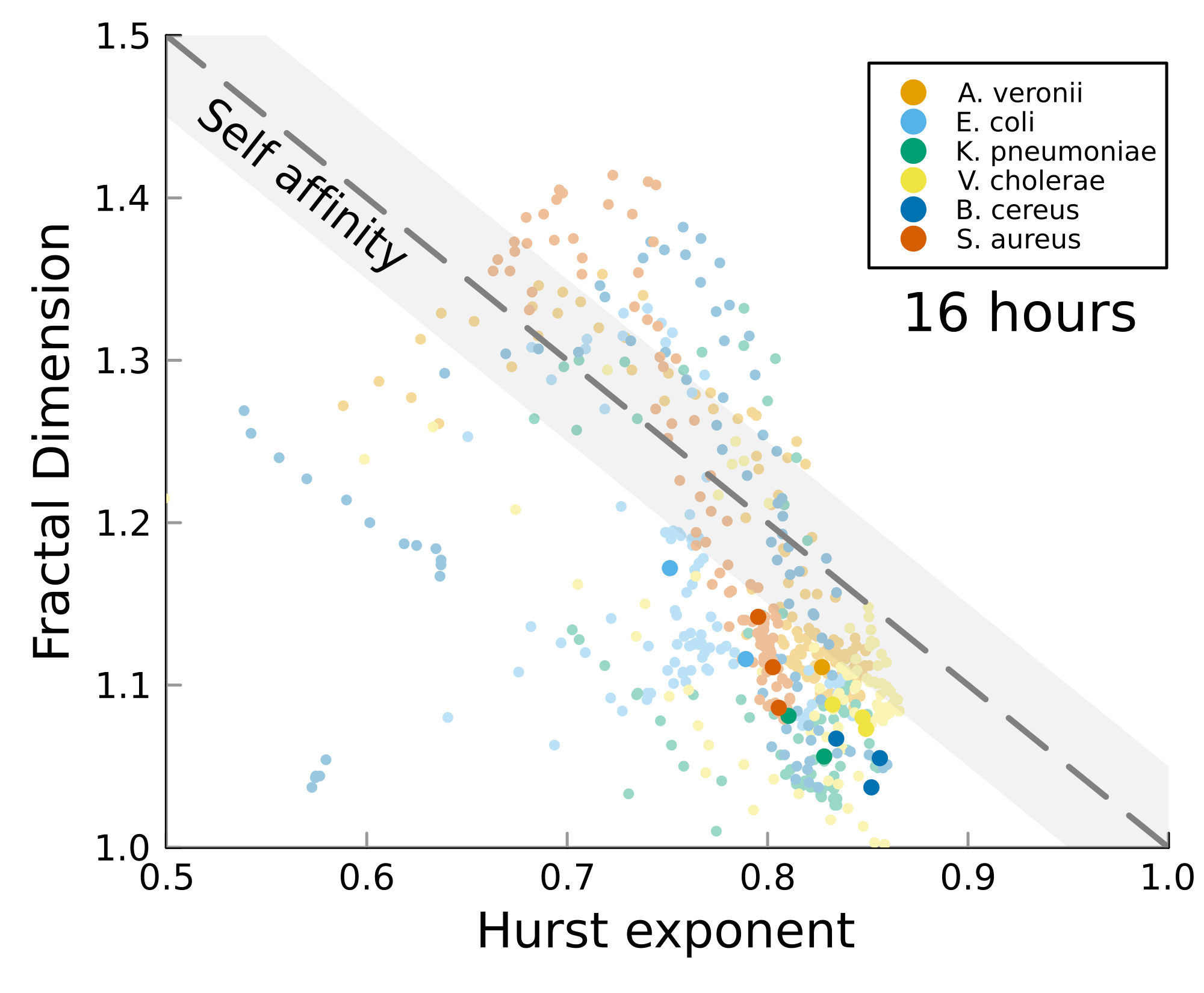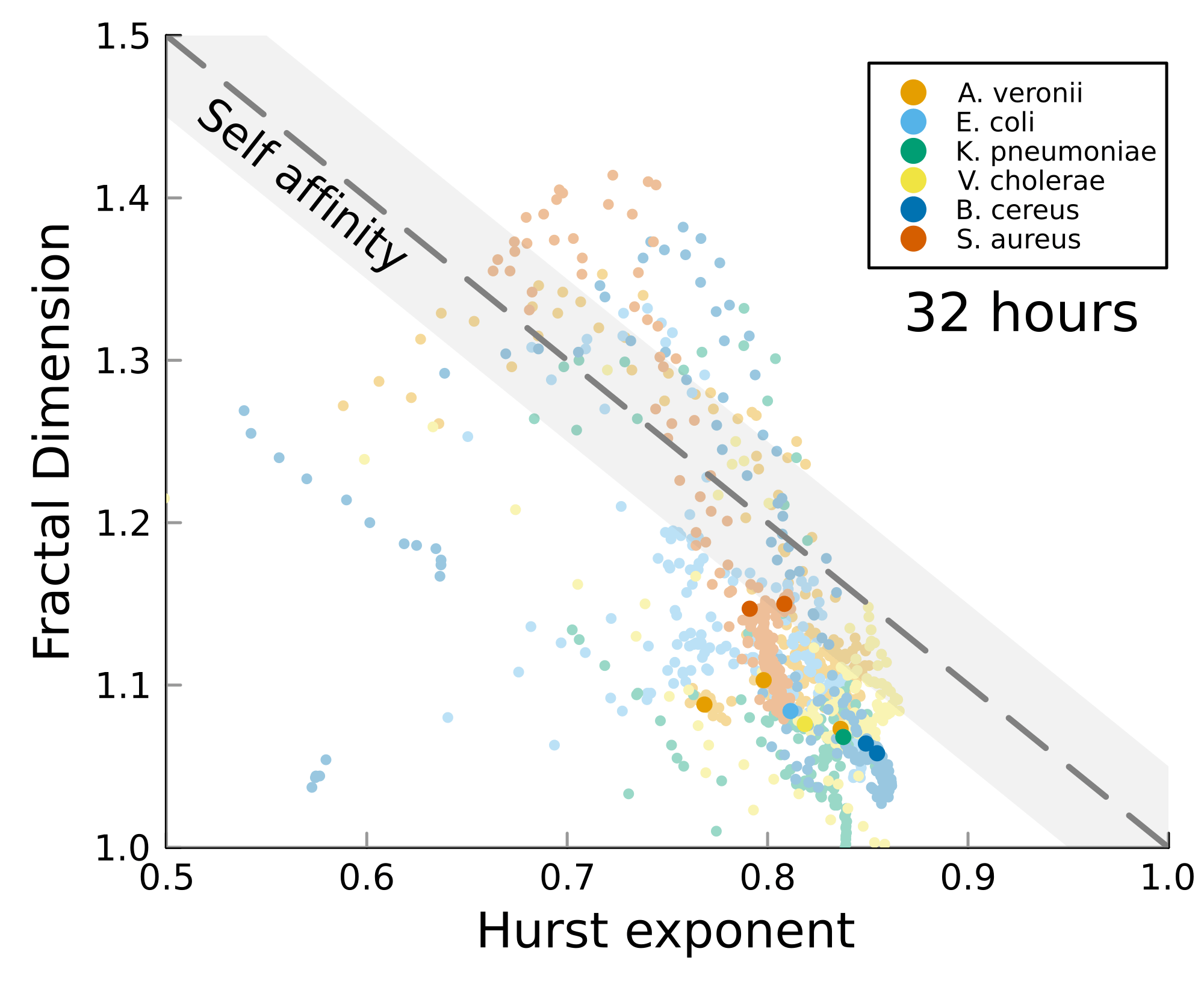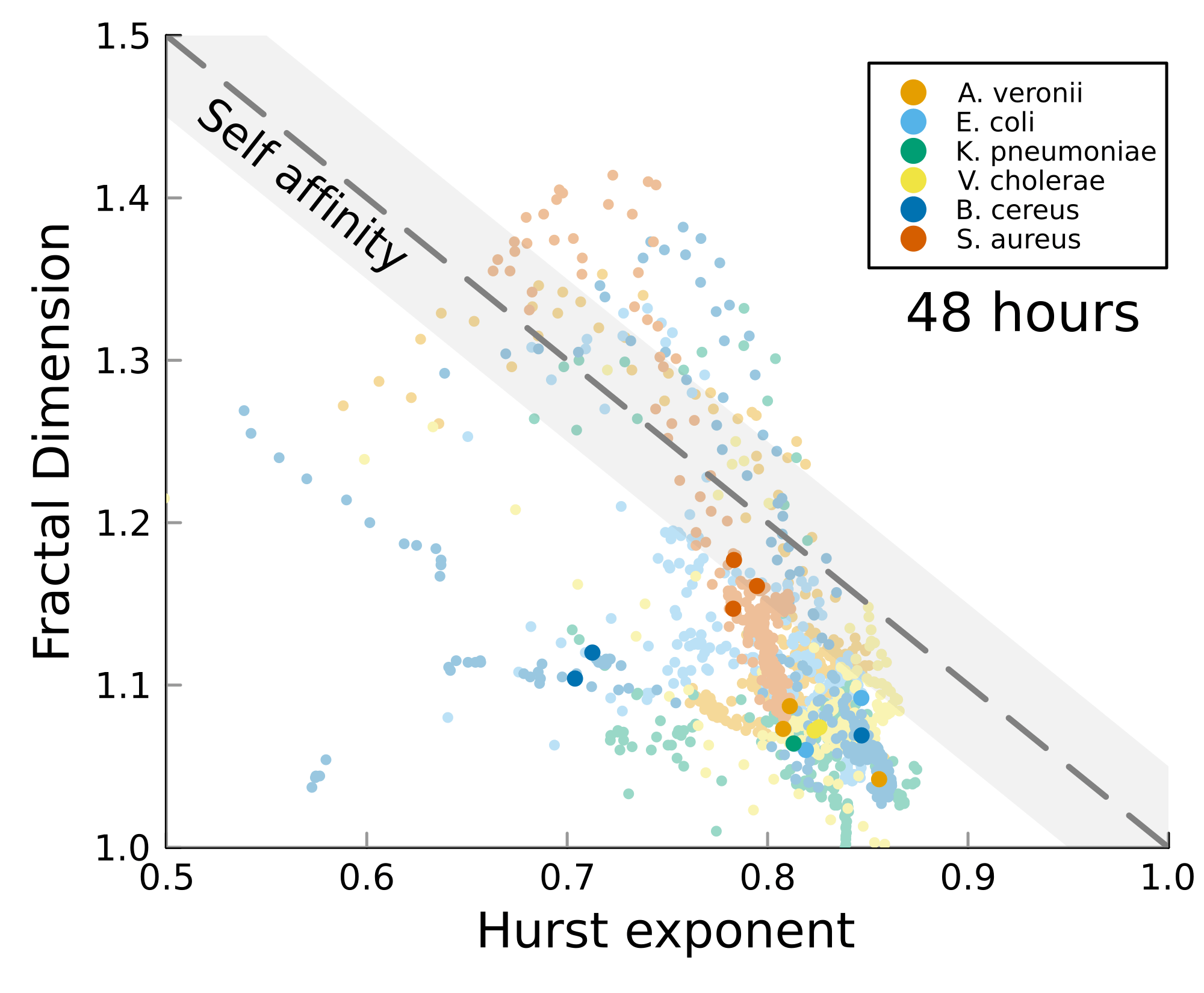
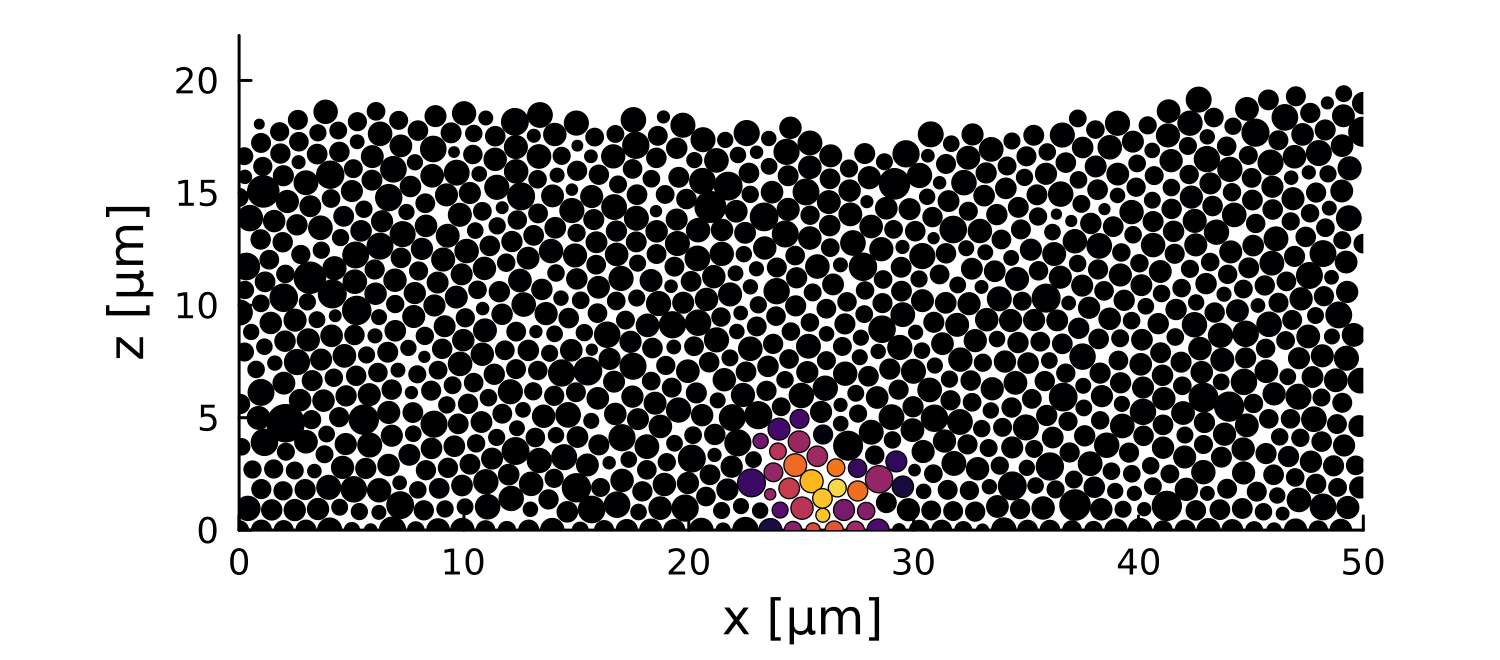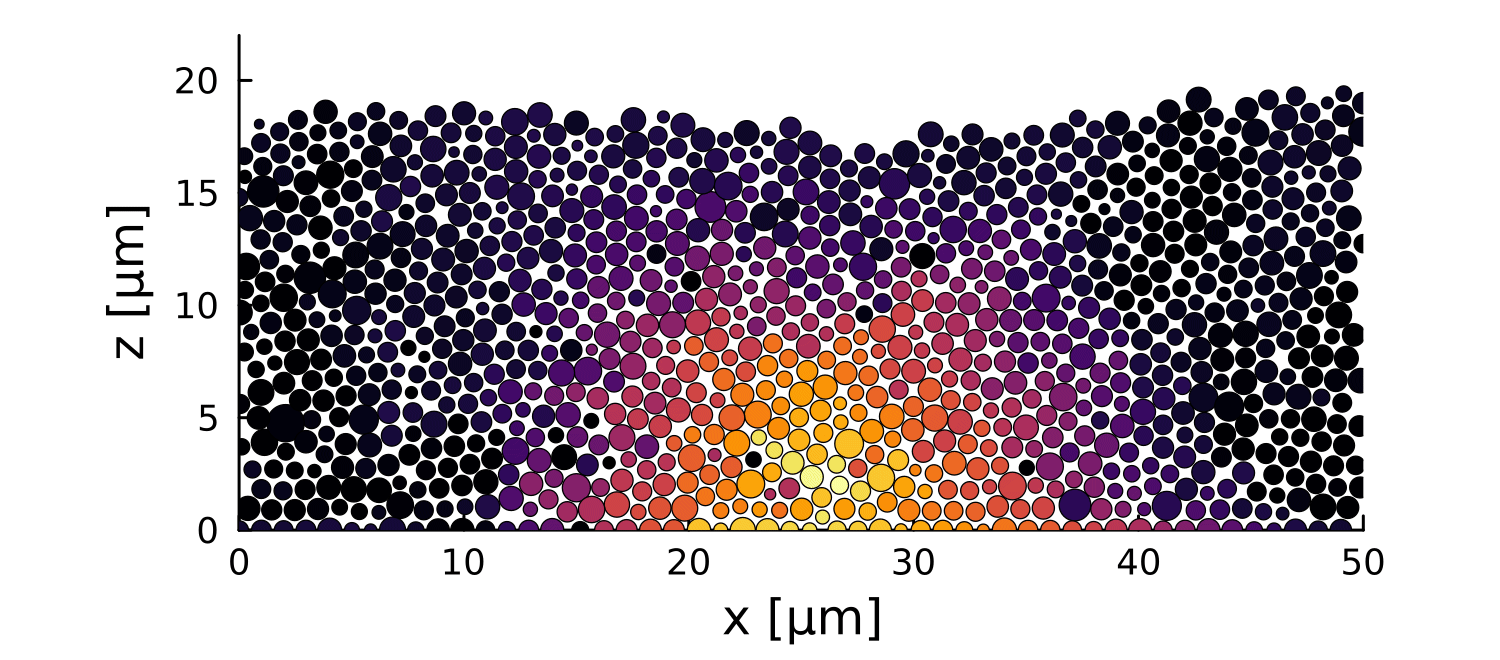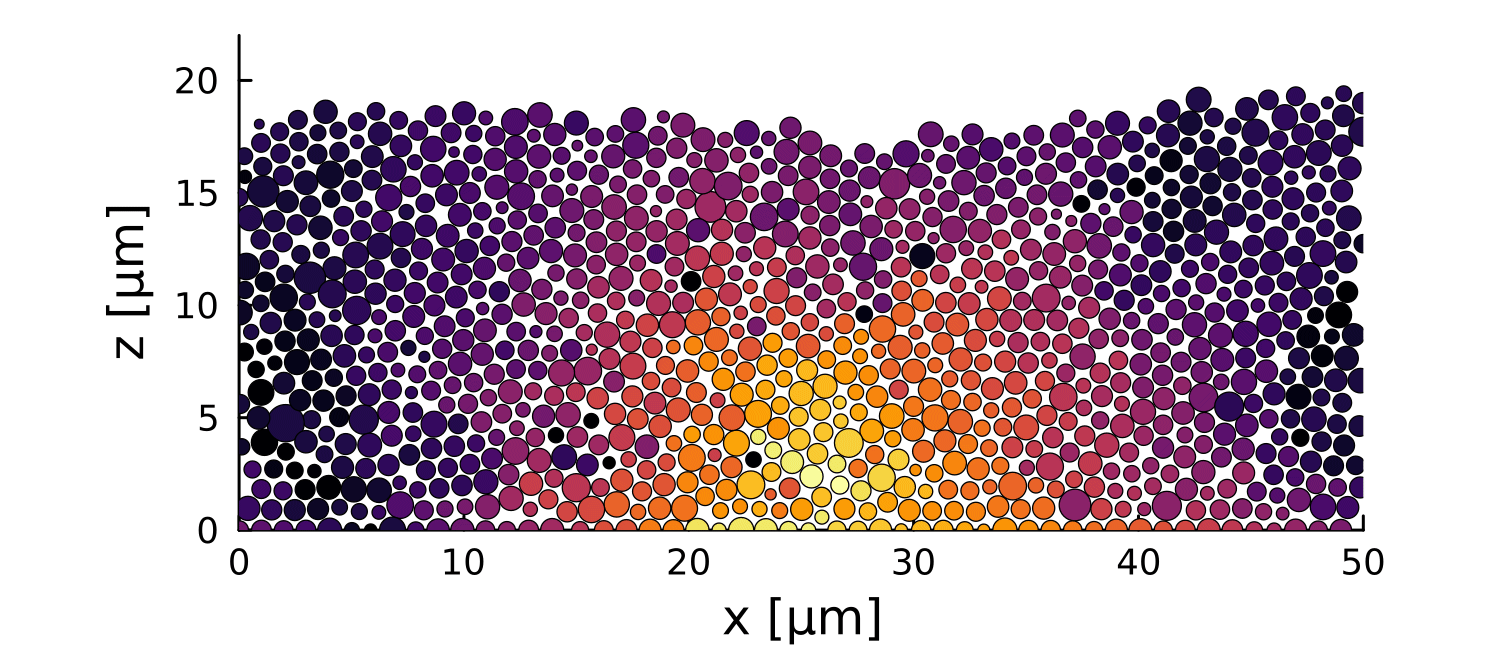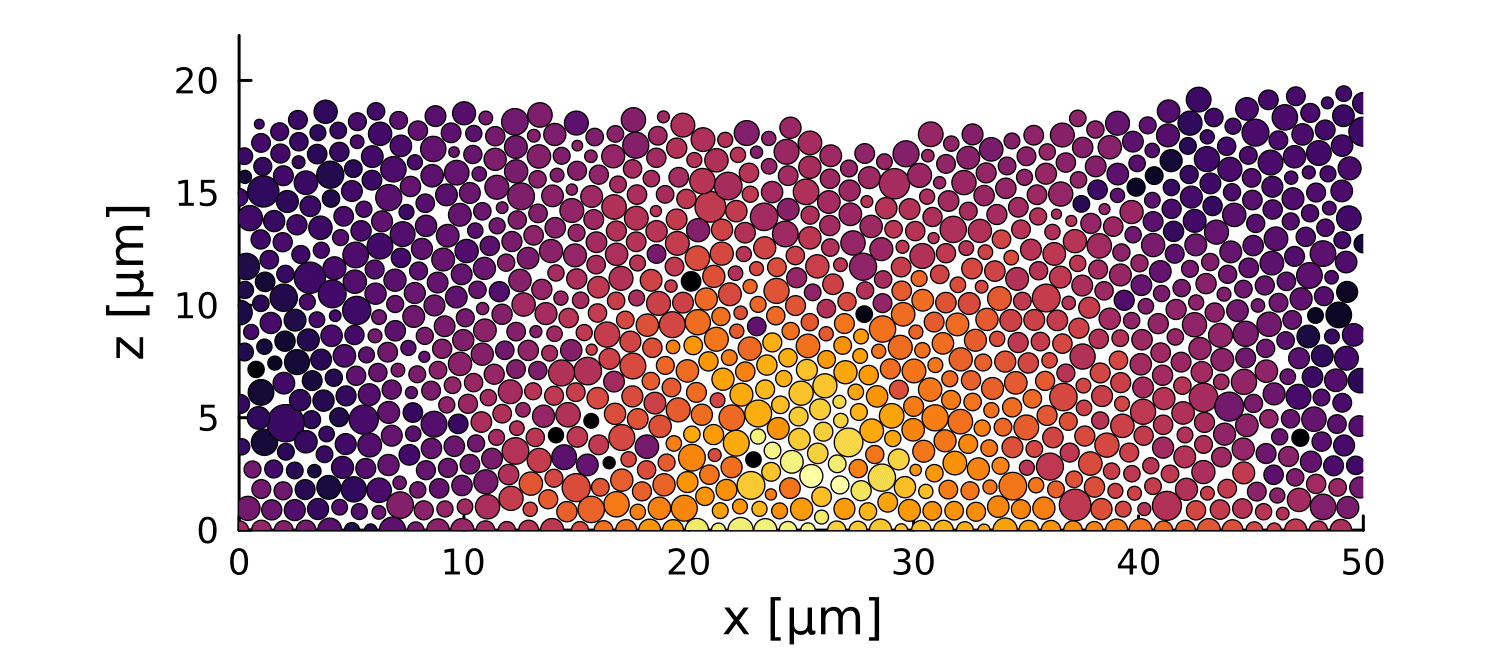
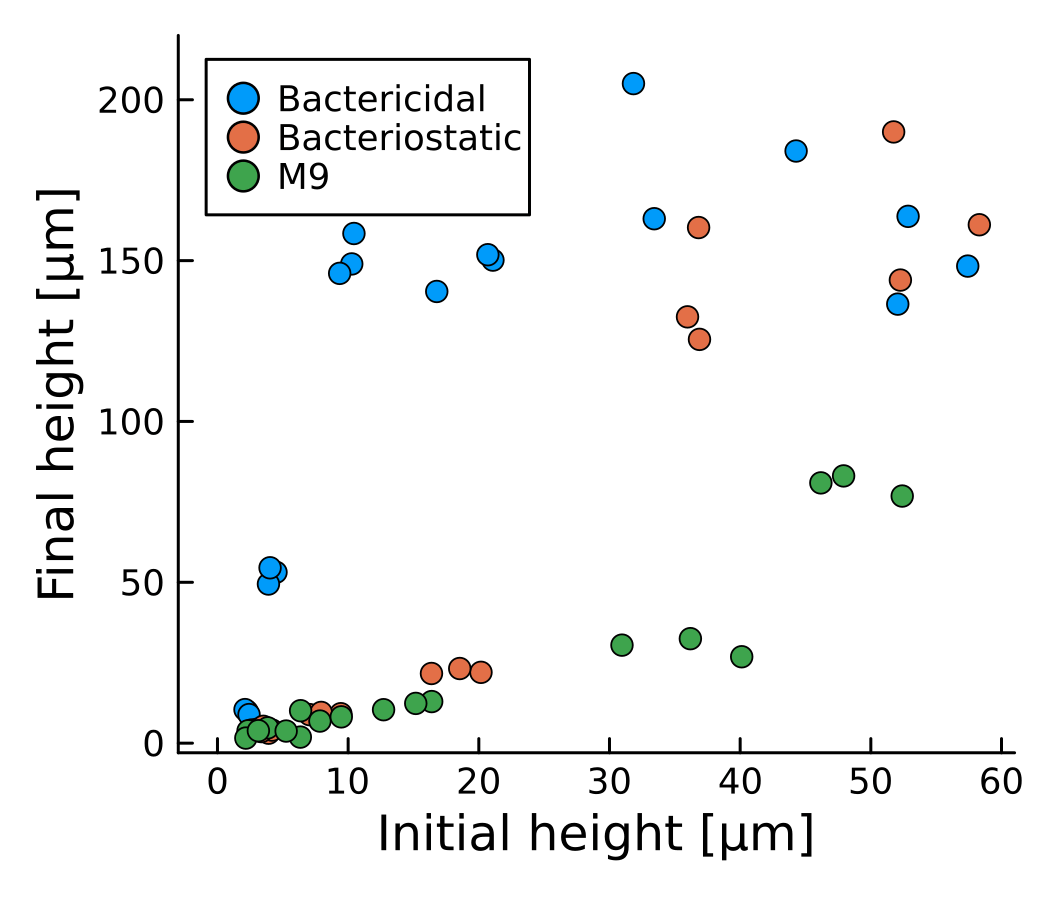
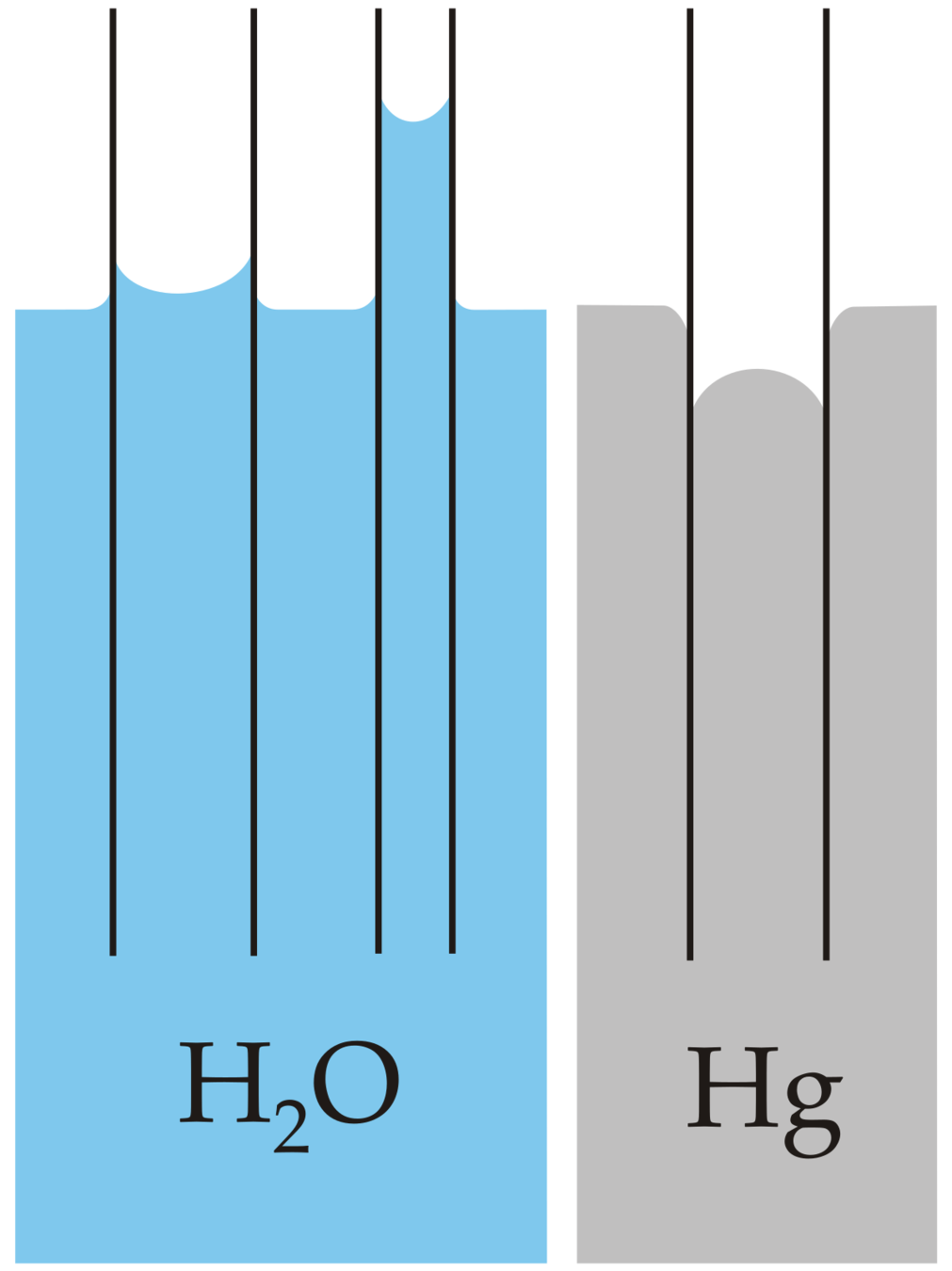
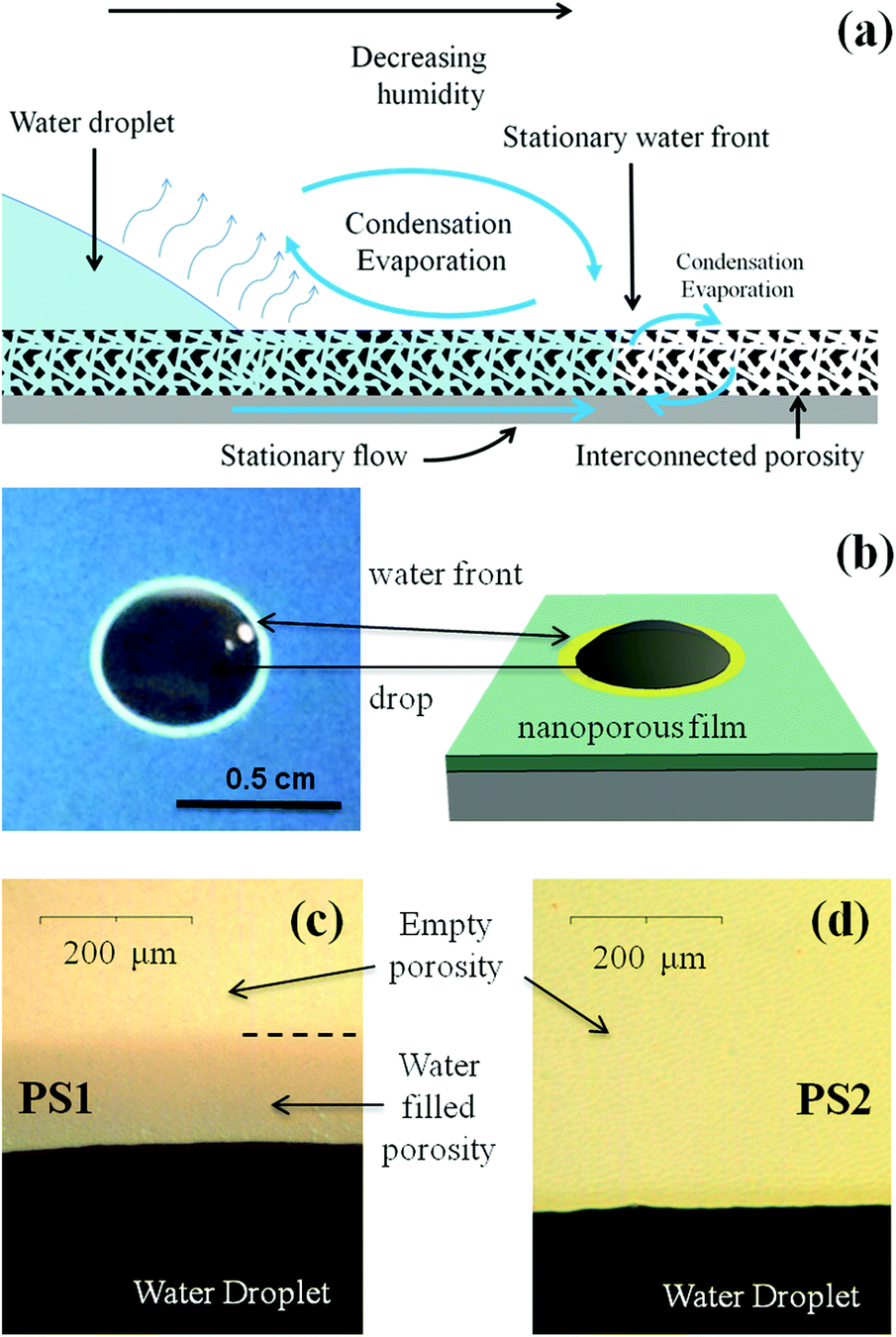
PhD Candidate in Quantitative Biosciences at GeorgiaTech. I am interested in biofilms, and how their topography evolves and what we could learn about their development by looking at them
characterization of
growth
Pablo Bravo
Topographic
biofilm
Quantitative Biosciences
PhD Defense
Outline
I. Biofilms and Interfaces
- Why and how to study
II. Vertical growth dynamics
III.Biofilm topographies
- How to measure vertical growth
- Behavior and clues
- Heuristic model
- Characterization
- Freezing
- Modeling
Biofilms are 3D structures
complex surface-attached
Surface
Interface
Cells
Extracellular matrix formed of polysaccharides, DNA, and proteins
Extracellular matrix formed of polysaccharides, DNA, and proteins
Surface
Interface
Cells
Biofilms are 3D structures
complex surface-attached
in the biofilm surface
\(1 cm\)
\(1 cm\)
Dietrich, L., et al. Journal of Bacteriology (2013)
Structures
Colonies in a laboratory setting
Each circle is a colony
Starting inoculums also exhibit the coffee ring effect!
Understanding vertical growth could provide insight in the developmental process
Visualizing Bacterial Colony Morphologies Using
Time-Lapse Imaging Chamber MOCHA
Peñil Cobo et al. 2017
cycle
The (expanded) biofilm
Sauer, K., et al. Nature Reviews Microbiology (2019)
Inside the biofilms: confocal/light-sheet
Hartmann, R., et al. Nature Microbiology (2021)
Images by Dr. Gabi Steinbach
Unprocessed
Processed
- How do aggregates grow?
- What are the underlying processes?
- Simple quantitative model?
Horizontal Growth
Growth
and accumulation
Morphologies and scaling of
advancing fronts
Matsuyama, T., et al. FEMS Microbiology Letters (1989)
Fujikawa, H. et al. JPSJ (1989)
Farrel, F.D.C., et al. Physical Review Letters (2013)
The same strain can exhibit different morphologies depending in the environment!
- Inside/outside interactions
- It is what we can see/measure
- Statistics
- Spatial and temporal information
- Toolbox and theories!
- Subject to material properties and activity
Why study interfaces?
Adkins, R., Kolvin, I., You, Z., et al. Science (2022)
Horizontal Growth
Vertical
Growth
Growth and accumulation
- How do aggregates grow?
- What are the underlying processes?
- Simple quantitative model?
- Multiple light sources in the instrument
- Super-resolution measurements
- Non-invasive
- No preparation needed
\( 0.5 mm\)
0
2
4
6
8
10
\(\Delta z\) (\( \mu m\))
Central region of a vibrio cholerae biofilm
Surface topography + intensity!
White-light interferometry
Biofilm topographies & Yunkerlab
Kalziqi, A., et al. PRL (2018)
Kalziqi, A., et al. ArXiv preprint (2019)
- Detect the amount of killing (T6SS)
- Viscosity through topography
- Rapid heteroresistance identification
Yan, J., et al. eLife (2019)
Outline
I. Biofilms and Interfaces
- Why and how to study
II. Vertical growth dynamics
III.Biofilm topographies
- How to measure vertical growth
- Behavior and clues
- Heuristic model
- Characterization
- Freezing
- Modeling
Using to measure
interferometry
biofilm growth
Homeland
Agar
Coffee Ring
Interferometry at the single-cell level
Surface topography and intensity from Interferometry
S. cerevisiae, 48 hours of growth.
Bravo 2022
Things didn't go quite well the first ~10 attempts
Hours
0
48
during bioflim growth
Two regimes
Two regimes in which vertical growth depends
linearly with the height of the colony
inside the colony
Nutrient dynamics
\(z\)
\frac{\partial c}{\partial t} = D \cdot \frac{\partial^2 c}{\partial z^2} - \lambda \cdot \frac{c}{k+c}
c(0, t) = c_0 \quad \quad \quad \dot{c}(h, t) = 0
Concentration in the substrate
No flux in the top
Region where cells can grow is finite
\int_0^h \frac{c(z)}{k+c(z)}dz \approx \text{min}(h, L)
Total growth of a colony saturates once they reach a critical length \(L\)
Diffusion constant
Consumption rate
Monod constant
inside the colony
Nutrient dynamics
\(z\)
\frac{\partial c}{\partial t} = D \cdot \frac{\partial^2 c}{\partial z^2} - \lambda \cdot \frac{c}{k+c}
c(0, t) = c_0 \quad \quad \quad \dot{c}(h, t) = 0
Concentration in the substrate
No flux in the top
Region where cells can grow is finite
\int_0^h \frac{c(z)}{k+c(z)}dz \approx \text{min}(h, L)
Total growth of a colony saturates once they reach a critical length \(L\)
Consumption rate
Diffusion constant
Monod constant
2560
in the agar?
Nutrient depletion
Agar is not running out of nutrients!
Colonies must be slowing down for a different reason
for vertical
biofilm growth
Heuristic model
Empirical data + biophysical insight:
- Fits the dynamics across timescales
- Captures two growth regimes
- \(D, \lambda, k \rightarrow L\)
\frac{\partial h}{\partial t} = \alpha \cdot \text{min}(h, L) - \beta \cdot h\\
Diffusion length
Growth rate
Decay rate
Improving the \(\Delta h\) calculations
Clean set
Not-so clean set
Clean set
Not so clean set
Supplemental: pluses and minuses
\(\alpha h \)
\(- \beta h \)
\( -\alpha \frac{h^2}{K_h} \)
\(- \beta h \)
\(\alpha h\)
\(\alpha G(h, h^*) \)
\(^{****}\)
Why is the prediction lower?
h_{\text{max}} = \frac{\alpha \cdot L}{\beta}
Growth
Decay
Small overestimation of \(\beta\) can lead to underestimating \(h_{\text{max}}\)
Measuring for 48h is going to dry the plate a bit more, even if we try to minimize it
High-tech containment chamber for timelapse measurements.
Even if the prediction gets corrected with time, residual changes very little!
Do the make sense?
parameters
\frac{\partial c}{\partial t} = D \cdot \frac{\partial^2 c}{\partial z^2} - \lambda \cdot \frac{c}{k+c}
\(800 \mu m^2 \cdot s^{-1}\)
\(38 \mu M\)
\(1.3\cdot10^3 \mu M \cdot s ^{-1}\)
E. coli growing in agar -> limited by L-serine
Using literature parameters we obtain
\(L = 14.8 \mu m\)
And using the interface model
\(L = 14.3 \pm 1 \mu m\)
2560
Do the make sense?
parameters
\frac{\partial c}{\partial t} = D \cdot \frac{\partial^2 c}{\partial z^2} - \lambda \cdot \frac{c}{k+c}
\(800 \mu m^2 \cdot s^{-1}\)
\(38 \mu M\)
\(1.3\cdot10^3 \mu M \cdot s ^{-1}\)
E. coli growing in agar -> limited by L-serine
Using literature parameters we obtain
\(L = 14.8 \mu m\)
And using the interface model
\(L = 14.3 \pm 1 \mu m\)
1920
Bootstrapping growth curves
Get the best fit for each sampled dataset (1000x)
Original dataset
Why is the prediction lower?
\(h_{\text{max}}\) \( [\mu m]\)
Bootstrapping on the 48h data we get distributions
\(\alpha\) \( [\mu m /hr]\)
\(\beta\) \( [\mu m /hr]\)
\(L\) \( [\mu m]\)
Aeromonas
Yeast (aa)
E. coli
48h fit
All fit
behavior
Long-time
- Measure colonies every 2 days
- Equilibrium in maximum height
-
Model height prediction:
\(h_{\text{max}} = \frac{\alpha L}{\beta}\)
-
Same behavior, different parameters
-
Good agreement even early!
Thinking about spatial dependence
Fit parameters \(\alpha, \beta, h^*\) to each trajectory
\( h_{\text{max}} = \frac{\alpha h^*}{\beta} \)
Merger initial conditions
Initial configuration is experimental (Gabi), except tweaking 0's and negative numbers.
in vertical growth
Universality
Experiments across a large cohort of microbes
- Bacteria and fungi
- Gram + and -
- Different shapes
- Different EPS production
- Novel measurements of vertical growth.
- Heuristic model that captures dynamics accurately
Summary
Modeling in 3D Yeast clusters
Shape of biofilms, and biofilm edge
Biofilm Topography
Outline
I. Biofilms and Interfaces
- Why and how to study
II. Vertical growth dynamics
III.Biofilm topographies
- How to measure vertical growth
- Behavior and clues
- Heuristic model
- Characterization
- Freezing
- Modeling
What is ?
Profiles are flat. A few cells in amplitude, over thousands of micrometers!
\(500 \mu m\)
biofilm topography
Using white-light interferometry, we can capture the profiles of a growing colonies for extended periods of time
Subtracting from the homeland?
- Width of perpendicular fluctuations in the height profile:
w_l(\mathbf{r}, t) = \langle (h (\mathbf{r}, t) - \langle h(\mathbf{r}, t) \rangle_l )^2 \rangle_l^{1/2}
\(\alpha\)
II. Quantifying fluctuations
Self similar systems link the fractal dimension \(FD\) and roughness \(\alpha\) with:
FD + \alpha = n + 1
Fractal Dimension FD
Measure of how complexity changes with scale
Surface roughness \(\alpha\)
are different between strains
Staphylococcus aureus
Bacillus cereus
Eschericia coli
- What is leading to the differences between profiles?
- How do we characterize the dynamics?
- Why does the topography freeze in later alligators?
\(2 mm\)
\(8 \mu m\)
Time since inoculation [hours]
\(0\)
\(24\)
\(48\)
Fluctuation dynamics
Fluctuations can
Aeromonas veronii
Eschericia coli
or
relax
increase
Timelapses of fluctuations
For visualization purposes, is it okay to interpolate?
Measurement time is not constant
Biofilm topographies are
smooth
Magnitude of fluctuations goes from 10%, to 0.1-1%!
Stainless steel (UL)
B
A
Are fluctuations ?
\(10^4\)
\(10^3\)
\(10^2\)
\(10^1\)
scale-free
Wavelengths of \(\lambda = L/2\) were removed in each step
\(S(k, t) \sim k^{-\nu}\)
- PSD exhibits \(1/f\) spectra
- Self organized criticality
- Observed in vacuum tubes, human hearts, brain activity, musical concertos.
at 40 hours of growth
\(S(k) [\mu m^4]\)
\(k [\mu m^{-1}]\)
PSD
Testing again
self-affinity
We can test self-affinity using the fractal dimension \(D\)
\(D + H = 2\)
\(D + H = n +1\), where \(n\) is the base dimension of the system
Topography dynamics as a consequence of growth through a viscoelastic material:
- Reach SA while growth is fast
- Relax when the colony is tall, and fluctuations get damped
- Width of perpendicular fluctuations in the height profile:
- With a roughness/Hurst scaling exponent \(\alpha, H\):
- And a growth exponent \(\beta\):
w_{\ell}(\mathbf{r}, t) = \langle (h (\mathbf{r}, t) - \langle h(\mathbf{r}, t) \rangle_{\ell} )^2 \rangle_{\ell}^{1/2}
\(w_{\ell}(t) \propto \ell^{H} \)
fluctuations
Dervaux, et al. 2014
Martinez-Calvo and Bhattacharjee, et al. 2022
\(H\)
\({\ell}_{\text{sat}}\)
\(w_{\text{sat}}\)
Quantifying
\( {\ell}\)
\( {\ell}\)
w_{\text{sat}}(t) \sim \begin{cases}
t^{\beta} & \text{for } t < t_{\times}\\
\text{constant} & \text{for } t > t_{\times}
\end{cases}
Filters, Fourier, and boundaries
- Boundaries are tricky
- Assumptions in Poly 2, or use more 'fancy' algorithms?
Butterworth \(\lambda = 500 \mu m\)
This worries me a little!
Spatial scaling:
Roughness stabilizes at \(H \sim 0.8\).
Biofilm interfaces, have been characterized at \(0.6-0.78\)
roughening
\(w_{\ell}(t) \propto \ell^{H} \)
\( {\ell}\)
\( {\ell}\)
| Paper | Roughness | ||
|---|---|---|---|
| On growth and form of Bacillus subtilis biofilms | ~2 | ~1.5 | 0.5-0.7 |
| Morphological instability and roughening of growing 3D bacterial colonies | ~1.5 | ~1 | 0.67 |
| Yunkerlab-Interferometry | ~3 | ~2.5 | 0.74-0.84 |
Sampling ranges in \(w_{loc}\) estimation
\(N_x\)
\(N_y\)
On growth and form of Bacillus subtilis biofilms
- Interpolated from fluorescence
- 0-10 hours
Dervaux, et al. 2014
- Local width
- Surface roughening
Morphological instability and roughening of growing 3D bacterial colonies
Martinez-Calvo and Bhattacharjee, et al. 2022
- Grown in 3D
- 0-97 hours
- Power spectral density
- 0-97 hours
Temporal scaling:
Saturation width decreases!
Something different
is happening after \(t_{\times}\)
saturation?
w_{\text{sat}}(t) \sim \begin{cases}
t^{\beta} & \text{for } t < t_{\times},\\
\text{constant} & \text{for } t > t_{\times}
\end{cases}
Scaling exponent varies between species and replicates
I
II
Topography
freezing
- Two interface stages:
- Active
- Frozen
- Qualitative behavior in all interfaces.
- No traveling waves
- Correlation length \(\xi\) increases slowly with time \(t\)
biofilm topographies
0
0.3
\(\Delta \vec{r}\) \([\mu m]\)
-4
-0.5
\(\log\Delta \vec{r}\) \([\mu m]\)
Modeling
1 perturbation
10 perturbations
- 2D soft disks mechanically interacting
- Bounded at the bottom
- Periodic on the sides
- Distribution of sizes around r =0.5µm
- Let system relax before perturbation
- Introduce a growth perturbation
In small colonies, displacements can reach the interface
In large colonies, displacements get dissipated before reaching the interface
Local disruptions change the topography
Displacement is homogeneous
Quantifying
topography change
- Topography change decreases with relative perturbation distance
- Variance also scales with \(d\)
- Cell displacement decays exponentially with distance to the perturbation.
\(d_0 \sim 13 \mu m\)
Interface dynamics and
growth
- Fluctuations reach a maximum defined by \(w_{\text{sat}}\)
- Growth saturates when colony reaches critical length \(L\)
- Strong correlation between fluctuation and growth dynamics
- Every additional layer, is a
damping element for fluctuations.
Outline
I. Biofilms and Interfaces
- Why and how to study
II. Vertical growth dynamics
III.Biofilm topographies
- How to measure vertical growth
- Behavior and clues
- Heuristic model
- Characterization
- Freezing
- Modeling
Vertical growth dynamics under
stress
What determines the antibiotic susceptibility of a biofilm?
- Antibiotic concentration
- Exposure time
- Biofilm size
- Thresholds observed for bactericidal and bacteriostatic preliminary results!
- Unexpected dynamics observed in
large coloneis
Before - 24h
Before - 36h
After - Growth
After - Carb
Preliminary Results - Growth and stress in MH
- \(h_0\) of 90 and 120 μm
- Growth seems to saturate at ~220μm
- Saturation height is consistent with and without transfer
- Chloramphenicol seems to have little effect in growth
- Carbenicillin is increasing height significantly
Awesome People
Yunker Lab
Dr. Peter Yunker
Dr. Gabi Steinbach
Dr. Alireza Zamani
Dr. Thomas Day
Dr. Miles Wetherington
Aawaz Pokhrel
Adam Krueger
Emma Bingham
Raymond Copeland
Maryam Hejri
Tremond Thomas
Lin Zhao
Committee Members
Dr. Brian Hammer
Dr. Sam Brown
Dr. Jennifer Curtis
Dr. Itamar Kolvin
Hammer Lab
Dr. Siu Lung Ng
Kathryn MacGillvray
Christopher Zhang
Ratcliff Lab
Dr. Will Ratcliff
Dr. Tony Burnetti
Dr. Rozenn Pineau
QBioS
Dr. Joshua Weitz
Dr. Andreea Magalie
Dr. Conan Zhao
CMDI
Dr. Ellinor Alseth
POLS
Topographic characterization of biofilm growth
- Measured biofilm-air interfaces with high spatial and temporal resolution
- Proposed a simple model for vertical growth dynamics
- Link between growth and fluctuation dynamics through topography freezing
4x speed
10 \( \mu L \) inoculation
11 days
Playing it safe vs crazier research paths
Passive transport
Would grass follow the height dynamics?
NO!
Capillary action is passive transport!
1. Biofilms are not homoegenous
2. Could we make artificial channels?
QBioS PhD Defense
By Pablo Bravo
QBioS PhD Defense
Discover how white-light interferometry can measure biofilm growth, their 3D structures, dynamics, and topographies. Presentation made for the QBioS 4th year Seminar at GeorgiaTech.
