Computational challenges on small grids: a series of vignettes
Parker Rule
MGGG
December 2, 2020
Why study (small) (square) grids?
Pedagogical value (Gridlandia!)
At the limits of what we can exhaustively enumerate
Sometimes resembles actual states
Iowa counties
Wikipedia
Texas counties
Wikipedia, Texas Tribune
Fun fact: Constitution of 1876 requires counties to be arranged in a grid when possible!
Finding global optima
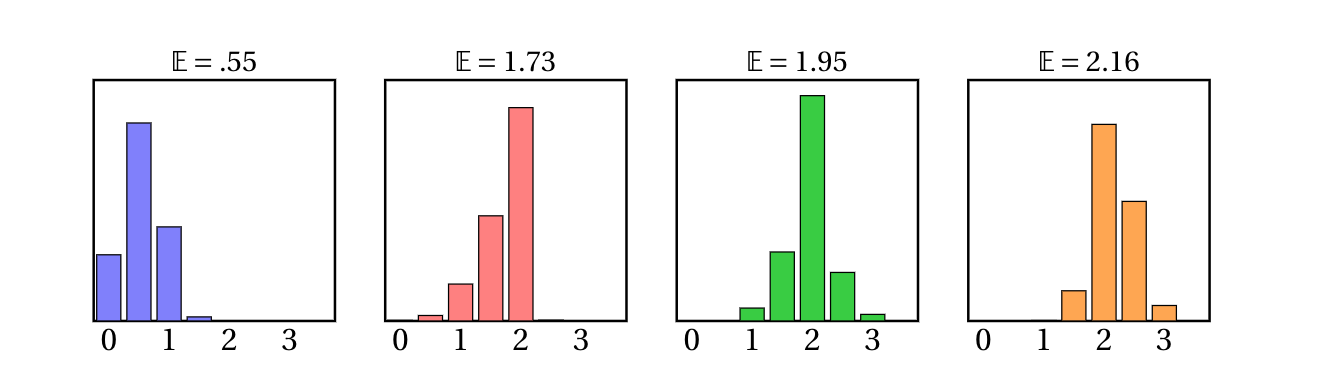
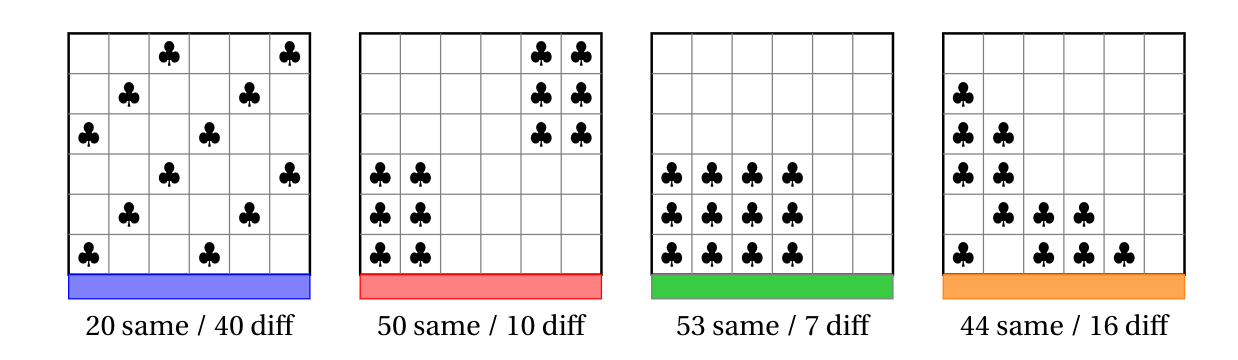
OptimalVotes.jl
Goal (6x6 grid → 6 districts, 12 club voters):
evaluate 1,251,677,700 vote distributions over 451,206 districtings
What is the best vote distribution for a party over all districtings?
What is the worst?
First-past-the-post voting introduces nonlinearities that make this problem hard.
Naively: 564,764,488,306,200 pairings
OptimalVotes.jl
Decompose districtings into polyominoes.
these are considered to be distinct.
OptimalVotes.jl
Approach (6x6 → 6):
Decompose ~450,000 districtings into ~2,500 polyominoes
Remove vote distributions that are redundant by symmetry
Compute all polyomino-vote distribution pairings to find best and worst expected seat shares
Solved in ~3 hours over hundreds of cores using Distributed.jl!
code: github.com/pjrule/OptimalVotes.jl
Approximation
Full enumeration is rather excessive.
(We did it for a very specific reason.)
In practice, the win probability of a polyomino can be estimated via (cheap) uniform sampling of vote distributions.
*Julia notebooks available upon request
Recall: the metagraph
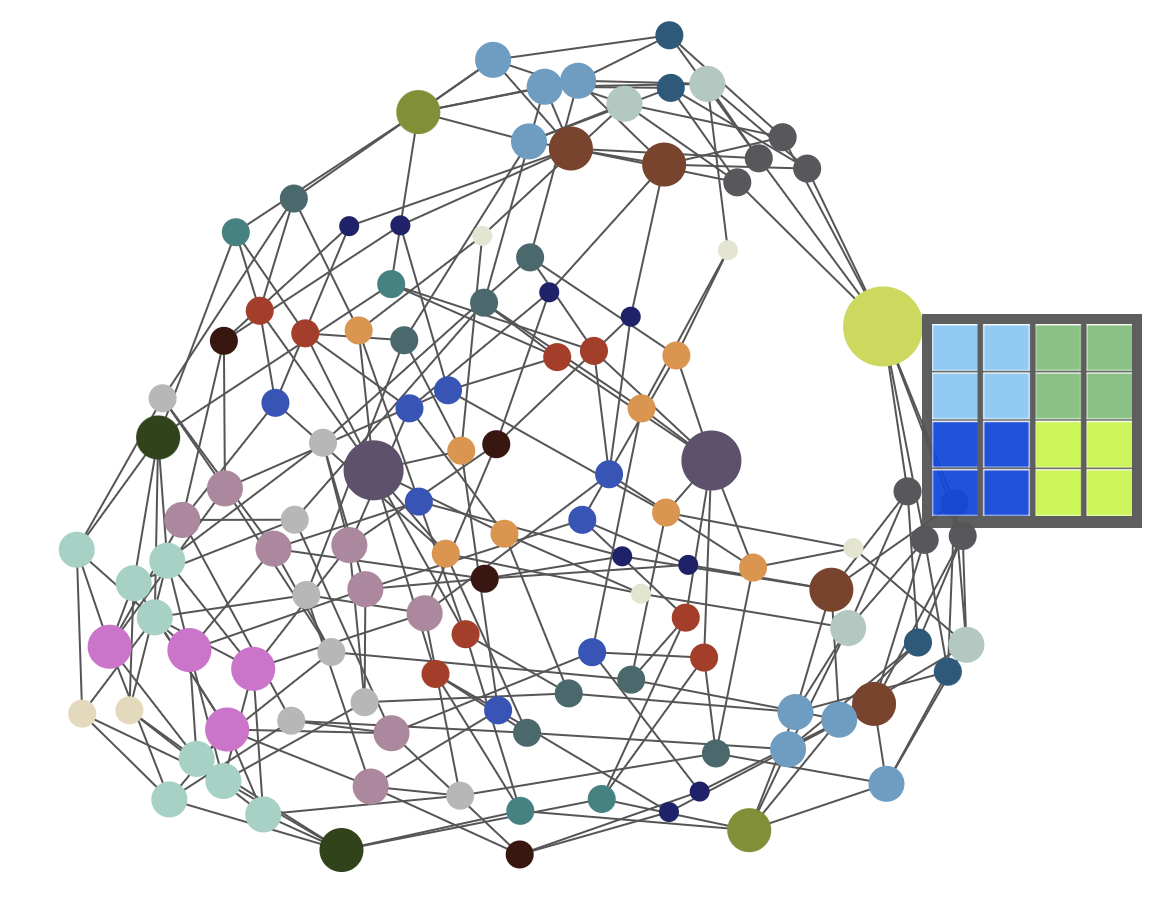
Two districting plans are adjacent in the ReCom metagraph if they are connected by a single ReCom step.
mggg.org/metagraph
7x7 → 7 metagraph
(in progress)
| Plans (nodes) | Edges | Min. degree | Max. degree | Diameter | |
|---|---|---|---|---|---|
| 2x2 → 2 | 2 | 1 | 1 | 1 | 1 |
| 3x3 → 3 | 10 | 16 | 3 | 4 | 3 |
| 4x4 → 4 | 117 | 372 | 4 | 12 | 6 |
| 5x5 → 5 | 4,006 | 23,716 | 2 | 21 | 10 |
| 6x6 → 6 | 451,206 | 4,995,543 | 5 | 87 | 12 |
| 7x7 → 7 | 158,753,814 | ? | ? | ? | ? |
not ∞, so connected
read: degree = number of neighbors
7x7 → 7 metagraph
(in progress)
Computational challenge: representing the plans alone requires several gigabytes of space (hard to store in memory)
Map/reduce architecture?
Could we do 8x8 → 8?
Know: 158,753,814 plans for 7x7 → 7
Know: 187,497,290,034 plans for 8x8 → 8
(~3 orders of magnitude)
Not outside the realm of possibility if we really wanted to (but why?)
New ZDD methods are thought to speed up enumeration (but may be hard to parallelize)
Connectedness, reconfiguration, and canonicalization
Conjecture: all balanced NxN → N partitions are ReCom-connected.
We know: the space of balanced NxN → N partitions is ReCom-connected. (N ≤ 6)
Question: is there a polynomial-time algorithm to reconfigure any plan into a canonical configuration
(e.g. vertical strips)?
(This type of question is challenging: for instance, we have tried and failed to produce a non-computational proof for the 6x6 → 3 case.)
Connectedness, reconfiguration, and canonicalization
Spanning tree calculator
Small grids
By Parker Rule
Small grids
- 572



