Uni Maths

Taster

Dr. Paul Johnson

Paul

• Topology: what's leftover from Geometry if can't measure distance or angles
• Graph Theory: Studying how "things" are "connected"

Studying "Shapes"

Fun and useful

Topology Joke

Henry Segerman

Videogames

Surface:

Locally looks 2-dimensional

Text

Manifold: 

Locally looks n-dimensional

 What n-dimensional manifolds are there?

How can we tell different manifolds apart?

What manifold do we live in?

Cosmic Microwave Background

Could they have made their videogame world a sphere?  

QUESTION 1:

QUESTION 2: Utilities

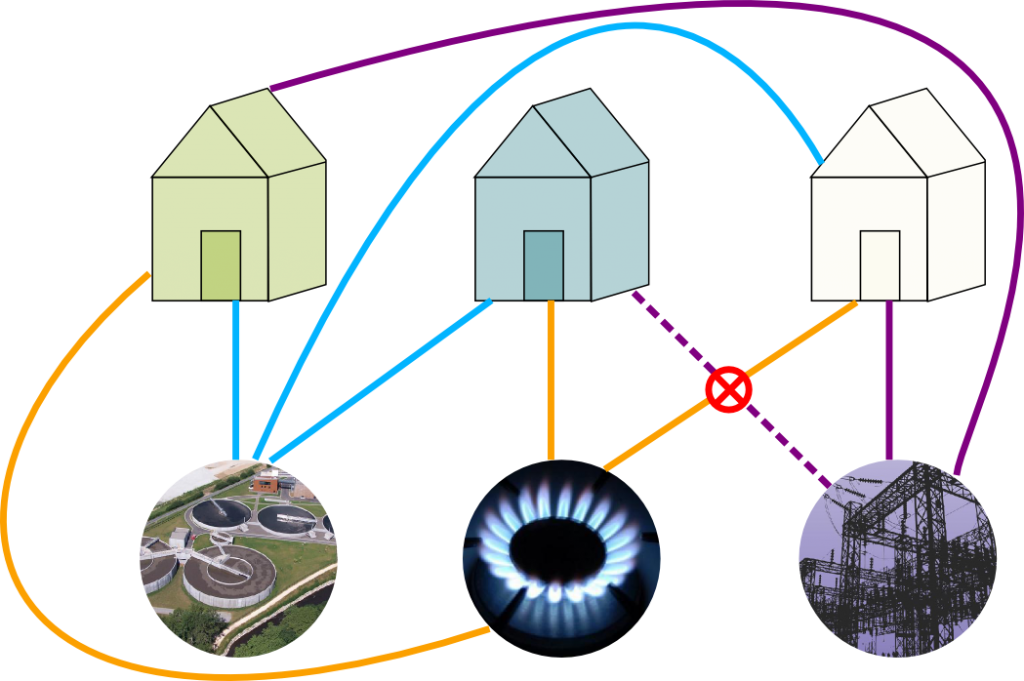
A failed attempt

Utilities question is impossible

But how can we know for sure?

How can we prove it?

Can we check every single possible way of connecting them, or are there infinite many different possibilities to try?

If it were possible, some connections would make a loop.

That loop would have an inside and an outside...

What connections are missing?

What if we were on the torus?

Graphs:

• Vertices: A set of "things"
• Edges: A set of "connections" between pairs of things

Text

"Epidemic dynamics on higher-dimensional small world networks"

The same graph, drawn different ways

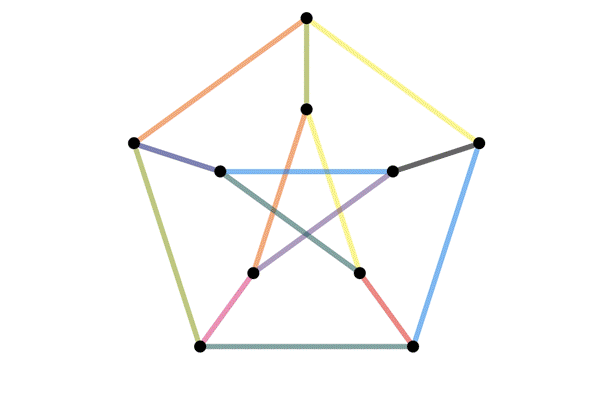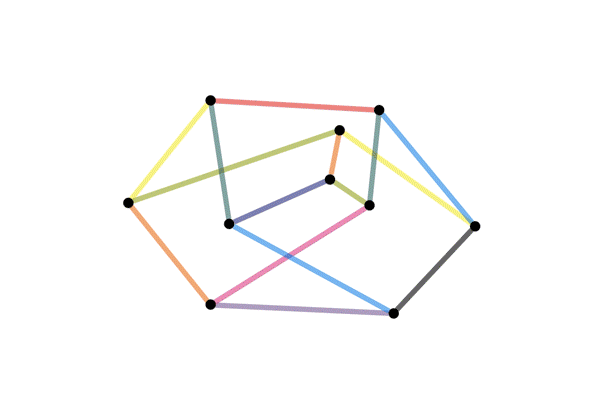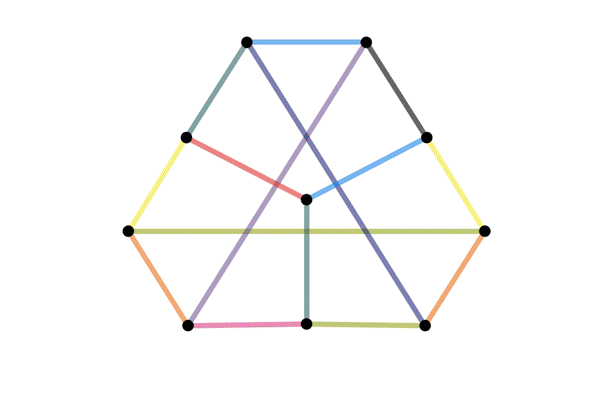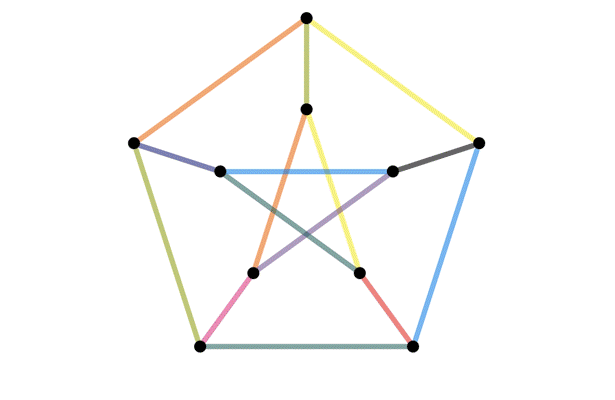
Definition: A graph is planar if it can be drawn on a piece of paper without any edges crossing.

Definition: The complete graph on n vertices, written K_n, is the graph with n vertices, and an edge between every pair of vertices

Definition: The complete bipartite graph K_{n,m} has n red vertices, m blue vertices, and an edge between every red vertex and every blue vertex.

Utilities Question: Is K_{3,3} planar?

What about other graphs?

If a graph is drawn on a plane, cuts the plane up into pieces called faces.

Graph      Vertices     Edges     Faces

Cube

Tetrahedron

Octahedron

Square Pyramid

Your Example

Notice any patterns?

The n-cycle C_n

Euler's Theorem

For any graph G drawn on the plane, we have:

E-V+F=2

A videogame graph will have V-E+F=0

Video game graph:

• Every vertex has four edges
• Every face has four edges

Locally, it looks like a grid: