Impossible Worlds

Videogames, topology and combinatorics

Topology "=" Shapes

Combinatorics "=" Counting

Topology Joke

Henry Segerman

Videogames

Surface:

Locally looks 2-dimensional

Manifold: 

Locally looks n-dimensional

Could they have made their videogame world a sphere?  

Naive Question:

Refining the question

Videogame assumptions:

1. Every region is a square
2. Four regions meet at each point

New claim: we can't cut there sphere up so that properties 1+2 hold

We can cut the sphere into pieces:

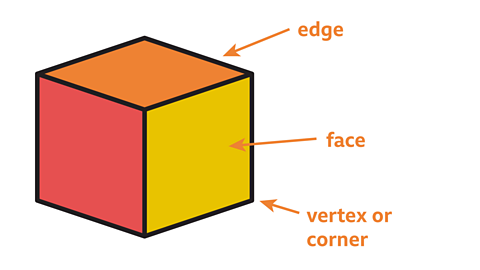
What can we say about the number of vertices, edges and faces in a decomposition of the sphere? 

Euler's Theorem:

Consider a connected graph drawn on the sphere, with v vertices, e edges, and f faces. Then :

v-e+f=2

To a new vertex:

Between existing vertices

• v increases by 1
• e increases by 1
• f remains unchanged

• v remains unchanged
• e increases by 1
• f increases by 1

Proof idea: Keep adding edges.

v-e+f doesn't change!

Return to the Torus Planet:

To show the designers couldn't have made a sphere, it's enough to prove their maps couldn't have v-e+f=2.

Need relations between v, e and f...

Count red arrows two ways

1. Every vertex has four arrows

2. Every edge has two arrows

So for a videogame graph,  4v=2e

Similar argument show that for a video game graph we have: 4f=2e

So 2v=e=2f

So v-e+f=v-2v+v=0

Violates Euler's Theorem!

Can finish our proof!

Homework: