K-Functions on Fibers
Joint work with
Hans Stephensen, Jon Sporring and Stefan sommer (DIKU)
Anne-Marie Svane and Rasmus Waagepetersen (AAU)
Stine Hasselholt (AU)
Content of talk
- Introduce point processes and Ripley's K-function
- Shape valued processes
- Currents metric and fiber K-function
- Result on myelin fibers

Point processes
A point process \(X\) on a metric space \(S\) is a measurable map from some probability space \((\Omega, F, P )\) into the space of locally finite subsets of \( S\).
Usually \( S= \mathbb R^n \)
Ripley's K-function for point processes \(X\) on \(\mathbb R^n\) is defined by
\(K(r) = \frac{1}{\lambda}\) E[ #events within distance r from point]
where \(\lambda \) is the density (number per unit area) of events.
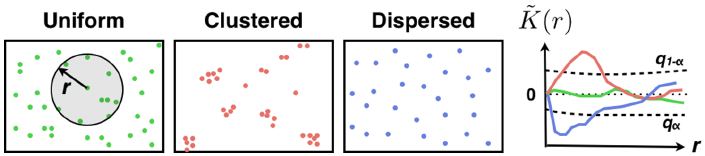
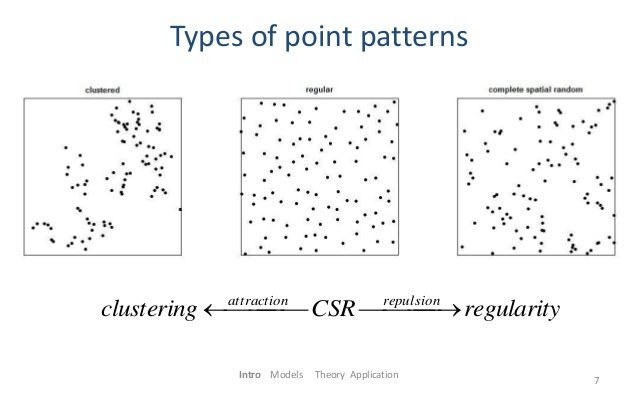
Ripley’s K-function is a well-known statistical tool for
- analyzing second order moment
structure of point processes - measuring deviance from complete
spatial randomness in point sets.
Ripley's K-function
Ripley’s K-function is a well-known statistical tool for
- analyzing second order moment
structure of point processes - measuring deviance from complete
spatial randomness in point sets.
Ripley's K-function
\(r\)
\( K(r)\)

Goal
Define a k-function for point processes where every point is a shape, for example fibers in \( \mathbb R^3\)
Issues
- Distance measure
- Well posed K-function
- Uniform shape process
Space of Currents
A piece-wise smooth curve \( \gamma \) is characterized by the path-integral over vector fields \(w\)
where \( \tau(x) \) is the tangent of \( \gamma \) at \(x\).
\(V_\gamma(w) = \int_\gamma w(x)^t\tau(x)d \lambda(x) \)
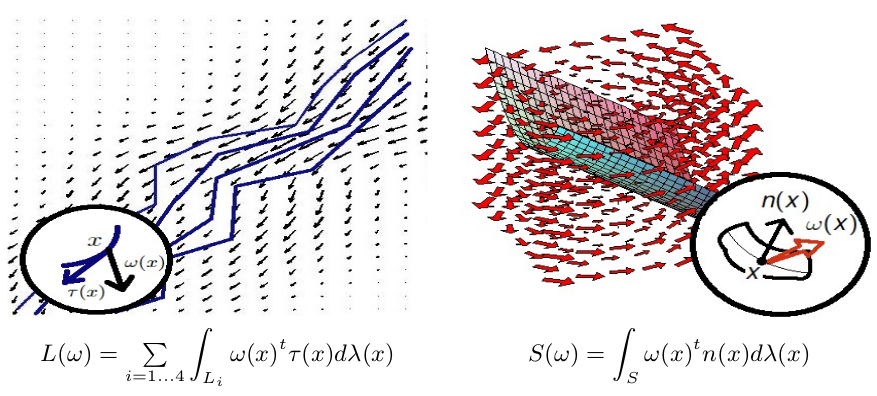
Thus, we can think of \( \gamma \) as a functional
\(V_\gamma\in W^* = \{ f:W\to \mathbb R | \text{linear and cont} \}. \)
This representation is called a current and formally the space of \(m\)-currents is the dual space of the differential \(m\)-forms.
By considering W as a RKHS, we get the inner product on \(W^*\)
\( \langle V_{\gamma_1}, V_{\gamma_2} \rangle = \int_{\gamma_1}\int_{\gamma_2} \tau_{\gamma_1}(x)^tK(x,y) \tau_{\gamma_2}(x) d\lambda(x)\lambda(y) \)
where \(K\) is the kernel of \(W\) and the induced distance measure
\( d_c(V_{\gamma_1}, V_{\gamma_2}) = ||V_{\gamma_1} - V_{\gamma_2} || \)
Space of Currents
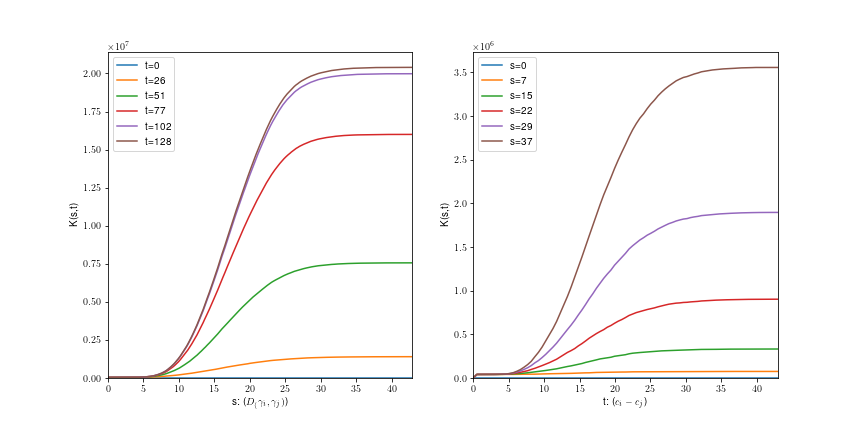
The K-function for fiber processes \(X\) observed in window \( W\) is
where c(.) denotes center point of curve, \(\nu(S_0) \) measure on centered curves and \( |W| \) size of window.
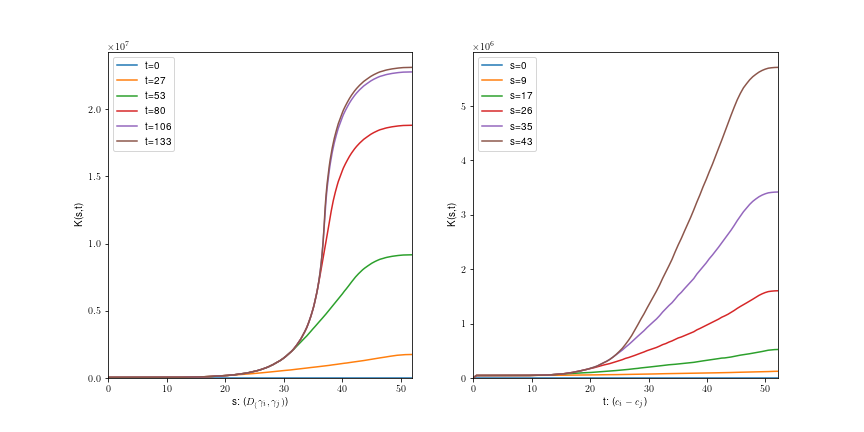
The K-function
- \( s \) shape parameter
- \(t\) spatial parameter
\( K(s,t) = \frac{1}{|W|\nu(S_0)} \sum \sum 1[||c(\gamma)-c(\gamma')|| \leq t, d_c(\gamma,\gamma')\leq s]\)
\( \gamma\in X:c(\gamma)\in W\)
\( \gamma' \neq \gamma \in X \)
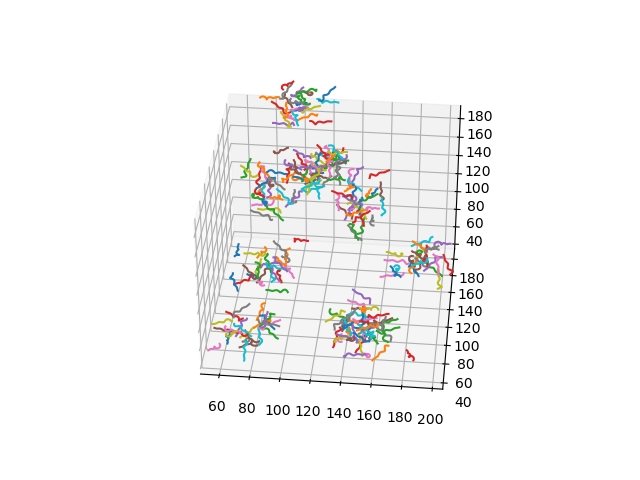
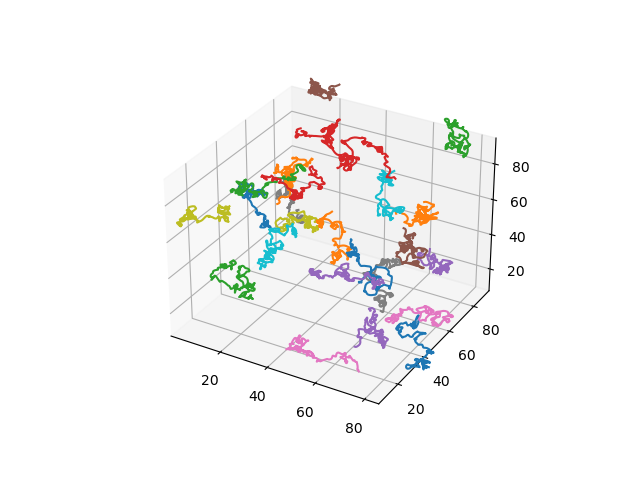
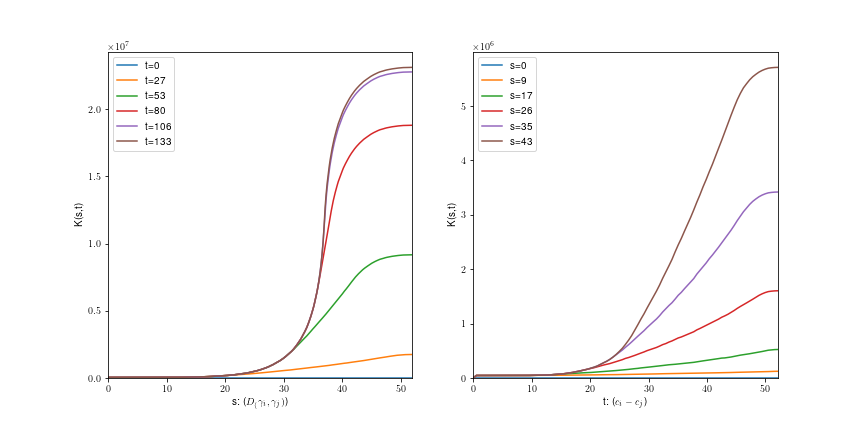
Uniform shape process
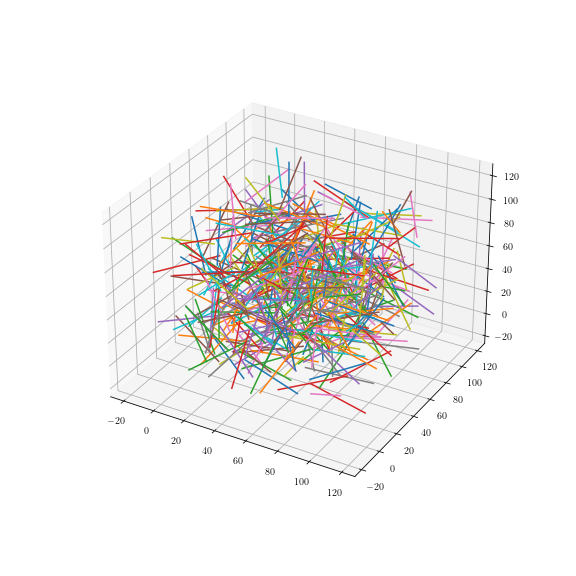
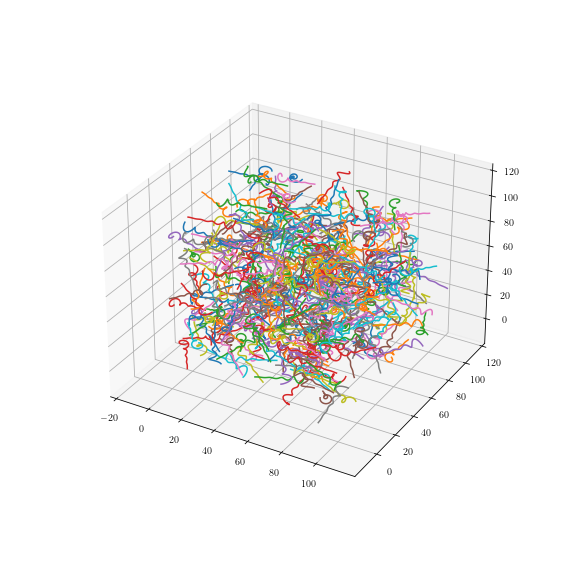
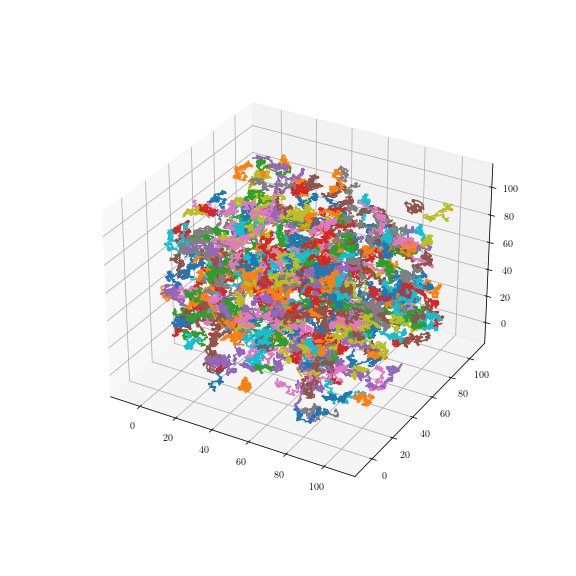
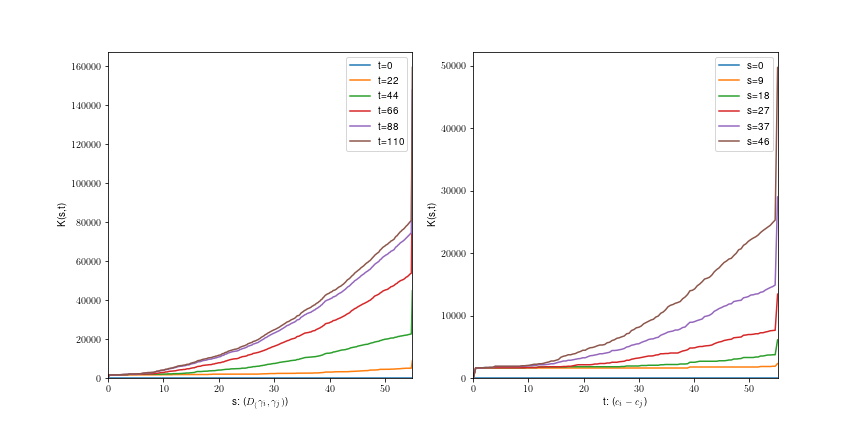
Uniformly
rotated lines:
Uniformly
rotated spirals:
Brownian motions:
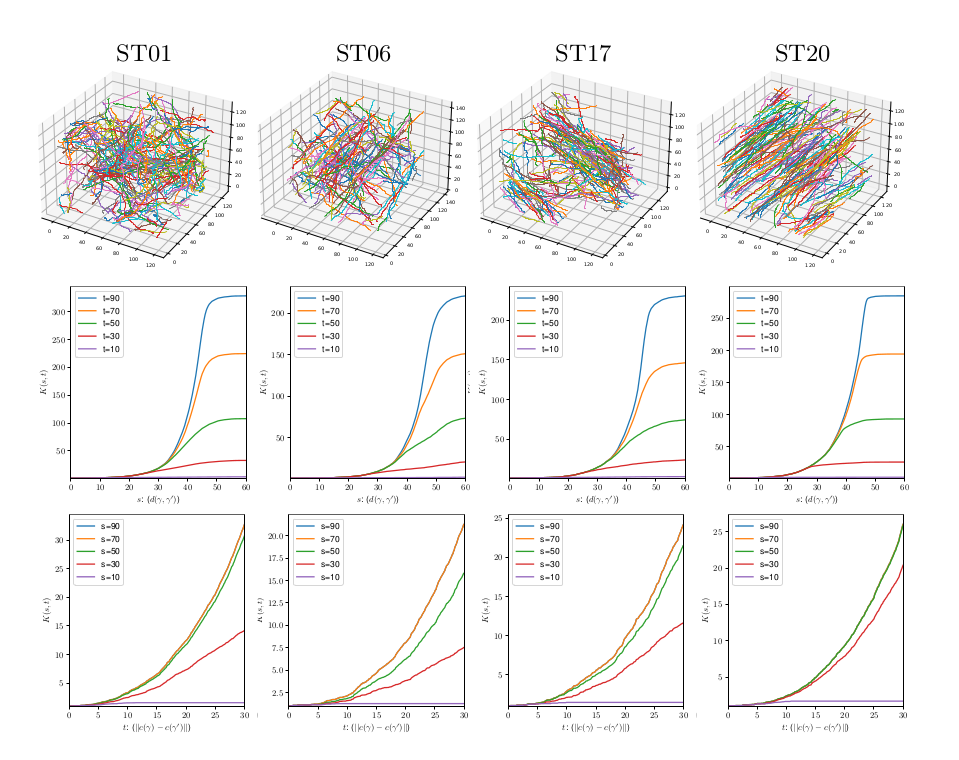
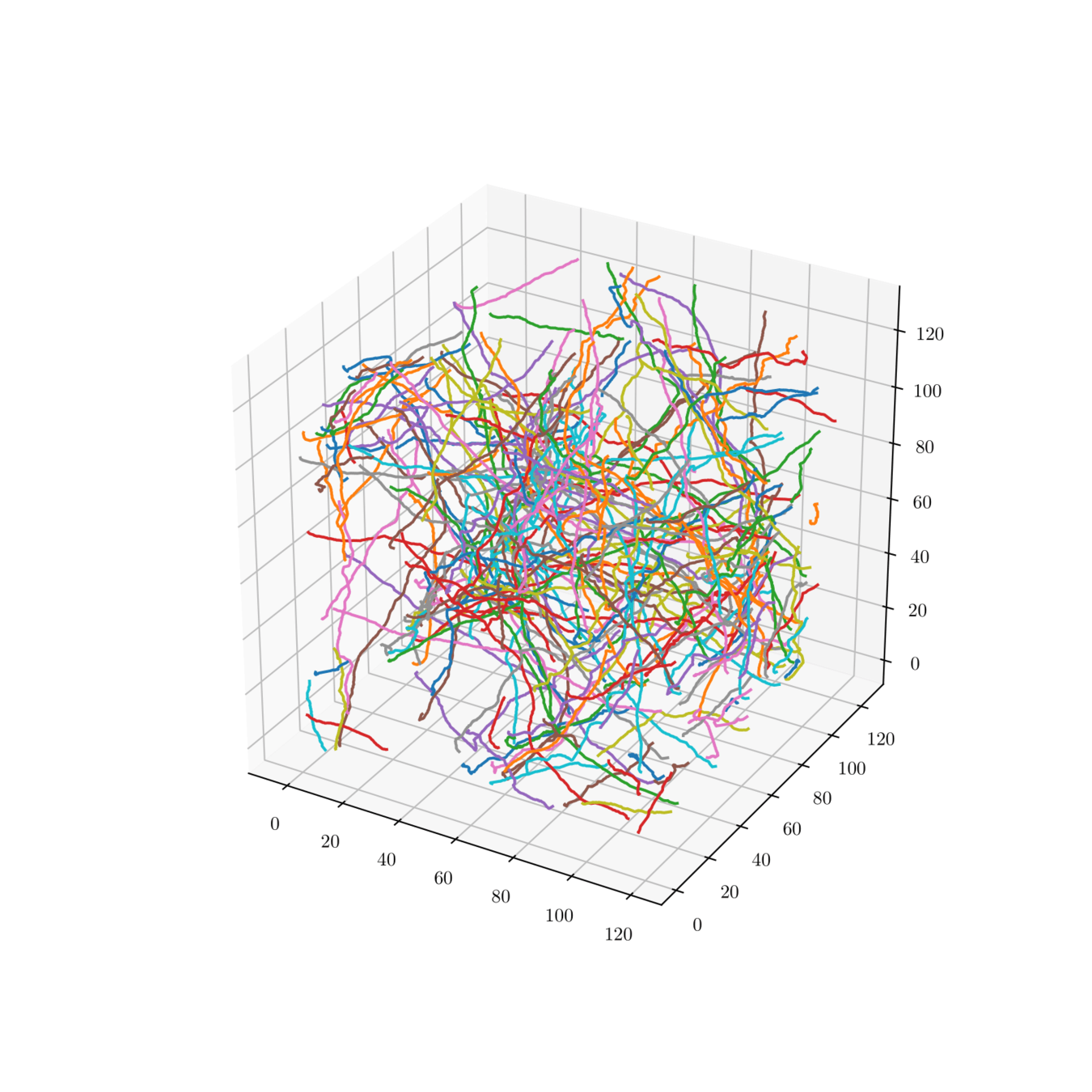
Myelin fibers
Future Work
- Improve uniform shape process comparison
- Review benefits from using currents metric
- Steel fibers in cement
Thank you for watching!
K-functions for Currents
By pernilleehh
K-functions for Currents
- 688



