Phase-Type Models in
Life Insurance

Dr Patrick J. Laub
Who am I?
- Software Engineering and Mathematics
- PhD between University of Queensland (Brisbane) and Aarhus University
- PhD supervisors:
- Søren Asmussen
- Phil Pollett

C'est moi!
- Computational methods for sums of random variables
Mackay



























Brisbane (University of Queensland)




Software experience
- Assembly
- Bash
- C
- C#
- C++
- CSS
- Dart
- HTML
- Java
- JavaScript
- Jekyll (Markdown)
- Julia
- LaTeX
- Mathematica
- Matlab
- Perl
- PHP
- Python
- R
- Ruby (on Rails)
- SQL
- Visual Basic








Sydney




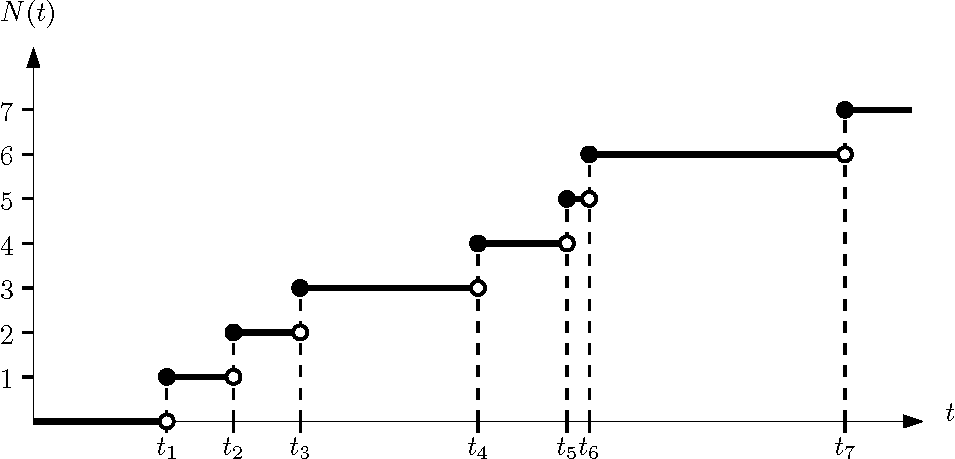
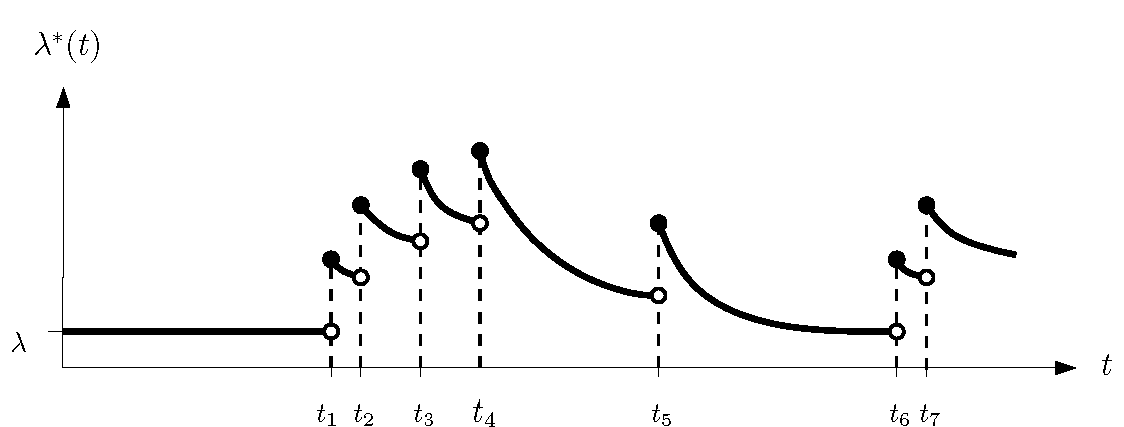
Masters: Hawkes Processes
Paper version of my thesis on https://arxiv.org/abs/1507.02822
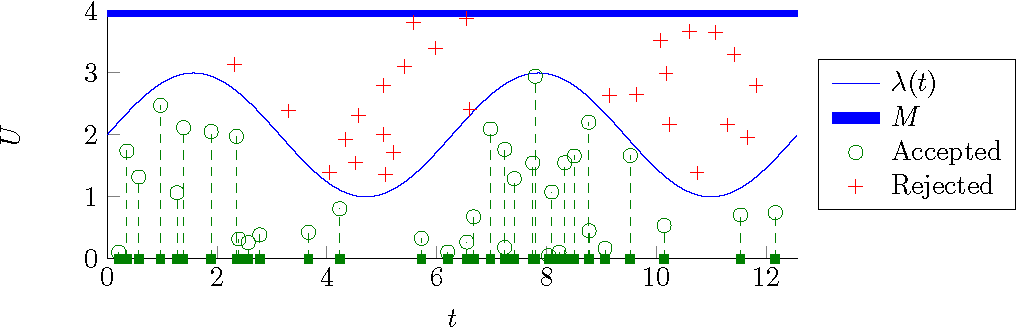
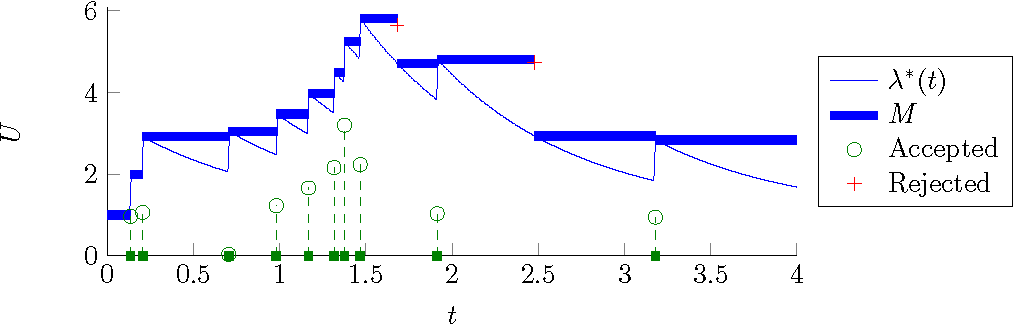
Monte Carlo
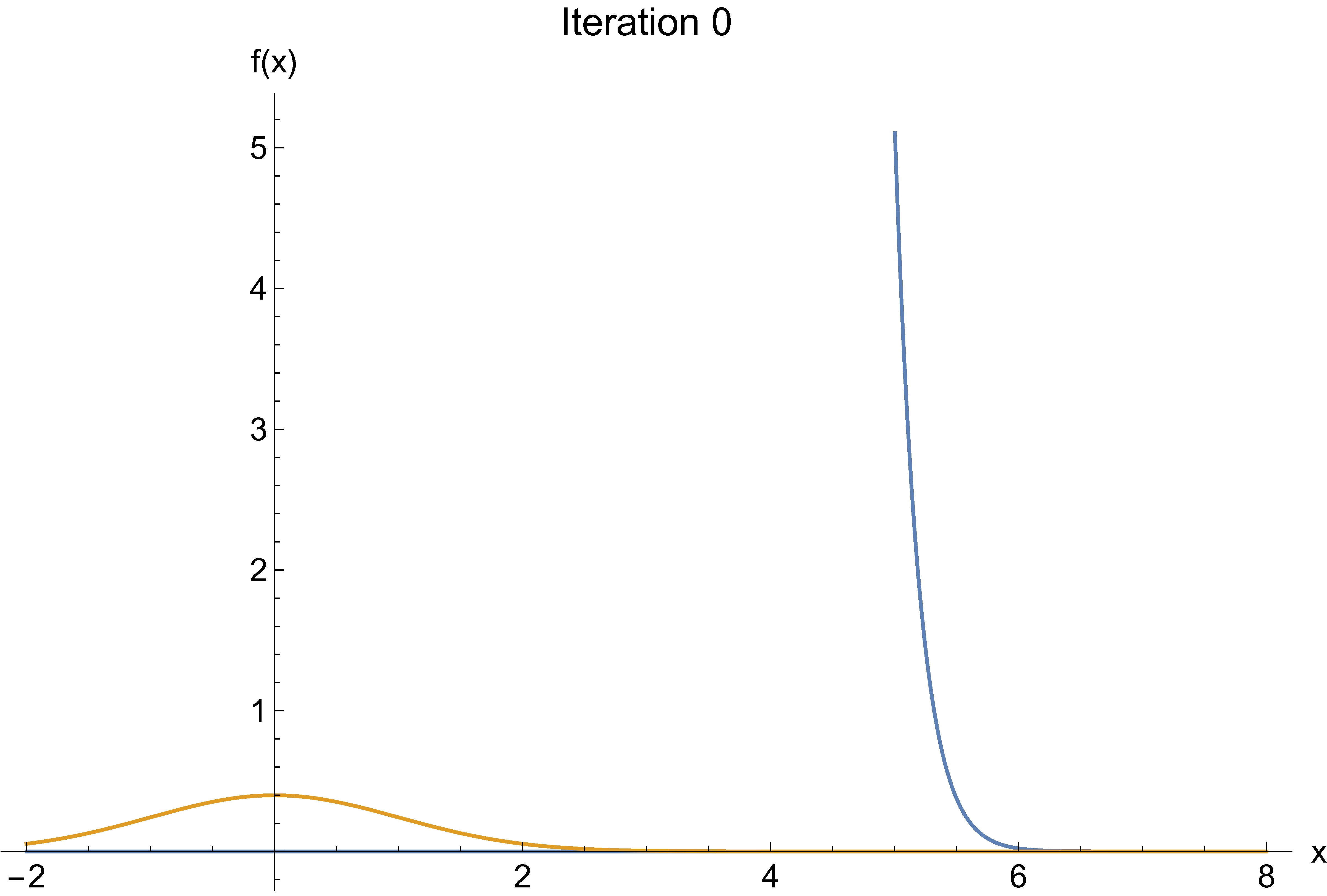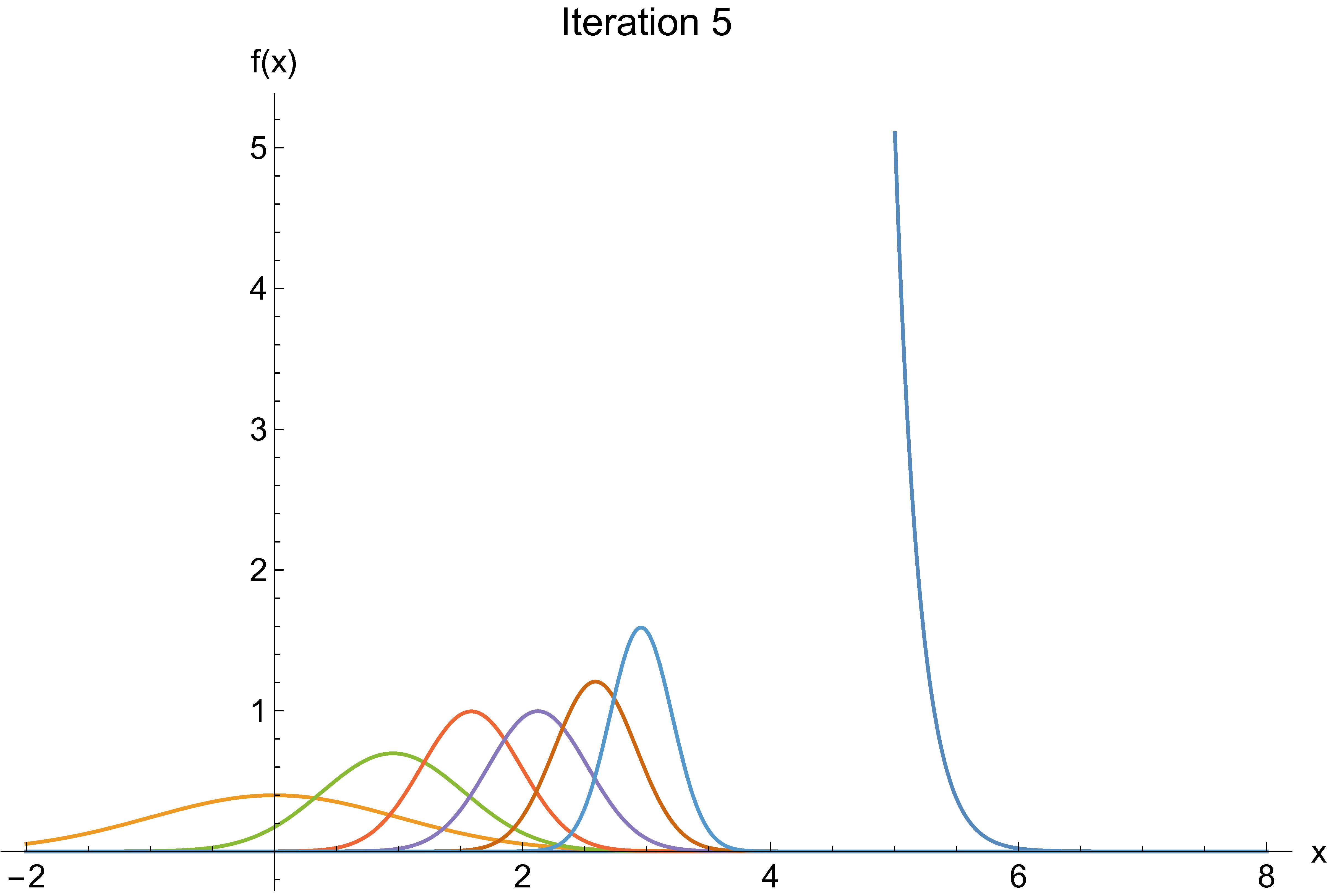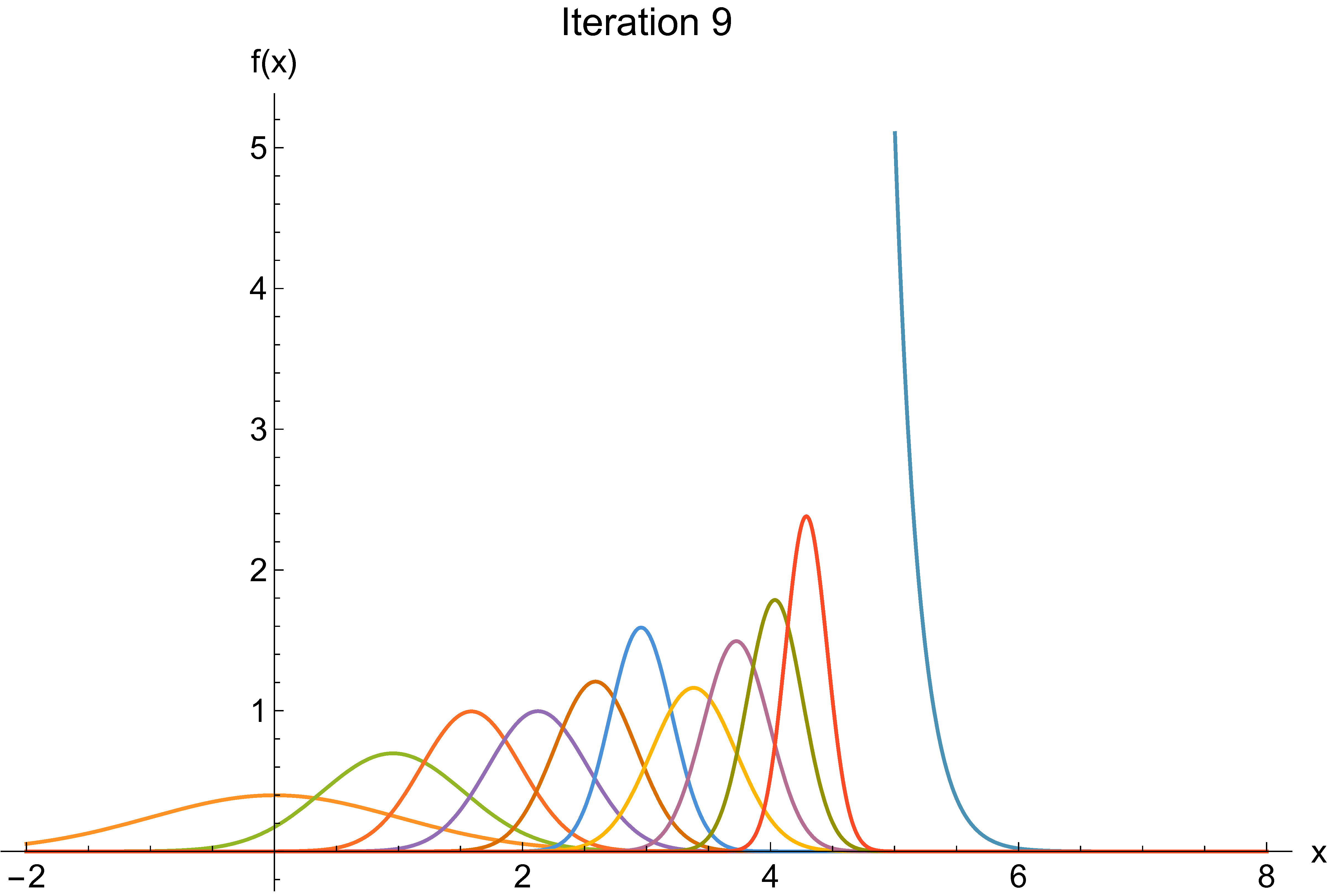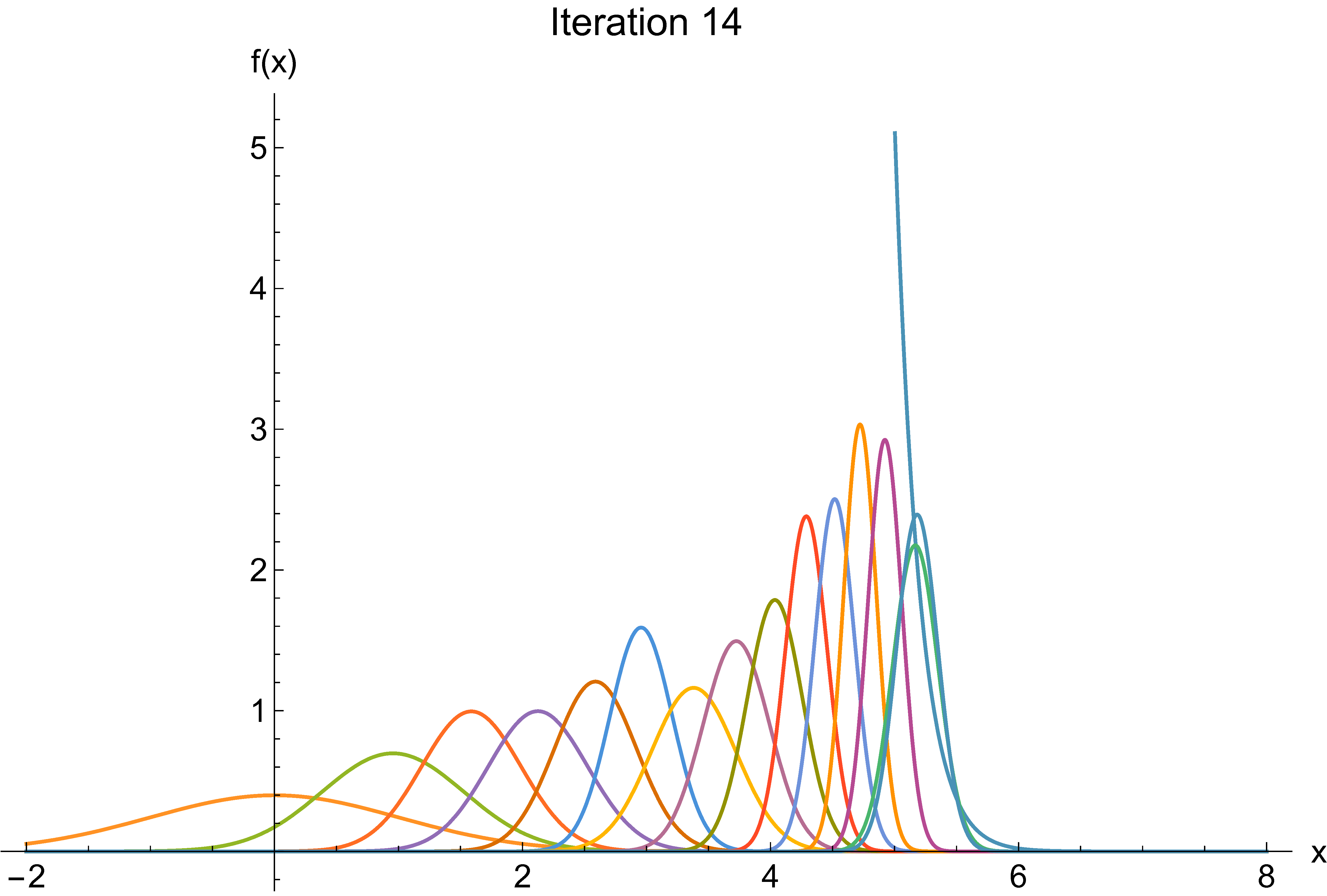
Cross-entropy example
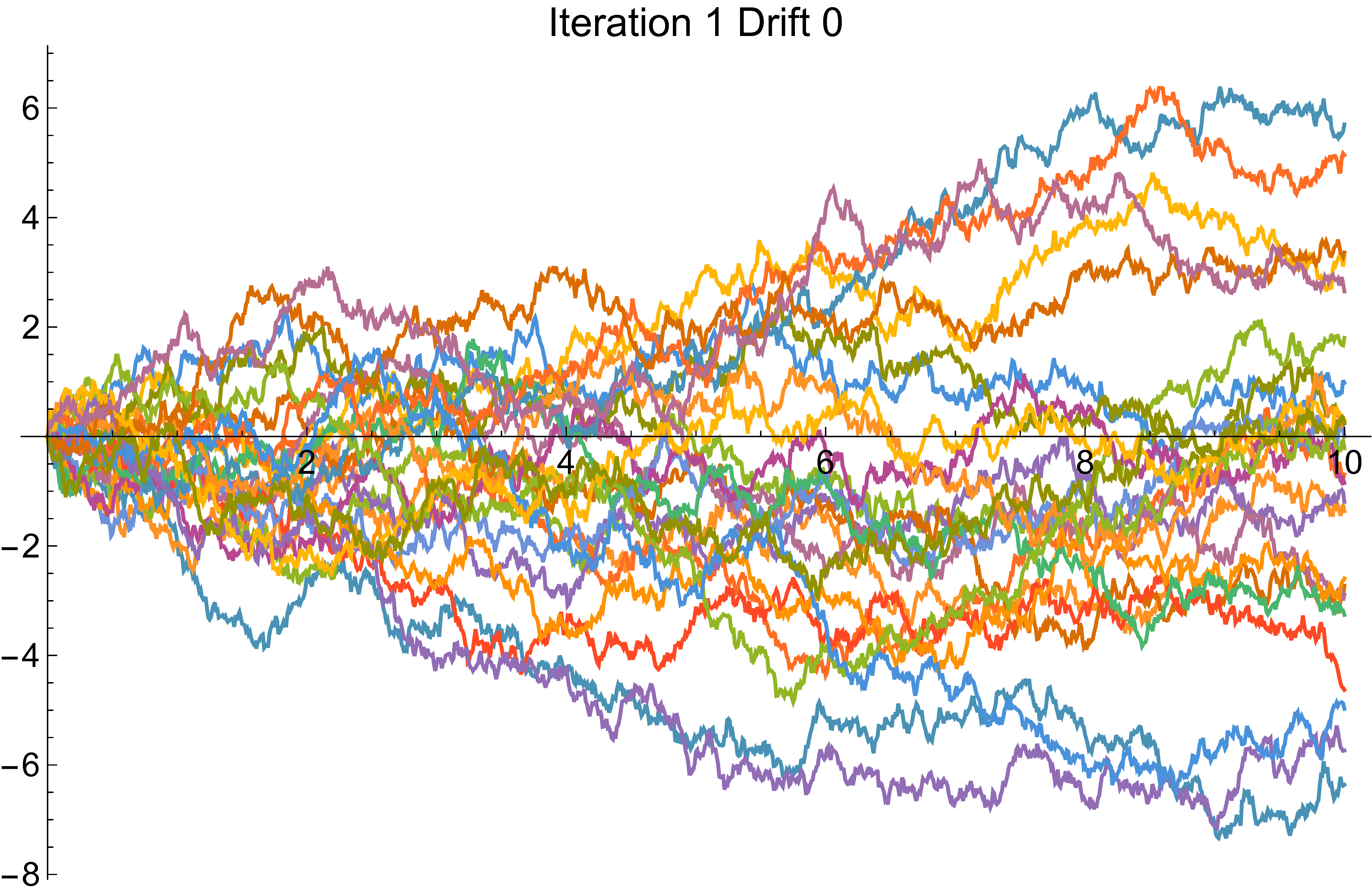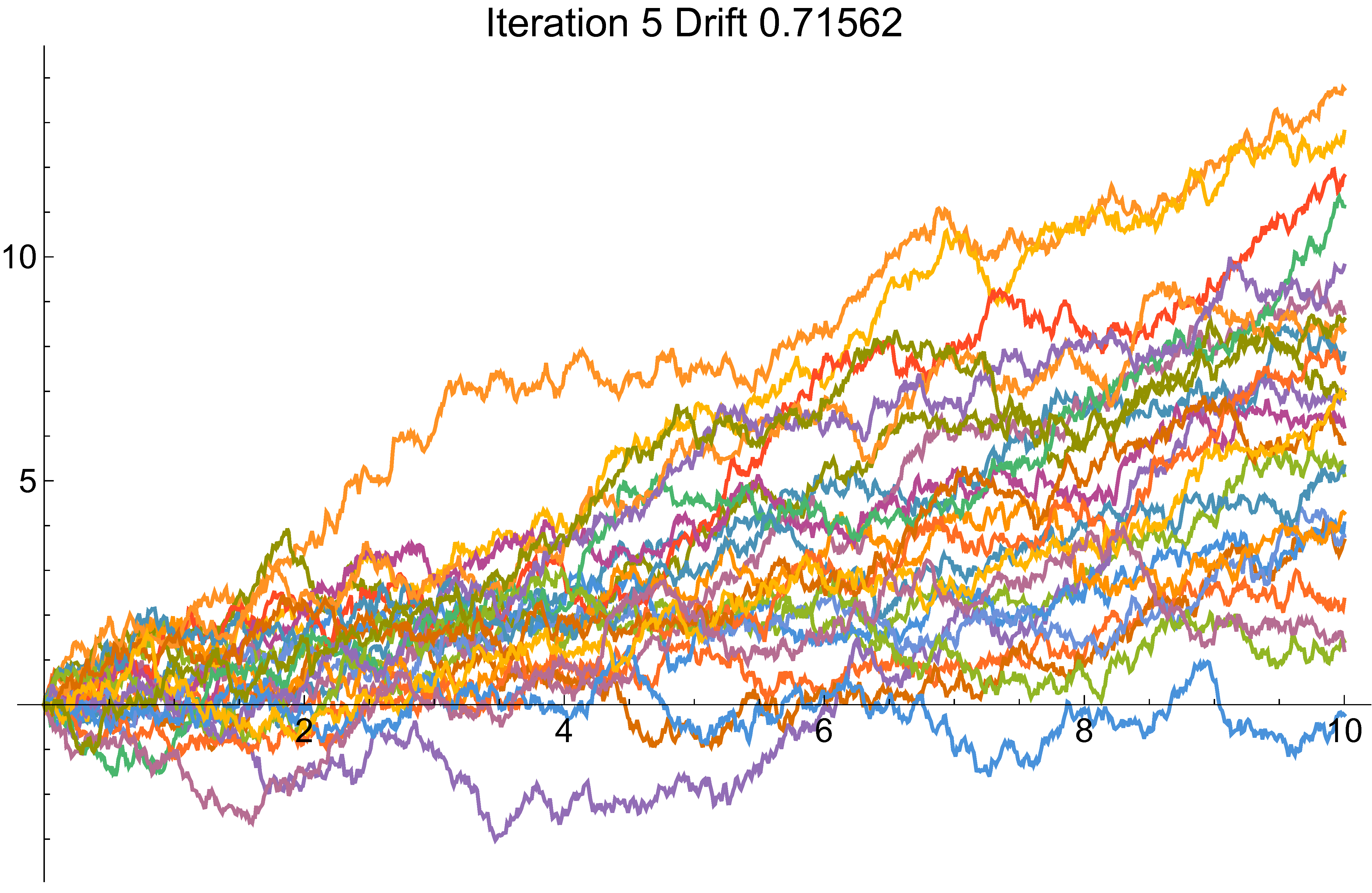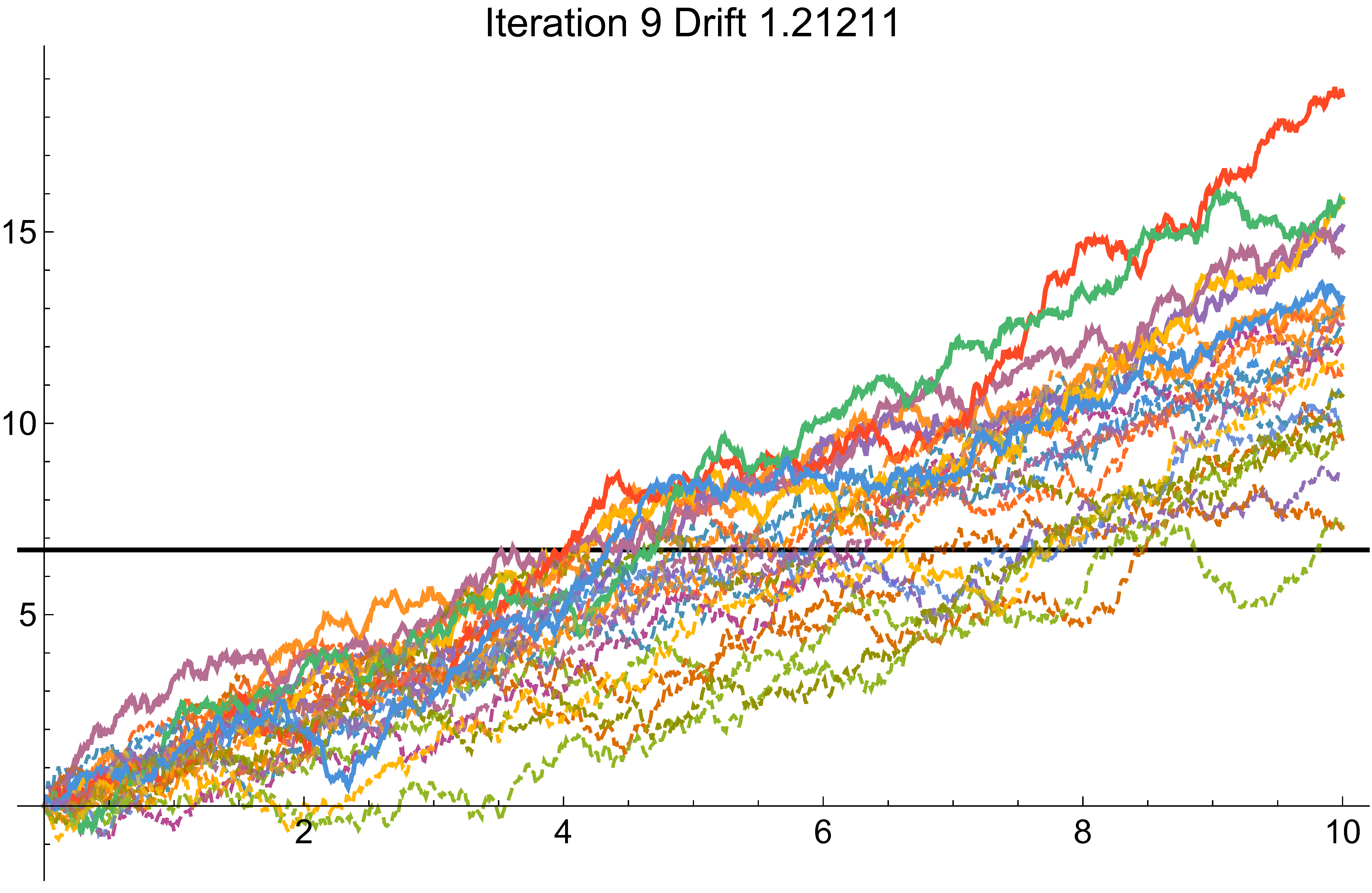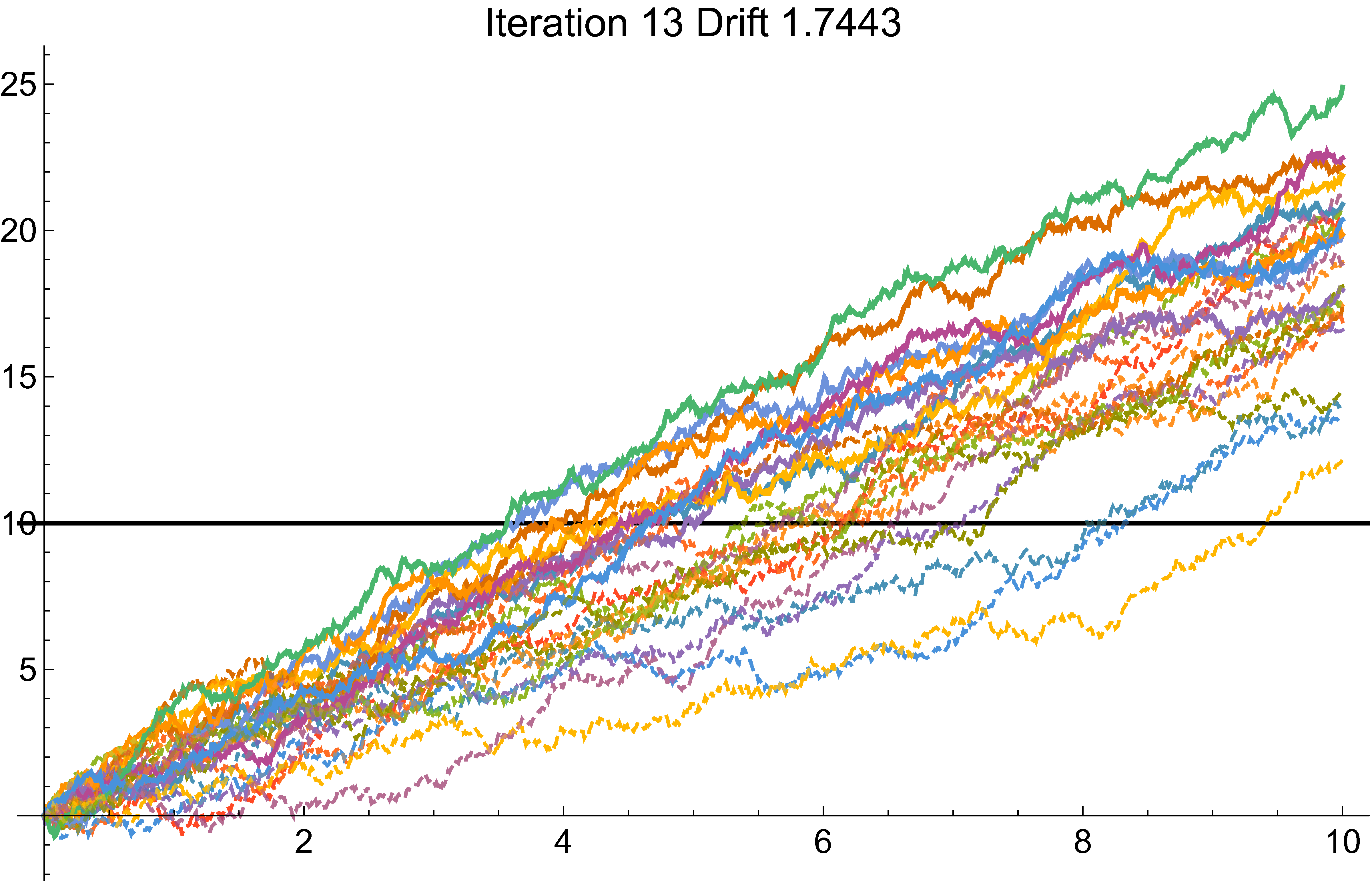
Cross-entropy example
PhD outline


| 2015 | Aarhus |
| 2016 Jan-Jul | Brisbane |
| 2016 Aug-Dec | Aarhus |
| 2017 | Brisbane/Melbourne |
| 2018 Jan-Apr (end) | China |
Supervisors: Søren Asmussen, Phil Pollett, and Jens L. Jensen
Laplace transform approximation for sums of dependent lognormals
No closed-form exists for a single lognormal
Asmussen, S., Jensen, J. L., & Rojas-Nandayapa, L. (2016). On the Laplace transform of the lognormal distribution. Methodology and Computing in Applied Probability


Orthogonal polynomial expansions
- Choose a reference distribution, e.g,
2. Find its orthogonal polynomial system
3. Construct the polynomial expansion

Pierre-Olivier Goffard
Asmussen, S., Goffard, P. O., & Laub, P. J. (2017). Orthonormal polynomial expansions and lognormal sum densities. Risk and Stochastics - Festschrift for Ragnar Norberg (to appear).

My Thesis
Søren visits Melbourne

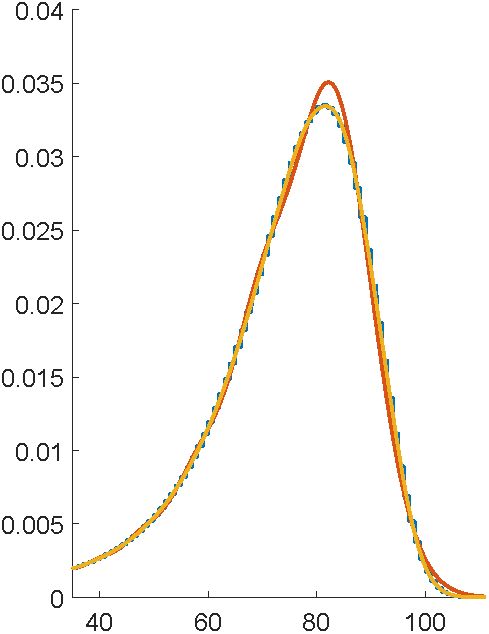
Problem: to model mortality via phase-type
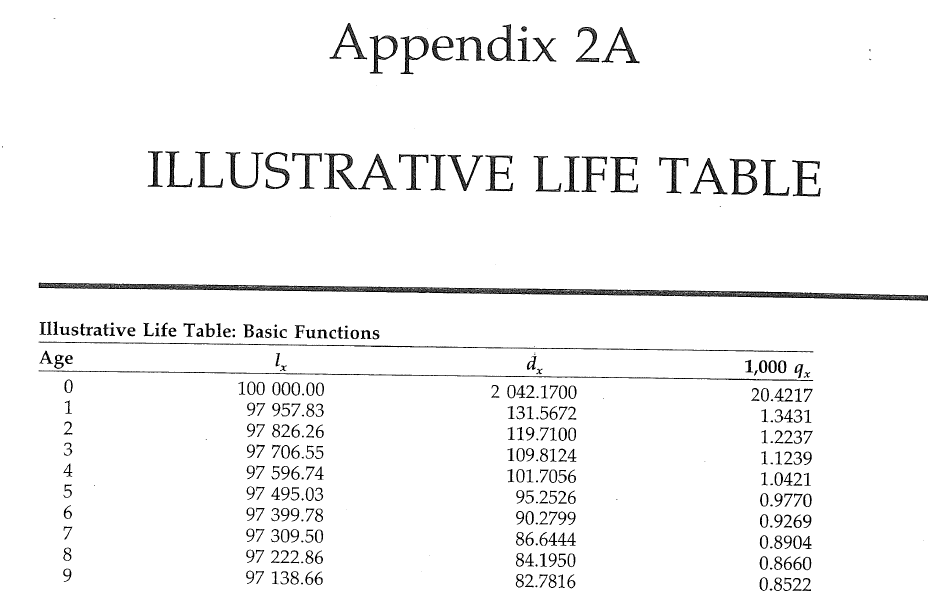
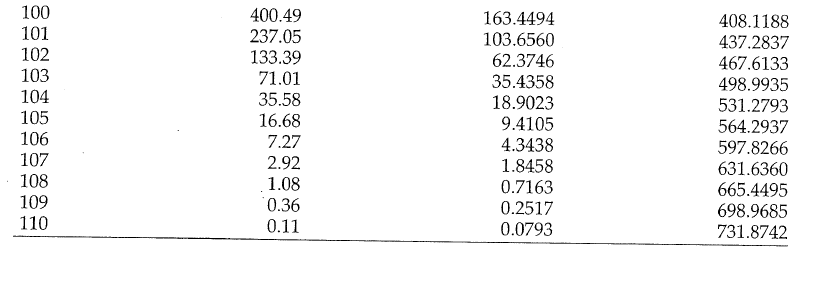
Bowers et al (1997), Actuarial Mathematics, 2nd Edition
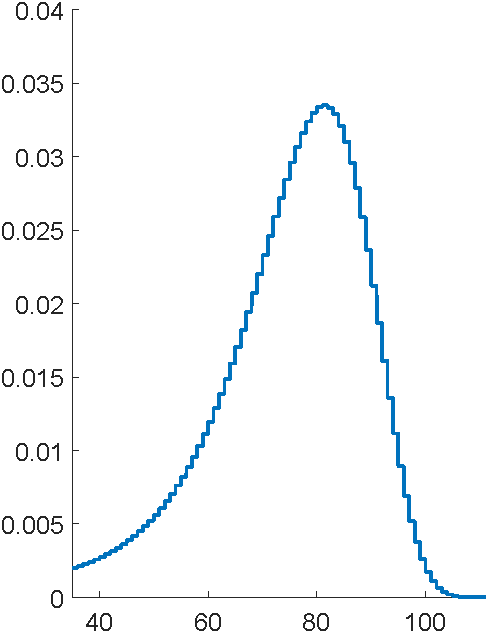
... using the C code EMpht



What are phase-type distributions?
Markov chain State space
Phase-type distributions
Markov chain State space
Phase-type definition
Markov chain State space
- Initial distribution
- Sub-transition matrix
- Exit rates
Phase-type properties
Matrix exponential
Density and tail
Moments
M.g.f
Phase-type generalises...
- Exponential distribution
- Sums of exponentials (Erlang distribution)
- Mixtures of exponentials (hyperexponential distribution)
Class of phase-types is dense

S. Asmussen (2003), Applied Probability and Queues, 2nd Edition, Springer
More cool properties
Closure under addition, minimum, maximum
... and under conditioning
Erlangization/Canadization
Phase-type can even approximate a constant!
Representation is not unique
Also, not easy to tell if any parameters produce a valid distribution
Lots of parameters to fit
- General
- Coxian distribution
- Generalised Coxian distribution
Generalised Coxian
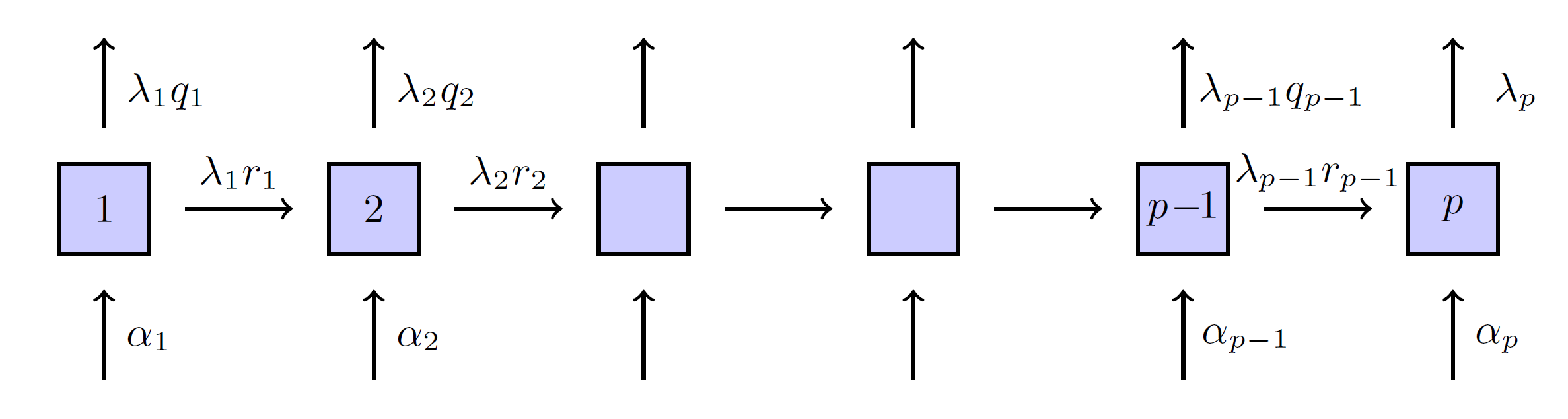
Two ways to view the phases
As meaningless mathematical artefacts
Choose number of phases to balance accuracy and over-fitting
As states which reflect some part of reality
Choose number of phases to match reality
X.S. Lin & X. Liu (2007) Markov aging process and phase-type law of mortality.
N. Amer. Act J. 11, pp. 92-109
M. Govorun, G. Latouche, & S. Loisel (2015). Phase-type aging modeling for health dependent costs. Insurance: Mathematics and Economics, 62, pp. 173-183.
Valuing equity-linked life insurance products
- Say the customer lives for years
- Payout at death is linked to equity
- Example:
- Guaranteed Minimum Death Benefit
- High Water Benefit
- Guaranteed Minimum Death Benefit
- Need
Simplest model
Assume:
- is exponentially distributed
- where is a Brownian motion
Then and are independent and exponentially distributed with rates
Wiener-Hopf Factorisation
-
is an exponential random variable
- is a Lévy process
Doesn't work for non-random time
Motivating theory

Accepted to Stochastic Models
Can read on https://arxiv.org/pdf/1803.00273.pdf
First attempts with EMpht
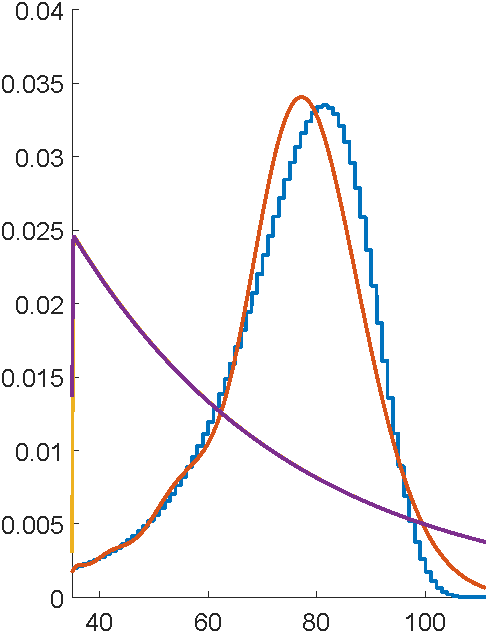
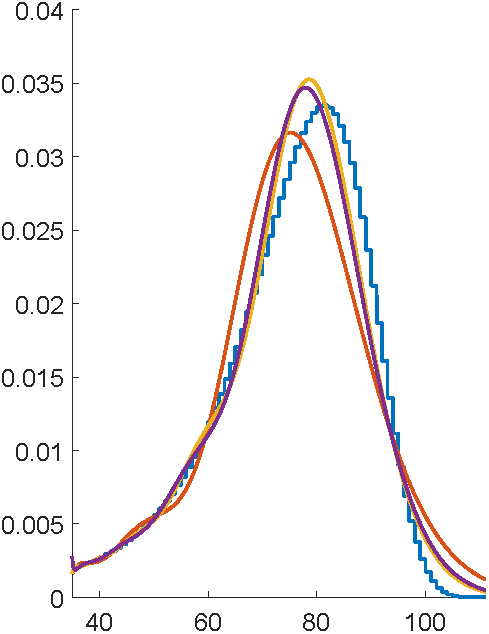
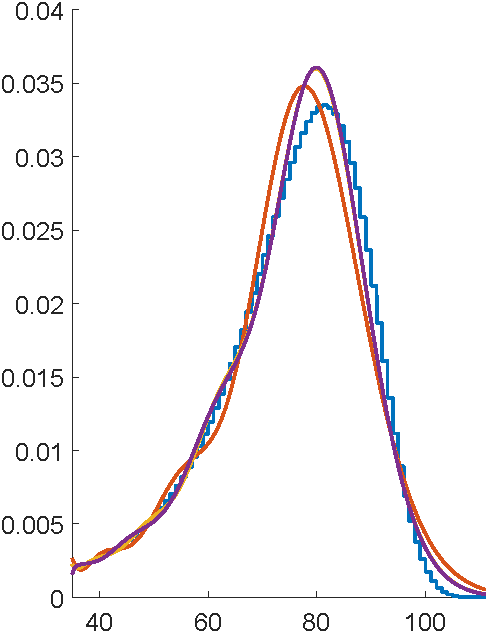



5 hours compute time
This is ancient technology...

Dennis Ritchie (creator of C) standing by the computer used to create C, 1972
Diving into the source
- Single threaded
- Homegrown matrix handling (e.g. all dense)
- Computational "E" step
- Instead solve a large system of DEs
- Hard to read or modify (e.g. random function)
Rewrite in Julia
void rungekutta(int p, double *avector, double *gvector, double *bvector,
double **cmatrix, double dt, double h, double **T, double *t,
double **ka, double **kg, double **kb, double ***kc)
{
int i, j, k, m;
double eps, h2, sum;
i = dt/h;
h2 = dt/(i+1);
init_matrix(ka, 4, p);
init_matrix(kb, 4, p);
init_3dimmatrix(kc, 4, p, p);
if (kg != NULL)
init_matrix(kg, 4, p);
...
for (i=0; i < p; i++) {
avector[i] += (ka[0][i]+2*ka[1][i]+2*ka[2][i]+ka[3][i])/6;
bvector[i] += (kb[0][i]+2*kb[1][i]+2*kb[2][i]+kb[3][i])/6;
for (j=0; j < p; j++)
cmatrix[i][j] +=(kc[0][i][j]+2*kc[1][i][j]+2*kc[2][i][j]+kc[3][i][j])/6;
}
}
}
This function: 116 lines of C, built-in to Julia
Whole program: 1700 lines of C, 300 lines of Julia
# Run the ODE solver.
u0 = zeros(p*p)
pf = ParameterizedFunction(ode_observations!, fit)
prob = ODEProblem(pf, u0, (0.0, maximum(s.obs)))
sol = solve(prob, OwrenZen5())https://github.com/Pat-Laub/EMpht.jl
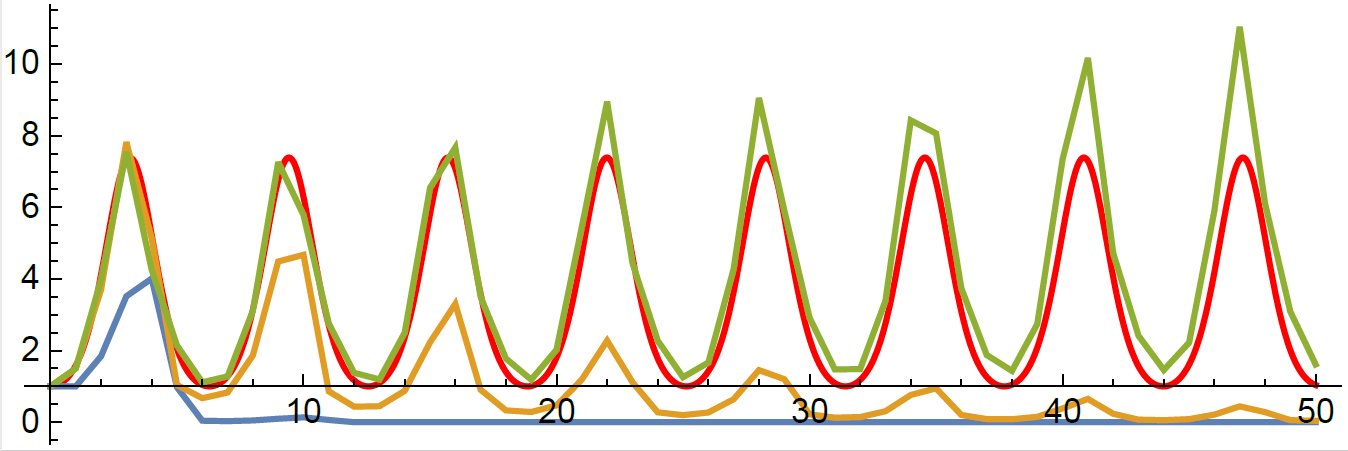

DE solver going negative
# Run the ODE solver.
u0 = zeros(p*p)
pf = ParameterizedFunction(ode_observations!, fit)
prob = ODEProblem(pf, u0, (0.0, maximum(s.obs)))
sol = solve(prob, OwrenZen5())
...
u = sol(s.obs[k])
C = reshape(u, p, p)
if minimum(C) < 0
(C,err) = hquadrature(p*p, (x,v) -> c_integrand(x, v, fit, s.obs[k]),
0, s.obs[k], reltol=1e-1, maxevals=500)
C = reshape(C, p, p)
end
Swap to quadrature in Julia
Swap to quadrature in Julia
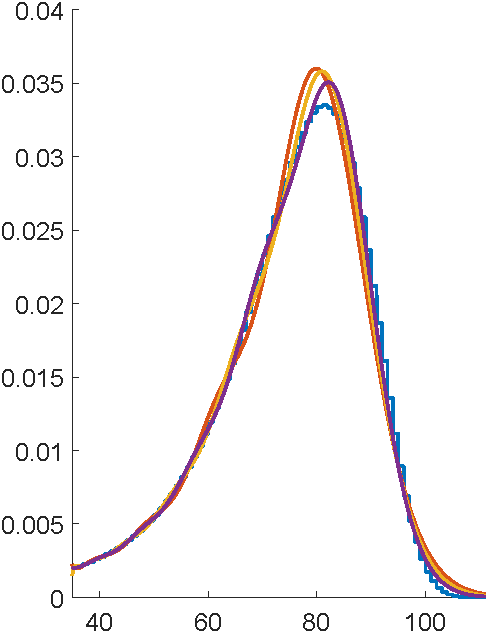
Rushing to complete



Submission deadline passes
Get to Lyon..






Uniformization magic


Uniformization magic
What was the point of all this again?
- The customer lives for years
- Need
- ... and we have it
where
Another cool thing
Contract over a limited horizon
Can use Erlangization so
and phase-type closure under minimums
What conclusion to draw?
... [Phase-types] are not well suited to approximating every distribution. Despite the fact that they are dense... the order of the approximating distribution may be disappointingly large... while the phase-type distributions are admittedly poorly suited to matching certain features, even low-order phase-type distributions do display a great variety of shapes...This rich family may be used in place of exponential distributions in many models without destroying our ability to compute solutions.
C.A. O'Cinneide (1999), Phase-type distributions: open problems and a few properties, Stochastic Models 15(4), p. 4

Phase-Type Models in Life Insurance
By plaub
Phase-Type Models in Life Insurance
- 1,379



