最大團問題
名詞解釋
圖Graph
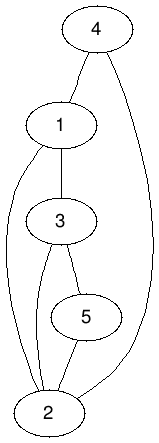
1. 圖由點和邊所組成
點:1, 2, 3, 4, 5
邊:(1, 4)、(3, 5)、...
2. 若兩個點由一條邊所連接,則稱此兩個點「相鄰」
ex:
3 與 5 相鄰
2 與 4 相鄰
3. 我們將點 v 的鄰居的集合
記為:\(N(v)\)
度數Degree
一個點所連出的邊的數量
ex:
deg(1) = 3
deg(5) = 2
deg(2) = 4

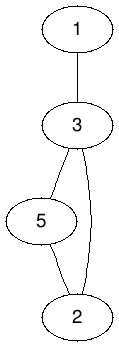
子圖Subgraph
給定一張圖G
取這張圖中的幾個點
並保留點之間的邊
所形成的圖稱為G的子圖

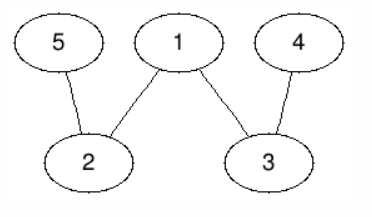
二分圖
一張圖G可以將點分成兩部分
每部分之間互相不相鄰
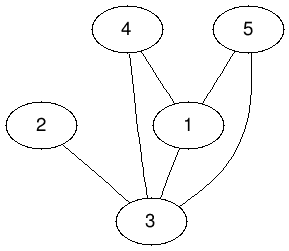
p-分圖
一張圖G可以將點分成 p 部分
每部分之間互相不相鄰
(圖by wiki)
完全p-分圖
一張圖G可以將點分成 p 部分
每部分之間互相不相鄰
並且不同部分之間兩兩相鄰
(圖by wiki)
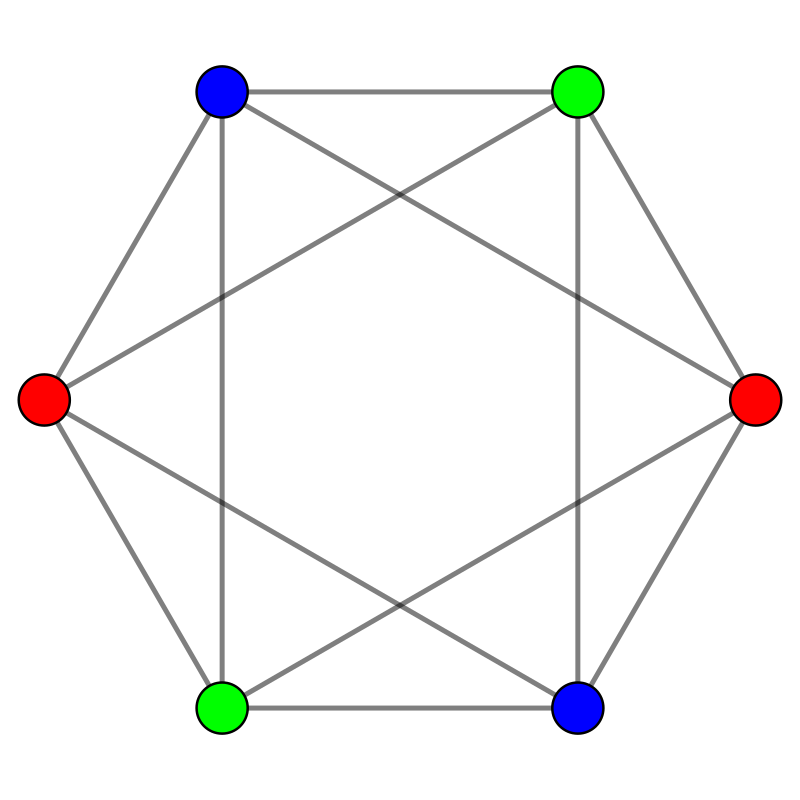
完全圖
Complete Graph
完全圖
給定一張圖
若這張圖中任兩點都相鄰
則稱為完全圖
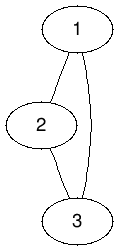
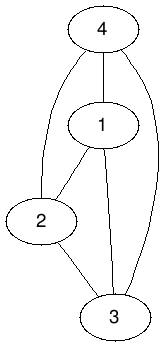
這是完全圖嗎?
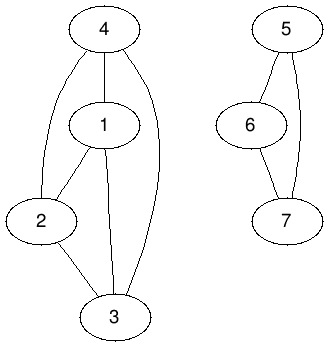
完全圖必須是「整張圖」的任兩點都相鄰
完全圖的性質
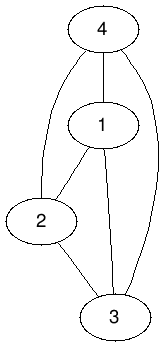
- 任兩點皆相鄰
- 每個點度數都一樣
- 總共有 \(\frac{V\times(V+1)}{2}\) 條邊
- 任兩點的距離為 \( 1 \)
- 任兩點的最遠距離為 \(V - 1\)
- 有漢米爾頓迴圈
...... etc.
完全圖的性質
完全圖的邊的數量是 \(O(V^2)\)
反過來說
完全圖的點的數量是 \(O(\sqrt E)\)
有一些關於完全圖的題目
可以藉由「完全圖的點與邊的數量很懸殊」
這個性質來進行剪枝
團Clique
團
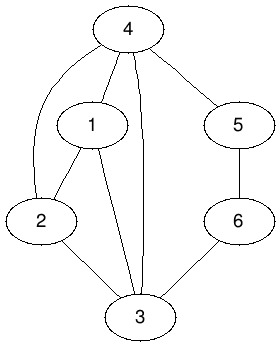
給定一張圖G
若其一個子圖G'是完全圖
則稱G'是G的一個團
ex:
{1, 2, 3}是團
{1, 2, 3, 4}是團
極大團 Maximal Clique
對於一個團
如果無法再加入任何一個點
則稱為極大團
ex:
{1, 2, 3}並非極大團
{3, 4, 5} 是極大團
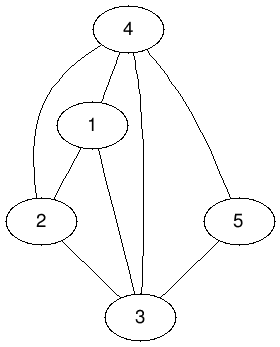
最大團 Maximum Clique
點數最多的團
稱作最大團
ex:
{1, 2, 3, 4}是最大團

給你一個 \(N\) 個點的完全圖
請問最大團的大小是多少?
給你一個 \(N\) 個點的樹
請問最大團的大小為多少?
練習題
一張圖可能有兩個相異的最大團嗎?
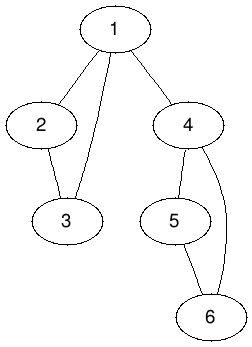
一張 p-分圖有多少個不同的極大團呢?
練習題
\(\prod\limits_{i=1}^p |V_i|\)
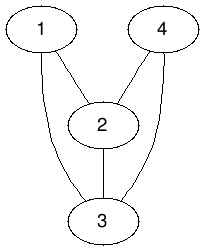
每一個部分都可以任意選一個點
尋找最大團
尋找最大團
給定一張 \(N\) 個點 \(M\) 條邊的圖
請問這張圖的最大團是多少?
這是NP-Complete問題QQ
尋找最大團
枚舉所有可能性
( 1 )
( 2 )
( 3 )
( 4 )
( 1, 2 )
( 1, 3 )
( 1, 4 )
( 2, 3 )
( 2, 4 )
( 3, 4 )
( 1, 2, 3 )
( 1, 2, 4 )
( 1, 3, 4 )
( 2, 3, 4 )
( 1, 2, 3, 4 )
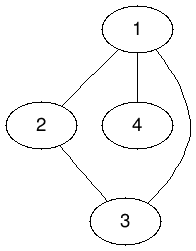
只有( 1, 2, 3 )是團
尋找最大團
枚舉所有可能性

共有 \(O(2^N)\) 種狀態
每種狀態要 \(O(N^2)\) 去檢查
複雜度: \(O(N^2\times2^N)\)
for (int i = 0; i < pow(2, n) - 1; i ++) {
vector<int> v;
for (int j = 0; j < n; j ++)
if ((i >> j) & 1)
v.push_back(j);
bool ok = 1;
for (int a : v) {
for (int b : v) {
if (a == b) continue;
if (a與b不相鄰) ok = 0;
}
}
if (ok) ans = max(ans, v.size());
}尋找最大團
枚舉所有可能性

共有 \(O(2^N)\) 種狀態
每個狀態要 \(O(N)\) 去檢查
複雜度: \(O(N\times2^N)\)
// s 是目前的團
void Dfs(int i) {
if (i > n) {
ans = max(ans, s.size());
return;
}
bool ok = 1;
for (int a : s)
if (i和a不相鄰)
ok = 0;
if (ok) {
s.insert(i);
Dfs(i + 1);
s.erase(i);
}
Dfs(i + 1);
}尋找最大團
剪枝:代價函數

共有 \(O(2^N)\) 種狀態
每個狀態要 \(O(N)\) 去檢查
複雜度: \(O(N\times2^N)\)
// s 是目前的團
void Dfs(int i) {
if (s.size() + (n - i) <= ans)
return;
if (i > n) {
ans = max(ans, s.size());
return;
}
bool ok = 1;
for (int a : s)
if (i和a不相鄰)
ok = 0;
if (ok) {
s.insert(i);
Dfs(i + 1);
s.erase(i);
}
Dfs(i + 1);
}找出極大團
找出極大團
一張圖最多有多少個不同的極大團呢?
給定一張 \(N\) 個點 \(M\) 條邊的圖
請求出「所有」這張圖的極大團
(極大團代表無法再加入任何額外的點)
找出極大團
考慮兩個沒有共同鄰居的兩個點:x, y
那麼 x 肯定不可能同時與 y 在同個極大團中
假設包含 x 的極大團的數量為: \(C_x\)
包含 y 的極大團的數量為: \(C_y\)
且不失一般性的,假設 \(C_x \leq C_y\)
那麼若是把 x 從圖上拔掉
並且加入一個點 x' 並且 x' 與 y 的所有鄰居都相鄰
那整張圖的極大團數量會如何變化呢?
找出極大團
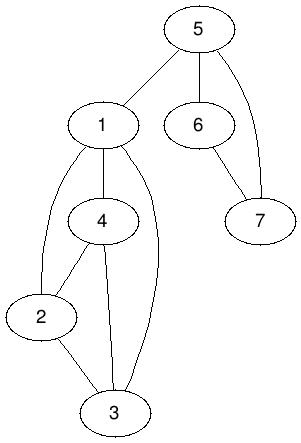
x = 7
y = 4
x' = 8
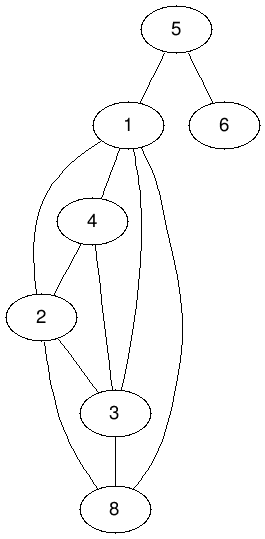
找出極大團
- 會多出 \(C_y\) 個極大團
- 「原本包含 x 的極大團的子圖」中,變成了真的極大團
變化量至少為: \(-C_x + C_y + 0 \geq 0\)
因此經過這樣的操作,極大團數量只有可能變多
那能夠一直執行操作直到甚麼時候呢?
找出極大團
最後會變成一張完全p-分圖
(此分析by tmt's blog)

完全p-分圖上的極大團數量為:
\(\prod\limits_{i=1}^{p}\lfloor V_i \rfloor\)
假設 \(\sum\limits_{i=1}^p V_i = N\) 根據分析可得
上式的最大值出現在: \(O(3^\frac{N}{3})\)
極大團的數量
一張圖中最多有 \(O(3^\frac{N}{3})\) 個極大團
因此這個問題不可能以多項式時間解決
給定一張 \(N\) 個點 \(M\) 條邊的圖
請求出所有這張圖的極大團
(極大團代表無法再加入任何額外的點)
可行嗎?
枚舉所有可能性

for (int i = 0; i < pow(2, n) - 1; i ++) {
vector<int> v;
for (int j = 0; j < n; j ++)
if ((i >> j) & 1)
v.push_back(j);
bool ok = 1;
for (int a : v) {
for (int b : v) {
if (a == b) continue;
if (a與b不相鄰) ok = 0;
}
}
if (ok) ans += 1;
}極大團:有可能可以再加入其他點
可行嗎?
枚舉所有可能性

for (int i = 0; i < pow(2, n) - 1; i ++) {
if (i是已經做過的點的子集的話) continue;
vector<int> v;
for (int j = 0; j < n; j ++)
if ((i >> j) & 1)
v.push_back(j);
bool ok = 1;
for (int a : v) {
for (int b : v) {
if (a == b) continue;
if (a與b不相鄰) ok = 0;
}
}
if (ok) ans += 1;
}複雜度:\(O(N^2\times 2^N)\)
Bron–Kerbosch algorithm
維護三個集合:R、P、X
對於我們目前所搜索到的極大團的子圖
必須要包含:
R中所有的點
P中部分的點
不包含X中任何點
演算法開始時, \(R=\{ \}, P=\{V\}, X=\{ \}\)
當 \(P = X = \{\}\) 時,R中所有點構成一個極大團
Bron–Kerbosch algorithm
algorithm BronKerbosch1(R, P, X) is
if P and X are both empty then
report R as a maximal clique
for each vertex v in P do
BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}R:目前構成團的那些點
P:可能可以加入團的那些點(候選的點)
X:已經搜索過的點,而不能再被加入
by wiki
Bron–Kerbosch algorithm
algorithm BronKerbosch1(R, P, X) is
if P and X are both empty then
report R as a maximal clique
for each vertex v in P do
BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}by wiki
P為空時,若X為空,則R為極大團
P為空時,若X非空,代表R可擴充
但X中的點都是做過的
Bron–Kerbosch algorithm
by wiki
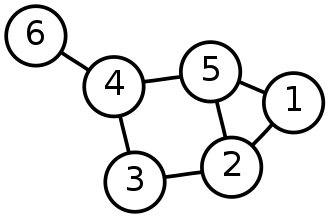
BronKerbosch2(Ø, {1,2,3,4,5,6}, Ø)
BronKerbosch2({2}, {1,3,5}, Ø)
BronKerbosch2({2,3}, Ø, Ø): output {2, 3}
BronKerbosch2({2,5}, {1}, Ø)
BronKerbosch2({1,2,5}, Ø, Ø): output {1,2,5}
BronKerbosch2({4}, {3,5,6}, Ø)
BronKerbosch2({3,4}, Ø, Ø): output {3,4}
BronKerbosch2({4,5}, Ø, Ø): output {4,5}
BronKerbosch2({4,6}, Ø, Ø): output {4,6}
BronKerbosch2({6}, Ø, {4}): no outputBron–Kerbosch algorithm
優化 by wiki
algorithm BronKerbosch2(R, P, X) is
if P and X are both empty then
report R as a maximal clique
choose a pivot vertex u in P ⋃ X
for each vertex v in P \ N(u) do
BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}對於一個極大團
要嘛包含 u (而 u 做過了)
要嘛至少包含一個不是 u 的鄰居的點
因此 u 的鄰居就不用搜了
Bron–Kerbosch algorithm
複雜度 by tmt's blog
為了盡可能優化
所以選的點 u 的 \(|N(u)|\) 要盡可能大
這件事情可以在 \(O(|P|^2)\) 內辦到
根據論文可知: \(T(N) = O(3^{\frac{N}{3}})\) = O(1.4422^N)
struct Maximum_Clique{
typedef bitset<MAXN> bst;
bst N[MAXN],empty;
int p[MAXN],n,ans;
void BronKerbosch2(bst R,bst P,bst X){
if(P==empty&&X==empty)
return ans=max(ans,(int)R.count()),void();
bst tmp=P|X;
int u;
if((R|P|X).count()<=ans) return;
for(int uu=0;uu<n;++uu){
u=p[uu];
if(tmp[u]==1) break;
}
//if (double(clock())/CLOCKS_PER_SEC > .999) return;
bst now2=P&~N[u];
for(int vv=0;vv<n;++vv){
int v=p[vv];
if(now2[v]==1){
R[v]=1;
BronKerbosch2(R,P&N[v],X&N[v]);
R[v]=0,P[v]=0,X[v]=1;
}
}
}
void init(int _n){n=_n;
for(int i=0;i<n;++i) N[i].reset();
}
void add_edge(int u,int v){N[u][v]=N[v][u]=1;}
int solve(){//remember srand
bst R,P,X;
ans=0,P.flip();
for(int i=0;i<n;++i) p[i]=i;
random_shuffle(p,p+n),BronKerbosch2(R,P,X);
return ans;
}
};pivot u的選擇
為了方便可以
直接random
(by BBQ's codebook)
Bron–Kerbosch algorithm
優化
還有一個根據The degeneracy of a graph
來優化的方法,但在此先跳過
有興趣的同學可以先自行研究看看
練習題
by tmt's blog
給定一張有 \(N\) 個點的圖G(以補圖的方式給出)
已知在G上有一個極大團的大小為\(\frac{2N}{3}\)
請設計一個演算法找出在G上一個大小至少為 \(\frac{N}{3}\)的團
練習題
- Zerojudge a858
- Codeforces D. Graph Subset Problem
- TIOJ在做投影片的時候掛掉了QQ
Zerojudge a858
給定 \(N\) 個點的完全圖
每條邊要嘛是紅色、要嘛是黑色
求這張圖總共有多少個同色的三角形
\(\binom{N}{3}\) 減掉非同色的三角形
D. Graph Subset Problem
給定一張 \(n\) 個點 \(m\) 條邊的圖和常數 \(k\)
如果存在一個子圖中,每個點的 \(deg\) 都大於 \(k\)
請輸出此子圖
若存在一個點數為 \(k\) 的團,則輸出此團
(\(n, m, k \leq 10^5\))
D. Graph Subset Problem
對於第一個小題
任何 \(deg\) 少於等於 \(k\) 的點都是沒用的
=>
將那些點一個一個拔掉,直到整張圖剩下 \(deg\) 大於 \(k\) 的點
或是整張圖是空的
D. Graph Subset Problem
對於第二小題
\(deg\) 小於 \(k-1\) 的點都是沒用的
=>
將那些點拔掉
若是圖是空的則無解
D. Graph Subset Problem
若圖非空
如果此時每個點的 \(deg\) 都大於 \(k - 1\)
則代表第一小題有解
=>
至少存在一個點的 \(deg = k - 1\)
D. Graph Subset Problem
假設那個點為 \(v\)
減查 \(v \cup N(v)\)是不是團
是=>找到
否=>拔掉這個點,繼續檢查剩下的圖
D. Graph Subset Problem
\(\sqrt{2m} < k\) 時,肯定無解
=>
\( k = O(\sqrt m\)
檢查完全圖的複雜度: \(O(k^2)\)
只需要檢查 \(O(\frac{m}{k})\) 個點 (why?)
複雜度為: \(O(mk) \leq O(m^\frac{3}{2})\)
最大團問題
By polarischiba
最大團問題
清大程式設計競技社 進階班課程
- 286



