序列問題
區間修改、區間加值
複習:何謂線段樹

出處:https://slides.com/sylveon/cp2019-spring
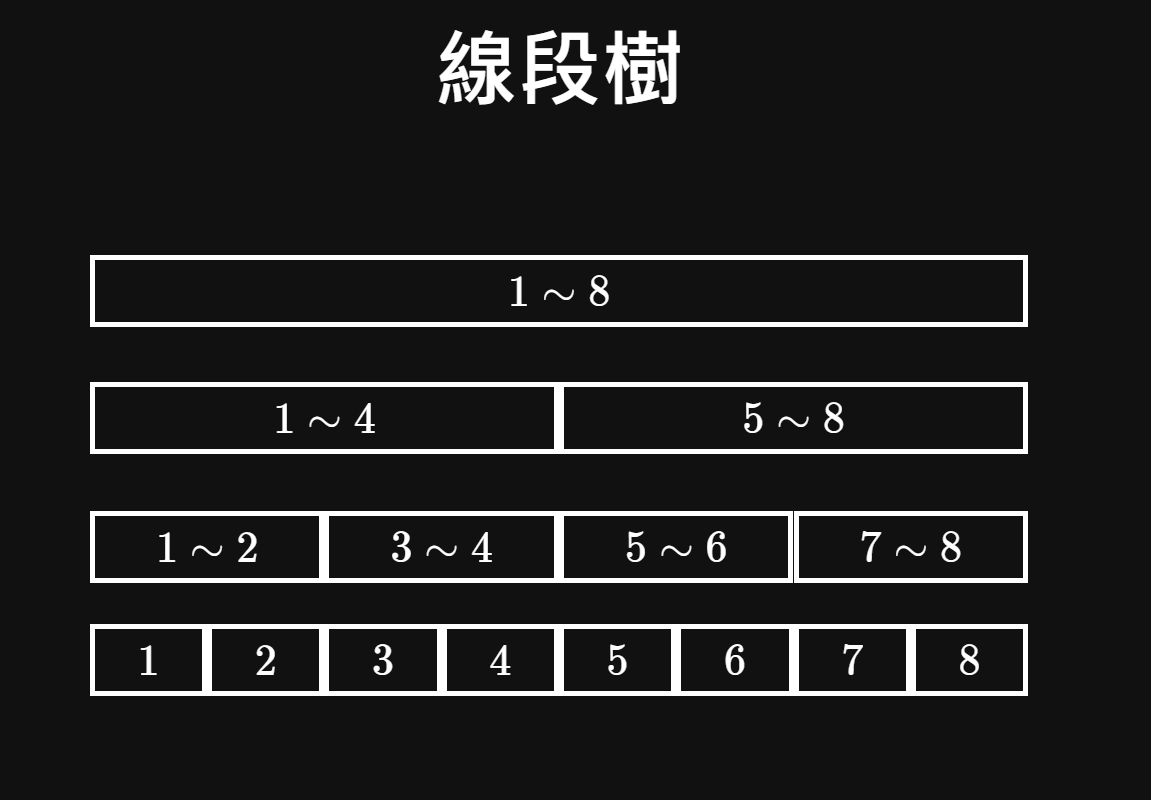
出處:https://slides.com/sylveon/cp2019-spring
區間加值、區間詢問
有數列 \(a_1, a_2, a_3, \cdots a_n\) ,想要做 \(Q\) 件事
- 求 \(a_i+a_{i+1}+\cdots+a_j\)
- 將 \(a_L, a_{L+1}, \cdots, a_R\) 中每個數字都加上 \(k\)
求區間和我會,但區間加值呢?
Lazy Tag的概念
將一個區間標記起來
代表這個區間中每個元素都要做「某種操作」
[1, 4]被打上了「7」這個lazy tag
則代表 \(a_1, a_2, \cdots a_4\)中每個值都要加上 7
Lazy Tag的樣子
1~8
1~4
7
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
8
2
Lazy Tag代表的意思
1~8
1~4
7
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
8
2
+28
+14
+7
但實際上沒有往下做!
想求1~7的答案
1~8
1~4
7
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
2
8
1~8
1~4
7
5~8
5~6
7~8
7
想求1~7的答案
1~8
1~4
7
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
8
2
想求3~6的答案?
1~8
1~4
7
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
8
2
1~8
1~4
7
3~4
怎麼辦?
將lazy tag往下推
1~8
1~4
7
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
8
2
1~4
1~2
7
3~4
7
3~4
7
5~8
5~6
lazy tag
要將 \(a_L, a_{L+1}, \cdots, a_R\) 都加上 \(k\) 的話
因為一次修改完全部太花時間了
所以先暫時不做,等到需要的時候再往下推
將3~5通通加上13
1~8
1~4
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
8
2
1~8
1~4
3~4
13
5~8
5~6
5
13
將4~6加上13
1~8
1~4
7
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
8
2
1~8
1~4
7
1~2
?
3~4
?
要分別填上甚麼數字呢?
將4~6加上13
5~8
3~4
7~8
5~6
1
3
4
5
6
7
8
2
1~8
1~4
1~2
7
3~4
7
3
?
4
?
將4~6加上13
5~8
3~4
7~8
5~6
1
3
4
5
6
7
8
2
1~8
1~4
1~2
7
3
7
4
20
5~8
5~6
13
lazy tag
- 將區間標記起來,代表「整個區間都要做某個操作」
- 未來路過那個區間的時候,再往下推就好
- 每個操作的複雜度和原本的線段樹一樣: \(O(\log N)\)
lazy tag
1~8
1~4
7
5~8
const int N = 500000;
int arr[4 * N + 10];
int tag[4 * N + 10];開兩個陣列,分別存節點的區間和與lazy tag
pull 與原本一樣
seg[0] = 10 + 7 = 17
seg[1] = 10
seg[2] = 7
int pull(int x, int y) {
return x + y;
}pull 與原本的線段樹一樣
建構線段樹也一樣
#define IL(X) ((X)*2+1)
#define IR(X) ((X)*2+2)
void build(int L, int R, int id) {
if (L == R) {
arr[id] = a[L];
return;
}
int M = (L + R) / 2;
build(L , M, IL(id));
build(M+1, R, IR(id));
arr[id] = pull(arr[IL(id)], arr[IR(id)]);
}將lazy tag往下推
void push(int L, int R, int id) {
arr[id] += tag[id] * (R - L + 1);
if (L != R) {
tag[IL(id)] += tag[id];
tag[IR(id)] += tag[id];
}
tag[id] = 0;
}(2)
注意因為是區間和
所以要乘上 \(R-L+1\)
(3)
如果 \(L == R\) 的話
代表到葉節點了
所以不必將lazy tag往下推
(7)
最後記得將這個節點的lazy tag歸零
想要求4的答案
1~8
1~4
7
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
8
2
1~8
1~4
7
想要求4的答案
5~8
1~2
7
3~4
7
7~8
5~6
1
3
4
5
6
7
8
2
1~8
1~4
1~2
3~4
想要求4的答案
5~8
1~2
7
3~4
7~8
5~6
1
3
7
4
7
5
6
7
8
2
1~8
1~4
已經推過的lazy tag記得歸零
3
4
查詢線段樹
int Query(int l, int r, int L, int R, int id) {
push(L, R, id);
if (l == L && r == R)
return arr[id];
int M = (L + R) / 2;
if (r <= M)
return Query(l, r, L , M, IL(id));
if (M < l)
return Query(l, r, M+1, R, IR(id));
return pull(
Query(l , M, L , M, IL(id)),
Query(M+1, r, M+1, R, IR(id))
);
}(2)
路過的時候記得推lazy tag
其餘都一樣
想求3~6的答案
1~8
1~4
7
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
8
2
1~8
1~4
7
路過就推一下
想求3~6的答案
1~8
5~8
1~2
3~4
7~8
5~6
1
3
4
5
6
7
8
2
1~8
1~4
1~2
7
3~4
7
5~8
5~6
除了要路過推一下以外,和原本的一模一樣
區間修改
void Modify(int l, int r, int k, int L, int R, int id) {
push(L, R, id);
if (l == L && r == R) {
tag[id] += k;
return;
}
int M = (L + R) / 2;
if (r <= M) Modify(l, r, k, L , M, IL(id));
else if (M < l) Modify(l, r, k, M+1, R, IR(id));
else {
Modify(l , M, k, L , M, IL(id));
Modify(M+1, r, k, M+1, R, IR(id));
}
push(L , M, IL(id));
push(M+1, R, IR(id));
arr[id] = pull(arr[IL(id)], arr[IR(id)]);
}(2)
路過的時候記得推一下
(4)
區間加值的時候
修改lazy tag即可
(15、16)
pull前
子孫的lazy tag
不一定是零
記得將子孫也push一下
其餘都一樣
將4~6加上13
1~8
1~4
7
5~8
1~2
3~4
7~8
21
5~6
1
3
4
5
6
7
8
2
1~8
1~4
7
將4~6加上13
5~8
3~4
7~8
21
5~6
1
3
4
5
6
7
8
2
1~8
1~4
1~2
7
3~4
7
將4~6加上13
5~8
3~4
7~8
21
5~6
1
3
4
5
6
7
8
2
1~8
1~4
1~2
7
3
7
4
20
5~8
5~6
13
pull 的時候要注意
以5~8為例子
3~4
7~8
21
1
3
5
6
13
7
8
2
1~8
1~4
1~2
7
3
7
4
20
5~8
5~6
13
5~6
7~8
5
13
6
7
21
8
21
因為和lazy tag有關的操作都是
遇到的時候「順便」做一下的
因此複雜度與原本的線段樹一樣,都是:
- 建造: \(O(N)\)
- 修改: \(O(\log N)\)
- 查詢: \(O(\log N)\)
總結
練習題
zerojudge
- d539 - 區間加值、區間最大值
- d799 - 區間加值、區間求和
TIOJ
- 1224 - 算一堆矩形的面積的聯集
- 1408
- 1836
Codeforces
- 292E
- 242E
- 301D
序列問題 - 區間修改、區間加值
By polarischiba
序列問題 - 區間修改、區間加值
清大程式設計競技社 進階班課程
- 345



