Basins of attraction of soft sphere packings are not fractal
Praharsh Suryadevara
Mathias Casiulis
Stefano Martiniani
Energy Landscapes



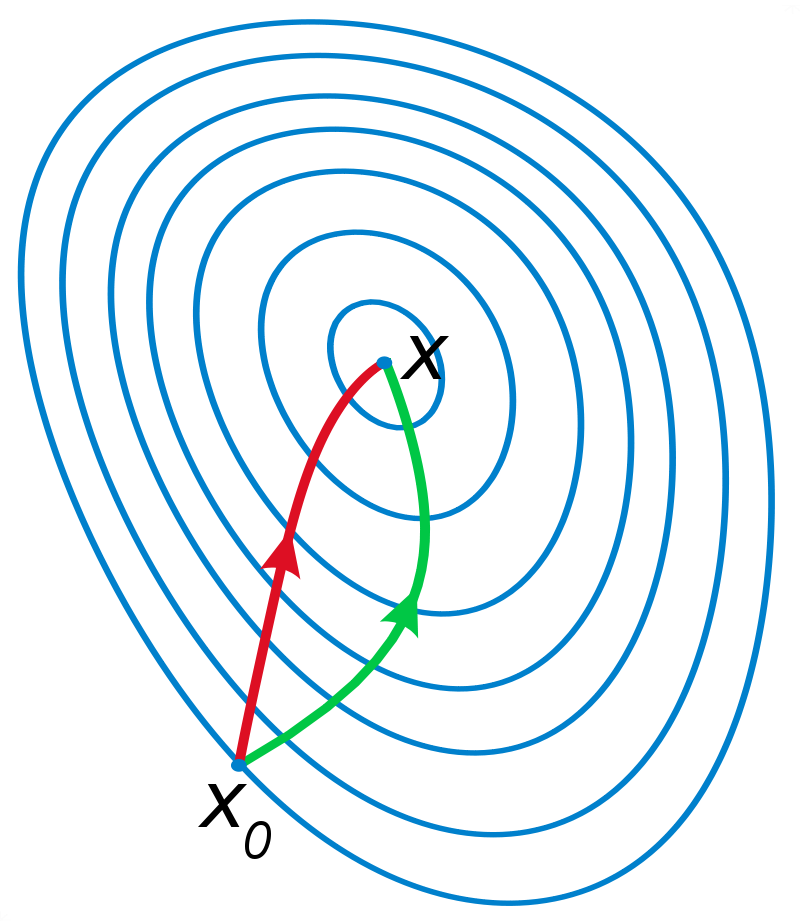
What is a basin?

\(V(x)\)
\(x\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
\(x_0\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
\(x_0\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
\(x_0\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
\(x_0\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
\(x_0\)
\(x_{min}\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
basin 2
Basin tiling (what we're interested in)
basin 1
basin 3
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
Insert slide on fractal basins
Basin identification in \((N-1)\times d\) dimensions
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
steepest descent
https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
Newton/Quasi-Newton methods (e.g. LBFGS)
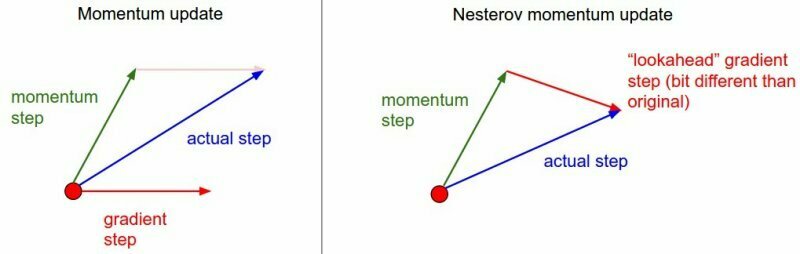
Momentum-based optimizers (e.g. FIRE)
Time
$$ x_{t+\Delta t} = x_t + \Delta t \nabla V(x_t)$$
Gradient Descent/Forward Euler infinitesimal stepsizes
Error
Optimizers accurate for small systems but not benchmarked moderate/large systems
??
Basin identification in \((N-1)\times d\) dimensions
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
steepest descent
https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
Optimizers
Forward Euler/Gradient descent
ODE Solvers
Expensive/Infeasible in high dimensions
Faster but accurate Methods?

Newton/Quasi-Newton methods (e.g. LBFGS)

Momentum-based optimizers (e.g. FIRE)
Basin identification in \((N-1)\times d\) dimensions
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
steepest descent
- Solving steepest descent in \((N-1) \times D\) for interacting potentials is expensive
- Previous work mostly relies on optimization algorithms as proxies for finding basins

Momentum-based optimizers (e.g. FIRE)

Newton/Quasi-Newton methods (e.g. LBFGS)
https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
Goal of this Talk
I want to show you, with new physics along the way, how to get features of the energy landscape accurately
Steepest Descent

Newton/Quasi-Newton methods (e.g. LBFGS)

Momentum-based optimizers (e.g. FIRE)
$$ x_{t+\Delta t} = x_t + \Delta t \nabla V(x_t)$$
Gradient Descent/Forward Euler




System
Bidisperse Hertzian soft spheres

$$ V_{ij}(r) =\begin{cases} \frac{\epsilon}{p} \left( 1 - \frac{r}{r_{i} + r_{j}} \right) ^{p} & r < r_{i} + r_{j} \\ 0 & r > r_{i} + r_{j}\end{cases}$$ with \(p\) = 2.5 and packing fraction \(\phi> \phi_j\)

landscape dimension \(d_l \sim (N-1)\times d\)
Slicing the energy landscape

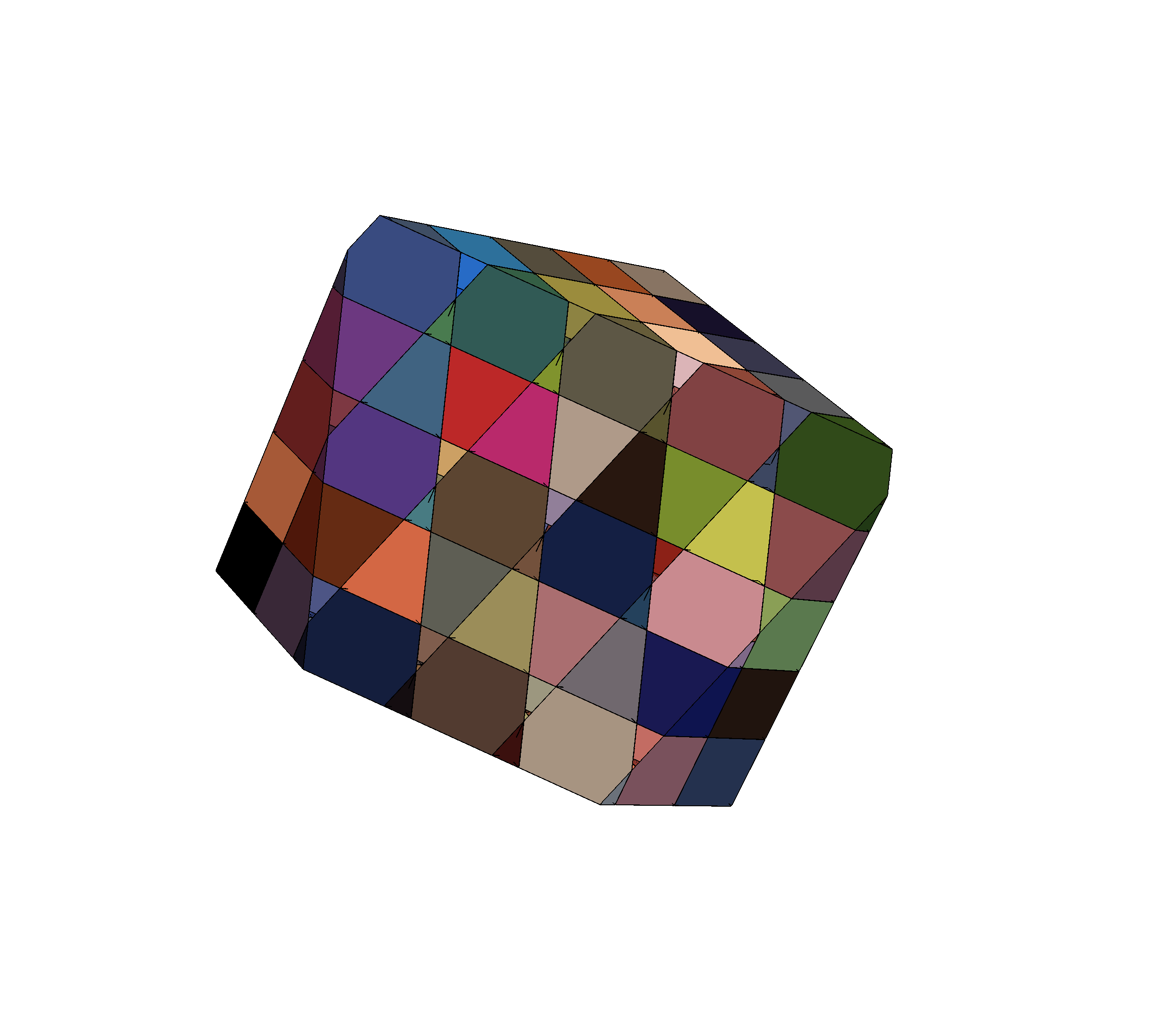
Each color is a basin
Imagine cubic basins in a regular grid
Slicing the energy landscape
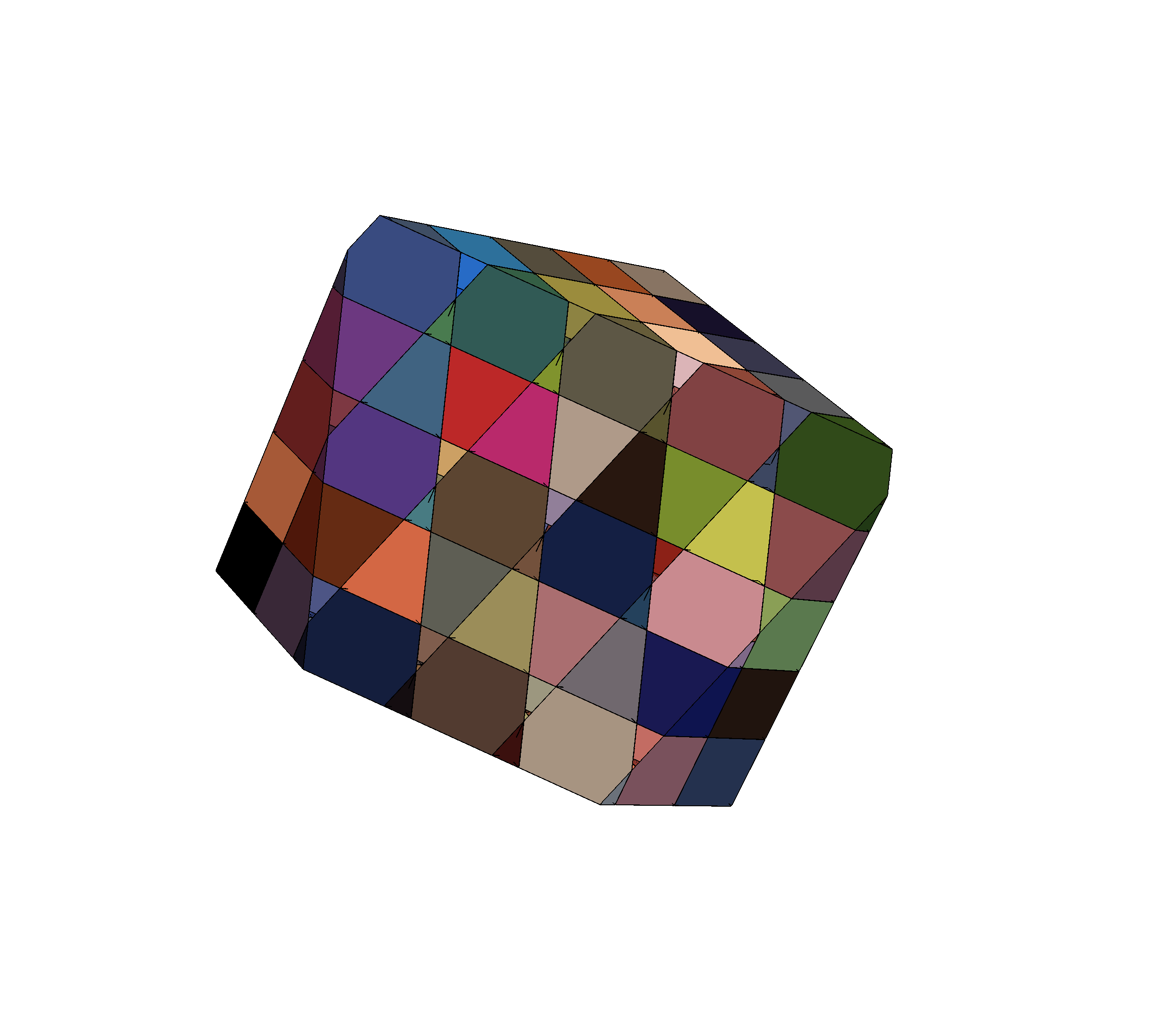
Each color is a basin
Imagine cubic basins in a regular grid
16 particle basin slice with FIRE
16 particle basin slice with FIRE
\(d_l \sim (N-1) d = 30\)
\(d_l \sim (N-1) d = 30\)
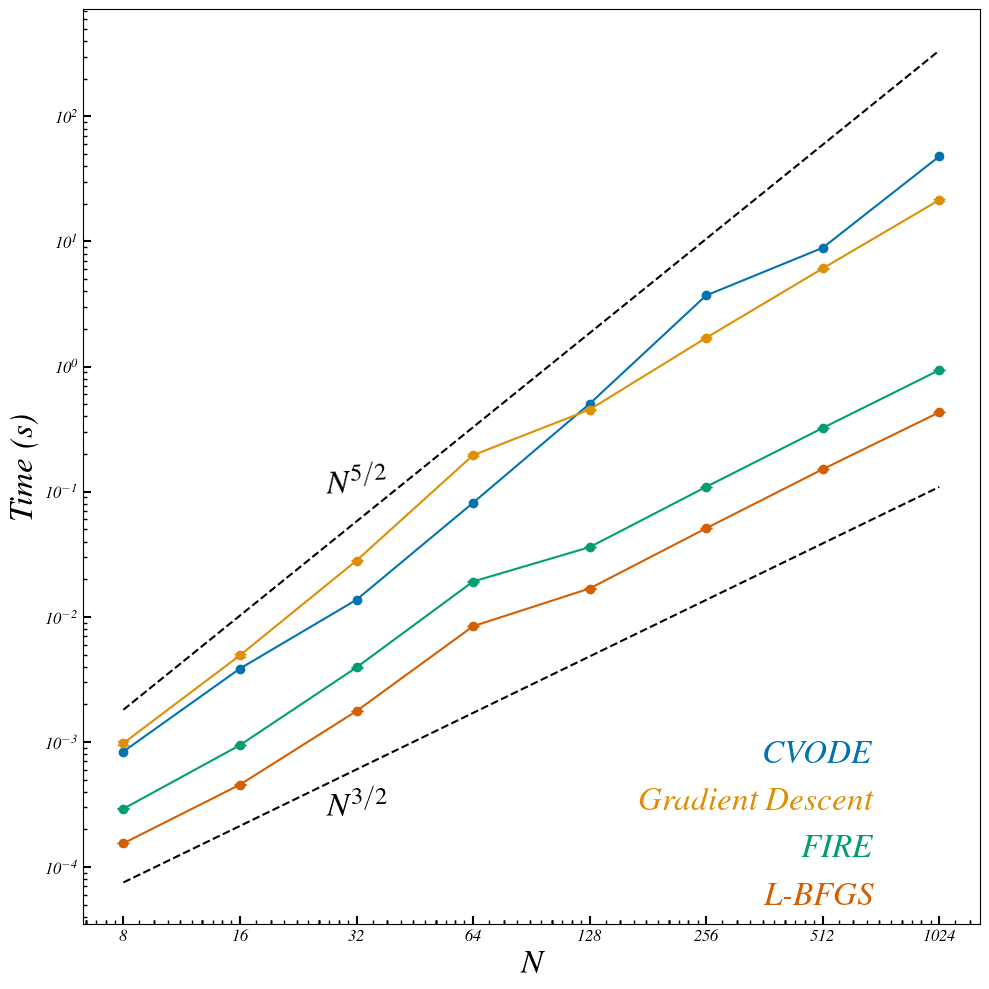
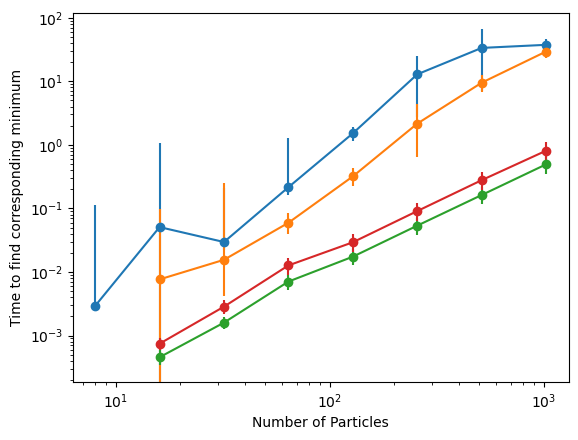
ODE Solver Comparison
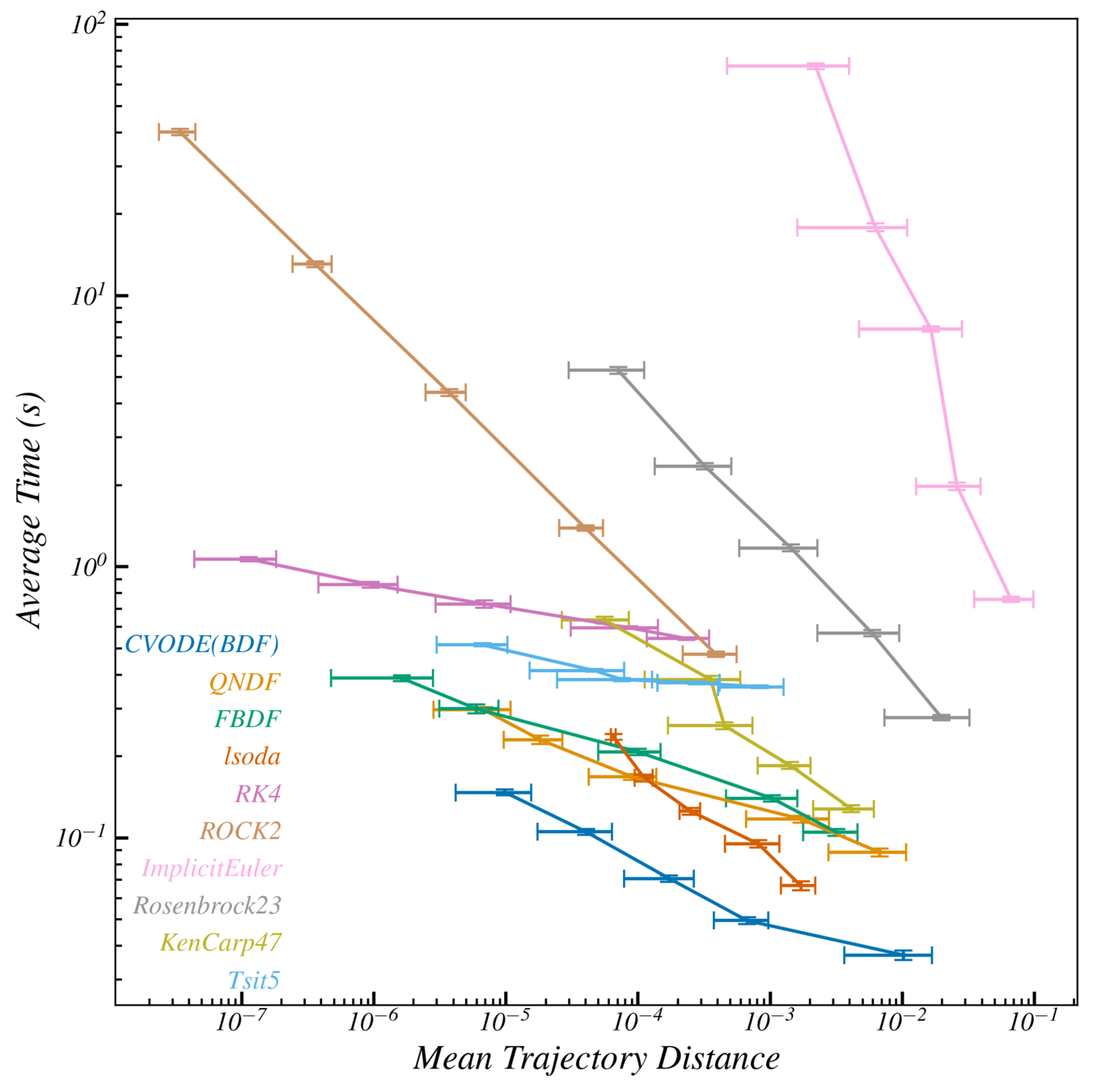
Better
true solution
ODE Solver Comparison

3 orders of magnitude faster than Implicit Euler at same error
Better
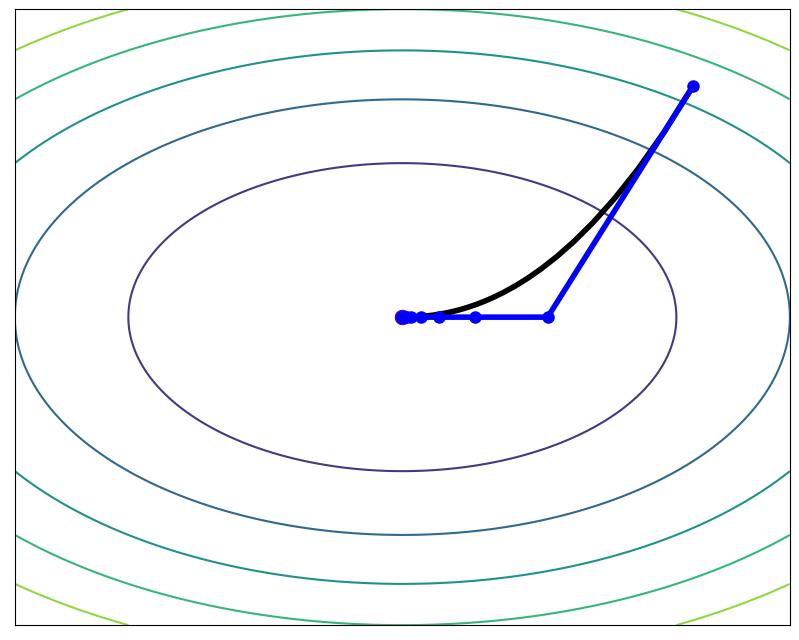
ODE solver solution
Max distance
Average over a 100 initial conditions
16 particle basin slice with FIRE
16 particle basin slice with FIRE
\(d_l \sim (N-1) d = 30\)
\(d_l \sim (N-1) d = 30\)
16 particle basin slice with CVODE
16 particle basin slice with CVODE
\(d_l \sim (N-1) d = 30\)
\(d_l \sim (N-1) d = 30\)
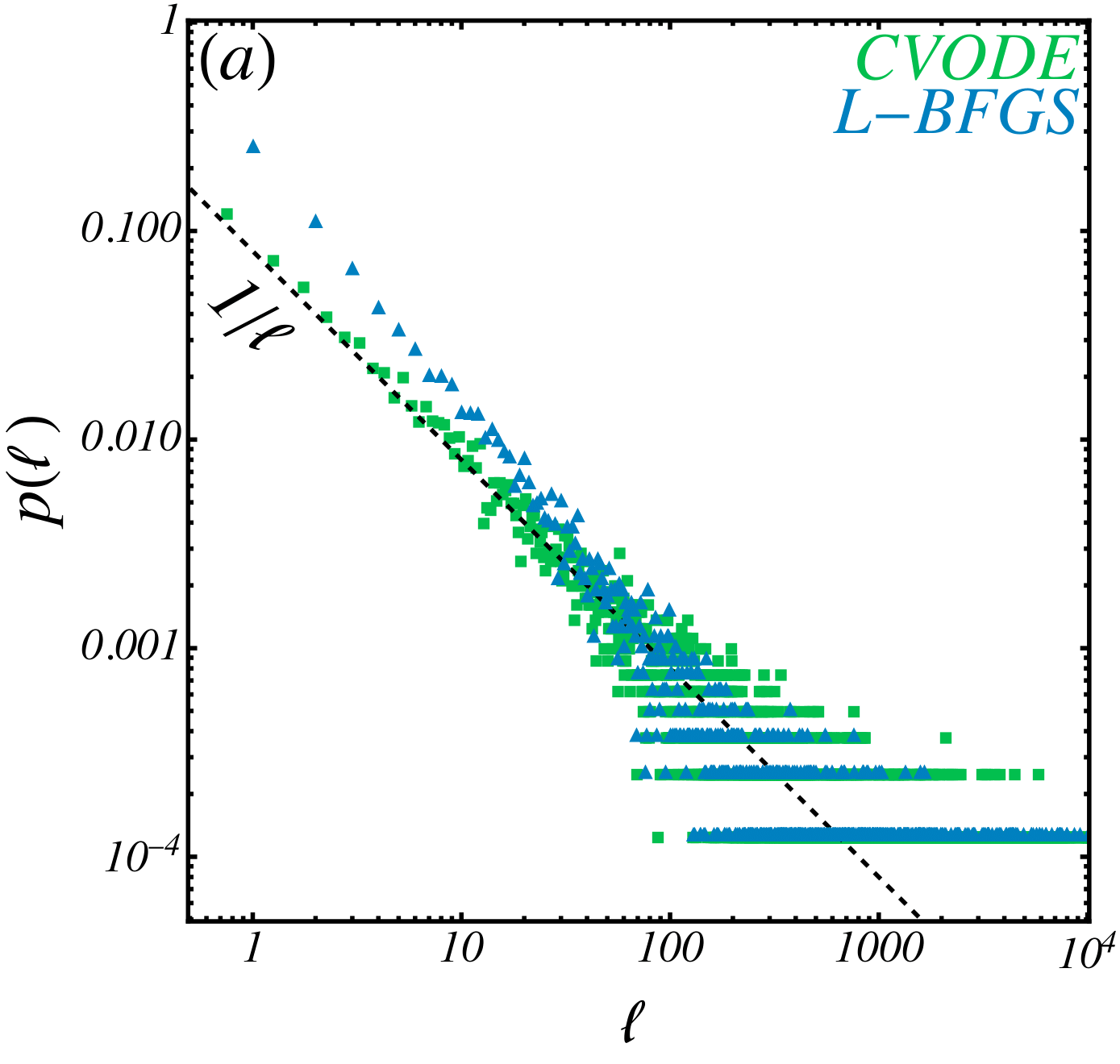
Exact Basins: 8 particles
Accuracy
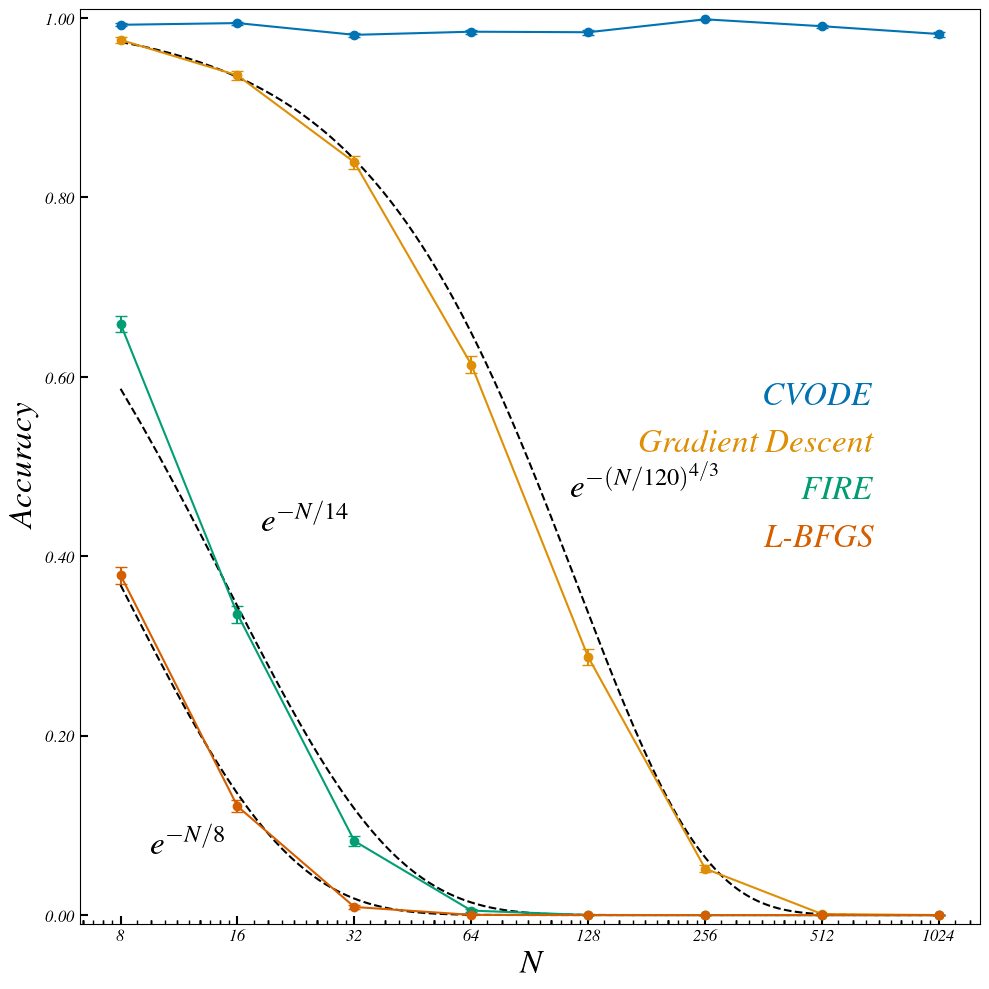
Accuracy



CVODE
FIRE
LBFGS
\(d_l \sim 254\)
\(N \sim 128 \)
Not a single sampled point matches
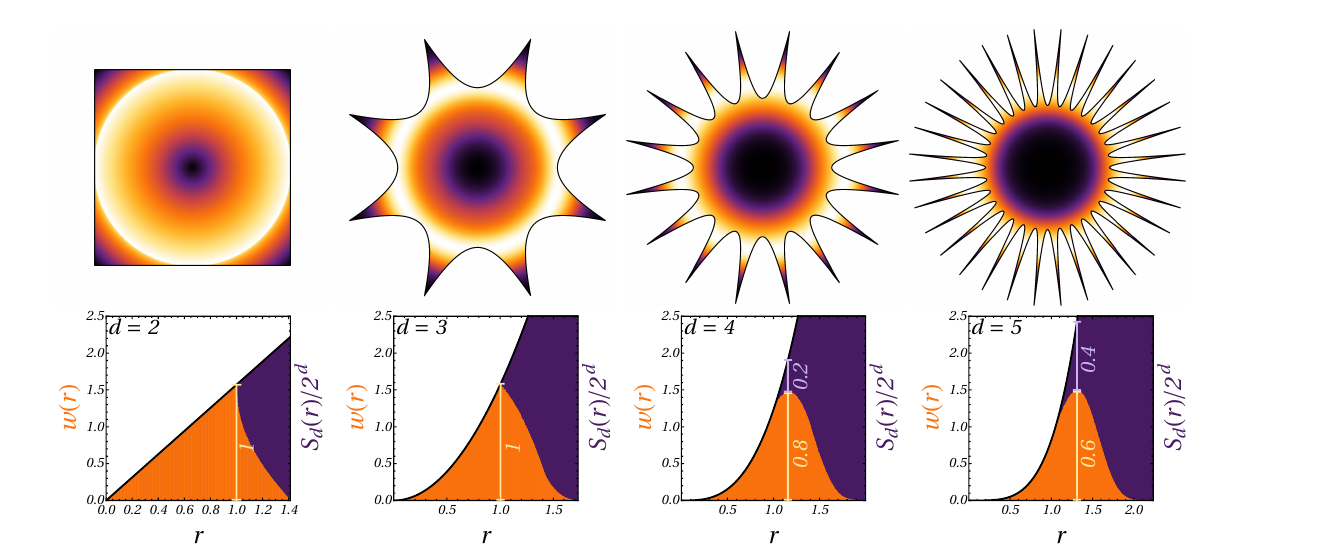
Areas to Volumes
\(V \sim l^d\)
\(log(V) \sim \log(l_1) + \log(l_2) + ...\)
The limiting distribution of \log(V) should go as Normal, if the mean and variance are well behaved and \(l\) isn't drawn from an already stable distribution
Distribution of lengths of basins
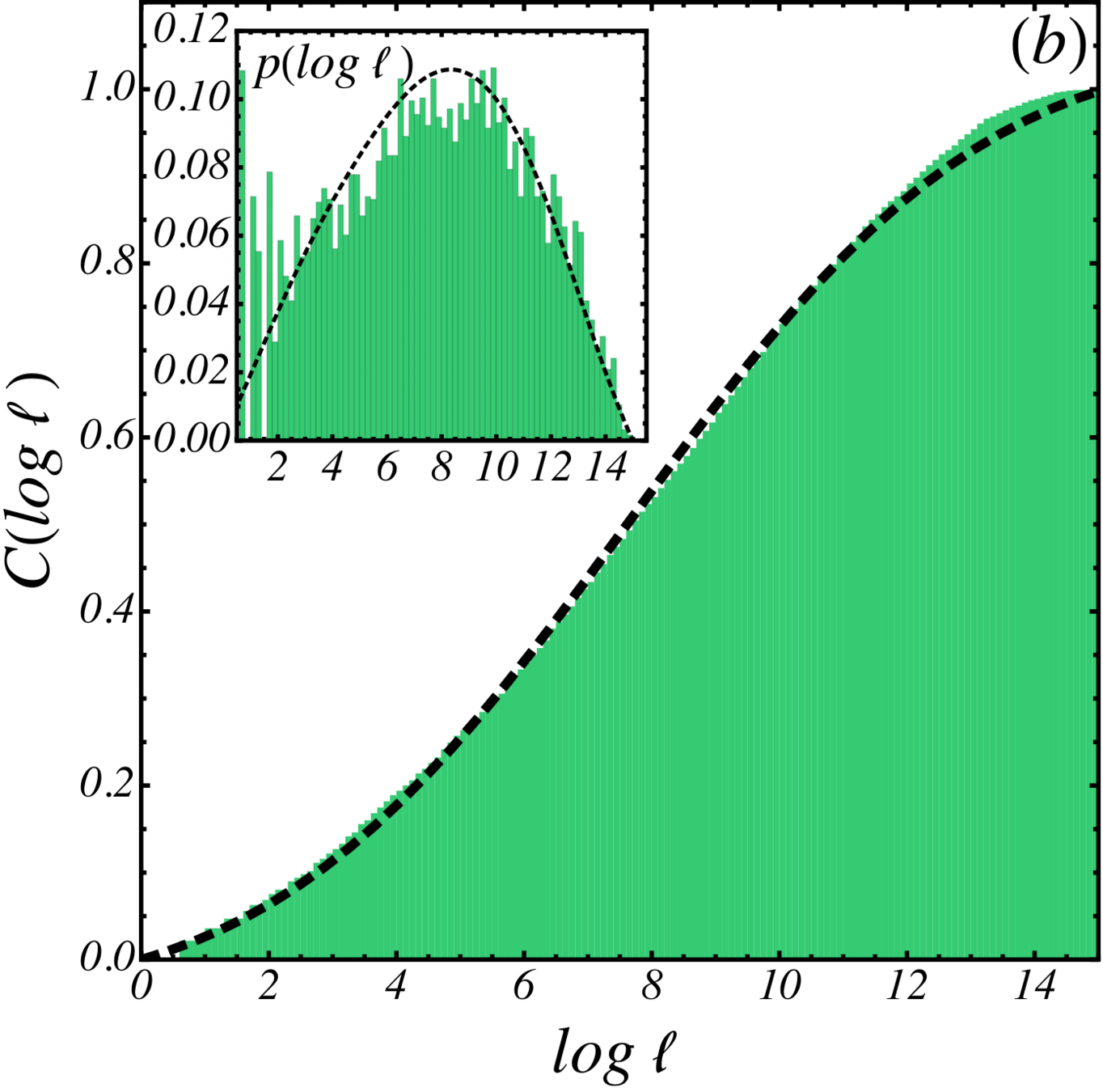
\(N=16\) \(d_l \sim 30\)

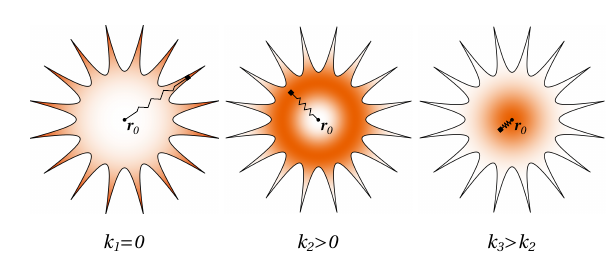
Basins in high dimensions
Casiulis et al. Papers in Physics 15 (2023): 150001
Most Probable: Maximum radial density

Probability of landing inside the basin
Hypercube \(~1000d\)
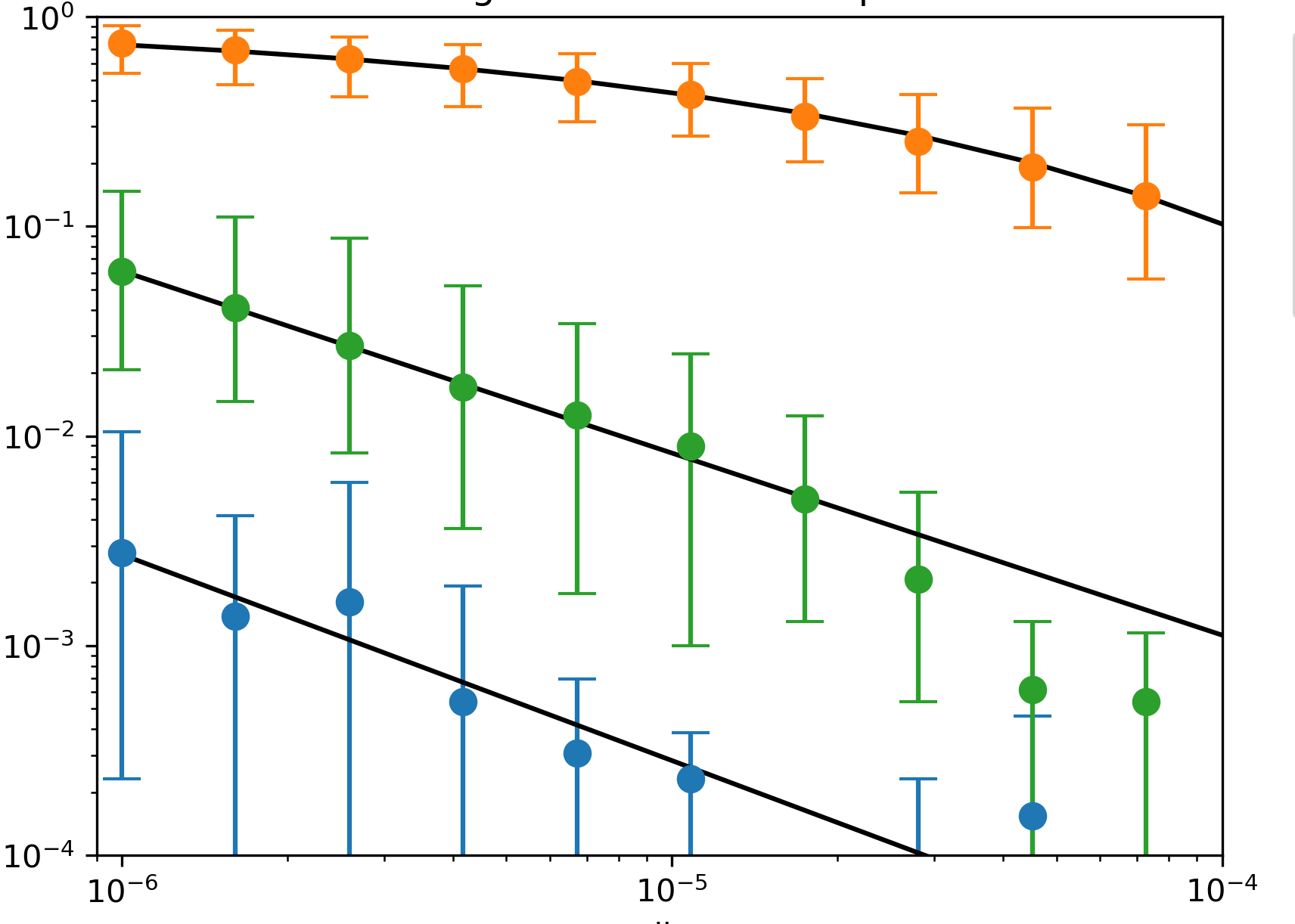
Survival probability in a tentacle
Casiulis et al. Papers in Physics 15 (2023): 150001-150001.

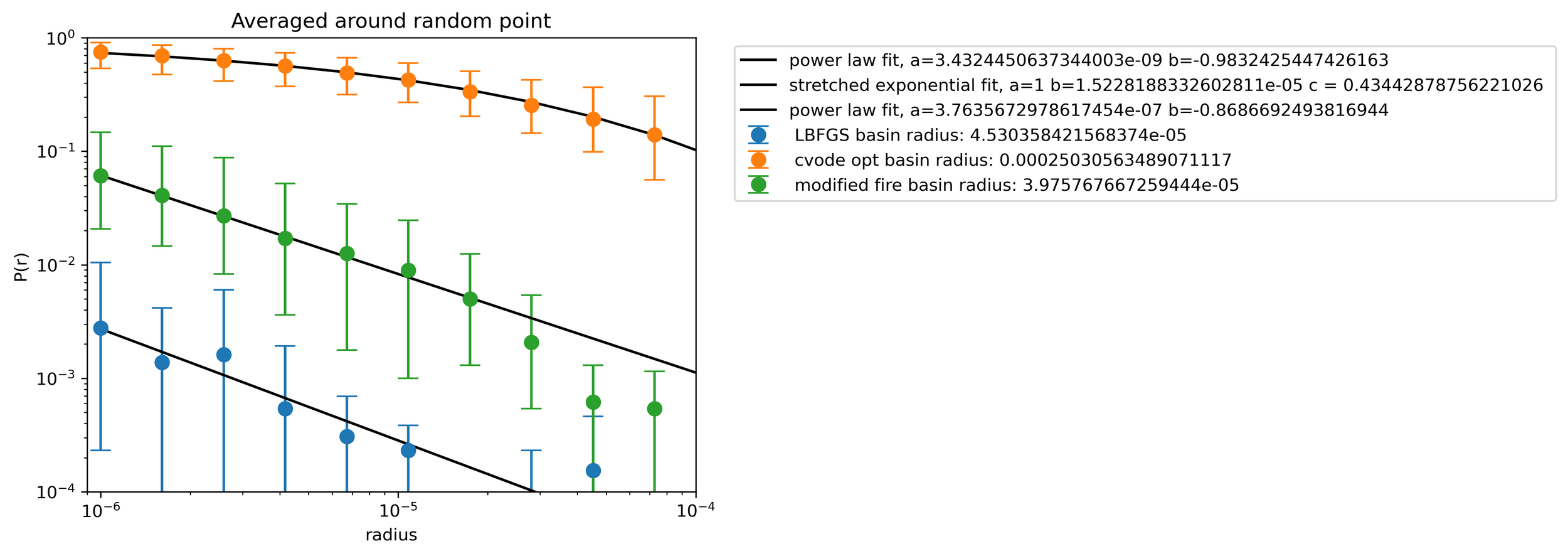
Survival Probability at r: Probability of staying inside basin taking uniform samples at radius r
Survival probability in a tentacle
Distance from point
CVODE
FIRE
LBFGS
\(P(r) = a x^b \)
Survival
Probability
CVODE
\(d_l = 2046 \)
\(P(r)=e^{-(r/r_0)^b}\)
\(1024\) particles
\(P(r) = a x^b \)
CVODE
Sampling basins in high dimensions
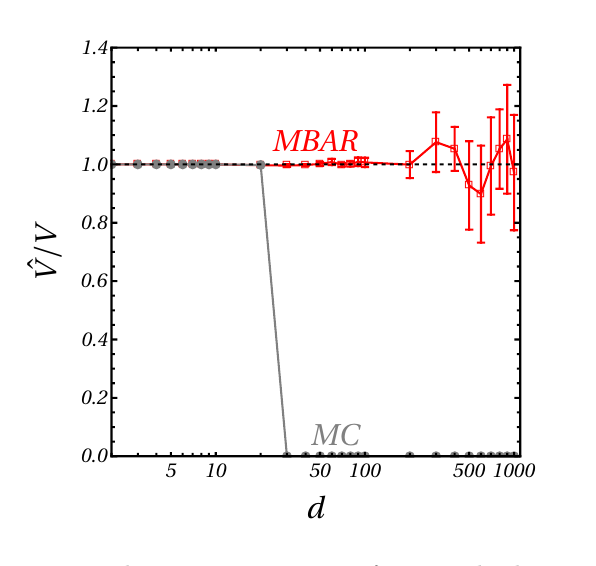
Brute force MC misses most of the volume!!
Umbrella sampling: Reconstruct uniform samples from MC walkers at different distances, which can be used to constuct volumes
Casiulis et al. Papers in Physics 15 (2023): 150001-150001.
Replica exchange
Calculating volumes in high dimensions
Casiulis et al. Papers in Physics 15 (2023): 150001-150001.
$$Z(k) = \int_{\mathbb{R}^N}^{} \mathcal{O}(x) e^{- \frac{1}{2} k \left|x-x_{0}\right|^{2}} dx$$
Partition function
Oracle (1 if inside basin. 0 if outside)
Spring (to control exploration)
$$ F(k) = - log(Z_{k}) $$
Free energy
$$ F(0) - F(k_{\infty}) = \int_{0}^{k_{\infty}} \frac{\partial F}{\partial k} dk = \int_{k_{\infty}}^{0} \langle \left| x-x_{0}\right|^{2} \rangle_{k} dk$$
Log volume (unknown)
Spring free energy
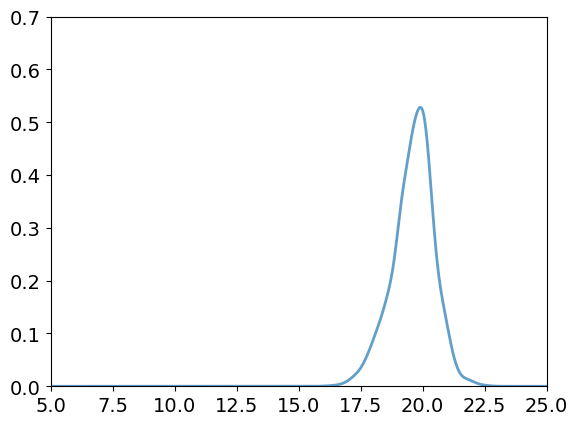
Accuracy within a single basin
\(128\) particles
\(d_l = 255 \)
Distance from minimum
Accuracy
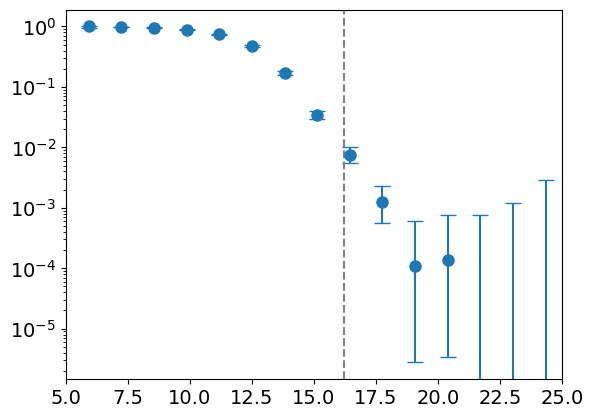
Most basin volume
Distance from minimum
Radial Density of Basin
Optimizer accuracy
Density
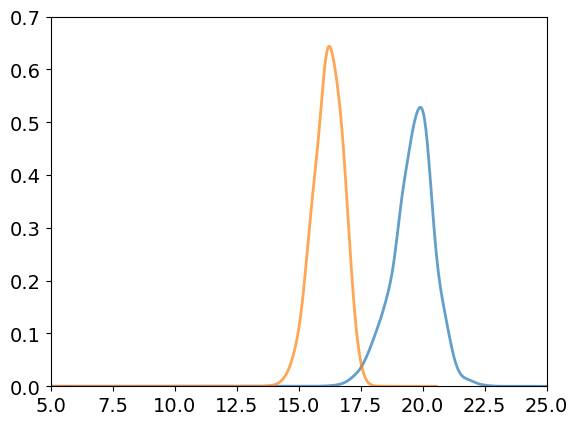
FIRE
CVODE
Take CVODE samples and minimize with FIRE
Accuracy within a single basin
\(128\) particles
\(d_l = 255 \)
Distance from minimum
Accuracy

Most basin volume
Distance from minimum
Radial Density of Basin
Optimizer accuracy
Density


FIRE
CVODE
Volumes of basins
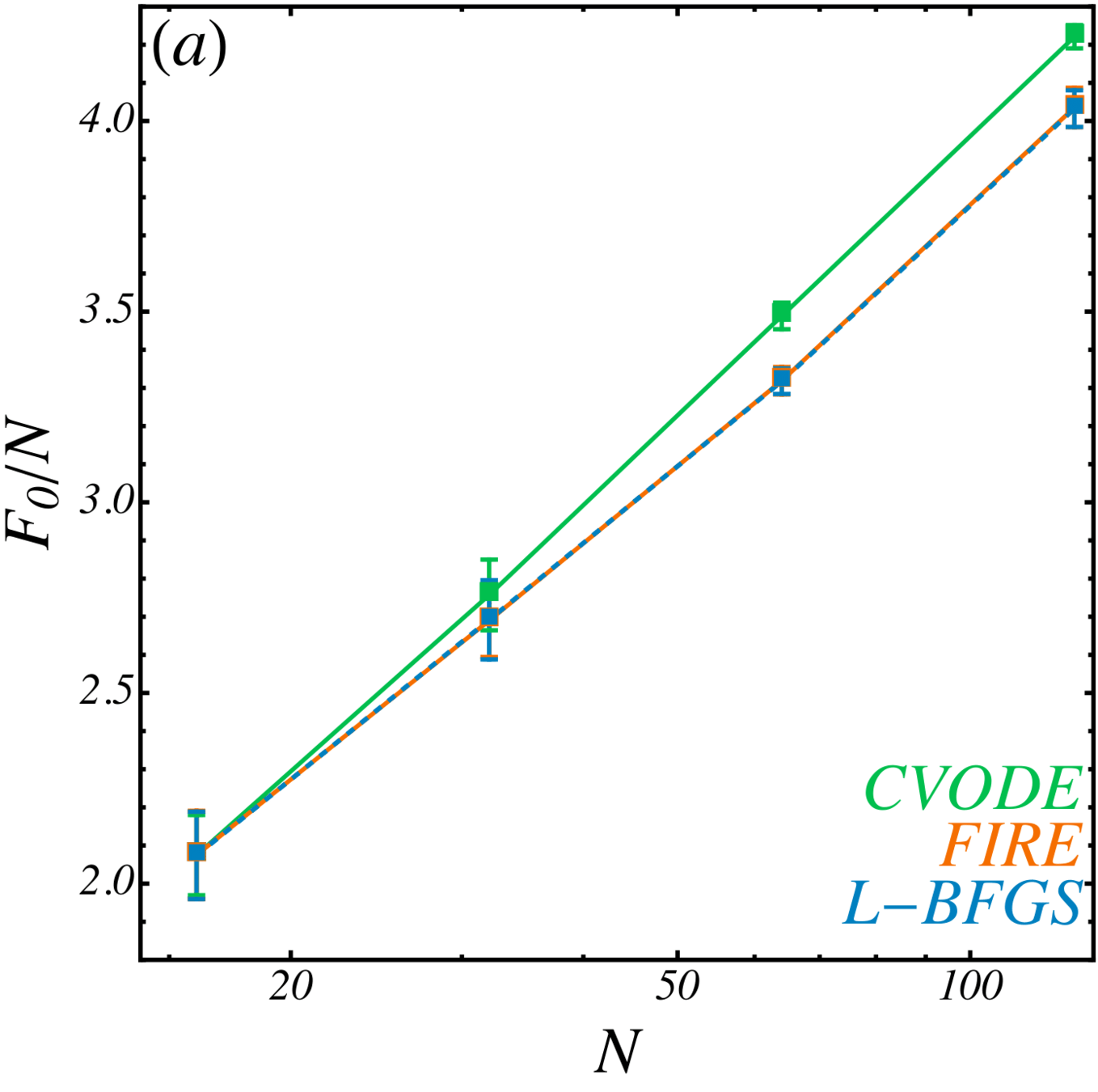
\(F_0 = - (1/N) \ln V \)
Edwards hypothesis

How probable is a packing?
Edwards: All packings are equally probable
Edwards conjecture: \(2d\)
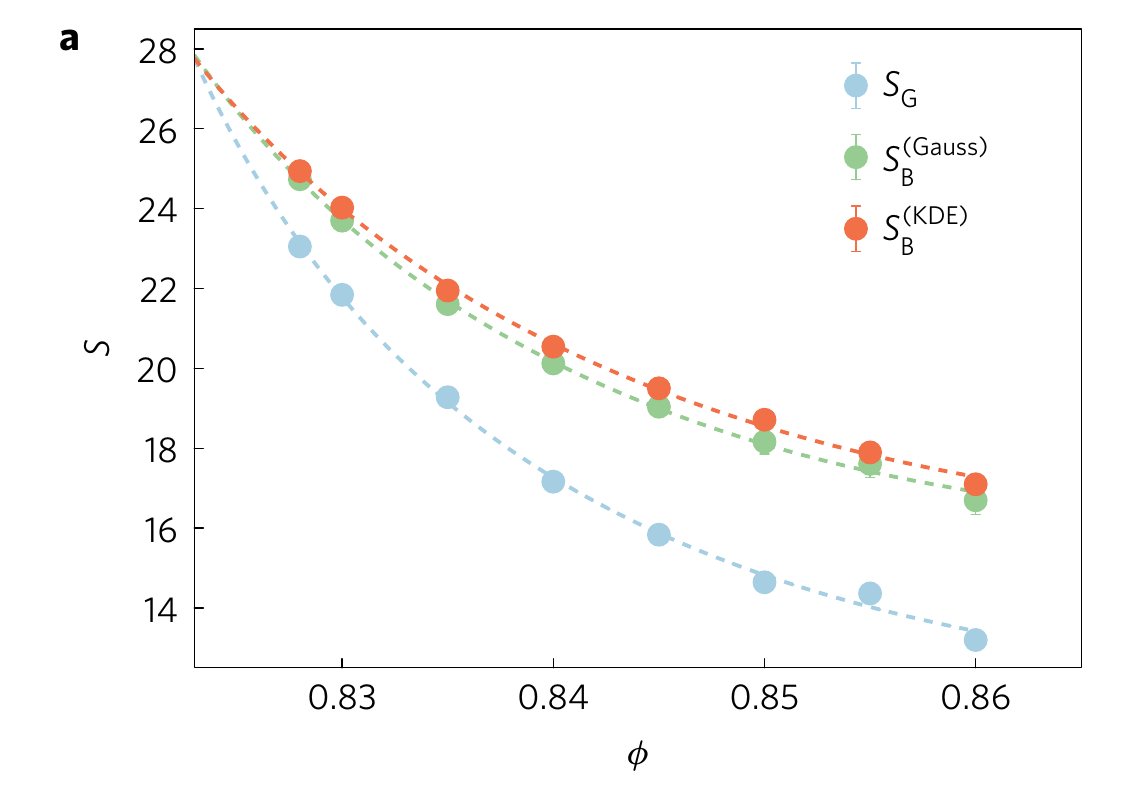
$$ S_G = - \sum_i p_i \ln p_i $$
$$ S_B = \ln(N_{packings}) $$
$$S_G=S_B \text{ at jamming}$$
Jamming
Martiniani, et al. Nature physics 13.9 (2017): 848-851.
Tested with FIRE, only tested computationally in 2d
packing probability
$$ N_{packings} = \frac{V_{space}}{\langle v_{basin} \rangle} $$
Counting by sampling
\(d\)
$$ N_{buildings} = \frac{L}{\langle\mathcal{d}\rangle} $$
Counting by sampling
$$ N_{packings} = \frac{V_{space}}{\langle v_{basin} \rangle} $$
- Choose a random initial condition
- Let the system relax
Stable packings are minima of the potential

Summary
- Basins are inaccurately identified with optimizer-based methods
- This has lead to biased calculations in previous published results
- Next steps: Check results for Edwards hypothesis in \(2d\) and check whether they hold in \(3d\)
Acknowledgments
Martiniani Lab

Stefano Martiniani

Mathias Casiulis




Fit data
Cubes in high dimensions
Casiulis et al. Papers in Physics 15 (2023): 150001-150001.
Most volume
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
steepest descent
basin 2
Basin Tiling (What we're interested in)
basin 1
basin 3
Can we do better?: Mixed Descent
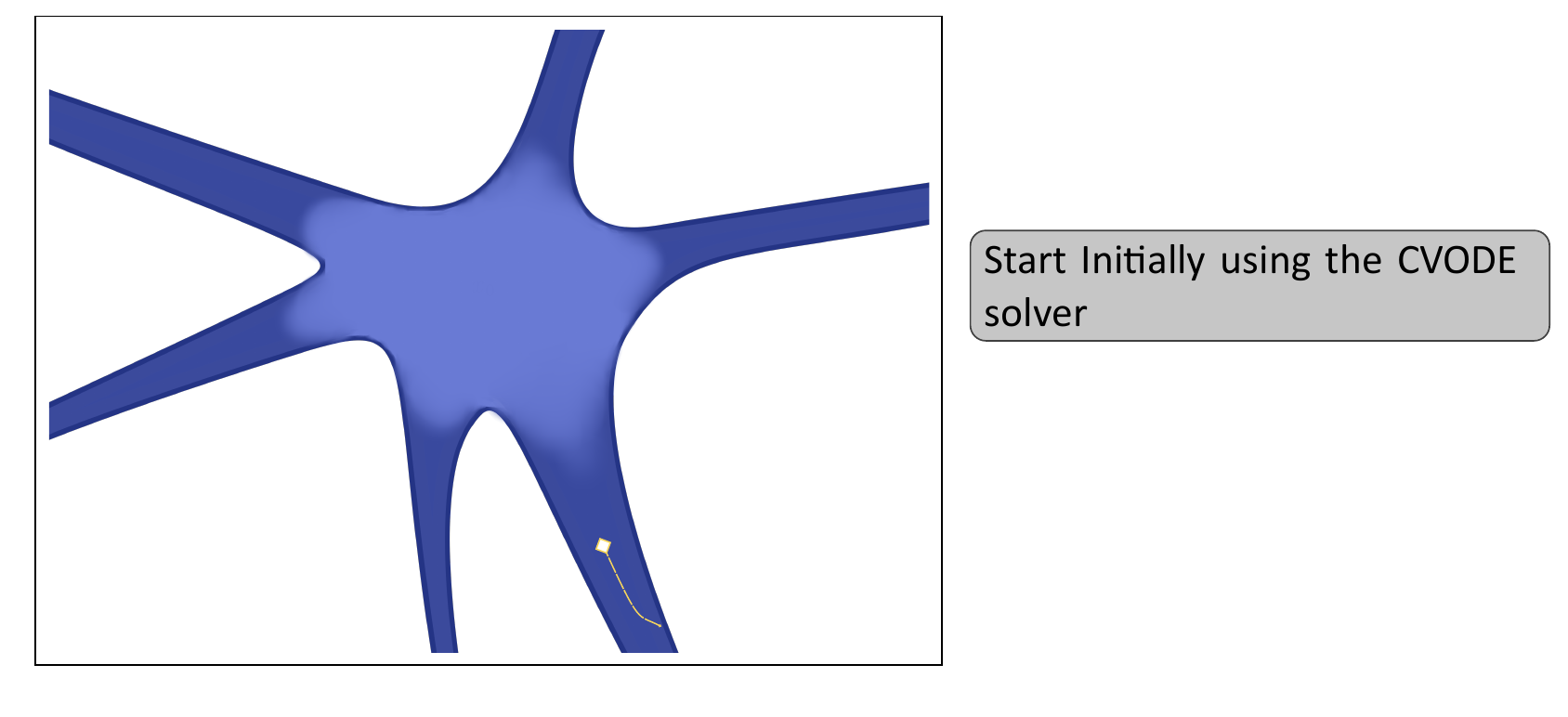
- Start with the CVODE solver
Basin identification
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
steepest descent
- Solving steepest descent in \(nD\) for interacting potentials is hard.
- a large volume of previous work mostly relies on optimization algorithms as proxies for finding basins
Method
- Use CVODE to solve the steepest descent equations
- CVODE is much faster than Gradient descent
- CVODE is much faster than scipy implemented stiff ODE methods
- Identify minima/optimize with pele (https://github.com/martiniani-lab/pele). Hard fork of Wales group code with additional functionality implemented
- Code implemented in basinerror (https://github.com/martiniani-lab/basinerror)
Goals for the talk
- I want to show you how to get basins of attraction in high dimensions accurately
- I want to show you how you can get them fast
Accuracy curves: Harmonic potential (2d)

CVODE: Results
How to get Global Accuracy
- Generate \(N\) steepest descent trajectories to the minima at very low \(rtol\) from random initial conditions
- verify that the minima don't change when you increase \(rtol\) $$\frac{N_\text{incorrect}}{N} < 0.01 $$

\(N\)
\(rtol\)
95 percent accuracy
Accuracy curves: Harmonic potential (2d)

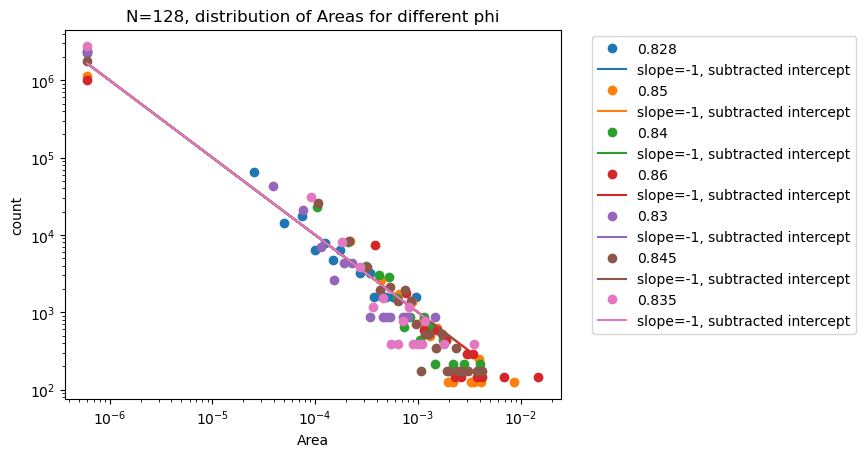
Areas

\(N=128\) \(d_l = 254\)
Polydisperse spheres
A fast and accurate algorithm
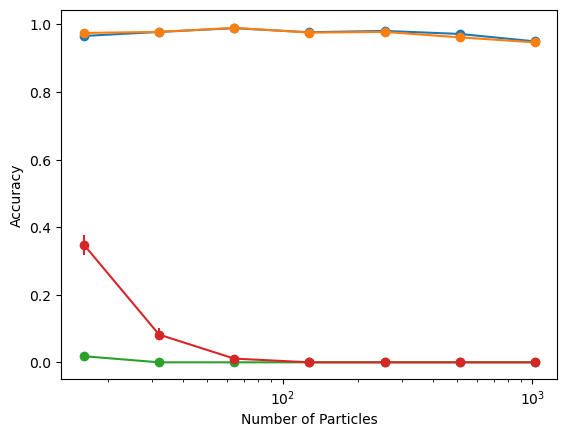
CVODE
Mixed Descent
FIRE
LBFGS
LBFGS
Mixed Descent
CVODE
FIRE
Counting by sampling
\(d\)
$$ N_{buildings} = \frac{D}{\langle\mathcal{d}\rangle} $$
Accuracy within a single basin
\(128\) particles
\(d_l = 14 \)
LBFGS
FIRE
Distance from minimum
Accuracy
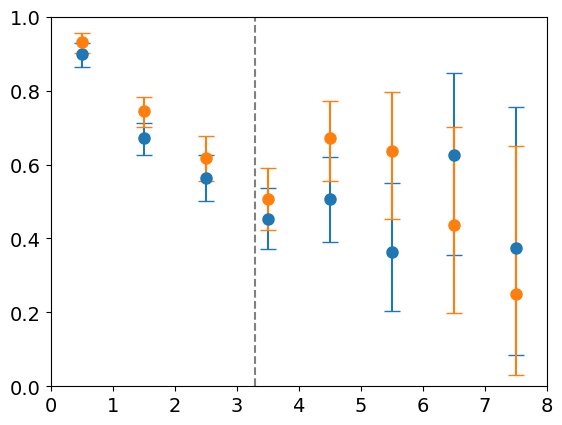
Most basin volume
Distance from minimum
Radial Density of Basin
Optimizer accuracy
Density
Monday morning Nov 2024
By Praharsh Suryadevara
Monday morning Nov 2024
- 173



