Graphs Key Concepts

Problems involving Graphs

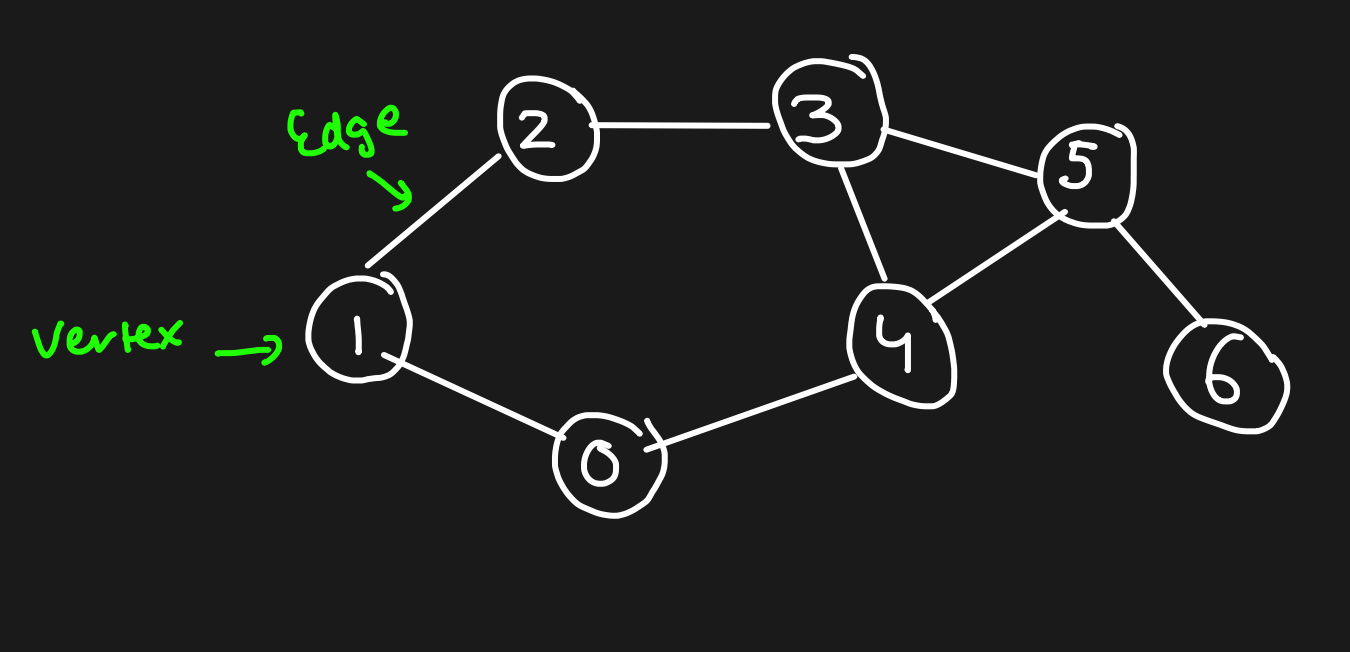
Types of Graph

1. Weighted Graph

2. Unweighted Graph

3. Undirected Graph

4. Directed Graph

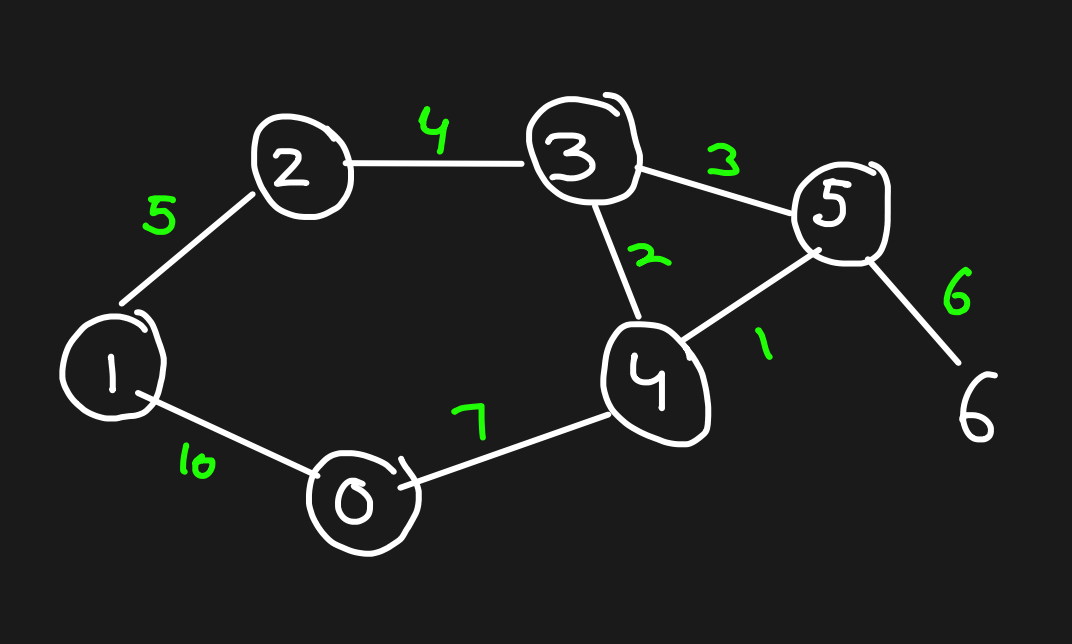
Weighted Graph

Graphs whose edges or paths have values called weights. Edges value can represent weight/cost/length

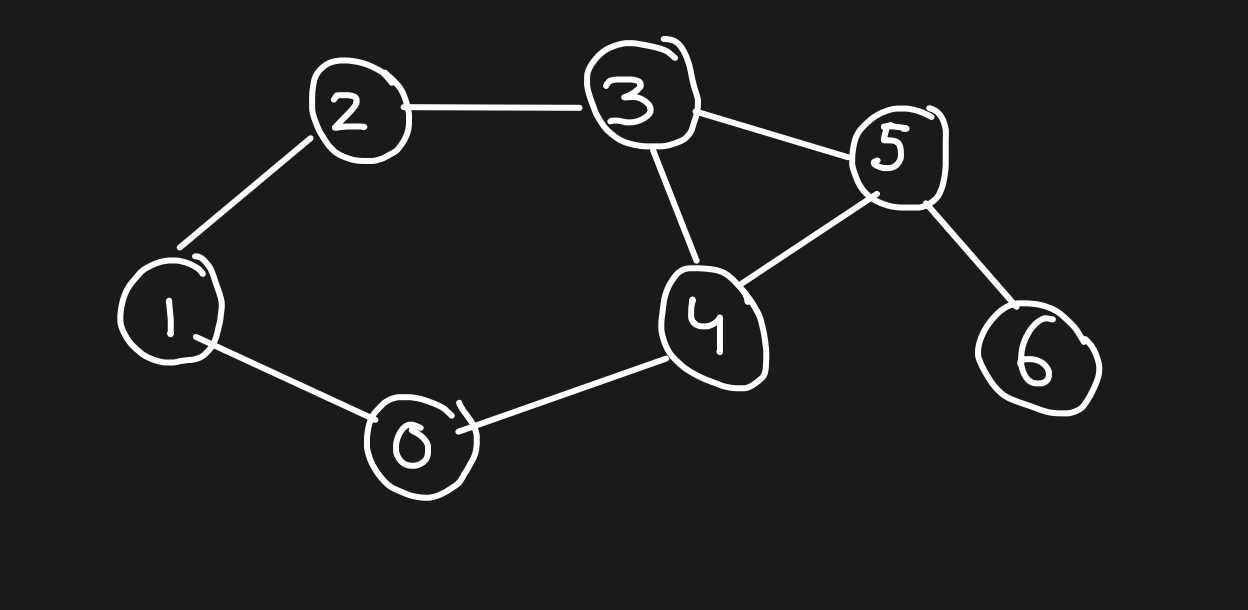
Unweighted Graph

There is no value or weight associated with the edge. By default, all the graphs are unweighted unless there is a value associated.

Undirected Graph

All edges are bi-directional.

For example - Friends connected on facebook

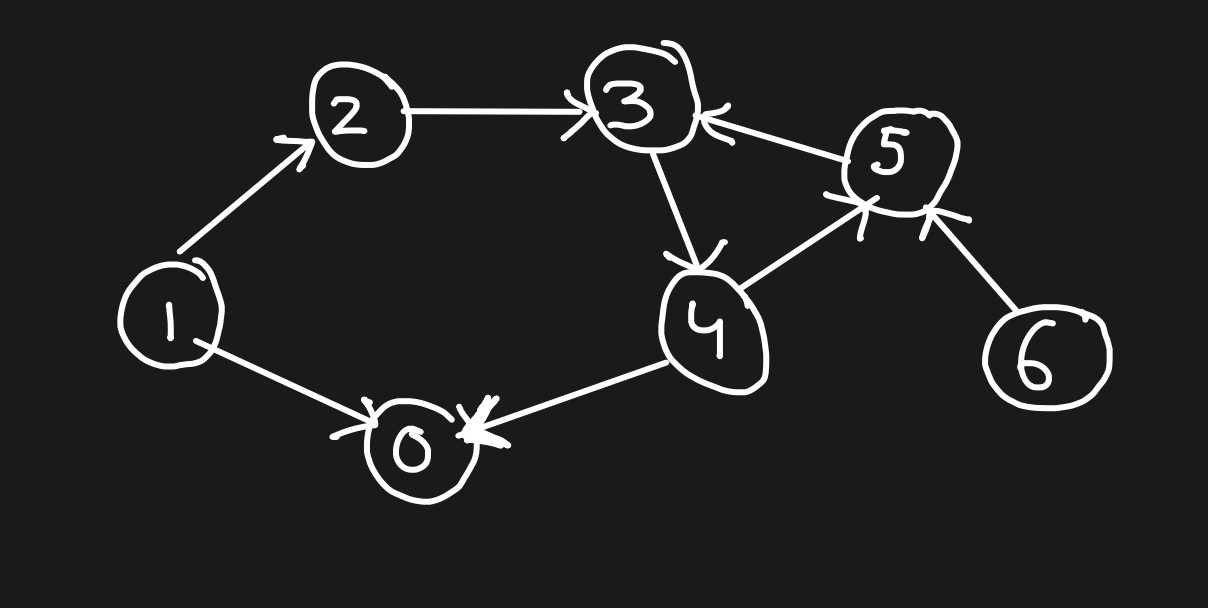
Directed Graph

Edges are directed from one node to another.
For example - Flights Routes, Flight Fares

Storing a Graph

• Adjacency Matrix

• Adjacency List

Adjacency Matrix

Adjacency List

Graph Traversals

• BFS (Breadth First Search)

• DFS (Depth First Search)

BFS

Time to Code  👩‍💻  

DFS

Undirected Graphs

🚀 Snakes & Ladders

Connected Components

🚀 Counting Pairs

Problem Statement ....

Cycle Detection-I

Undirected Graphs

🚀 Dijkshtra's Algorithm

    Shortest Paths

- Weighted Graphs

- Single Source Shortest Paths (SSSP)

🚀 Shortest Path Algorithms

Single Source Shortest Path

1. BFS

2. Dijkstra's

3. Bellman Ford

All-Pairs Shortest Path

4. Floyd Warshall

🚀 Shortest Path Algorithms

Single Source Shortest Path

1. BFS

2. Dijkstra's

3. Bellman Ford

All-Pairs Shortest Path

4. Floyd Warshall

Single Source

Shortest Path

Simple BFS Algorithm

We can use BFS, for unweighted graphs!

🚀 Dijkshtra's Algorithm

    Shortest Paths

• Weighted Graphs
• Single Source Shortest Paths (SSSP)
• Greedy Algorithm
• Dijkstra doesn’t work for Graphs with negative weight edges

🚀 Bellman Ford

• Weighted Graphs
• Single Source Shortest Paths (SSSP)
• Bellman-Ford works for graphs with negative weight edges.

🚀 Floyd Warshall

Weighted Graphs

Single All Pairs Shortest Paths (APSP) 

Dynamic Programming based algorithm.

1. BFS (SSSP on unweighted graph) 

2. Dijkstra's (SSSP on weighted graph)

3. Bellman Ford (SSSP on weighted graph with -ve edges) 

4. Floyd Warshall (APSP on all graphs)

Time to Code  👩‍💻  

Disjoint Set Union👨‍💻👩‍💻

Data Structure

DSU Data Structure

1. Find

2. Union

Minimum Spanning Trees

Minimum Spanning Tree

Problem Statement: Given a connected, undirected and weighted graph G, select a subset of edges E' such that graph G is conncected and total weight of selected edges E' is minimum.

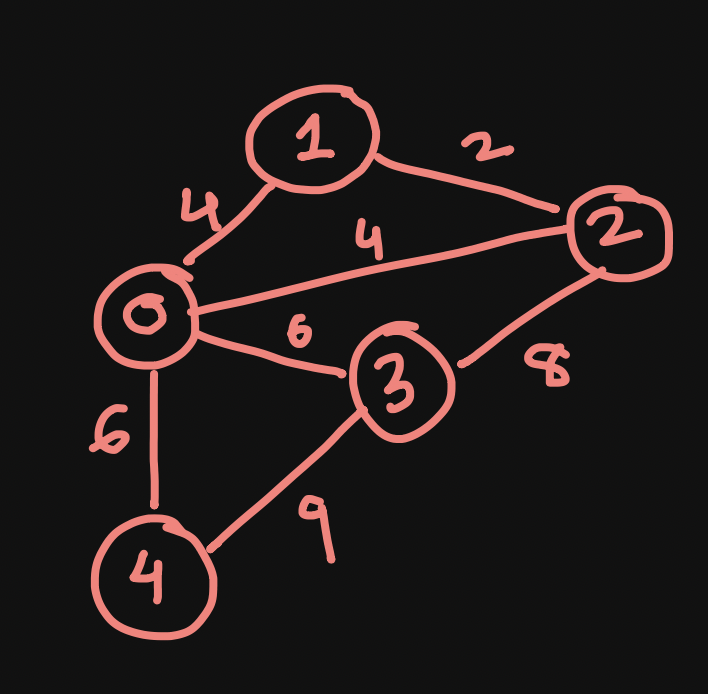
Minimum Spanning Tree

Example

Minimum Spanning Tree

V-1 Edges to form a tree and keep the graph connected

Real Life Application

• Building Roads for Villages
• Connecting remote Villages via roads, each village is vertex and each edge is road. Minimise the total cost of building roads.

Minimum Spanning Tree

Popular Algorithms

• Prim's Algorithm
• Kruskal's Algorithm

🚀 Prims's Algorithm

    for MST

• Greedy Algorithm
• Uses a priority queue

🚀 Kruskal's Algorithm

    for MST

• Greedy Algorithm
• Stores graph as a edge list
• DSU for detecting Cycle
• O(ELogV)

Topological Sorting

Directed Acyclic Graphs

Biparite Graph

Strongly Connected Components