高翊恩
Parity
魔術方塊中的奇偶性
Index
貼心提醒
- 可能有一點排列組合
- 可能有一點群論
不懂的找賴泓安
魔術方塊的狀態數
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 每個角塊有自己的位置\(\Rightarrow8!\)
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 每個角塊有自己的位置\(\Rightarrow8!\)
- 每個角塊有自己的方向\(\Rightarrow3^8\)
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 每個角塊有自己的位置\(\Rightarrow8!\)
- 每個角塊有自己的方向\(\Rightarrow3^8\)
- 每個邊塊有自己的位置\(\Rightarrow12!\)
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 每個角塊有自己的位置\(\Rightarrow8!\)
- 每個角塊有自己的方向\(\Rightarrow3^8\)
- 每個邊塊有自己的位置\(\Rightarrow12!\)
- 每個邊塊有自己的方向\(\Rightarrow2^{12}\)
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 每個角塊有自己的位置\(\Rightarrow8!\)
- 每個角塊有自己的方向\(\Rightarrow3^8\)
- 每個邊塊有自己的位置\(\Rightarrow12!\)
- 每個邊塊有自己的方向\(\Rightarrow2^{12}\)
總狀態數\(=8!\times3^8\times12!\times2^{12}\)
\(\approx5.19\times10^{20}\)
總狀態數\(=8!\times3^8\times12!\times2^{12}\)
\(\approx5.19\times10^{20}\)
總狀態數\(=8!\times3^8\times12!\times2^{12}\)
\(\approx5.19\times10^{20}\)
是不是多了什麼?
總狀態數\(=8!\times3^8\times12!\times2^{12}\)
\(\approx5.19\times10^{20}\)
是不是多了什麼?




魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 角塊位置\(\Rightarrow8!\)
- 角塊方向\(\Rightarrow3^8\)
- 邊塊位置\(\Rightarrow12!\)
- 邊塊方向\(\Rightarrow2^{12}\)
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 角塊位置\(\Rightarrow8!\)
- 角塊方向\(\Rightarrow3^8\)
- 邊塊位置\(\Rightarrow12!\)
- 邊塊方向\(\Rightarrow2^{12}\)
禁止角塊對調\(\Rightarrow\times\frac{1}{2}\)
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 角塊位置\(\Rightarrow8!\)
- 角塊方向\(\Rightarrow3^8\)
- 邊塊位置\(\Rightarrow12!\)
- 邊塊方向\(\Rightarrow2^{12}\)
禁止角塊對調\(\Rightarrow\times\frac{1}{2}\)
禁止角塊自旋\(\Rightarrow\times\frac{1}{3}\)
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 角塊位置\(\Rightarrow8!\)
- 角塊方向\(\Rightarrow3^8\)
- 邊塊位置\(\Rightarrow12!\)
- 邊塊方向\(\Rightarrow2^{12}\)
禁止角塊對調\(\Rightarrow\times\frac{1}{2}\)
禁止角塊自旋\(\Rightarrow\times\frac{1}{3}\)
禁止邊塊對調\(\Rightarrow\times\frac{1}{2}\)
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 角塊位置\(\Rightarrow8!\)
- 角塊方向\(\Rightarrow3^8\)
- 邊塊位置\(\Rightarrow12!\)
- 邊塊方向\(\Rightarrow2^{12}\)
禁止角塊對調\(\Rightarrow\times\frac{1}{2}\)
禁止角塊自旋\(\Rightarrow\times\frac{1}{3}\)
禁止邊塊對調\(\Rightarrow\times\frac{1}{2}\)
禁止邊塊自旋\(\Rightarrow\times\frac{1}{2}\)
魔術方塊的狀態數
將一顆魔術方塊隨意轉動,能夠轉出多少種不一樣的狀態?
- 角塊位置\(\Rightarrow8!\)
- 角塊方向\(\Rightarrow3^8\)
- 邊塊位置\(\Rightarrow12!\)
- 邊塊方向\(\Rightarrow2^{12}\)
禁止角塊對調\(\Rightarrow\times\frac{1}{2}\)
禁止角塊自旋\(\Rightarrow\times\frac{1}{3}\)
禁止邊塊對調\(\Rightarrow\times\frac{1}{2}\)
禁止邊塊自旋\(\Rightarrow\times\frac{1}{2}\)
總狀態數\(\approx5.19\times10^{20}\times\frac{1}{2}\times\frac{1}{3}\times\frac{1}{2}\times\frac{1}{2}\)
\(\approx2.16\times10^{19}\)
總狀態數\(\approx5.19\times10^{20}\times\frac{1}{2}\times\frac{1}{3}\times\frac{1}{2}\times\frac{1}{2}\)
\(\approx2.16\times10^{19}\)
總狀態數\(\approx5.19\times10^{20}\times\frac{1}{2}\times\frac{1}{3}\times\frac{1}{2}\times\frac{1}{2}\)
\(\approx2.16\times10^{19}\)
BRUH.
為什麼還是錯的?
總狀態數\(\approx5.19\times10^{20}\times\frac{1}{2}\times\frac{1}{3}\times\frac{1}{2}\times\frac{1}{2}\)
\(\approx2.16\times10^{19}\)
BRUH.
為什麼還是錯的?

神奇J-b perm
神奇J-b perm
給定一顆轉亂的方塊,但只能使用以下操作:
- x
- y
- z
- J-b perm
是否對於每一種狀態都可以將其復原?
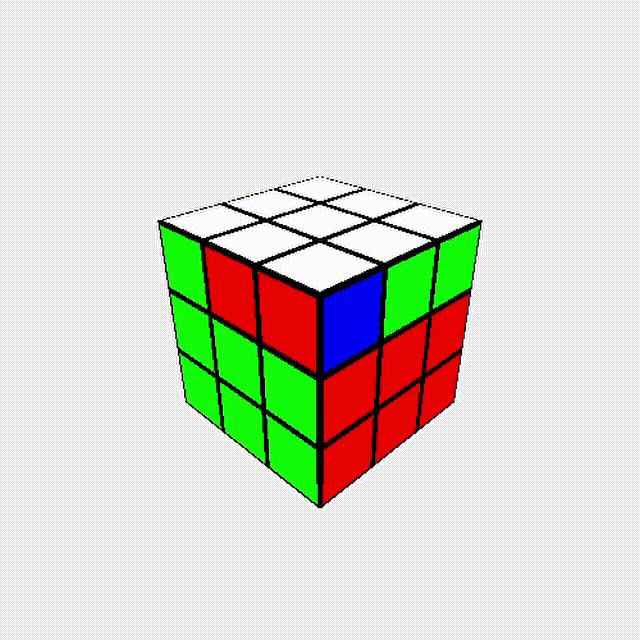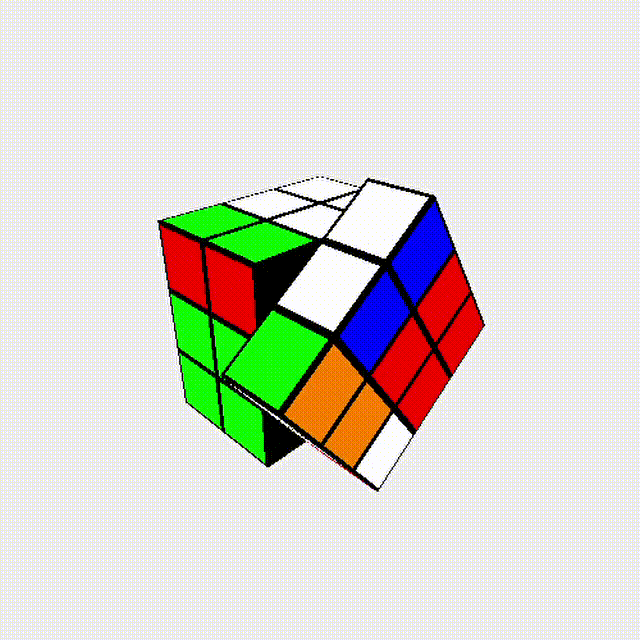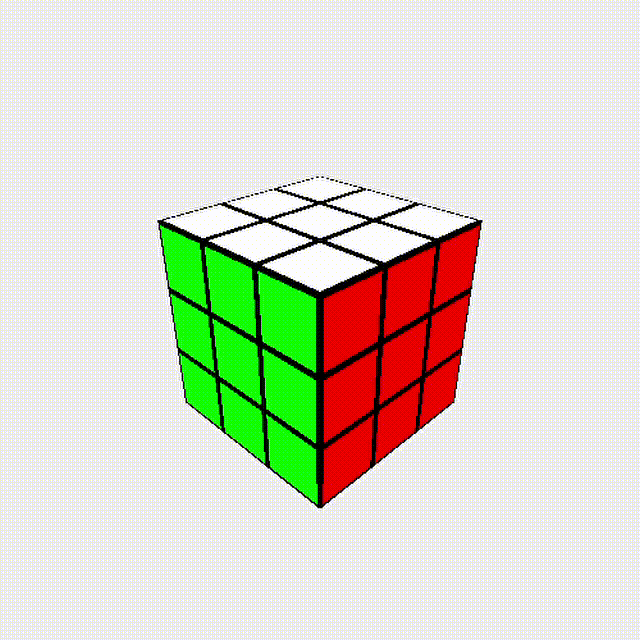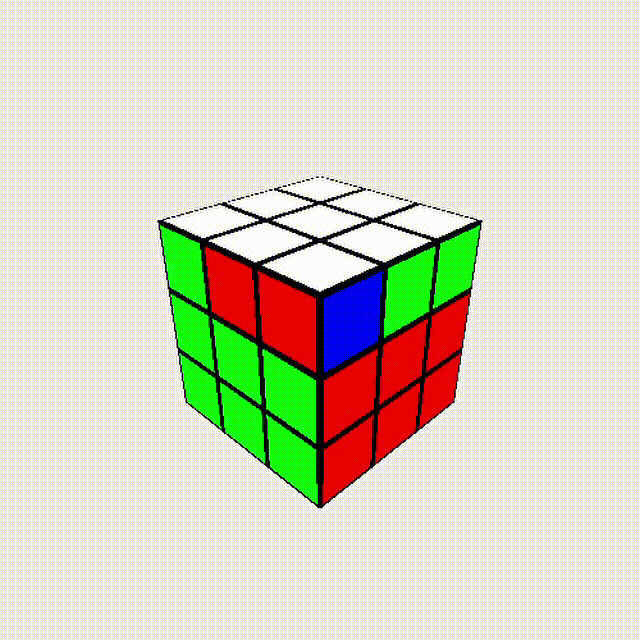
我們來看一個現象:
我們來看一個現象:
我們來看一個現象:
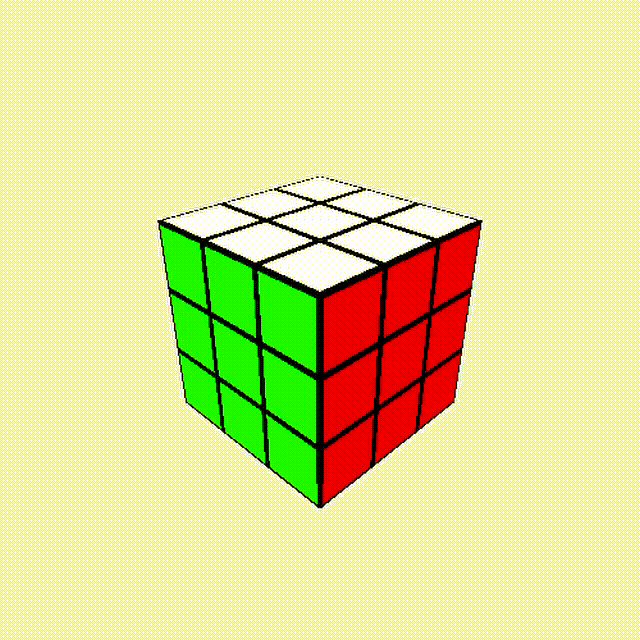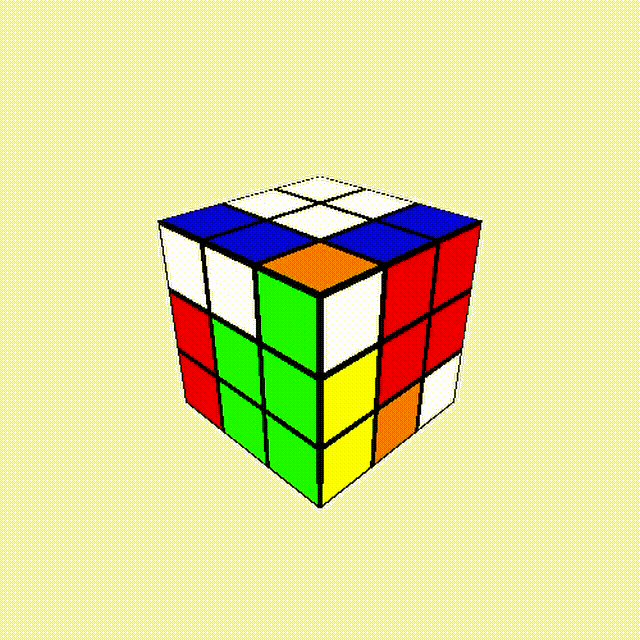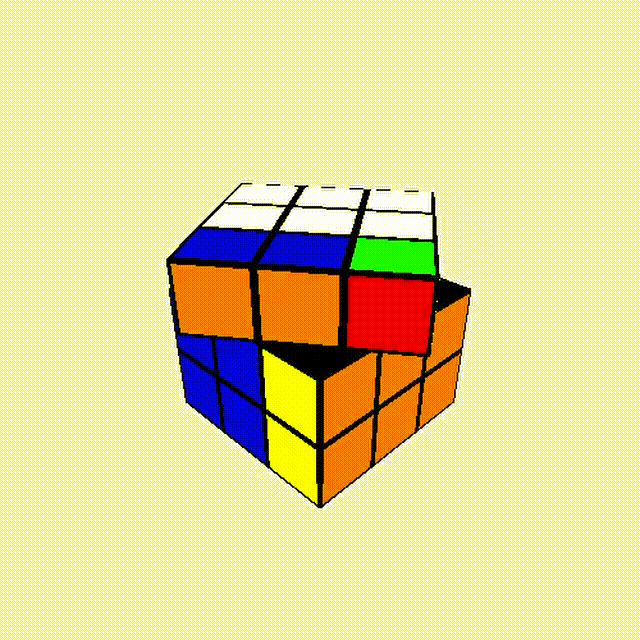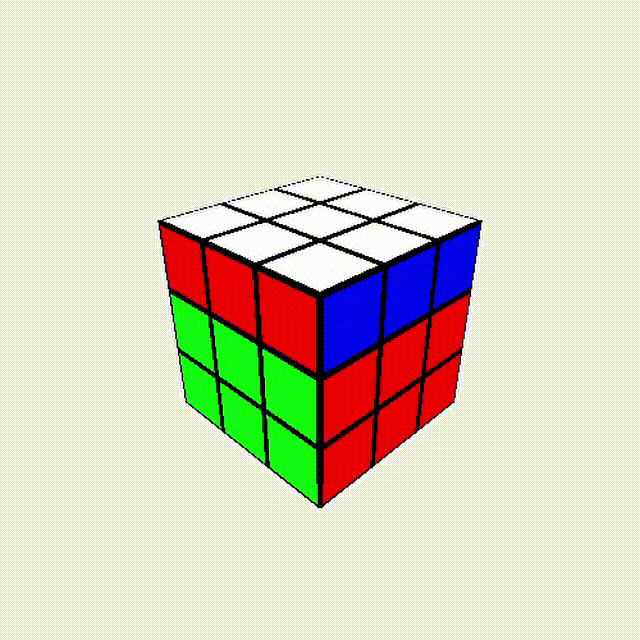
J-b + y + J-b + y + J-b + y2 = U !!!
J-b + y + J-b + y + J-b + y2 = U !!!
換句話說:任何外層轉動的操作\(=3\)個J-b perm
J-b + y + J-b + y + J-b + y2 = U !!!
換句話說:任何外層轉動的操作\(=3\)個J-b perm
J-b perm 可視為方塊轉動的最基本單位
Parity
J-b perm
到底在幹嘛?
J-b perm
到底在幹嘛?
交換\(1\)組邊塊,且
交換\(1\)組角塊
J-b perm
到底在幹嘛?
交換\(1\)組邊塊,且
交換\(1\)組角塊
可不可以只換邊塊、角塊其中\(1\)個?
最怪的地方來了
其實我們可以一起交換任意一組邊塊和任意一組角塊!
從J-b perm到Pairty
從J-b perm到Pairty

從J-b perm到Pairty

邊塊交換數:0
角塊交換數:1
從J-b perm到Pairty

邊塊交換數:0
角塊交換數:1
從J-b perm到Pairty

從J-b perm到Pairty

邊塊交換數:1
角塊交換數:0
從J-b perm到Pairty

邊塊交換數:1
角塊交換數:0
從J-b perm到Pairty

從J-b perm到Pairty

邊塊交換數:1
角塊交換數:1
從J-b perm到Pairty

邊塊交換數:1
角塊交換數:1
從J-b perm到Pairty
從J-b perm到Pairty
邊塊交換數:8
角塊交換數:6
從J-b perm到Pairty
邊塊交換數:8
角塊交換數:6
其他種類的Parity
- 三階的另一個pairty
- 四階、高階邊塊反轉
- square-X
- 數字華容道
俄羅斯方塊
Parity
By pring
Parity
- 254



