Quantum Computing:

State of Play

Justin Dressel, Ph.D.
Institute for Quantum Studies, Chapman University

 

OC ACM Chapter Meeting, May 16th, 2018

Quantum Computing : Media Hype

What is a "Quantum" Computer?

IBM, Superconducting quantum computer

Main Idea : Computation is Physics

  • Traditional computation uses classical physics
    • Turing Machines : data tape and a moving read/write head for bits






       
  • The physical world is better described by quantum physics
    • Atoms, Molecules : do not generally behave like Turing Machines
       
  • Does quantum physics change the possibilities of computation?
    • Yes.  The theory of computation must be extended

Anything "Turing Complete" can simulate a Turing Machine, and thus all classical computation.

 

Even Microsoft Excel

or Minecraft

Classical Physics & Bits

  • Classical Bits
    • Electrical signals : bits are high/low voltages on metallic wires




       

    • Magnetic domains : bits are spin configurations in arrays of atoms

Bits are definite physical configurations (0 or 1)

Quantum Physics and Qubits

New "coherent" features for quantum bits (qubits)

  • ​Superpositions of 0 and 1 can also be definite​
    A bit has two possible definite states.
    A qubit has a definite state for each point on the surface of a unit sphere.     
     
  • Entanglement breaks modularity : More is different
    1 qubit requires 2 continuous angles to cover its spherical state space
    N qubits require 2(2^N-1) continuous angles to cover their state space (not 2N)
    Exponential scaling of parameters with qubit number, not linear!
     
  • Time-symmetry : logic gates must be reversible
    Qubit states follow smooth continuous orbits on the unit sphere
     
  • Measurement forces probabilistic description
    When measured, qubit randomly collapses to 0 or 1 based on state proximity

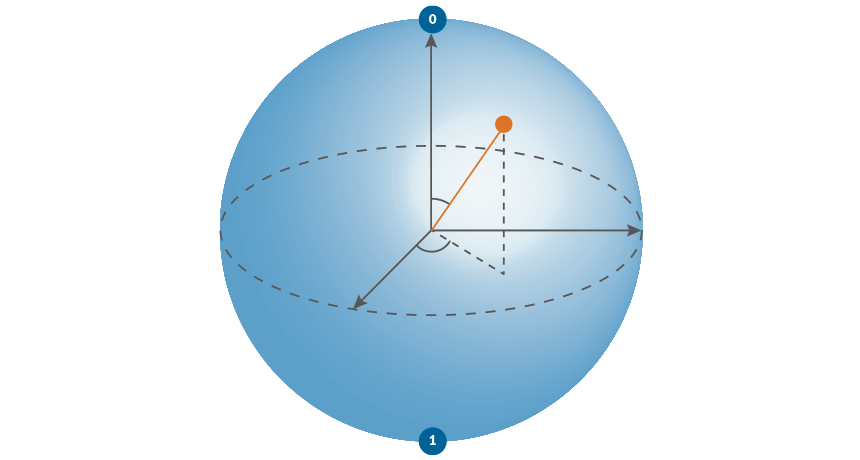
These coherent features wash out (or "decohere") on the macro-scale to produce the classical picture

Probabilistic Bits vs. Quantum Bits

  • Probabilistic state: 1 parameter

     
  • Evolution can only flip:
  • Measurement obeys Bayes' rule:
z = {\small P(1) - P(0) \in [-1,1]},\quad {\small (P(1) + P(0) = 1)}
P(1|r) = \frac{P(r|1)P(1)}{P(r|1)P(1)+P(r|0)P(0)}
1\;{\small (z=1)}
0\;{\small (z=-1)}
z
  • Probabilistic state: 3 parameters



     
  • Evolution precesses in circle: 
  • Measurement obeys Bayes' rule
\lvert 1\rangle \;{\small (z=1)}
\lvert 0\rangle \;{\small (z=-1)}
\lvert +\rangle \;{\small (x=1)}
\lvert -\rangle \;{\small (x=-1)}
\lvert -i\rangle \qquad\;\;{\small (y=-1)}
\vec{\rho} = {(x,y,z) \in [-1,1]^{\times 3}},\quad {\small (x^2+y^2+z^2 \leq 1)}
\lvert i\rangle
x + iy = e^{-(i\phi+d)/2}\,2\sqrt{P(1)P(0)}
0 \leftrightarrow 1, \; {\small (z \to -z)}
\partial_t \vec{\rho} = \vec{\Omega} \times \vec{\rho}

Classical Bit

Quantum Bit

Shares same "z-axis"

Decoheres as projection to indefinite classical state on z-axis

Only 2 definite states: 0 or 1

 

z-axis connecting them is indefinite, or probabilistic

Surface of sphere are definite states

Inside sphere are indefinite states

Gate-based Quantum Computation

Idea : Treat quantum logic as superset of reversible logic

  • Use reversible classical computation as a starting point
    Quantum computation should "decohere" to this classical model
    • Usual AND, OR, NAND gates are not reversible
    • Reversible logic gates : NOT, CNOT, Toffoli






       
  • Upgrade the bits in these gates to qubits

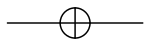
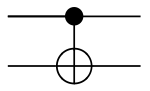
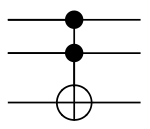
NOT

CNOT (controlled-NOT)

Toffoli (controlled-controlled-NOT)

x \mapsto 1\oplus x
(x, y) \mapsto (x, x\oplus y)
(x, y, z) \mapsto (x, y, xy\oplus z)

Gate-based Quantum Computation

3 new features in quantum generalization

  1. Parallelism of gates over superpositions of qubit states



     
  2. Random classical bits obtained when measuring qubits


     
  3. New gates to produce superpositions from classical bit states

NOT

|\psi\rangle = \alpha |0\rangle + \beta |1\rangle \mapsto \hat{X}|\psi\rangle = \alpha |1\rangle + \beta |0\rangle
|\psi\rangle
\hat{X}|\psi\rangle
|\psi\rangle = \alpha |0\rangle + \beta |1\rangle \Rightarrow \begin{cases}0, & P(0)=|\alpha|^2\\ 1, & P(1)=|\beta|^2 \end{cases}
|\psi\rangle
\hat{H}|\psi\rangle

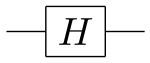
Hadamard

|\psi\rangle =|1\rangle \mapsto \hat{H}|\psi\rangle = \frac{1}{\sqrt{2}}|0\rangle - \frac{1}{\sqrt{2}}|1\rangle

Negatives in the "probability amplitudes" for the superpositions allow for "destructive interference" since they can cancel positives

Is a quantum computer more powerful?

  • The answer to this is unknown. However there are strong indications it is.
     
  • Rough logic of why it likely to be more powerful:
    • (+) Parallelization of computations over superpositions
      • This parallelization can exponentially speed up a single computation
         
    • (-) Randomness of measurement kills the parallelization speedup
      • Computations generally are exponentially repeated due to uncertainty
         
    • (+) Destructive interference can eliminate most uncertainty
      • Prior to measurement, interference can reduce most outcomes to zero probability, leaving only a few information-dense possibilities
      • This can at least partially restore the speedup expected from parallelism

Example:  Quantum (Fast) Fourier Transform

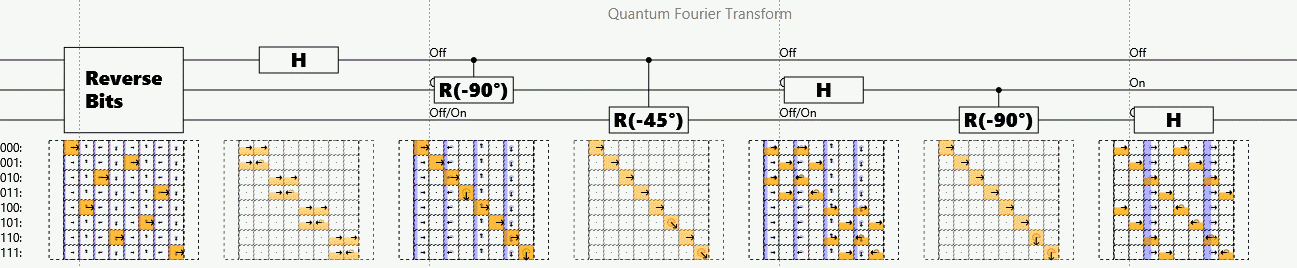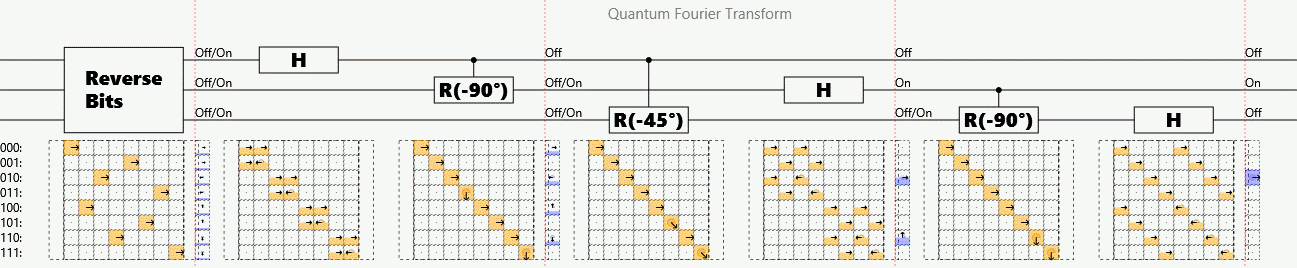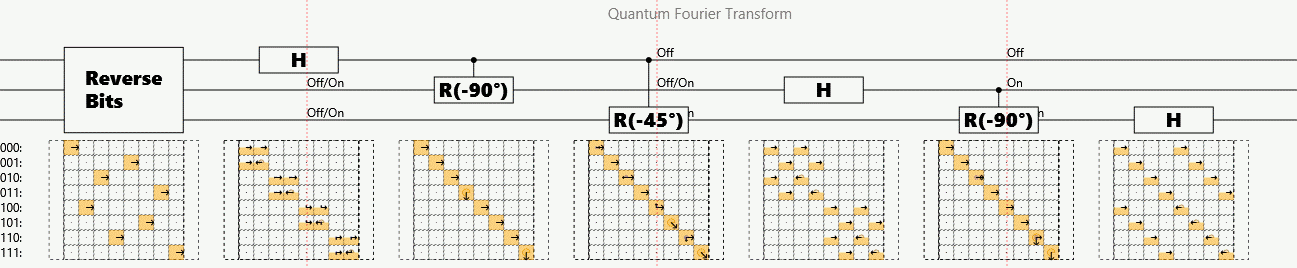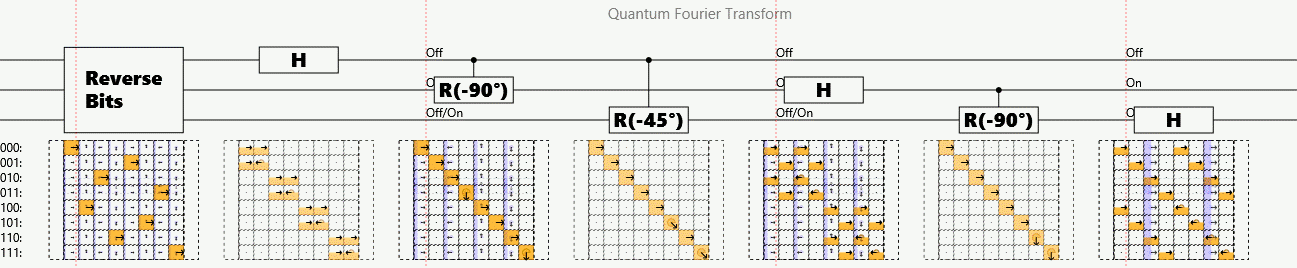
Suppose a periodic sequence can be encoded as the amplitudes of a superposition

The quantum Fourier transform (QFT) finds periodicity in polynomial operations

# steps per n bits: 

|\psi\rangle = |000\rangle + i|001\rangle - |010\rangle -i|011\rangle + |100\rangle + i|101\rangle - |110\rangle -i|111\rangle
\Rightarrow \hat{F}|\psi\rangle = |010\rangle

Detects that each successive phase factor is:

(e^{2\pi i / 8})^2
2^n(2^{n+1}-1) \text{ (DFT)} \longrightarrow 3n 2^n \text{ (FFT)} \longrightarrow (n^2 + n)/2 \text{ (QFT)}

Caveat: Answer stored as superposition. Must randomly sample outputs to measure.

(source)

Example:  Shor's Algorithm

To factorize an n-bit integer, reduce the problem to a period-finding problem, then apply the quantum Fourier transform to exponentially speed it up. Since the resulting superpositions are periodic by construction, the main caveat of the QFT is mitigated.

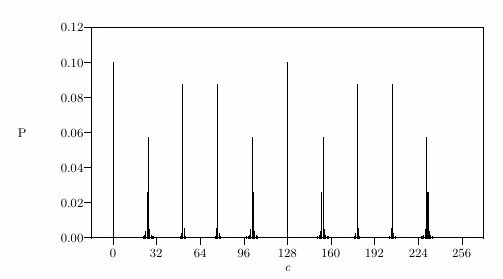
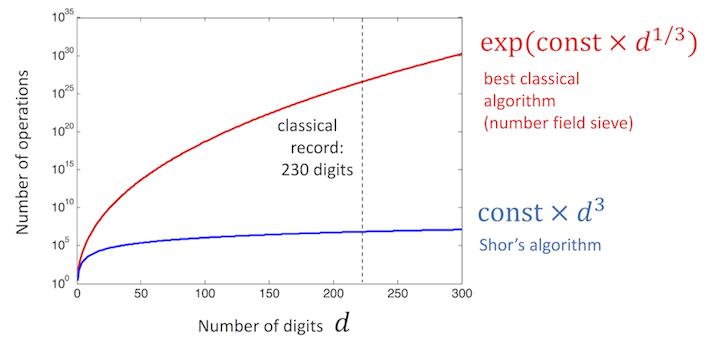
O(e^{1.7 (\log n)^{1/3}(\log\log n)^{2/3}}) \text{ (number sieve)}\longrightarrow O((\log n)^2(\log\log n)(\log\log\log n)) \text{ (Shor)}

Measured output : sparse,

easy to sample

Useful for breaking encryption!

Public key encryption (RSA) relies on the factoring of integers to be difficult

How close are we to

practical quantum computers?

We already have them!    ... sort of

2 main competing implementations (others in development):

  1. Trapped ions
         UMD : 53 qubits
     
  2. Superconducting circuits
         Google : 72 qubits
         IBM : 50 qubits
         Rigetti Computing : 19 qubits
         UC Berkeley : 10 qubits

But these numbers do not tell the complete story

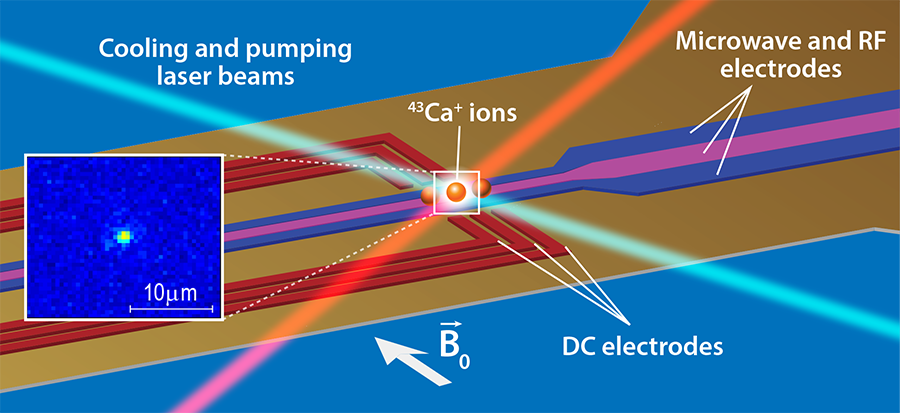
Technology 1 : Trapped Ions

A trapped ion qubit is a superposition of the lowest two magnetic hyperfine energy levels of an ion (like Ytterbium or Calcium)

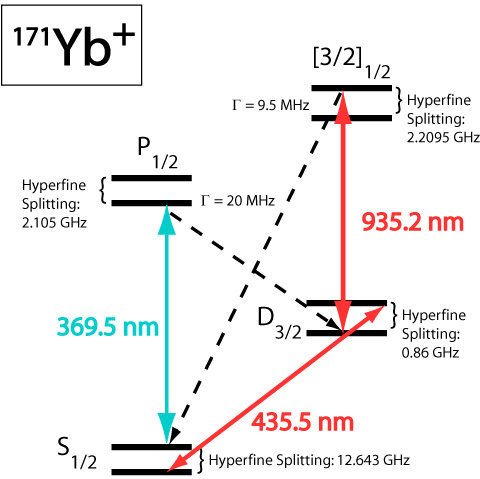
Such ions are trapped and cooled with lasers, then manipulated with more lasers

A superconducting (transmon) qubit is a superposition of the lowest two energy levels of a charge oscillation (an "artificial atom") across a nonlinear inductive tunnel barrier attached to a capacitive antenna

Technology 2 : Superconducting Qubits

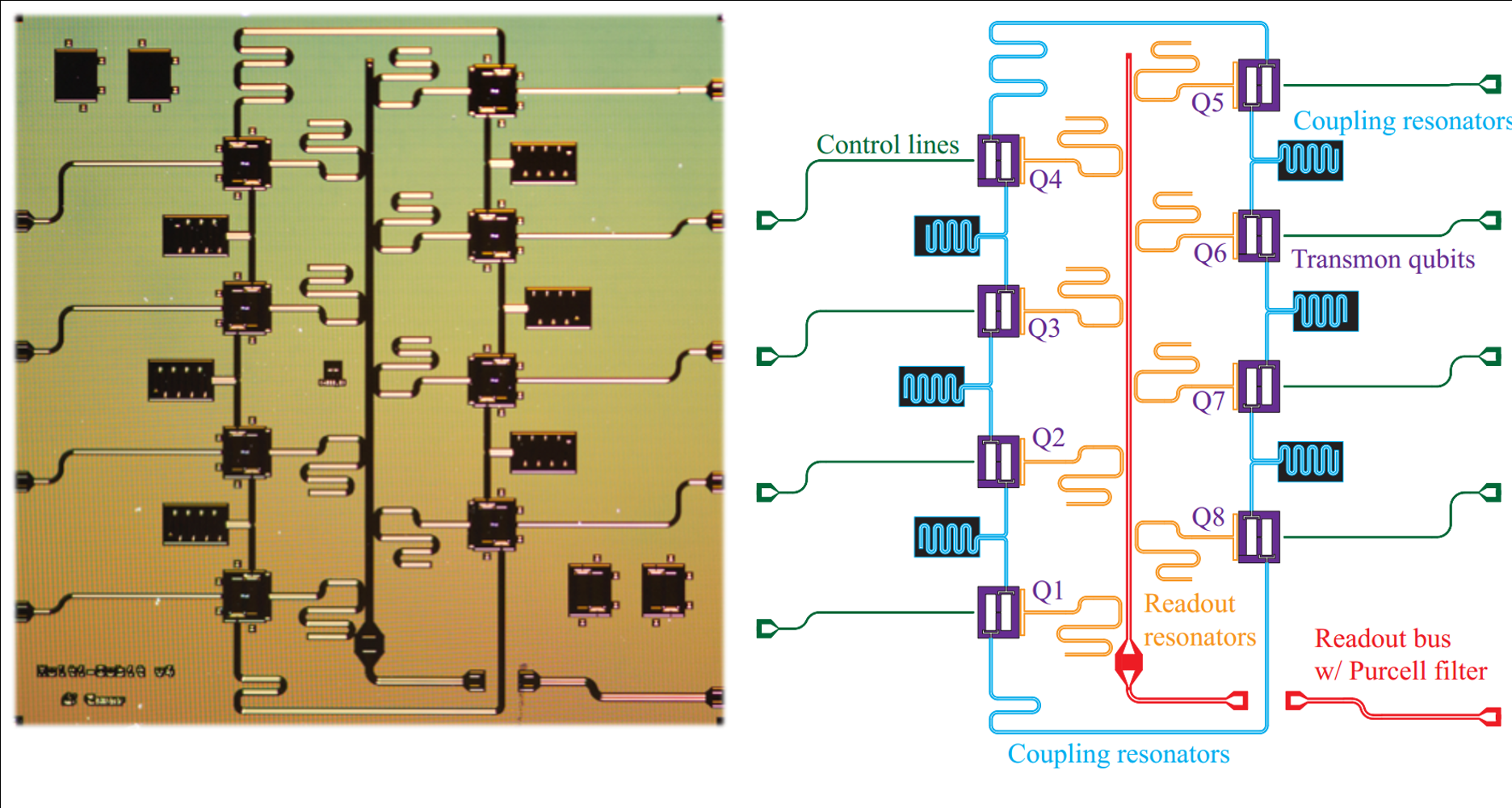
UC Berkeley : 8 qubit chip

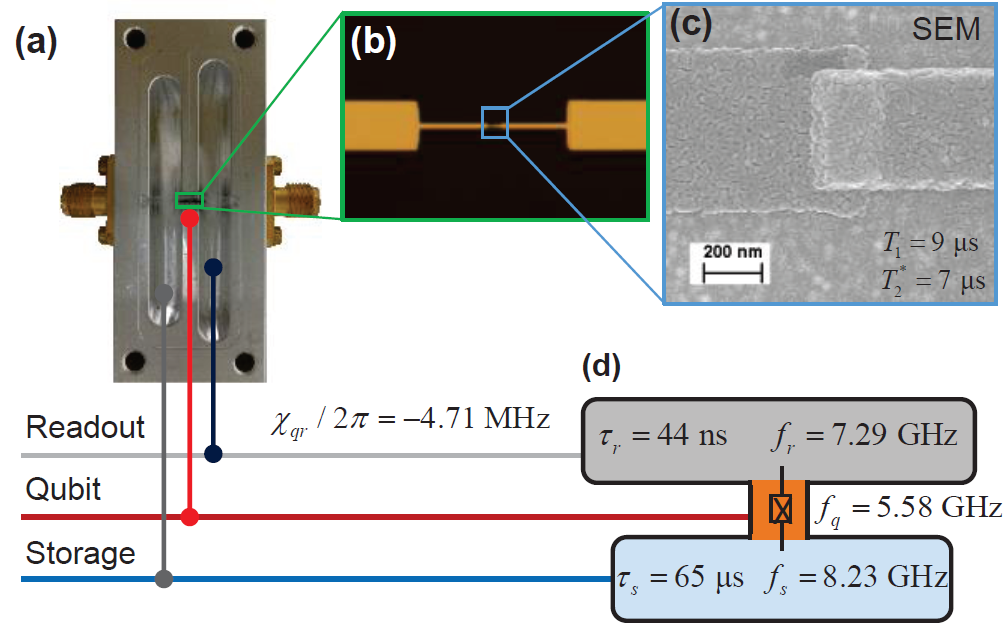
Controlled with all electrical AC signals at microwave frequencies

Cooled to mK temperatures

Yale : Transmon SEM

Chris Monroe, UMD

53 Trapped Fluorescing Ions, UMD

Government Labs

(MIT Lincoln Labs,

Sandia National Labs,

Laboratory for the Physical Sciences,

NIST)

 

Levitating trapped
ions as qubits

 

YouTube video of Trapped Ion Design Concept

Hartmut Neven,

John Martinis,

 

Google Quantum AI Lab

Bristlecone Chip

72 qubits

Jay Gambetta,

 Jerry Chow

 

IBM Q

IBM Q Prototype

50 qubits

Rigetti Computing

Rigetti 19Q Processor

19 qubits

How Many Qubits is "Enough"?

  • Suppose our goal is to implement Shor's Algorithm to factor an n-bit integer.  For example, strong RSA encryption uses 2048-bit keys.
    • Need: 2n qubits minimum to implement algorithm
      • RSA needs 4096 qubits - about 2 orders of magnitude more than state-of-the-art quantum computing hardware (a few years away)
    • Caveat: qubits need to be perfect - no laboratory qubit is perfect
       
  • Hidden resource cost : Quantum Error Correction
    • Quantum coherence is very sensitive
    • To protect against decoherence, need to encode quantum information redundantly
       
    • Idea : compose "Logical" qubits out of many "Physical" qubits
0 \mapsto 000
1 \mapsto 111

If one bit flips, can detect and correct via majority-voting

|\psi\rangle = \alpha|0\rangle + \beta |1\rangle \mapsto \alpha |000\rangle + \beta |111\rangle

Classical Bit Error Correction

Qubit Error Correction

Same basic idea, but now applied to superpositions

Main problem: cannot "look" at the bits directly due to measurement collapse

 

Resolution: measure parities of bits instead

|\psi\rangle = \alpha|0\rangle + \beta |1\rangle \mapsto \alpha |000\rangle + \beta |111\rangle

Qubit Error Correction

Problem: qubits can do more than just flip - more can go wrong

 

Resolution: redundantly encode several types of information at once (e.g., multiple axes of the sphere), and measure several types of parities to fully detect and correct errors

 

Remarkably, protecting two independent types of error is sufficient to protect against all errors

Simple bitflip protection is not quite enough.

The "Surface Code"

A very clever way to implement full quantum error correction for a 2D lattice of nearest-neighbor-coupled qubits is the "surface code"

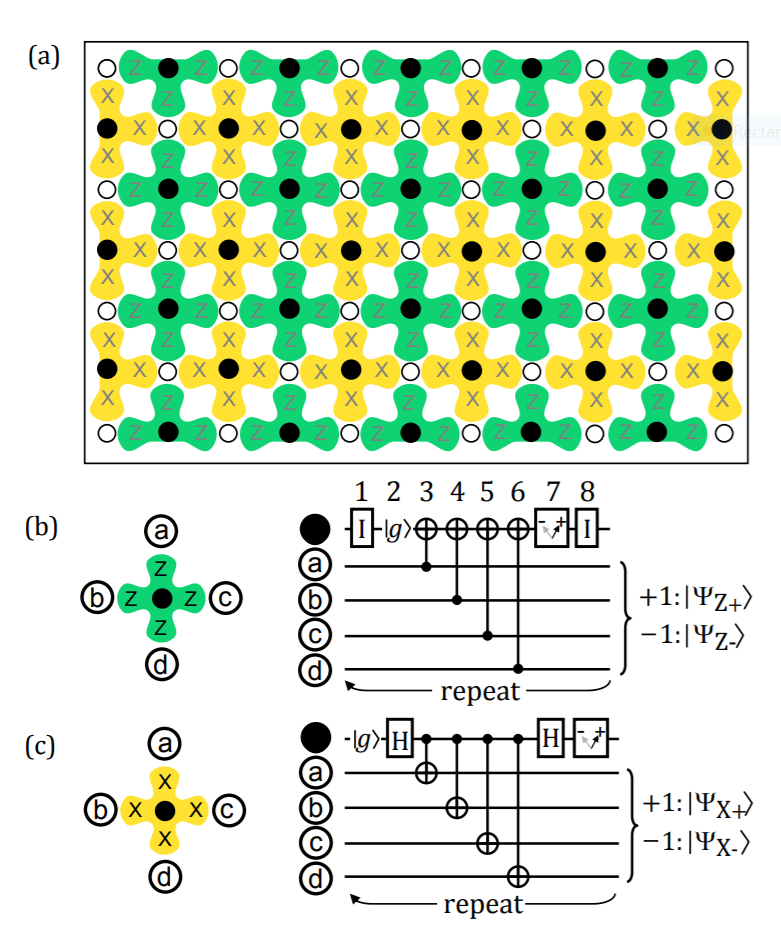
Idea : Create three interspersed lattices

  1. Data qubit lattice - white dots
    (stores quantum info.)
     
  2. X qubit lattice - black dots, yellow (measures XXXX parities)
     
  3. Z qubit lattice - black dots, green
    (measures ZZZZ parities)

Can encode redundant information across entire area of the lattice to reduce error rate for the resulting logical qubit

Phys. Rev. A 86, 032324 (2012)

"Surface Code" Logical Qubit

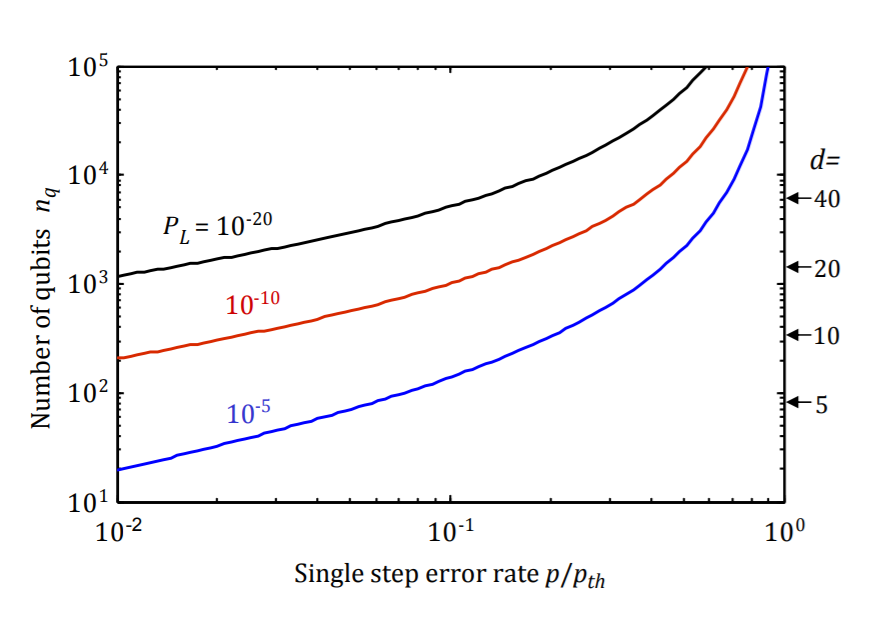
Shor's Algorithm needs a logical error rate of around 1e-20 per step

 

If each step has an error rate ~1e-3
(typical in very good hardware), then about 1e4 physical qubits will be needed to encode each logical qubit!

Phys. Rev. A 86, 032324 (2012)

Updated Estimate for Shor's Algorithm

  • n = 2048 bits for secure RSA encryption
  • Need a minimum of 2n logical qubits for n bits
  • Need 1e4 physical qubits per logical qubit
  • Need another factor of 15 overhead for algorithmic details (state distillation)

 

Minimum qubit number :                       

 

  • Adding in the time-axis:
    • Algorithm requires 3e11 Toffoli gates
    • For superconducting qubits ~100ns per Toffoli gate
       

Factoring run-time :             

10^9

Phys. Rev. A 86, 032324 (2012)

27\text{ hr}

Side note : Can reduce run-time by adding more qubits

(Compare to 6.4 quadrillion years for a classical desktop computer running the number sieve)

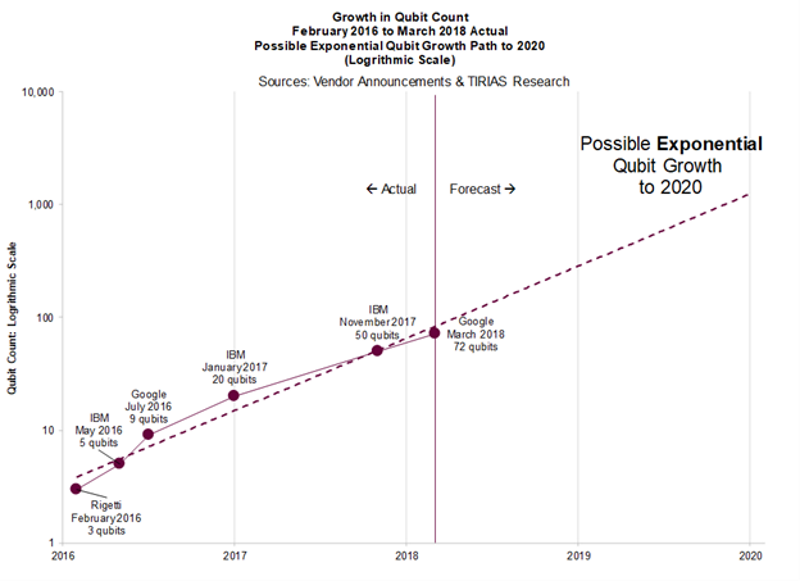
How Long Until A Billion Qubits?

Growth in qubit number is currently exponential

If growth continues exponentially (with both fidelity and technical substrate scaling favorably) then we can expect chips with one billion qubits in:

 ~10-15 years

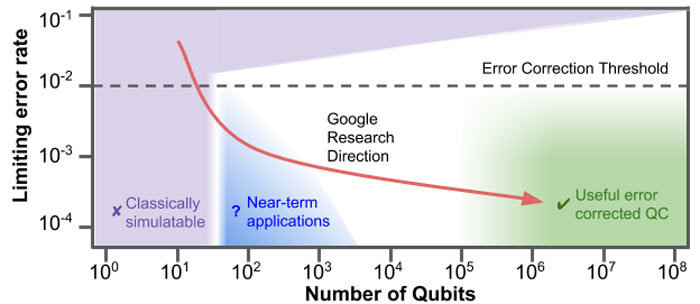
What can we do until then?

We are now reaching the scale that is no longer possible to simulate using classical supercomputers.

 

The current challenge is to find "near-term" applications for the existing quantum devices.

We are here

Google Slides

Quantum Simulation

Idea : Quantum systems more easily simulate other quantum systems
(Proposed by Feynman in 1985)

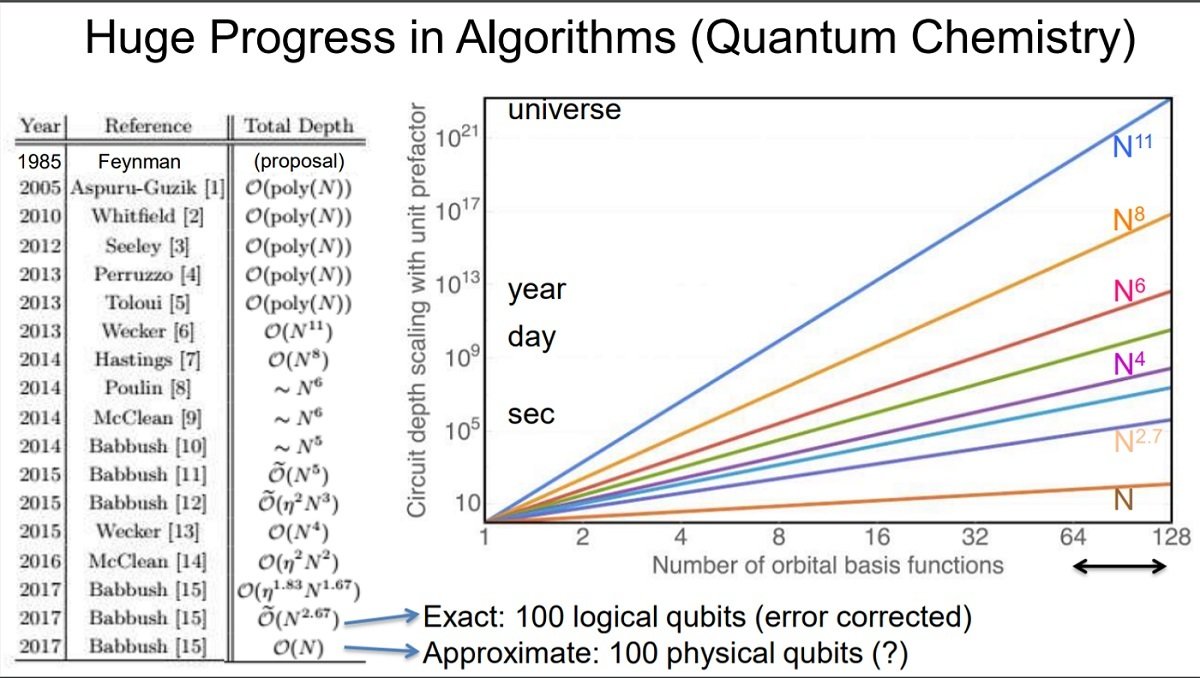
Quantum Chemistry is an obvious application

 

Recent algorithms need only ~1e2 physical qubits for approximate solutions,
or
 ~1e2 logical qubits for
exact solutions

Google Slides

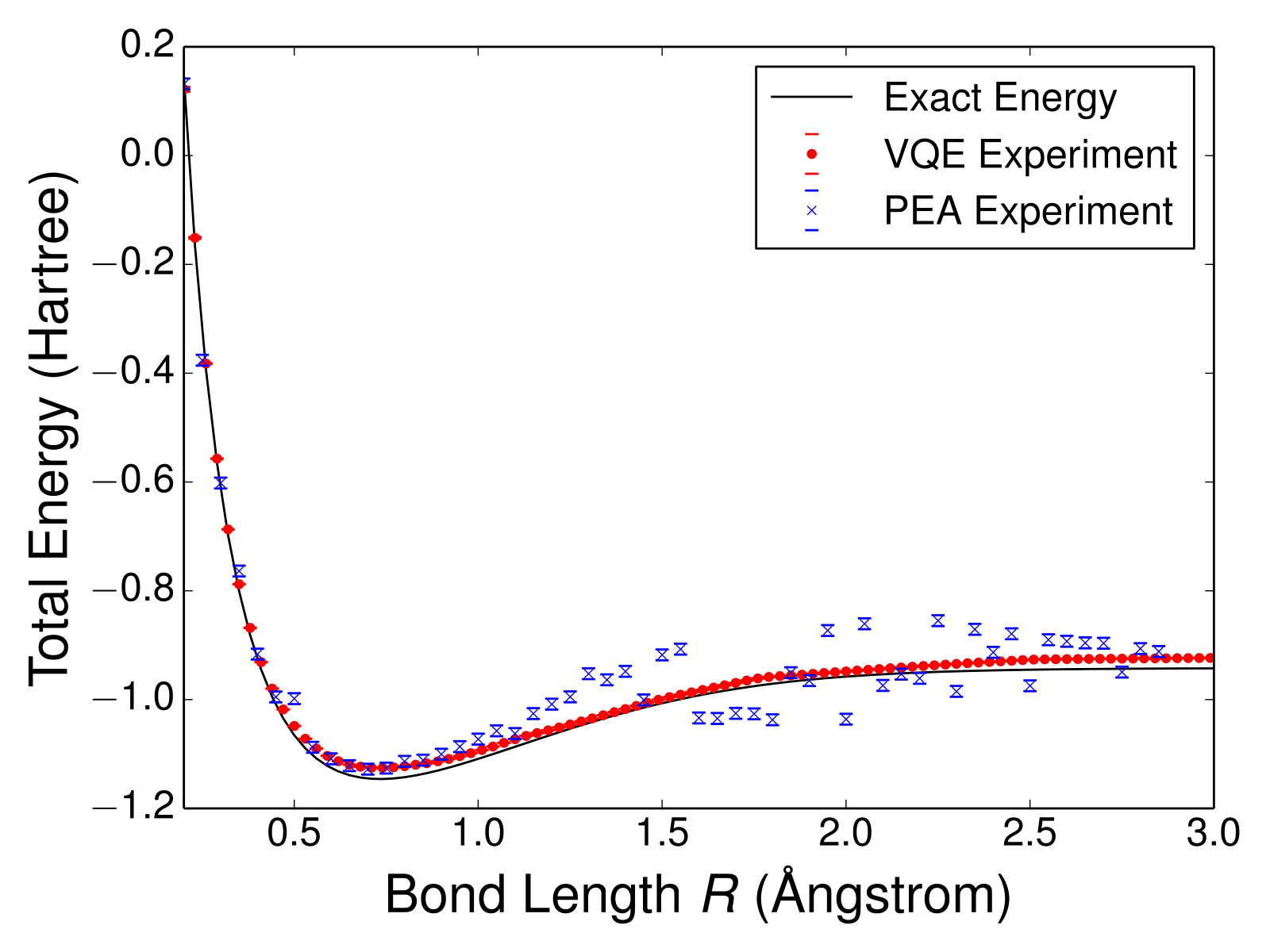
Experimental Progress already Underway

2016 Google Experiment

Two quantum algorithms for computing the bond energy for an H2 molecule using 3 qubits, compared to the numerical calculation using a classical computer

 

Experimental data already viable

 

For larger molecules, classical computers will no longer be able to numerically calculate these energies

Program a Quantum Computer Now

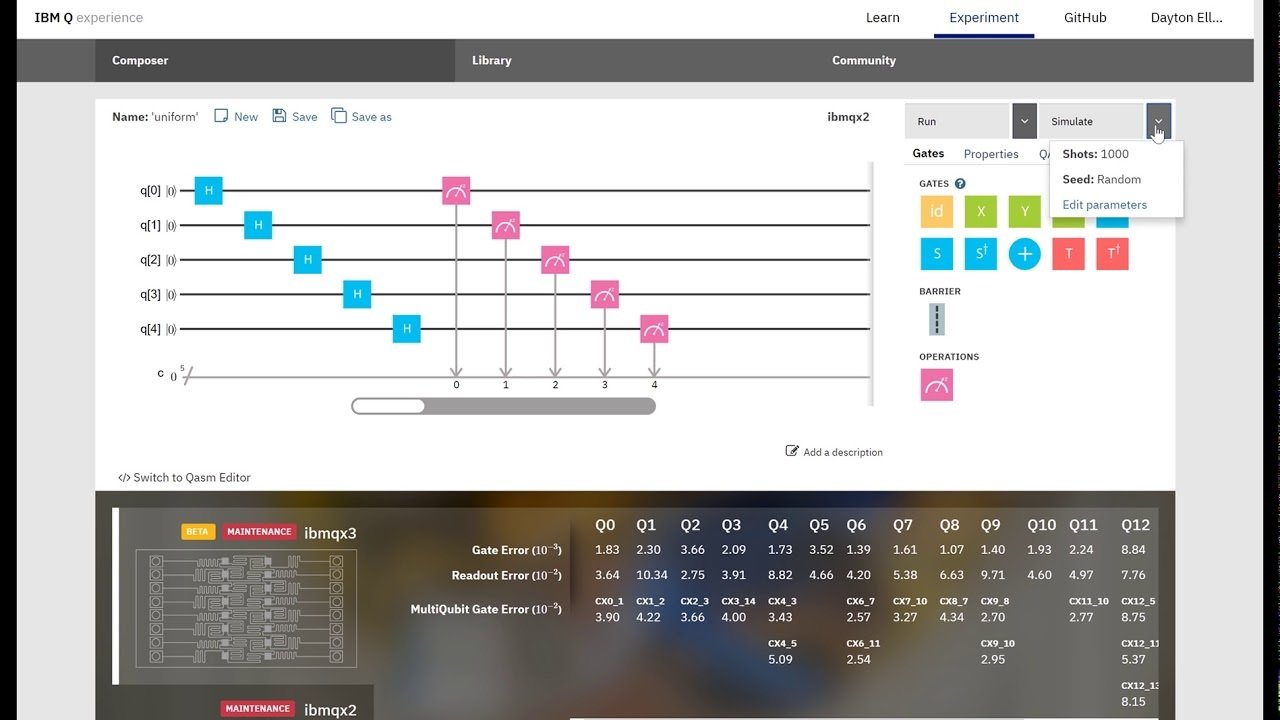
IBM Quantum Experience : Cloud Computer

(16 qubits free, 20+ paid)

Quantum Software Stacks

Microsoft : Q#, Quantum Dev Kit, LiQui|>

IBM : QISKit SDK

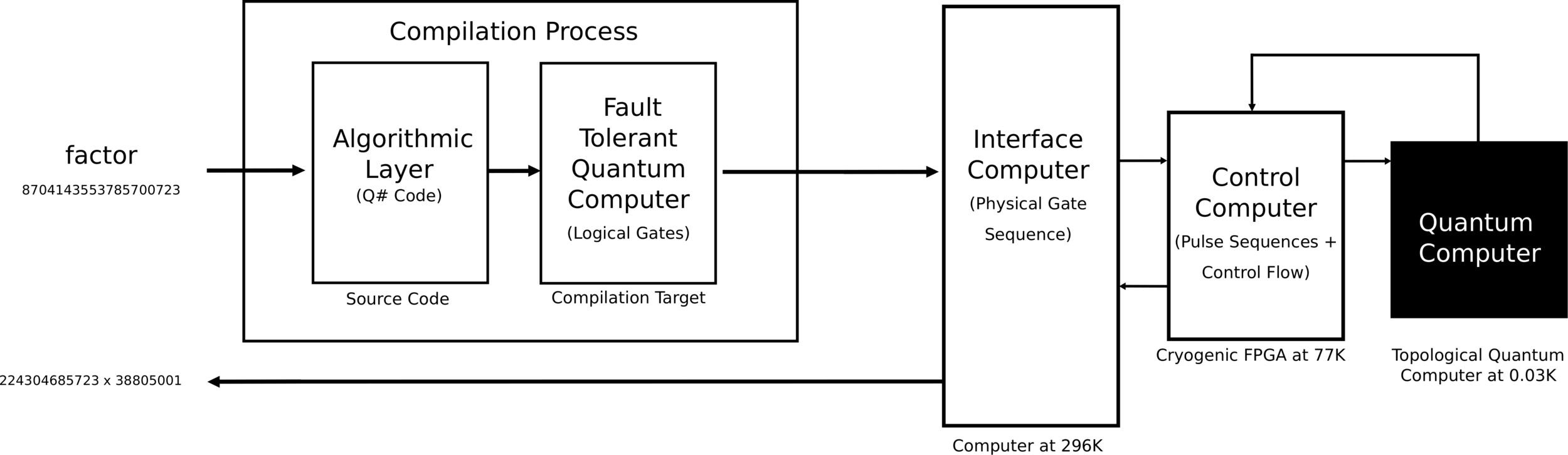
operation Teleport(msg : Qubit, there : Qubit) : () {
    body {
        using (register = Qubit[1]) {
            let here = register[0];
            H(here);
            CNOT(here, there);
            CNOT(msg, here);
            H(msg);
            // Measure out the entanglement.
            if (M(msg) == One)  { Z(there); }
            if (M(here) == One) { X(there); }
        }
    }
}
from qiskit import ClassicalRegister, QuantumRegister
from qiskit import QuantumCircuit, execute
from qiskit.tools.visualization import plot_histogram

# set up registers and program
qr = QuantumRegister(16)
cr = ClassicalRegister(16)
qc = QuantumCircuit(qr, cr)

# rightmost eight (qu)bits have ')' = 00101001
qc.x(qr[0])
qc.x(qr[3])
qc.x(qr[5])

# second eight (qu)bits have superposition of
# '8' = 00111000
# ';' = 00111011
# these differ only on the rightmost two bits
qc.h(qr[9]) # create superposition on 9
qc.cx(qr[9],qr[8]) # spread it to 8 with a CNOT
qc.x(qr[11])
qc.x(qr[12])
qc.x(qr[13])

# measure
for j in range(16):
    qc.measure(qr[j], cr[j])

More Quantum Software Stacks

Rigetti Computing : Forest, Quil, PyQuil

Opensource : ProjectQ

from math import pi

def qft3(q0, q1, q2):
    p = Program()
    p.inst( H(q2),
            CPHASE(pi/2.0, q1, q2),
            H(q1),
            CPHASE(pi/4.0, q0, q2),
            CPHASE(pi/2.0, q0, q1),
            H(q0),
            SWAP(q0, q2) )
    return p
from projectq import MainEngine
from projectq.backends import CircuitDrawer

from teleport import create_bell_pair

# create a main compiler engine
drawing_engine = CircuitDrawer()
eng = MainEngine(drawing_engine)

create_bell_pair(eng)

eng.flush()
print(drawing_engine.get_latex())

Conclusions

Quantum computing is already here (mostly).

 

It is only a matter of time before a quantum computer accomplishes a task that is currently impossible on any classical computer.

 

 

Thank you!

Quantum Computing : State of Play

By Justin Dressel

Quantum Computing : State of Play

OC ACM Chapter Meeting, May 16, 2018

  • 3,204

More from Justin Dressel