Operator Techniques for
Continuous Quantum Measurements in
Circuit Quantum Electrodynamics
Justin Dressel
Institute for Quantum Studies
Schmid College of Science and Technology
Chapman University
Advances in Operator Theory
with Applications to Mathematical Physics, Chapman 2024
Outline
-
Superconducting Qubits
- Circuit QED Overview
- Harmonic Oscillators
- Transmon Qubits
-
Qubit Measurement
- Dispersive Readout
- Continuous Measurement
- Quantum Trajectories
- Operator Methods
With simulations by Cory Panttaja
Superconducting Qubits
Mesoscopic coherence of collective charge motion at \(\mu\)m scale
EM Fields of charge motion described by Circuit QED
Anharmonic oscillator potentials treated as artificial atoms
Lowest two energy levels treated as a quantum bit (qubit)
Qubit levels controlled and measured by resonant microwave field drives
Quantum Circuits: Basic Idea
Canonically conjugate dynamical variables: \([\hat{\Phi}, \hat{Q}] = i\hbar\)
-
inductive (magnetic) flux: \(\hat{\Phi} = \Phi_0\,\hat{\phi}\), \(\Phi_0 = \hbar/2e\)
-
capacitive (electric) charge: \(\hat{Q} = (2e)\,\hat{n}\)
Dimensionless conjugate variables: \( [\hat{\phi},\,\hat{n}] = i\)
Capacitor energy: \(\displaystyle \hat{H}_C = \frac{\hat{Q}^2}{2C} = E_C\,(2\hat{n})^2, \quad E_C = \frac{e^2}{2C}\)
Inductor energy: \(\displaystyle \hat{H}_L = \frac{\hat{\Phi}^2}{2L} = \frac{E_L}{2}\,\hat{\phi}^2, \qquad\; E_L = \frac{\Phi_0^2}{L}\)
Circuit Classical Electrodynamics
Definitions:
- Map hardware into a circuit of nodes connected by branches
Each branch is a 2-point lumped circuit element like a capacitor, inductor, etc.
- Define voltage and current for each branch via EM fields directly,
as well as the flux and charge stored in each element:
- Define reference ground node and spanning tree of active nodes connected to both capacitors and inductors - the active fluxes to ground and their time-derivatives become the key Lagrangian variables
, and (2017) . doi: 10.1002/cta.2359.
v_b(t) = \int_b \vec{E}(\vec{r},t)\cdot d\vec{\ell}
i_b(t) = \frac{1}{\mu_0}\oint_b \vec{B}(\vec{r},t)\cdot d\vec{s}
\Phi_b(t) = \int_{-\infty}^t v(t')dt'
Q_b(t) = \int_{-\infty}^t i(t')dt'
\phi_n(t) = \sum_{b\in\mathcal{B}}\Phi_b(t)
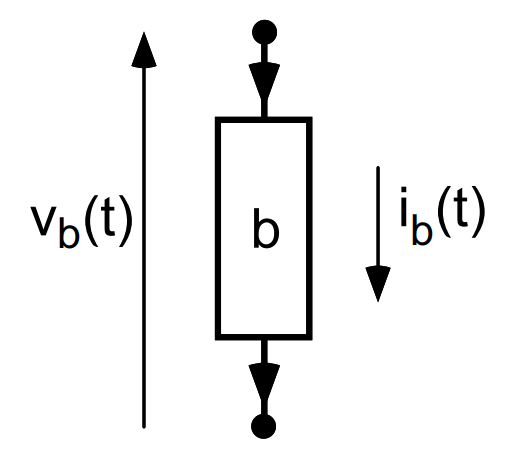
Branches \(b\in\mathcal{B}\) in spanning tree path that connects node \(n\) to ground through a sequence of capacitors
\mathcal{L} = \mathcal{E}_{\text{kin}}[\{\dot{\phi}_n\}] - \mathcal{E}_{\text{pot}}\left[\{\phi_n\}\right]
\displaystyle q_n \equiv \frac{\partial \mathcal{L}}{\partial \dot{\phi}_n}
Correct conjugate charge to active node flux \(\phi_n\)
\{ \phi_n,\ q_n \}_{\text{PB}} = \pm 1
(\(+1\) capacitive, \(-1\) inductive)
Circuit Quantum Electrodynamics
- Three primary circuit elements: capacitor, inductor, and Josephson junction
Energies of node elements written in terms of canonical variables:
, and (2017) . doi: 10.1002/cta.2359.
i_L(t) = \frac{\Phi(t) - \Phi_0}{L}
v_C(t) = \frac{Q(t) - Q_0}{C}
i_{J}(t) = I_0\,\sin\left(\frac{\Phi(t) - \Phi_0}{\hbar/2e}\right)
\mathcal{E}_C = \frac{(Q - Q_0)^2}{2C} = \frac{C\,\dot{\phi}^2}{2} = \frac{q^2}{2C}
\mathcal{E}_L = \frac{(\phi - \phi_0)^2}{2L}
\mathcal{E}_J = \frac{(\hbar/2e)^2}{L_J}\left[1 - \cos\left(\frac{(\phi - \phi_0)}{\hbar/2e}\right)\right]
L_J = \frac{(\hbar/2e)}{I_0}
\{
"Kinetic" energy:
"Potential" energy:
- Canonically Quantize dynamical variables for each node: (same as quantizing \(\vec{E},\vec{B}\) )
\{\phi,\,q\}_{\text{PB}} \to \displaystyle \frac{1}{i\hbar}[\hat{\Phi},\,\hat{Q}]
Magnetic Flux and Electric Charge
analogous to
Position and Momentum coordinates
Harmonic Oscillator (LC Resonator)
Capacitor energy: \(\displaystyle \hat{H}_C = \frac{\hat{Q}^2}{2C} = E_C\,(2\hat{n})^2, \quad E_C = \frac{e^2}{2C}\)
Inductor energy: \(\displaystyle \hat{H}_L = \frac{\hat{\Phi}^2}{2L} = \frac{E_L}{2}\,\hat{\phi}^2, \qquad\; E_L = \frac{\Phi_0^2}{L} = \frac{(\hbar/2e)^2}{L} \)
Resonator energy: \(\displaystyle \hat{H}_r = \hat{H}_C + \hat{H}_L = E_C\,(2\hat{n})^2 + \frac{E_L}{2}\,\hat{\phi}^2 \)
Bosonic amplitude: \(\displaystyle \hat{a} = \frac{1}{\sqrt{2}}\left( \frac{\hat{\Phi}}{\Phi_z} + i \frac{\hat{Q}}{Q_z} \right), \quad [\hat{\Phi},\,\hat{Q}] = i\hbar \implies [\hat{a},\,\hat{a}^\dagger] = 1 \)
Zero-point Action: \( \Phi_z\,Q_z = \hbar \), Impedance: \(\displaystyle \frac{\Phi_z}{Q_z} = \sqrt{\frac{L}{C}} \)
Dimensionless Form: \(\displaystyle \hat{a} = \frac{1}{\sqrt{2}}\left( \frac{\hat{\phi}}{\sqrt{\epsilon}} + i \sqrt{\epsilon}\,\hat{n} \right), \qquad \epsilon = \sqrt{\frac{8\,E_C}{E_L}} = \frac{\Phi_z^2}{\Phi_0^2} = \frac{(2e)^2}{Q_z^2} \)
\(\displaystyle \implies \quad \hat{H}_r = \hbar\,\omega_r\,\left(\hat{a}^\dagger\hat{a} + \frac{1}{2}\right) \), Frequency: \(\displaystyle \omega_r = \frac{1}{\sqrt{LC}} = \sqrt{8\,E_C E_L} = \epsilon\,E_L \)
Josephson Junction energy: \(\displaystyle \hat{H}_J = E_J\,\left(1 - \cos\hat{\phi}\right) \approx \frac{E_J}{2}\,\hat{\phi}^2 - \frac{E_J}{4!}\hat{\phi}^4 + \cdots \)
\(\displaystyle \hat{\phi} = \frac{\hat{\Phi}}{\Phi_0}, \quad E_J = \frac{\Phi_0^2}{L_J} \) Tunnel junction introduces nonlinearity to circuit
\(\displaystyle \hat{H} = \hat{H}_C + \hat{H}_J = E_C\,(2\hat{n})^2 + E_J\,(1 - \cos\hat{\phi}) \approx \hbar\omega_p\left(\frac{1}{2} + \hat{b}^\dagger\hat{b} + \epsilon\hat{V}\right) \)
\(\displaystyle \hat{b} = \frac{1}{\sqrt{2}}\left( \frac{\hat{\phi}}{\sqrt{\epsilon}} + i \sqrt{\epsilon}\,\hat{n} \right), \; \epsilon = \sqrt{\frac{8\,E_C}{E_J}}, \quad \omega_p = \frac{1}{\sqrt{L_J C}} = \sqrt{8\,E_J E_C} \)
\(\displaystyle \hat{V} = -\frac{1}{4!}\left(\frac{\hat{b}+\hat{b}^\dagger}{\sqrt{2}}\right)^4 + \frac{\epsilon}{6!}\left(\frac{\hat{b}+\hat{b}^\dagger}{\sqrt{2}}\right)^6 \) Anharmonic Perturbation
\(E_J\)
\(E_C\)
Quantum Pendulum: Nonlinear Resonator
Replacing the inductor with a Josephson tunnel junction introduces nonlinearity to circuit
Transmon Qubit
Cosine potential acts like an artificial atom
Distinct level spacings allow targeted control of specific pairs of levels
Frequency gaps in the microwave regime
Large capacitor protects against charge noise
Distinct behavior from optical regime with real atoms:
- Engineered chips permit ultra-strong and deep-strong coupling regimes that are difficult to achieve with atoms
- Lower frequencies than optics make transients more relevant
- Emission can be directionally controlled down waveguides to minimize collection loss and increase detection efficiency
\hbar\omega_q
\hbar(\omega_q - \delta_q)
\omega_q/2\pi \sim \text{4--7GHz}
\delta_q/2\pi \sim \text{100--300MHz}
\(\displaystyle \hat{H} \approx E_0\,\hat{1} + \hbar\omega_q\,|1\rangle\!\langle 1| + \hbar(2\omega_q - \delta_q)\,|2\rangle\!\langle 2| \approx \frac{E_0}{2}\hat{1} - \frac{\hbar\omega_q}{2}\hat{\sigma}_z \)
\(E_J\)
\(E_C\)
Large shunt capacitor \(\displaystyle \frac{E_J}{E_C} \approx 100 \)
\(\displaystyle \hat{H} = \hat{H}_C + \hat{H}_J = E_C\,(2\hat{n})^2 + E_J\,(1 - \cos\hat{\phi}) \)
\(\displaystyle \hat{\sigma}_z = |0\rangle\langle 0| - |1\rangle\langle 1| \)
qubit subspace
Qubit Pauli Z
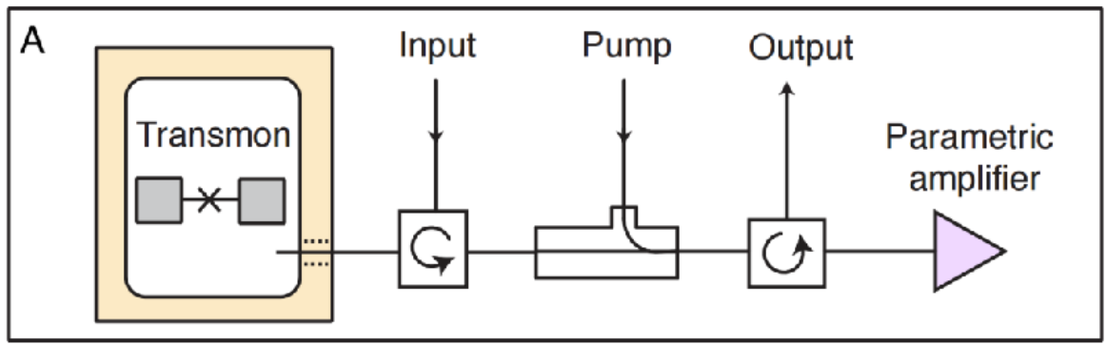
How do we measure a qubit?
Problem:
Qubit is on a chip inside a fridge near absolute zero.
How does one "measure the energy eigenstates" of the qubit
without causing unwanted changes to those energy states?
Solution:
Indirectly peek at the qubit energy using traveling microwaves:
- Dispersively couple the qubit to a strongly detuned resonator
- Probe the resonator with a resonant microwave tone
- Amplify the reflected microwave signal after interaction
- Measure the returned microwave signal and compare it to original
- Frequency shifts in the collected signal correlated to the qubit state
- Learning information updates the quantum state (Bayes' rule)
The energy states of the qubit can be inferred without allowing energy transitions between the qubit and readout resonator
This is an indirect "non-demolition measurement" of the qubit energy.
C_J
L_J
C_c
C_r
- Resonator + Transmon:
C_J
L_J
C_c
\hat{H} = \hat{H}_q + \hat{H}_r + \hat{H}_c
g = \displaystyle \frac{C_c\sqrt{\omega_q\omega_r}}{2\sqrt{C_r(C_J+C_c)}}
\hat{H}_c \approx \hbar g (\hat{a} + \hat{a}^\dagger)(\hat{b} + \hat{b}^\dagger)
\chi = \displaystyle\delta_q\frac{g^2}{\Delta^2}
X-X (capacitive) coupling
Dispersive approximation:
|\Delta| \equiv |\omega_q - \omega_r| \gg |g|
\hat{H}_c \approx 2\chi\,\hat{b}^\dagger\hat{b}\,\hat{a}^\dagger\hat{a} \approx \chi\,\hat{\sigma}_z\,\hat{a}^\dagger\hat{a}
Resonator and qubit strongly detuned
\hat{H}_q + \hat{H}_r + \hat{H}_c \approx \displaystyle -\hbar\omega_q \frac{\hat{\sigma}_z}{2} + \hbar(\omega_r + \chi\hat{\sigma}_z)\hat{a}^\dagger\hat{a}
\omega_r \mapsto \omega_r \pm \chi
Resonator frequency acquires a shift determined by qubit energy state
\Rightarrow
Transmon-Resonator Coupling
C_r
Transmission-line Fields
C_J
L_J
C_c
\hat{H} = \hat{H}_q + \hat{H}_r + \hat{H}_c + \hat{H}_t + \hat{H}_{rt}
\displaystyle \hat{H}_t = \int_0^\lambda \left[\frac{\hat{q}(x)^2}{2c} + \frac{(\partial_x\hat{\phi}(x))^2}{2l}\right]dx = v \int_0^\lambda(\hat{A}^\leftarrow(x)^2 + \hat{A}^\rightarrow(x)^2)dx = \sum_{k=-\infty}^\infty\hbar\omega_k\frac{\hat{c}_k^\dagger \hat{c}_k + \hat{c}_k \hat{c}_k^\dagger}{2}
C_{rt}
(OUT: to amplifier and detector)
(IN: from signal generator)
(2017)
[\hat{\phi}_t(x),\hat{q}_t(x')] = i\hbar\delta(x-x')
[\hat{A}^\rightleftharpoons(s),\hat{A}^\rightleftharpoons(s')] = \frac{i\hbar}{2}\partial_s\delta(s-s')
[\hat{c}_k,\hat{c}^\dagger_{k'}] = \delta_{kk'}
\hat{A}^\rightleftharpoons(s = t \mp x/v) = \displaystyle \frac{1}{2\sqrt{v}}\left(\frac{\partial_s\hat{\phi}(s)}{\sqrt{l}} \pm \frac{\hat{q}(s)}{\sqrt{c}}\right)
v = \frac{1}{\sqrt{lc}}
\displaystyle\hat{c}_k = \sqrt{\frac{2v}{\lambda}}\int_0^\lambda \hat{A}^\rightarrow(x)\frac{e^{-ikx}}{\sqrt{\hbar\omega_k}}dx, \; k>0
c,l
Capacitance, Inductance per unit length
Z_t = \sqrt{\frac{l}{c}}
Transmission line: local quantum fields
C_r
Local traveling waves:
Global harmonic modes:
\hat{H}_{rt} = \hat{\Phi}\hat{I}(x=0)
= \sqrt{\frac{\hbar Z_r}{2}}(\hat{a}+\hat{a}^\dagger)\sqrt{\frac{1}{Z_t}}\partial_t(\hat{A}^\rightarrow(t) - \hat{A}^\leftarrow(t))
\equiv \frac{\hbar}{2}i\sqrt{\kappa}(\hat{a}+\hat{a}^\dagger)(\hat{c}_{\text{in}}-\hat{c}_{\text{in}}^\dagger - \hat{c}_{\text{out}} + \hat{c}_{\text{out}}^\dagger)
\kappa \equiv \displaystyle \omega_r \frac{Z_r}{Z_t}
\hat{c}_{\text{in}}
\equiv -i\sqrt{\frac{v}{\lambda}}\sum_{k=0}^\infty\sqrt{\frac{\omega_k}{\omega_r}}\,\hat{c}_{-k}
\hat{c}_{\text{out}}
\equiv -i\sqrt{\frac{v}{\lambda}}\sum_{k=0}^\infty\sqrt{\frac{\omega_k}{\omega_r}}\,\hat{c}_{k}
Resonator decay rate near \(\omega_r\)
Input-output (boundary) condition:
\hat{\Phi}_r = \hat{\phi}_t(x=0)
\Rightarrow \sqrt{\kappa}\,\hat{a} = \hat{c}_{\text{in}} + \hat{c}_{\text{out}}
Resonator-Transmission-line Coupling
C_J
L_J
C_c
\hat{H} = \hat{H}_q + \hat{H}_r + \hat{H}_c + \hat{H}_t + \hat{H}_{rt}
C_{rt}
(OUT: to amplifier and detector)
(IN: from signal generator)
C_r
= \frac{\hbar}{2}\sqrt{\frac{Z_r}{Z_t}}(\hat{a}+\hat{a}^\dagger)\sqrt{\frac{v}{\lambda}}\sum_{k=0}^\infty\sqrt{\omega_k}(\hat{c}_{-k} + \hat{c}^\dagger_{-k} -\hat{c}_k -
\hat{c}^\dagger_k)
\hat{H} = \hbar(\omega_r + \chi\hat{\sigma}_z)\hat{a}^\dagger\hat{a} + \frac{\hbar}{2}i\sqrt{\kappa}(\hat{a}+\hat{a}^\dagger)(\hat{c}_{\text{in}}-\hat{c}_{\text{in}}^\dagger - \hat{c}_{\text{out}} + \hat{c}_{\text{out}}^\dagger)
\sqrt{\kappa}\,\hat{a} = \hat{c}_{\text{in}} + \hat{c}_{\text{out}}
Effective Resonator Evolution
C_J
L_J
C_c
C_{rt}
(OUT: to amplifier and detector)
(IN: from signal generator)
C_r
\displaystyle \frac{d\hat{a}}{dt} = -i(\omega_r + \chi\hat{\sigma}_z)\hat{a} -i\frac{\sqrt{\kappa}}{2}(\hat{c}_{\text{in}} - \hat{c}_{\text{in}}^\dagger - \hat{c}_{\text{out}} + \hat{c}_{\text{out}}^\dagger)
\( \langle c_{\text{in}}(t) \rangle = -i(\varepsilon(t)/\sqrt{\kappa}) \, e^{-i\omega_d t} \)
\Delta = \omega_r - \omega_d
\displaystyle \frac{d\hat{a}}{dt} = -i(\Delta + \chi\hat{\sigma}_z)\hat{a} - \frac{\kappa}{2}\hat{a} -i(\varepsilon(t) + \hat{v}(t))
Quantum Langevin Equation (RWA):
Vacuum fluctuations
\hat{c}_{\rm out}(t) = \sqrt{\kappa}\,\hat{a}(t) + i \varepsilon(t)/\sqrt{\kappa} - \hat{v}(t)
Reflected field in transmission line:
[\hat{v}(t),\hat{v}^\dagger(t')] = \delta(t-t')
Dispersive Microwave Readout
Quantum-limited on-chip amplifiers (built from Josephson junctions using their nonlinear inductance):
-
Josephson Parametric Amplifier (JPA):
- narrow-band reflected 3-wave mixer
- usually operated in phase-sensitive (squeezed) mode
-
one output homodyne signal for a single quadrature of the microwave signal: \(I(t)\)
-
Traveling-Wave Parametric Amplifier (TWPA):
- broad-band amplification over transmission-line propagation
- only operates in phase-preserving (unsqueezed) mode
- two output heterodyne signals for both orthogonal quadratures of the microwave signal: \((I(t), Q(t))\)
Outgoing signal is further amplified to enhance phase difference in steady-state resonator modes
One (informational) quadrature encodes
qubit state information as a displacement of the signal
The orthognal (phase) quadrature encodes
photon number fluctuations inside the resonator
Dispersive Microwave Readout
\hat{c}_{\rm out}(t) = \sqrt{\kappa}\,\hat{a}(t) + i \varepsilon(t)/\sqrt{\kappa} - \hat{v}(t)
Traveling reflected field:
Finite bandwidth detector absorbs
compact wavelet mode of field:
\hat{b}(t) = \int_{t-\Delta t}^t\hat{c}_{\rm out}(t')w(t - t')\frac{dt'}{\sqrt{\Delta t}} \approx \sqrt{\kappa \Delta t}\,\hat{a}(t) + \hat{d}(t)
\langle\hat{d}(t)\rangle = -i\int_{t-\Delta t}^t \varepsilon(t')w(t - t')\frac{dt'}{\sqrt{\kappa\Delta t}}, \qquad [\hat{d}(t),\hat{d}^\dagger(t)] = 1 \qquad \implies \qquad [\hat{b}(t),\hat{b}^\dagger(t)] = 1
Exact wavelet is unimportant for short duration \(\Delta t\), but bosonic commutator must be preserved.
Amplification and loss are beamsplitter and Bogoliubov (squeezing) transformations of this mode.
\hat{b}(t) \mapsto \sqrt{\eta_c G}\,(e^{i\phi}\cosh(r)\hat{b}(t) + e^{-i\phi}\sinh(r)\hat{b}^\dagger(t)) + \hat{w}(t), \qquad e^r = G_\phi, \qquad [\hat{w}(t),\hat{w}^\dagger] = \eta_c G + D
\(\eta_c\): Collection inefficiency, \(G\): phase-preserving gain,
\(G_\phi\): phase-sensitive gain, \(\phi\): amplified quadrature angle, \(D\): additional (Gaussian) noise
Measured Signal
\begin{aligned}
\hat{b} &= \displaystyle \sqrt{\eta_c G \kappa \Delta t}\,\left(e^{i\phi}\cosh(r)\left(\hat{a} + \frac{\hat{d}}{\sqrt{\kappa \Delta t}}\right) + e^{-i\phi}\sinh(r)\left(\hat{a}^\dagger + \frac{\hat{d}^\dagger}{\sqrt{\kappa \Delta t}}\right) + \frac{\hat{w}}{\sqrt{\eta_c G\kappa\Delta t}}\right) \\
&\equiv \sqrt{\eta_c G \kappa \Delta t}\;\hat{r}, \qquad [\hat{r}(t),\hat{r}^\dagger(t)] = \displaystyle 1 + \frac{1}{\kappa\Delta t} + \frac{D}{\eta_c G \kappa \Delta t} = 1 + \frac{\tau_m}{\Delta t}
\end{aligned}
\(\tau_m\): Measurement integration time for unit signal-to-noise ratio
\(\eta\): Net measurement inefficiency, \(\eta_c\): Collection inefficiency
\(G\): phase-preserving gain, \(G_\phi = e^r\): phase-sensitive gain, \(\phi\): amplified quadrature angle
\(D\): additional Gaussian noise
\(\kappa\): resonator decay rate, \(\Delta t\): inverse bandwidth of detector
\tau_m = \displaystyle \frac{1 + D/\eta_c G}{\kappa} \equiv \frac{1}{\eta\kappa}, \qquad \eta \equiv \frac{\eta_c G}{\eta_c G + D}
Phase-preserving Measurements
\begin{aligned}
\hat{b} &= \displaystyle \sqrt{\eta_c G \kappa \Delta t}\,\left(\hat{a} + \frac{\hat{d}}{\sqrt{\kappa \Delta t}} + \frac{\hat{w}}{\sqrt{\eta_c G\kappa\Delta t}}\right) \equiv \sqrt{\eta_c G \kappa \Delta t}\;\hat{r}, \\
&[\hat{r}(t),\hat{r}^\dagger(t)] = 1 + \frac{\tau_m}{\Delta t} = 1 + \frac{1}{\eta\kappa\Delta t}
\end{aligned}
\displaystyle \eta \equiv \frac{\eta_c G}{\eta_c G + D}
Readout signal \(\hat{r}\) approximates complex Gaussian random variable with variance \(1/\eta\kappa\Delta t\) and mean \(\langle\hat{a}\rangle\) set by the spectrum \(\alpha\) of \(\hat{a}\).
\begin{aligned}
dP(r|\hat{\rho}) &= \text{Tr}(d\hat{P}(r)\,\hat{\rho}) = \iint dP_Q(r|\alpha)\,P(\alpha | \hat{\rho})\,d^2\alpha, \\
dP_Q(r|\alpha) &= \frac{d^2r}{\pi}\sqrt{\frac{\eta\kappa\Delta t}{\pi}}\,\exp\left[-\eta\kappa\Delta t|r - \alpha|^2\right] = \frac{\bra{\alpha}d\hat{P}(r)\ket{\alpha}}{\pi}
\end{aligned}
\(r\) samples Husimi-Q distribution for each \(\alpha\) in \(\hat{\rho}\)
Phase-preserving Measurements
\begin{aligned}
dP(r|\hat{\rho}) &= \text{Tr}(d\hat{P}(r)\,\hat{\rho}) = \iint dP_Q(r|\alpha)\,P(\alpha | \hat{\rho})\,d^2\alpha, \\
dP_Q(r|\alpha) &= \frac{d^2r}{\pi}\sqrt{\frac{\eta\kappa\Delta t}{\pi}}\,\exp\left[-\eta\kappa\Delta t|r - \alpha|^2\right] = \frac{\bra{\alpha}d\hat{P}(r)\ket{\alpha}}{\pi}
\end{aligned}
The \(Q\)-representation encodes eigenvalues \(\alpha\) for normally-ordered field-operator products.
The POVM \(d\hat{P}(r)\) can be evaluated and factored into a pair of Kraus operators \(\hat{M}_r\) and \(\hat{N}\)
\begin{aligned}
d\hat{P}(r) &\equiv d^2r\,p_0(r)\,\exp(\eta\kappa\Delta t\,r\hat{a}^\dagger)[1 - \eta\kappa\Delta t]^{\hat{a}^\dagger\hat{a}}
\exp(\eta\kappa\Delta t\,r^*\hat{a}) \equiv d^2r\,p_0(r)\,(\hat{N}\hat{M}_r)^\dagger\,(\hat{N}\hat{M}_r), \\
p_0(r) &= \sqrt{\frac{\eta \kappa\Delta t}{\pi}}\, \exp(-\eta\kappa\Delta t\,|r|^2), \\
\hat{M}_r &\equiv \exp(\eta\kappa\Delta t\, r^*\hat{a}), \\
\hat{N} &\equiv [1-\eta\kappa\Delta t]^{\hat{a}^\dagger\hat{a}/2} \approx \exp(-\eta\kappa\Delta t\hat{a}^\dagger\hat{a}/2)
\end{aligned}
Phase-preserving Measurements
This yields a simple prescription for both simulating measured records \(r(t)\) and updating the quantum state \(\hat{\rho}\) given a measured \(r(t)\):
\begin{aligned}
r(t) &= \langle \hat{a}(t) \rangle + \xi(t), \\
dP(\xi) &= \sqrt{\frac{\eta \kappa\Delta t}{\pi}}\, \exp(-\eta\kappa\Delta t\,|\xi|^2), \\ \\
\hat{M}_r &\equiv \exp(\eta\kappa\Delta t\, r^*\hat{a}), \\
\hat{N} &\approx \exp(-\eta\kappa\Delta t\hat{a}^\dagger\hat{a}/2), \\
\hat{U}_{\Delta t} &= \exp(-i\Delta t \hat{H}/\hbar)
\end{aligned}
\begin{aligned}
\hat{\rho}(t + \Delta t) &\propto \hat{N}\hat{M}_r\hat{U}_{\Delta t}\hat{\rho}(t)\hat{U}^\dagger_{\Delta t}\hat{M}^\dagger_r\hat{N}^\dagger + (1-\eta)\kappa\Delta t\hat{a}\hat{U}_{\Delta t}\hat{\rho}\hat{U}^\dagger_{\Delta t}\hat{a}^\dagger
\end{aligned}
For small time steps \(\Delta t\) and efficient measurements \(\eta = 1\),
this evolution becomes equivalent to stochastic non-Hermitian Hamiltonian evolution for the resonator-qubit system:
\displaystyle \frac{\hat{H}}{\hbar} = \frac{\omega_q}{2}\hat{\sigma}_z + (\omega_r + \chi\hat{\sigma}_z - i\kappa/2)\hat{a}^\dagger\hat{a} + i\kappa r^*(t)\hat{a}, \qquad r(t) = \langle \hat{a}(t) \rangle + \xi(t)
Phase-preserving Measurements
This method is simple enough that a freshman undergraduate student was able to code it up in Python.
Plots courtesy of Cory Panttaja
Regime 1:
\(2\chi/\kappa = 1\)
\(2\Omega/\kappa = 1\)
\(2\varepsilon/\kappa = 1/8\)
weak
measurement
Phase-preserving Measurements
Plots courtesy of Cory Panttaja
Regime 2:
\(2\chi/\kappa = 1\)
\(2\Omega/\kappa = 1\)
\(2\varepsilon/\kappa = 1/2\)
wimpy
measurement
Phase-preserving Measurements
Plots courtesy of Cory Panttaja
Regime 3:
\(2\chi/\kappa = 1\)
\(2\Omega/\kappa = 1\)
\(2\varepsilon/\kappa = 1\)
frustrated
measurement
Phase-preserving Measurements
Plots courtesy of Cory Panttaja
Regime 4:
\(2\chi/\kappa = 1\)
\(2\Omega/\kappa = 1\)
\(2\varepsilon/\kappa = 2\)
strong
measurement
Conclusions
- Superconducting qubits naturally use continuous measurements, which have much more detailed information and potential utility than just integrating them to obtain binary projective measurements
- Quantum trajectories of monitored joint qubit-resonator states can now be readily simulated and analyzed using a novel operator method
- There is very interesting behavior to explore in transient and low-probability regimes that requires this more comprehensive treatment of measurement
Thank you!
And thanks to
Cory Panttaja
Operator methods for continuous quantum measurements in circuit quantum electrodynamics
By Justin Dressel
Operator methods for continuous quantum measurements in circuit quantum electrodynamics
Advances in Operator Theory with Applications to Mathematical Physics, Chapman University, 11/22/2024
