Continuous Monitoring and Feedback Control
of Superconducting Qubits


Justin Dressel
Institute for Quantum Studies
Schmid College of Science and Technology
Chapman University
UT Arlington, 2025/03/26



Outline
-
Superconducting Qubits
- Circuit QED Overview
- Transmon Qubits
-
Continuous Measurement
- Dispersive Readout
- Quantum Trajectories
-
A Tour of Recent Results
- State Tracking
- Zeno-dragging Gates
- Feedback State Stabilization
- Continuous Error Correction
- LSTM RNN State Tracking

Superconducting Qubits
Mesoscopic coherence of collective charge motion at \(\mu\)m scale, mK temperature
EM Fields of charge motion described by Circuit QED

Anharmonic oscillator potentials treated as artificial atoms, with lowest 2 levels as qubit
Qubit levels controlled by resonant microwave field drives
Qubit levels measured via dispersive frequency-shift of coupled microwave resonator mode
Circuit QED Overview

Canonically conjugate dynamical variables: \([\hat{\Phi}, \hat{Q}] = i\hbar\)
-
inductive (magnetic) flux: \(\hat{\Phi} = \Phi_0\,\hat{\phi}\), \(\Phi_0 = \hbar/2e\)
-
capacitive (electric) charge: \(\hat{Q} = (2e)\,\hat{n}\)
Dimensionless conjugate variables: \( [\hat{\phi},\,\hat{n}] = i\)

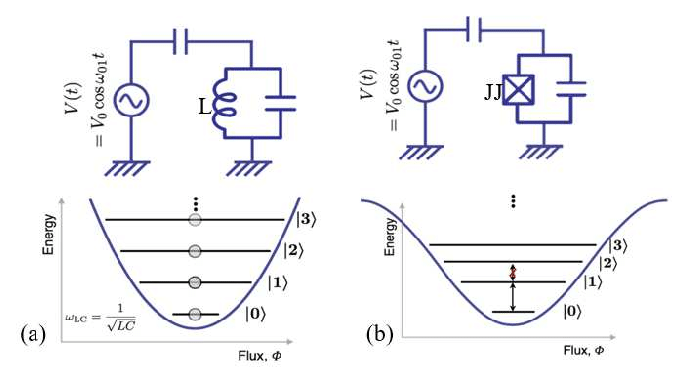
Example: Harmonic Oscillator
Useful circuit, but bad qubit:
Can't isolate specific level pairs since
all energy gaps are identical
Josephson Junction: \(\displaystyle \hat{H}_J = E_J\,\left(1 - \cos\hat{\phi}\right) \approx \frac{E_J}{2}\,\hat{\phi}^2 - \frac{E_J}{4!}\hat{\phi}^4 + \cdots \)
\(\displaystyle \hat{\phi} = \frac{\hat{\Phi}}{\Phi_0}, \quad E_J = \frac{\Phi_0^2}{L_J} \) Acts as nonlinear inductance => anharmonic oscillator
Shunting with large capacitor shields from charge noise



\(E_J\)
\(E_C\)
Quantum Pendulum (Transmon)

Nonlinearity makes energy gaps different
Energy level pairs now addressable as qubits
In reality, ~7 levels are bound in the cosine well
The bottom two levels are the most stable qubit
Microwave drive resonant with qubit energy gap
induces single-qubit gates (controlled Rabi oscillations)
\(\displaystyle \hat{H} = E_0\,\hat{1} + \hbar\omega_q\,|1\rangle\!\langle 1| + \hbar(\omega_q - \delta_q)\,|2\rangle\!\langle 2|+ \cdots \)
Transmon Qubits as Artificial Atoms
Cosine potential acts like a binding potential well
Below an ionization threshold, energies are discretized
(Above the threshold, unbound energies are continuous)
Distinct behavior from optical regime with real atoms:
- Engineered chips permit ultra-strong and deep-strong coupling regimes that are difficult to achieve with atoms
- Lower frequencies than optics make transients more relevant
-
Emission can be directionally controlled down waveguides to minimize collection loss and increase detection efficiency
- These atoms are super-cool (~4 mK)
\(\displaystyle \hat{H} \approx E_0\,\hat{1} + \hbar\omega_q\,|1\rangle\!\langle 1| + \hbar(\omega_q - \delta_q)\,|2\rangle\!\langle 2| \)


Measuring a Transmon Qubit
Problem:
Qubit is on a chip inside a fridge near absolute zero.
How does one "measure the energy eigenstate" of the qubit without causing unwanted changes to those energy states?


Solution:
Indirectly peek at the qubit energy by dispersively coupling
the qubit to a strongly detuned resonator, then
probing that resonator with a microwave tone.
The frequency shift of the leaked and amplified tone stores information about the energy state of the qubit without allowing energy transitions between the qubit and resonator.
This type of measurement that does not disturb energy eigenstates in the process of measuring the energy is called a
"quantum non-demolition (QND) measurement".

Dispersive Readout: Quantum Filtering
Reconstructing qubit information from an amplified and noisy homodyne record is a challenging filtering problem!
Need to process stochastic voltage records to isolate tiny phase-differences
(classical signal filtering)
The corresponding qubit/resonator state evolution must then be inferred
(quantum state filtering)
Amazingly, all you need is Bayes' Rule from probability theory
and the Born rule from quantum mechanics to derive how
the state partially collapses with information gain!
Problem:
The microwave probe tone must be compared to the original source, using homodyne or heterodyne measurements.
These signals are noisy due to the intrinsic vacuum noise of the source, which dominates the tiny amount of qubit information per unit time.

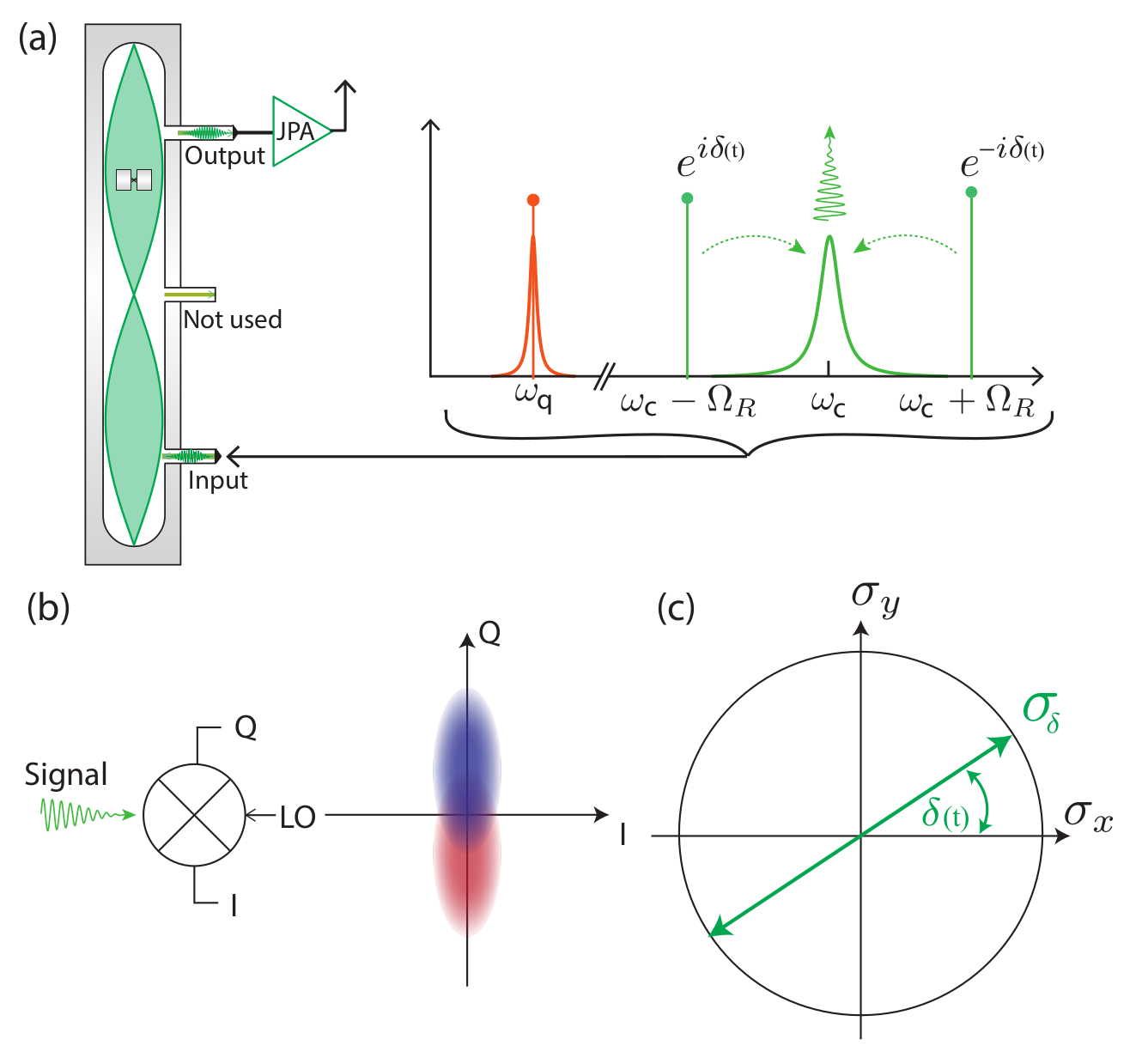
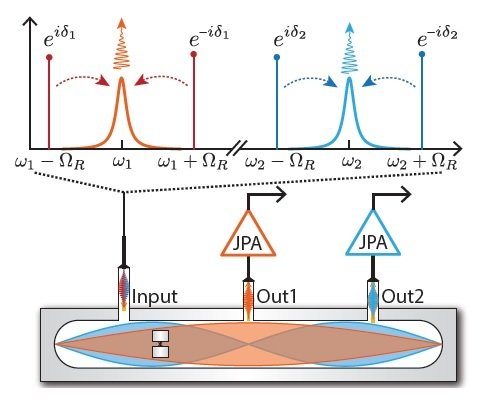
Dispersive Readout: Amplification
Without quantum-limited on-chip pre-amplification, this technique wouldn't work due to the weak signal.
With pre-amplification, the weak signal is boosted above noise thresholds for later HEMTs.
Quantum-limited amplifiers (built from Josephson junctions using their nonlinear inductance):
-
Josephson Parametric Amplifier (JPA):
- narrow-band reflected 3-wave mixer
- can operate in phase-sensitive (squeezed, above) or phase-preserving (unsqueezed) modes
-
Traveling Wave Parametric Amplifier (TWPA):
- broad-band amplification over transmission-line propagation
- only operates in phase-preserving (unsqueezed) mode
Outgoing signal is further amplified to enhance phase difference in steady-state resonator modes
One (informational) quadrature encodes the qubit state information as a displacement of the signal distribution
The other (phase) quadrature encodes photon number fluctuations inside the resonator

Single shot "projective" readout
using phase-sensitive amplifier to isolate informational quadrature
Integrated noisy signals clearly distinguish definite qubit states
and can detect "quantum jumps" between them (useful for syndrome detection)
Prevents normal dynamics from occurring (quantum Zeno effect)
Strong Continuous Monitoring
Stronger coupling yields more distinguishable resonator states
More information per unit time yields more rapid projection to the stationary eigenstates of the coupling
=> Strong continuous measurement

For each trajectory, the qubit state is affected less per unit time
but the same average information can be collected over an ensemble
Weak coupling can "gently" monitor average information during dynamics,
yielding a gradual collapse to an eigenstate as information accumulates.
Weak Continuous Monitoring
Weaker coupling yields
less distinguishable resonator states
Less information per unit time yields
slower projection to the coupling eigenstates
=> Weak continuous measurement
Following Bayes' rule, the qubit state randomly walks as probabilities are updated with each small amount of information in the signal

Modern UC Berkeley Planar Chip: 8 Transmons
Bus doubles as Purcell filter,
coupled to traveling wave parametric amplifier (TWPA)
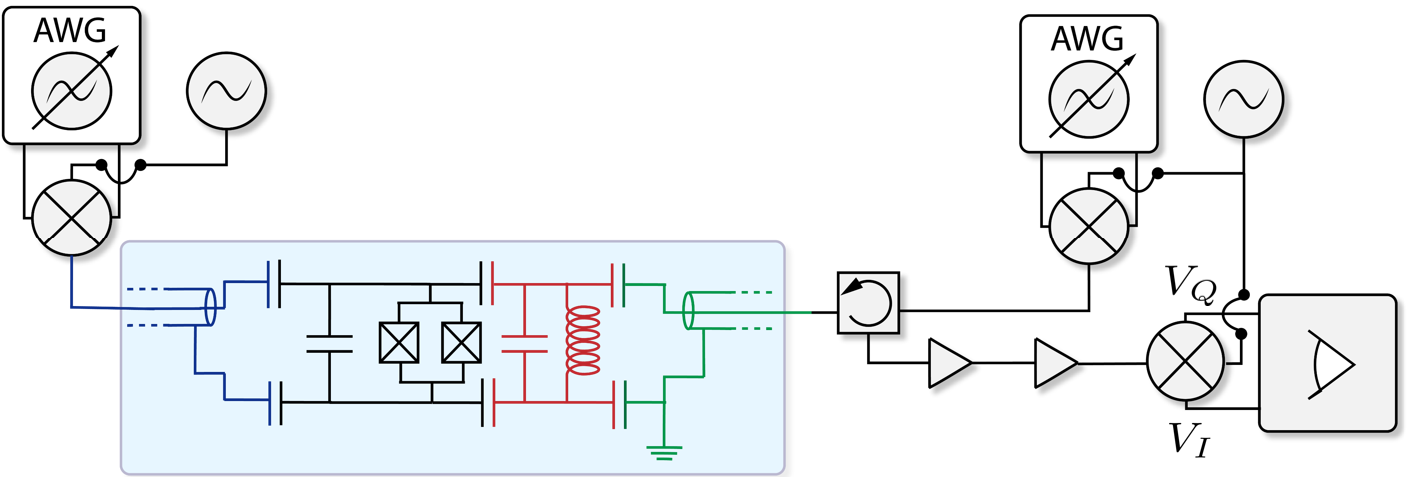
(Stripline) Resonator couples capacitively to both bus and transmon for qubit readout
Double-junction Transmon couples to both readout resonator and a separate control line
Control uses a resonant (Rabi) drive where envelope area is the rotation angle
TWPA
Bus is pumped to excite resonator. Reflected part of the field and leaked resonator field are amplified by the TWPA, which is phase-preserving
Distinguishable resonator phase is made visible in a heterodyne measurement
A Brief Tour of Recent Work using
Continuous Measurements
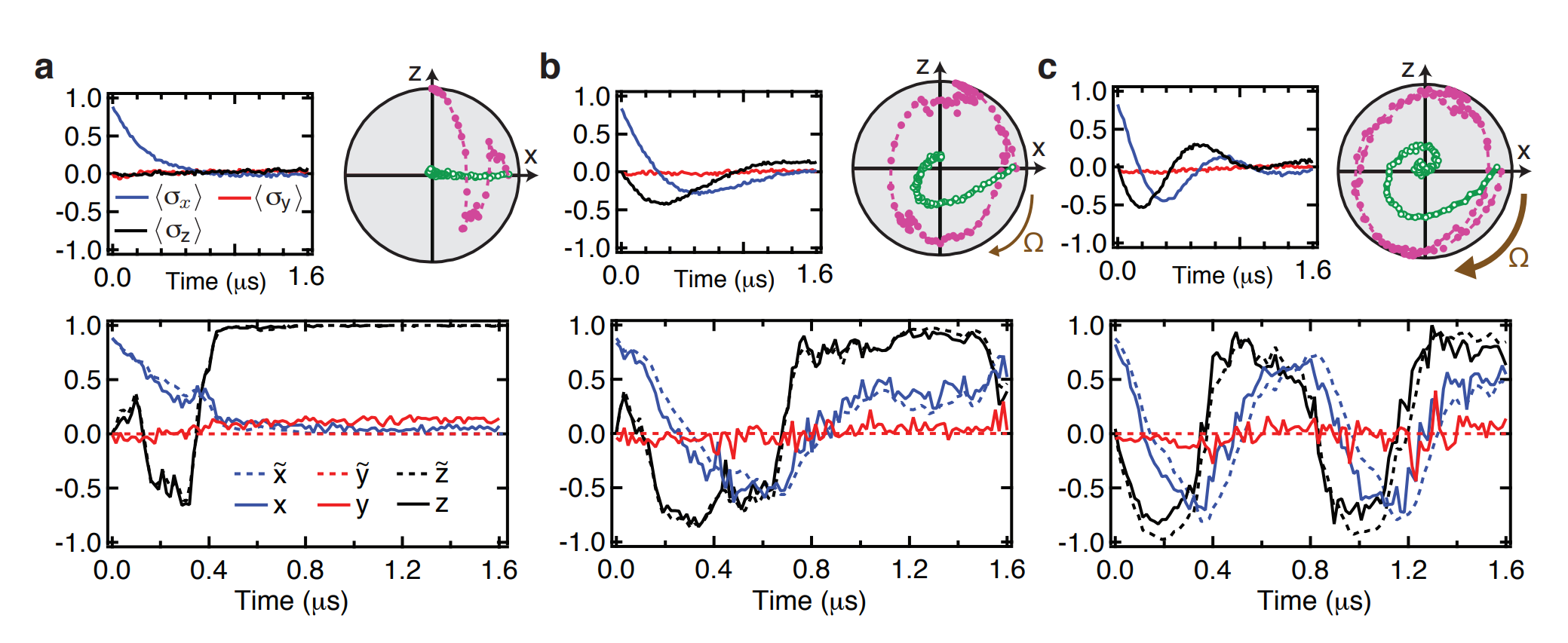
Monitored Rabi Drive
JD and Siddiqi Group, Nature 511, 570 (2014)
Partial collapses compete with unitary dynamics
Ensemble-averaging the stochastic evolution recovers smooth dissipative (Lindblad) dynamics
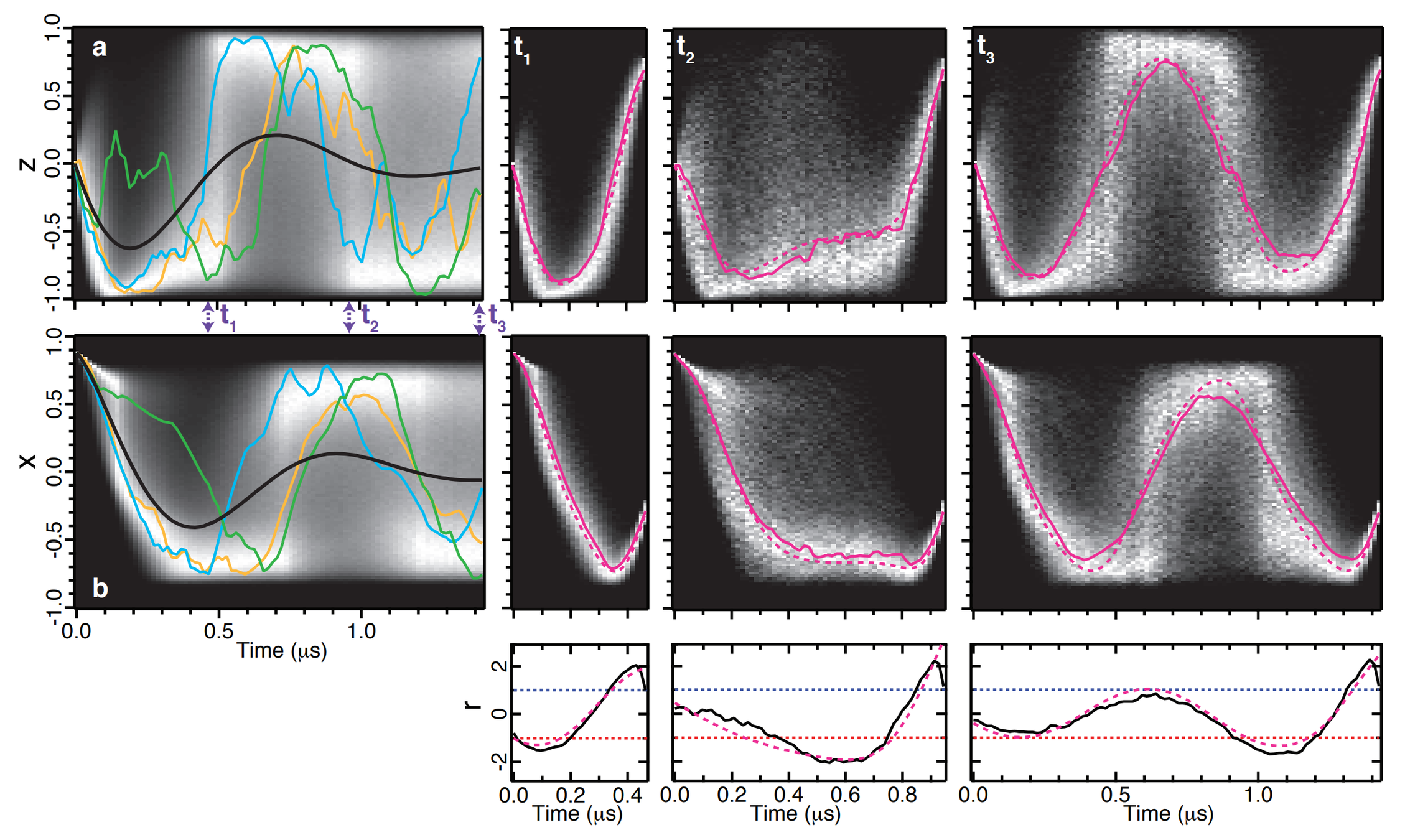
Post-selected State Dynamics
JD and Siddiqi Group, Nature 511, 570 (2014)
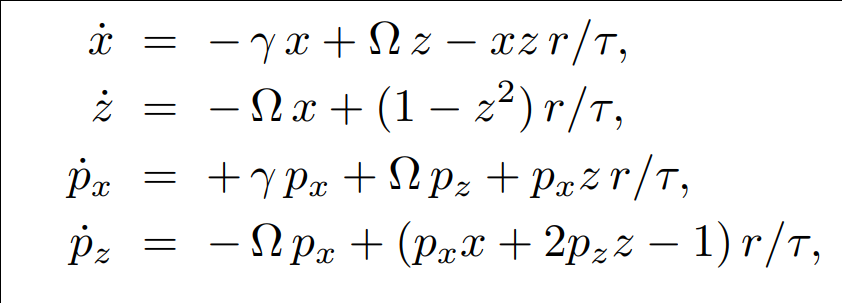
Experimental most probable path matches ODE solution derived from stochastic path integral
JD and Jordan Group, PRA 88, 042110 (2013)
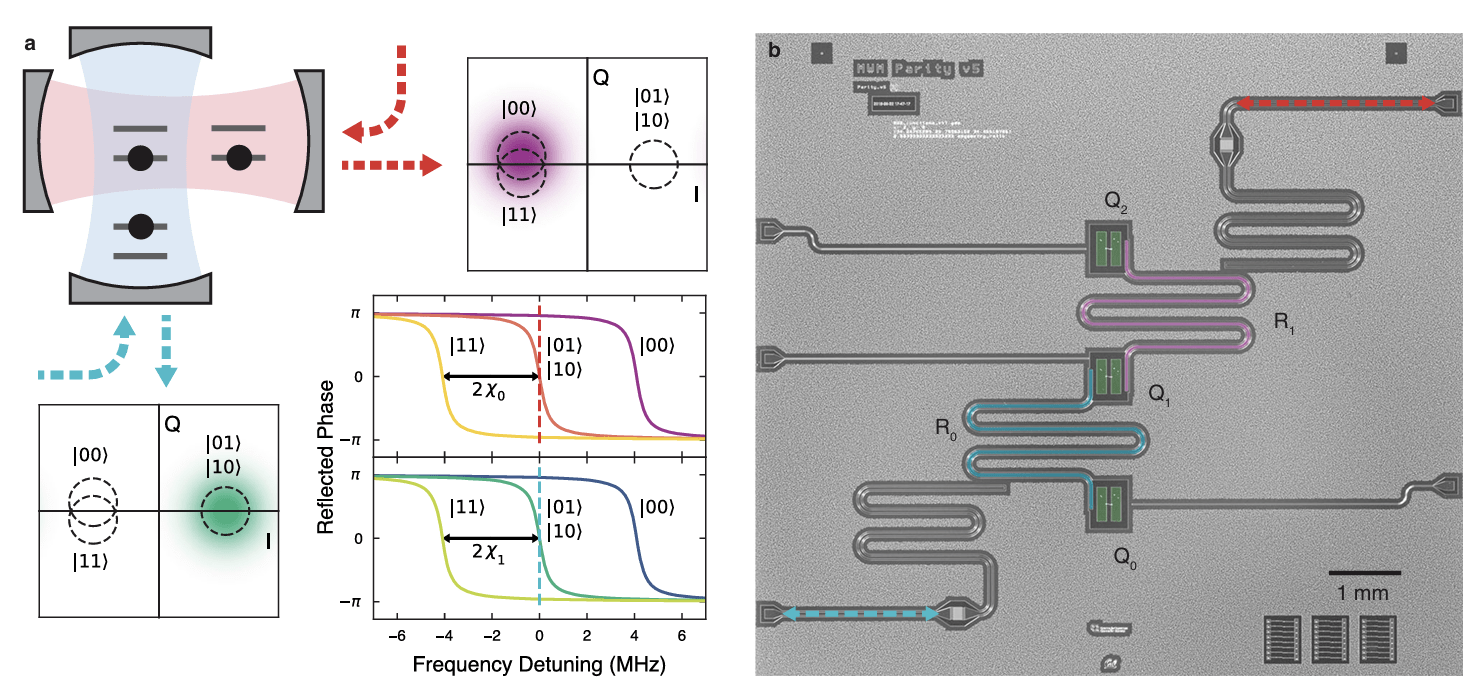
Siddiqi group, JD, Nature Communications 13, 2307 (2022)
2 parity syndromes of 3 qubits monitored continuously and strongly
Zeno effect protects code space, readout alerts when flip needs correction
Continuous Quantum (Bit-flip) Error Correction
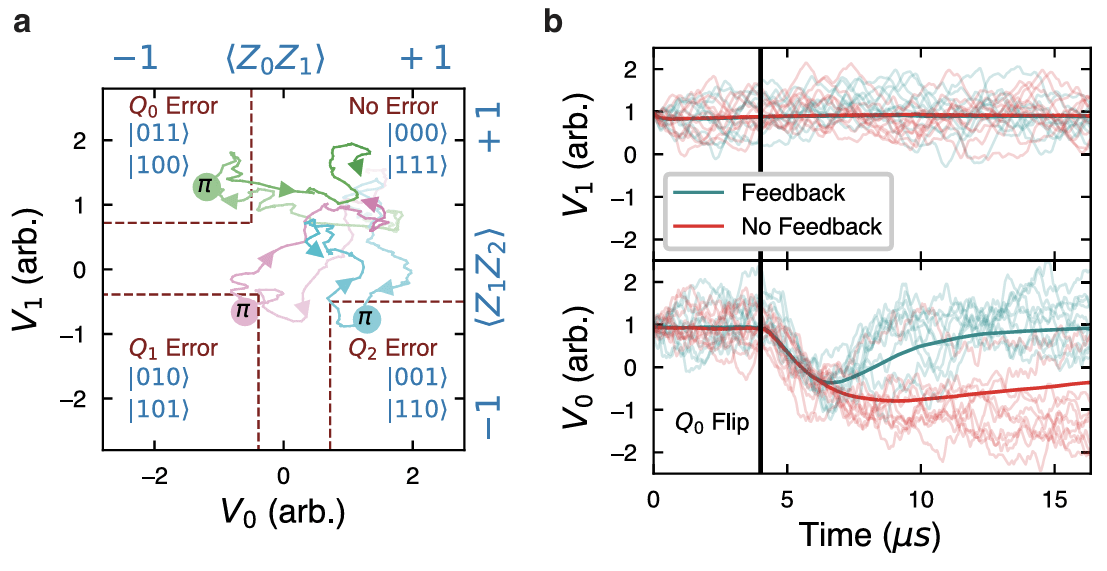
Siddiqi group, JD, Nature Communications 13, 2307 (2022)
Continuous Quantum (Bit-flip) Error Correction
2 parity syndromes of 3 qubits monitored continuously and strongly
Zeno effect protects code space, readout alerts when flip needs correction
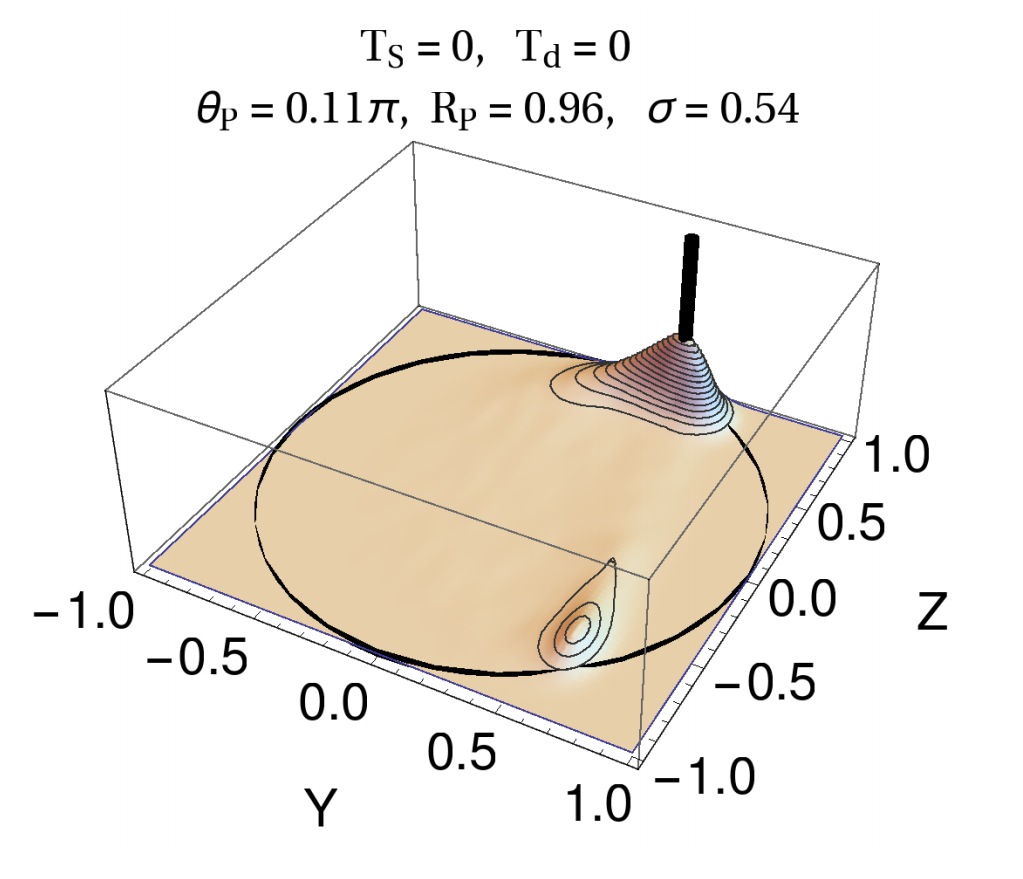
Feedback State Stabilization
Linear feedback (with very small temporal delays) can stabilize the qubit state to targeted regions of the Bloch sphere.
JD and Jordan Group, PRA 96, 022311 (2017)
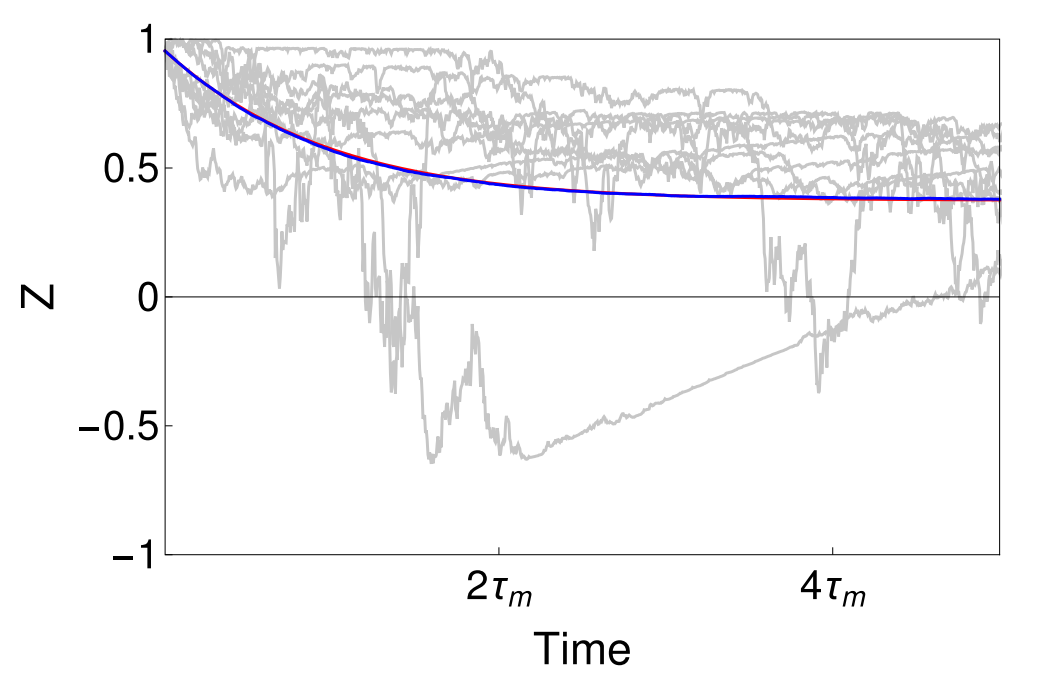
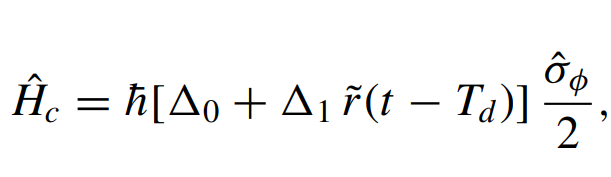
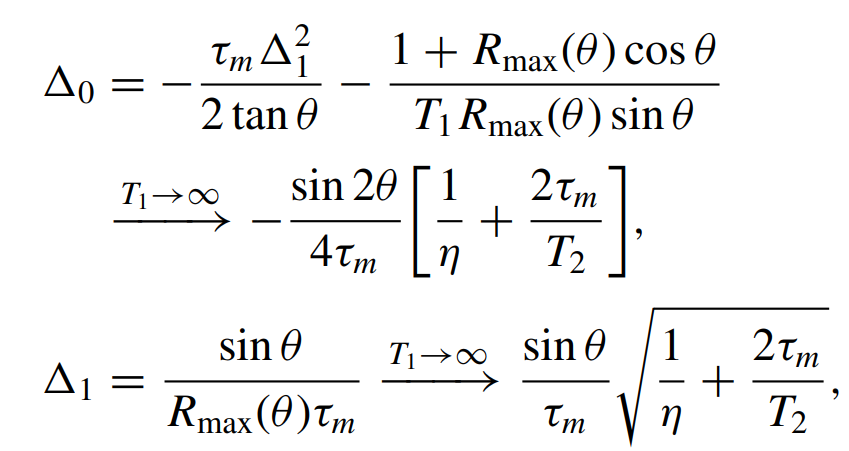
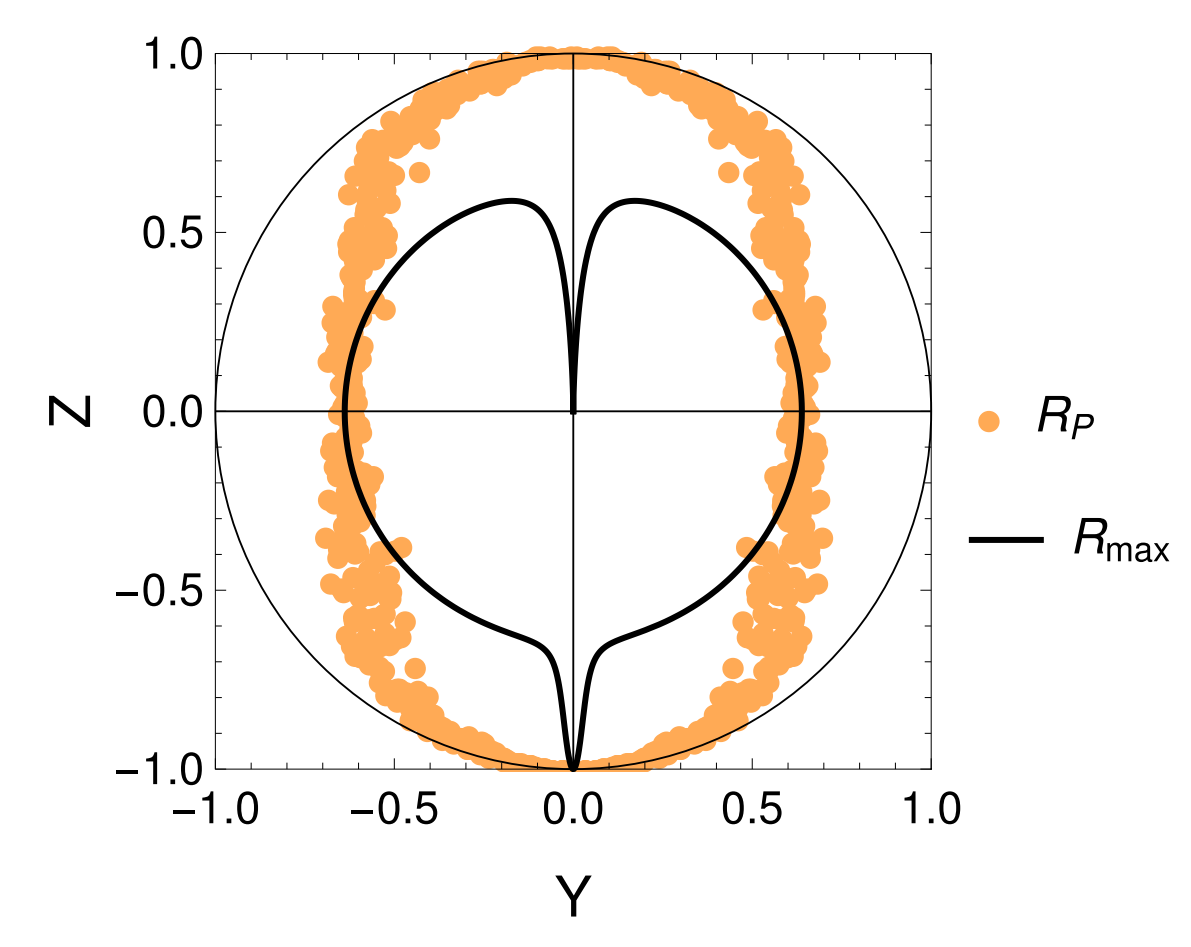
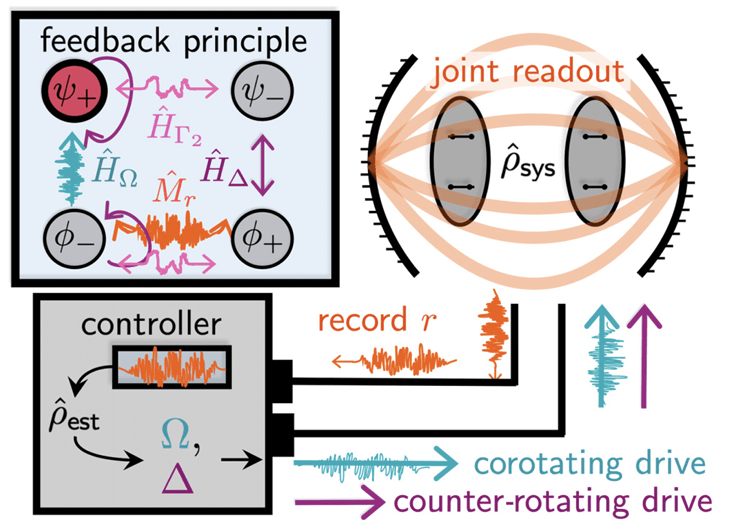
Levenson-Falk, JD, PRApplied 21, 024022 (2024)
Two drives, parity measurement, and feedback stabilize Bell state
Non-Markovian noise sources suppressed by measurement and dynamical decoupling from drives (theory + simulations)
Entangled State Stabilization with Feedback
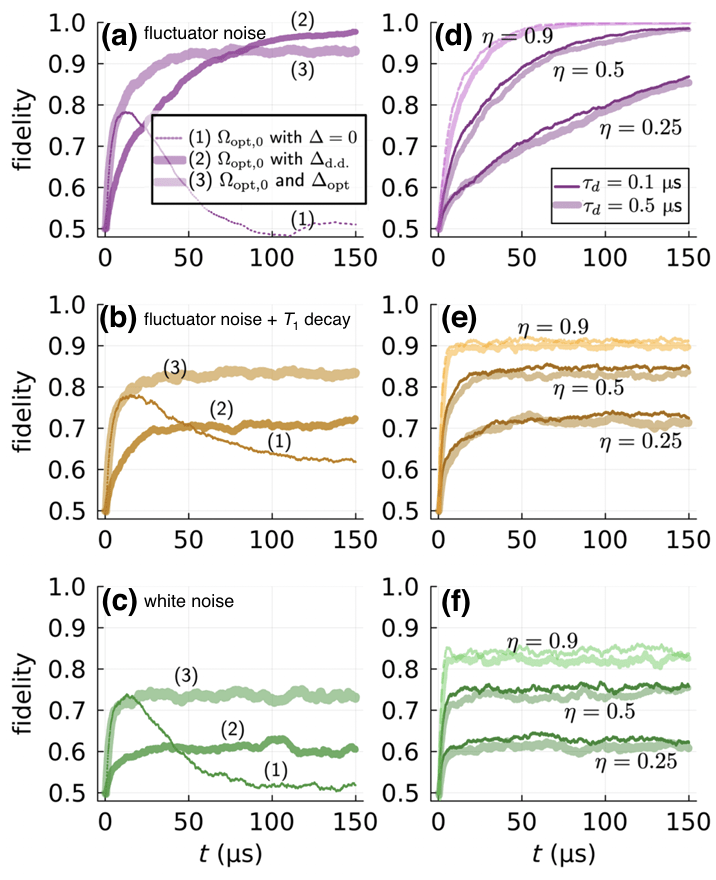
- Symmetrically detuned pumps
- Beats stroboscopically measure rotating qubit
- Yields displacement coupling
- Allows tunable measurement axis
- Multiple cavity modes = multiple observables
Displacement coupling:
Siddiqi group, Nature 538, 491 (2016)
Stroboscopic Displacement Coupling
Rotating frame:
Incoherent Zeno-Dragging Qubit Gate
Idea : use time-varying measurement axes to drag the quantum state around the Bloch sphere using the quantum Zeno effect
The record tracks the state well in this regime, so can be used as a herald for high-fidelity gates
Non-unitary gate
(measurement-based)

Stroboscopic displacement coupling can be time-varying
JD, Siddiqi group, PRL 120, 020505 (2018)
Jumps : Faster drag speeds allow trajectories to jump to the opposite pole, decreasing ensemble-averaged dragging fidelity
Jump-axis : Dragging dynamics causes lag of actual Zeno-pinned behind the measurement axis by a fixed angle
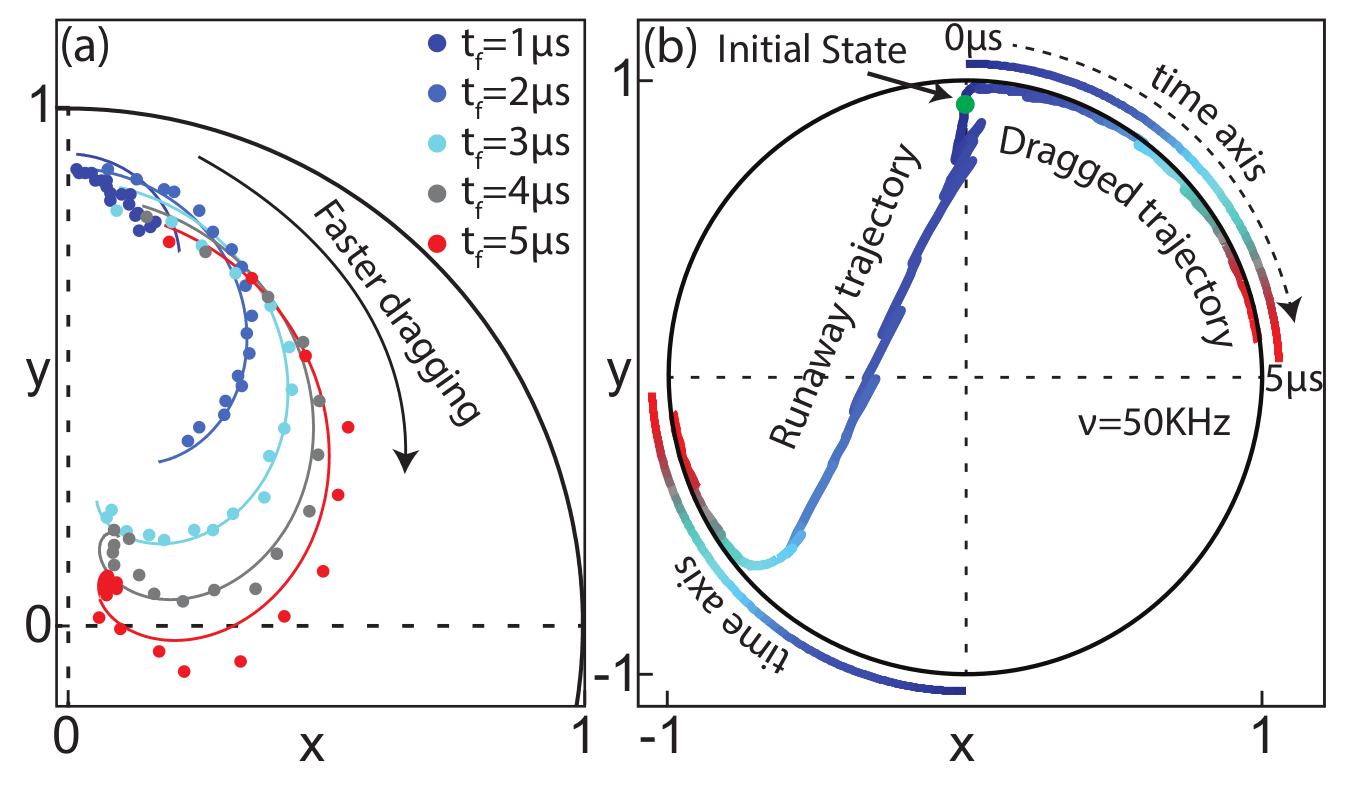
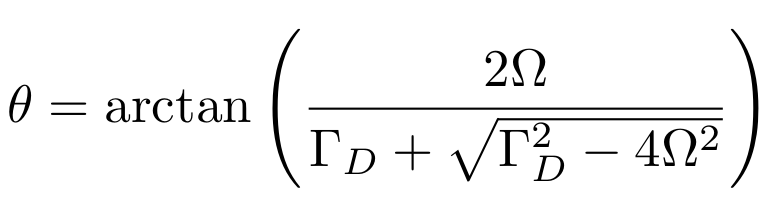
JD, Siddiqi group, PRL 120, 020505 (2018)
Pinned to poles : Other than the jumps, state remain pinned to lagged measurement poles
Incoherent Zeno-Dragging Qubit Gate
Siddiqi group, Nature 538, 491 (2016)
4 pumps, symmetrically detuned from 2 resonator modes
2 simultaneous noncommuting observables
Partial collapses compete with each other, preventing full collapse to a stationary state
If observables are maximally non-commuting, creates persistent phase-diffusion in Bloch sphere
Noncommuting Observable Measurement
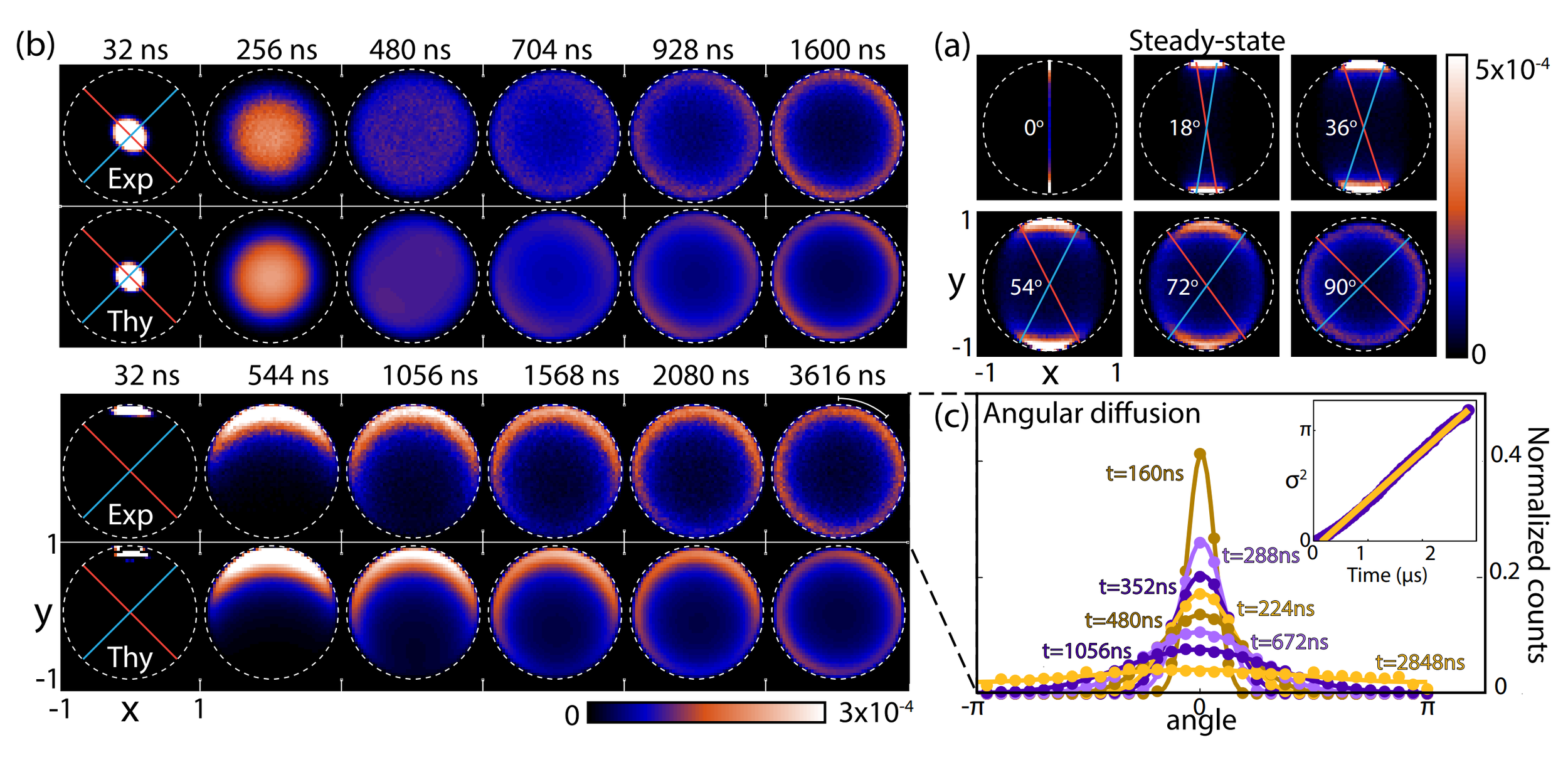
Siddiqi group, Nature 538, 491 (2016)
State purifies, but diffuses randomly
Basins of attraction if measurement axes are nearly aligned
Noncommuting Observable Measurement
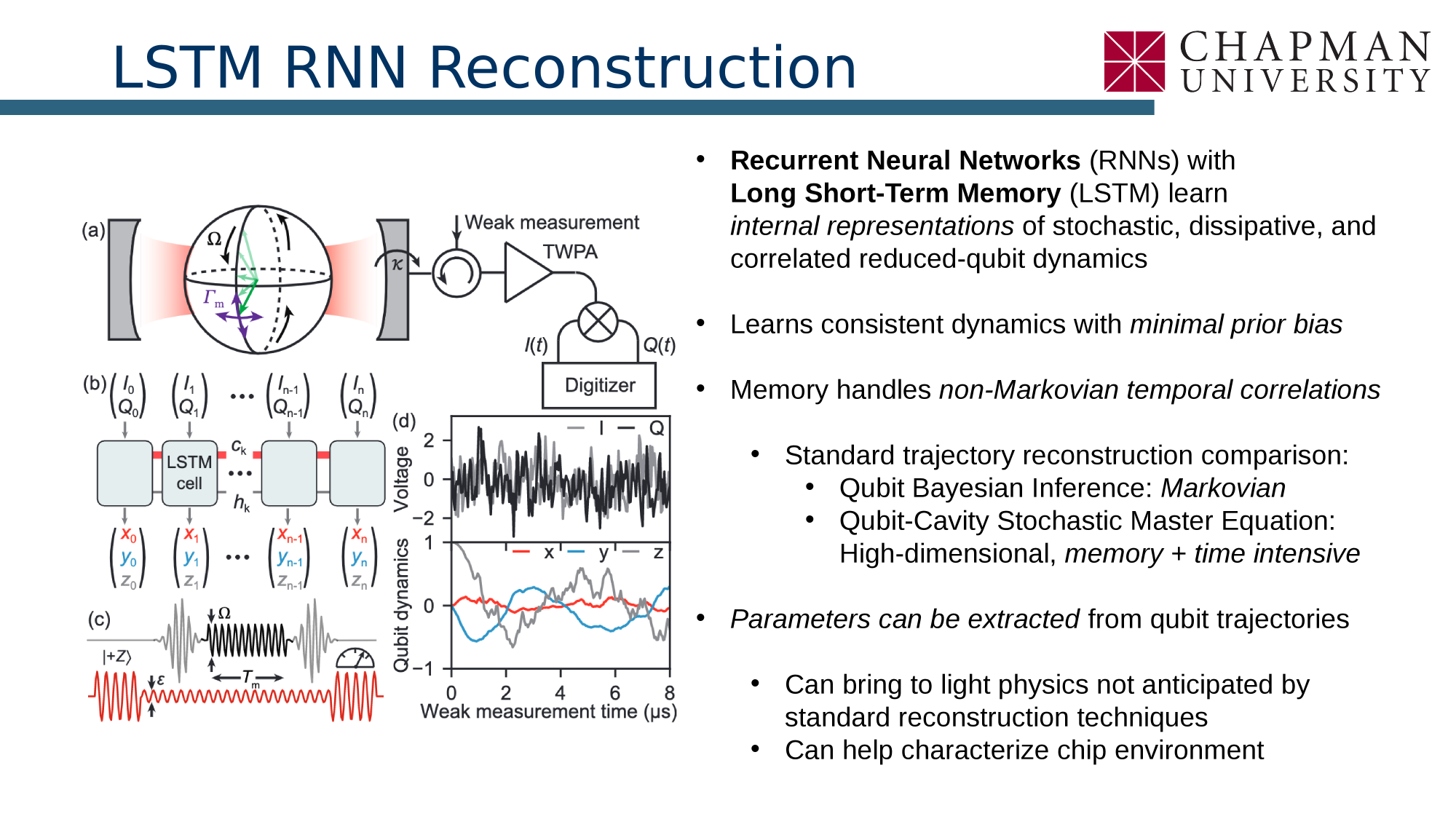
Machine Learning of Quantum Trajectories
Siddiqi group, JD, PRX 12, 031017 (2022)

Machine Learning of Quantum Trajectories
Siddiqi group, JD, PRX 12, 031017 (2022)
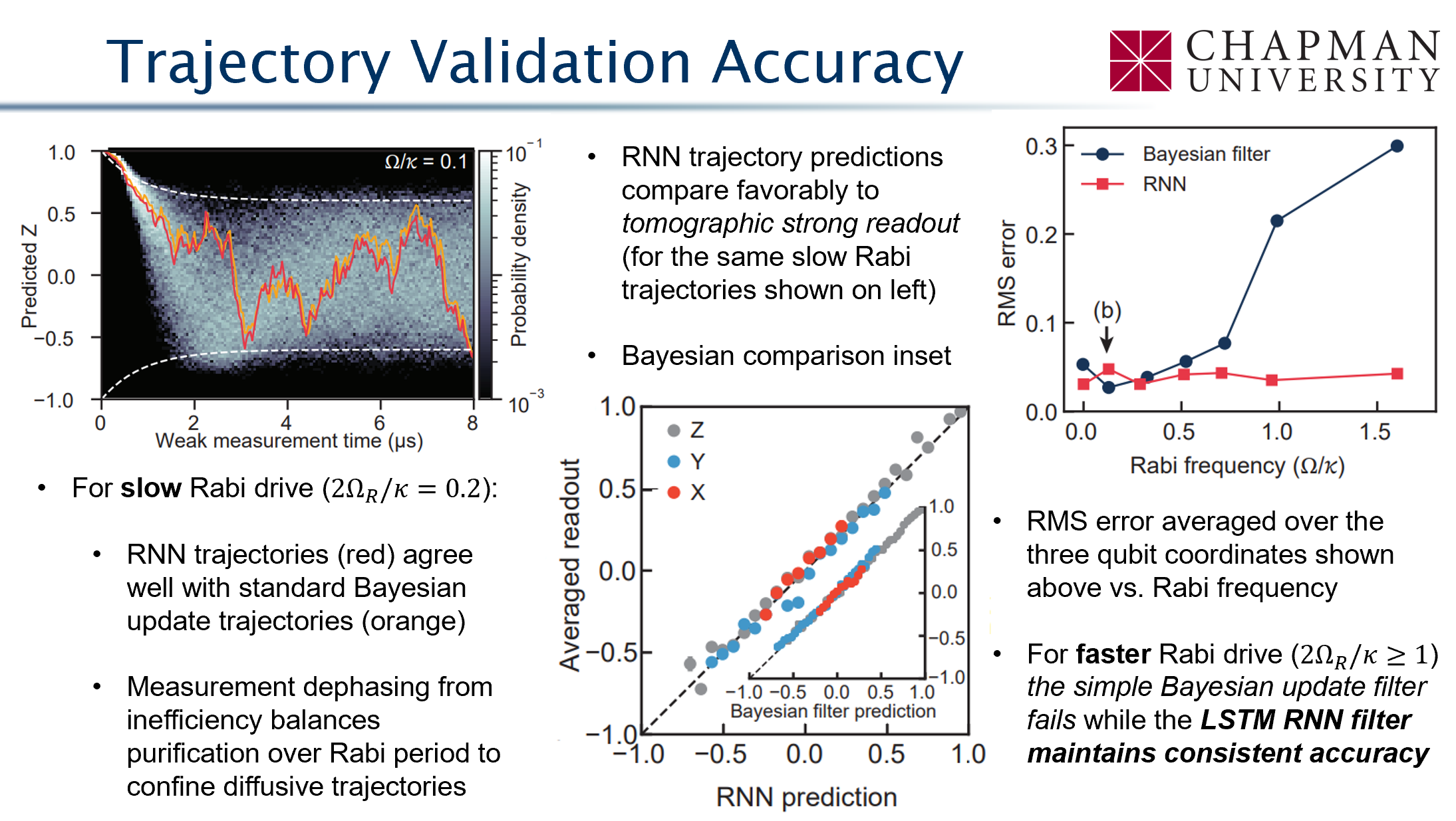
Machine Learning of Quantum Trajectories
Siddiqi group, JD, PRX 12, 031017 (2022)
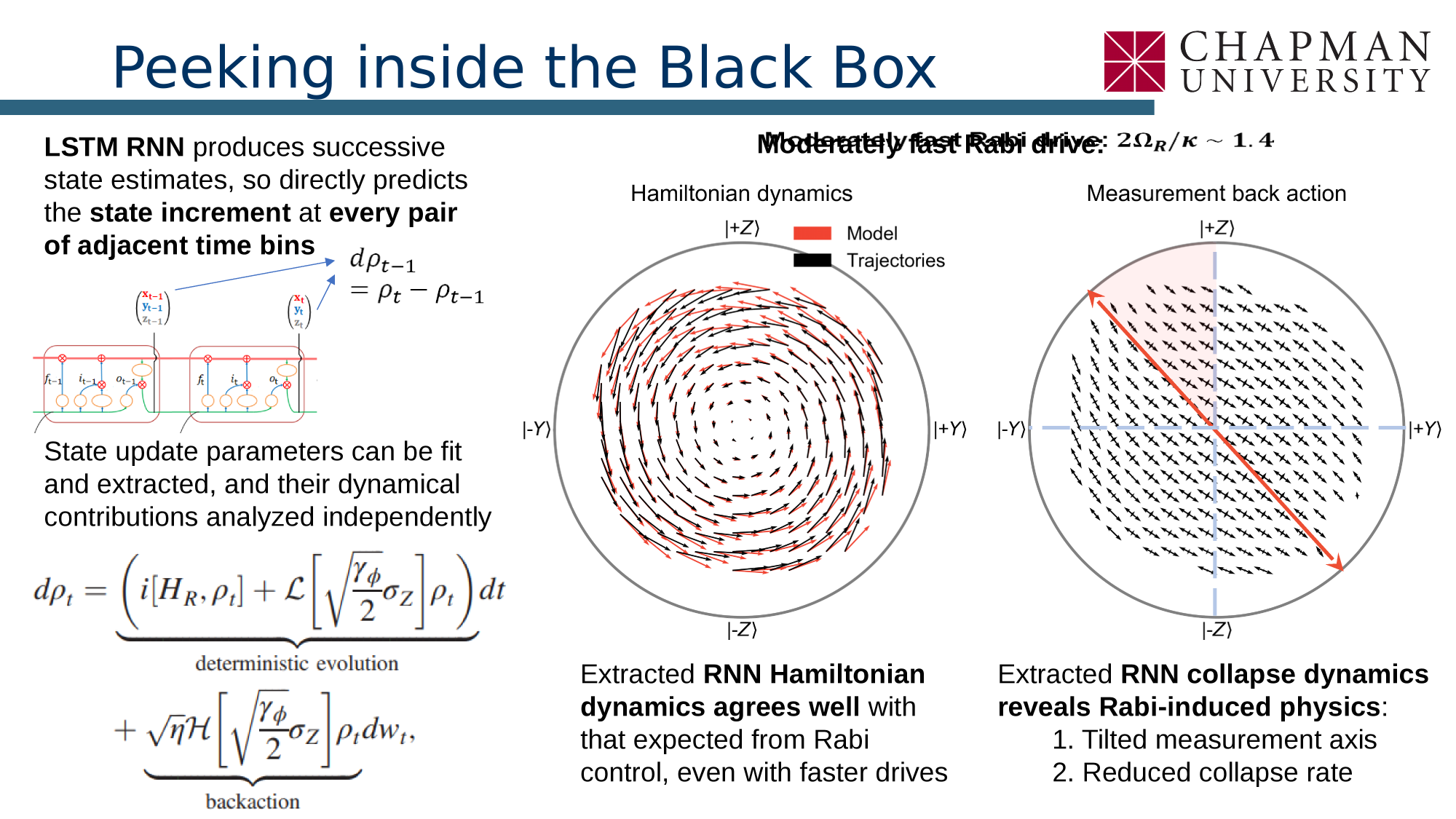
Machine Learning of Quantum Trajectories
Siddiqi group, JD, PRX 12, 031017 (2022)
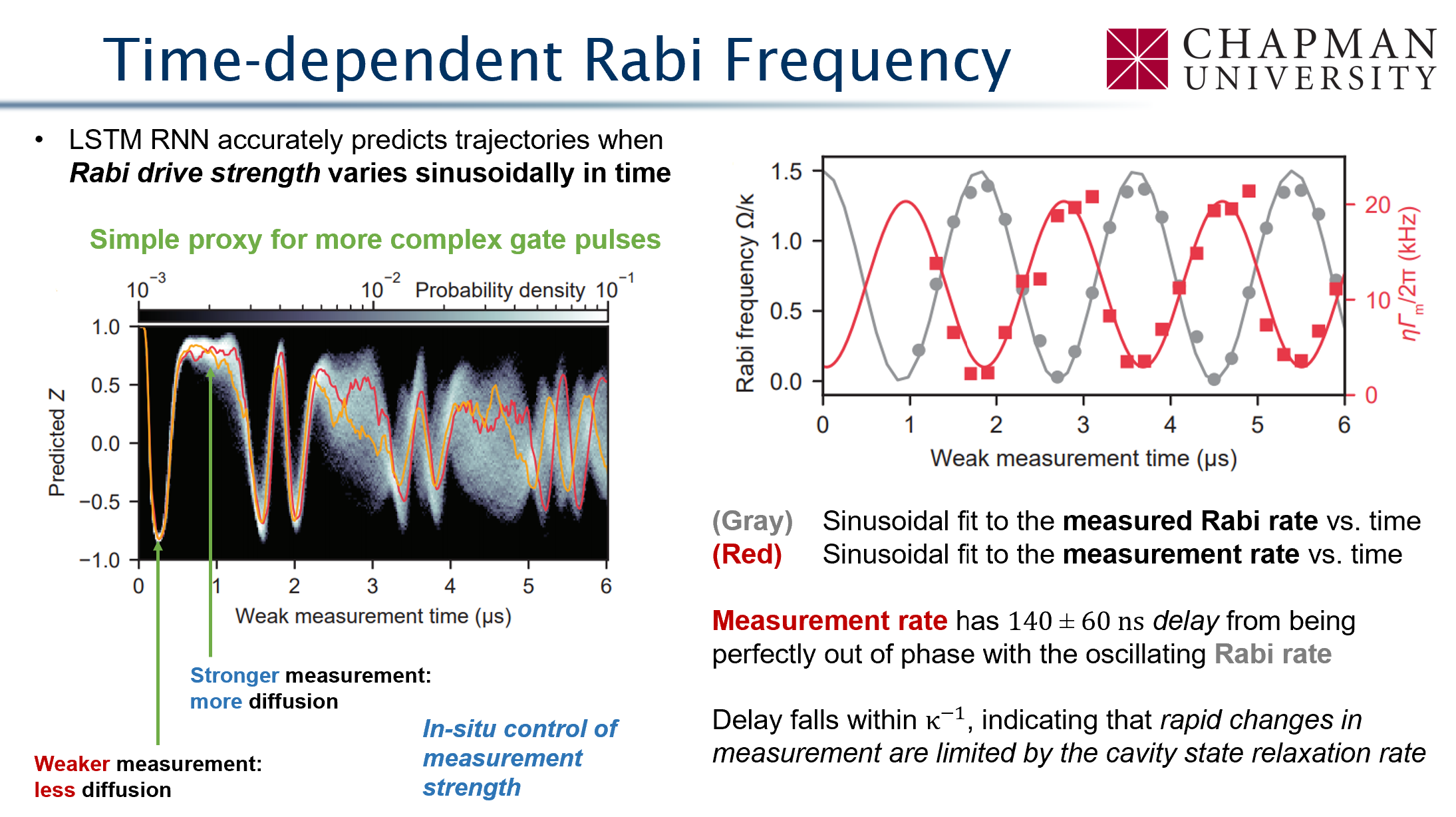
Machine Learning of Quantum Trajectories
Siddiqi group, JD, PRX 12, 031017 (2022)
Conclusions

-
Superconducting qubits are super-cool(ed)
-
Superconducting qubits naturally use continuous measurements, which have much more detailed information and potential utility than just integrating them to obtain standard binary projective measurements
- Continuous measurements have a variety of uses, from tracking the state, to state stabilization with feedback, to error correction and Zeno dragged incoherent gates, and more!
Thank you!

Individual quantum state trajectories filtered from the readout are verified via spot checking predicted subensembles with tomography
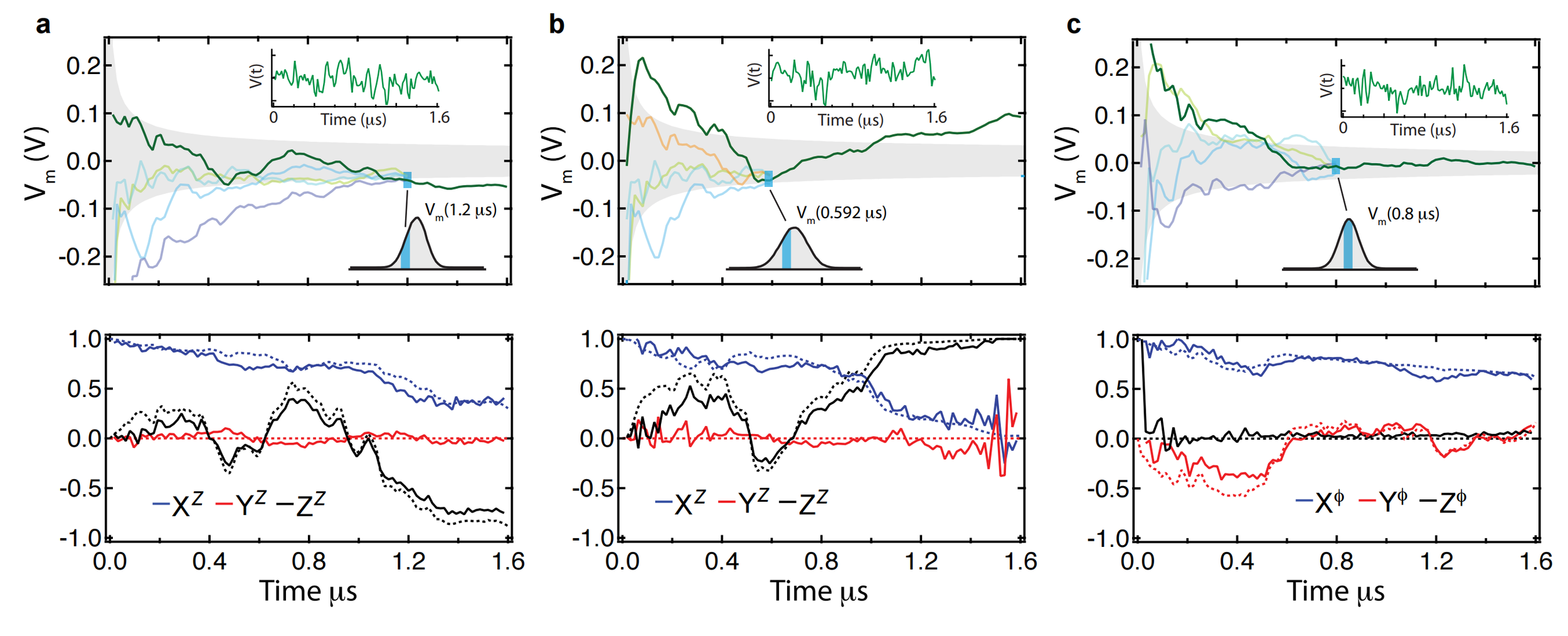
Approach:
- Perform a random tomographic pulse at the end of each data run
- Spot check subensembles of data to verify tomography of final state
Quantum State Trajectories
Murch et al., Nature 502, 211 (2013)

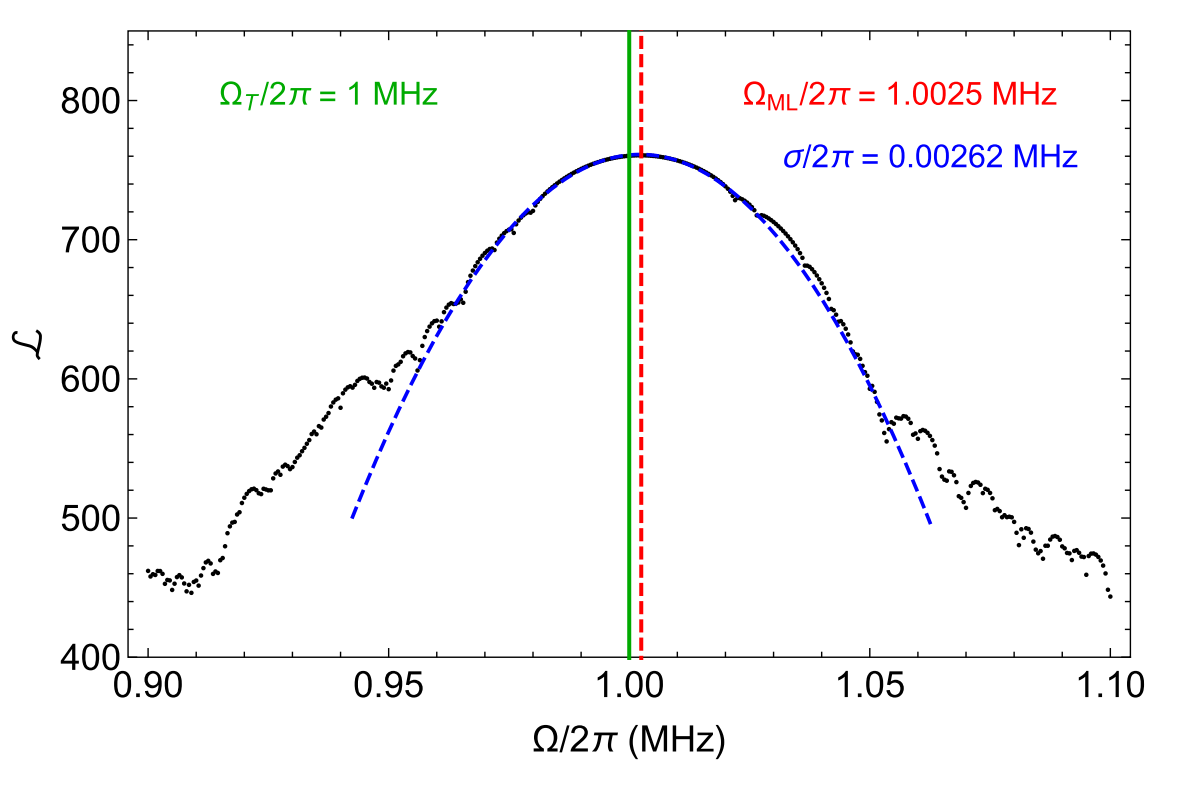
Tracking Drifting Parameters
Maximum likelihood techniques allow extraction of parameters drifts from stochastic records with reasonable precision
JD and Jordan Group, PRA 95, 012314 (2017)
Continuous Monitoring and Feedback Control of Superconducting Qubits
By Justin Dressel
Continuous Monitoring and Feedback Control of Superconducting Qubits
UT Arlington, Invited Talk, 2025/03/26; The precision control offered by modern superconducting processors has enabled the implementation and use of time-continuous monitoring of quantum information using coupled microwave cavities. This talk reviews how these measurements are implemented and gives a tour of recent experimental and theoretical uses for the technique, including measurement-based gates using the quantum Zeno effect and state stabilization using feedback control.
- 238



