Strengthening weak measurements for qubit tomography and multitime correlators
Justin Dressel
Schmid College of Science and Technology
Institute for Quantum Studies
Chapman University
January 16, 2019
Justin Dressel (PI)
José Raúl Gonzales Alonso (postdoc)
Razieh Mohseninia (postdoc)
Shiva Barzili (grad student)
Lucas Burns (grad student, spring 2019)
Amy Lam (undergrad)
Luis Pedro García-Pintos (postdoc - now at UMB)
Taylor Lee Patti (undergrad - now at Harvard)
William Parker (undergrad - now at U Oregon)
Aaron Grisez (undergrad - founder of Qhord.com)
Chapman Crew
Outline
-
Strengthening Weak Value Tomography
- Weak Value Tutorial
- Weak Value Tomography
- Strong Weak Values with Neutrons
-
Strengthening Qubit Correlator Measurements
- Weakly Measured Correlators
- Generalized Qubit Measurements
- Strongly Measured Correlators
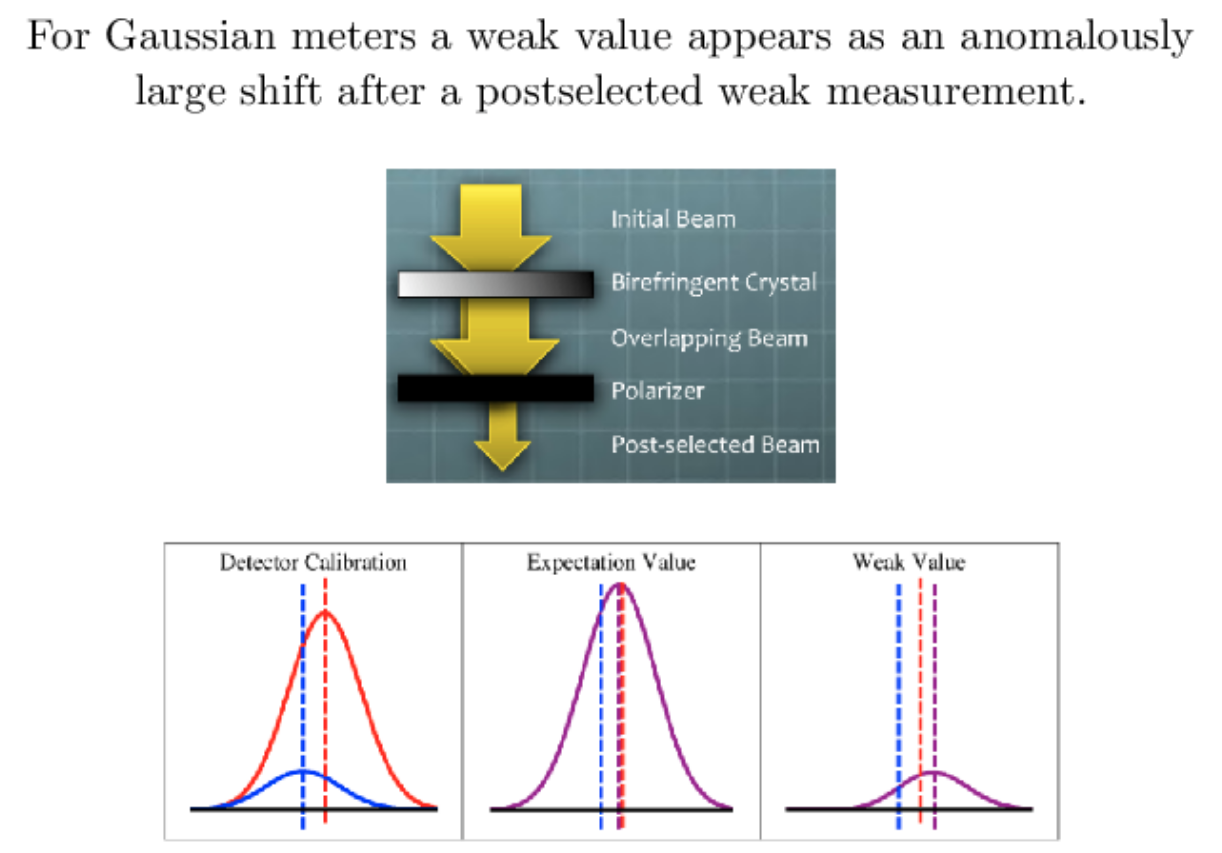
What is a Weak Value?
Roughly, it is a conditioned expectation value under weak detector coupling that can have surprising properties
Aharonov, Albert, Vaidman (AAV), PRL 1988
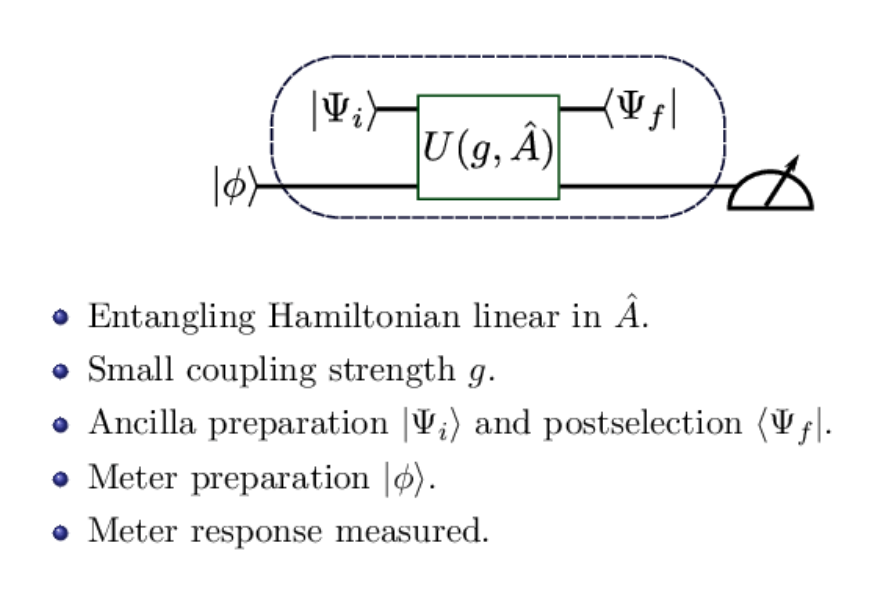
What is a Conditioned Expectation Value?
A conditioned expectation value is the conditioned response of an indirectly coupled and properly calibrated meter
Pang, Dressel, Brun, PRL 113, 030401 (2014)
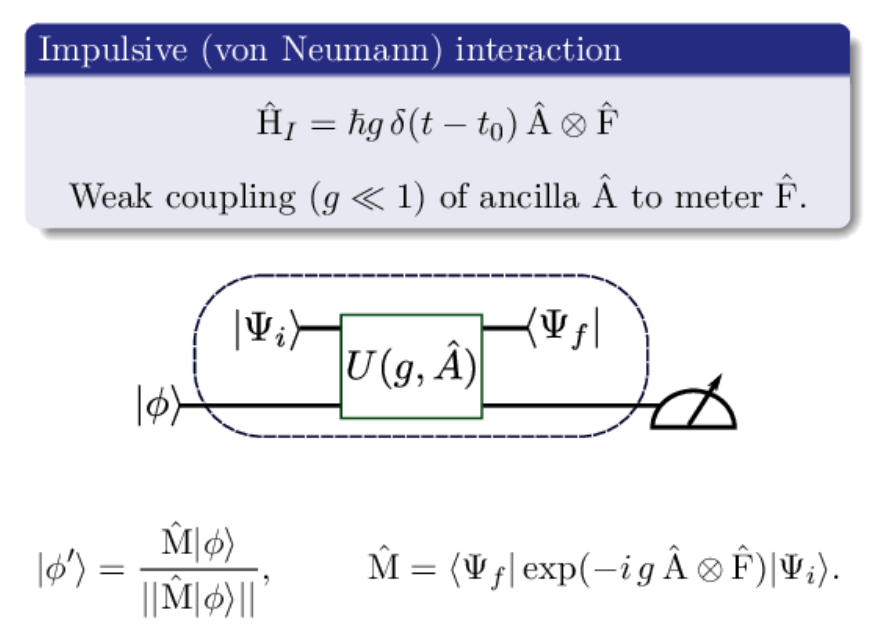
The detector response is encapsulated in the "measurement operator", which is a partial matrix element of the interaction propagator
Pang, Dressel, Brun, PRL 113, 030401 (2014)
What is a Conditioned Expectation Value?
What is a Weak Value?
Weak values appears as the key complex system parameters that characterize the detector response. Generally all infinite orders \((A^n)_w\) are needed, but for weaker coupling the first order suffices
Pang, Dressel, Brun, PRL 113, 030401 (2014)
Kofman, Ashab, Nori, Physics Reports 520, 43 (2012)
Dressel, Jordan, PRL 109, 230402 (2012)
Detector parameters:
System parameter:
Pang, Dressel, Brun, PRL 113, 030401 (2014)
What is a Weak Value?
Typically, only the linear response regime is considered, where the weak value is directly proportional to the detector response
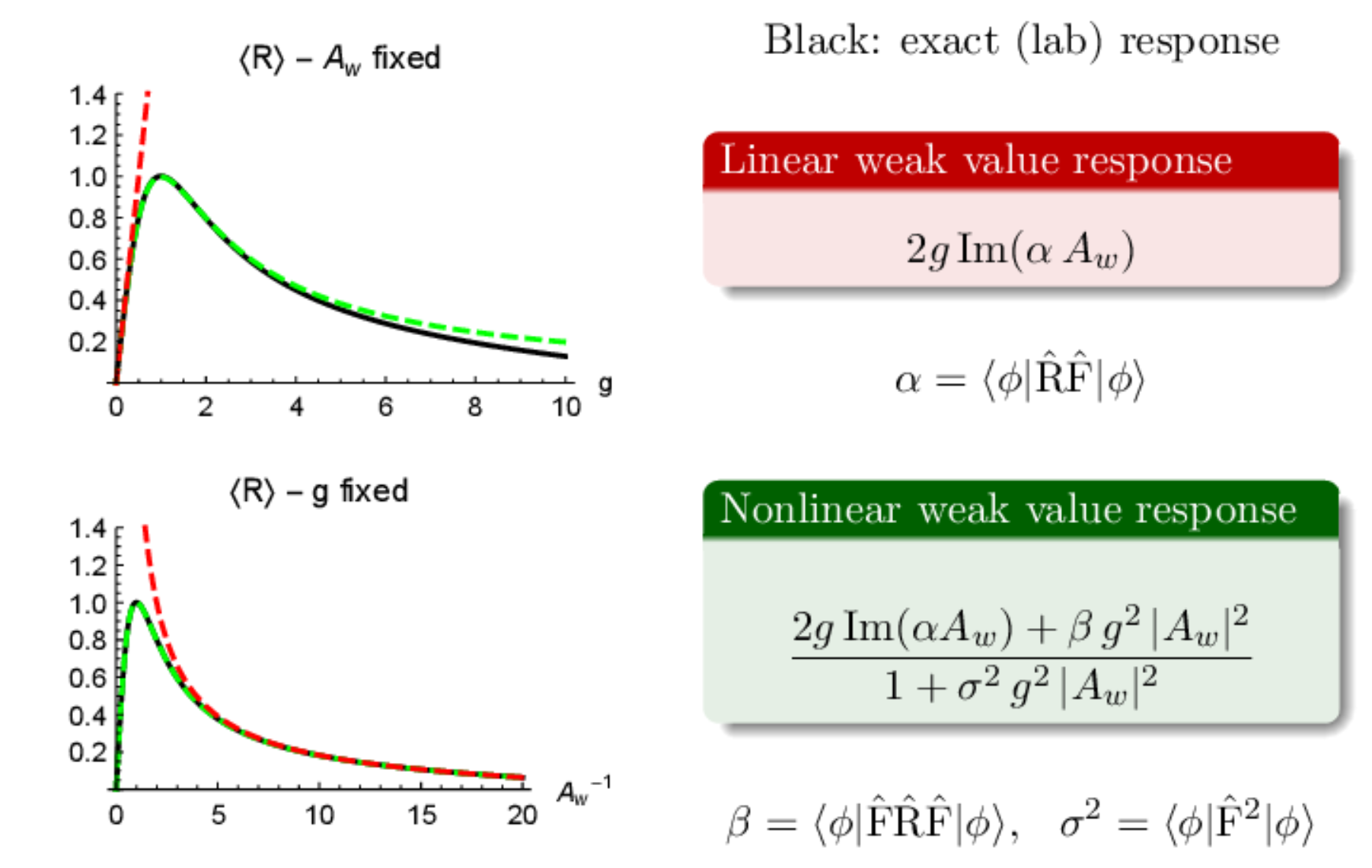
What is a Weak Value?
Even keeping only the first-order weak value, the nonlinear expression is remarkably accurate even for moderately large coupling strengths
Example: Sagnac Interferometer
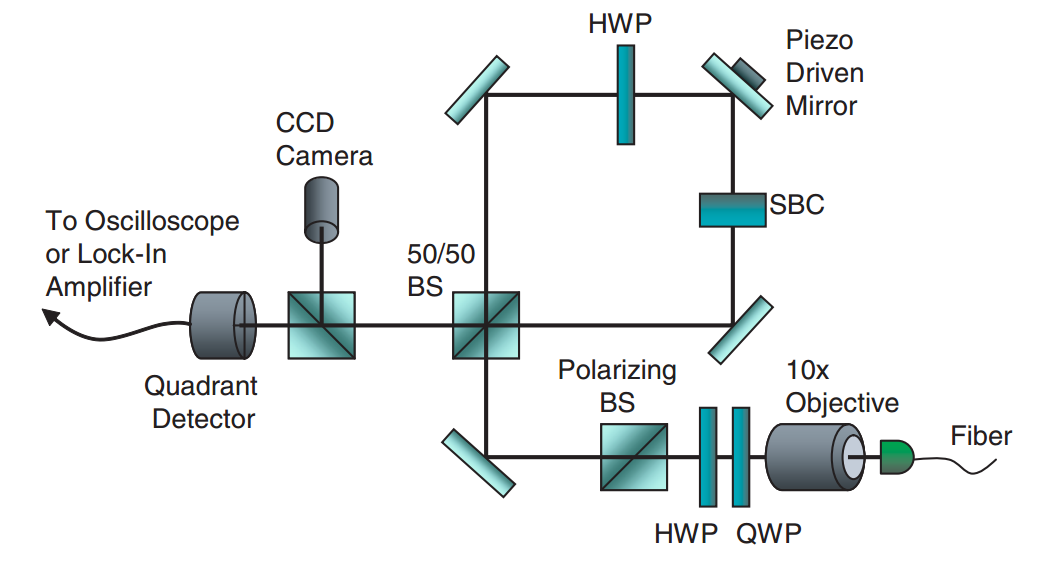
Prototype experiment: Howell lab, Rochester
PRL 102, 173601 (2009)
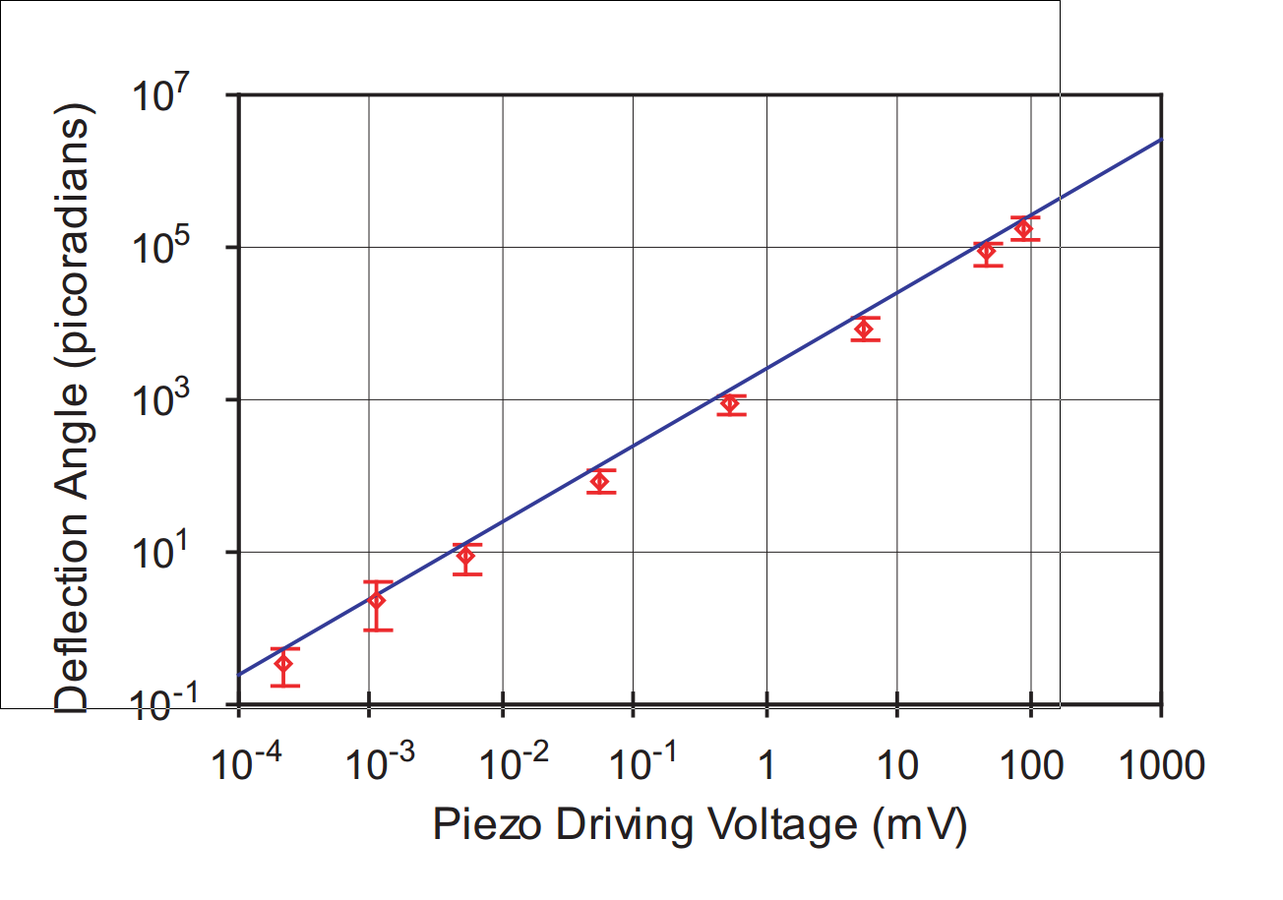
Ultra-sensitive to beam deflection: ~560 femto-radians of tilt detected
\phi\;\text{(phase offset)}
k\;\text{(tilt)}
x\;\text{(signal)}
\sigma\;\text{(beam waist)}
Weak Value Analysis
|i\rangle \propto i|\!\circlearrowleft\rangle + |\!\circlearrowright\rangle
|f\rangle \propto e^{i\phi/2}|\!\circlearrowleft\rangle - ie^{-i\phi/2}|\!\circlearrowright\rangle
|\psi, i\rangle \to \langle p, f | \exp(-i k \hat{x}\hat{W}) | \psi, i \rangle \approx \langle f | i \rangle \langle p - k W_w | \psi \rangle
\hat{W} = |\!\circlearrowleft\rangle\langle\!\circlearrowleft | - |\!\circlearrowright\rangle\langle\!\circlearrowright |
W_w = \frac{\langle f |\hat{W}|i\rangle}{\langle f | i \rangle} = i\cot\frac{\phi}{2} \approx \frac{2i}{\phi}
\phi\;\text{(phase offset)}
k\;\text{(tilt)}
x\;\text{(signal)}
\sigma\;\text{(beam waist)}
Angular tilt (transverse momentum) amplified by large weak value.
Weak value regime
k\sigma \ll \phi \ll 1
Dark port has single lobe that approximates displaced a Gaussian centered at:
\langle x/\sigma \rangle \propto (\mathbf{k}/\phi)\sigma
Tiny beam deflections can be distinguished, but with low output intensity.
I \propto \phi^2
Exact Collimated Analysis
|i\rangle = \frac{i|\!\circlearrowleft\rangle + |\!\circlearrowright\rangle}{\sqrt{2}}
|f\rangle = \frac{e^{i\phi/2}|\!\circlearrowleft\rangle - ie^{-i\phi/2}|\!\circlearrowright\rangle}{\sqrt{2}}
|\psi, i\rangle \to \langle x, f | \exp(-i k \hat{x}\hat{W}) | \psi, i \rangle = \langle x|\hat{M}_f\,|\psi\rangle = i\sin(\phi/2 - kx)\langle x | \psi\rangle
\hat{W} = |\!\circlearrowleft\rangle\langle\!\circlearrowleft\! | - |\!\circlearrowright\rangle\langle\!\circlearrowright\! |
\phi\;\text{(phase offset)}
k\;\text{(tilt)}
x\;\text{(signal)}
\sigma\;\text{(beam waist)}
\hat{M}_f = \langle f | \exp(-i k \hat{x}\hat{W}) | i \rangle = i \sin(\phi/2 - k\hat{x})
P(x) = |\langle x,f| \psi,i\rangle|^2 = \sin^2(\phi/2 - kx)\,P_0(x) = \frac{\sin^2(\phi/2 - kx)}{\sqrt{2\pi\sigma^2}} e^{-(x/\sigma)^2/2}
Original profile of beam becomes modulated.
JD et al., PRA 88 , 023801 (2013)
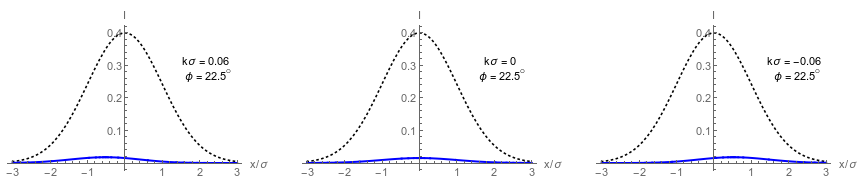
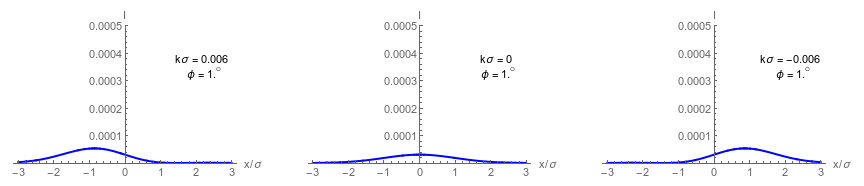
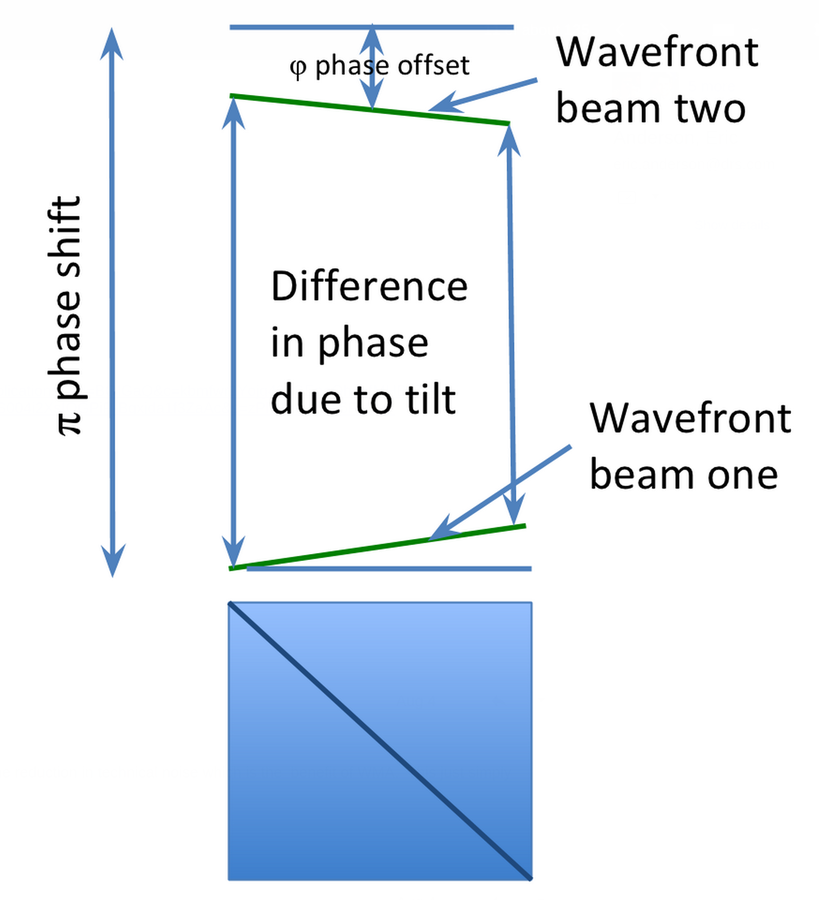
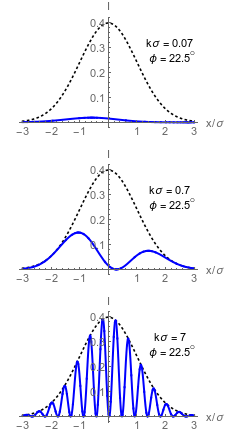
Collimated Dark Port Profiles
Left: Wavefront tilt mechanism producing spatial modulation
Right : Asymmetric dark port profiles in different regimes
Dashed envelope: input beam intensity
Solid curve:
dark port intensity
Top right:
weak value regime
Middle right:
double lobe regime
Bottom right:
misaligned regime
k\sigma \ll \phi \ll 1
\phi\ll k\sigma \ll 1
\phi\ll 1 \ll k\sigma
Weak Value Tomography
\displaystyle |\psi\rangle = \alpha |H\rangle + \beta |V\rangle
\displaystyle c \equiv \frac{\langle D|H \rangle}{\langle D | \psi \rangle} = \frac{\langle D|V \rangle}{\langle D | \psi \rangle}
\displaystyle \implies c|\psi\rangle = \frac{\langle D| H \rangle \langle H | \psi \rangle}{\langle D | \psi \rangle} |H\rangle + \frac{\langle D | V \rangle \langle V | \psi \rangle}{\langle D | \psi \rangle} |V\rangle
Measurable weak values
Determining these also determines the state, up to a simple renormalization
Unnormalized initial state:
Arbitrary constant, in terms of unbiased "postselection" basis
Unknown state:
Dressel, et al. RMP 86, 307 (2014)
Task: Measure the path state of a neutron inside a neutron interferometer using its coupled spin freedom as a probe
Denkmayr, Dressel, et al. PRL 118, 010402 (2017)
- Spin-up neutrons preselected by silicon crystal Bragg condition of interferometer
- DC coil (ST1) rotates spin to +X (initial spin state prepared at this point)
- Sapphire slab (PS) phase shifts relative paths (initial path state prepared at this point)
- Helmholtz coils (HCs) perform path-dependent spin rotations by tunable angle alpha
- After interferometer, DC coil (ST2) and CoTi supermirror (A) spin-polarizes neutrons
- Only neutrons at O-Det are analyzed (postselection completed here)
- Measuring average spin response allows determination of path weak values, and thus the intermediate path state inside the interferometer
|\Psi_i\rangle = (c_+ |P_I\rangle + c_- |P_{II}\rangle)\otimes |S_x; +\rangle
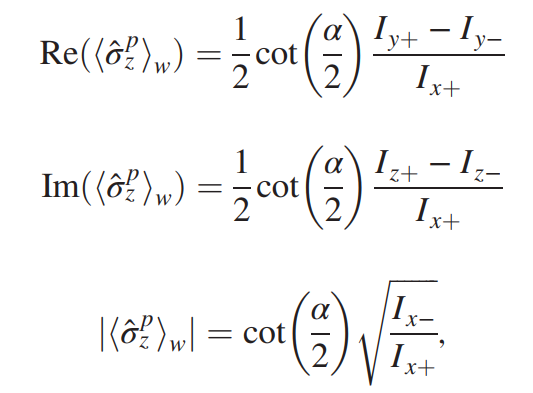
Denkmayr, Dressel, et al. PRL 118, 010402 (2017)
\displaystyle |P_i\rangle = \frac{\langle\hat{\Pi}^p_{z+}\rangle_w |P_I\rangle + \langle\hat{\Pi}^p_{z-}\rangle_w |P_{II}\rangle }{\sqrt{|\langle\hat{\Pi}^p_{z+}\rangle_w |^2 + |\langle\hat{\Pi}^p_{z-}\rangle_w |^2}}
\displaystyle \langle\hat{\Pi}^p_{z\pm}\rangle_w = \frac{1 \pm \langle \hat{\sigma}_z^p\rangle_w}{2}
Expressions exact for any relative spin-splitting angle alpha
Usual linear response regime when alpha small
Angle alpha selected here
Spin measurement axis selected here
Arbitrary-strength Path Weak Values
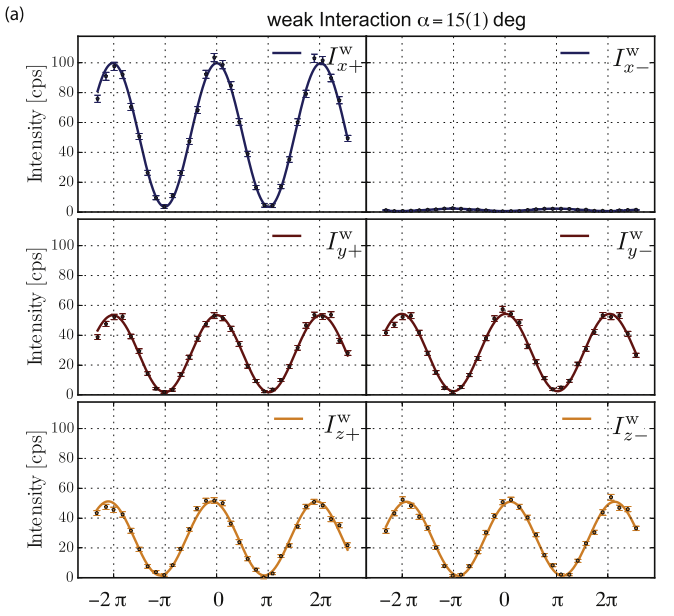
Relative phase of path state varied, keeping relative magnitudes the same (only imaginary weak value nonzero)
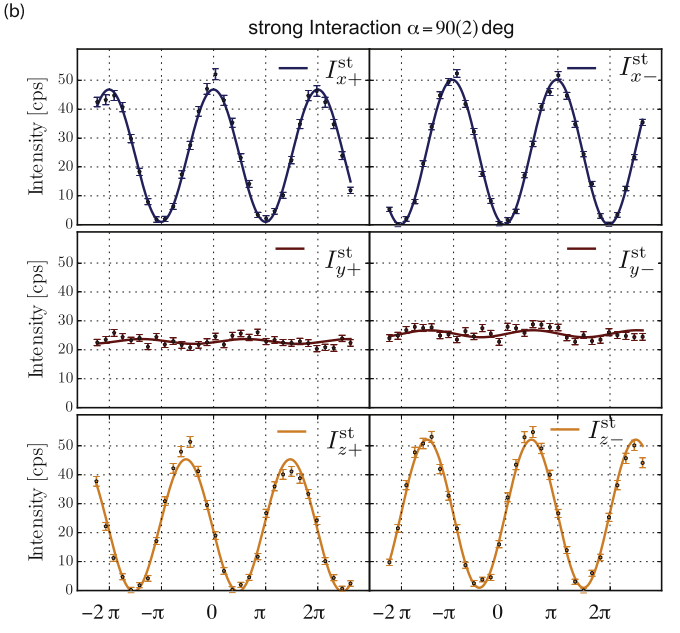
Weak (left) and Strong (right) measurements compared
Different-looking responses yield same weak value reconstructions
Denkmayr, Dressel, et al. Physica B (2018)
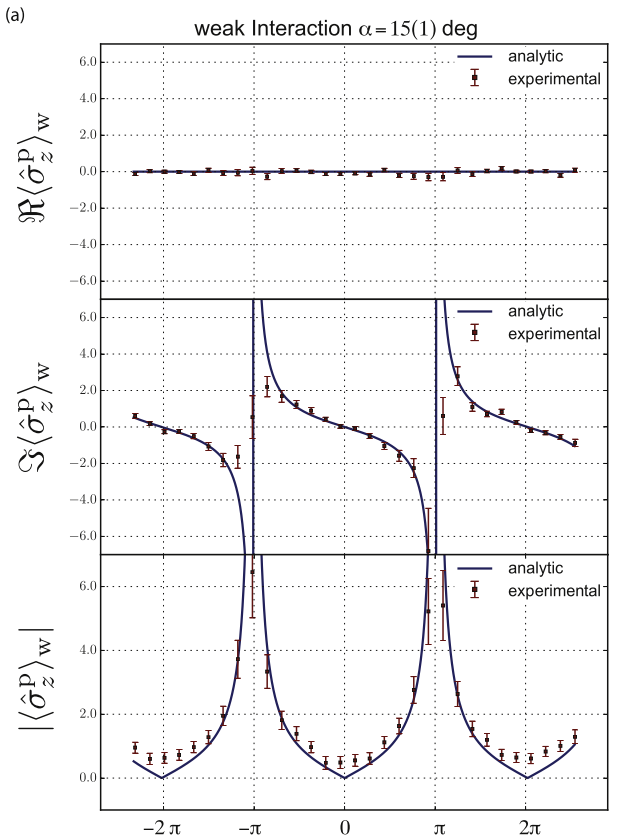
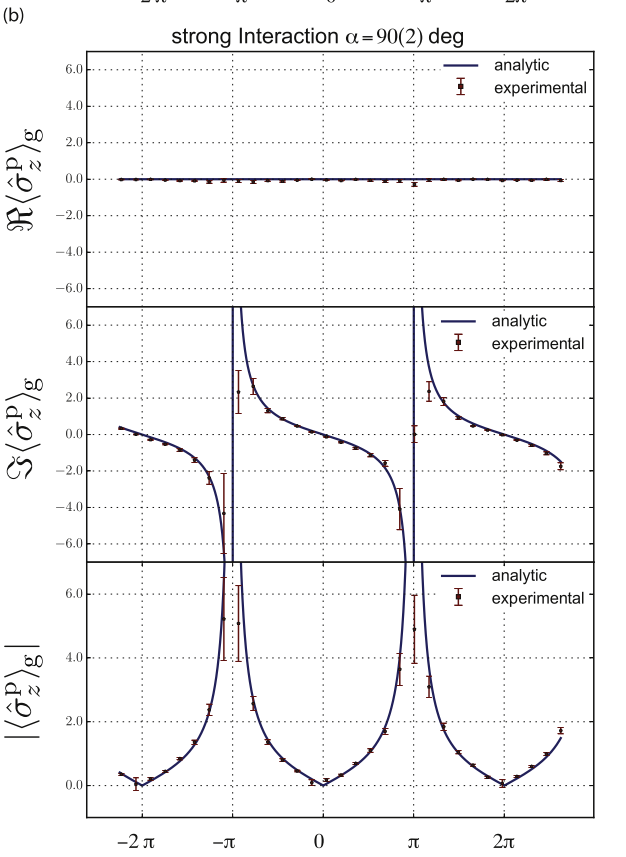
Same Weak Values : Stronger has better accuracy and precision
Denkmayr, Dressel, et al. Physica B (2018)
Outline
-
Strengthening Weak Value Tomography
- Weak Value Tutorial
- Weak Value Tomography
- Strong Weak Values with Neutrons
-
Strengthening Qubit Correlator Measurements
- Weakly Measured Correlators
- Generalized Qubit Measurements
- Strongly Measured Correlators
Recall Weak Measurement
What happens when you make several weak measurements in a row?
Pang, Dressel, Brun, PRL 113, 030401 (2014)
\hat{M} = \langle \psi_f | \exp(-i (g/2) \hat{A}\otimes \hat{D} ) |\psi_i \rangle \approx \sqrt{p}\,\hat{1} + (g/2)\,\hat{A} + O(g^2)
Crude idea : measurement operator approximately linearizes in weak measurement regime (linear response regime)
Post-interaction system state couples to anticommutator to linear order in coupling:
\displaystyle \text{Tr}(\hat{M}\hat{\rho}\hat{M}^\dagger) \approx p + g\sqrt{p}\,\text{Tr}\left[\frac{\hat{A}\hat{\rho}+\hat{\rho}\hat{A}}{2}\right] + O(g^2)
Sequences of measurements create nested anticommutator terms to lowest order in the joint couplings
\displaystyle \text{Tr}(\hat{N}\hat{M}\hat{\rho}\hat{M}^\dagger\hat{N}^\dagger) \approx p_1p_2 + g_1\sqrt{p_1}p_2\,\text{Tr}\left[\frac{\{\hat{A}_1,\hat{\rho}\}}{2}\right] + g_2\sqrt{p_2}p_1\,\text{Tr}\left[\frac{\{\hat{A}_2,\hat{\rho}\}}{2}\right] + g_1g_2\sqrt{p_1p_2}\,\text{Tr}\left[\frac{\{\hat{A}_2,\{\hat{A}_1,\hat{\rho}\}\}}{4}\right] + \cdots
\displaystyle \text{Tr}(\hat{N}\hat{M}\hat{\rho}\hat{M}^\dagger\hat{N}^\dagger) \approx p_1p_2 + g_1\sqrt{p_1}p_2\,\text{Tr}\left[\frac{\{\hat{A}_1,\hat{\rho}\}}{2}\right] + g_2\sqrt{p_2}p_1\,\text{Tr}\left[\frac{\{\hat{A}_2,\hat{\rho}\}}{2}\right] + g_1g_2\sqrt{p_1p_2}\,\text{Tr}\left[\frac{\{\hat{A}_2,\{\hat{A}_1,\hat{\rho}\}\}}{4}\right] + \cdots
-
Benefit : Isolating such a nested commutator term gives access to interesting temporal correlation information that is sensitive to coherence (e.g., quasiprobability characterizations of the dynamics : Yunger Halpern, Swingle, Dressel PRA 9, 042105 (2018))
-
Problem : Isolating this term means subtracting away unwanted terms, including the higher-order coupling terms, which is difficult in practice with realistic measurements
- Miracle : For qubits, this term can be isolated exactly with any measurement strengths g (Dressel, et al. PRA 98, 012032 (2018) )
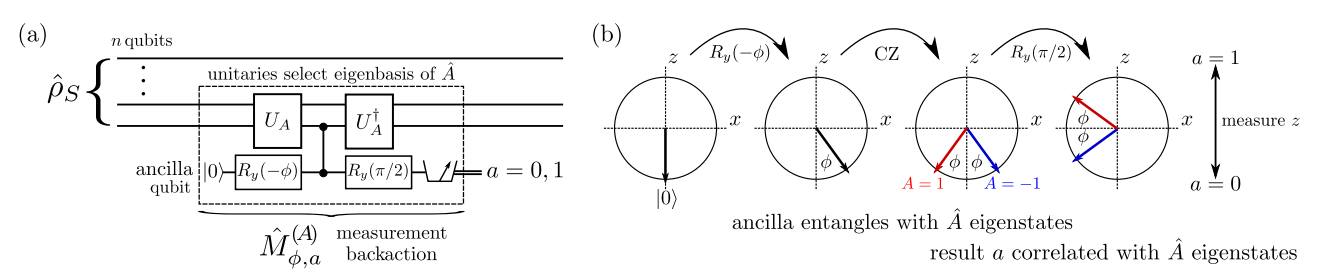
Arbitrary Strength Qubit Measurements
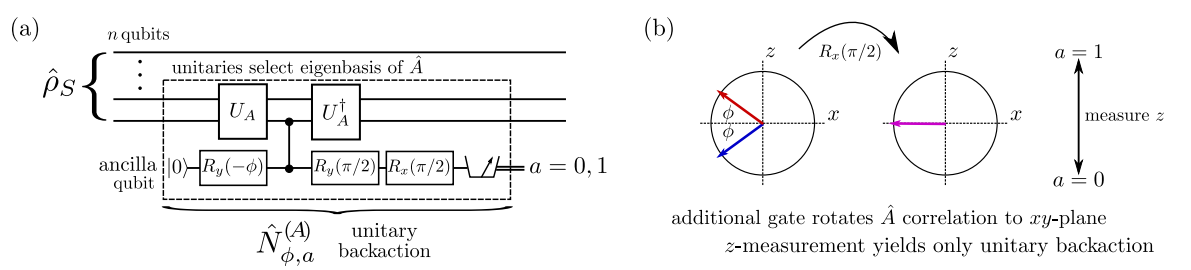
Informative Measurement:
Non-Informative Measurement:
\displaystyle \hat{M}_{\phi,a}^{(A)} = \frac{1}{\sqrt{2}}\left[ \cos\frac{\phi}{2}\hat{1} -(-1)^a \sin\frac{\phi}{2}\hat{A}\right]
\displaystyle \hat{N}_{\phi,a}^{(A)} = \frac{1}{\sqrt{2}}\left[ \cos\frac{\phi}{2}\hat{1} +i(-1)^a \sin\frac{\phi}{2}\hat{A}\right]
Dressel, et al. PRA 98, 012032 (2018)
\displaystyle \sum_{a=0,1} \alpha_{\phi,a}\,\hat{M}_{\phi,a}^{\dagger(A)}\hat{M}_{\phi,a}^{(A)} = \hat{A}
\displaystyle \alpha_{\phi,a} = \frac{(-1)^{a+1}}{\sin\phi}
Generalized spectral decomposition
(Works for observables A that square to the identity)
Arbitrary Strength Qubit Measurements
Informative Measurement:
White, Mutus, Dressel, et al. npj Quantum Information 2, 15022 (2016)
\displaystyle \hat{M}_{\phi,a}^{(A)} = \frac{1}{\sqrt{2}}\left[ \cos\frac{\phi}{2}\hat{1} -(-1)^a \sin\frac{\phi}{2}\hat{A}\right]
\displaystyle \sum_{a=0,1} \alpha_{\phi,a}\,\hat{M}_{\phi,a}^{\dagger(A)}\hat{M}_{\phi,a}^{(A)} = \hat{A}
\displaystyle \alpha_{\phi,a} = \frac{(-1)^{a+1}}{\sin\phi}
Generalized spectral decomposition
Generalized measurement method already used experimentally with superconducting qubits (Google)
Arbitrary Strength Qubit Measurements
Informative Measurement:
White, Mutus, Dressel, et al. npj Quantum Information 2, 15022 (2016)
Arbitrary Strength Qubit Measurements
Informative Measurement:
\displaystyle \hat{M}_{\phi,a}^{(A)} = \frac{1}{\sqrt{2}}\left[ \cos\frac{\phi}{2}\hat{1} -(-1)^a \sin\frac{\phi}{2}\hat{A}\right]
Dressel, et al. PRA 98, 012032 (2018)
Useful corollaries:
\displaystyle \sum_{a=0,1} \alpha_{\phi,a}\,\hat{M}_{\phi,a}^{\dagger(A)}\hat{M}_{\phi,a}^{(A)} = \hat{A}
\displaystyle \alpha_{\phi,a} = \frac{(-1)^{a+1}}{\sin\phi}
\displaystyle \sum_{a=0,1} \alpha_{\phi,a}\,\hat{M}_{\phi,a}^{(A)}\hat{\rho}\hat{M}_{\phi,a}^{\dagger(A)} = \frac{\{\hat{A},\hat{\rho}\}}{2}
Anticommutators isolated perfectly for any coupling strength
\displaystyle \sum_{a_1,\ldots,a_m=0,1} \alpha_{\phi_1,a_1}\cdots\alpha_{\phi_m,a_m}\,P(a_1,\ldots,a_m) = \left\langle\frac{\{\cdots\{\{\hat{A}_m,\hat{A}_{m-1}\},\hat{A}_{m-2}\}\cdots,\hat{A}_1\}}{2^{m-1}}\right\rangle_\rho
Nested anticommutator averages can be measured directly for any coupling strength
Arbitrary Strength Qubit Measurements
Non-Informative Measurement:
Dressel, et al. PRA 98, 012032 (2018)
Useful corollaries:
\displaystyle \alpha_{\phi,a} = \frac{(-1)^{a+1}}{\sin\phi}
\displaystyle \sum_{a=0,1} \alpha_{\phi,a}\,\hat{N}_{\phi,a}^{(A)}\hat{\rho}\hat{N}_{\phi,a}^{\dagger(A)} = \frac{[\hat{A},\hat{\rho}]}{2i}
Commutators also isolated perfectly for any coupling strength
\displaystyle \sum_{\tilde{a}_1,\ldots,a_m=0,1} \alpha_{\phi_1,\tilde{a}_1}\cdots\alpha_{\phi_m,a_m}\,P(\tilde{a}_1,\ldots,a_m) = \left\langle\frac{[\cdots\{\{\hat{A}_m,\hat{A}_{m-1}\},\hat{A}_{m-2}\}\cdots,\hat{A}_1]}{2^{m-2}(2i)}\right\rangle_\rho
Nested commutator averages can also be measured directly for any coupling strength
\displaystyle \hat{N}_{\phi,a}^{(A)} = \frac{1}{\sqrt{2}}\left[ \cos\frac{\phi}{2}\hat{1} +i(-1)^a \sin\frac{\phi}{2}\hat{A}\right]
Arbitrary Strength Qubit Measurements
Dressel, et al. PRA 98, 012032 (2018)
\displaystyle \alpha_{\phi,a} = \frac{(-1)^{a+1}}{\sin\phi}
\displaystyle \sum_{a=0,1} \alpha_{\phi,a}\,\hat{N}_{\phi,a}^{(A)}\hat{\rho}\hat{N}_{\phi,a}^{\dagger(A)} = \frac{[\hat{A},\hat{\rho}]}{2i}
\displaystyle \hat{N}_{\phi,a}^{(A)} = \frac{1}{\sqrt{2}}\left[ \cos\frac{\phi}{2}\hat{1} +i(-1)^a \sin\frac{\phi}{2}\hat{A}\right]
\displaystyle \hat{M}_{\phi,a}^{(A)} = \frac{1}{\sqrt{2}}\left[ \cos\frac{\phi}{2}\hat{1} -(-1)^a \sin\frac{\phi}{2}\hat{A}\right]
\displaystyle \sum_{a=0,1} \alpha_{\phi,a}\,\hat{M}_{\phi,a}^{(A)}\hat{\rho}\hat{M}_{\phi,a}^{\dagger(A)} = \frac{\{\hat{A},\hat{\rho}\}}{2}
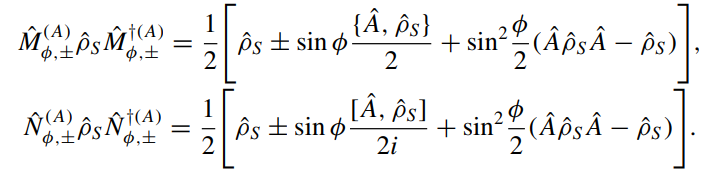
Why does this work? What about state collapse?
(Lindblad) decoherence terms from the measurement cancel in the average
Any marginalization of results exposes the collapse-based disturbance
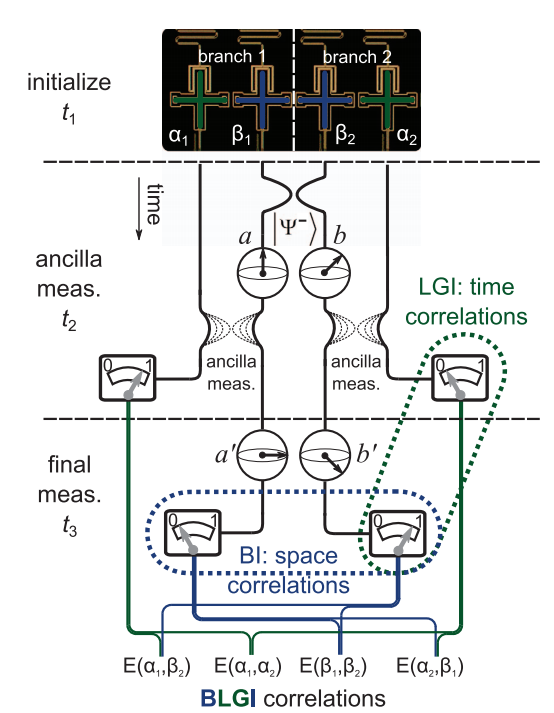
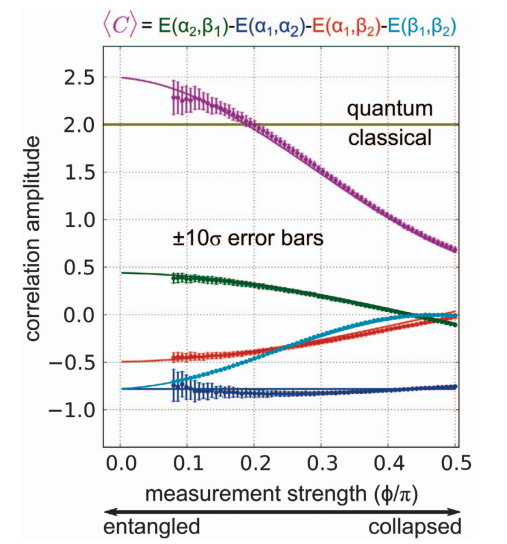
Strongly Measured 2-Point Correlator
Dressel, et al. PRA 98, 012032 (2018)
\displaystyle \hat{U}_t^\dagger\hat{M}_{\phi,b}^{(B)}\hat{U}_t = \frac{1}{\sqrt{2}}\left[ \cos\frac{\phi}{2}\hat{1} -(-1)^b \sin\frac{\phi}{2}\hat{B}(t)\right]
2-point temporal qubit correlators may be directly measured using any measurement strength
These are common theoretical objects that are usually inaccessible in measurements directly
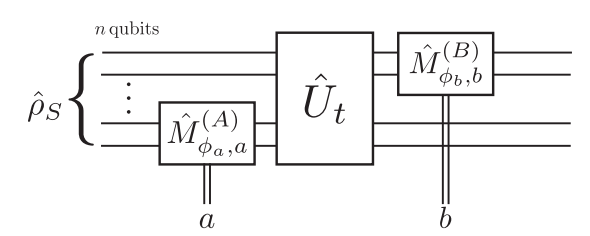
Bracketing measurement by unitary evolutions probes a Heisenberg-evolved operator
The final unitary may be omitted as inconsequential to the measured average
\displaystyle \sum_{a,b=0,1} \alpha_{\phi_a,a}\cdots\alpha_{\phi_b,b}\,P(a,b) = \left\langle\frac{\{\hat{B}(t),\hat{A}\}}{2}\right\rangle_\rho = \text{Re}\langle\hat{B}(t)\hat{A}\rangle_\rho
\displaystyle \sum_{a,b=0,1} \alpha_{\phi_a,\tilde{a}}\cdots\alpha_{\phi_b,b}\,P(\tilde{a},b) = \left\langle\frac{[\hat{B}(t),\hat{A}]}{2i}\right\rangle_\rho = \text{Im}\langle\hat{B}(t)\hat{A}\rangle_\rho
Strongly Measured 4-Point Correlator
Dressel, et al. PRA 98, 012032 (2018)
4-point temporal qubit out-of-time-ordered correlators may be directly measured using any measurement strength
These are recently explored theoretical objects connected with information scrambling and chaos
\displaystyle \sum_{a,b,a',b'=0,1} \alpha_{\phi_a,a}\alpha_{\phi_b,b}\alpha_{\phi_{a'},a'}\alpha_{\phi_{b'},b'}\,P(a,b,a',b') = \left\langle\frac{\{\{\{\hat{B}(t),\hat{A}\},\hat{B}(t)\},\hat{A}\}}{2^3}\right\rangle_\rho = \frac{1 + \text{Re}\langle\hat{B}(t)\hat{A}\hat{B}(t)\hat{A}\rangle_\rho}{2}
\displaystyle \sum_{\tilde{a},b,a',b'=0,1} \alpha_{\phi_a,\tilde{a}}\alpha_{\phi_b,b}\alpha_{\phi_{a'},a'}\alpha_{\phi_{b'},b'}\,P(\tilde{a},b,a',b') = \left\langle\frac{[\{\{\hat{B}(t),\hat{A}\},\hat{B}(t)\},\hat{A}]}{2^2(2i)}\right\rangle_\rho = \frac{\text{Im}\langle\hat{B}(t)\hat{A}\hat{B}(t)\hat{A}\rangle_\rho}{2}
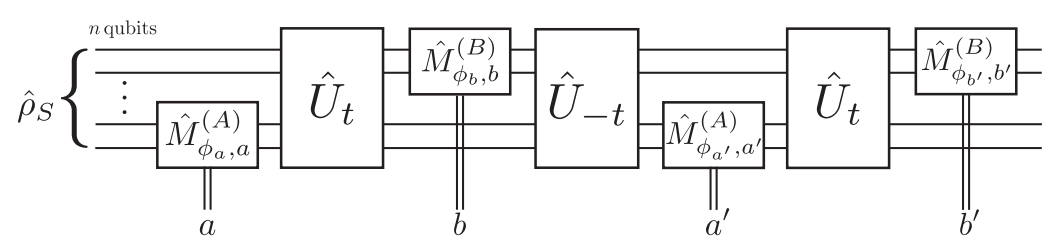
(one reversed evolution needed)
Conclusions
- Weak values are better when made strong
- Nested (anti)commutators are accessible for qubits at any strength
- 2- and 4-point qubit correlators can be directly measured
- Follow-up research in the works:
- Measuring qubit quasiprobabilities strongly with multiple setups
- Measuring qutrit correlators with arbitrary strength
- Investigation of out-of-time-ordered correlators experimentally
Thank you!
Superconducting Qubits:
Review and recent results
Superconducting Qubits
\hbar\omega_q
\hbar(\omega_q - \delta_q)
\hbar(\omega_q - 2\delta_q)
Mesoscopic quantum coherence of collective charge motion at \(\mu\)m scale
EM Fields produced by charge motion described by Circuit QED
Lowest levels of anharmonic oscillator potentials treated as artificial atoms
Typical Transmon Parameters
\displaystyle \hat{H} = \hbar\hat{\Omega} = \frac{\hbar\omega_q}{2}\hat{\sigma}_z
\hbar\omega_q
\hbar(\omega_q - \delta_q)
\hbar(\omega_q - 2\delta_q)
\omega_q/2\pi \sim \text{4--7GHz}
\delta_q/2\pi \sim \text{100--300MHz}
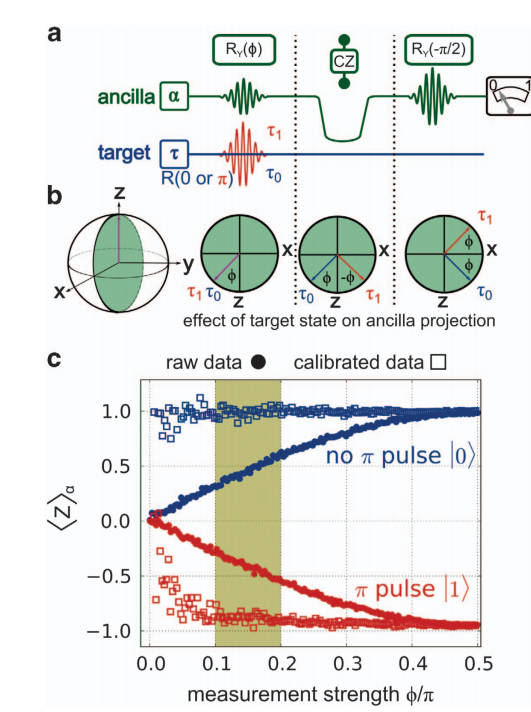
Microwave Measurement
Note : Without a quantum-limited amplifier, this doesn't work!
The Josephson Parametric Amplifier (JPA) and Traveling Wave Parametric Amplifier (TWPA) boost signal enough for later HEMTs in the readout chain to resolve the information.
"3D Transmon"
\hbar\omega_q
\hbar(\omega_q - \delta_q)
\hbar(\omega_q - 2\delta_q)
\displaystyle \hat{H}_r = \hbar\omega_r\hat{a}^\dagger\hat{a}
Cavity mode:
\omega_r/2\pi \sim \text{5--7GHz}
|\Delta|\equiv|\omega_q-\omega_r| \gg g
\displaystyle \hat{H}_{c} = \hbar g(\hat{a}+\hat{a}^\dagger)\hat{\sigma}_x
g/2\pi \sim \text{100MHz}
Detuned (dispersive) regime (RWA):
\displaystyle \hat{H}_c \sim \hbar \chi\,\hat{a}^\dagger\hat{a}\,\hat{\sigma}_z
X-X Coupling:
\displaystyle \chi \sim \left[\frac{g}{\Delta}\right]^2\!\delta_q \sim 1\text{MHz}
\displaystyle {\small \chi \neq \frac{g^2}{|\Delta|}}
Korotkov group, Phys. Rev. A 92, 012325 (2015)
Martinis group, Phys. Rev. Lett. 117, 190503 (2016)
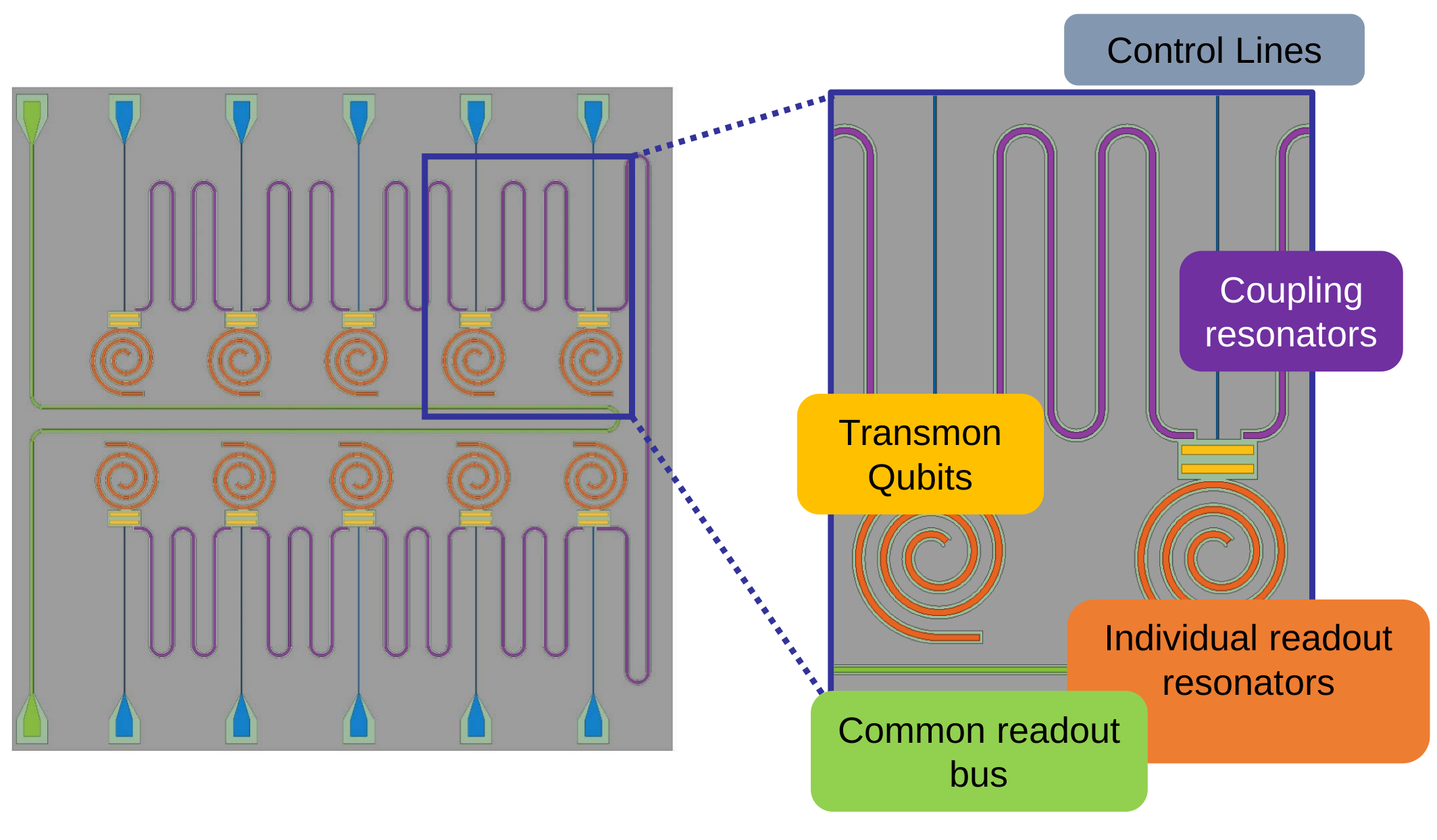
2D planar chip schematic
Bus acts as Purcell filter, coupled to traveling wave parametric amplifier (TWPA)
\omega_r/2\pi \sim \text{5--7GHz}
g/2\pi \sim \text{100MHz}
\displaystyle \chi \sim \left[\frac{g}{\Delta}\right]^2\!\delta_q \sim 1\text{MHz}
\omega_q/2\pi \sim \text{4--7GHz}
\delta_q/2\pi \sim \text{100--300MHz}
Similar parameters:
v1
v3
Coming soon: two-layer design of 20+ qubits
separated from control circuitry
(similar to Google Bristlecone + IBM Q)
Now on v8+
T_2 \sim 100\mu\text{s}
T_1 \sim 60\mu\text{s}
UCB 2D planar chip
Multiplexed 10 qubit control and readout
Single shot "projective" readout :
typical quantum computing goal
Microwave Measurement
A Brief Tour of Recent Results
Individual quantum state trajectories filtered from the readout are verified via spot checking predicted subensembles with tomography
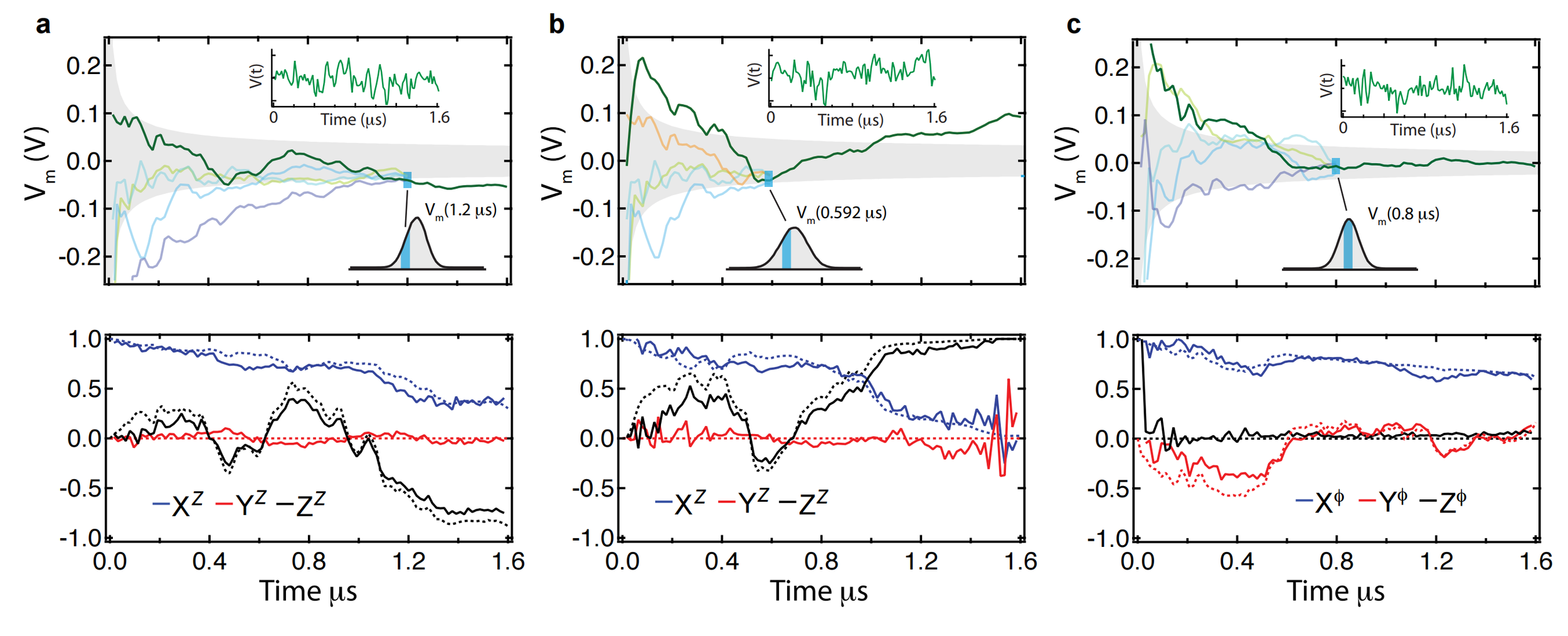
Approach:
- Perform a random tomographic pulse at the end of each data run
- Spot check subensembles of data to verify tomography of final state
Quantum Trajectories
Murch et al., Nature 502, 211 (2013)
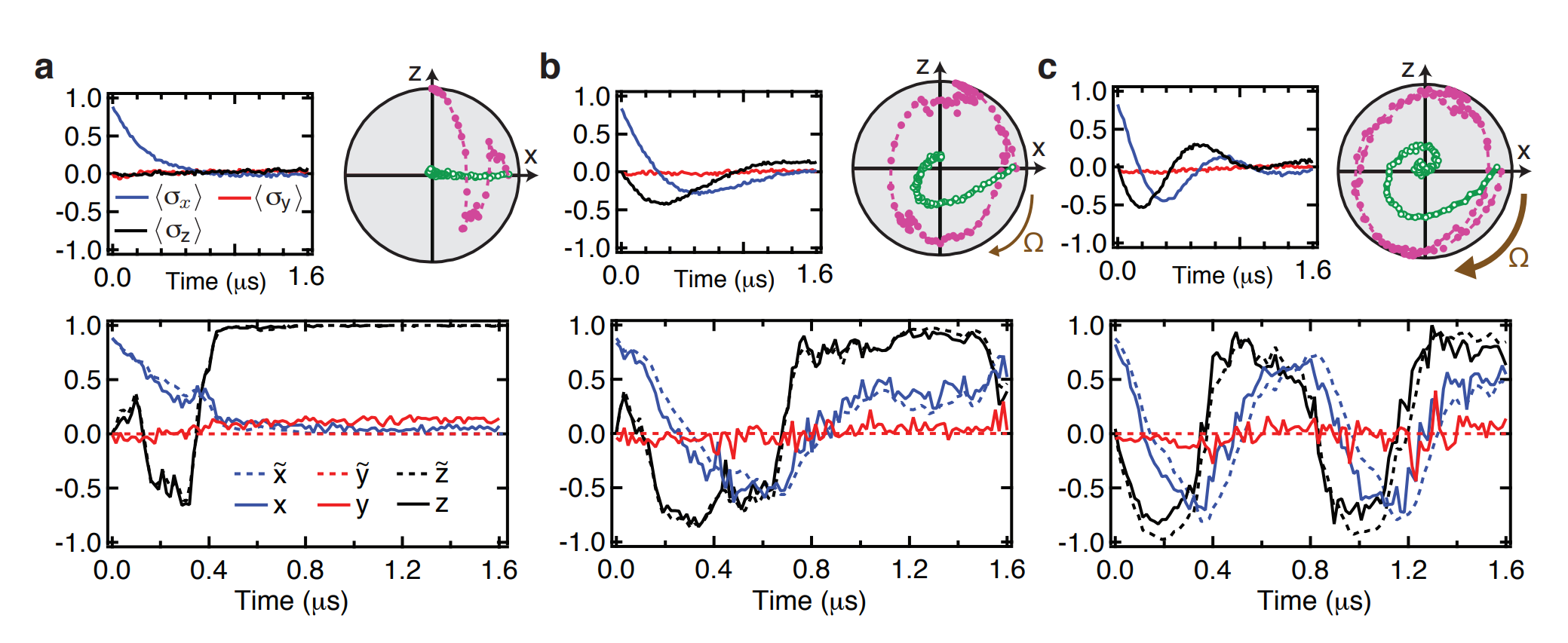
Monitored Rabi Drive
JD and Siddiqi Group, Nature 511, 570 (2014)
Partial collapses compete with unitary dynamics
Ensemble-averaging the stochastic evolution recovers the usual Lindblad dynamics
Conditioned State Dynamics
JD and Siddiqi Group, Nature 511, 570 (2014)
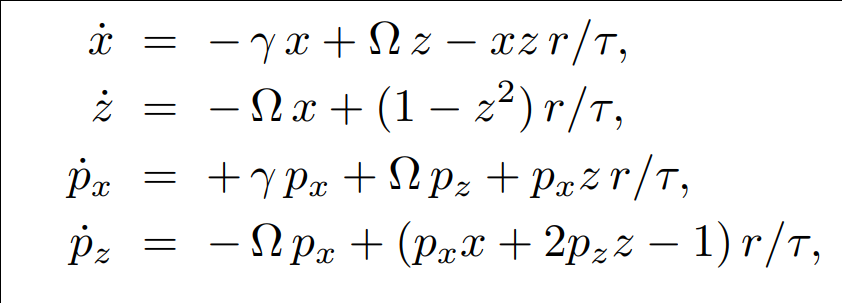
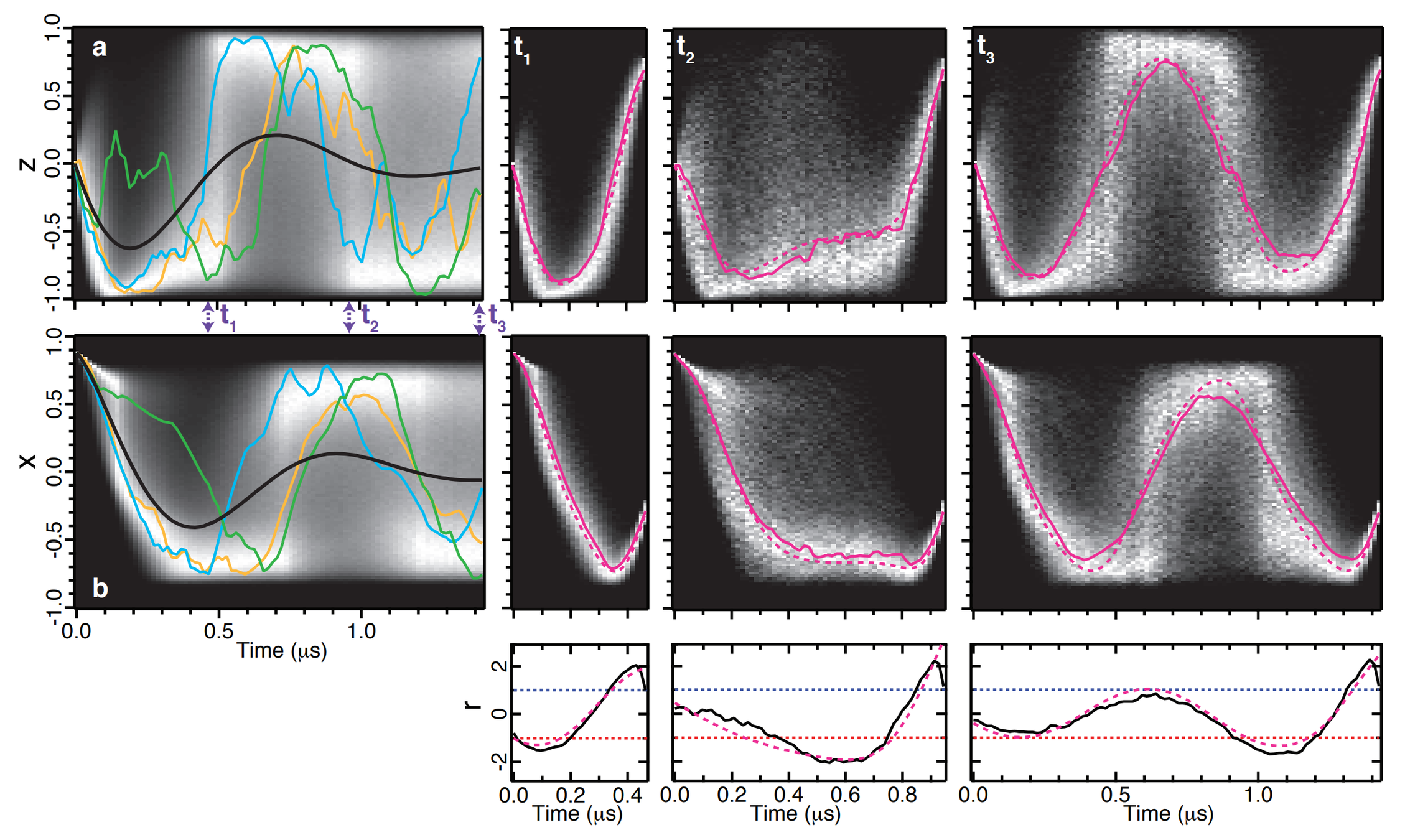
Experimental most probable path matches ODE solution derived from stochastic path integral
JD and Jordan Group, PRA 88, 042110 (2013)
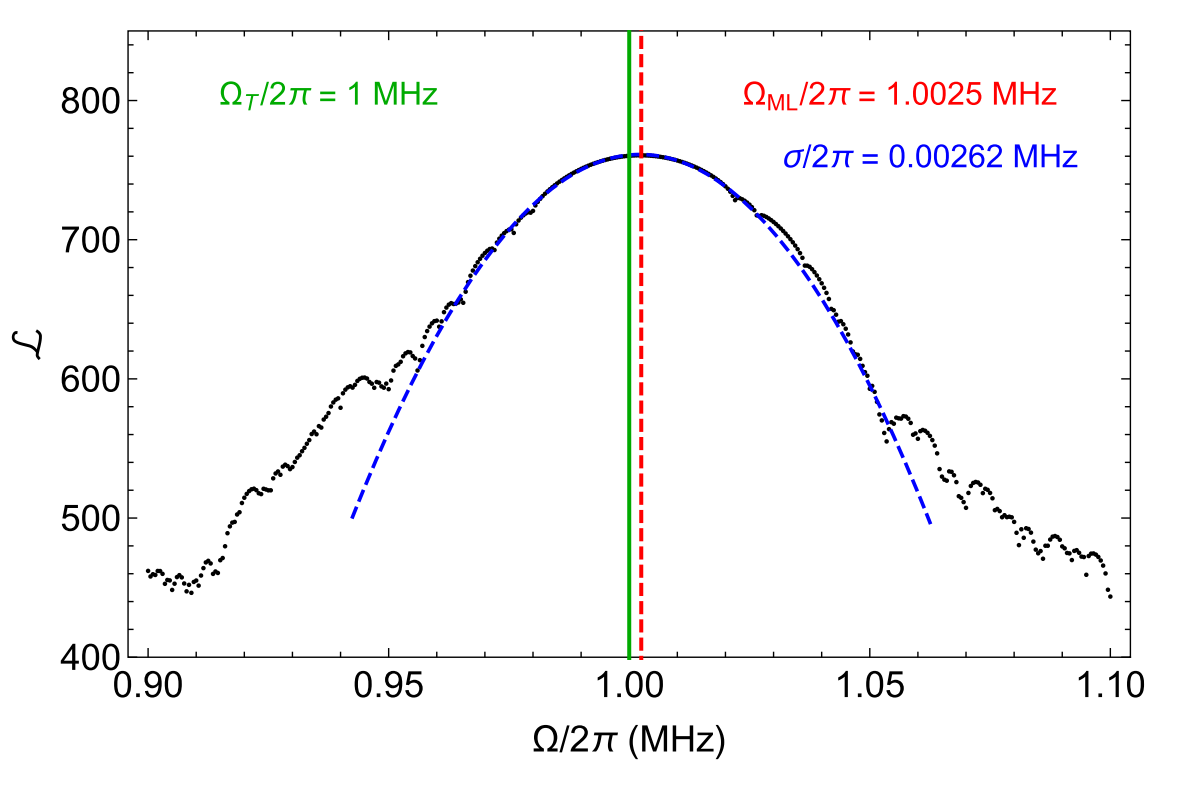
Tracking Drifting Parameters
Maximum likelihood techniques allow extraction of parameters drifts from stochastic records with reasonable precision
JD and Jordan Group, PRA 95, 012314 (2017)
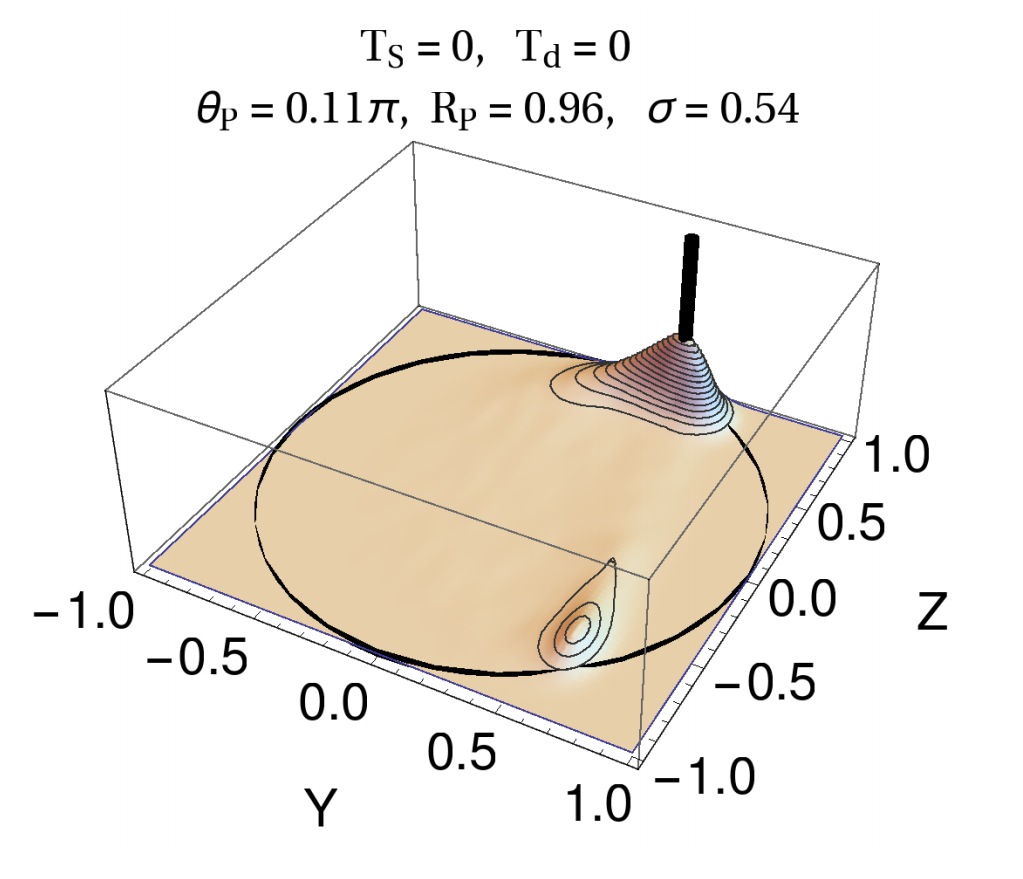
Feedback State Stabilization
Linear feedback (with very small temporal delays) can stabilize the qubit state to targeted regions of the Bloch sphere.
JD and Jordan Group, PRA 96, 022311 (2017)
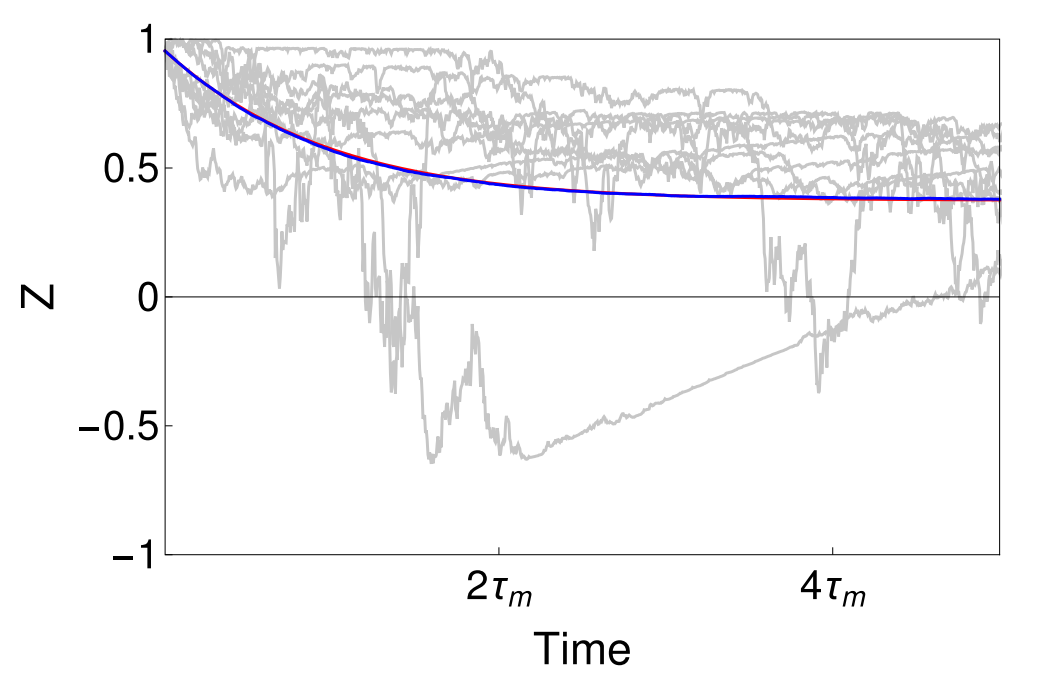
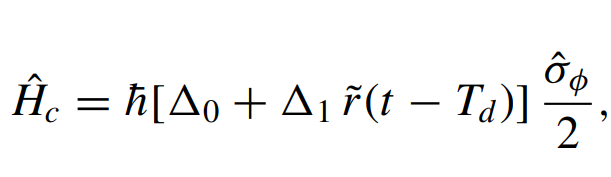
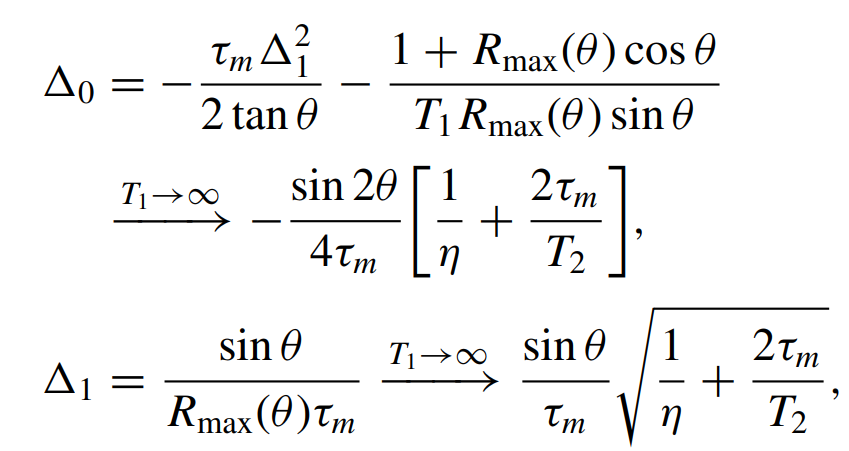
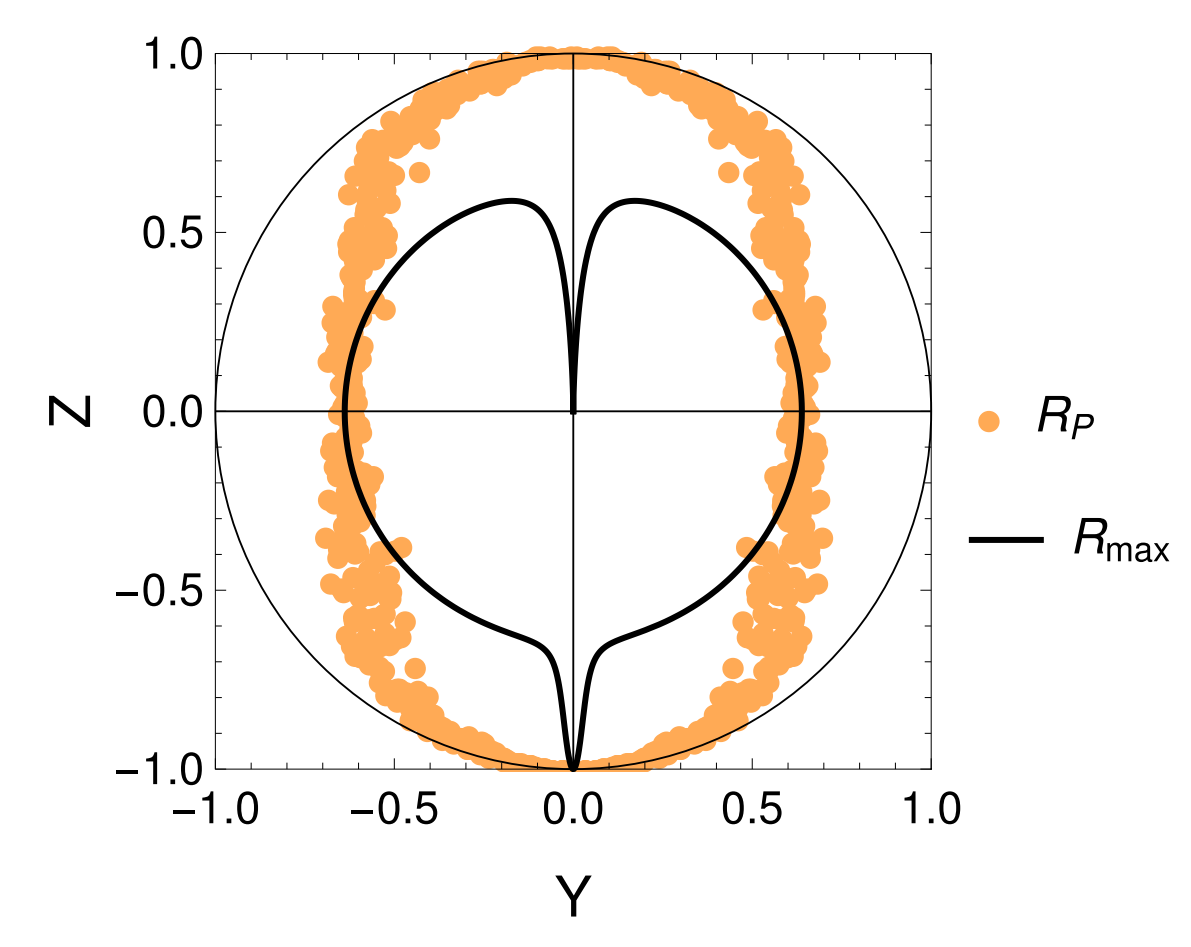
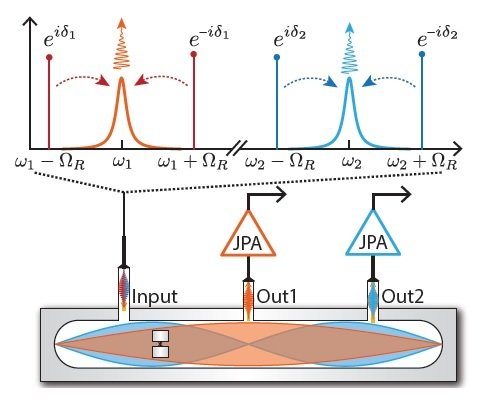
- Symmetrically detuned pumps
- Beats stroboscopically measure rotating qubit
- Yields displacement coupling
- Allows tunable measurement axis
- Multiple cavity modes = multiple observables
\hat{H}^{\text{rf}}_{\text{q-r}} = \chi\,(\hat{a}+\hat{a}^\dagger)\,\hat{\sigma}_{\delta}
Displacement coupling:
\hat{\sigma}_{\delta} = \cos\delta\,\hat{\sigma}^{\text{rf}}_x + \sin\delta\,\hat{\sigma}^{\text{rf}}_y
Siddiqi group, Nature 538, 491 (2016)
Stroboscopic Displacement Coupling
\hat{H}_{\text{q}} = \frac{\hbar\Omega_R}{2}\hat{\sigma}_x
Rotating frame:
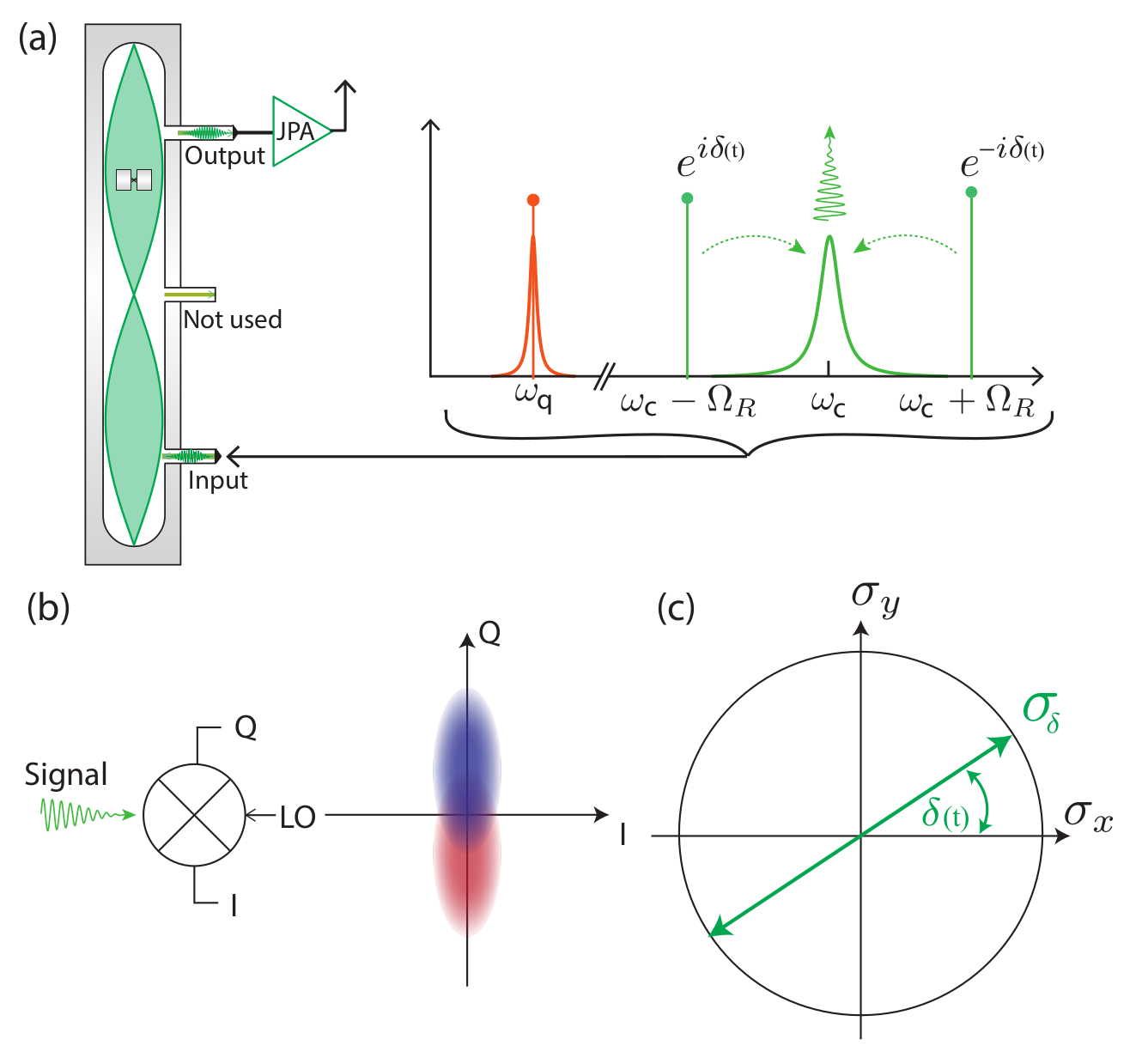
Incoherent Zeno-Dragging Qubit Gate
Idea : use time-varying measurement axes to drag the quantum state around the Bloch sphere using the quantum Zeno effect
The record tracks the state well in this regime, so can be used as a herald for high-fidelity gates
Non-unitary gate
(measurement-based)
\hat{H}_{\text{q-r}}(t) = \chi\,(\hat{a}+\hat{a}^\dagger)\,\hat{\sigma}_{\delta(t)}
\hat{\sigma}_{\delta(t)} = \cos\delta(t)\,\hat{\sigma}_x + \sin\delta(t)\,\hat{\sigma}_y
Stroboscopic displacement coupling can be time-varying
JD, Siddiqi group, PRL 120, 020505 (2018)
Jumps : Faster drag speeds allow trajectories to jump to the opposite pole, decreasing ensemble-averaged dragging fidelity
Jump-axis : Dragging dynamics causes lag of actual Zeno-pinned behind the measurement axis by a fixed angle
\Omega = 2\pi\,v : \text{dragging frequency}
\Gamma_D = 1/2\tau_m\eta : \text{measurement dephasing rate}
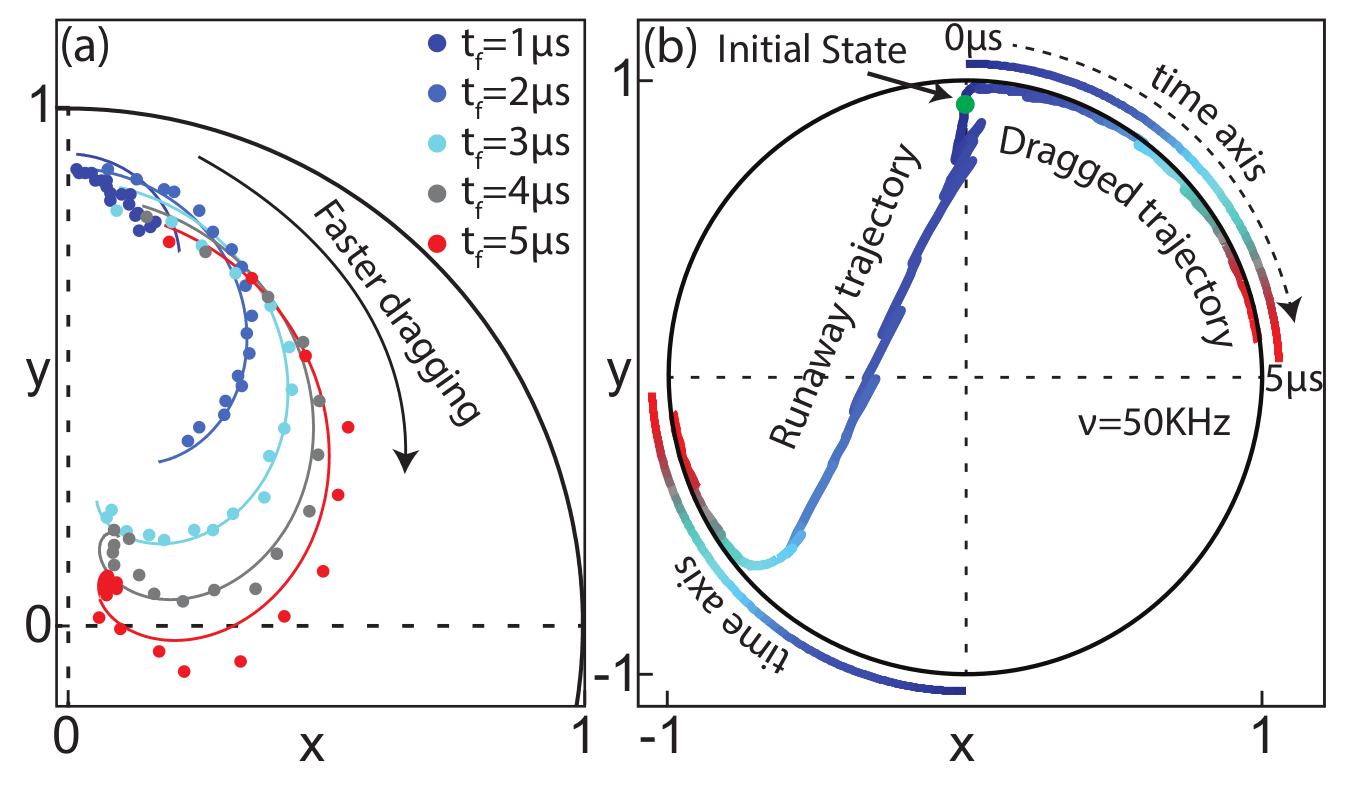
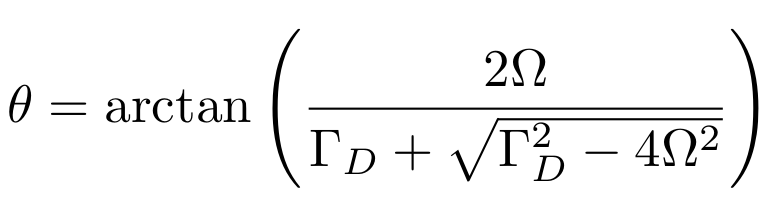
JD, Siddiqi group, PRL 120, 020505 (2018)
Pinned to poles : Other than the jumps, state remain pinned to lagged measurement poles
Incoherent Zeno-Dragging Qubit Gate
\Omega = 2\pi\,v : \text{dragging frequency}
\Gamma_D = 1/2\tau_m\eta : \text{measurement dephasing rate}
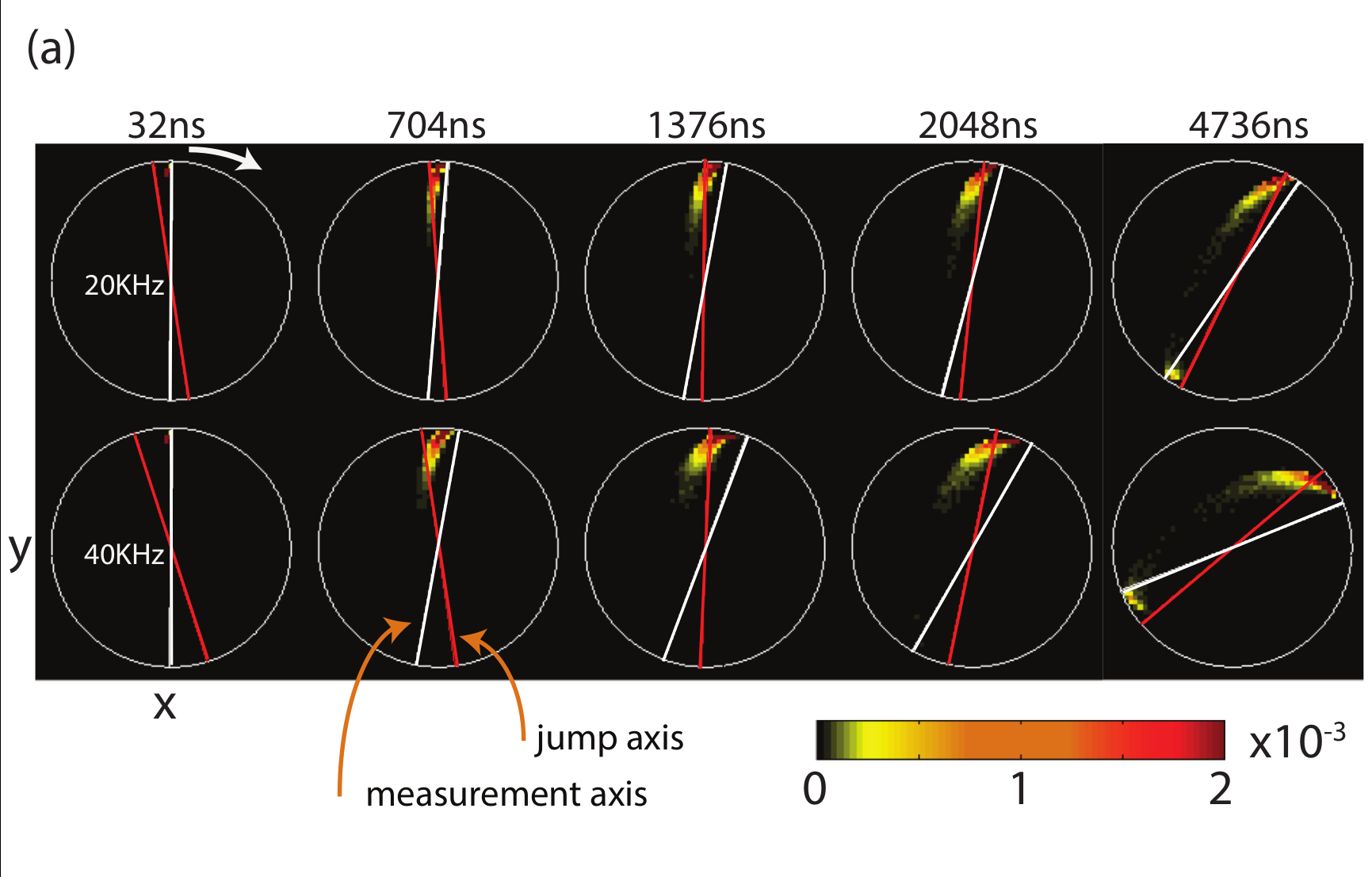
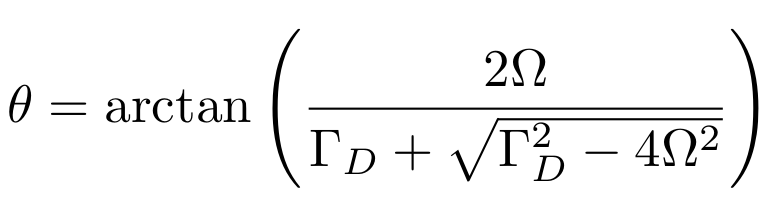
State collapses to jump-axis
JD, Siddiqi group, PRL 120, 020505 (2018)
Incoherent Zeno-Dragging Qubit Gate
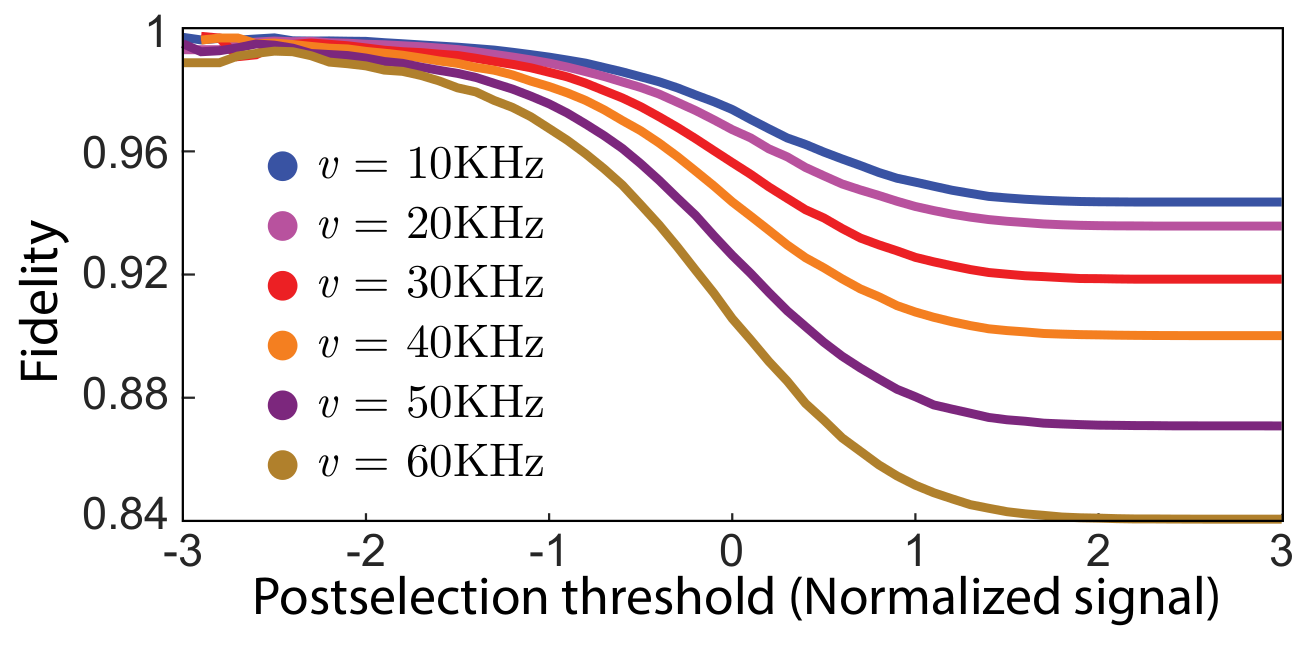
Post-selecting on trajectories with an average readout with a value >1 keeps only trajectories that did not jump, heralding a reasonably high-fidelity dragging gate for that subset
Alternatively, the jump may be observed, then corrected later
JD, Siddiqi group, PRL 120, 020505 (2018)
Incoherent Zeno-Dragging Qubit Gate
Siddiqi group, Nature 538, 491 (2016)
4 pumps, symmetrically detuned from 2 resonator modes
2 simultaneous noncommuting observables
Partial collapses compete with each other, preventing full collapse to a stationary state
If observables are maximally non-commuting, creates persistent phase-diffusion in Bloch sphere
Noncommuting Observable Measurement
\hat{H}^{\text{rf}}_{\text{q-r}} = \chi_1\,(\hat{a}+\hat{a}^\dagger)\,\hat{\sigma}_{\delta_1} + \chi_2\,(\hat{b}+\hat{b}^\dagger)\,\hat{\sigma}_{\delta_2}
\hat{\sigma}_{\delta_k} = \cos\delta_k\,\hat{\sigma}^{\text{rf}}_x + \sin\delta_k\,\hat{\sigma}^{\text{rf}}_y
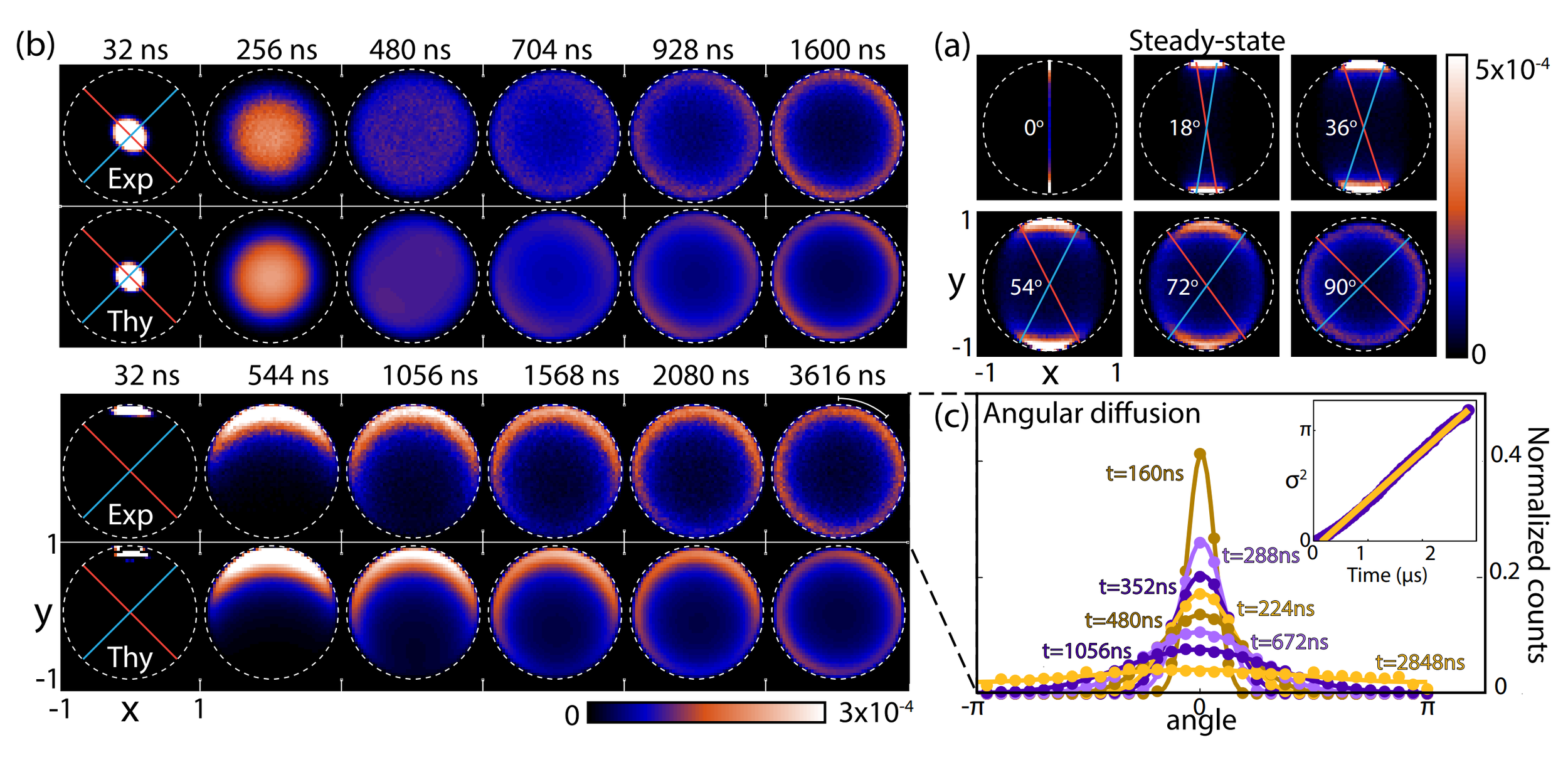
Siddiqi group, Nature 538, 491 (2016)
State purifies, but diffuses randomly
Basins of attraction if measurement axes are nearly aligned
Noncommuting Observable Measurement
Siddiqi group, Nature 538, 491 (2016)
State disturbance can be measured
Result agrees with the lower bound set by the Maccone-Pati relation involving the sum of variances:
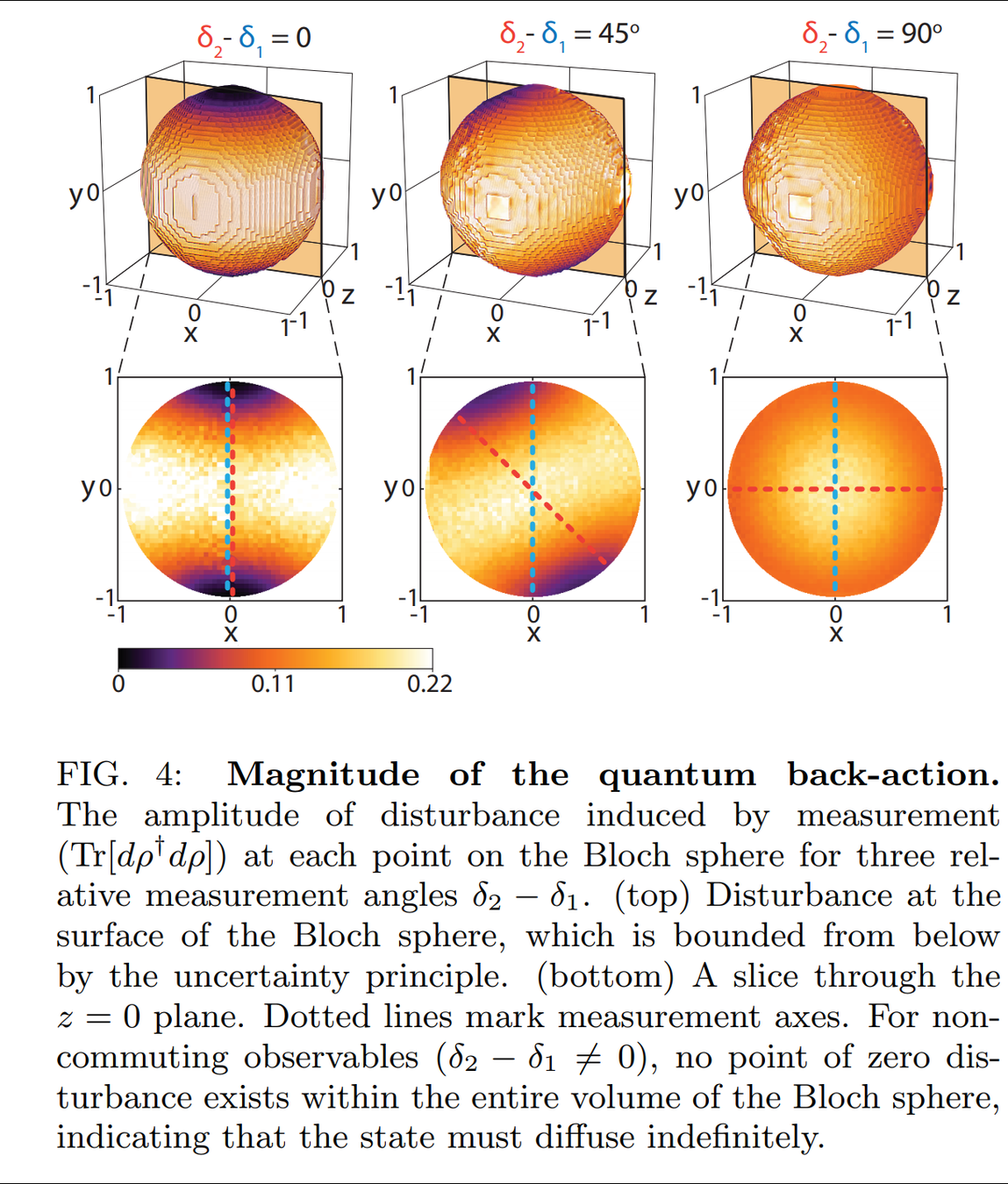
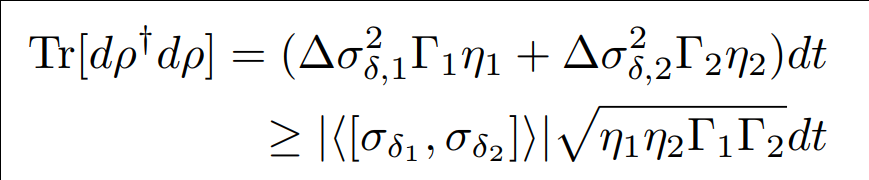
Uncertainty relation forces the random state diffusion when measuring incompatible axes
Noncommuting Observable Measurement
Circuit Quantum Electrodynamics
Ideas:
- Size scale of device (\(\mu\)m) is smaller than the characteristic wavelength of superconducting Cooper pairs:
quantum coherence is relevant to the motion
- Cooper pairs (bosons) condense into
collective charge motion that is well described by an effective "center of charge", much like rigid bodies are described by an effective center of mass in classical mechanics
- Collective charge motion along superconducting wires can be described by the
currents and voltages it produces, which are then easily related to measurable capacitances, inductances, and impedances
- Quantization of the conjugate variables of flux and charge follows from the usual quantization of the electromagnetic field
How do we model collective mesoscopic quantum coherence?
Circuit QED (Technical Details)
Definitions:
- Map hardware into a circuit of nodes
connected by branches (e.g., capacitor, inductor, etc.)
- Define voltage and current for each branch via EM fields,
as well as the flux and charge stored in each element:
- Define ground node and tree of active nodes connecting both capacitors and inductors - the fluxes to ground are the dynamical circuit variables
, and (2017) . doi: 10.1002/cta.2359.
v_b(t) = \int_b \vec{E}(\vec{r},t)\cdot d\vec{\ell}
i_b(t) = \frac{1}{\mu_0}\oint_b \vec{B}(\vec{r},t)\cdot d\vec{s}
\Phi_b(t) = \int_{-\infty}^t v(t')dt'
Q_b(t) = \int_{-\infty}^t i(t')dt'
\phi_n(t) = \sum_{b\in\mathcal{B}}\Phi_b(t)
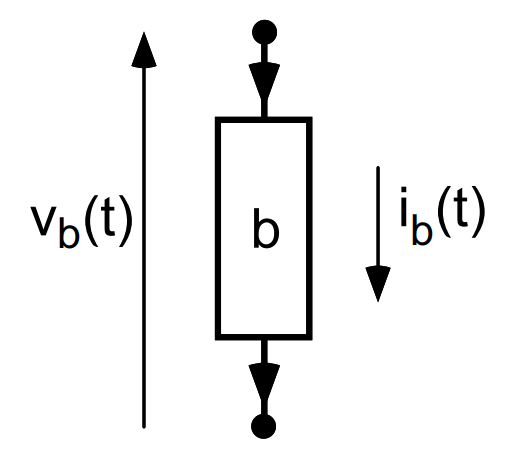
Branches \(b\in\mathcal{B}\) in path connecting node \(n\) to ground through capacitors
\mathcal{L} = \mathcal{E}_{\text{kin}}[\{\dot{\phi}_n\}] - \mathcal{E}_{\text{pot}}\left[\{\phi_n\}\right]
\displaystyle q_n \equiv \frac{\partial \mathcal{L}}{\partial \dot{\phi}_n}
charge conjugate to node flux \(\phi_n\)
\{ \phi_n,\ q_n \}_{\text{PB}} = \pm 1
(\(+1\) capacitive, \(-1\) inductive)
- Primary circuit elements:
capacitor, inductor, and Josephson junction
, and (2017) . doi: 10.1002/cta.2359.
i_L(t) = \frac{\Phi(t) - \Phi_0}{L}
v_C(t) = \frac{Q(t) - Q_0}{C}
i_{J}(t) = I_0\,\sin\left(\frac{\Phi(t) - \Phi_0}{\hbar/2e}\right)
\mathcal{E}_C = \frac{(Q - Q_0)^2}{2C} = \frac{C\,\dot{\phi}^2}{2} = \frac{q^2}{2C}
\mathcal{E}_L = \frac{(\phi - \phi_0)^2}{2L}
\mathcal{E}_J = \frac{(\hbar/2e)^2}{L_J}\left[1 - \cos\left(\frac{(\phi - \phi_0)}{\hbar/2e}\right)\right]
L_J = \frac{(\hbar/2e)}{I_0}
\{
"Kinetic" energy:
"Potential" energy:
- Canonical quantization : (equivalent to quantizing \(\vec{E},\vec{B}\) )
\{\phi,\,q\}_{\text{PB}} \to \frac{1}{i\hbar}[\hat{\phi},\,\hat{q}]
\hat{a} \equiv \frac{1}{\sqrt{2}}(\frac{\hat{\phi}}{\phi_z} + i \frac{\hat{q}}{q_z})
\phi_z\,q_z = \hbar
\phi_z / q_z \equiv Z_0
[\hat{a},\,\hat{a}^\dagger] = \hat{1}
Circuit QED (Technical Details)
(An)harmonic Oscillators
- Resonator:
, and (2017) . doi: 10.1002/cta.2359.
\hat{H} = \frac{\hat{q}_J^2}{2C_J} + \frac{(\hbar/2e)^2}{L_J}\left[1 - \cos\left(\frac{\hat{\phi}_J}{\hbar/2e}\right)\right]
L_J = \frac{(\hbar/2e)}{I_0}
\hat{H}_r = \frac{\hat{q}^2}{2C} + \frac{\hat{\phi}^2}{2L} = \hbar\omega_r(\hat{a}^\dagger\hat{a} + \frac{1}{2})
\hat{a} \equiv \frac{1}{\sqrt{2}}(\frac{\hat{\phi}}{\phi_z} + i \frac{\hat{q}}{q_z})
\phi_z\,q_z = \hbar
\phi_z / q_z = \sqrt{\frac{L}{C}}
\omega_r = \sqrt{\frac{1}{LC}}
- Transmon:
Josephson junction shunted by large capacitance:
\(E_J/E_C \sim 100, \; E_J = \frac{(\hbar/2e)^2}{L_J}, \; E_C = \frac{e^2}{2C_J} \)
\hat{H}_q \approx \hbar\omega_q(\hat{b}^\dagger\hat{b} + \frac{1}{2}) - \frac{\hbar\delta_q}{12}(\hat{b}+\hat{b}^\dagger)^4
C_J
L_J
\omega_q = \frac{\sqrt{8 E_J E_C}}{\hbar}
\delta_q = \frac{E_C}{\hbar}
\hat{b} \equiv \frac{1}{\sqrt{2}}(\frac{\hat{\phi}_J}{\phi_{J,z}} + i \frac{\hat{q}_J}{q_{J,z}})
\phi_{J,z}\,q_{J,z} = \hbar
\phi_{J,z} / q_{J,z} = \sqrt{\frac{L_J}{C_J}}
Qubit - Resonator Coupling
- Resonator + Transmon:
, and (2017) . doi: 10.1002/cta.2359.
C_J
L_J
C_c
\hat{H} = \hat{H}_q + \hat{H}_r + \hat{H}_c
g = \frac{C_c\sqrt{\omega_q\omega_r}}{2\sqrt{C_r(C_J+C_c)}}
\hat{H}_c \approx \hbar g (\hat{a} + \hat{a}^\dagger)(\hat{b} + \hat{b}^\dagger)
\chi = \delta_q\frac{g^2}{\Delta^2}
Dispersive approximation, including rotating-wave approx (RWA):
|\Delta| \equiv |\omega_q - \omega_r| \gg |g|
\hat{H}_c \approx 2\chi\,\hat{b}^\dagger\hat{b}\,\hat{a}^\dagger\hat{a} \approx \chi\,\hat{\sigma}_z\,\hat{a}^\dagger\hat{a}
\hat{H}_q \approx \hbar\omega_q \frac{\hat{\sigma}_z}{2}
\omega_r \mapsto \omega_r \pm \chi
Resonator frequency depends
on transmon energy levels
\Rightarrow
Transmission Line Coupling
- Resonator + Transmon + Transmission Line:
, and ( 2017 ) . doi: 10.1002/cta.2359 .
C_J
L_J
C_c
\hat{H} = \hat{H}_q + \hat{H}_r + \hat{H}_c + \hat{H}_t + \hat{H}_{rt}
\displaystyle \hat{H}_t = \int_0^\lambda (\frac{\hat{q}(x)^2}{2c} + \frac{(\partial_x\hat{\phi}(x))^2}{2l})dx = v \int_0^\lambda(\hat{A}^\leftarrow(x)^2 + \hat{A}^\rightarrow(x)^2)dx = \sum_{k=-\infty}^\infty\hbar\omega_k\frac{\hat{c}_k^\dagger \hat{c}_k + \hat{c}_k \hat{c}_k^\dagger}{2}
C_{rt}
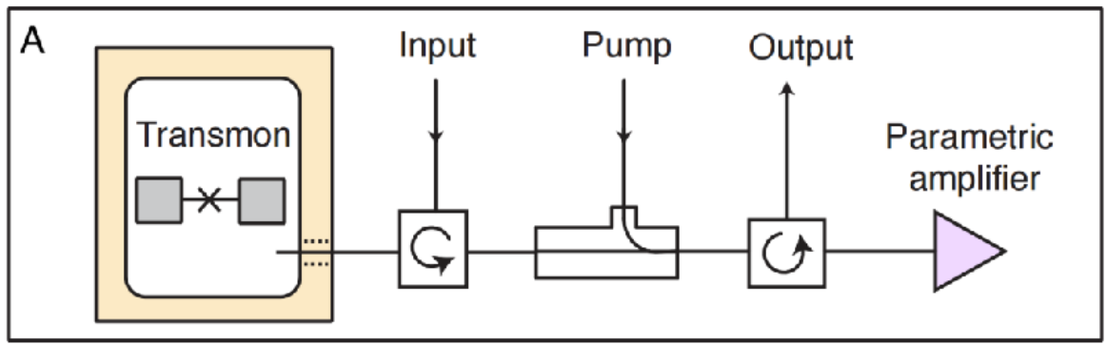
(OUT: to amplifier and detector)
(IN: from signal generator)
( 2017 ) .
[\hat{\phi}_t(x),\hat{q}_t(x')] = i\hbar\delta(x-x')
[\hat{A}^\rightarrow(x),\hat{A}^\rightarrow(x')] = \frac{i\hbar}{2}\partial_x\delta(x-x')
[\hat{c}_k,\hat{c}^\dagger_{k'}] = \delta_{kk'}
\hat{A}^\rightleftharpoons(x) = \frac{1}{2\sqrt{v}}(\frac{\hat{q}(x)}{\sqrt{c}} \mp \frac{\partial_x\hat{\phi}(x)}{\sqrt{l}})
v = \frac{1}{\sqrt{lc}}
\displaystyle\hat{c}_k = \sqrt{\frac{2v}{\lambda}}\int_0^\lambda \hat{A}^\rightarrow(x)\frac{e^{-ikx}}{\sqrt{\hbar\omega_k}}dx, \; k>0
c,l
Capacitance, Inductance per unit length
Z_t = \sqrt{\frac{l}{c}}
, and ( 2017 ) . doi: 10.1002/cta.2359 .
C_J
L_J
C_c
\hat{H} = \hat{H}_q + \hat{H}_r + \hat{H}_c + \hat{H}_t + \hat{H}_{rt}
\hat{H}_t = \sum_{k=-\infty}^\infty\hbar\omega_k(\hat{c}_k^\dagger \hat{c}_k + \frac{1}{2})
C_{rt}
(OUT: to amplifier and detector)
(IN: from signal generator)
( 2017 ) .
\hat{H}_{rt} = \hat{\Phi}\hat{I}(x=0)
= \frac{\hbar}{2}\sqrt{\frac{Z_r}{Z_t}}(\hat{a}+\hat{a}^\dagger)\sqrt{\frac{v}{\lambda}}\sum_{k=0}^\infty\sqrt{\omega_k}(\hat{c}_{-k} + \hat{c}^\dagger_{-k} -\hat{c}_k -
\hat{c}^\dagger_k)
v = \frac{1}{\sqrt{lc}}
Z_t = \sqrt{\frac{l}{c}}
\equiv \frac{\hbar}{2}i\sqrt{\kappa}(\hat{a}+\hat{a}^\dagger)(\hat{c}_{\text{in}}+\hat{c}_{\text{in}}^\dagger - \hat{c}_{\text{out}} - \hat{c}_{\text{out}}^\dagger)
\kappa \equiv \omega_r \frac{Z_r}{Z_t}
\hat{c}_{\text{in}}
\equiv -i\sqrt{\frac{v}{\lambda}}\sum_{k=0}^\infty\sqrt{\frac{\omega_k}{\omega_r}}\,\hat{c}_{-k}
\hat{c}_{\text{out}}
\equiv -i\sqrt{\frac{v}{\lambda}}\sum_{k=0}^\infty\sqrt{\frac{\omega_k}{\omega_r}}\,\hat{c}_{k}
Resonator decay rate near \(\omega_r\)
Boundary condition:
\hat{\Phi}_r = \hat{\phi}_t(x=0)
\Rightarrow \sqrt{\kappa}\,\hat{a} - \hat{c}_{\text{in}} = \hat{c}_{\text{out}}
"Input-output relation"
Transmission Line Coupling
Strengthening weak measurements for qubit tomography and multitime correlators
By Justin Dressel
Strengthening weak measurements for qubit tomography and multitime correlators
Chapman University, MPC Seminar 10/4/2018; RIKEN Invited Seminar 1/16/2019
