Graph Neural Network - K-Hop, MHAGNN, PPGNs

Problem with Standard GNN

Subhankar Mishra, Sachin Kumar

BL2403, School of Computer Sciences, NISER

week-4 | GitHub | Resource Doc

Text

Text

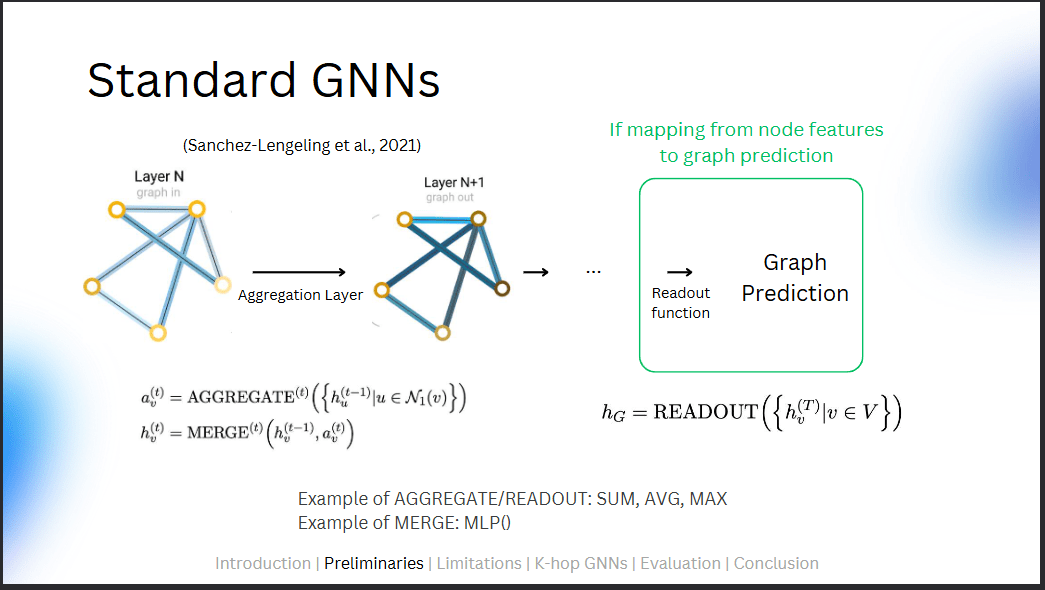
Limitations 1

Text

Text

Assume all nodes with same degree have the same feature vector

• In regular graphs, all nodes have the same feature vector

• Regular graph: All nodes have the same degree

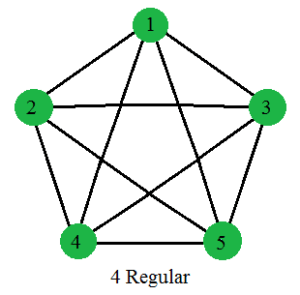
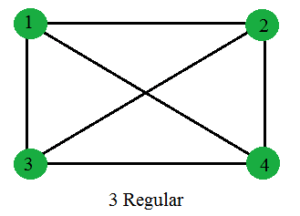
Standard GNNs produce the same representation for the nodes of all regular graphs of a specific size and degree

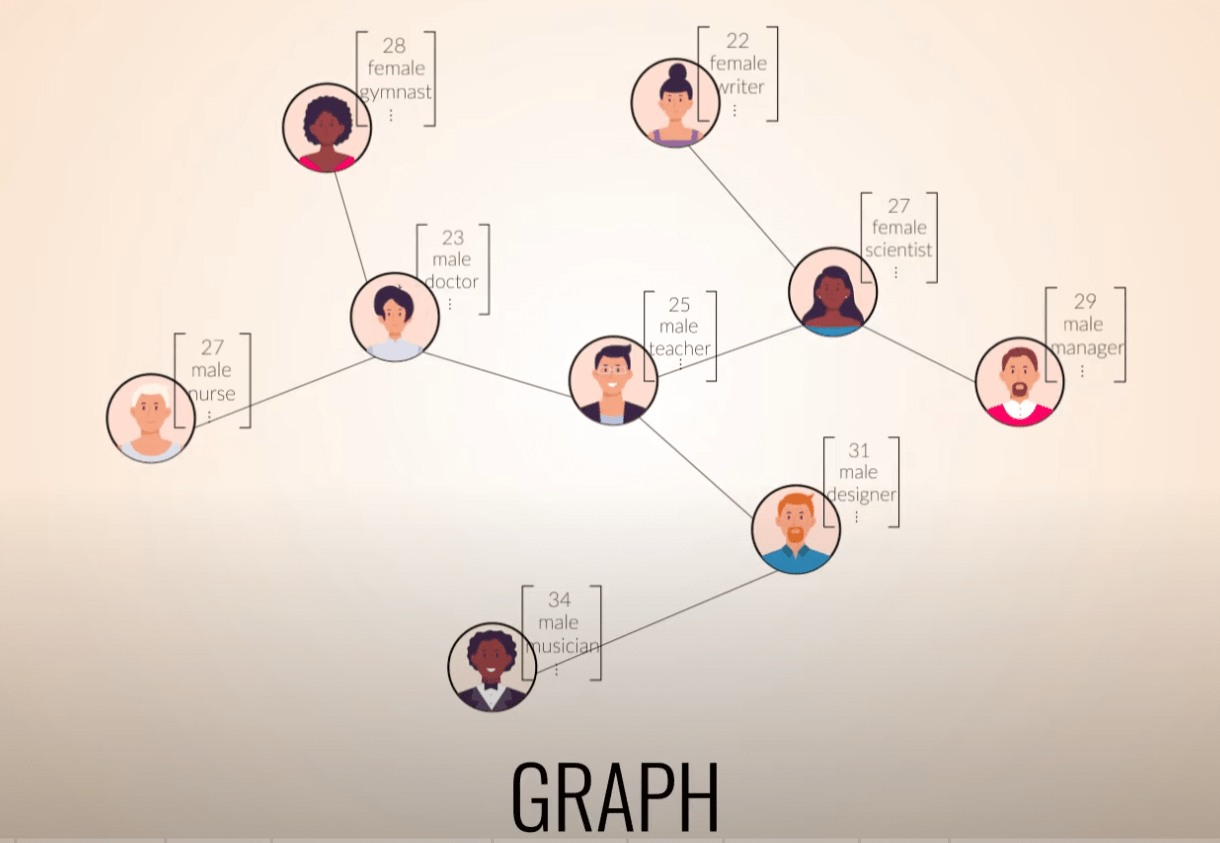
Graphs

Text

Text

Non-Isomorphic Graphs?

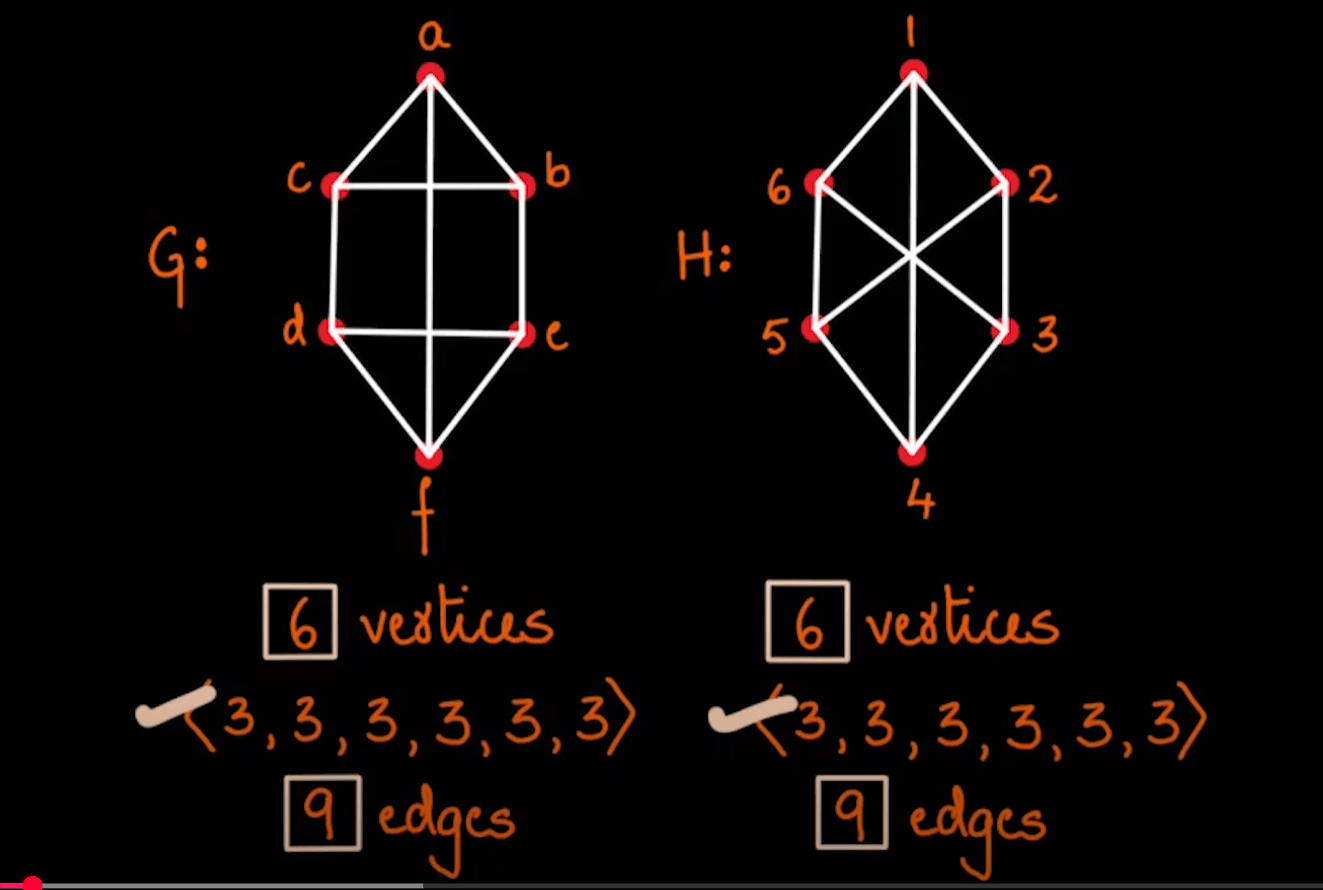
Graphs

Text

Text

Non-Isomorphic Graphs?

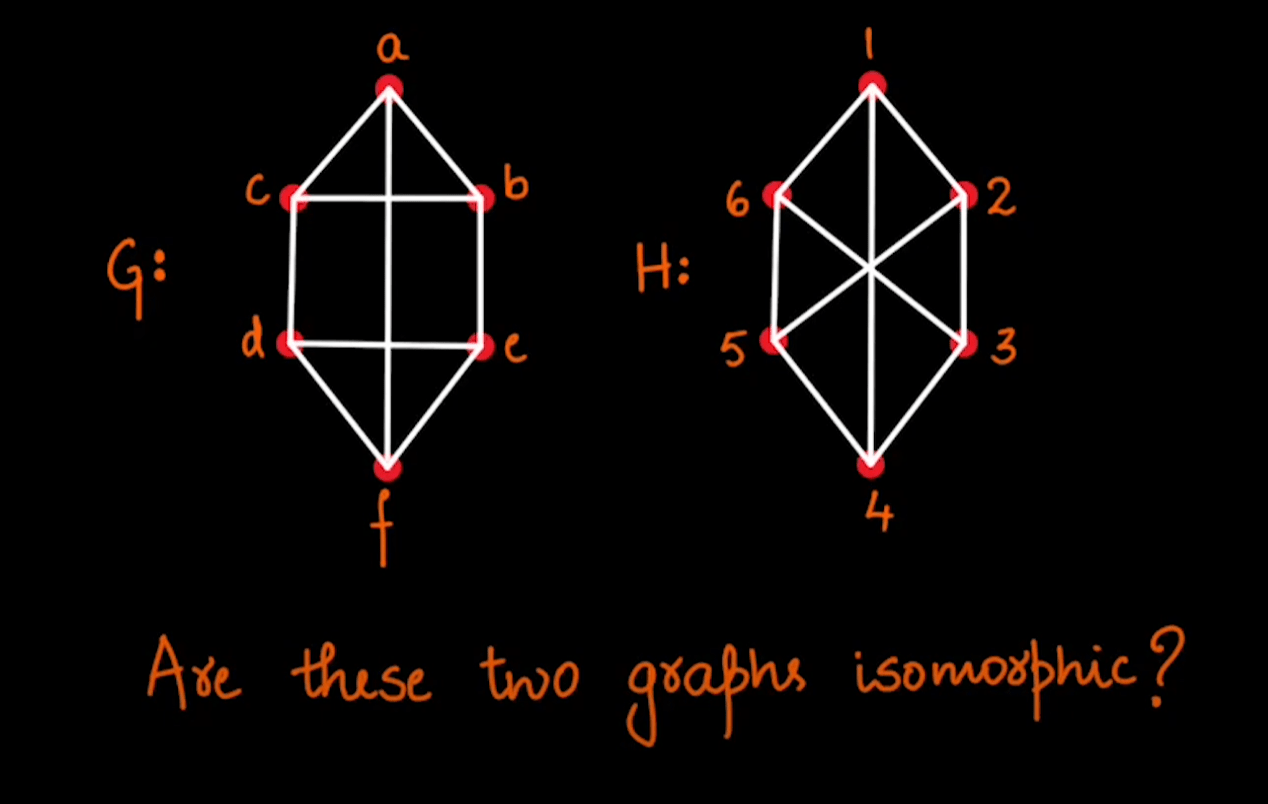
Graphs

Text

Text

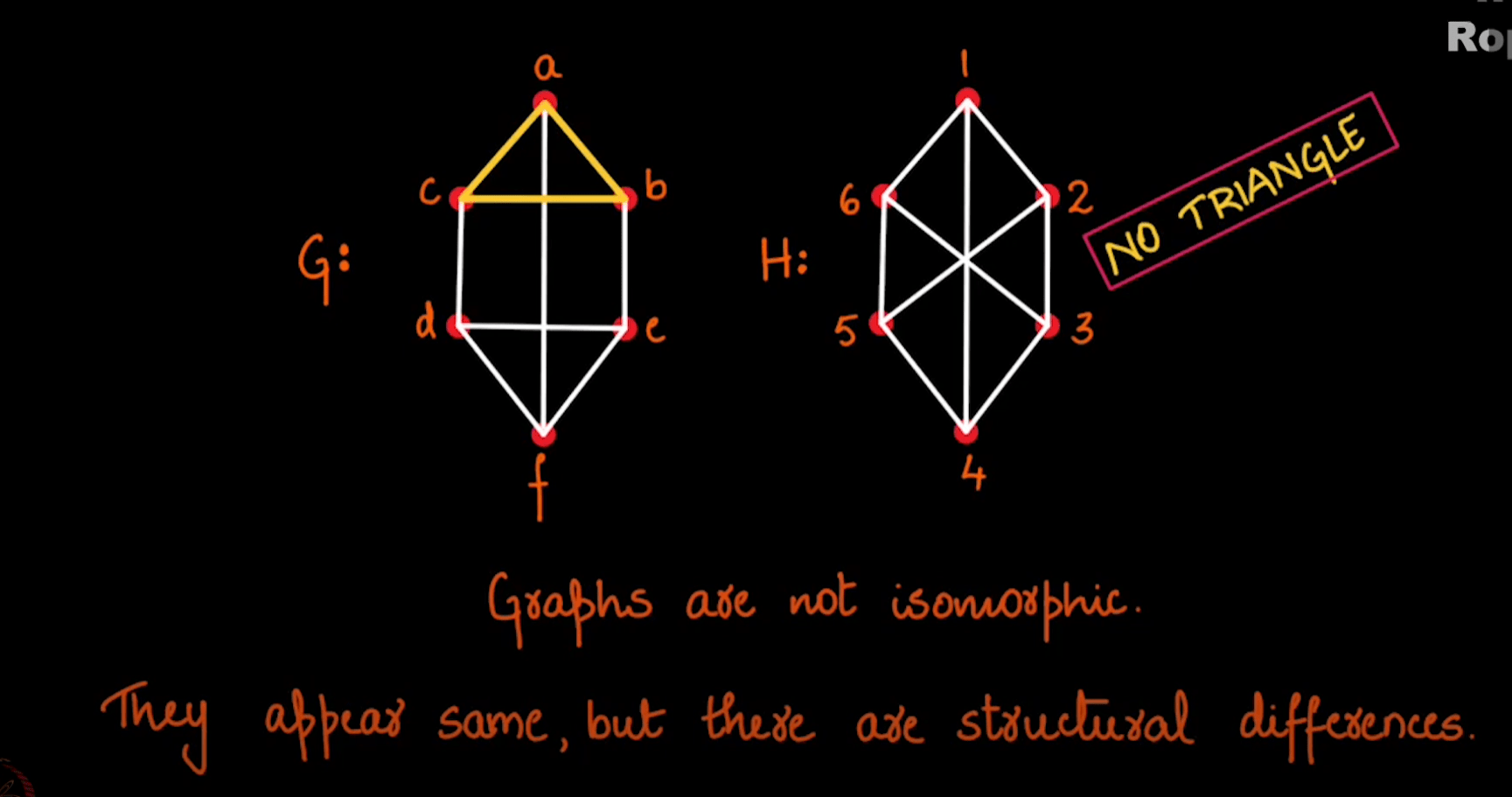
Non-Isomorphic Graphs No

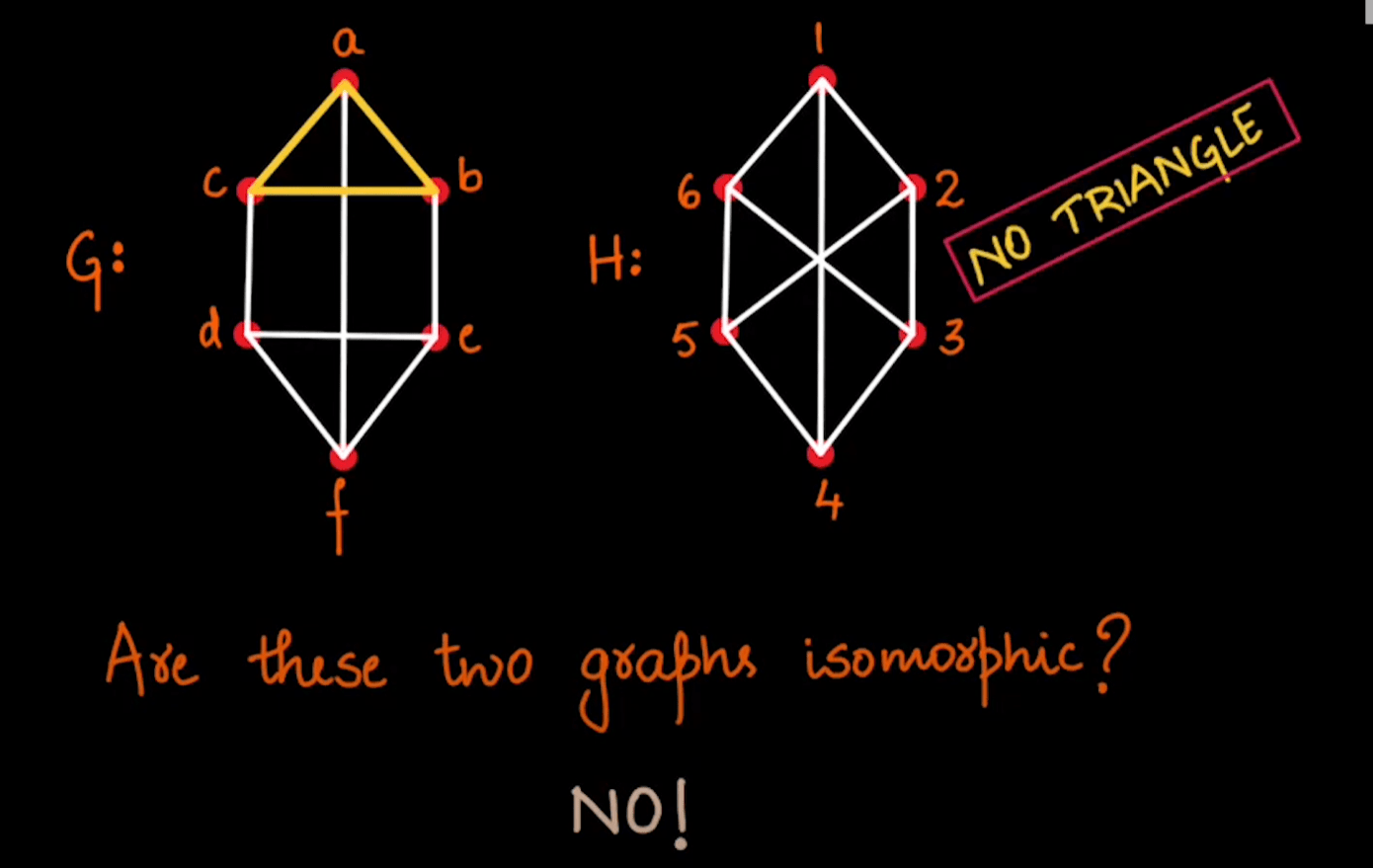
Graphs

Text

Text

Non-Isomorphic Graphs

Standard GNNs produce the same representation for the nodes of all regular graphs of a specific size and degree

Graphs

Text

Text

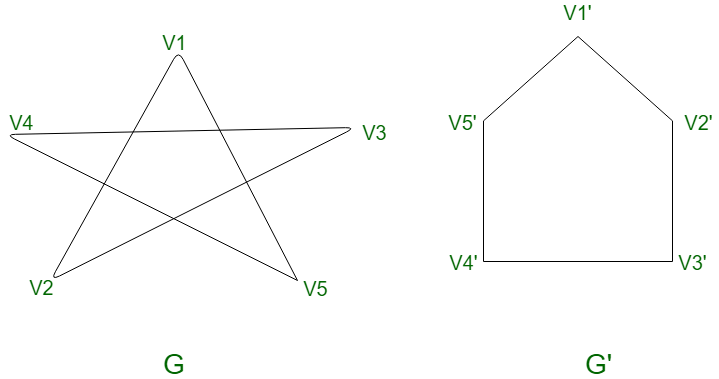
Isomorphic Graphs

Limitations 2

Text

Text

with Non-Isomorphic Graphs

Limitations 2

Text

Text

with Non-Isomorphic Graphs

Limitations 2

Text

Text

with Non-Isomorphic Graphs

Limitations 3

Text

Text

Oversmoothing  & Oversquashing

Text

Text

Oversmoothing  & Oversquashing

Text

Text

Oversmoothing  & Oversquashing

Text

Text

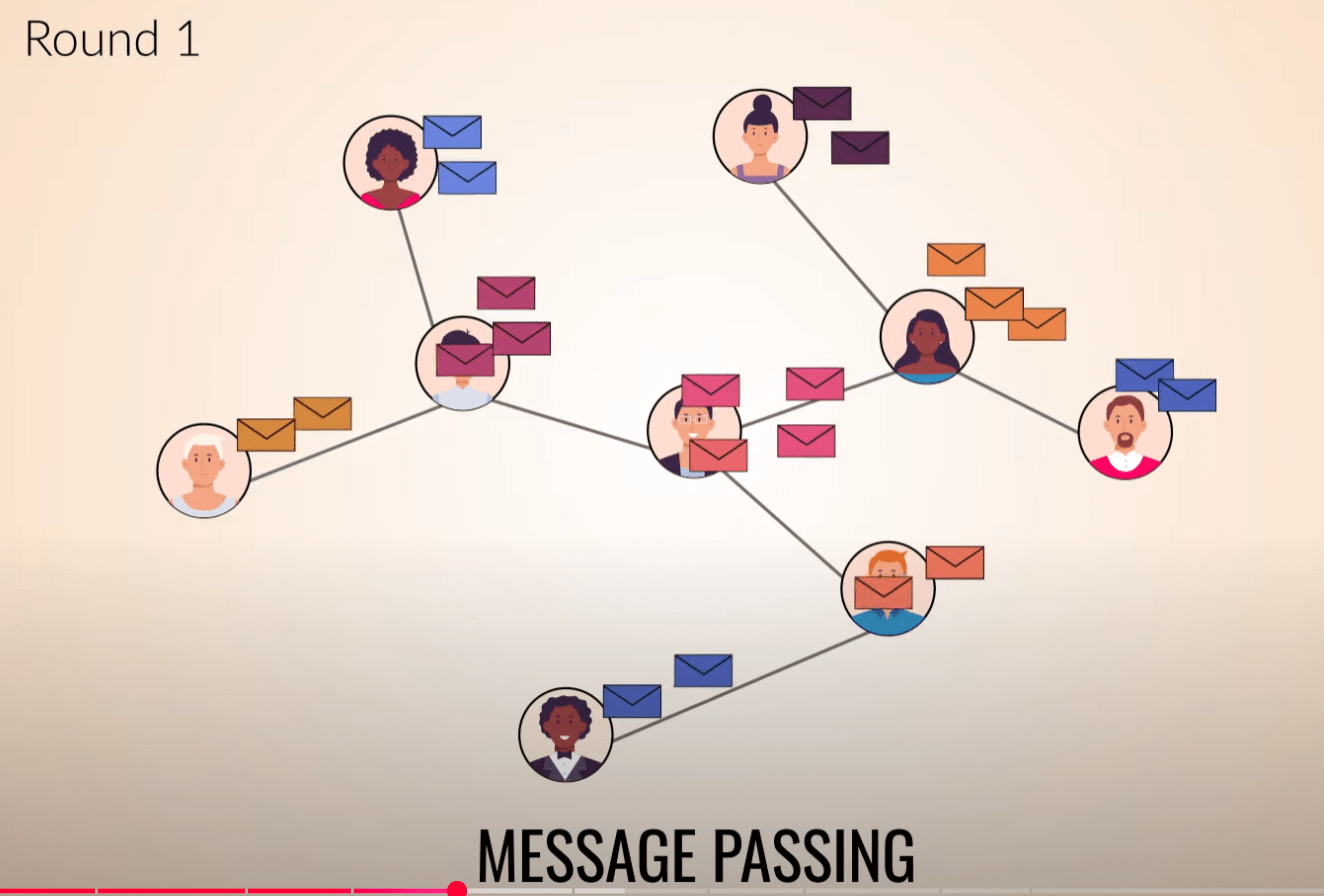
K-Hop GNN

Text

Text

Standard GNN

K-Hop GNN

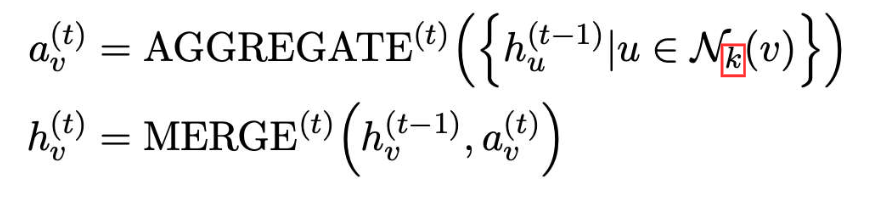
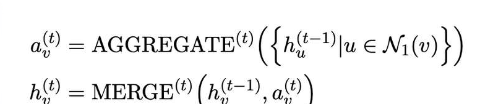
Ask friends of friends and their friends

K-Hop GNN

Text

Text

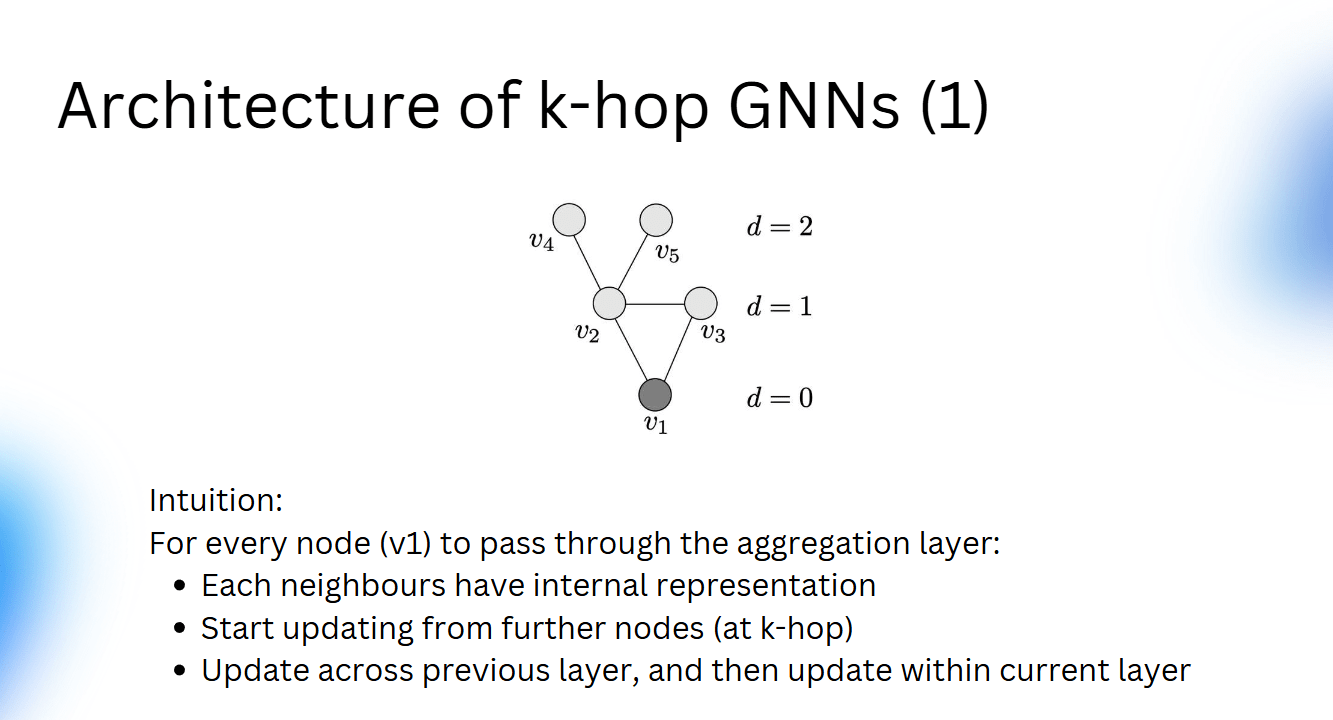
K-Hop GNN

Text

Text

Standard GNN

K-Hop GNN

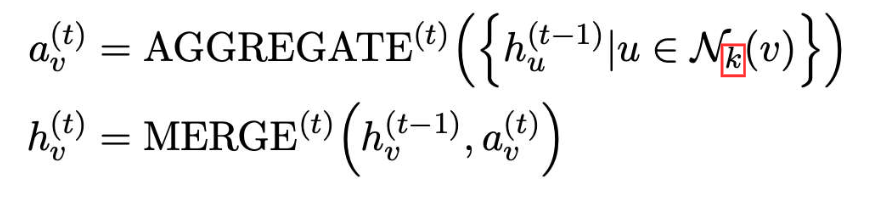
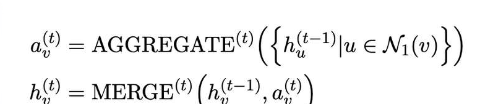
Does that solve the problem?
What do you think?

Does it create new problems🤔

K-Hop GNN

Text

Text

Yes
You can't assign equal importance to all the message coming from K-Hop.

You need to assign weight to each Hop so you can have important information only

Multi-Hop Attention Graph Neural Network

• Multi-hop message passing: Extract embeddings from 1-hop, 2-hop, … k-hop neighbors.

• Attention fusion: An attention module assigns weights to each hop’s embedding.

• Final embedding: A weighted sum of multi-hop embeddings forms the node representation.

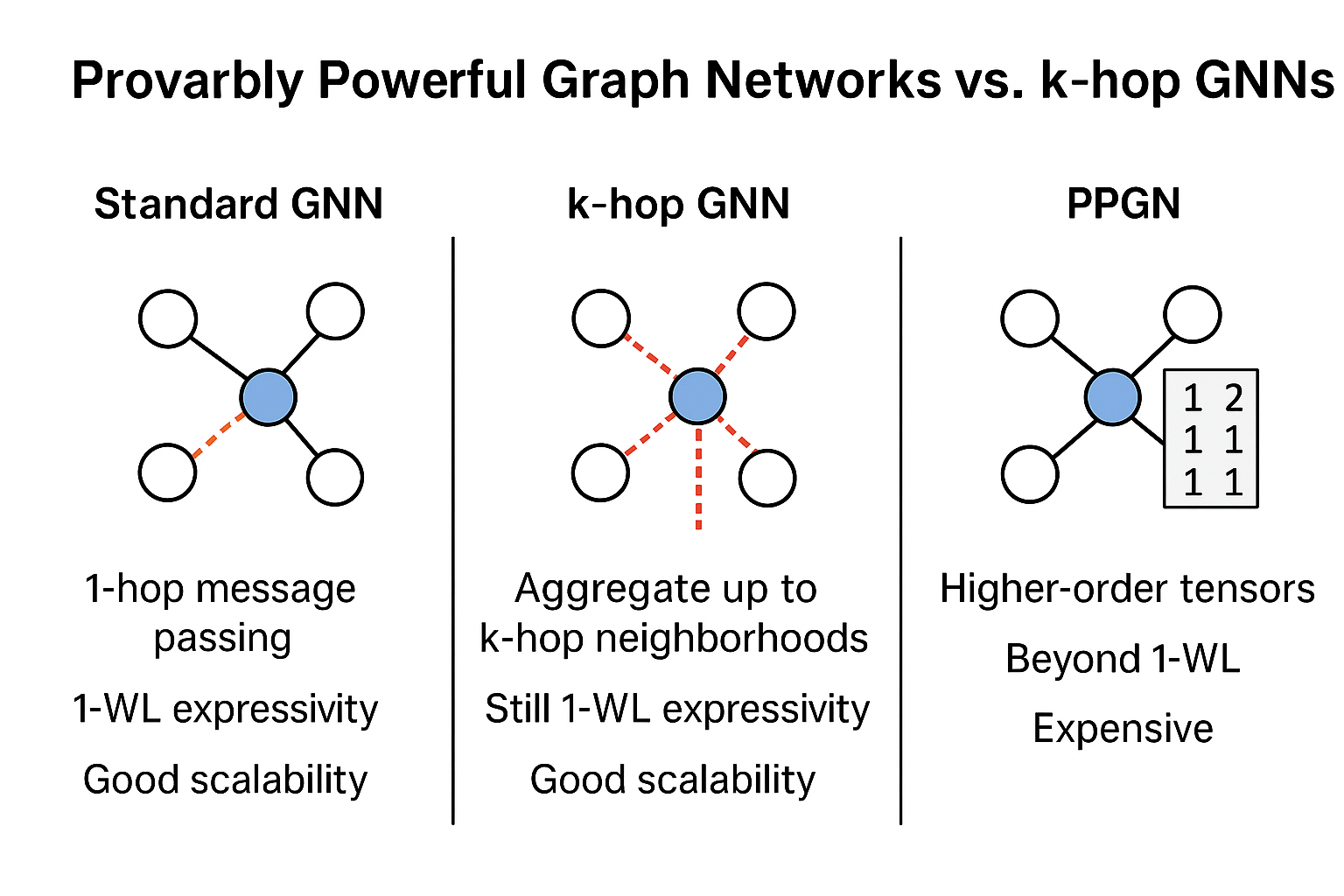
Provably Powerful Graphs Networks(PPGNs)

Text

Text

Classical GNNs cannot capture higher-order structures (like cliques, cycles, regularity) that go beyond local neighborhoods.

• They are designed to be at least as powerful as the k-dimensional Weisfeiler–Lehman test (k-WL) with $k\ge 3$.

• This means they can distinguish graphs that 1-WL (and hence standard GNNs) fail to separate.

• In practice, they can capture higher-order interactions like:

  • Detecting whether a graph is regular

  • Recognizing graph symmetries

  • Counting small substructures (motifs, cliques, cycles)

Provably Powerful Graphs Networks(PPGNs)

Text

Text

Classical GNNs cannot capture higher-order structures (like cliques, cycles, regularity) that go beyond local neighborhoods.

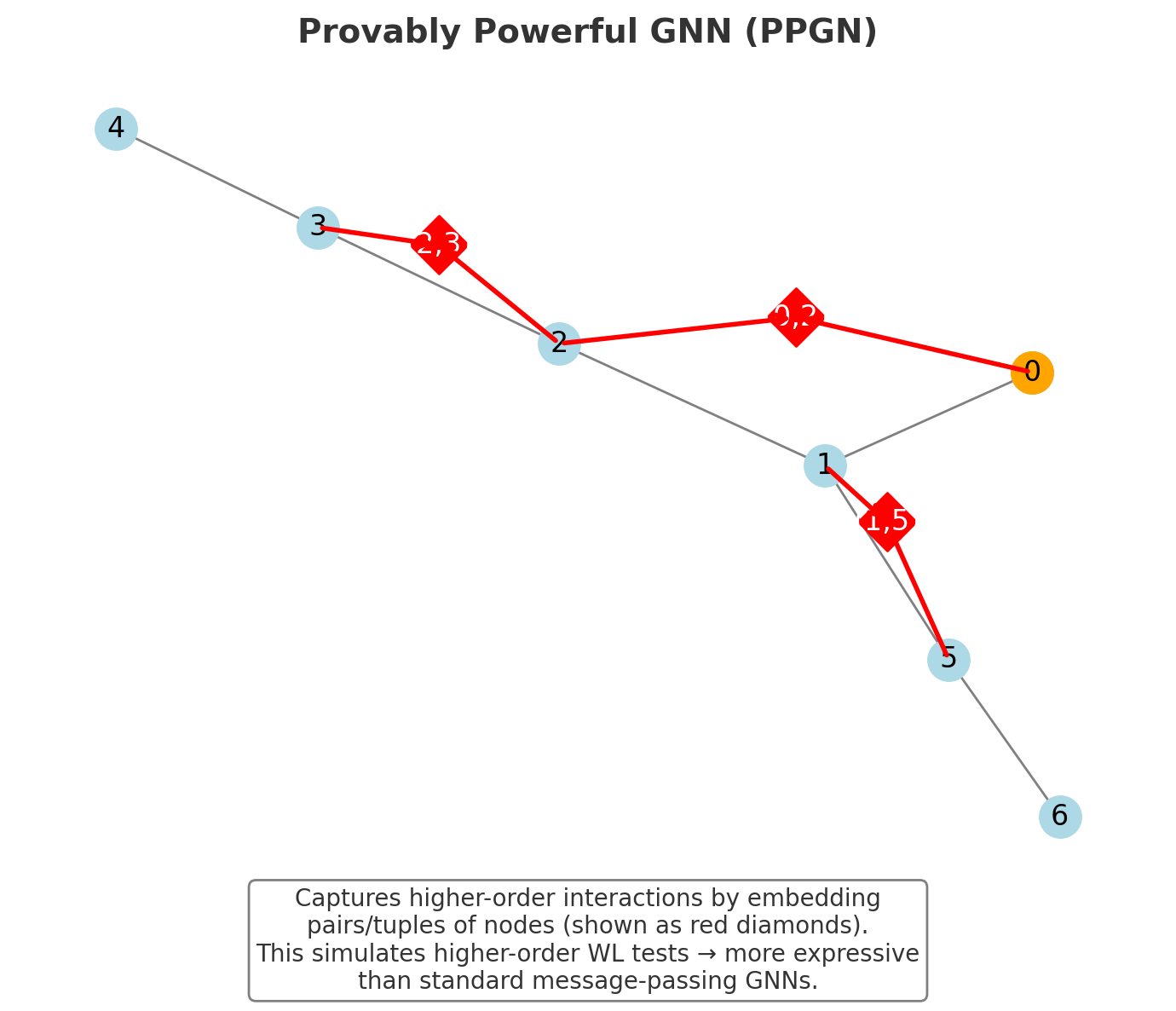
Provably Powerful Graphs Networks(PPGNs)

Text

Text

Classical GNNs cannot capture higher-order structures (like cliques, cycles, regularity) that go beyond local neighborhoods.

K-Hop GNN vs Multi-Hop Attention GNN vs PPGN

Text

Text

k-hop GNN (left): gathers all nodes within k-hops (green) of the target node (orange).

Multi-Hop Attention GNN (middle): still considers multi-hop neighbors, but pays different levels of attention (big green node = more important, small green = less important).

Provably Powerful GNN (right): doesn’t just aggregate neighbors — it also considers higher-order relationships (red arrows show interactions between pairs of nodes).

Thank you for attending the talk!

Text

Text

week-4 | GitHub | Resource Doc