p?題解
By NTUCSIE 系學會學術部 陳家陞
重新解釋一下題目
遍歷所有點 回到起點的最短路
但是有一些限制
符合限制的最佳解
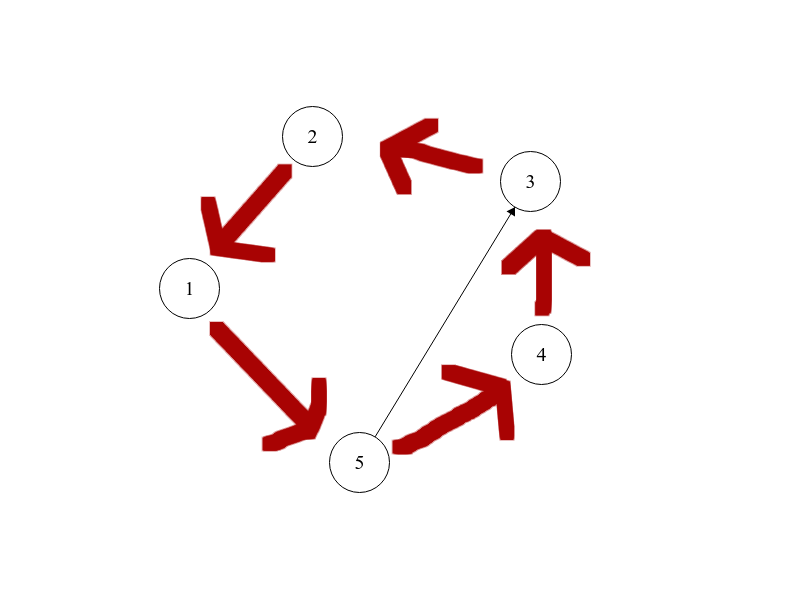
距離的算法也不太一樣
| 1 | 5 | 13 | 25 |
| 1 | 3 | 5 | 7 |
| 1 | 1 | 1 | 1 |
| 2 | ||||
| 1 | ||||
| 0 | ||||
| 0 | 1 | 2 | 3 |
dist(2^1,3)
最直觀的做法
跑過所有可能的排列
用「表格法」算出每種距離

| 1 | 5 | 13 |
| 1 | 3 | 5 |
| 1 | 1 | 1 |
| 1 | z | c |
| 1 | y | b |
| 1 | x | a |
...
然後挑最近的那一條

時間複雜度是……
(n-1)! × n^2 × n^k × n × n
排列數 × 檢查 × 路線距離
(19-1)! × 19^2 × 19^(1e6+7) × 19 × 19
代入 n = 19, k = 1e6+7
大概是 3 × 10^1278783
假設電腦 10^8指令 /sec
就只要跑
3×10^1278775秒而己哦
好方法
拆成兩個部份
-
有相依關係的旅行銷售員問題
-
德拉努瓦(Delannoy)數
旅行銷售員 With 相依關係
動態規劃解法
目標:(n-1)! to 2^(n-1)
6e15 v.s. 262144
狀態
dp[x][S]
從x開始
經過S中所有的元素
到起點的最短距離
轉移式
dp[x][S]
= min(dist(x,i) + dp[i][S-{x}])
for all i in S-{x}
德拉努瓦數 加上 初等數論
Delannoy = (0,0)->(n,m) 路徑數
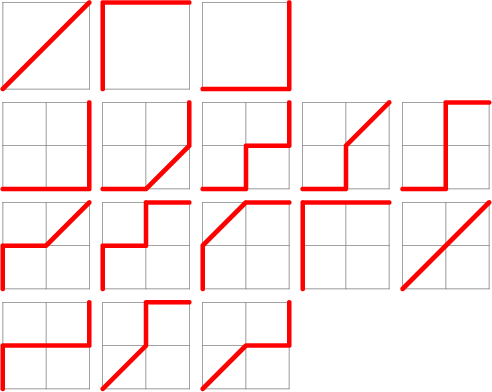
把↗看成是→↑的變種

假設一個造型有i組→↑
那變種的數量就是2^i
經過一番理解
可以知道總路徑數為
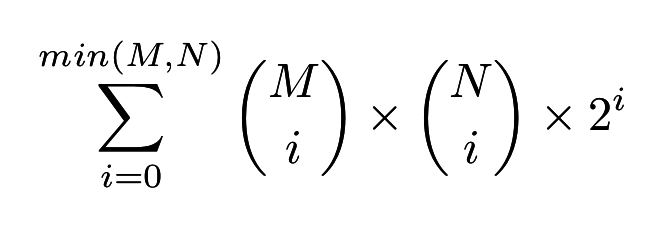
但是
當M = 19^(1e6+7)
怎麼找組合數?
遙遠的數學
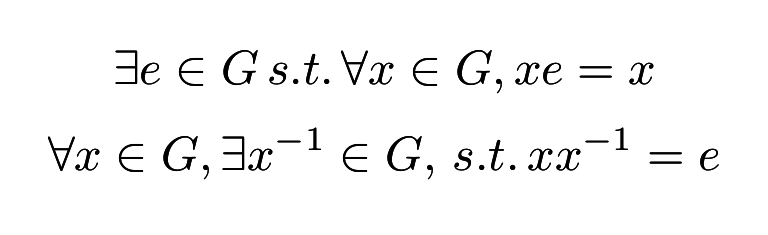
用一般的乘法來理解
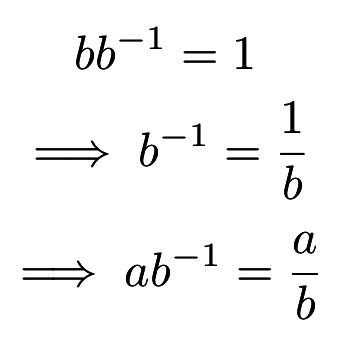
有餘數的乘法
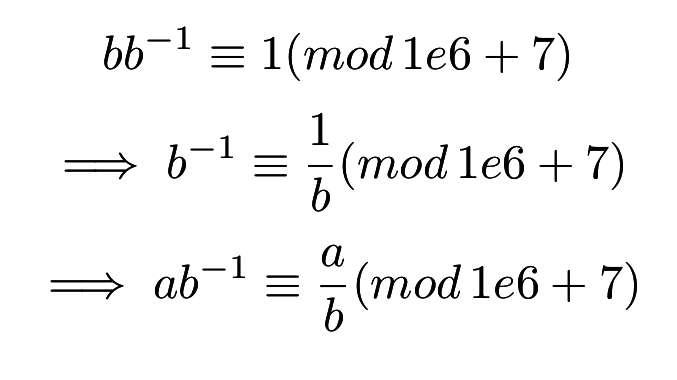
二項式
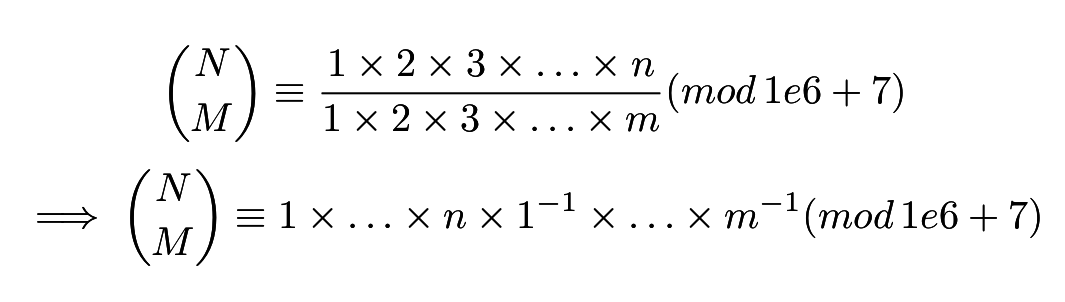
怎麼求模的乘法反元素?
費馬小定理
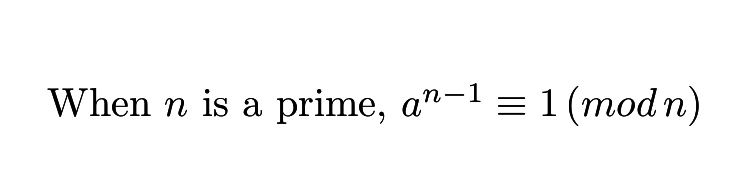
費馬小定理
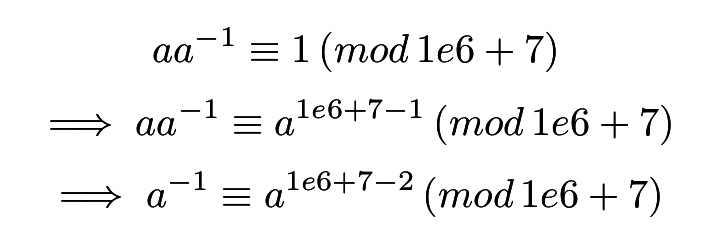
原式變成
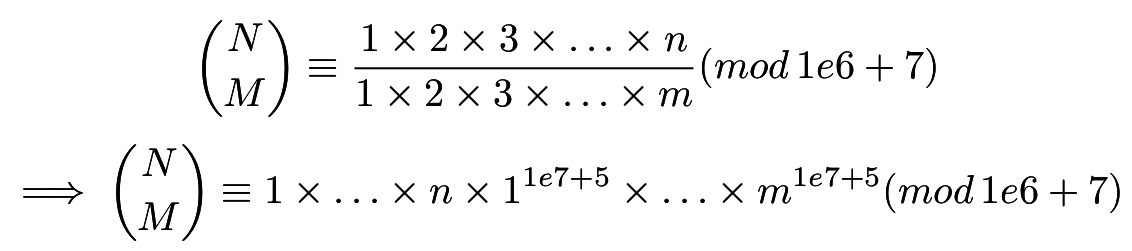
回到這張圖
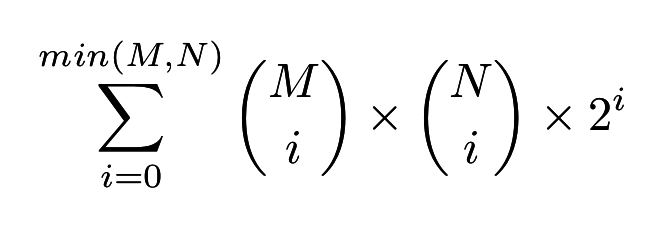
大功告成
總結做法
先對距離建表
德拉努瓦數 + 費馬小定理
再用建出來的距離
做2^n個狀態的DP
p?題解
By qitar888
p?題解
- 566



