Estatística

Data Science & Big Data 

Rafael Erbisti

Aula 2 - Estatística Descritiva

 Estatística descritiva

  • Resumo dos dados por meio de tabelas e gráficos
  • Muitas vezes queremos resumir ainda mais estes dados, apresentando um ou alguns valores que “representem” toda a série
  • Exemplo: considere interesse em estudar a eficácia de uma nova escova dental infantil. Os dados obtidos em um experimento são apresentados a seguir

 Estatística descritiva

## No R

x.antes = c(2.18, 2.05, 1.05, 1.95, 0.28, 2.63, 1.50, 0.45, 0.70, 1.30, 1.25, 0.18, 3.30,
            1.40, 0.90, 0.58, 2.50, 2.25, 1.53, 1.43, 3.48, 1.80, 1.50, 2.55, 1.30, 2.65)
x.depois = c(0.43, 0.08, 0.18, 0.78, 0.03, 0.23, 0.20, 0.00, 0.05, 0.30, 0.33, 0.00, 0.90,
             0.24, 0.15, 0.10, 0.33, 0.33, 0.53, 0.43, 0.65, 0.20, 0.25, 0.15, 0.05, 0.25)

# Gráfico
par(mfrow=c(1,2), mar=c(4,4,1,0.5))
hist(x.antes,prob=1,xlab="índice de placa bacteriana",main="Histograma: antes",
     xlim=c(0,4),nclass=4,col="gray50")
hist(x.depois,prob=1,xlab="índice de placa bacteriana",main="Histograma: depois",
     xlim=c(0,4),nclass=4,col="gray50")

 Estatística descritiva

  • VARIÁVEL – são os resultados da observação de uma determinada característica de interesse.

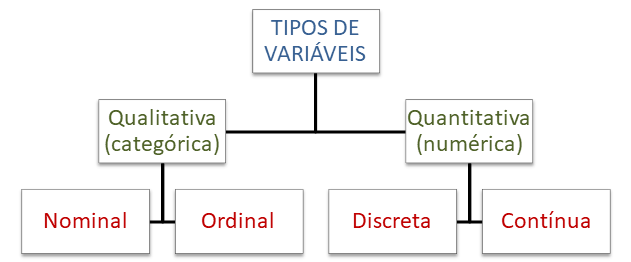
 Estatística descritiva

  • VARIÁVEIS QUALITATIVAS – indicam qualidade ou atributo do indivíduo pesquisado. Exemplos: estado civil, sexo, grau de instrução etc.
  1. Nominais – não existe ordenação nos resultados. Exemplos: estado civil, sexo, religião etc.
  2. Ordinais – existe certa ordenação dos resultados. Exemplos: classe social (alta, média ou baixa), grau de instrução (1º grau, 2º grau e superior) etc.

 Estatística descritiva

  • VARIÁVEIS QUANTITATIVAS – indicam números resultantes de uma contagem ou mensuração.
  1. Discretas – os possíveis valores formam um conjunto finito ou enumerável. É frequentemente resultante de uma contagem. Exemplos: número de filhos (1,2,3,...), idade em anos etc.
  2. Contínuas – os possíveis valores formam um intervalo de números reais. Resultam, frequentemente, de uma mensuração. Exemplos: altura, peso, salário etc. 

 Estatística descritiva

Qual é o tipo das seguintes variáveis?

  1. Índice da BOVESPA
  2. Número de casos de dengue no Rio de Janeiro
  3. Regiões do Brasil
  4. Conceito final no curso de Estatística (A,B,C ou D)
  5. Prêmio de seguros
  6. Proporção de eleitores do Bolsonaro
  7. Escolaridade dos brasileiros

 Análise gráfica

Quais gráficos utilizar se as variáveis forem...

  1. QUALITATIVAS?

2. QUANTITATIVAS?

barras, pizza (setor)

histograma, linhas, dispersão

Fonte: Censo demográfico - IBGE, 2000.

Fonte: Pnad - IBGE.

 Análise gráfica no R

1. Gráfico de barras

Arquivo: "Pesquisa2008.csv".

table(pesq$Escolaridade)  # retorna a tabela de frequência da variável "Escolaridade" 
                          # do dataframe "pesq"

barplot(table(pesq$Escolaridade),ylim=c(0,20),xlab="Escolaridade",ylab="Frequência",
        main="Alunos por escolaridade")

2. Gráfico de pizza

pie(table(pesq$Sexo),main="Alunos por sexo")

 Análise gráfica no R

3. Histograma

hist(pesq$Peso,main="Distribuição dos alunos por peso (Kg)",xlab="peso (kg)",ylab="Frequência")

4. Gráfico de dispersão

plot(pesq$Peso,pesq$Altura,xlab="peso(kg)",ylab="altura (m)",pch=20,
     main="Peso (Kg) vs. altura (m)")

5. Gráfico de linhas

ano = c(2008,2009,2010,2011,2012,2013,2014,2015,2016,2017)
roubos = c(45,32,16,19,15,31,19,32,31,43)

cel.data = data.frame(ano,roubos)
cel.data

plot(cel.data$ano,cel.data$roubos,type="l",xlab="Ano",ylab="nº roubos de celular",
     main="Roubos de celular no centro do Rio \n outubro de cada ano")

 Medidas de resumo

Medidas de posição

Medidas de dispersão

Separatrizes

Média

Mediana

Moda

Variância

Desvio-padrão

Amplitude

Coeficiente de Variação

Quartil

Percentil

 Média aritmética simples

Média aritmética simples: é a soma das observações dividida pelo número de observações.

\bar{x}=\dfrac{\textrm{soma dos elementos}}{\textrm{número de elementos}} = \frac{\sum_{i=1}^{n}x_i}{n}
xˉ=soma dos elementosnuˊmero de elementos=∑i=1nxin\bar{x}=\dfrac{\textrm{soma dos elementos}}{\textrm{número de elementos}} = \frac{\sum_{i=1}^{n}x_i}{n}
# No R:

x = c(21,20,25,22,24,25,21,21,23,21,22,24,90)
 
x.barra = mean(x)
x.barra
[1] 27.61538

 Média aritmética ponderada

Média aritmética ponderada: é a soma ponderada das observações dividida pelo número de observações.

\bar{x}=\dfrac{\textrm{soma dos elementos ponderados}}{\textrm{número de elementos}} = \frac{\sum_{i=1}^{n}f_i x_i}{n}
xˉ=soma dos elementos ponderadosnuˊmero de elementos=∑i=1nfixin\bar{x}=\dfrac{\textrm{soma dos elementos ponderados}}{\textrm{número de elementos}} = \frac{\sum_{i=1}^{n}f_i x_i}{n}
## No R:

x = c(21,20,25,22,24,23,90)
f = c(4,1,2,2,2,1,1)
 
x.barra = weighted.mean(x,f)
x.barra
[1] 27.61538

 Mediana

Mediana: é o "meio" de uma lista ordenada de números.

\tilde{x}=x_{(\frac{n+1}{2})}, \textrm{se $n$ impar}
x~=x(n+12),se n impar\tilde{x}=x_{(\frac{n+1}{2})}, \textrm{se $n$ impar}
\textrm{Sejam os dados ordenados } x_{(1)} < x_{(2)} < \ldots < x_{(n)},
Sejam os dados ordenados x(1)&lt;x(2)&lt;…&lt;x(n),\textrm{Sejam os dados ordenados } x_{(1)} &lt; x_{(2)} &lt; \ldots &lt; x_{(n)},
\tilde{x}=\dfrac{x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)}}{2}, \textrm{se $n$ par}
x~=x(n2)+x(n2+1)2,se n par\tilde{x}=\dfrac{x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)}}{2}, \textrm{se $n$ par} 
## No R:

x = c(21,20,25,22,24,25,21,21,23,21,22,24,90)
 
x.til = median(x)
x.til
[1] 22

 Média vs. Mediana

A média é afetada por valores extremos (altos ou baixos).

Fonte: Pnad/2017 - IBGE.

Distribuição da renda domiciliar per capita por cor - Brasil 2017

 Moda

Moda: valor mais frequente nos dados.

## No R:

library(DescTools)

x = c(21,20,25,22,24,25,21,21,23,21,22,24,90)
 
mod = Mode(x)
mod
[1] 21

 Assimetria

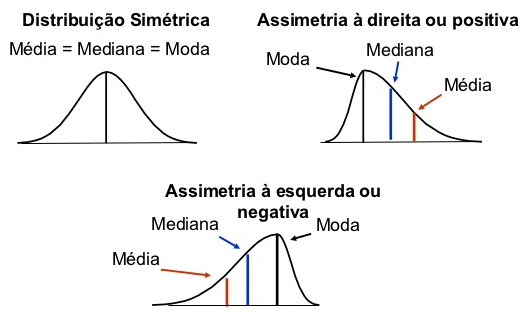
 Medidas de dispersão

O resumo de um conjunto de dados por uma única medida representativa de posição central esconde a informação sobre a variabilidade.

Grupo A: 3, 4, 5, 6, 7

Grupo B: 1, 3, 5, 7, 9

Grupo C: 5, 5, 5, 5, 5

Grupo D: 2, 5, 5, 7, 6

Grupo E: 4, 5, 5, 6, 5

\bar{x} = 5
xˉ=5\bar{x} = 5

Notas de grupos de alunos

Podemos dizer que os grupos têm o mesmo desempenho?

Idade de alunos de 3 turmas

Podemos dizer que as turmas são semelhantes em termos de idade?

 Amplitude

Amplitude: é distância entre o mínimo e o máximo.

\Delta=\textrm{maximo}-\textrm{minimo}=x_{(n)}-x_{(1)}
Δ=maximo−minimo=x(n)−x(1)\Delta=\textrm{maximo}-\textrm{minimo}=x_{(n)}-x_{(1)}
  1. não consegue caracterizar a distribuição dos valores entre o mínimo e o máximo;
  2. é baseada em duas observações, independentemente do número total de observações.

Limitações:

## No R:

x = c(21,20,25,22,24,25,21,21,23,21,22,24,90)
 
amplitude = max(x)-min(x)   # ou a função range(x)
amplitude
[1] 70

 Variância

Variância: considera os tamanhos dos desvios  de cada observação em relação à média.

\sigma^2=\dfrac{\textrm{soma dos desvios ao quadrado}}{\textrm{número total de elementos}}=\dfrac{\sum_{i=1}^{n} (x_i-\bar{x})^2}{n}
σ2=soma dos desvios ao quadradonuˊmero total de elementos=∑i=1n(xi−xˉ)2n\sigma^2=\dfrac{\textrm{soma dos desvios ao quadrado}}{\textrm{número total de elementos}}=\dfrac{\sum_{i=1}^{n} (x_i-\bar{x})^2}{n}

Limitações:

  1. não está na mesma unidade dos dados;
  2. afetado por valores extremos.
## No R:

x = c(21,20,25,22,24,25,21,21,23,21,22,24,90)
 
v = var(x)  # variância amostral
v
[1] 354.0897

Observação: é possível definir a variância usando o divisor (n-1) no lugar de (n); essa é a diferença entre os conceitos de variância amostral e variância populacional.

 Desvio-padrão

Desvio-padrão: é a raiz quadrada da variância.

\sigma=\sqrt{\sigma^2}=\sqrt{\dfrac{\sum_{i=1}^{n} (x_i-\bar{x})^2}{n}}
σ=σ2=∑i=1n(xi−xˉ)2n\sigma=\sqrt{\sigma^2}=\sqrt{\dfrac{\sum_{i=1}^{n} (x_i-\bar{x})^2}{n}}
## No R:

x = c(21,20,25,22,24,25,21,21,23,21,22,24,90)
 
v = sd(x)  # desvio-padrão amostral
v
[1] 18.81727
  • Uma forma de se obter uma medida de dispersão com a mesma unidade dos dados.

 Coeficiente de variação

Coeficiente de variação: medida de dispersão relativa (adimensional) da variação de um conjunto de dados.

CV=\dfrac{\textrm{desvio-padrão}}{\textrm{média}}\times 100=\dfrac{\sigma}{\bar{x}} \times 100
CV=desvio-padra˜omeˊdia×100=σxˉ×100CV=\dfrac{\textrm{desvio-padrão}}{\textrm{média}}\times 100=\dfrac{\sigma}{\bar{x}} \times 100
## No R:

x = c(21,20,25,22,24,25,21,21,23,21,22,24,90)
 
cv = sd(x)/mean(x)*100
cv
[1] 68.14054
  • Expressa a variabilidade dos dados retirando a influência da ordem de grandeza da variável.
  • interpretado como a variabilidade dos dados em relação à média. Quanto menor o CV mais homogêneo é o conjunto de dados.

 Separatrizes

  • Tanto a média como o desvio-padrão podem não ser medidas adequadas para representar um conjunto de dados, pois:
  1. são afetados, de forma exagerada, por valores extremos;
  2. apenas com esses dois valores não temos ideia da simetria ou assimetria da distribuição dos dados.

Principais SEPARATRIZES:

  • Quartis
  • Decis
  • Percentis

 Separatrizes

x_{(1)} < x_{(2)} < \ldots < x_{(n)},
x(1)&lt;x(2)&lt;…&lt;x(n),x_{(1)} &lt; x_{(2)} &lt; \ldots &lt; x_{(n)},

1. Quartis

2. Decis

3. Percentis

Sejam os dados ordenados

## No R:

x = c(21,20,25,22,24,25,21,21,23,21,22,24,90)

q = quantile(x,probs=c(0.05,0.1,0.5,0.75))
q
  5%  10%  50%  75% 
20.6 21.0 22.0 24.0

 Separatrizes

Fonte: Pnad/2017 - IBGE.

Distribuição da renda domiciliar per capita - Brasil 2017

 Box-plot

Box-plot: construído a partir dos quartis.

  1. ilustra as principais características de uma distribuição;
  2. muito útil na comparação de distribuições
## No R:

library(datasets)
library(help="datasets")

data("airquality")
help("airquality")

airquality

boxplot(airquality$Temp~airquality$Month,ylab="temperatura (ºF)",xlab="meses",
        names=c("Maio","Junho","Julho","Agosto","Setembro"),pch=20,col=rainbow(5),
        main="Temperatura em NY em 1973")

 Box-plot

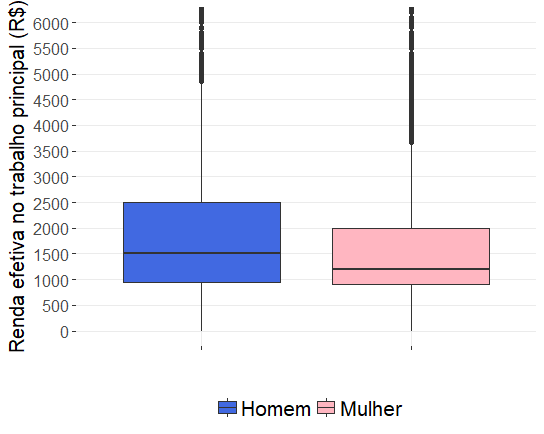
Distribuição da renda no trabalho principal por sexo - Brasil 2017

Fonte: Pnad/2017 - IBGE.

Curso-Wida - Aula 2

By rafaerbisti

Made with Slides.com

Curso-Wida - Aula 2

Estatística descritiva

  • 380

More from rafaerbisti