Estatística
Data Science & Big Data
Rafael Erbisti
Aula 5 - Modelos estatísticos e tomada de decisão
Introdução
Modelos estatísticos: modelos probabilístico cuja finalidade é a modelagem do sistemas de interesse em termos de suas características.
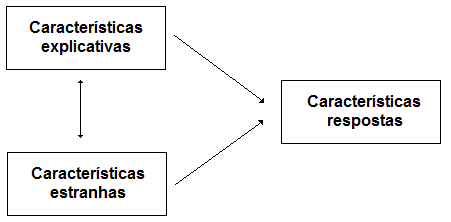
Introdução
y=x
y=x+\epsilon
Associação linear
Instrumentos exploratórios para padrões de associação:
- Gráfico de dispersão
- Coeficiente de correlação linear
## No R:
base = read.csv2(file=paste(diretorio,"oxigenio.csv",
sep=""),header=TRUE)
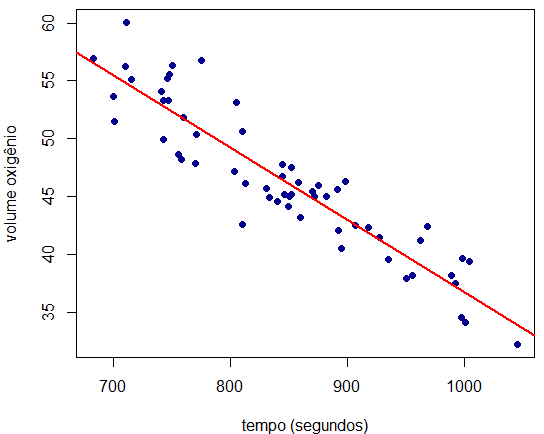
# gráfico de dispersão
plot(base$tempo,base$volume,xlab="tempo (segundos)",
ylab="volume oxigênio",pch=16,col="darkblue")
# coeficiente de correlação
cor(base$tempo,base$volume)
[1] -0.9228064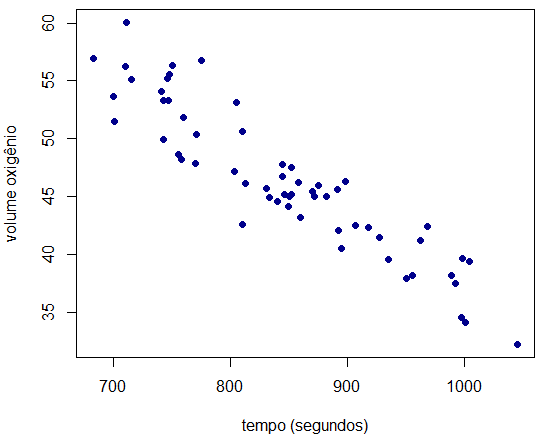
Correlação linear
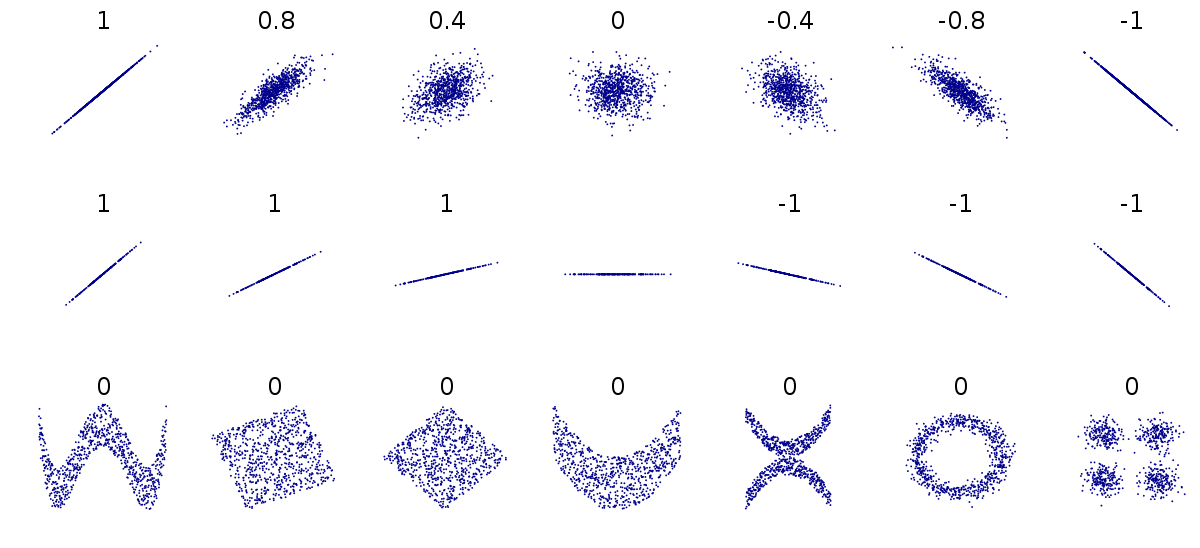
Correlação espúria
Correlação espúria: existência de relação estatística entre duas ou mais variáveis, mas sem significado teórico.
correlação = 99,3%
Correlação espúria
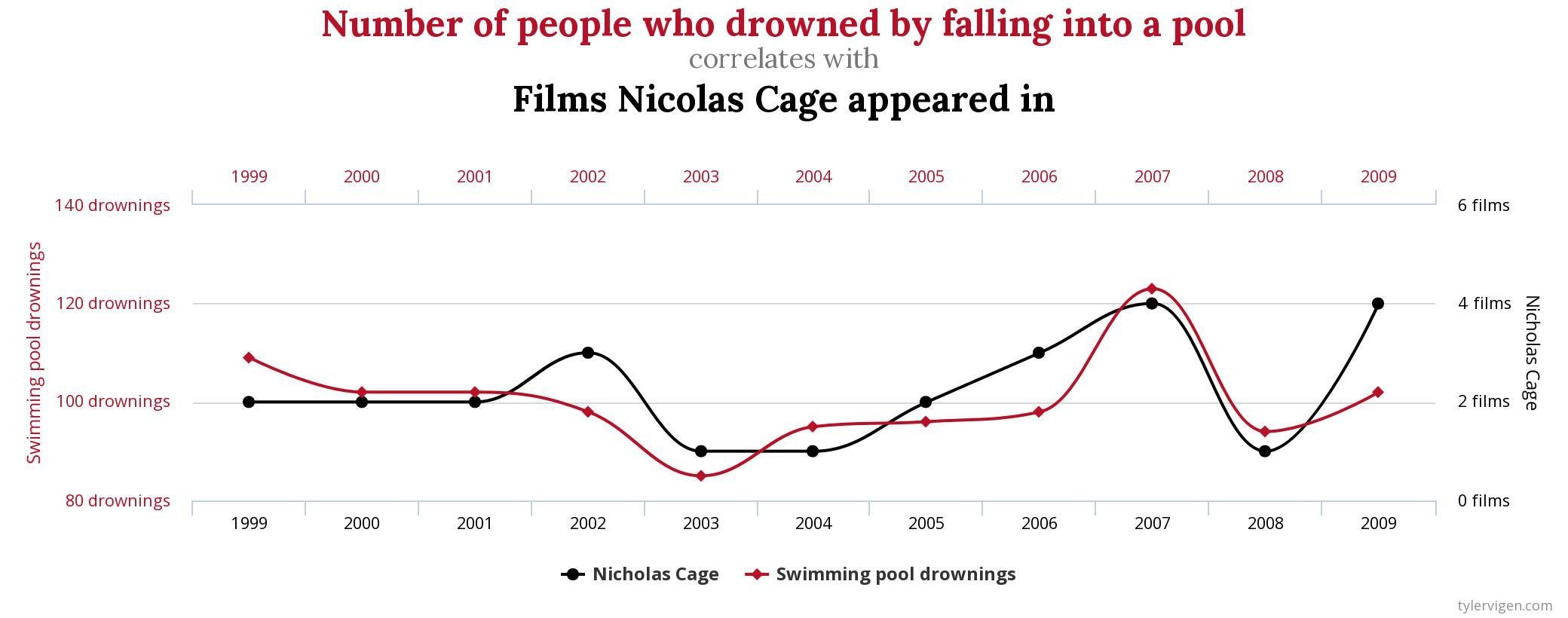
correlação = 66,6%
Modelos de Regressão
Modelo de regressão linear
Simples
(1 regressora)
Múltiplo
(2 ou + regressoras)
- Regressão linear simples: uma maneira formal de expressar as características fundamentais da associação linear entre duas variáveis
Y=\alpha+\beta X + \epsilon
\epsilon: \textrm{ erro aleatório}
X: \textrm{ variável explicativa}
\alpha \textrm{ e } \beta: \textrm{ parâmetros desconhecidos}
Y: \textrm{ variável resposta}
-
-
-
-
Modelos de Regressão
## No R
model.fit = lm(base$volume~base$tempo)
summary(model.fit)
Call:
lm(formula = base$volume ~ base$tempo)
Residuals:
Min 1Q Median 3Q Max
-5.9922 -1.8530 0.2574 1.4114 5.9676
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 99.25977 2.91575 34.04 <2e-16 ***
base$tempo -0.06258 0.00343 -18.24 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.437 on 58 degrees of freedom
Multiple R-squared: 0.8516, Adjusted R-squared: 0.849
F-statistic: 332.8 on 1 and 58 DF, p-value: < 2.2e-16
plot(base$tempo,base$volume,xlab="tempo (segundos)",ylab="volume oxigênio",pch=16,col="darkblue")
abline(model.fit,col=2,lwd=2)Resultados e decisões
Taxa de retorno à educação na cidade do Rio de Janeiro - 2000
- comparação entre a população que vive na favela e a que não vive
- modelo de regressão linear que explique renda no trabalho principal
- interpretação dos coeficientes da variável escolaridade comparada nos grupos favela e não-favela
Resultados e decisões
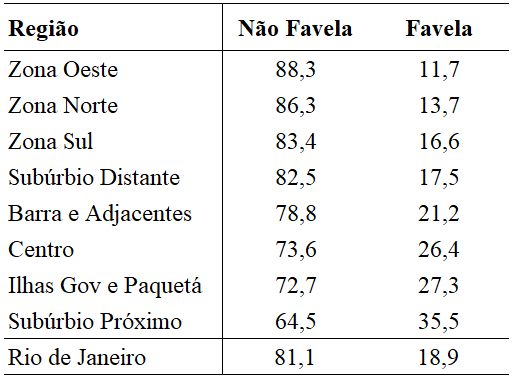
Fonte: Censo 2000 - IBGE.
Distribuição da população por setor - (em %)
Resultados e decisões
Fonte: Censo 2000 - IBGE.
Distribuição da população por grupos - (em %)
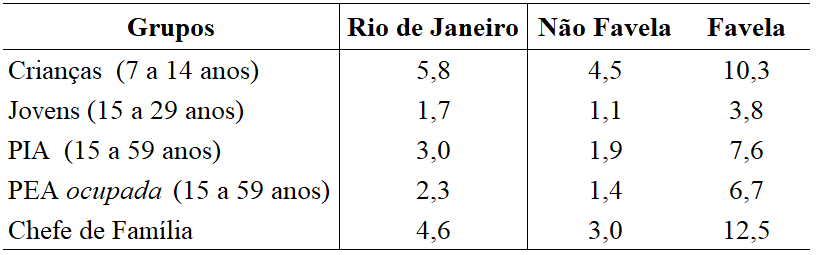
Resultados e decisões
Fonte: Censo 2000 - IBGE.
Rendimento médio no trabalho principal por ano de estudo (em R$)
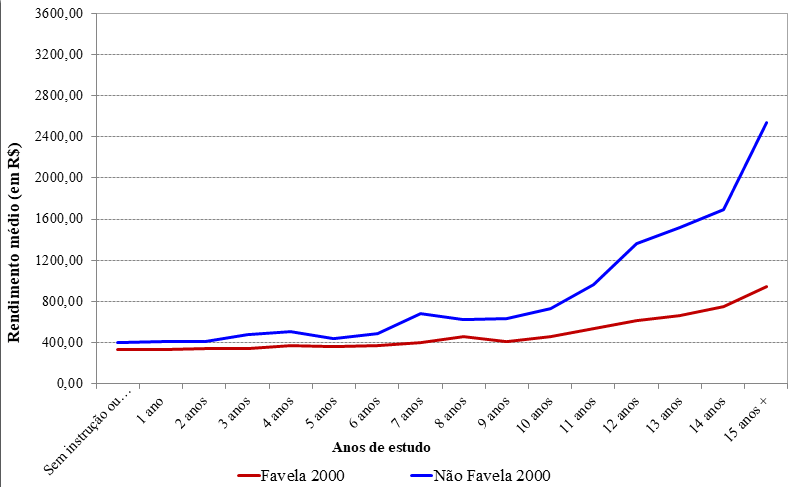
Resultados e decisões
Modelo de regressão ajustado:
log Y = \alpha + \beta_1 E + \beta_2 M + \beta_3 S + \beta_4 C + \beta_5 F + \beta_6 T + \beta_7 A + \beta_8 R
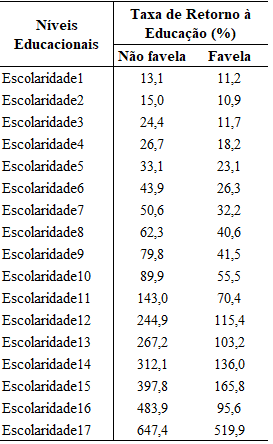
Resultados e decisões
Consumo industrial de energia elétrica - Mato Grosso (jan/10 - Dez/14)
- modelos de séries temporais para predizer o consumo no período de 24 meses
- Período de previsão: janeiro/2015 até dezembro/2016
Que cuidados devemos ter?
Nossa decisão depende apenas do resultado do modelo?
Será que nossa experiência não deve ser considerada?
Fonte: Agência Nacional de Energia Elétrica - ANEEL.
Resultados e decisões
Consumo industrial de energia elétrica - Mato Grosso (jan/10 - Dez/14)
1. Resultado da previsão a partir do modelo estatístico adequado
Resultados e decisões
2. Resultado da previsão a partir do modelo estatístico adequado comparado ao dado realizado
Consumo industrial de energia elétrica - Mato Grosso (jan/10 - Dez/14)
Resultados e decisões
Análise Espaço-Temporal da Distribuição dos Casos de Dengue na Cidade do Rio de Janeiro
- 70 semanas epidemiológicas: começando em jan/2001
Fonte: Dissertação do mestrado em estatística do IM/UFRJ de Gustavo Ferreira.
Resultados e decisões
Análise Espaço-Temporal da Distribuição dos Casos de Dengue na Cidade do Rio de Janeiro
Fonte: Dissertação do mestrado em estatística do IM/UFRJ de Gustavo Ferreira.
Curso-Wida - Aula 5
By rafaerbisti
Curso-Wida - Aula 5
Modelagem e decisões
