Raíra Marotta

Estatística

Curso Big Data e Data Science  INFNET

Aula 7 - Introdução a Inferência Estatística

 Introdução

Modelos estatísticos: modelos probabilístico cuja finalidade é a modelagem do sistemas de interesse em termos de suas características.

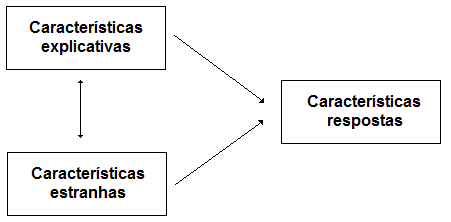
 Introdução

y=x
y=x+\epsilon

 Associação linear

Instrumentos exploratórios para padrões de associação:

  1. Gráfico de dispersão
  2. Coeficiente de correlação linear
## No R:
p_load(HistData)
data("GaltonFamilies")

# gráfico de dispersão
galton_pai_filho <- GaltonFamilies%>%
                      filter(gender == "male")%>%
                      select(father, childHeight)  


ggplot(data = galton_pai_filho) +
  aes(x = father, y = childHeight) +
  geom_point(color = "#0c4c8a") +
  theme_minimal()

# coeficiente de correlação
cor(base$tempo,base$volume)
[1] 0.3923835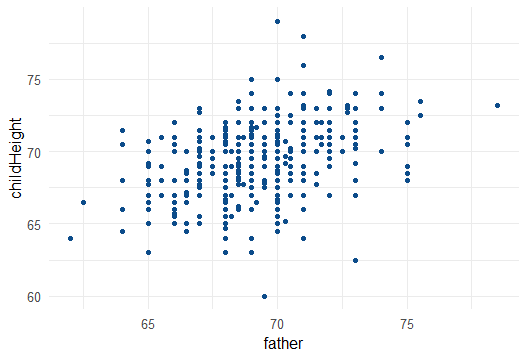

 Correlação linear

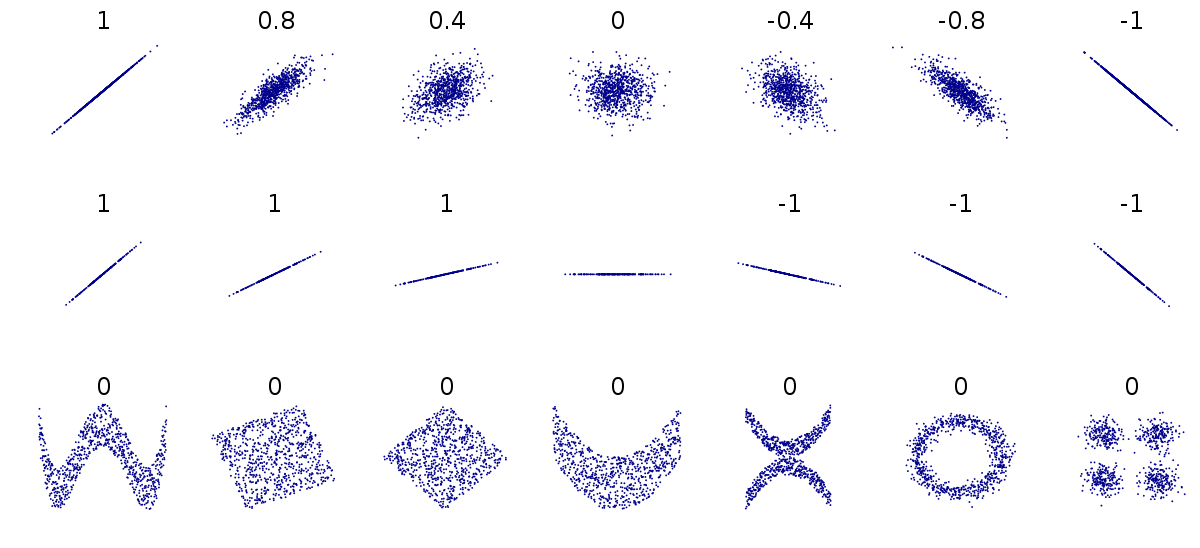
 Correlação espúria

Correlação espúria: existência de relação estatística entre duas ou mais variáveis, mas sem significado teórico. 

correlação = 99,3%

 Modelos de Regressão

Modelo de regressão linear

Simples

(1 regressora)

Múltiplo

(2 ou + regressoras)

  • Regressão linear simples: uma maneira formal de expressar as características fundamentais da associação linear entre duas variáveis
Y=\alpha+\beta X + \epsilon
\epsilon: \textrm{ erro aleatório}
X: \textrm{ variável explicativa}
\alpha \textrm{ e } \beta: \textrm{ parâmetros desconhecidos}
Y: \textrm{ variável resposta}

-

-

-

-

 Modelos de Regressão

## No R

modelo <- lm(childHeight ~ father, data = galton_pai_filho)
summary(modelo)

Call:
lm(formula = galton_pai_filho$childHeight ~ galton_pai_filho$father)

Residuals:
    Min      1Q  Median      3Q     Max 
-9.3959 -1.5122  0.0413  1.6217  9.3808 

Coefficients:
                        Estimate Std. Error t value
(Intercept)             38.36258    3.30837  11.596
galton_pai_filho$father  0.44652    0.04783   9.337
                        Pr(>|t|)    
(Intercept)               <2e-16 ***
galton_pai_filho$father   <2e-16 ***
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.416 on 479 degrees of freedom
Multiple R-squared:  0.154,	Adjusted R-squared:  0.1522 
F-statistic: 87.17 on 1 and 479 DF,  p-value: < 2.2e-16


plot(galton_pai_filho$father,galton_pai_filho$child, pch = 20, xlab = " Altura do pai",
     ylab = "Altura do filho")
abline(modelo, col = 2, lwd = 2)

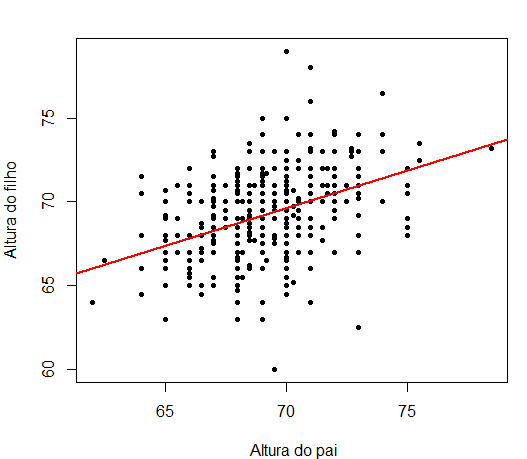
 Resultados e decisões

Consumo industrial de energia elétrica - Mato Grosso (jan/10 - Dez/14)

  • modelos de séries temporais para predizer o consumo no período de 24 meses
  • Período de previsão: janeiro/2015 até dezembro/2016

Que cuidados devemos ter?

Nossa decisão depende apenas do resultado do modelo?

Será que nossa experiência não deve ser considerada?

Fonte: Agência Nacional de Energia Elétrica - ANEEL.

 Resultados e decisões

Consumo industrial de energia elétrica - Mato Grosso (jan/10 - Dez/14)

1. Resultado da previsão a partir do modelo estatístico adequado

 Resultados e decisões

2. Resultado da previsão a partir do modelo estatístico adequado comparado ao dado realizado

Consumo industrial de energia elétrica - Mato Grosso (jan/10 - Dez/14)

 Resultados e decisões

Análise Espaço-Temporal da Distribuição dos Casos de Dengue na Cidade do Rio de Janeiro

  • 70 semanas epidemiológicas: começando em jan/2001

Fonte: Dissertação do mestrado em estatística do IM/UFRJ de Gustavo Ferreira.

 Resultados e decisões

Análise Espaço-Temporal da Distribuição dos Casos de Dengue na Cidade do Rio de Janeiro

Fonte: Dissertação do mestrado em estatística do IM/UFRJ de Gustavo Ferreira.

Infnet - Aula 8

By Raíra Marotta

Source: rafaerbisti

Infnet - Aula 8

Modelagem e decisões

  • 317

More from Raíra Marotta