Aula 2 - Estatística Descritiva
Raíra Marotta
Estatística
Estatística Descritiva
- É em geral utilizada no início da análise de dados.
- Tem como objetivo tirar conclusões de forma simples através de gráficos e tabelas que representem de forma resumida uma (possivelmente) grande massa de dados.
- Exemplo: considere interesse em estudar a eficácia de uma nova escova dental infantil. Os dados obtidos em um experimento serão apresentados a seguir.
Estatística Descritiva
Variável: Característica do elemento investigado no estudo de interesse.
Estatística Descritiva
VARIÁVEIS QUALITATIVAS têm como possíveis realizações qualidades ou atributos do indivíduo em estudo. Exemplos: sexo, estado civil, grau de instrução, etc...
As variáveis qualitativas podem ser classificadas como:
- Nominais: não existe ordenação nas possíveis realizações da variável de interesse. Exemplos: religião, estado civil, sexo...
- Ordinais: existem ordenações nas possíveis realizações da variável de interesse. Exemplos: classe social (baixa, média, alta).
Estatística Descritiva
VARIÁVEIS QUANTITATIVAS tem como possíveis realizações os resultados de uma contagem ou mensuração.
As variáveis quantitativas podem ser classificadas como:
- Discretas: os possíveis resultados formam um conjunto finito ou infinito enumerável e que resultam, frequentemente, de uma contagem. Exemplos: número de filhos em uma família (0,1,2,...).
- Contínuas: os possíveis resultados formam um conjunto infinito não enumerável, ou seja, pertencem a um intervalo de R e resultam de uma mensuração. Exemplos: altura, peso...
Estatística Descritiva
Observações Importantes
Note que, dependendo da maneira como a variável é medida, ela pode ser classificada de formas diferentes.
Exemplo: a variável idade se medida em anos poderia ser classificada como quantitativa discreta enquanto se medimos anos e dias (2,4 anos, 3,2 anos) podemos classificá-la como quantitativa contínua.
Por que é preciso classificar as variáveis de interesse corretamente?
Porque as técnicas usadas para resumir e analisar os dados dependem do tipo de variável em estudo.
Estatística descritiva
Qual é o tipo das seguintes variáveis?
- Índice da BOVESPA
- Número de casos de dengue no Rio de Janeiro
- Regiões do Brasil
- Conceito final no curso de Estatística (A,B,C ou D)
- Prêmio de seguros
- Proporção de eleitores do Bolsonaro
- Escolaridade dos brasileiros
Análise gráfica
Quais gráficos utilizar se as variáveis forem...
- QUALITATIVAS?
2. QUANTITATIVAS?
barras, pizza (setor)
histograma, linhas, dispersão
Fonte: Censo demográfico - IBGE, 2000.
Fonte: Pnad - IBGE.
Medidas de Resumo
Medidas resumo são usadas para resumir ainda mais a informação vinda dos dados, fornecendo valores que representam os dados de forma global.
Medidas de Posição
Média
Mediana
Moda
Medidas de Dispersão
Variância
Desvio-padrão
Amplitude
Intervalo Interquartílico
Média Aritmética
Média aritmética simples: é a soma das observações dividida pelo número de observações
"Ponto de equilíbrio"
\bar{x}=\dfrac{\textrm{soma dos elementos}}{\textrm{número de elementos}} = \frac{\sum_{i=1}^{n}x_i}{n}
# Fui a feira e gastei R$ 40 reais em 5 itens.
# Quanto gastei em média por item?
40
______ = 8
5 Média Aritmética
Média aritmética ponderada: é a soma ponderada das observações dividida pelo número de observações.
\bar{x}=\dfrac{\textrm{soma dos elementos ponderados}}{\textrm{número de elementos}} = \frac{\sum_{i=1}^{n}f_i x_i}{n}
# Comprei 3 blusas, por R$ 50 cada e 2 shorts, por R$ 80 cada.
# Quanto gastei em média por item?
3 x 50 + 2 x 80
_________________ = 62
5 Mediana
Mediana: Observação que ocupa a posição central nos dados ordenados em ordem crescente.
Mediana
\tilde{x}=x_{(\frac{n+1}{2})}, \textrm{se $n$ impar}
\textrm{Sejam os dados ordenados } x_{(1)} < x_{(2)} < \ldots < x_{(n)},
\tilde{x}=\dfrac{x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)}}{2}, \textrm{se $n$ par}
Mediana
# Na turma do meu filho há 5 crianças.
# João - 4 anos
# Pedro - 3 anos
# Maria - 2 anos
# Marta - 3 anos
# José - 5 anos
Qual a mediana das idades ?
R: 3 anos
# Uma nova aluna com 2 anos entrou na turma.
# E agora? Qual a nova mediana das idades?
R: 3 anos?
# E a média mudou?Mediana x Média
A média é afetada por valores extremos (altos ou baixos).
Fonte: Pnad/2017 - IBGE.
Distribuição da renda domiciliar per capita por cor - Brasil 2017
Moda
Moda: realização mais frequente nos dados.
Medidas de dispersão
O resumo de um conjunto de dados por uma única medida representativa de posição central esconde a informação sobre a variabilidade.
Grupo A: 3, 4, 5, 6, 7
Grupo B: 1, 3, 5, 7, 9
Grupo C: 5, 5, 5, 5, 5
Grupo D: 2, 5, 5, 7, 6
Grupo E: 4, 5, 5, 6, 5
\bar{x} = 5
Notas de grupos de alunos
Podemos dizer que os grupos têm o mesmo desempenho?
Idade de alunos de 3 turmas
Podemos dizer que as turmas são semelhantes em termos de idade?
Medidas de dispersão
Amplitude: é distância entre o mínimo e o máximo.
\Delta=\textrm{maximo}-\textrm{minimo}=x_{(n)}-x_{(1)}
- não consegue caracterizar a distribuição dos valores entre o mínimo e o máximo;
- é baseada em duas observações, independentemente do número total de observações.
Limitações:
Variância
Variância: considera os tamanhos dos desvios de cada observação em relação à média.
\sigma^2=\dfrac{\textrm{soma dos desvios ao quadrado}}{\textrm{número total de elementos}}=\dfrac{\sum_{i=1}^{n} (x_i-\bar{x})^2}{n}
Limitações:
- não está na mesma unidade dos dados;
- afetado por valores extremos.
Observação: é possível definir a variância usando o divisor (n-1) no lugar de (n); essa é a diferença entre os conceitos de variância amostral e variância populacional.
Desvio Padrão
Desvio-padrão: é a raiz quadrada da variância.
\sigma=\sqrt{\sigma^2}=\sqrt{\dfrac{\sum_{i=1}^{n} (x_i-\bar{x})^2}{n}}
- Uma forma de se obter uma medida de dispersão com a mesma unidade dos dados.
Coeficiente de variação
Coeficiente de variação: medida de dispersão relativa (adimensional) da variação de um conjunto de dados.
CV=\dfrac{\textrm{desvio-padrão}}{\textrm{média}}\times 100=\dfrac{\sigma}{\bar{x}} \times 100
- Expressa a variabilidade dos dados retirando a influência da ordem de grandeza da variável.
- interpretado como a variabilidade dos dados em relação à média. Quanto menor o CV mais homogêneo é o conjunto de dados.
Separatrizes
- A média e variância são medidas muito influenciadas por observações discrepantes. Por isso buscamos medidas alternativas tal como a mediana, que é mais robusta.
- Apenas com esses dois valores não temos ideia da simetria ou assimetria da distribuição dos dados.
Principais SEPARATRIZES:
- Quartis
- Decis
- Percentis
Separatrizes
x_{(1)} < x_{(2)} < \ldots < x_{(n)},
1. Quartis
2. Decis
3. Percentis
Sejam os dados ordenados
Separatrizes
Fonte: Pnad/2017 - IBGE.
Distribuição da renda domiciliar per capita - Brasil 2017
Alguns nomes particulares são usados para alguns quantis mais usados:
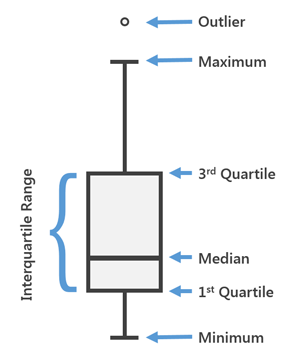
Separatrizes
Desvio Interquartílico
Máximo
Mínimo
Mediana
Outlier
3º Quartil
1º Quartil
- q1 = q(0, 25): primeiro quartil;
- q2 = q(0, 50): mediana;
- q3 = q(0, 75): terceiro quartil;
Assimetria
Moda
Média
Médiana
Moda
Moda
Média
Média
Médiana
Médiana
Assimetria positiva
Assimetria negativa
Distribuição simétrica
Aula2
By Raíra Marotta
