Raíra Marotta
Estatística
Curso Big Data e Data Science
Aula 6 - Distribuição Normal
Padronização
Suponha que temos variáveis com escalas diferentes e gostaríamos de poder compará-las.
Uma possível solução envolve padronizá-las.
Esse processo envolve:
- subtrair a média;
- dividir pelo desvio padrão
Interpretação: número de desvios que cada valor dista da média.
Padronização
## No R:
#Simulando 10 números
x <- sample(10,size = 10)
[1] 3 4 5 7 2 8 9 6 10 1
mean(x)
[1] 5.5
sd(x)
[1] 3.02765
# Retirando a média
desvios.media = x - mean(x)
[1] -2.5 -1.5 -0.5 1.5 -3.5 2.5 3.5 0.5 4.5 -4.5
# Dividindo pelo desvio padrao
z = (desvios.media)/sd(x)
z
[1] -0.8257228 -0.4954337 -0.1651446 0.4954337 -1.1560120
[6] 0.8257228 1.1560120 0.1651446 1.4863011 -1.4863011z_i = \frac{x_i - \bar{x}}{\sqrt{\sigma^2}}
Padronização
Padronizar os dados não muda sua forma, somente sua escala.
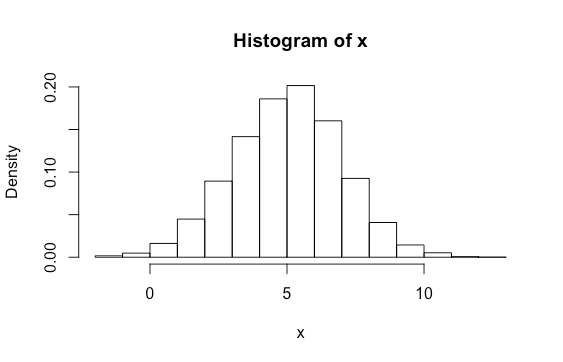
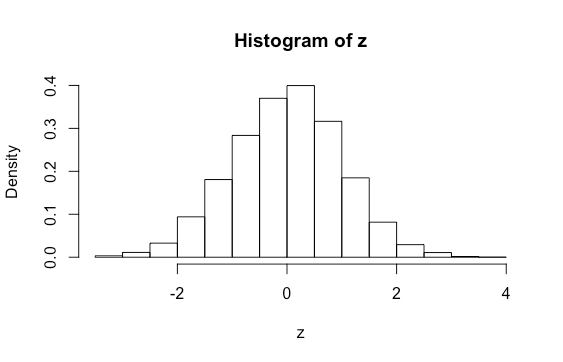
## No R:
x <- rnorm(5000, 5, 2)
z <- (x- mean(x))/sd(x)
hist(x, freq = FALSE)
hist(z, freq = FALSE)Padronização
Padronizar os dados não muda sua forma, somente sua escala.
## No R:
x <- rnorm(5000, 5, 2)
z <- (x- mean(x))/sd(x)
hist(x, freq = FALSE)
hist(z, freq = FALSE)Normal
MODELO NORMAL: muito comum e o mais importante em toda a estatística. Chamado também de modelo Gaussiano.
X \sim Normal(\mu,\sigma^2) \hspace{0.3cm} \Longrightarrow \hspace{0.3cm} f(k) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-1}{2\sigma^2}(k-\mu)^2}\textrm{ , } -\infty < k < \infty.
Normal
PROPRIEDADES
- E(X) =
- V(X) =
\mu
\sigma^2
Seja X uma v.a com distribuição
N(\mu_x, \sigma_x^2)
X + Y \sim N(\mu_x + \mu_y, \sigma_x^2 + \sigma_y^2)
e Y uma v.a com
distribuição
N(\mu_y, \sigma_y^2)
\bar{X} \sim N(\mu, \sigma^2/n)
Normal Padrão
Chamamos de normal padrão a distribuição normal que tem média 0 e desvio padrão 1.
# Normal padrão
curve(dnorm(x, 0, 1), lwd =2, xlim=c(-4,4),
ylab = "f(x)",xlab = "x" )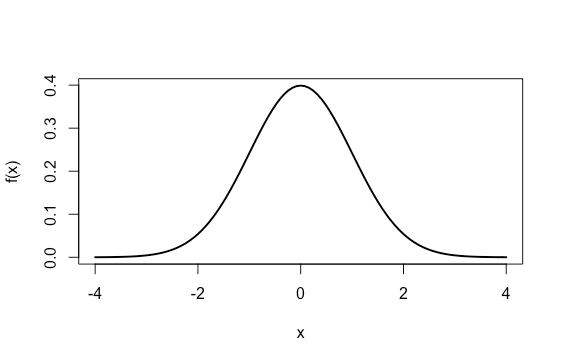
Normal Padrão
- A área da curva entre -1 e 1 é de aproximadamente 68%;
- A área da curva entre -2 e 2 é de aproximadamente 95%;
- A área da curva entre -3 e 3 é de aproximadamente 99%;
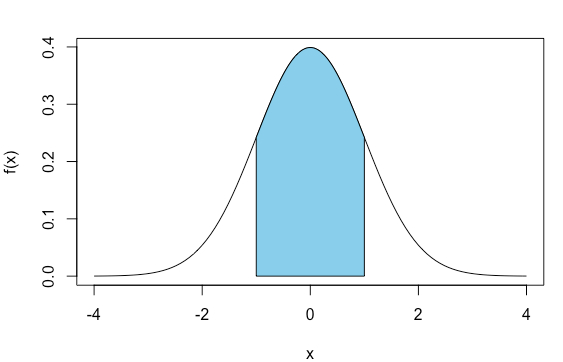
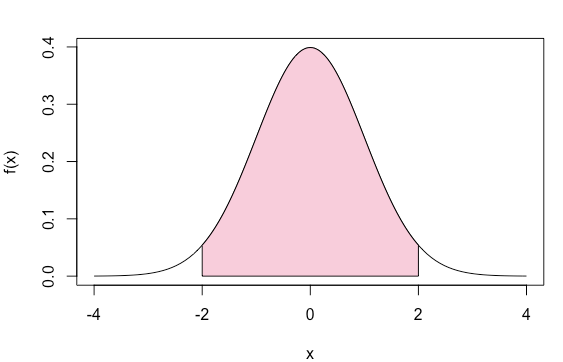
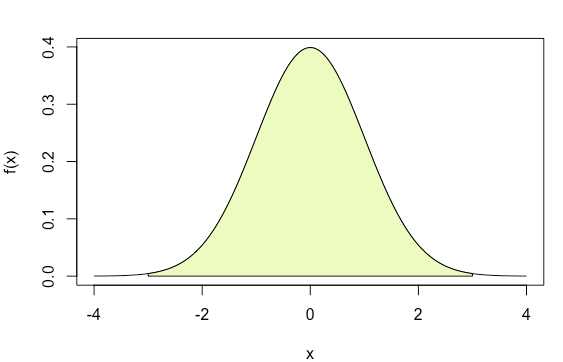
Tabela Normal
Aproximação Normal
Suponha que a altura de um grupo de crianças tenha em média 1.2m e desvio padrão 0.3m.
- Qual a probabilidade de uma criança selecionada ao acaso ter entre 1m e 1.5m?
1.0m
1.5m
Média: 1.2m SD: 0.3m
1.0m
1.5m
Média: 1.2m SD: 0.3m
1.2m
Aproximação Normal
1.0m
1.5m
Média: 1.2m SD: 0.3m
1.2m
Padronizando: z = (1-1.2)/0.3 = - 0.66
Padronizando: z = (1.5-1.2)/0.3 = 1
Aproximação Normal
1.0m
1.5m
Média: 1.2m SD: 0.3m
1.2m
Padronizando: z = (1-1.2)/0.3 = - 0.66
Padronizando: z = (1.5-1.2)/0.3 = 1
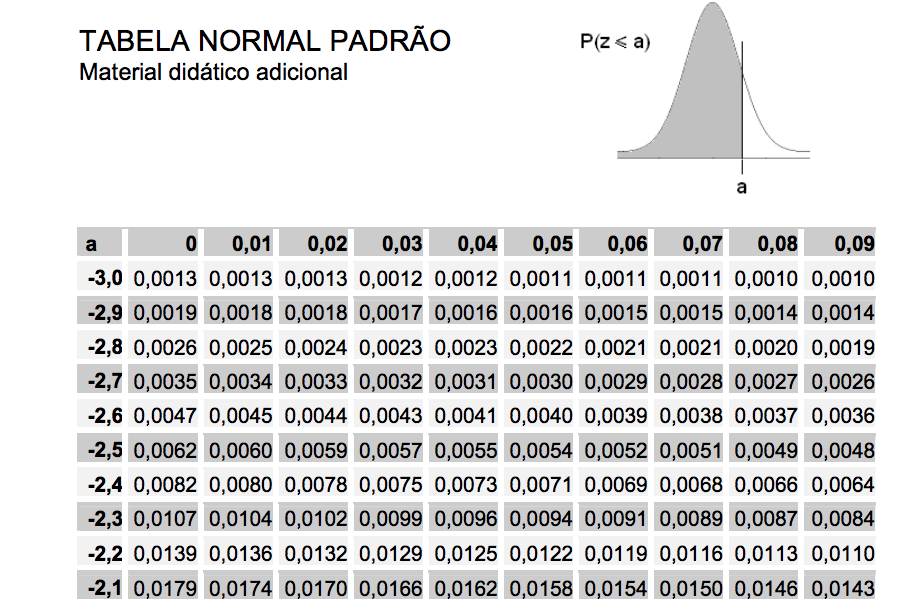
Olhe na tabela!!
Aproximação Normal
P(Z < 1) - P(Z < -0.66) =
= 0.8413 - 0.2546 =
= 0.5867
Aproximação Normal
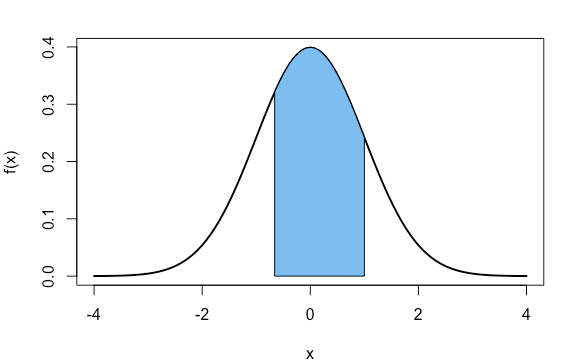
# Exercício tabela normal -----
# Suponha que a altura de um grupo de crianças tenha em média 1.2m e desvio padrão 0.3m.
# Qual a probabilidade de uma criança selecionada ao acaso ter entre 1m e 1.5m?
lower.x <- -0.66
upper.x <- 1
step <- (upper.x - lower.x) / 100
sigma <- 1
mu <- 0
bounds <- c(mu-4*sigma, mu+4*sigma)
cord.x <- c(lower.x,seq(lower.x,upper.x,step),upper.x)
cord.y <- c(0,dnorm(seq(lower.x,upper.x,step),mu,sigma),0)
curve(dnorm(x,mu,sigma),xlim=bounds,
ylab = "f(x)",xlab = "x", lwd = 2 )
polygon(cord.x,cord.y,col='#7bbcf2')
pnorm(1,0,1) - pnorm(-0.66,0,1)
Aproximação Normal
QQ plot
Utilizado para checar se uma determinada distribuição de frequências se adequa a uma determinada distribuição de probabilidades
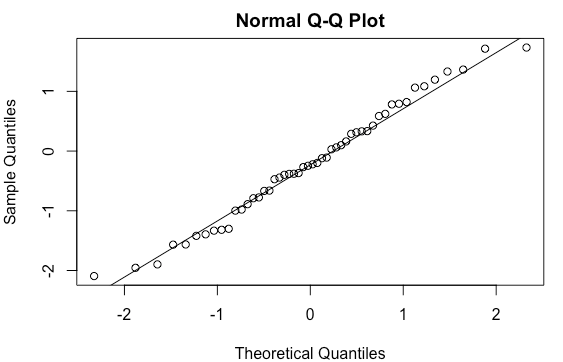
Teorema Central do Limite na prática
Segundo o TCL, quando o tamanho da amostra é suficientemente grande, a distribuição da soma é uma distribuição aproximadamente normal.
Isso indica que a distribuição da média também é normal.
## No R:
p <- 0.2
N.repeticoes <- 10000
N.amostra <- 1000
X.barra <- replicate(N.repeticoes, {
X <- sample(c(0,1), size=N.amostra, replace=TRUE, prob=c(1-p, p))
mean(X)
})
hist(X.barra, freq = FALSE, breaks = 10)
qqnorm(X.barra)
qqline(X.barra)
Infnet - Aula 6
By Raíra Marotta
