ELEMENTARY,
MY DEAR WATSON

PART II

 

AKA: SDRI seventh meetup

SEPTEMBER 2016

Software Defined Radio Israel

WHAT IS

THE CONNECTION BETWEEN 

ALICE

AND

OPTIMUS PRIME?

THE FANTASTIC STORY

OF

COMPLEX NUMBERS

NEXT TIME...

FOURIER

AND

OTHER TRANSFORMATIONS

IT ALL BEGINS WITH SERIES'

\sum _{ n=0 }^{ \infty }{ { a }_{ n }={ a }_{ 1 }+{ a }_{ 2 }+{ a }_{ 3 }+{ a }_{ 4 }... }
∑n=0∞an=a1+a2+a3+a4...\sum _{ n=0 }^{ \infty }{ { a }_{ n }={ a }_{ 1 }+{ a }_{ 2 }+{ a }_{ 3 }+{ a }_{ 4 }... }
\sum _{ n=0 }^{ \infty }{ { f }_{ n }\left( x \right) ={ f }_{ 1 }\left( x \right) +{ f }_{ 2 }\left( x \right) +{ f }_{ 3 }\left( x \right) +{ f }_{ 4 }\left( x \right) +... }
∑n=0∞fn(x)=f1(x)+f2(x)+f3(x)+f4(x)+...\sum _{ n=0 }^{ \infty }{ { f }_{ n }\left( x \right) ={ f }_{ 1 }\left( x \right) +{ f }_{ 2 }\left( x \right) +{ f }_{ 3 }\left( x \right) +{ f }_{ 4 }\left( x \right) +... }

OUR MOTIVATION:

DESCRIBE A FUNCTION WITH...OTHER FUNCTIONS

AND

BECOME...

(AND THE OTHER WAY AROUND)

FOR

EXAMPLE:

all kinds of series'

  • Geometric series

 

  • Taylor series

 

  • Laurent series

 

And more...

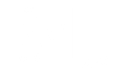
\sum_{n=0}^\infty \frac{ \, x^n}{n!}
∑n=0∞xnn!\sum_{n=0}^\infty \frac{ \, x^n}{n!}
\sum _{ n=-\infty }^{ \infty }{ { { a }_{ n }x }^{ n } }
∑n=−∞∞anxn\sum _{ n=-\infty }^{ \infty }{ { { a }_{ n }x }^{ n } }

FOURIER SERIES

SERIES THAT IS COMBINED FROM SINES AND COSINES

{ s }_{ N }\left( x \right) =\frac { { a }_{ 0 } }{ 2 } +\sum _{ n=1 }^{ N }{ \left[ { a }_{ n }\cos { \left( \frac { 2\pi nx }{ P } \right) + } { b }_{ n }\sin { \left( \frac { 2\pi nx }{ P } \right) } \right] }
sN(x)=a02+∑n=1N[ancos(2πnxP)+bnsin(2πnxP)]{ s }_{ N }\left( x \right) =\frac { { a }_{ 0 } }{ 2 } +\sum _{ n=1 }^{ N }{ \left[ { a }_{ n }\cos { \left( \frac { 2\pi nx }{ P } \right) + } { b }_{ n }\sin { \left( \frac { 2\pi nx }{ P } \right) } \right] }

A BASIC EXAMPLE:

{ s }_{ }\left( x \right) =1+3\cos { \left( x \right) }
s(x)=1+3cos(x){ s }_{ }\left( x \right) =1+3\cos { \left( x \right) }
{ a }_{ 0 }=2,\quad { a }_{ 1 }=3,\quad { a }_{ n>1 },b_{ n>0 }=0
a0=2,a1=3,an>1,bn>0=0{ a }_{ 0 }=2,\quad { a }_{ 1 }=3,\quad { a }_{ n>1 },b_{ n>0 }=0
P(period)=2\pi
P(period)=2πP(period)=2\pi

HOW DOES A SQUARE WAVE LOOKS LIKE?

FOURIER TRANSFORM

  • FOURIER SERIES COEFFICIENTS REPRESENT THE "ENERGY" OF THEIR CORRESPONDING "FREQUENCY"
  • THE COMBINATION OF ALL THE COEFFICIENTS IS THE "SPECTRAL CONTENT" OF THE ORIGINAL FUNCTION (OR SIGNAL)
  • THE PROCESS OF FINDING THE COEFFICIENTS IS CALLED "FOURIER TRANSFORM"

HOW TO PERFORM A FOURIER TRANSFORM? 

SIGNALS IN NATURE ARE CONTINUOUS IN TIME AND VALUE, AND THEREFORE WE DEFINE THE CONTINUOUS FOURIER TRANSFORM - CFT:

\Im \left\{ h\left( x \right) \right\} \left( f \right) =\int _{ -\infty }^{ \infty }{ h\left( x \right) { e }^{ -2\pi jxf }dx }
ℑ{h(x)}(f)=∫−∞∞h(x)e−2πjxfdx\Im \left\{ h\left( x \right) \right\} \left( f \right) =\int _{ -\infty }^{ \infty }{ h\left( x \right) { e }^{ -2\pi jxf }dx }
j=\sqrt { -1 }
j=−1j=\sqrt { -1 }

BUT IN THE REAL WORLD...

- SIGNALS ARE NOT REALLY CONTINUOUS, BUT RATHER A VECTOR OF VALUES ( = DISCRETE TIME) WHICH ARE FROM A FINITE SET OF VALUES (SAY, A BYTE SIZE)

 

- THEREFORE, THE FOURIER TRANSFORM SHOULD BE ABLE TO HANDLE  THOSE SIGNALS TOO. HENCE: DISCRETE FOURIER TRANSFORM - DFT

X_{ k }=\sum _{ n=0 }^{ N-1 }{ x_{ n }\left[ \cos { \left( -\frac { 2\pi nk }{ N } \right) + } j\sin { \left( -\frac { 2\pi nk }{ N } \right) } \right] }
Xk=∑n=0N−1xn[cos(−2πnkN)+jsin(−2πnkN)]X_{ k }=\sum _{ n=0 }^{ N-1 }{ x_{ n }\left[ \cos { \left( -\frac { 2\pi nk }{ N } \right) + } j\sin { \left( -\frac { 2\pi nk }{ N } \right) } \right] }

DFT vs. FFT

  • DFT is very easy to understand, however it takes time to  evaluate
  • FFT (Fast Fourier Transform) is an algorithm that can evaluate DFT very fast - given that the vector size is a power of 2

dspguide.com

common transforms

things we didn't talk about

but are very important

REAL LIFE ARE COMPLEX

THERE (SOME) MORE MATH INTO IT

Elementary, My dear Watson. Part 2

By raziele

Made with Slides.com

Elementary, My dear Watson. Part 2

SDRI sixth meetup

  • 1,113

More from raziele