Qualifying Exam
Rebecca Barter
advised by
Jas Sekhon and Bin Yu
May 15, 2018
Projects I'm going to talk about
The fundamental problem of transplantation
Current approaches to increasing supply
Live donor chains
Blum et al. (2015, 2016): Finding the optimal chain using stochastic matching on a graph
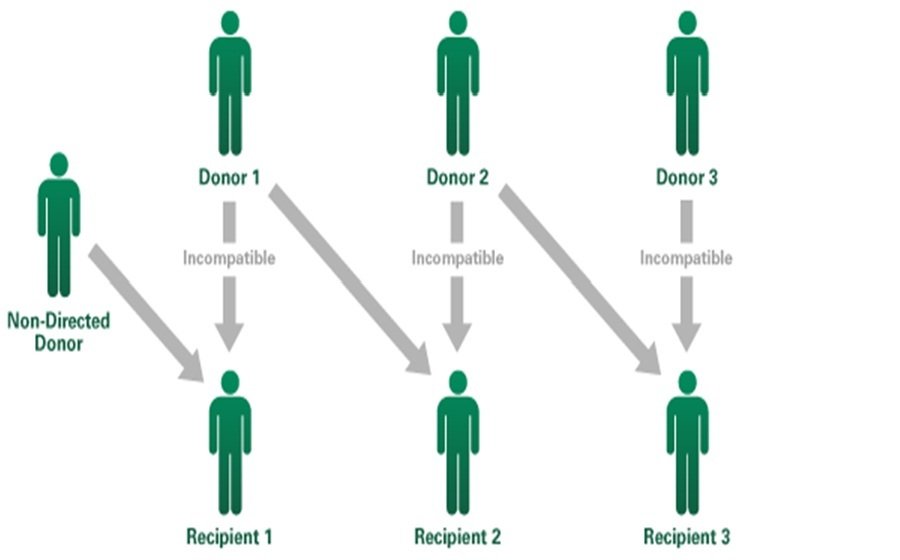
Rees et al. (2009): A Nonsimultaneous, Extended, Altruistic-Donor Chain
Roth et al. (2009): Kidney exchange
Increasing rates of deceased organ donation
Organs from other sources
Shepherd et al. (2014): International comparisons between opt-in vs opt-out systems
Rithalia et al. (2009): The impact of presumed consent
Pierson et al. (2009)
The current status of xenotransplantation
Atala et al. (2009) synthetic organ (bladder) transplantation
Given that there is a shortage of supply...
Our focus is on how to allocate the livers available from deceased donors
Rethinking
deceased donor liver allocation
in the US
Every month over
700
people are added to the liver tx waitlist
In that same month, only
450
people will receive a liver transplant
117,000
people have been listed since 2002
64,000
people have received a liver transplant since 2002
Of those listed since 2002:
21,000
died waiting for a liver
became too sick
got better
15,000
8,000
4,000
living donor
Livers are a precious resource
How should transplant organizations decide how to allocate livers for transplant?
Many possible allocation metrics:
- waited longest
- shortest survival w/out transplant
- longest survival with transplant
-
benefit the most from transplant
- quality of life
- survival
Keller et al. (2014), Ethical considerations surrounding survival benefit-based liver allocation
Freeman et al. (2014) Who should get a liver graft?
Sickest first: the MELD score
(Model for End-Stage Liver Disease)
- Originally designed to predict 3-month transplant-free survival in transjugular intrahepatic portosystemic shunt (TIPS) patients (Malinchoc et al, 2000)
- Later deemed useful for estimating prognosis for chronic liver disease (Kamath et al., 2001, 2007)
- Adopted by UNOS for liver allocation in 2002
This study was based on 231 patients at 4 US medical centers and validated on 71 patients from the Netherlands
MELD = 10 \times \Big[ 0.957 \log(\textbf{creatinine}) + 0.378 \log (\textbf{bilirubin}) + 1.12 \log (\textbf{INR})\Big] + 6.43
The donor liver is given to the person on the waitlist with the highest MELD score
Defining a waitlist:
Blood type and Geography
Image source: https://unos.org/transplantation/matching-organs/regions/
Image source: https://sites.google.com/site/esrdandkidneytranpslant/
MELD and transplant-free survival
*Data from a single OPO in CA with 3,500 patients and where 85% are transplant-free at 3 months
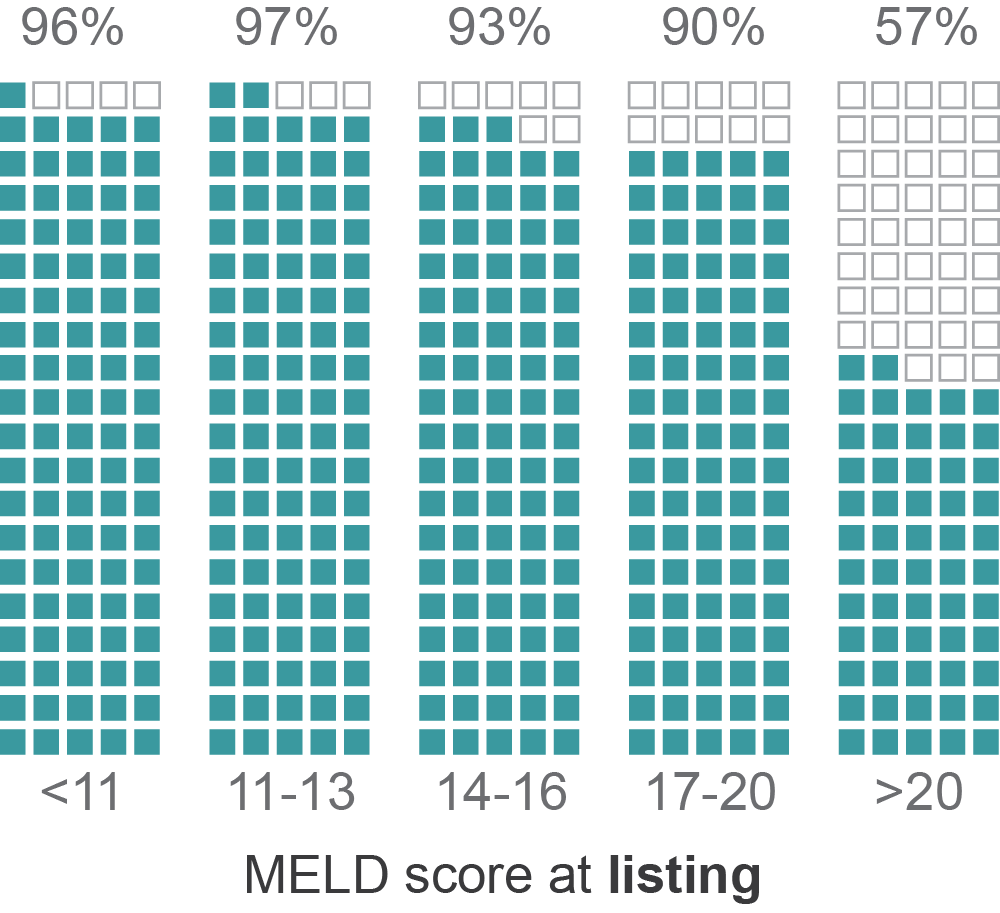
Percent alive at 3 months
(transplant-free)
Criticisms of MELD in the literature
MELD is a poor predictor of post-transplant survival
The current weighting (of INR, bilirubin and creatinine) may not be optimal
MELD should include serum albumin
Meyers et al. (2013), Revision of MELD to include serum albumin improves prediction of mortality on the liver transplant waiting list
Sharma et al. (2008), Re-weighting the model for end stage liver disease score components
Patients with the highest MELD are those with the worst post-transplant outcomes
Klein et al. (2013), Predicting Survival after Liver Transplantation Based on Pre-Transplant MELD Score: a Systematic Review of the Literature
Siparsky et al. (2014), Organ allocation in liver transplantation
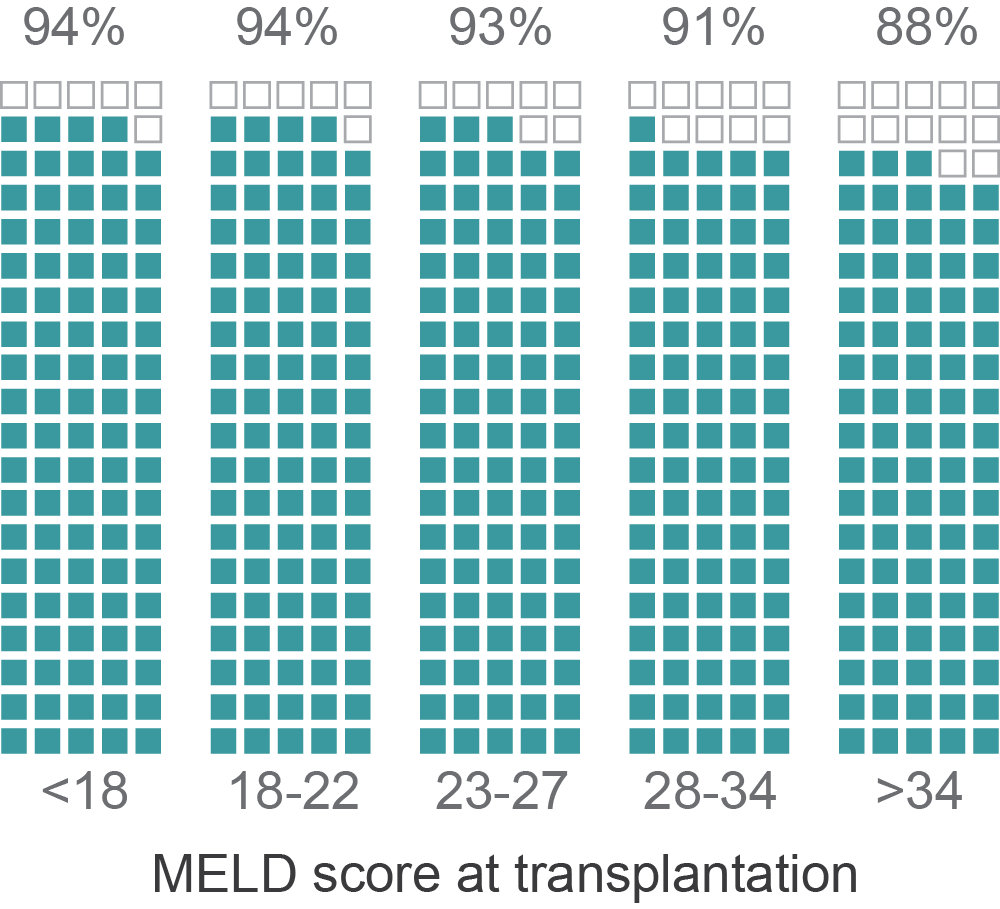
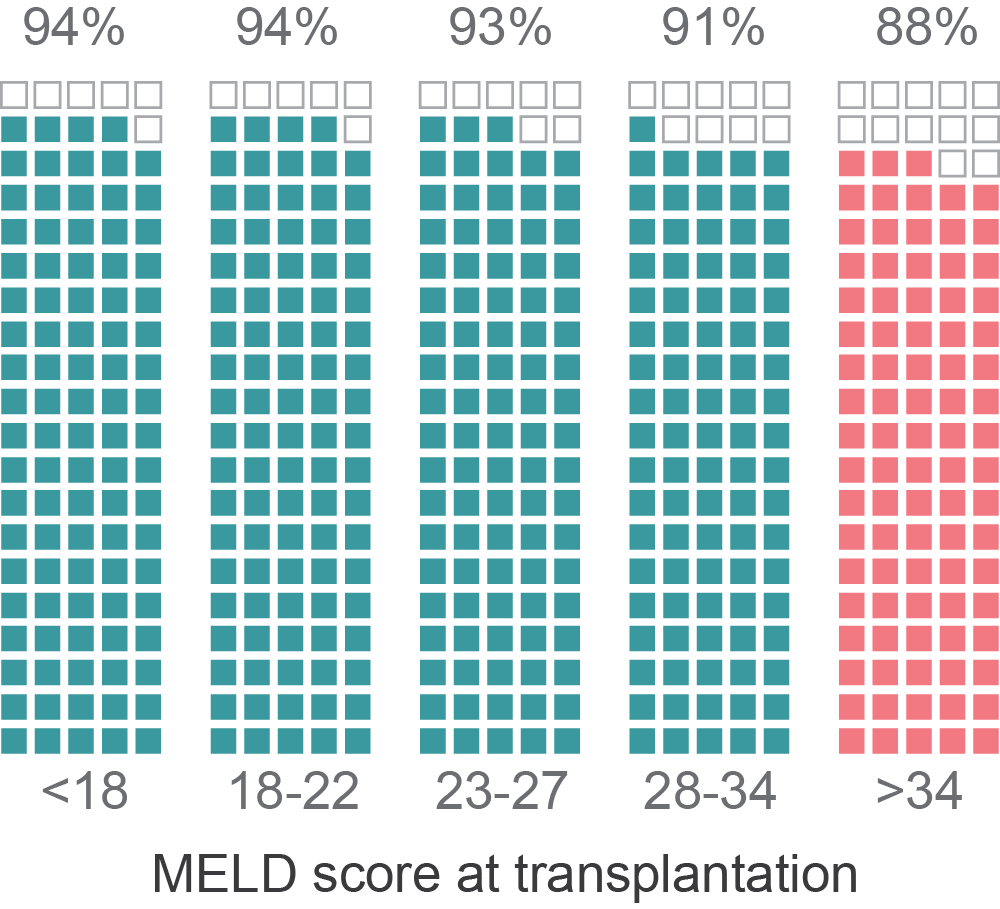
Percent alive at 6 months (post-transplant)
Percent alive at 6 months (post-transplant)
transplantation
transplantation
Estimating transplant benefit
Defining transplant benefit
benefit
survival with a transplant
survival without
a transplant
Fundamental problem of causal inference:
We can only observe one!!!
Existing approaches to estimating benefit
Control outcome
(censored)
Treated
outcome
11/01/2003
11/01/2003
Control outcome
(observed)
Merion et al. (2005)
Shaubel et al. (2009)
Difference between 5-yr predicted survival for two Cox models
Single Cox model with transplant indicator
Deals with censoring using inverse probability of censoring weighting (Robins and Finkelstein, 2000)
Do not address bias from censoring
Informative censoring:
Earlier censoring = higher and/or more rapidly increasing MELD score
Confounding:
Difference in MELD score between control and treatment
Merion et al. (2005), Shaubel et al. (2009)
Do not address potential confounding
Do not address potential confounding
The data isn't really designed to compare transplanted versus untransplanted...
Transplanted
first
Transplanted
last
With the UNOS data, we are far from a random experiment:
Sickest
Healthiest
Our approach: redefining transplant benefit
Redefining our causal effect
Consider the causal effect on survival of
increasing wait time to transplantation
(i.e. receiving a transplant now vs later)
In 2 weeks
In one year
In 2 months
4 yrs
3.5 yrs
3 yrs
What is t = 0?
A specific MELD score, e.g. first time MELD is 18
Redefining our causal effect
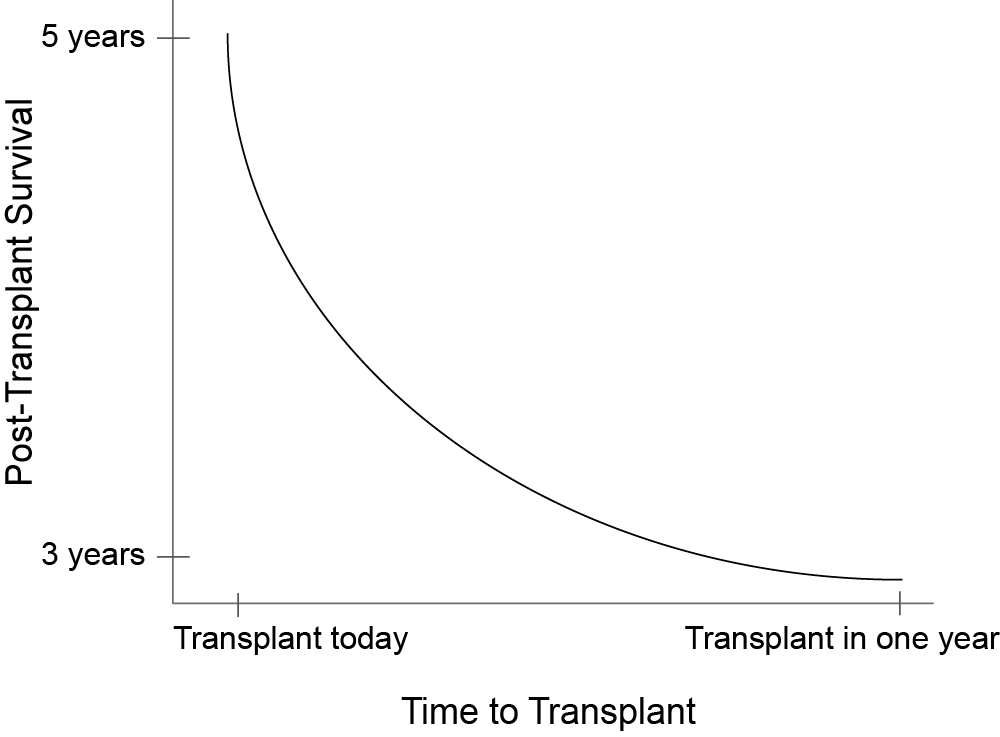
If we could observe the outcome of all possible wait times for an individual...
Unfortunately we only observe one point on the individual's curve
Maybe we can populate the curve with observations with other similar patients
The problem is that patients with a shorter wait time tend to be sicker...
Sickness is a confounder!
Can we find features of the data that allow us to do comparisons across wait times that are "as if random"?
Exploiting randomness in the data
Two sources of randomness in wait times
Wait time differs by blood type
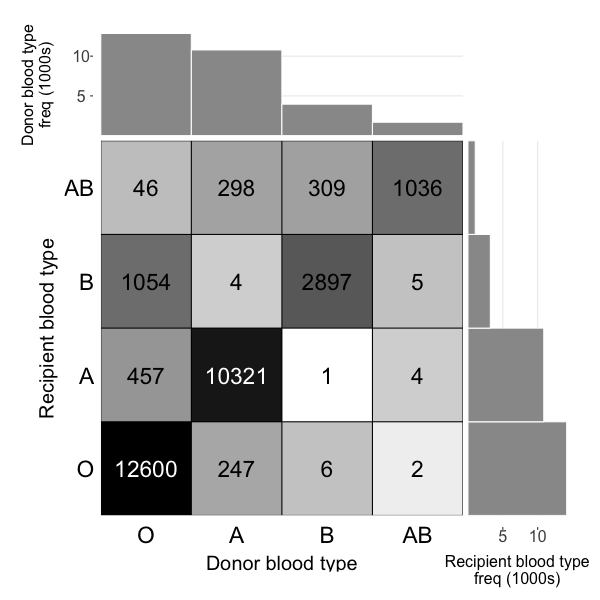
Wait time differs by blood type
(Universal donor)
(Universal recipient)
A quick foray into instrumental variables
Instrumental Variables
\textrm{dead in 1yr}_i = \beta_0 + \beta_1 \textrm{(tx in 1mo)}_i + ~~...~~ + \epsilon_i
terms we can control for
terms we can't control for
(e.g. future MELD)
Correlated
AB
O
AB is 23% more likely than O to be transplanted in 1 month
AB is 7% less likely than O to die within 1 year
Causal effect of tx in 1mo on death in 1yr:
\frac{\textrm{Effect of AB on death in 1yr}}{\textrm{Effect of AB on tx in 1mo}} = \frac{-0.07}{0.23} = -0.30
Exclusion restriction!
Imbens & Angrist (1994), Identification and estimation of local average treatment effects
Exclusion restriction
The instrument affects the outcome only through the treatment
- Blood type B is correlated with higher life expectancy (Shimizu et al (2004))
- Blood type B is correlated with lower life expectancy (Brecher et al. (2015))
- No correlation between blood type and life expectancy (Vasto (2011))
Research on link between blood type and race:
Research on link between life expectancy and race:
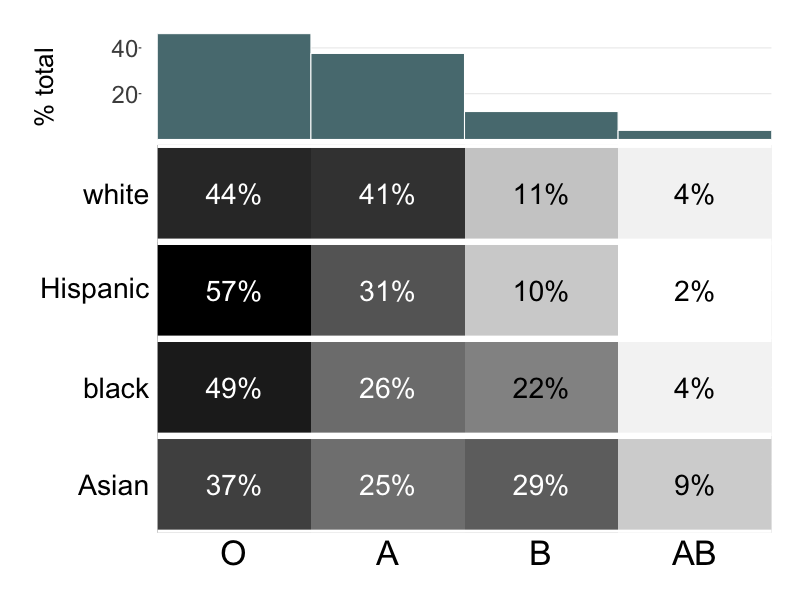
This matches what the literature says...
O'Neil (2001), Modern Human Variation: Distribution of Blood Types
Research on direct link between blood type and life expectancy:
Lots of literature showing a correlation between race and life expectancy
- Thielke et al. (2015) Sex, Race, and Age Differences in Observed Years of Life, Healthy Life, and Able Life among Older Adults in The Cardiovascular Health Study
- Cantu et al. (2014) New estimates of racial/ethnic differences in life expectancy with chronic morbidity and functional loss: evidence from the National Health Interview Survey
Other assumptions
Relevance of instrument
Monotonicity
SUTVA
Exchangeability of instrument
The treatment assignment of an individual has no effect on the potential outcomes of any other individual
The instrument has a nonzero effect on the instrument
The instrument has a monotonic effect on the treatment across the population. I.e. it either always increases or does not change (but never decreases) the probability of treatment
The instrument does not share any common causes with the outcome (possibly after conditioning on observed covariates)
Two-stage least squares
\textrm{dead in 1yr}_i = \alpha + \beta \textrm{(tx in 1mo)}_i + ... + \epsilon_i
Two stage least squares estimation of :
\beta
Stage 1: regress the treatment on the instrument
\textrm{(tx in 1mo)}_i = \gamma_0 + \gamma_1 \textrm{A}_i + \gamma_2 \textrm{B}_i + \gamma_3 \textrm{AB}_i + \gamma_4 \textrm{OPO}_i + \gamma_5 \textrm{ethnicity}_i + \nu_i
instruments
(blood type dummies)
Stage 2: regress the outcome on the predicted treatment
\textrm{(dead in 1yr)}_i = \beta_0 + \beta_1 \textrm{(tx in 1mo)}_i + \beta_2 \textrm{OPO}_i + \beta_3 \textrm{ethnicity}_i + \epsilon_i
predicted treatment
(from first stage)
treatment
outcome
Things get complicated when trying to adapt to survival models
(Terza et al. 2008, Wan et al. (2015), Cai et al. (2011), Tchetgen Tchetgen et al. (2015))
IV as Two-stage least squares
\hat{\beta}_{2SLS} = \frac{Cov(Y, ~\hat{T})}{Var(\hat{T})}
= \frac{Cov(Y, ~\gamma_0 + \gamma_1Z)}{Var(\gamma_0 + \gamma_1 Z)}
=\frac{1}{\gamma_1} \frac{ Cov(Y, Z)}{ Var(Z)}
= \frac{Var(Z)}{Cov(T, Z)} \frac{Cov(Y, Z)}{Var(Z)}
= \frac{Cov(Y, Z)}{Cov(T, Z)}
= \hat{\beta}_{IV}
T_i = \gamma_0 + \gamma_1 Z_i + \nu_i
Y_i = \beta_0 + \beta_{2SLS} \hat{T}_i + \epsilon_i
Y_i = \omega_0 + \omega_1 Z_i + \epsilon_i
\hat{\beta}_{IV} = \frac{\omega_1}{\gamma_1}
2SLS
IV (Wald)
T_i = \gamma_0 + \gamma_1 Z_i + \nu_i
A sequential IV approach
(that doesn't deal with hazard models!)
IV for survival outcomes
Survival models
\textrm{wait time}_i = \gamma_0 + \gamma_1 \textrm{A}_i + \gamma_2 \textrm{B}_i + \gamma_3 \textrm{AB}_i + \gamma_4 \textrm{OPO}_i + \gamma_5 \textrm{ethnicity}_i+ \nu_i
Stage 1: OLS to predict wait time
Tchetgen Tchetgen et al. (2015) Instrumental variable estimation in a survival context
Cox model is non-collapsable:
Use an additive model instead
(estimate the marginal causal effect on hazard of transplantation one week earlier)
Stage 2: Additive hazard model (predictor substitution)
\lambda(t) = \beta_0(t) + \beta_1 \textrm{(wait time)} + \beta_2 \textrm{OPO}_i(t) + \beta_3 \textrm{ethnicity}_i(t) + \epsilon_i(t)
(Alt) Stage 2: Additive hazard model (residual inclusion / control function)
\lambda(t) = \beta_0(t) + \beta_1 \textrm{(wait time)} + \beta_2\Big( \textrm{(wait time) - (wait time)} \Big)
+ \beta_3 \textrm{OPO}_i(t) + \beta_4 \textrm{ethnicity}_i(t) + \epsilon_i(t)
Results show that Predictor Substitution is inconsistent but residual inclusion is consistent.(Terza et al. (2008), Wan et al. (2015), Cai et al. (2011))
Results
Marginal causal effect on hazard of waiting one extra week for a transplant
Residual inclusion estimate:
0.000000867 (-0.000000878, 0.00000325)
Residual inclusion estimate:
0.000000832 (-0.000000137, 0.00000322)
A sequential IV approach
1
2
(MELD 18)
3
4
5
6
7
8
9
Month (t)
A = (0, 0, 1, 1, 1, 1, 1, 1, 1)
Y = (0, 0, 0, 0, 1, 1, 1, 1, 1)
A = (0, 0, 0, 0, 0, 0, 0, 0, 0)
Y = (0, 1, 1, 1, 1, 1, 1, 1, 1)
A = (0, 0, 0, 0, 0, 1, 1, 1, 1)
Y = (0, 0, 0, 0, 0, 0, 0, 0, 0)
A = (0, 0, 0, 0, 0, 0, 0, 0, 0)
Y = (0, 0, 0, 0, 0, 0, 0, 0, 0)
A = (0, 0, 0, 1, 1, 1, 1, 1, 1)
Y = (0, 0, 0, 0, 0, 0, 0, 0, 0)
A = (0, 0, 0, 0, 0, 0, 0, 0, 0)
Y = (0, 0, 0, 0, 0, 0, 0, 0, 0)
2SLS (1)
Y = death by month 1
A = tx by month 1
Z = blood type
0
2SLS (3)
Y = death by month 3
A = tx by month 3
Z = blood type
2SLS (2)
Y = death by month 2
A = tx by month 2
Z = blood type
The effect of receiving a transplant...
The effect on death by 24 months
of
receiving a transplant by 24 months
versus
not having receiving a transplant yet
(\textrm{Death by 24mo})_i = \alpha + \beta (\textrm{tx by 24mo})_i + \epsilon_i
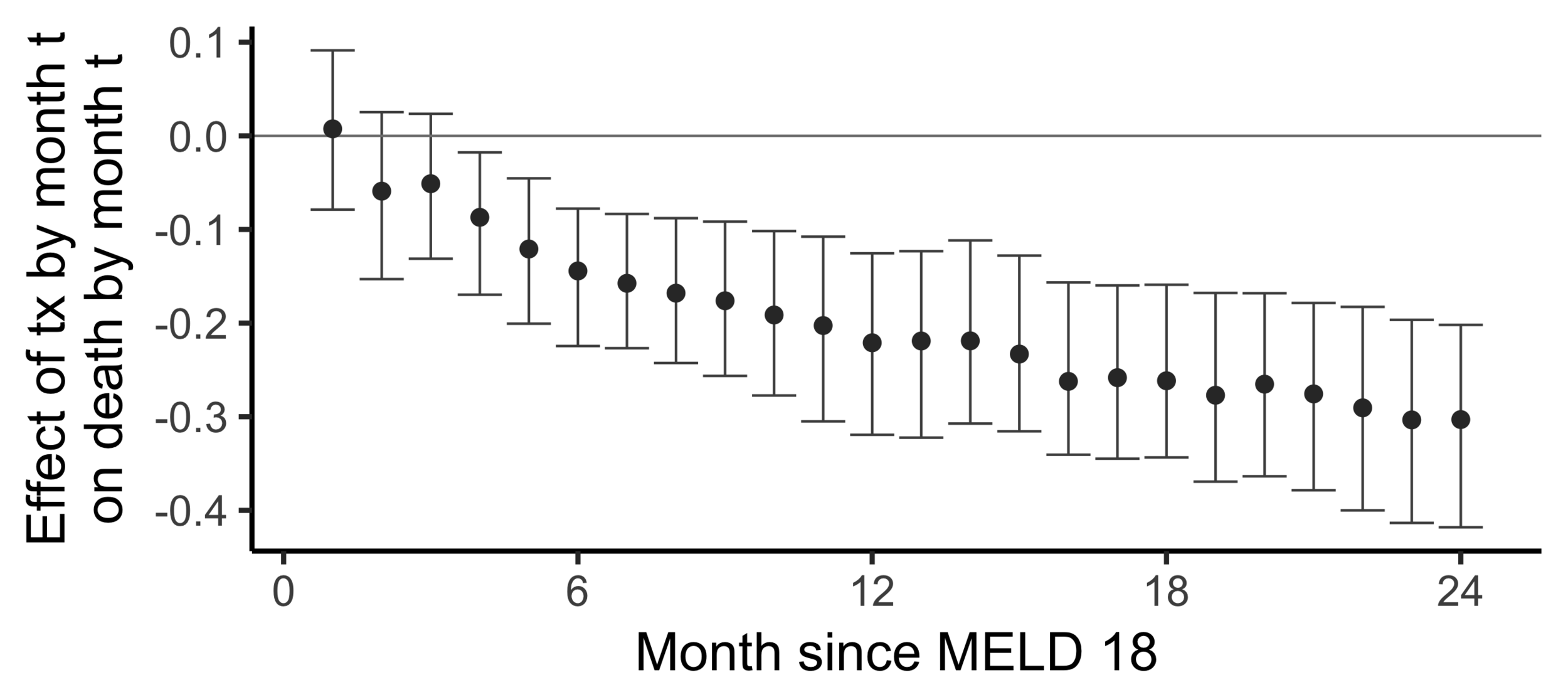
(2SLS estimate)
Subsampling stability
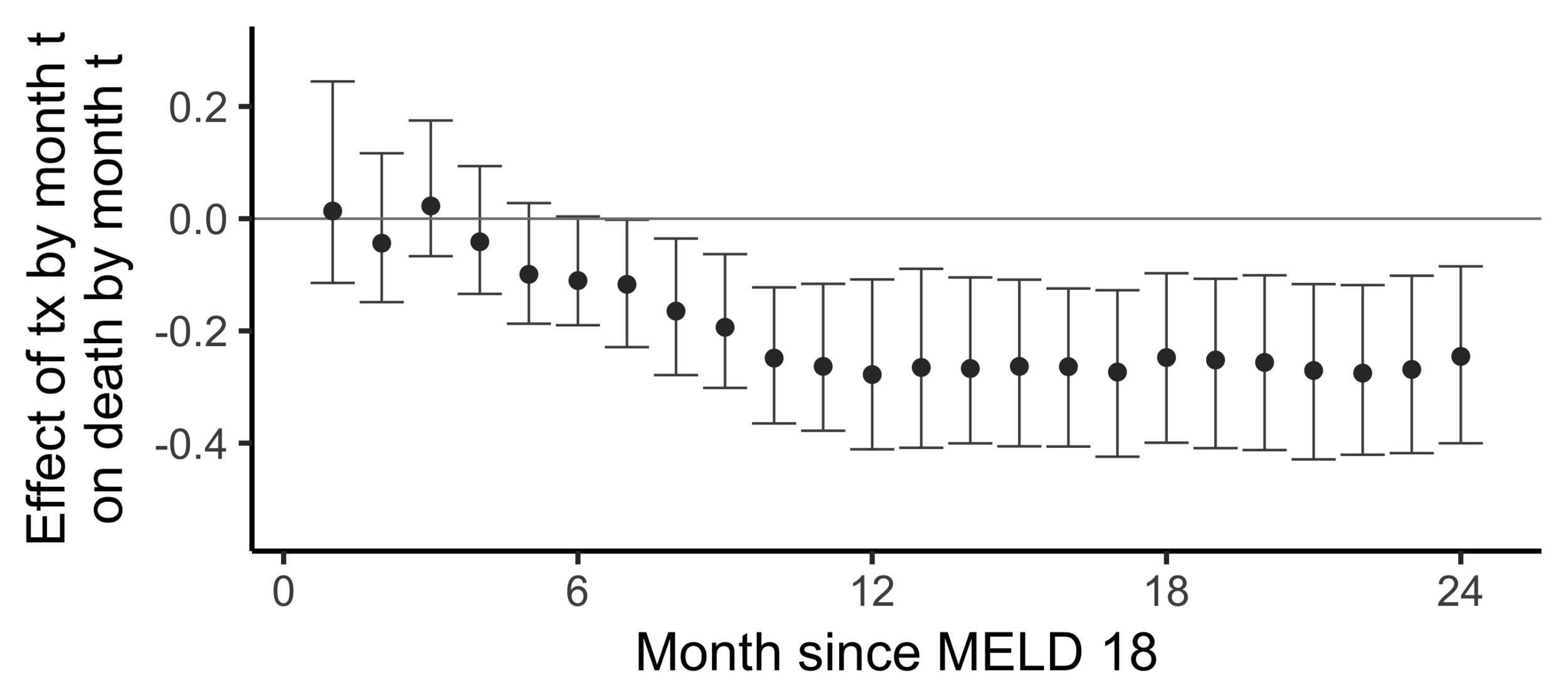
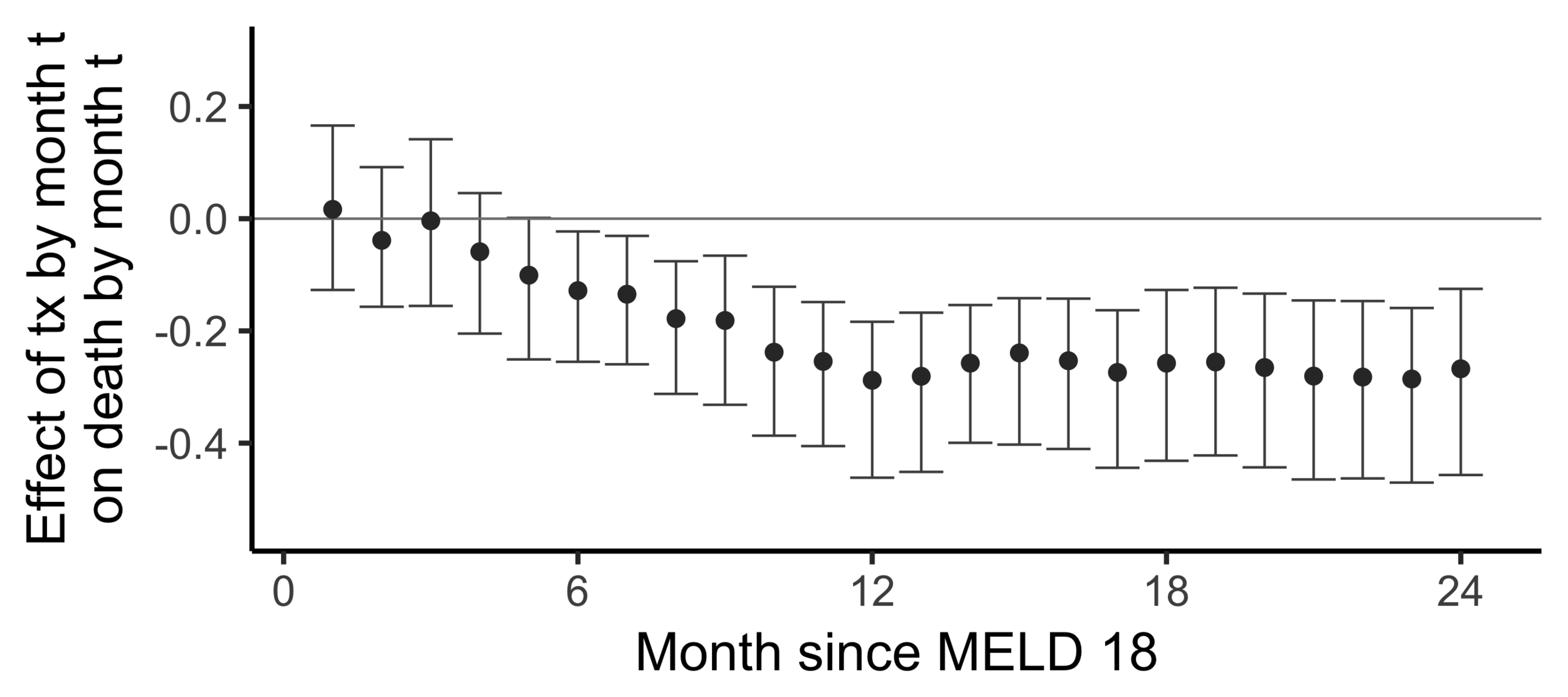
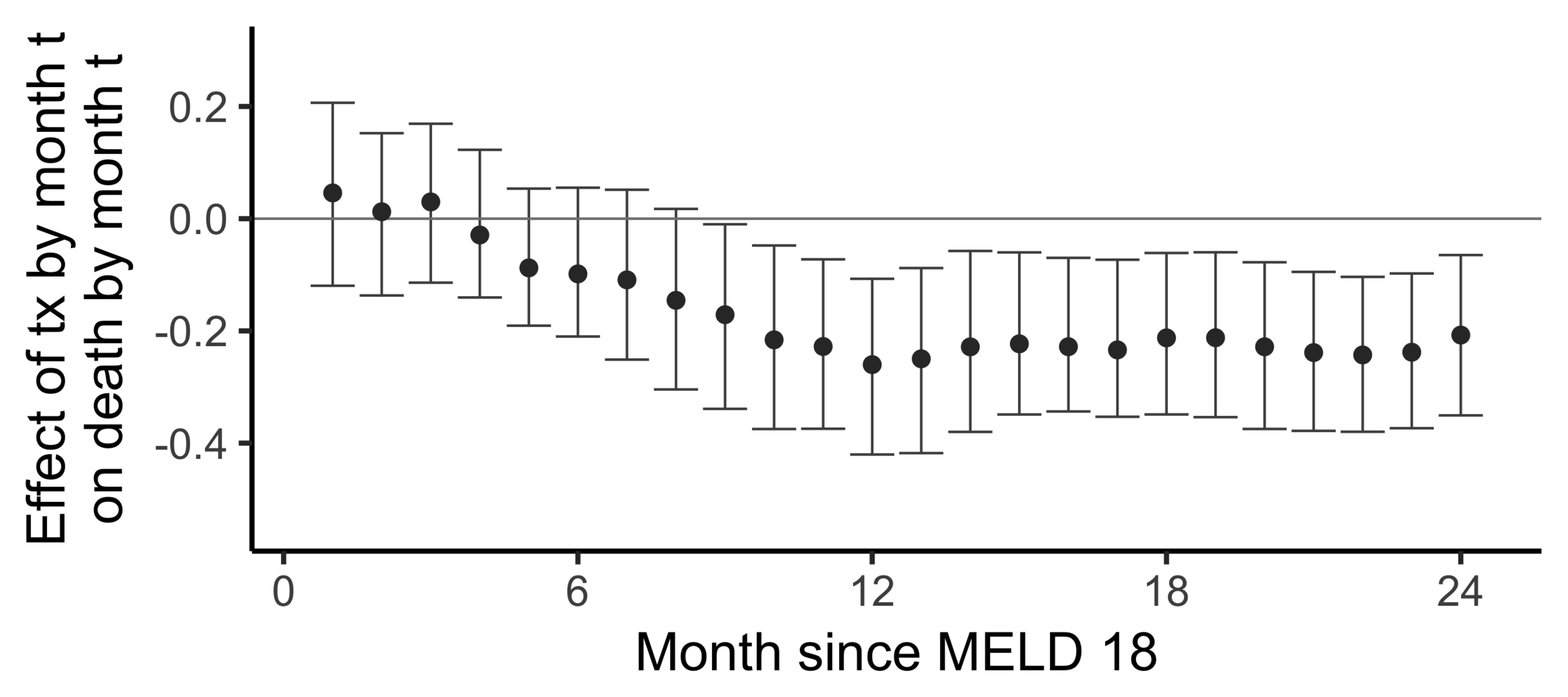
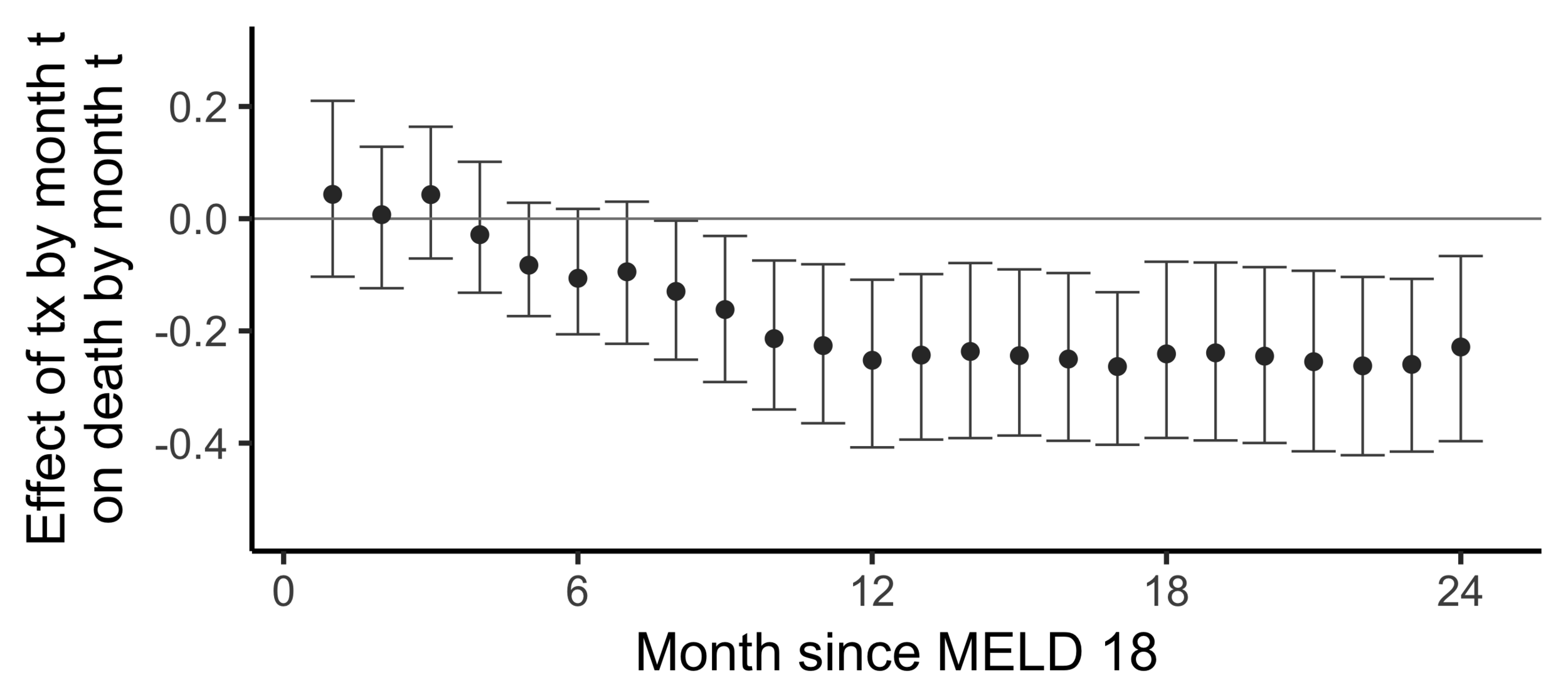
Stability with respect to MELD
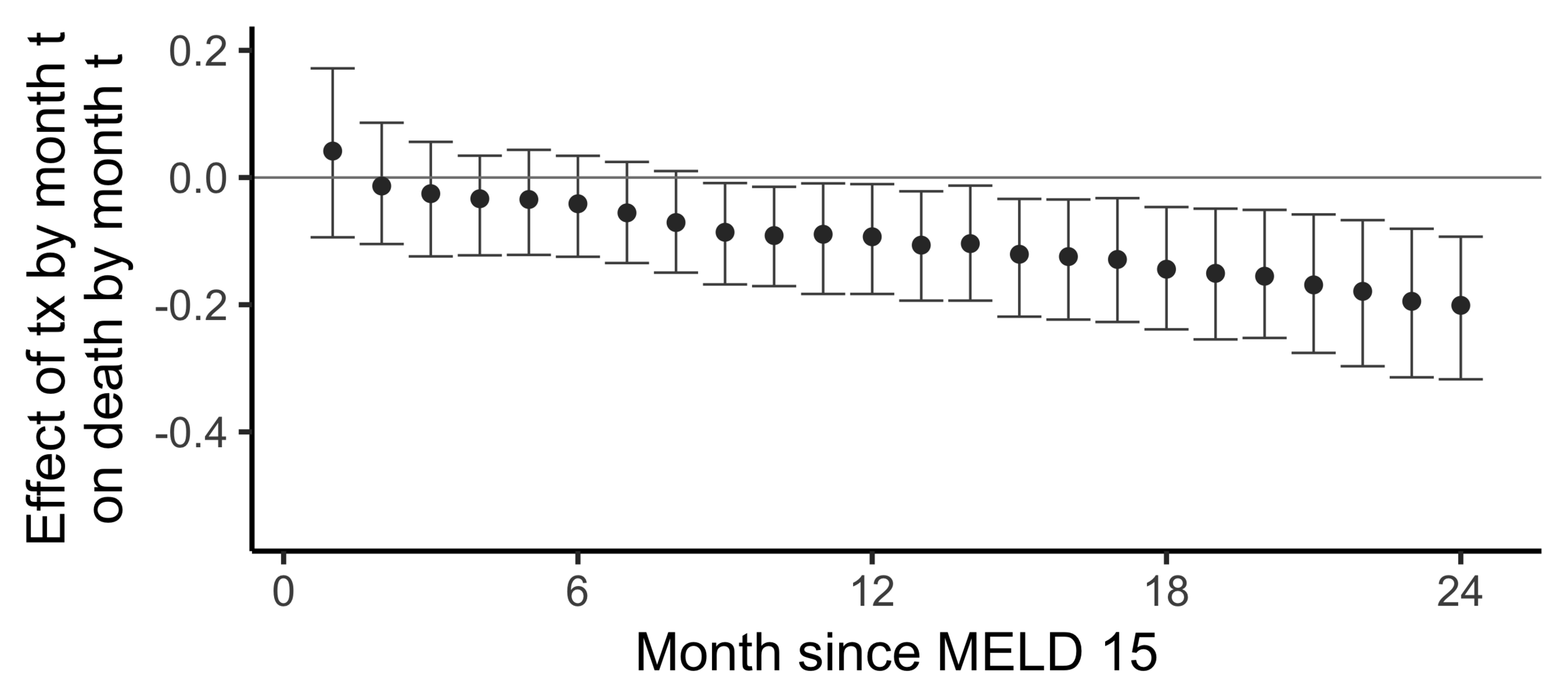
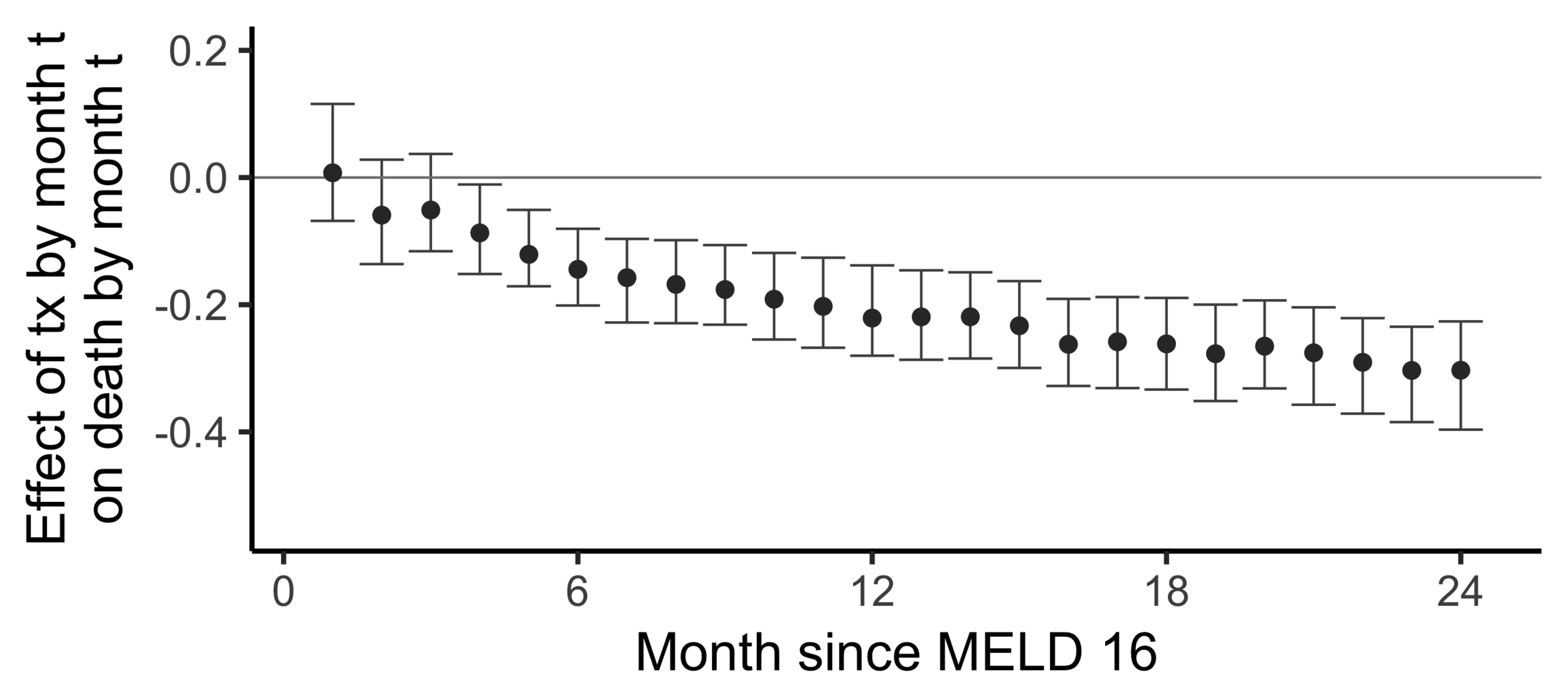
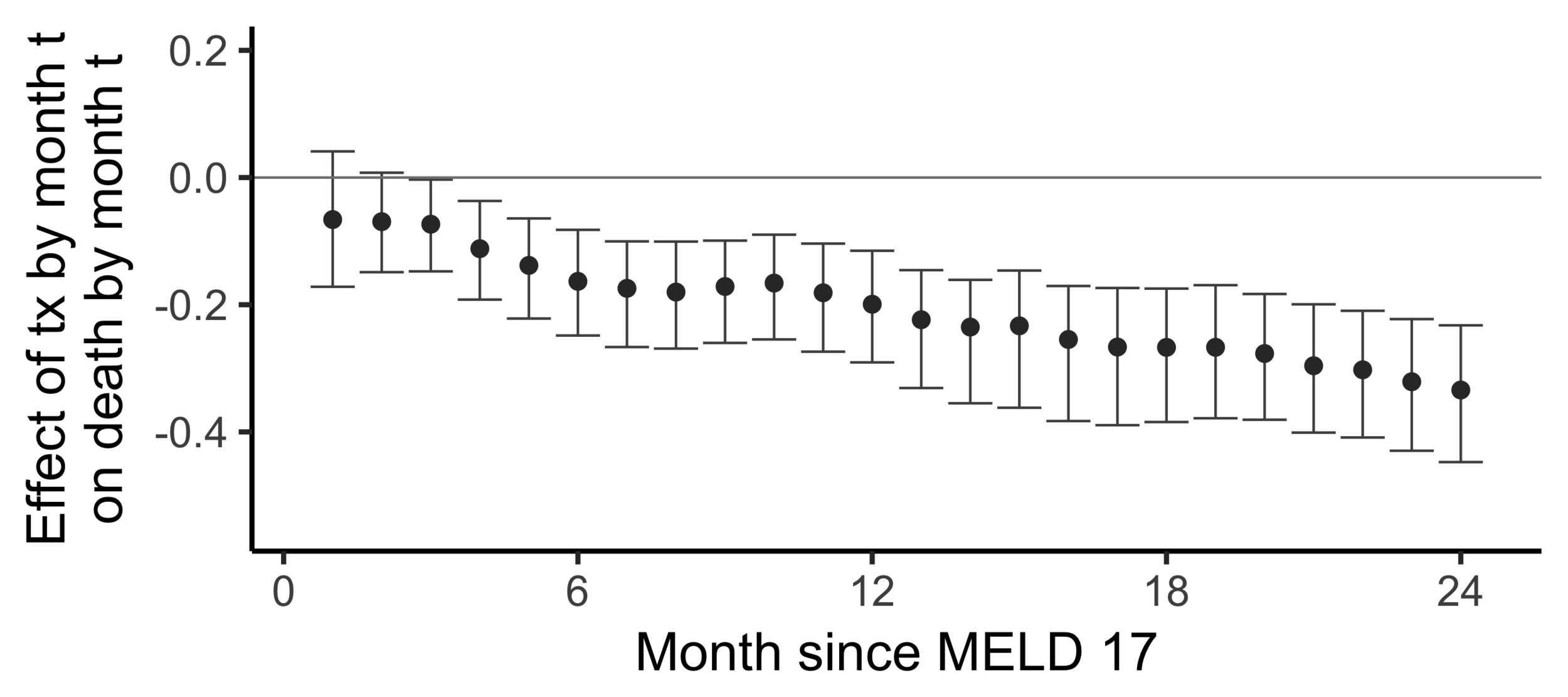
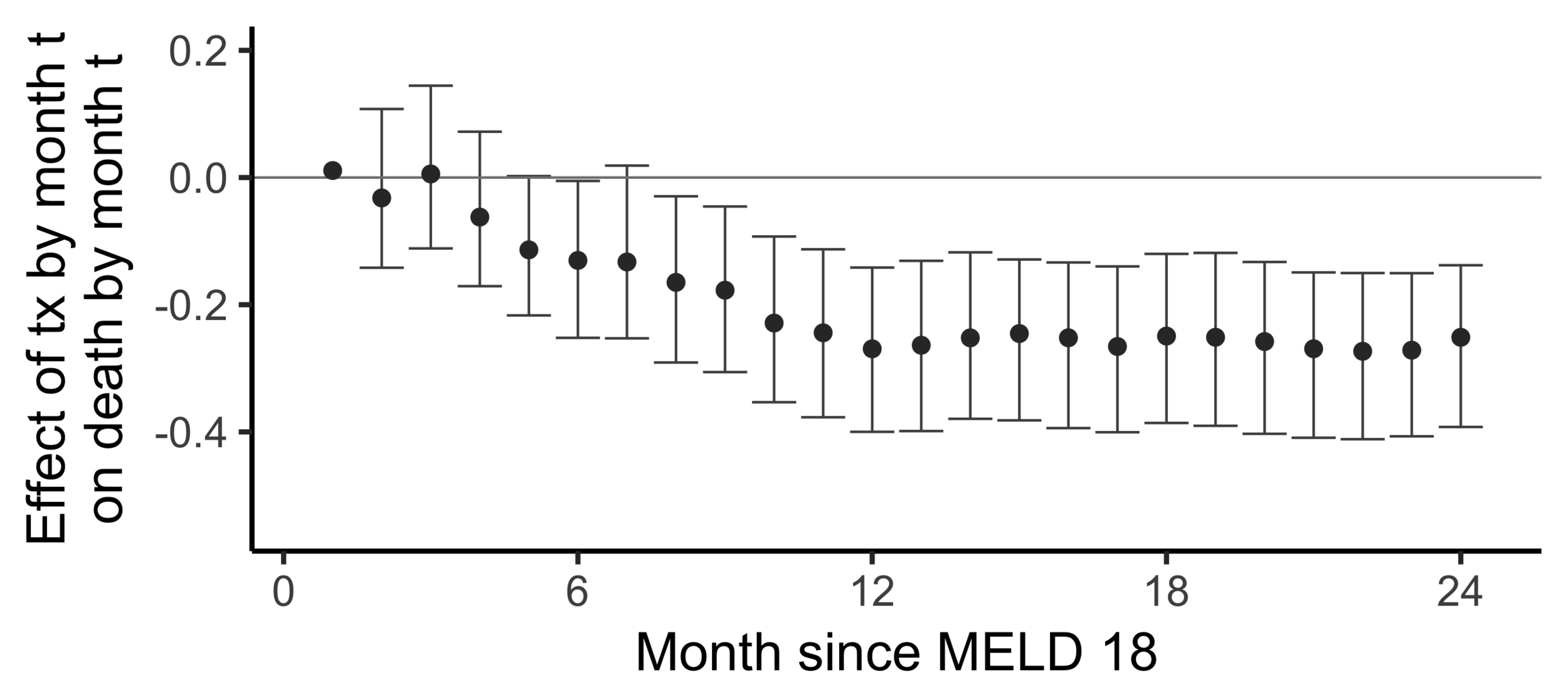
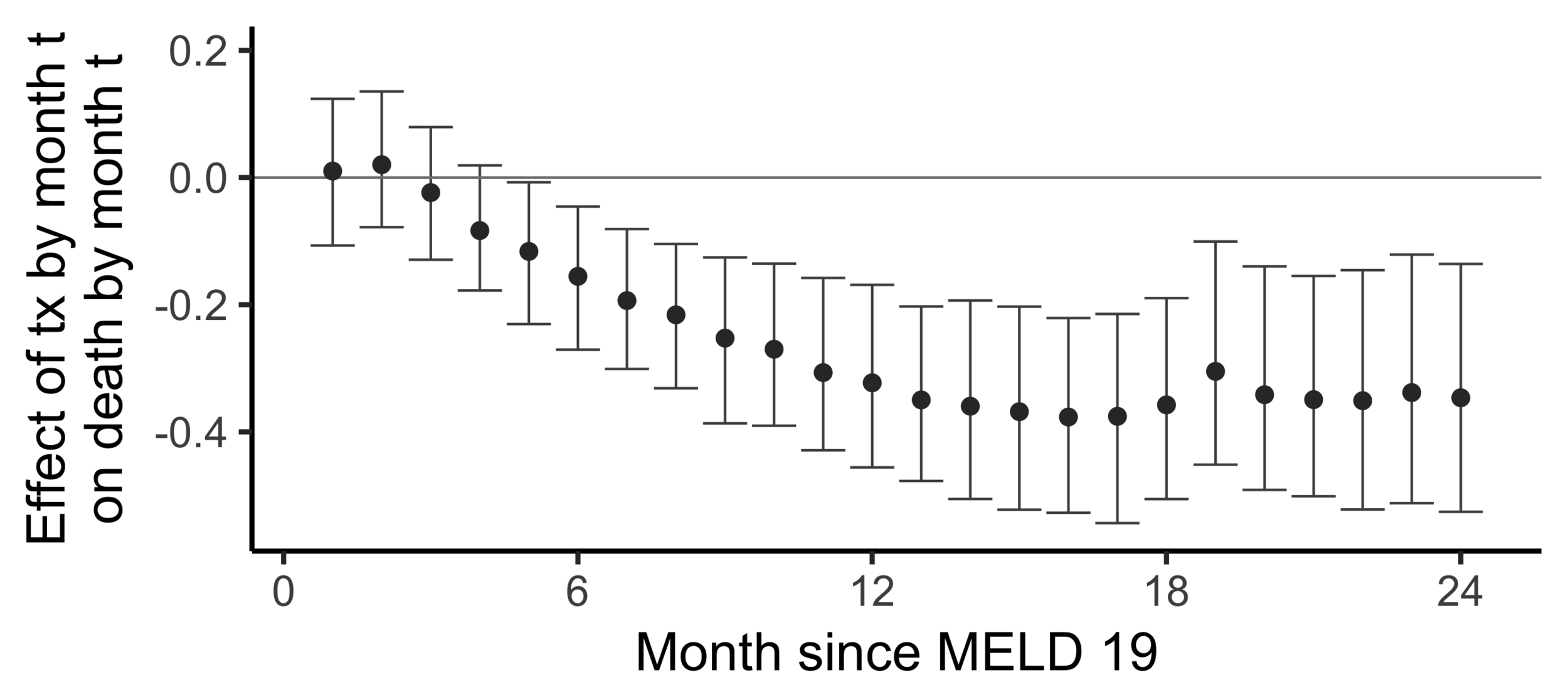
A sequential non-parametric approach
1
2
(MELD 18)
3
4
5
6
7
8
9
Month (t)
A = (0, 0, 1, 2, 3, 4, 5, 6, 7)
Y = (0, 0, 0, 0, 1, 1, 1, 1, 1)
A = (0, 0, 0, 0, 0, 0, 0, 0, 0)
Y = (0, 1, 1, 1, 1, 1, 1, 1, 1)
A = (0, 0, 0, 0, 0, 1, 2, 3, 4)
Y = (0, 0, 0, 0, 0, 0, 0, 0, 0)
A = (0, 0, 0, 0, 0, 0, 0, 0, 0)
Y = (0, 0, 0, 0, 0, 0, 0, 0, 0)
A = (0, 0, 0, 1, 2, 3, 4, 5, 6)
Y = (0, 0, 0, 0, 0, 0, 0, 0, 0)
A = (0, 0, 0, 0, 0, 0, 0, 0, 0)
Y = (0, 0, 0, 0, 0, 0, 0, 0, 0)
The effect on death by month 24
of
being transplanted one month earlier than actually transplanted
(\textrm{Death by 24mo})_i = \alpha + \beta (\textrm{months since tx})_i + \epsilon_i
Effect on the chance of death by 24 months of being transplanted 6 months earlier:
-0.014 \times 6 = -8.4\%
-0.014 -
The effect of receiving a transplant earlier
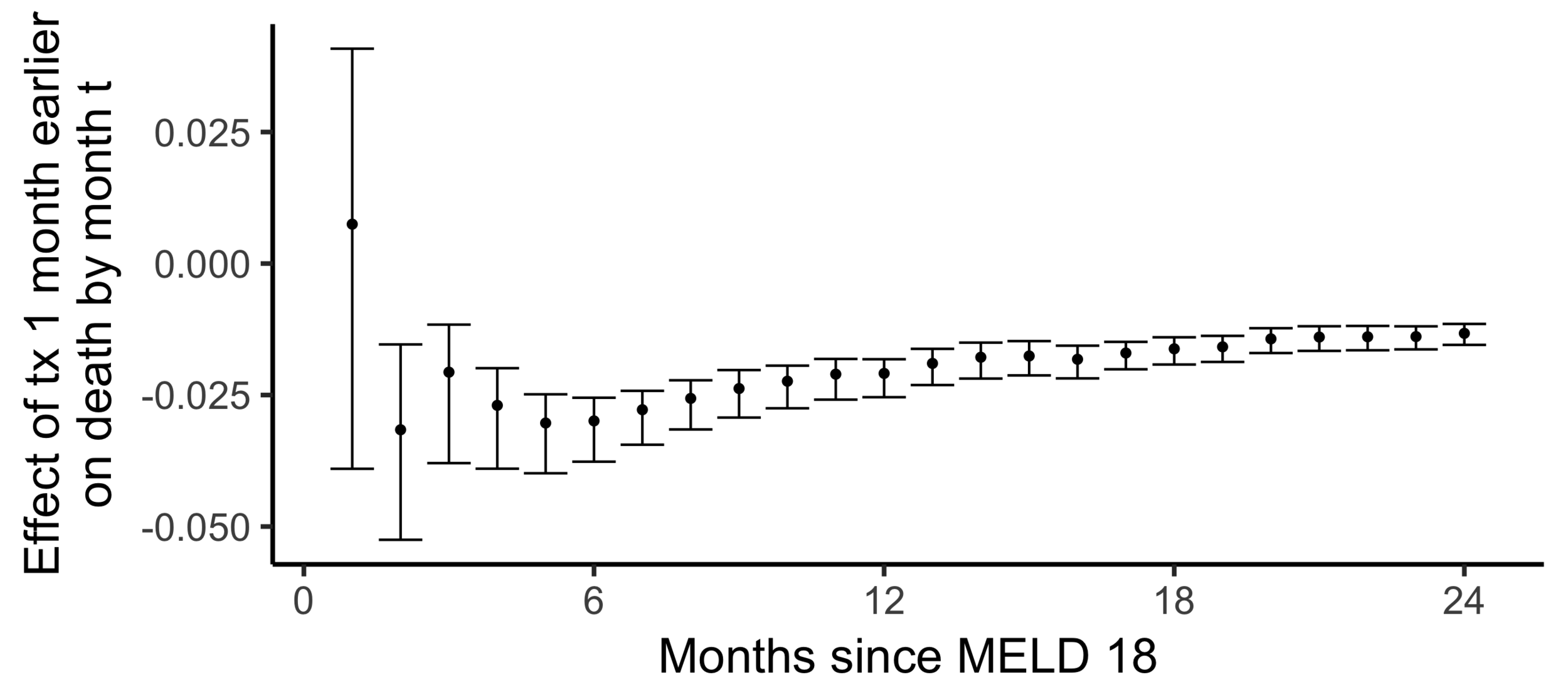
(2SLS estimate)
Subsampling stability
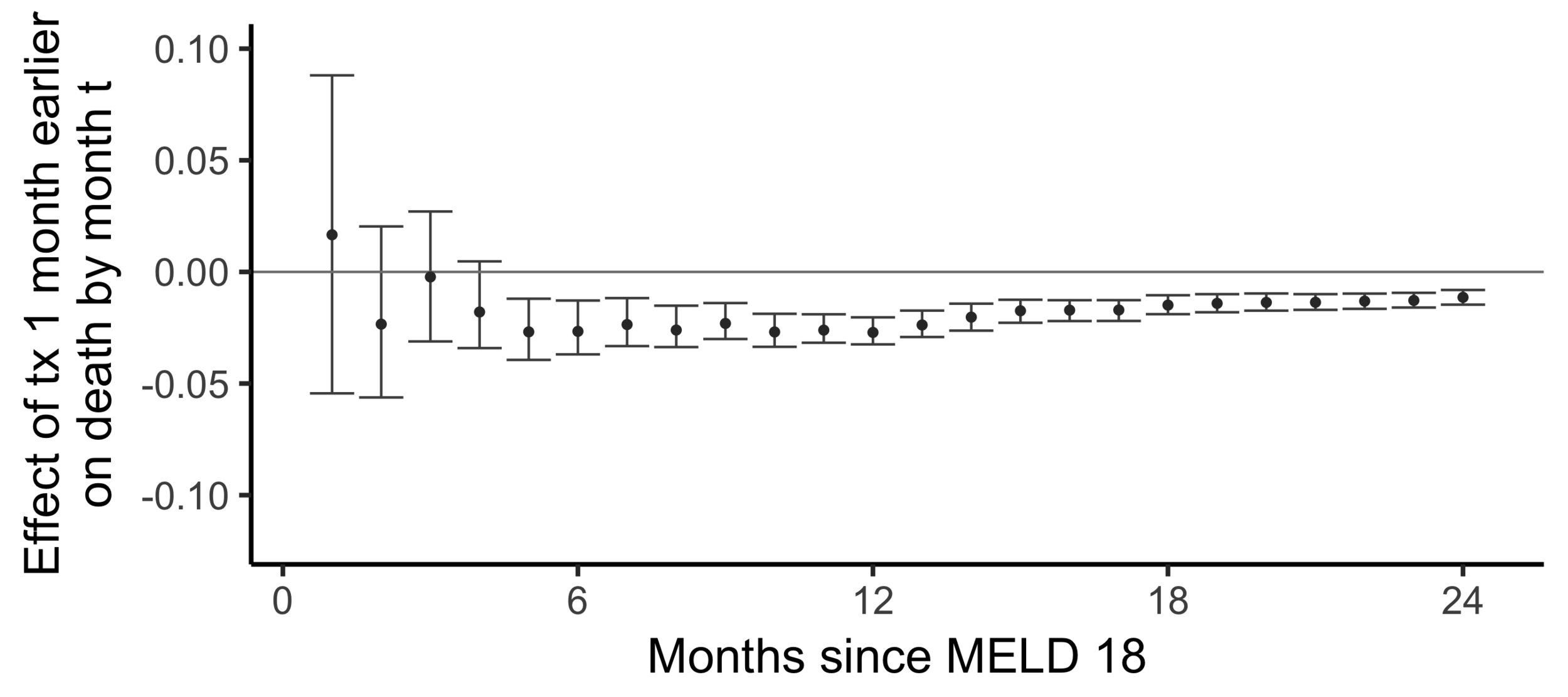
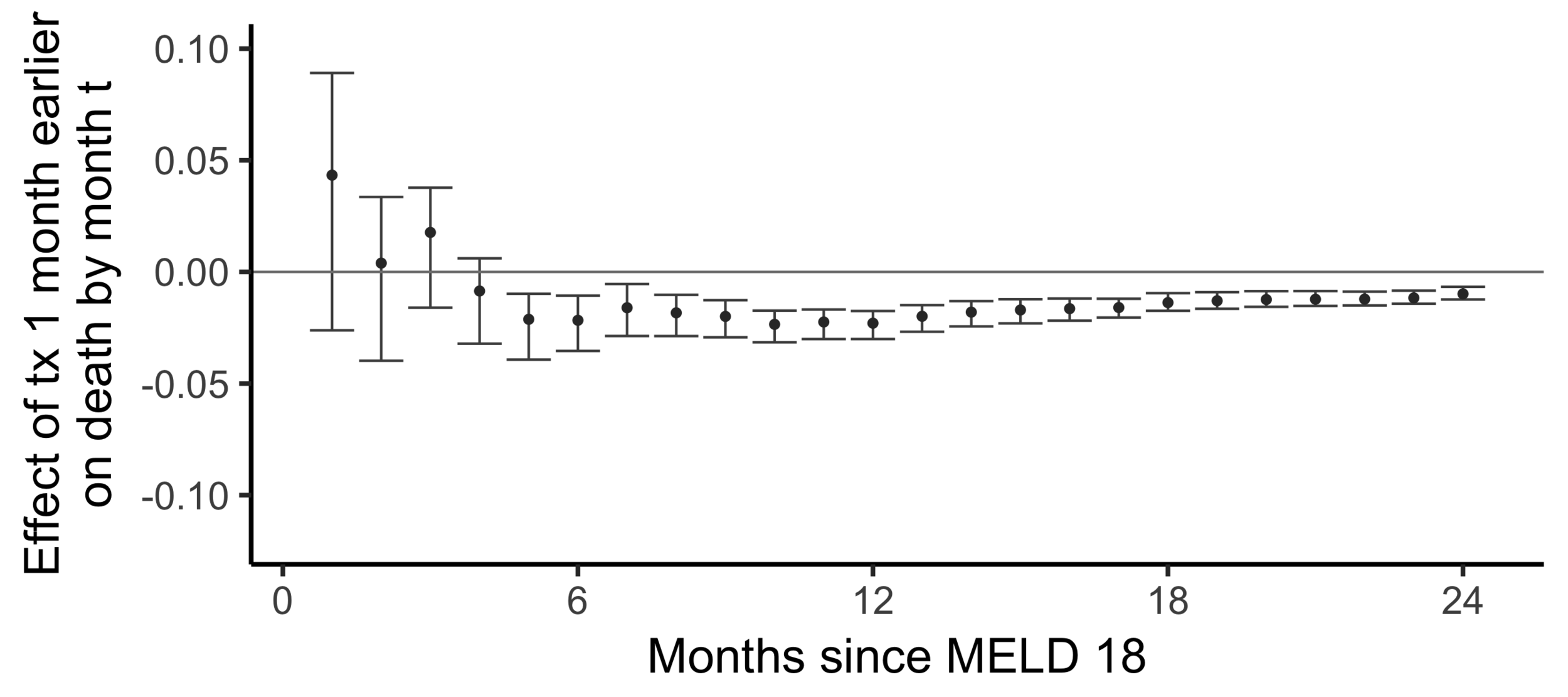
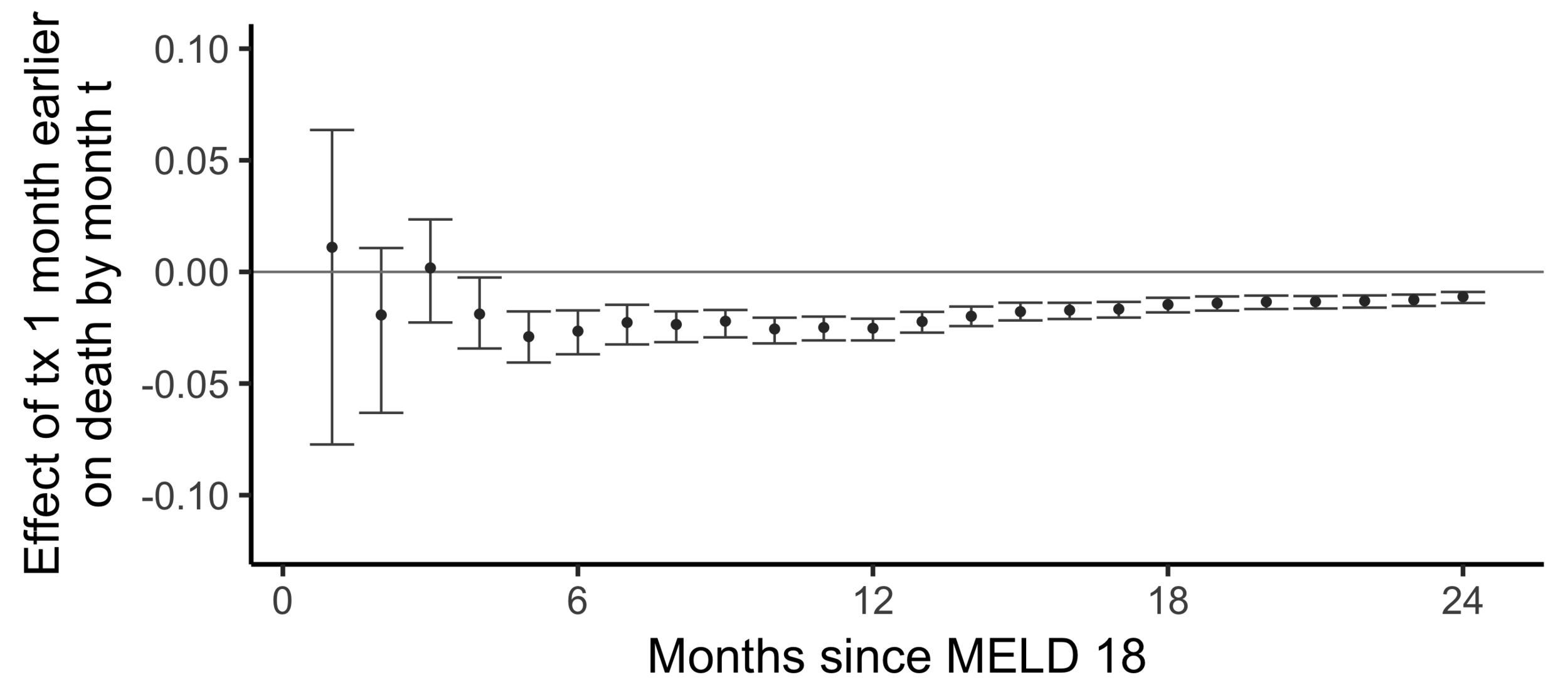
Stability with respect to MELD
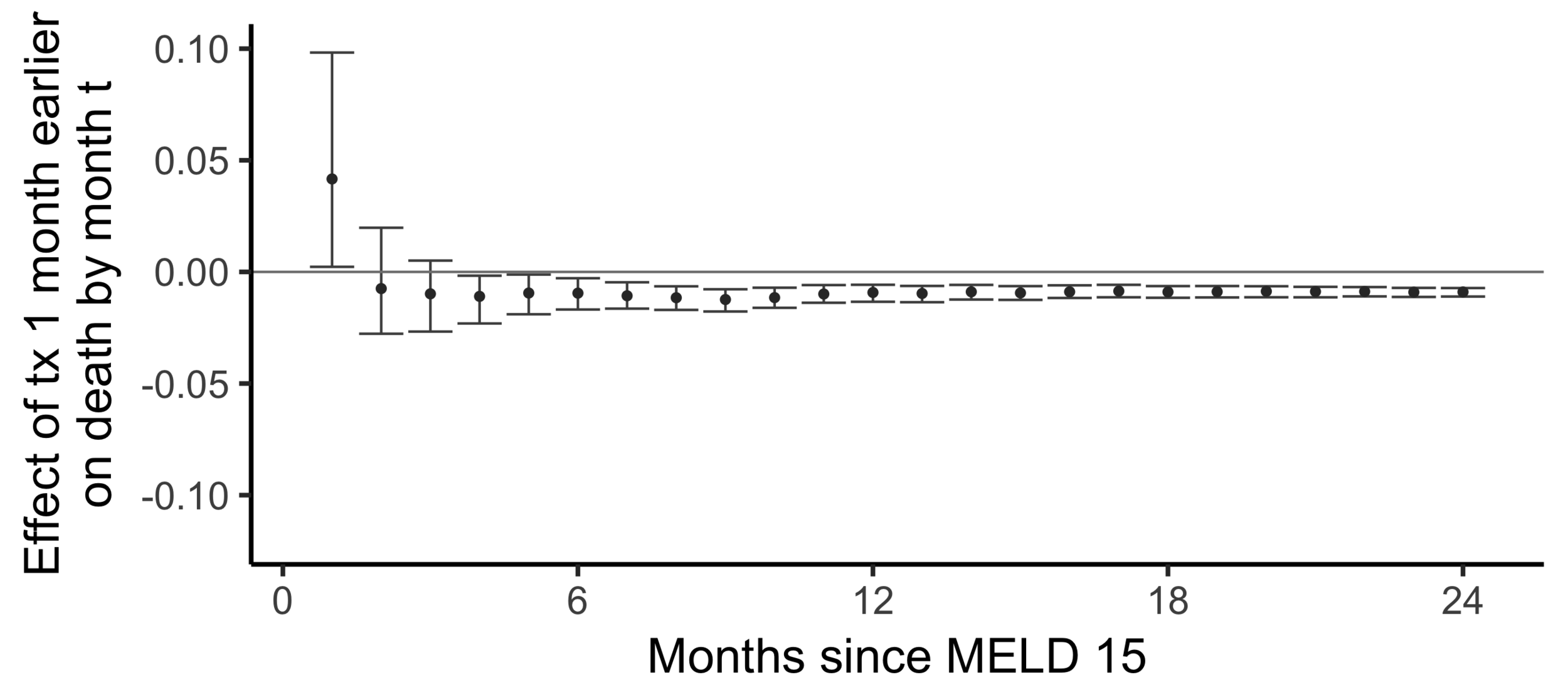
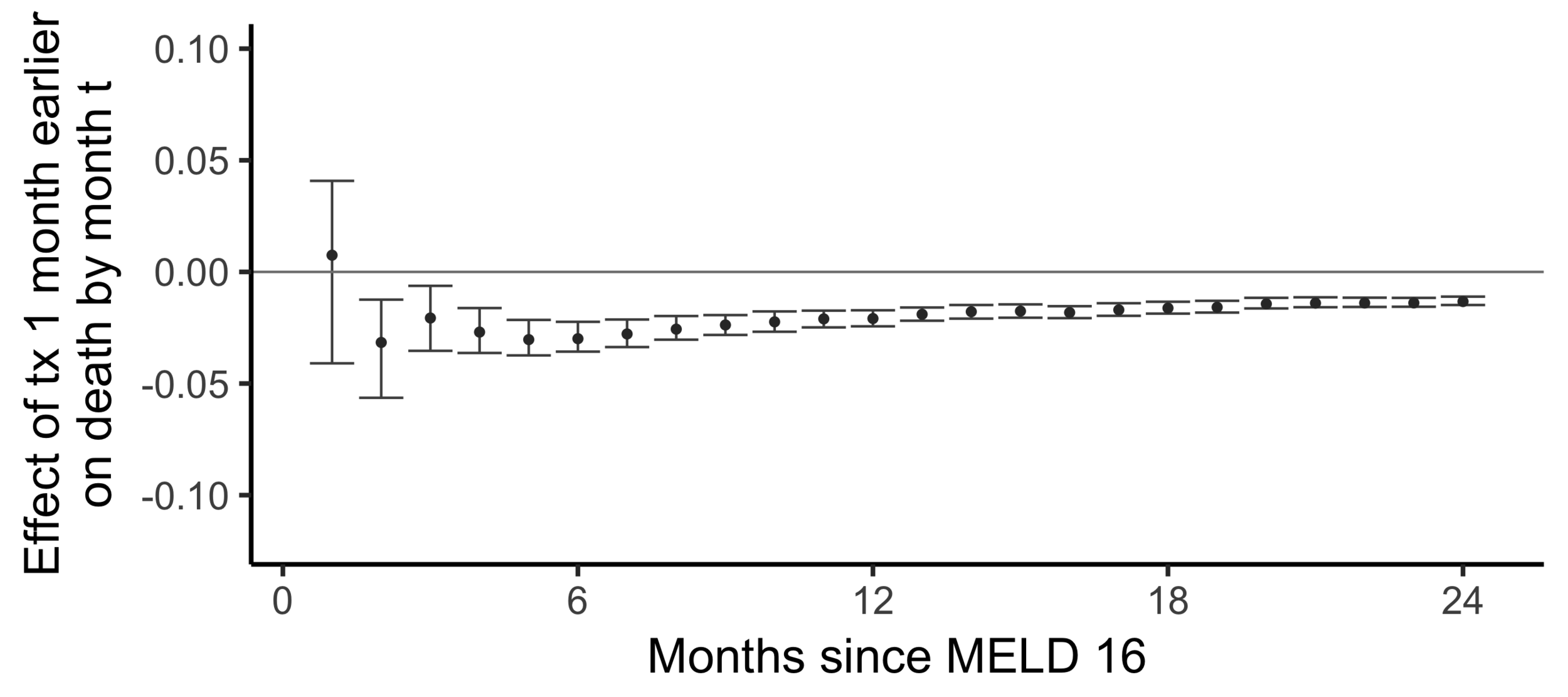
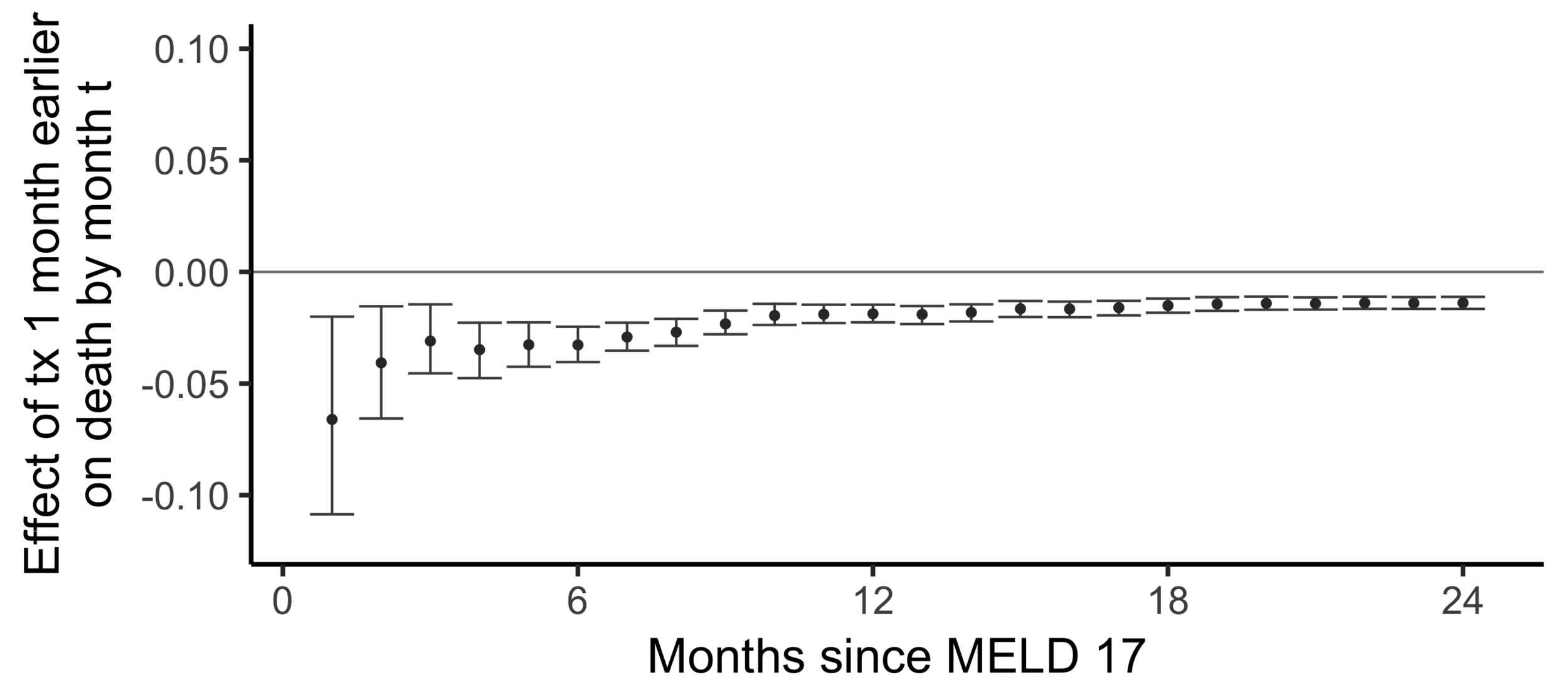
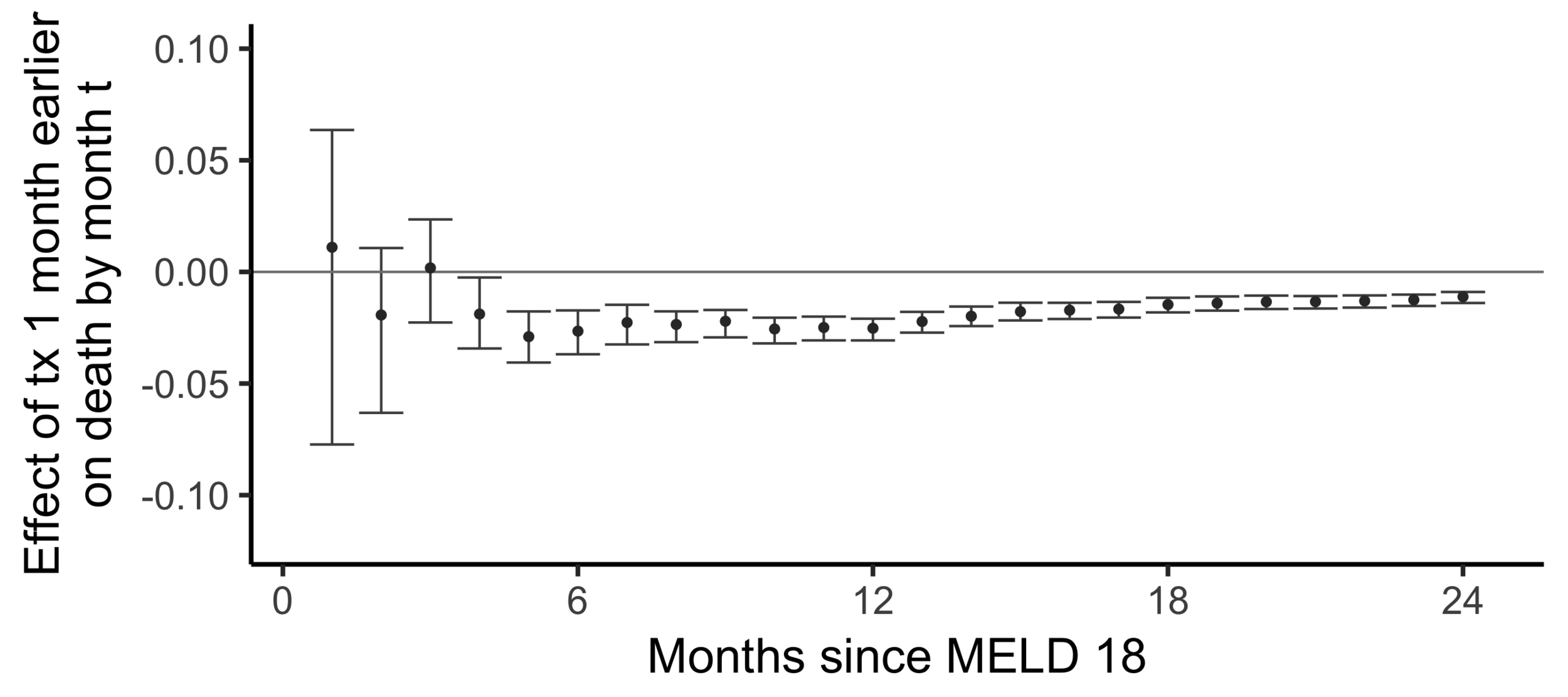
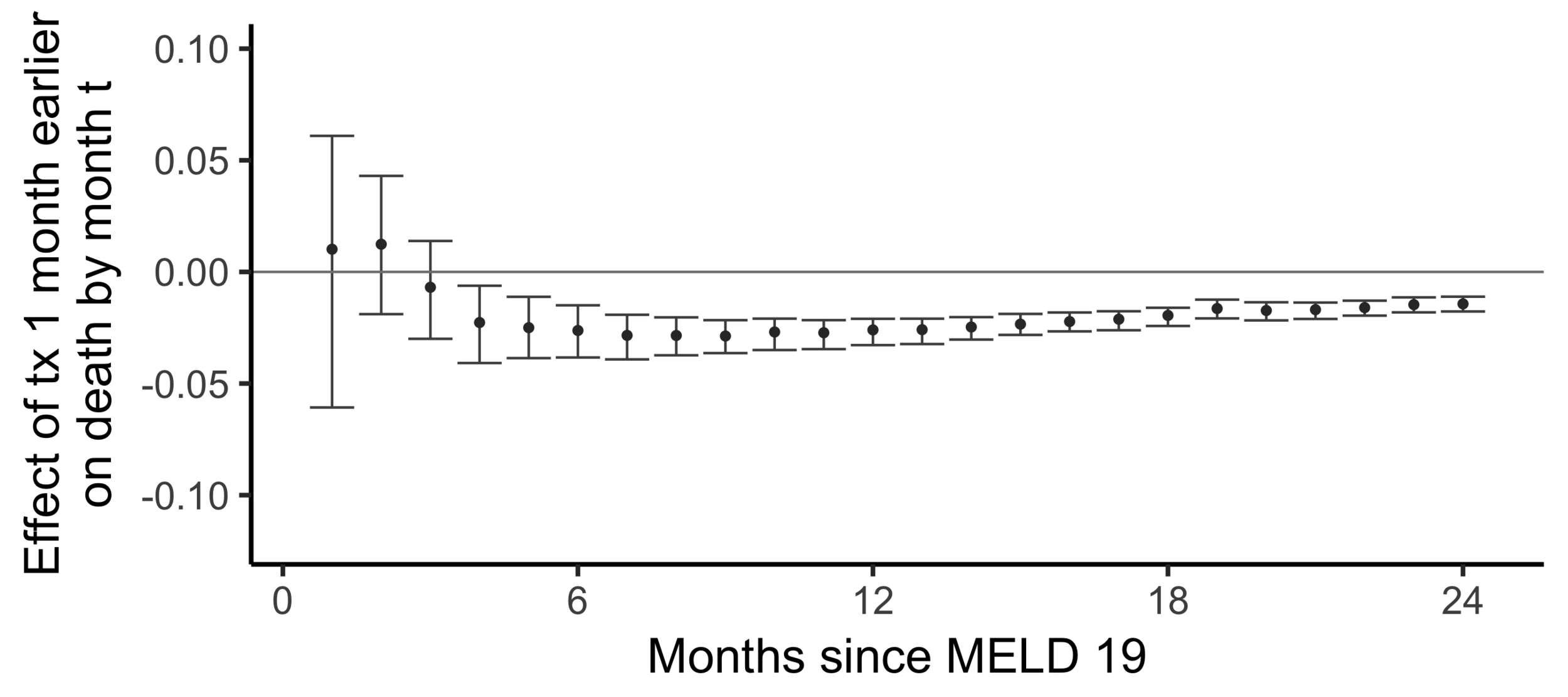
Comparing wait times by state
Wait time differs by state
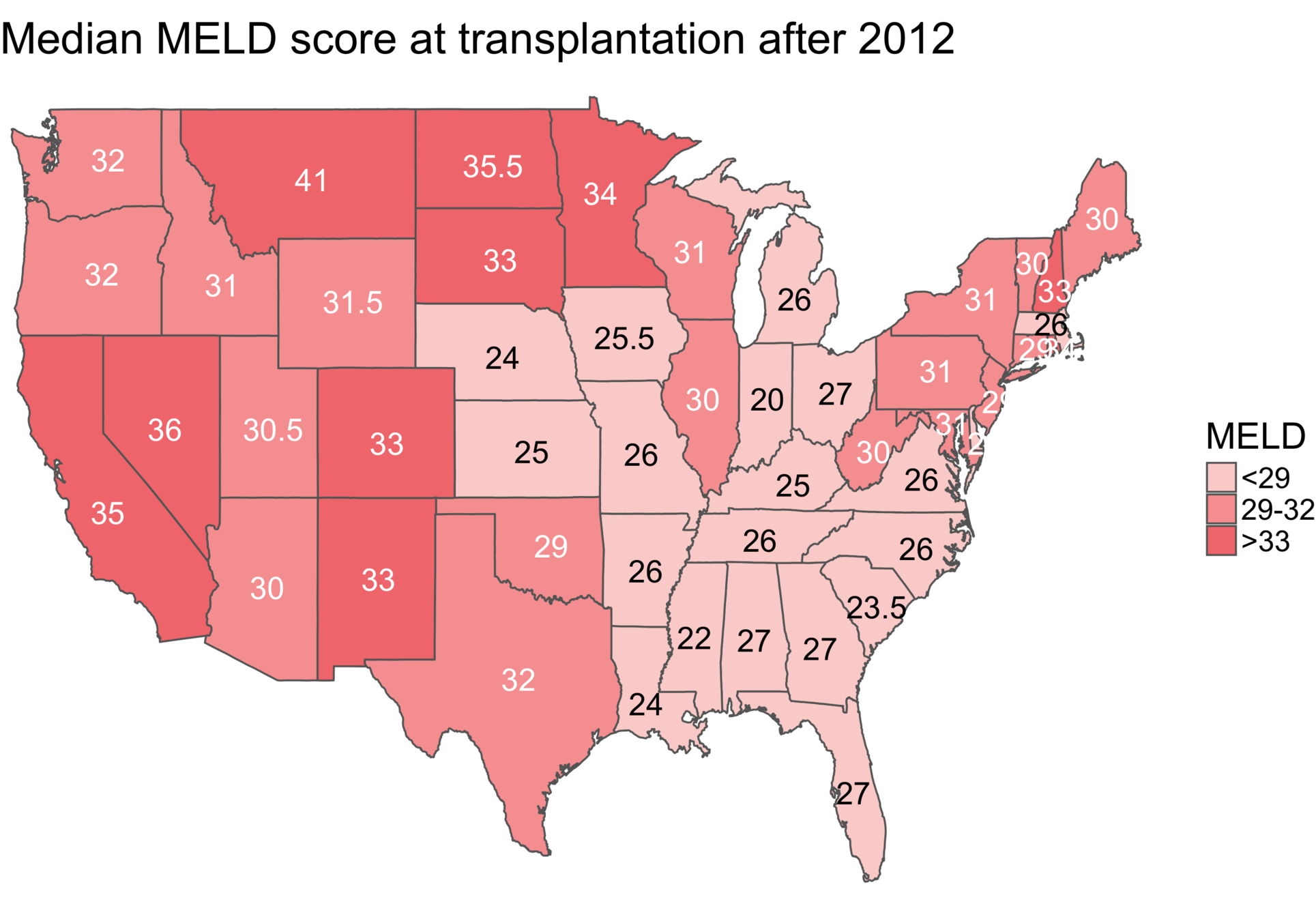
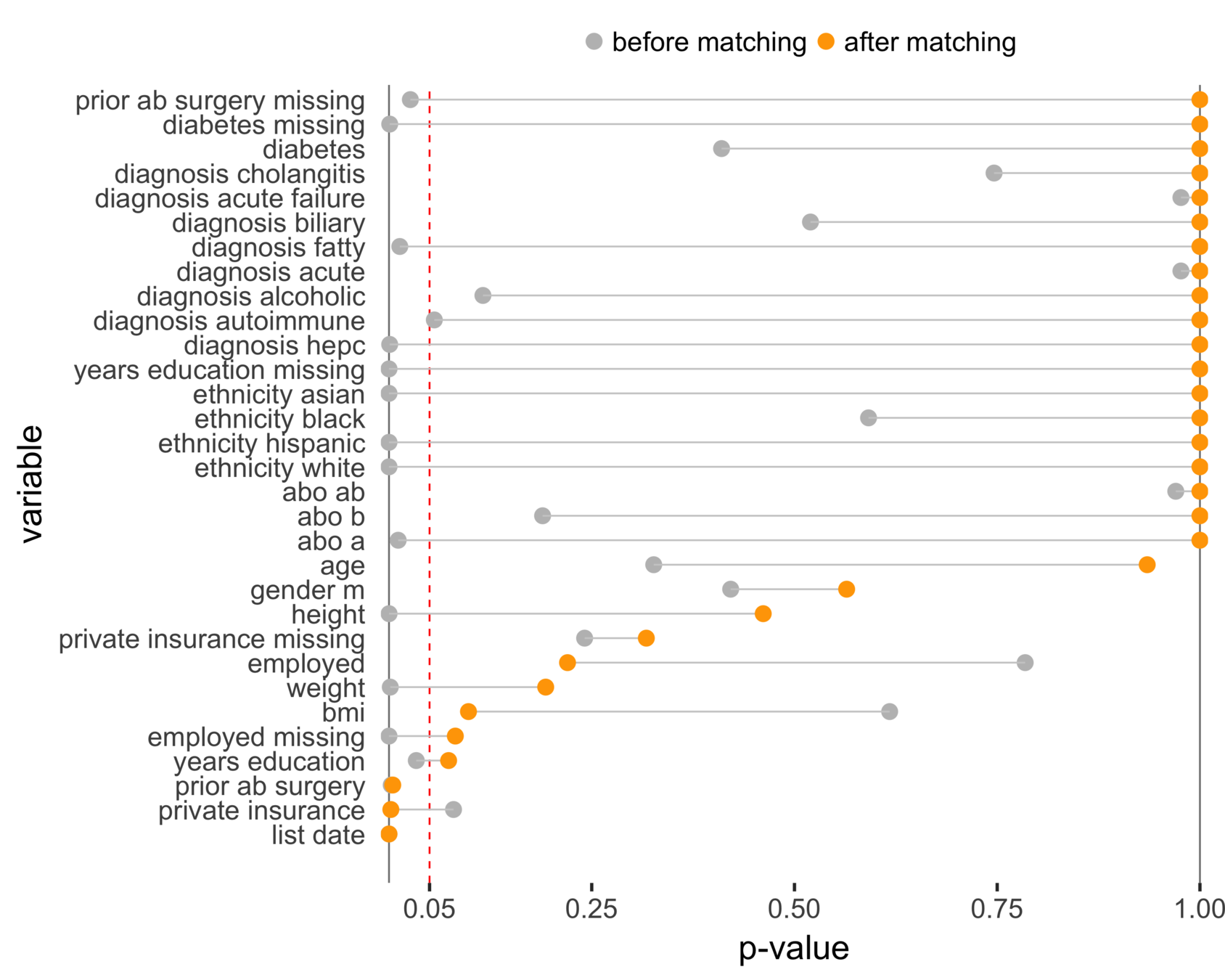
Matching CA and NC
Sekhon (2011), Multivariate and Propensity Score Matching Software with Automated Balance Optimization: The Matching Package for R
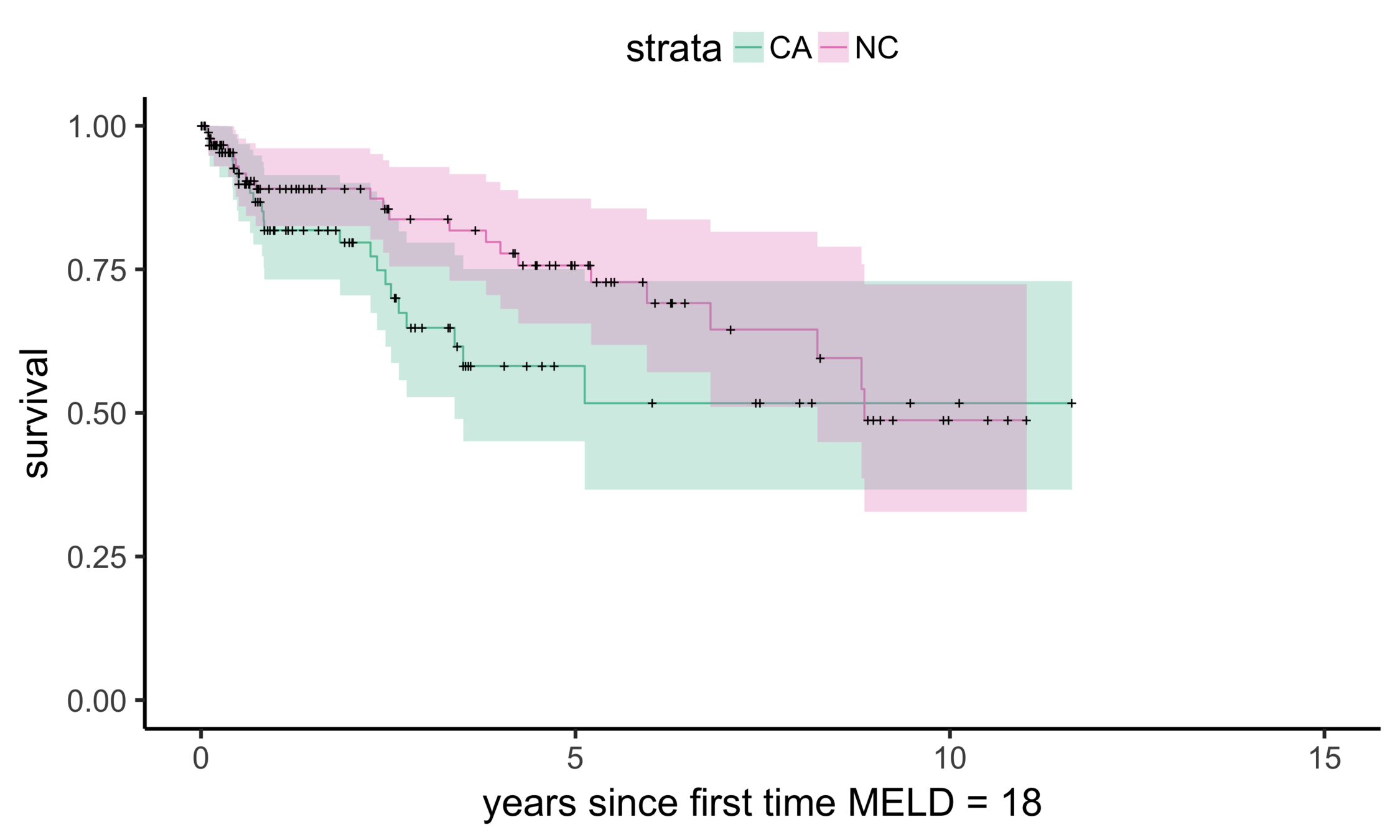
CA (MELD 38)
NC (MELD 24)
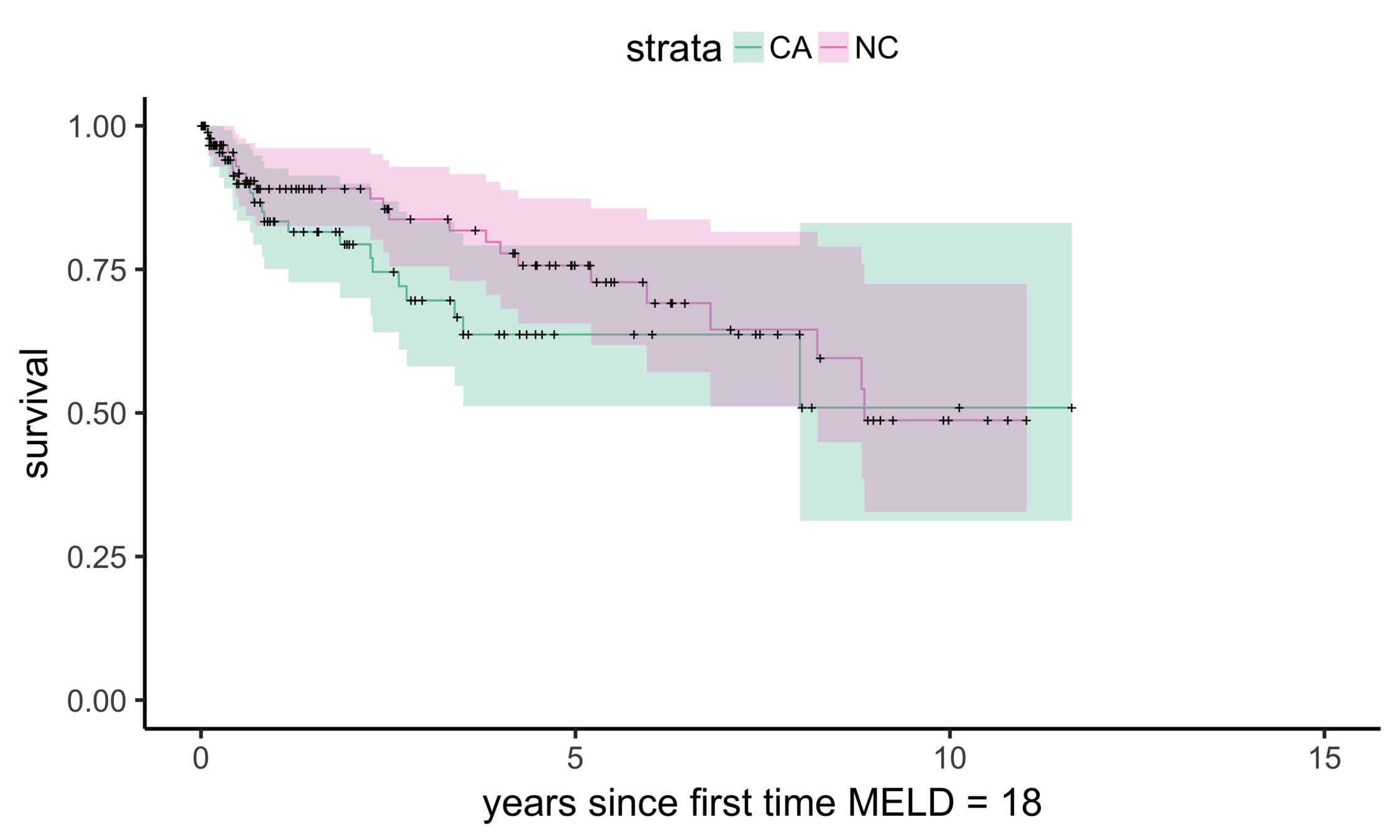
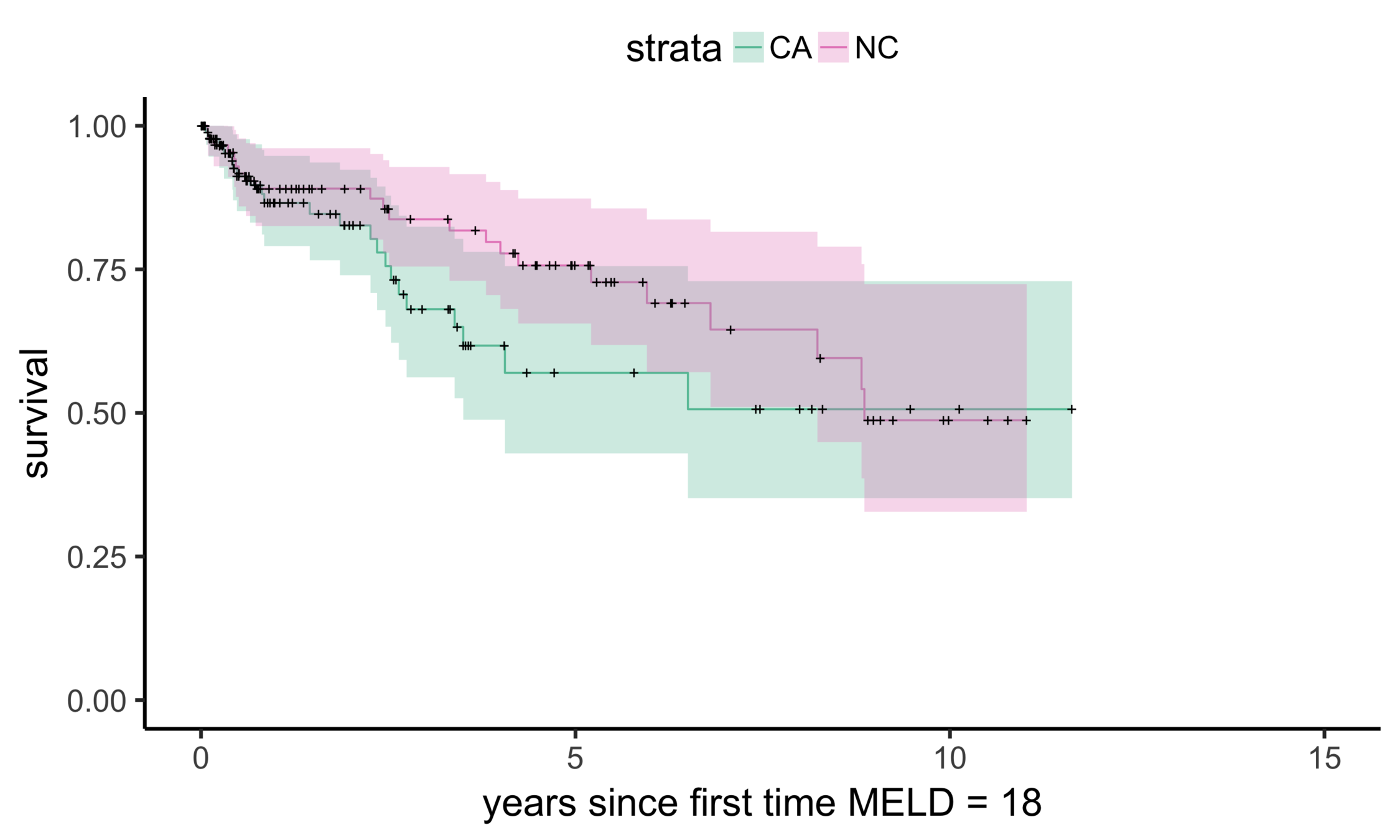
Matching CA (n = 686) to NC (n = 150)
Balance (NC & CA)
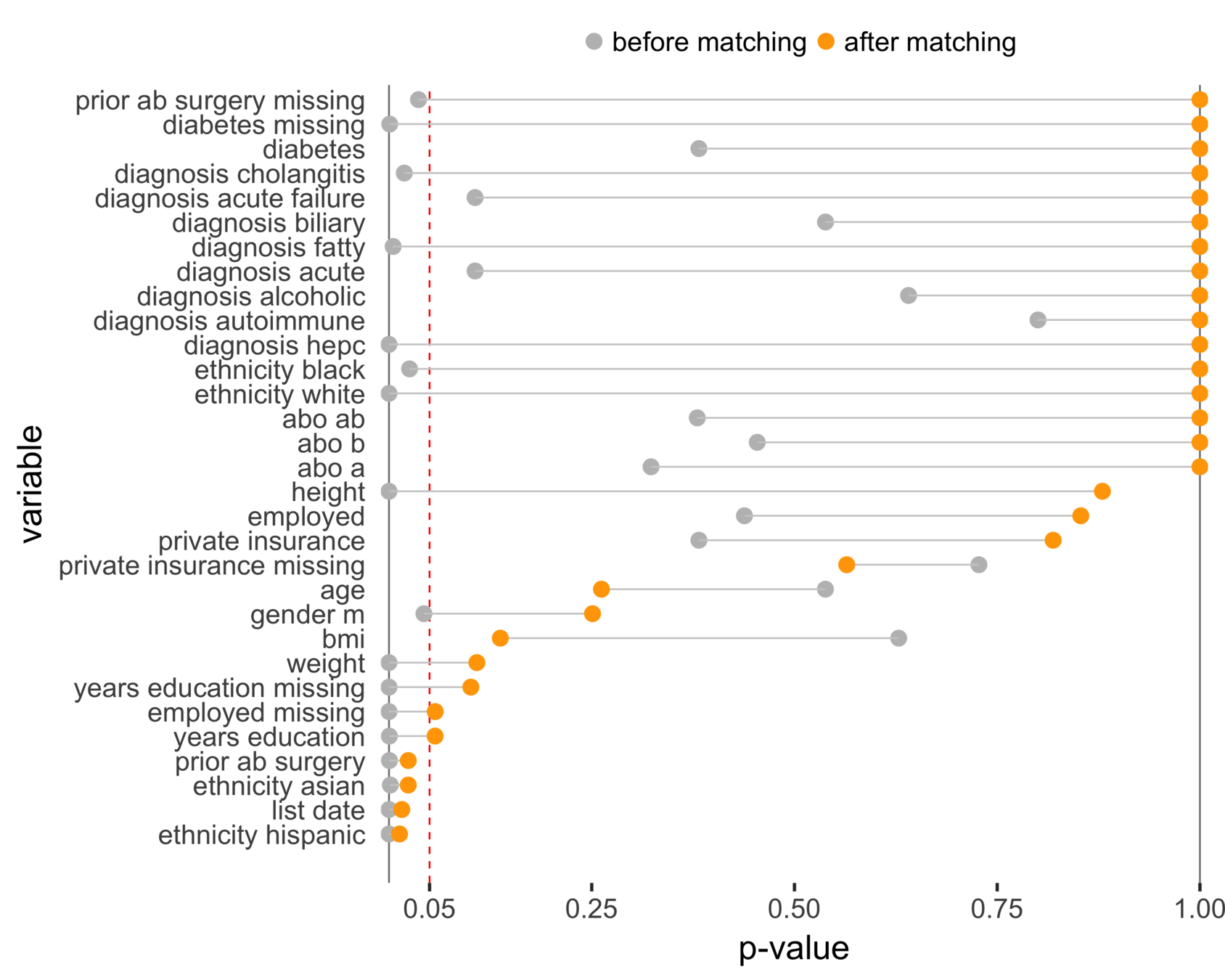
Stability: equivalent comparisons
CA (MELD 38)
OH (MELD 24)
Matching CA (n = 686) to OH (n = 195)
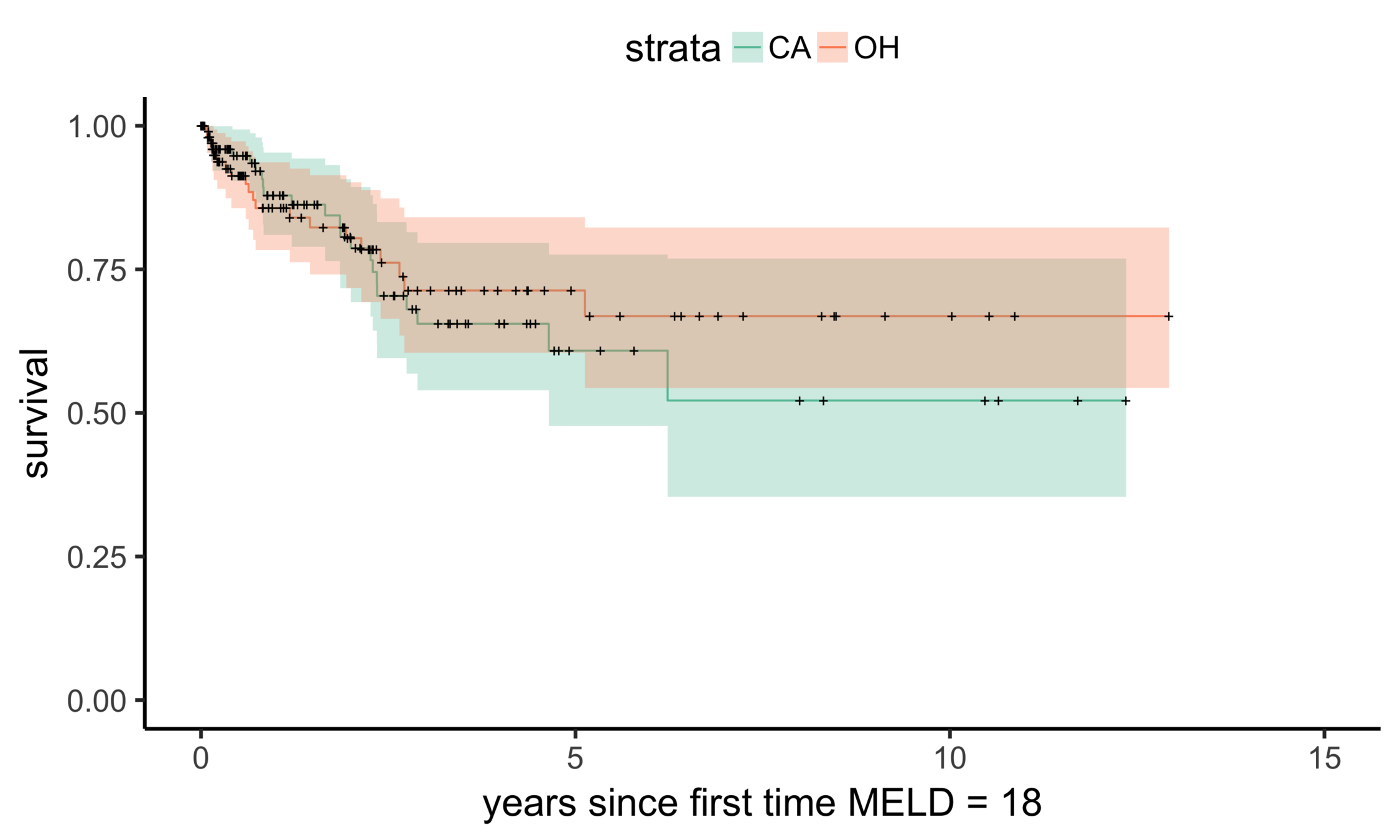
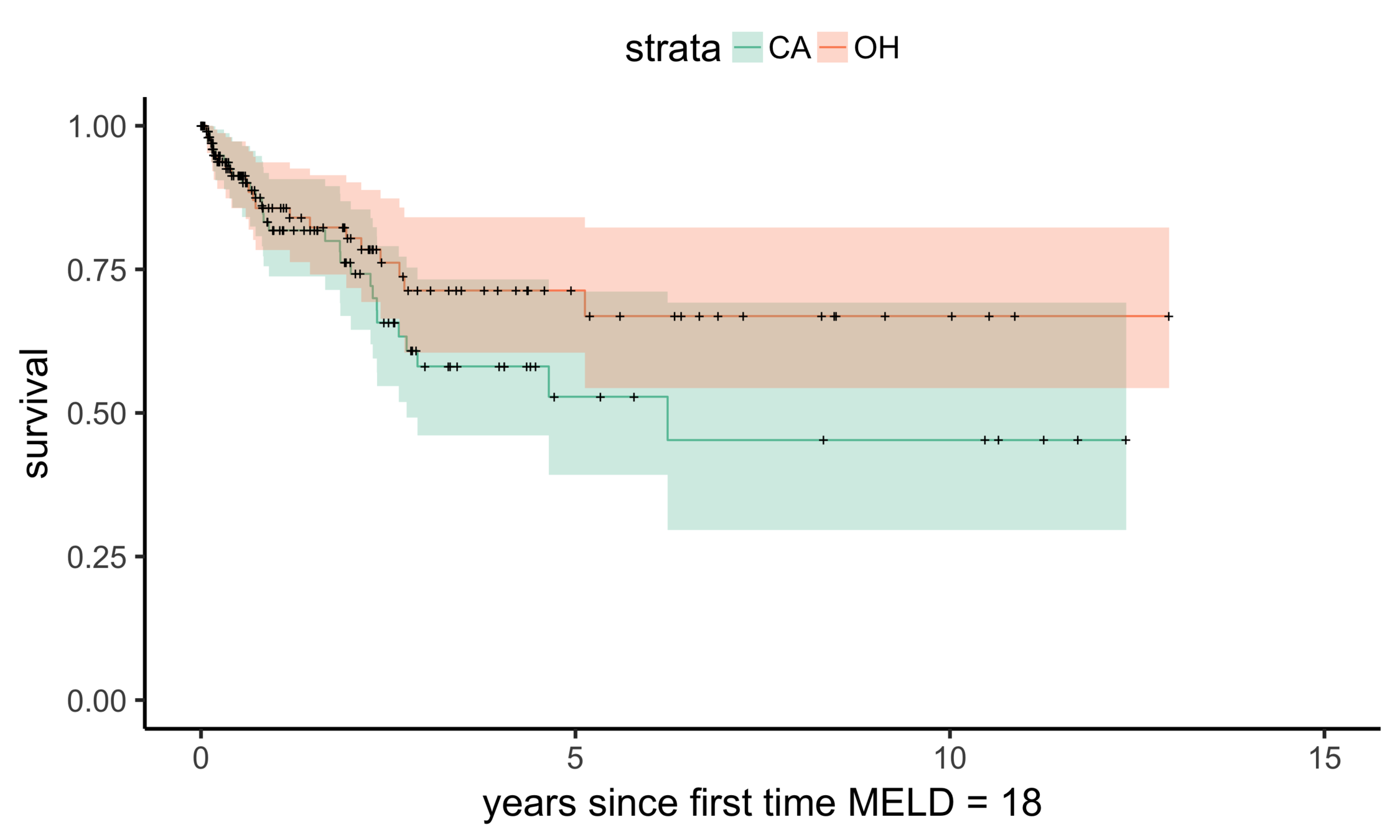
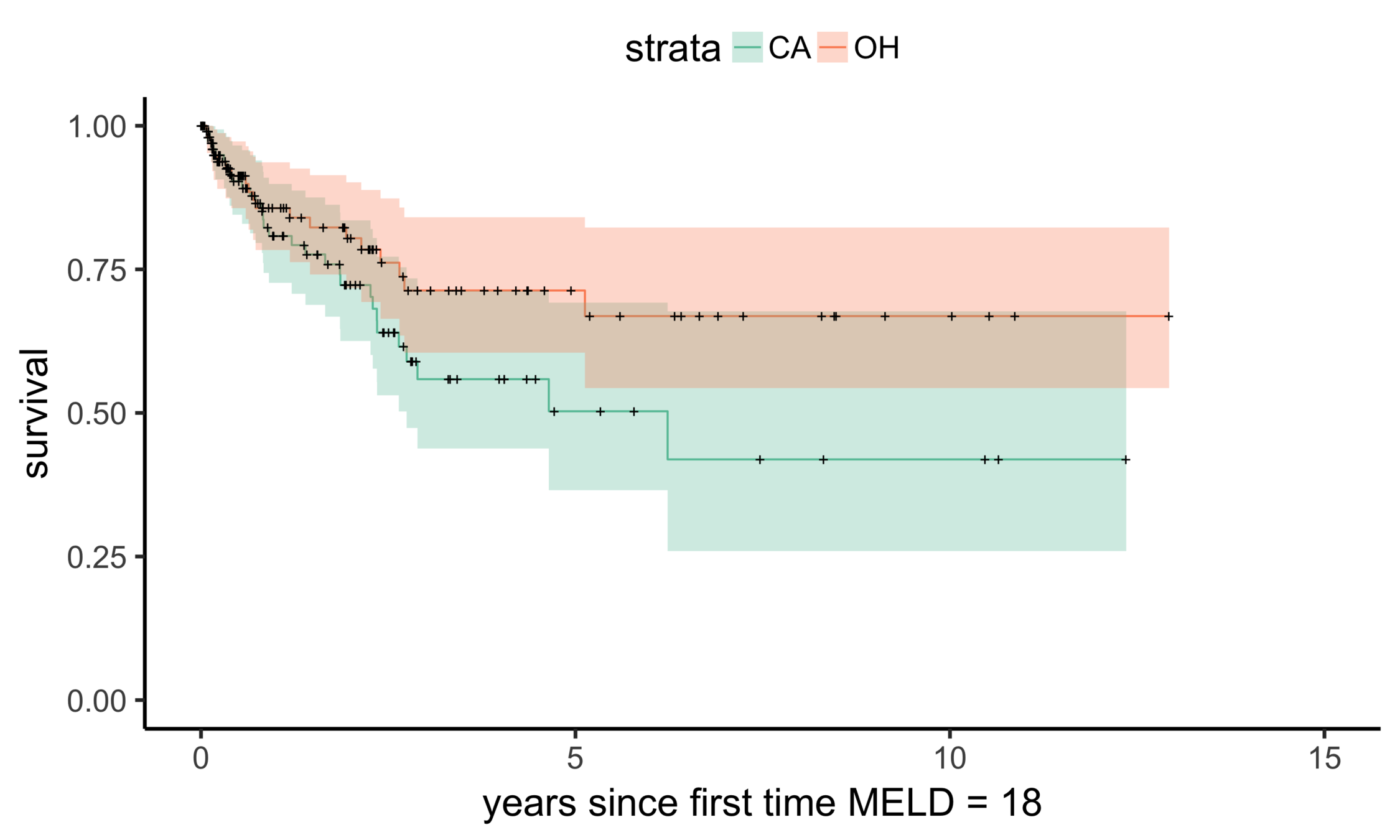
Balance (CA & OH)
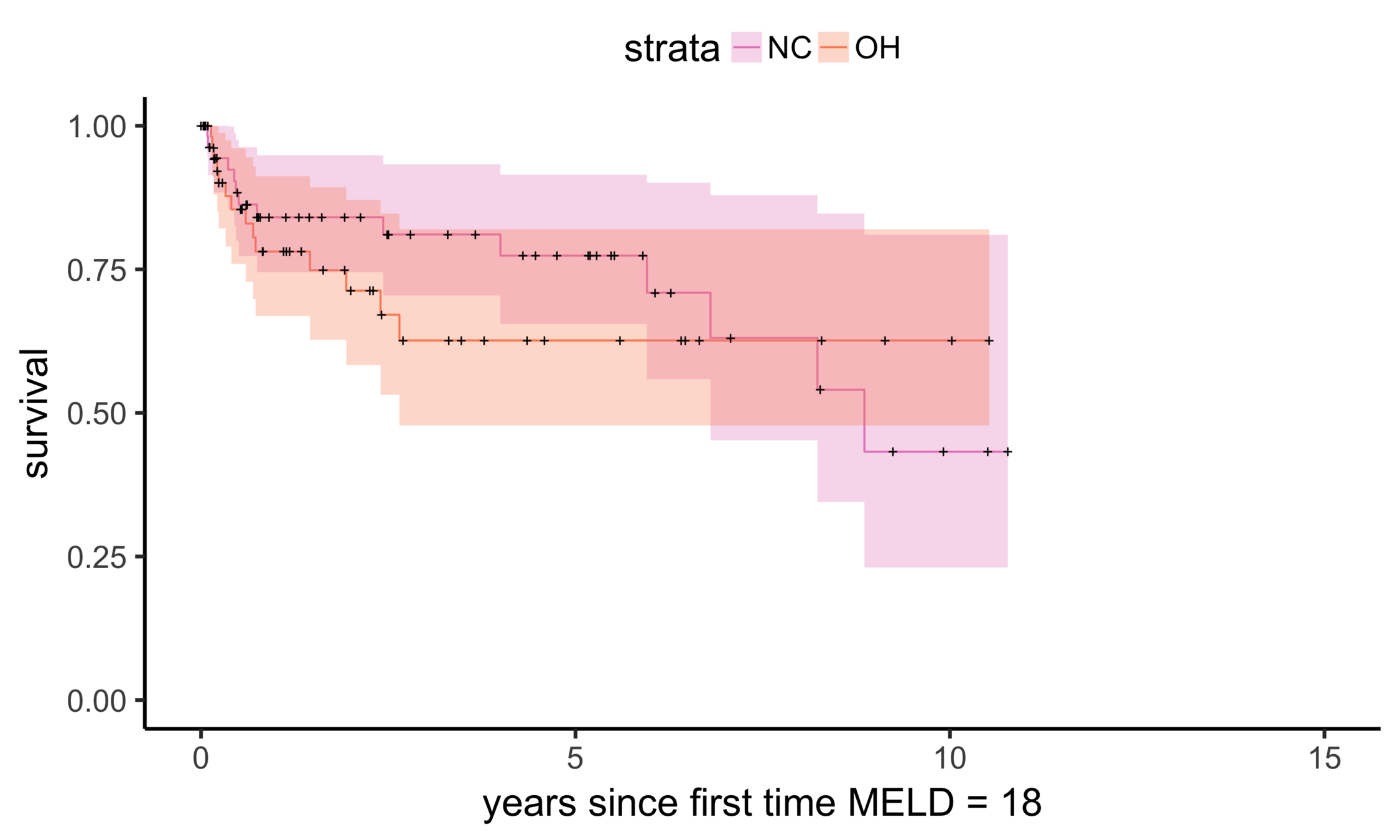
Stability: null comparisons
NC (MELD 24)
OH (MELD 24)
Matching OH (n = 195) vs NC (n = 150)
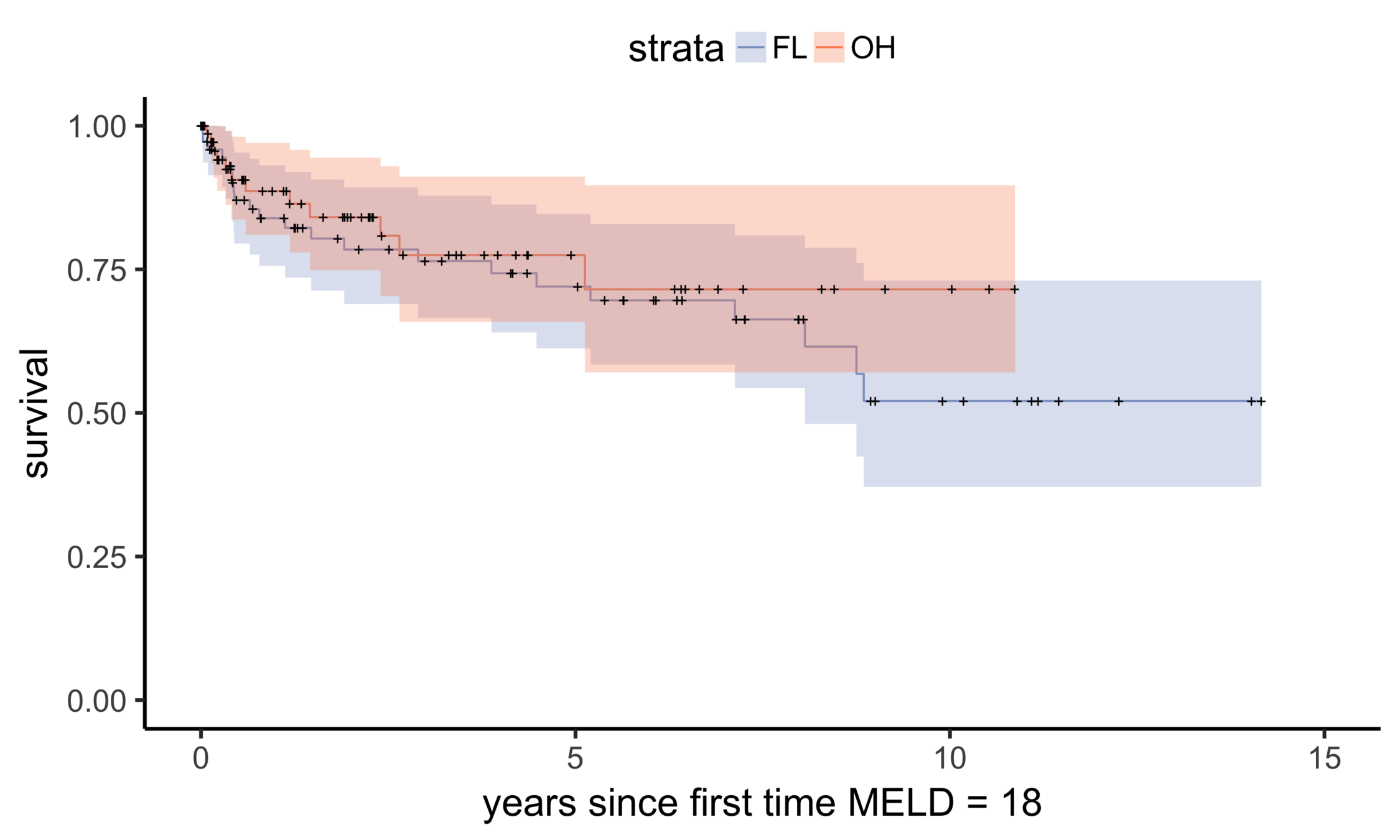
OH (MELD 24)
FL (MELD 24)
Matching OH (n = 195) vs FL (n = 305)
Recap
vs
A = (0, 0, 1, 1, 1, 1, 1, 1, 1)
Y = (0, 0, 0, 0, 1, 1, 1, 1, 1)
What did we learn?
It is very difficult to quantify the effect of transplantation wait time on survival.
Results imply a benefit of being transplanted sooner rather than later.
Where next (UNOS)?
Is there a considerable benefit in being transplanted sooner? For who? How much?
What is the best way to estimate benefit for current patients on the waitlist?
Should allocations policies be altered? If so, how?
Can we estimate benefit on quality of life?
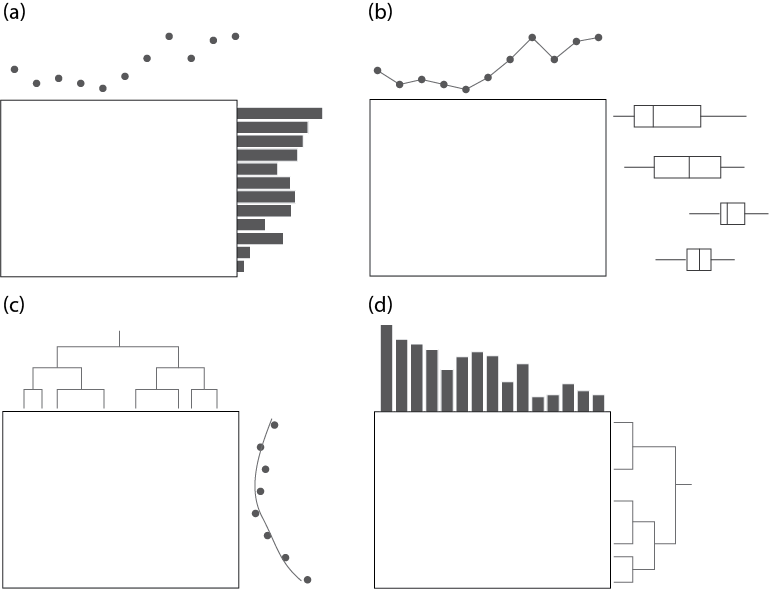
Superheat
package
an
Heatmaps
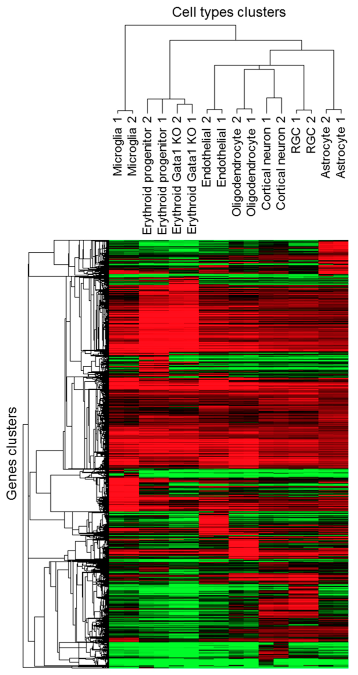
Trakhtenberg et al. (2016) Cell types differ in global coordination of splicing and proportion of highly expressed genes
Clustering &
Dendrogram
Wilkinson (1994)
Eisen et al. (1998)
Loua (1873), Atlas statistique de la population de Paris
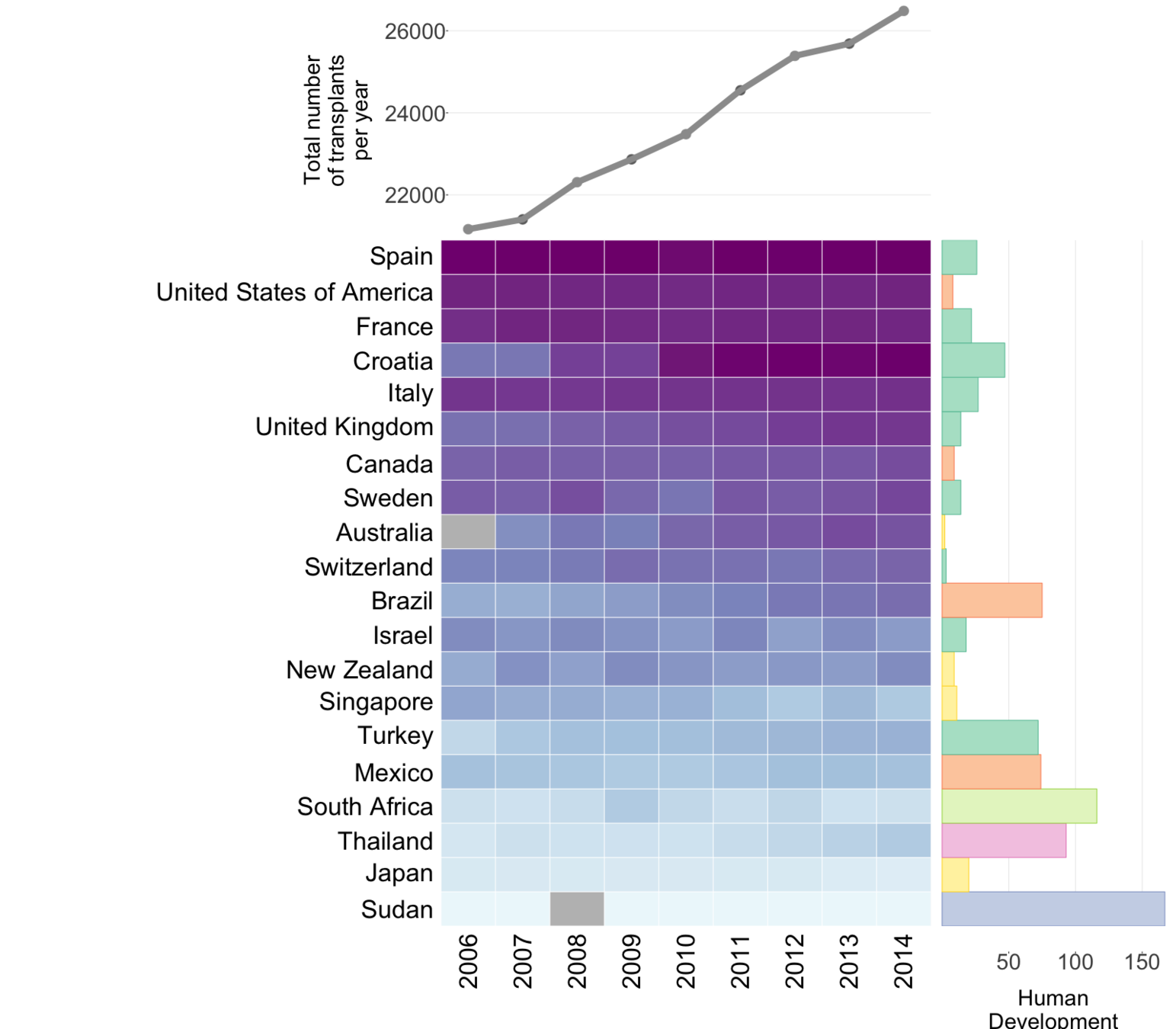
Global organ donation trends over time
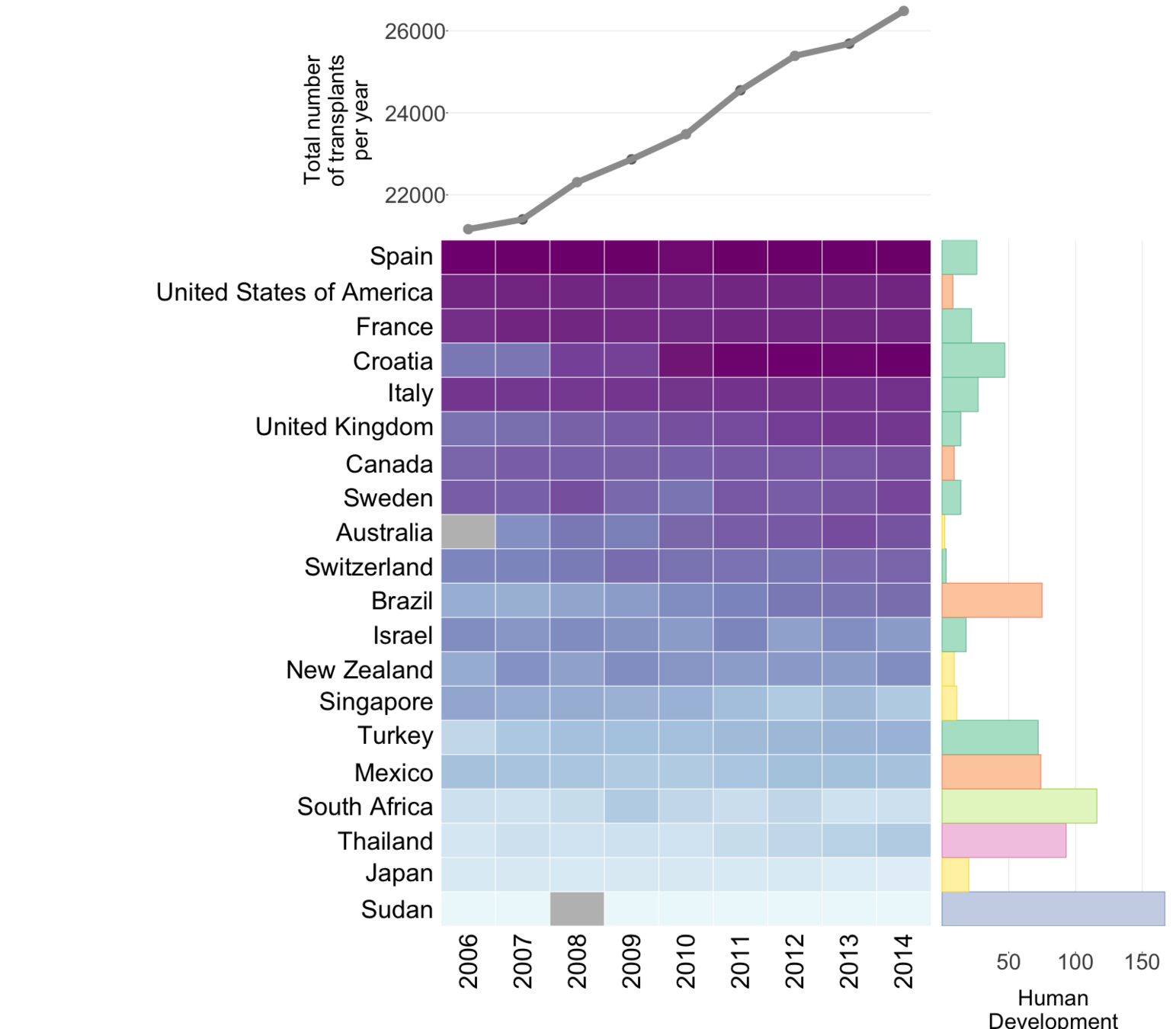
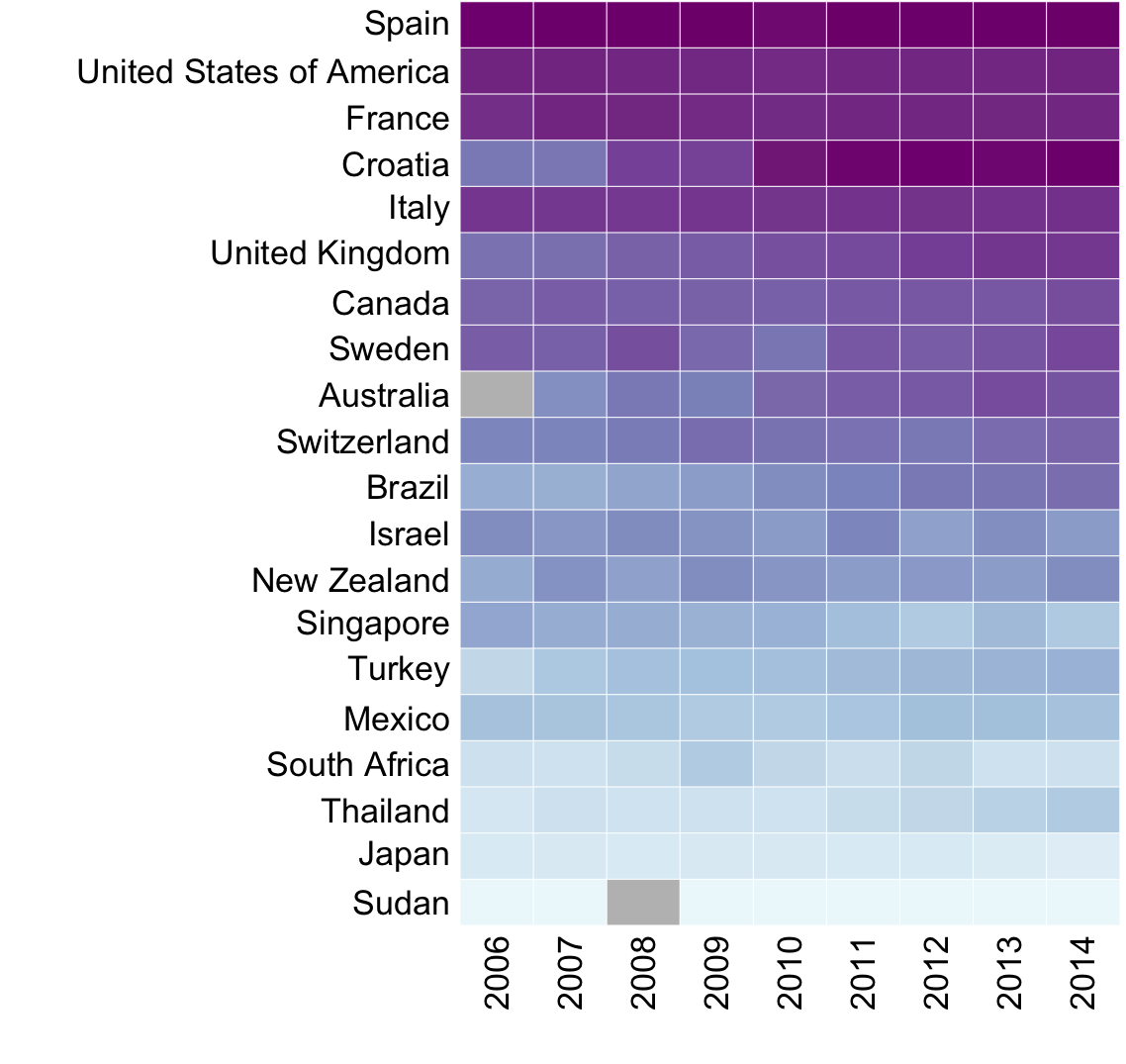
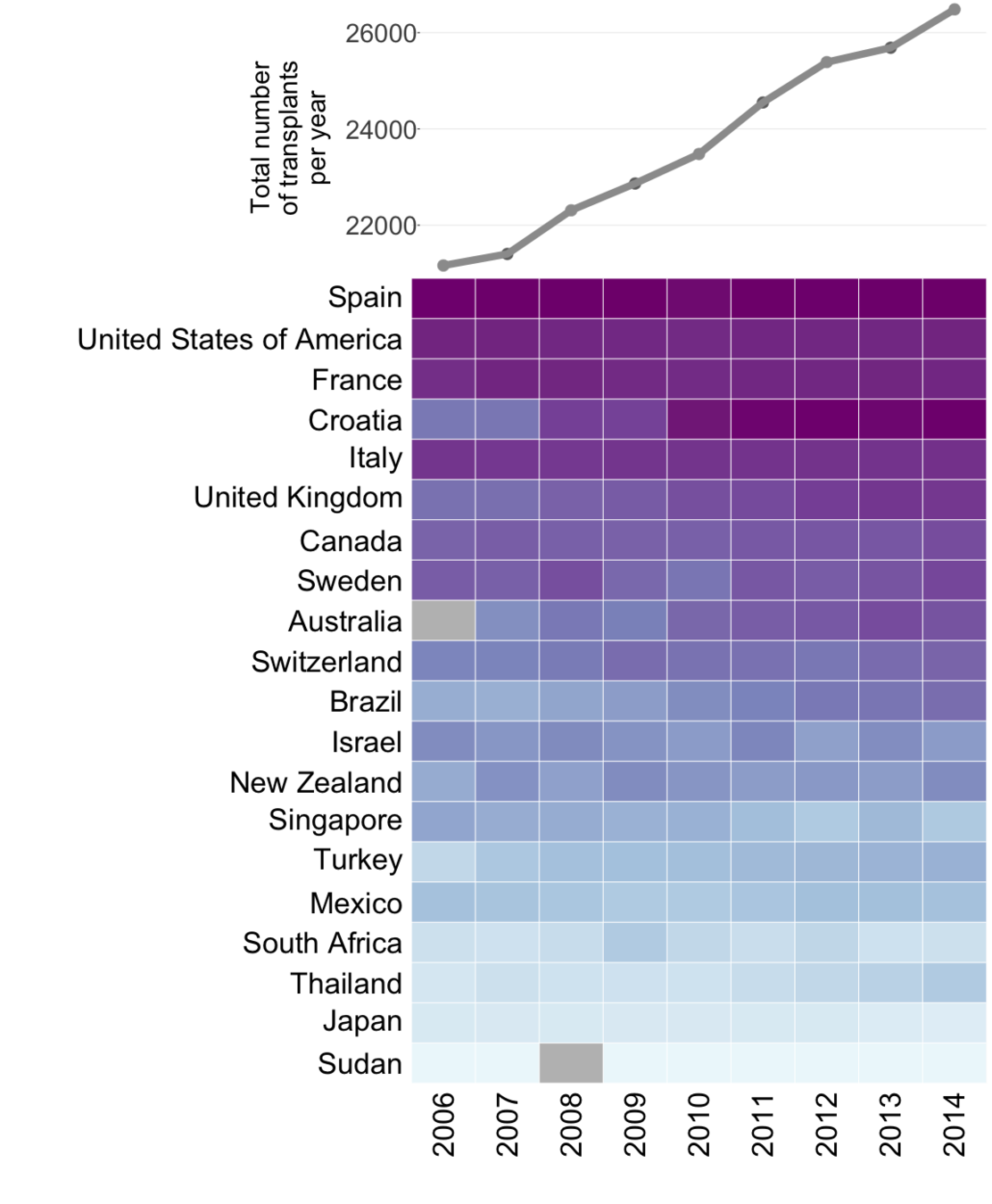
Organ donation trends
with a trendline
and
human development
index ranking
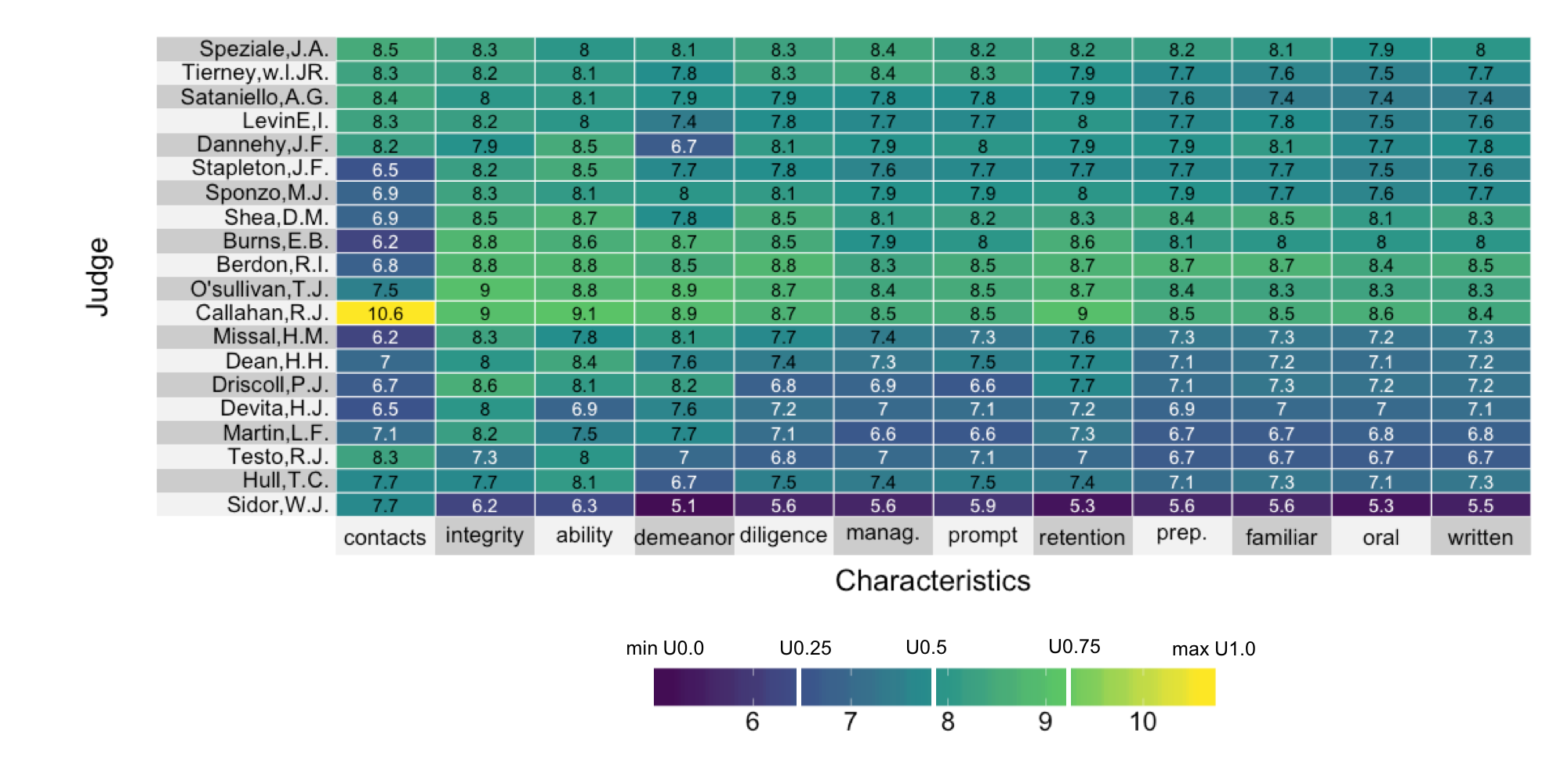
Visualizing lawyer's ratings on US Supreme Court judges
A linear color map
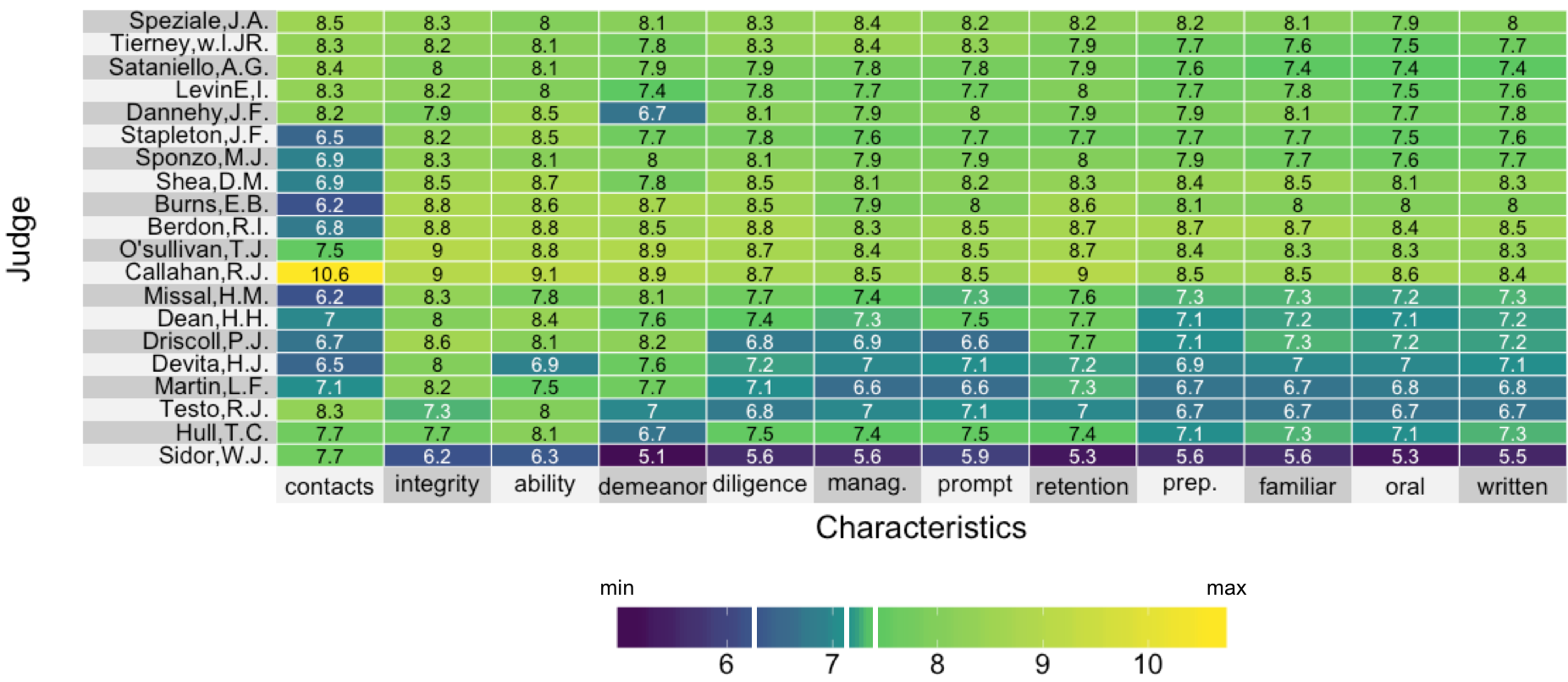
A manual color map
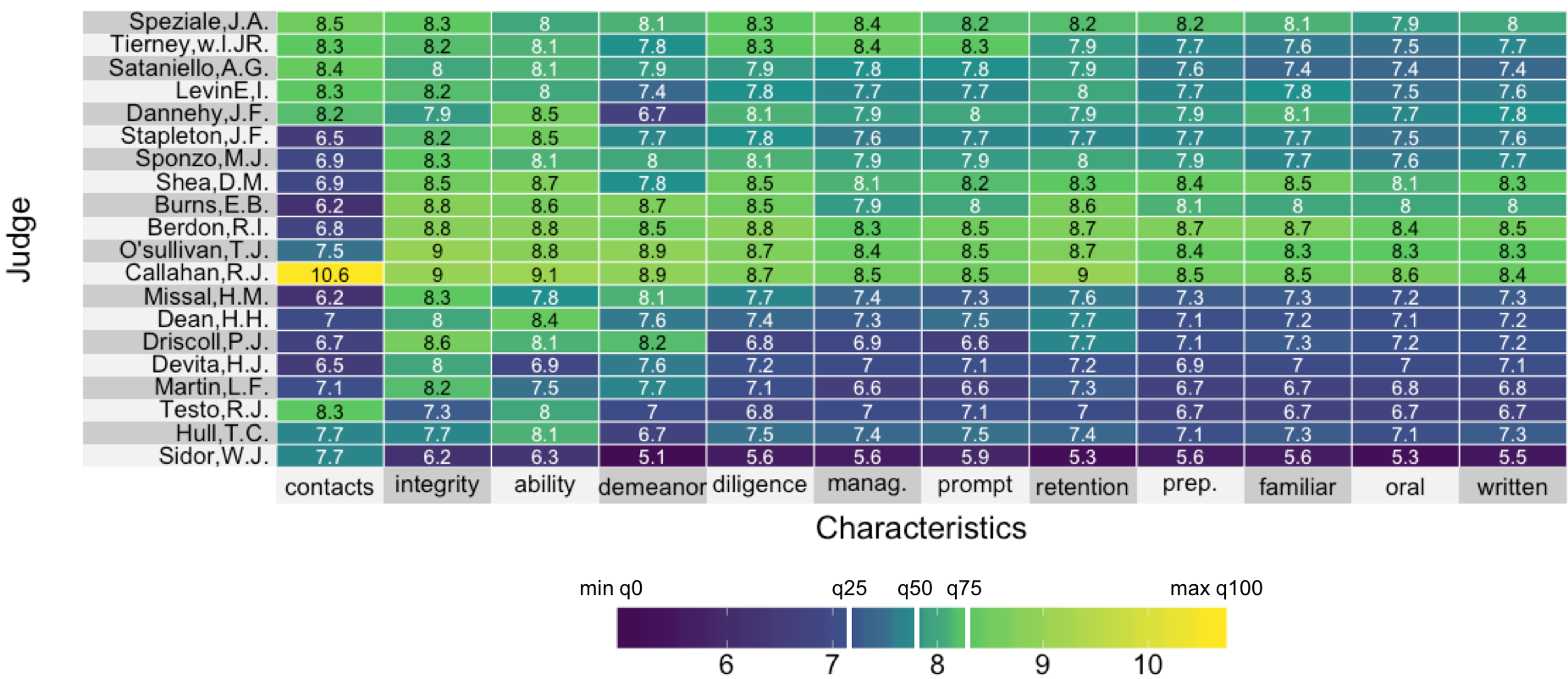
A quantile color map
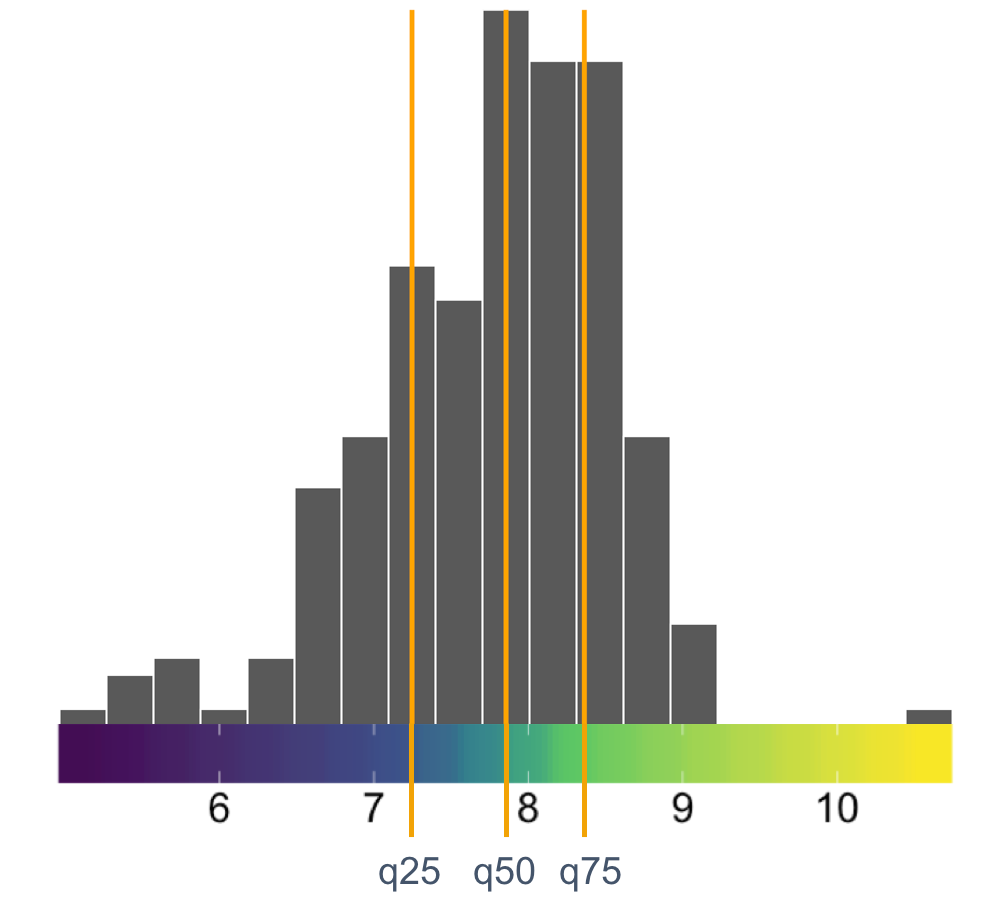
uperheat success!
Where next (PhD)?
(Open data platform with Colin Wu)
Qualifying Exam talk: Assessing the current liver transplant allocation algorithm
By Rebecca Barter
Qualifying Exam talk: Assessing the current liver transplant allocation algorithm
Slides for liver allocation project (UNOS data)
