XOR8 HASH FUNCTION
B04902073 洪崇凱
B02208025 蔡誌烜
B02705025 賴冠廷
Complexity
md5, sha1
djb2, sdbm
sum8, xor8
B02208025
B02407068
B03701137
B03208028
B04705045
︙
studentID
djb2
xor8
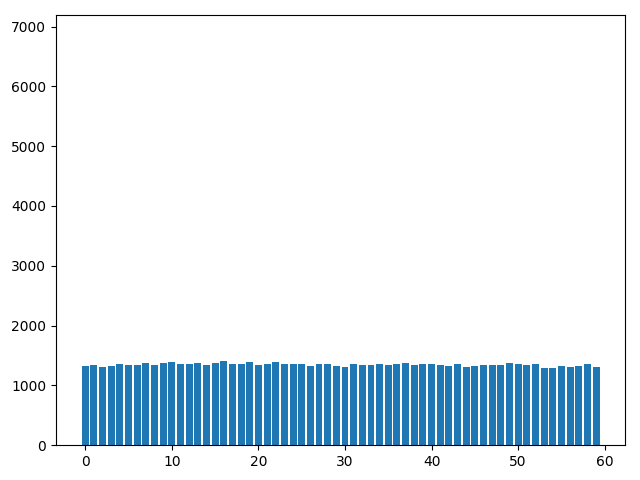
'B02208025'
hash
read
djb2:
xor8:
hash'
| B | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 5 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
Since XOR is bit-independent, symmetric and reflexive...
每項有 n bits 做 XOR ⇒ n 維向量做運算 ⇒
Conclusion 1A
最優(分散最平均)
個桶子有
倍碰撞
個桶子沒用
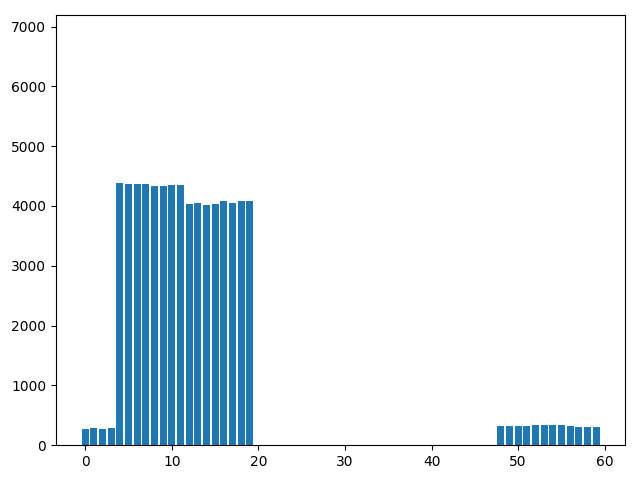
Optimization 1
Optimization 1
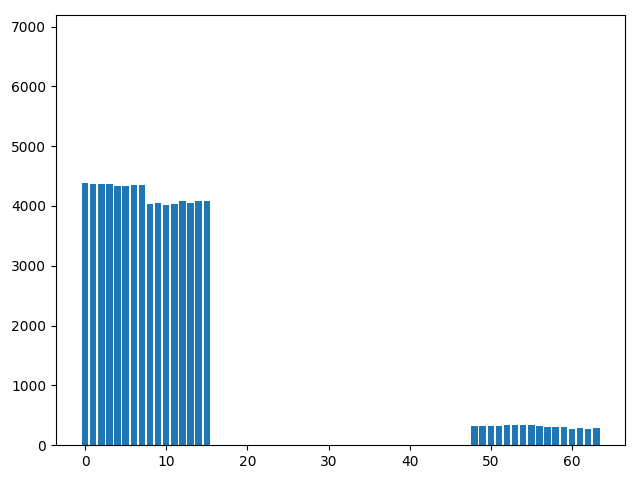

Conclusion 2A
當 xor 中有一項遵守 Uniform Distribution
最後結果同樣遵守 Uniform Distribution
By Induction
Conclusion 2B
當各項有相同性質,即
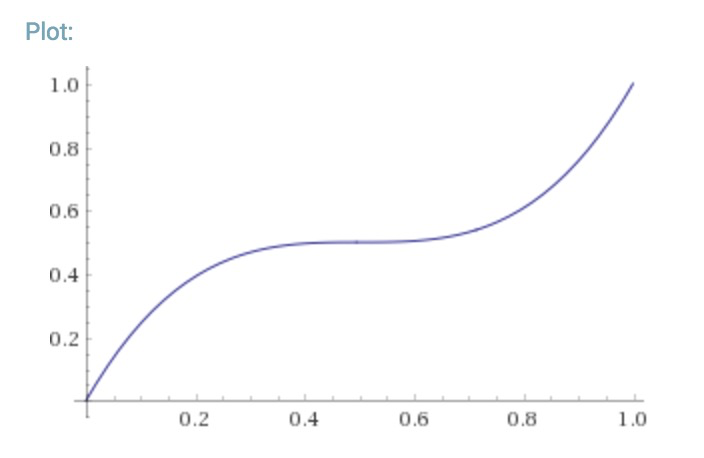
Optimization 2
'B02 208 025'
DEC
HEX
HEX
Optimization 2
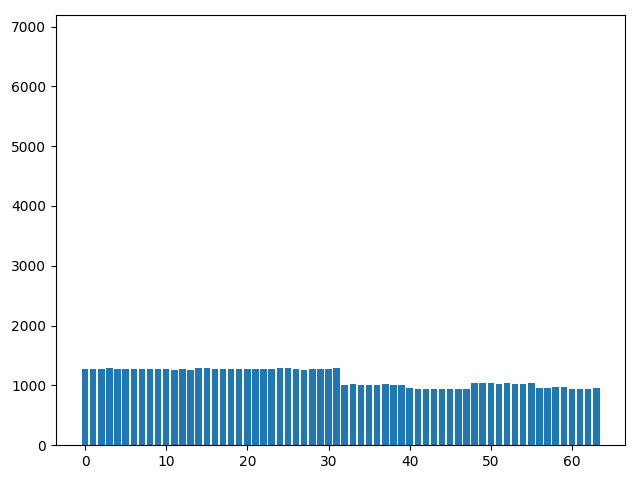

'B02 208 025'
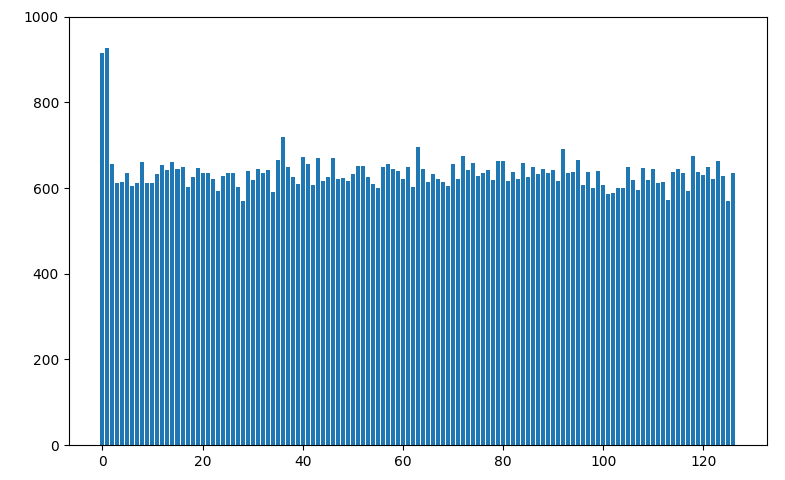
- Random
- Hash
- Histogram Equilization
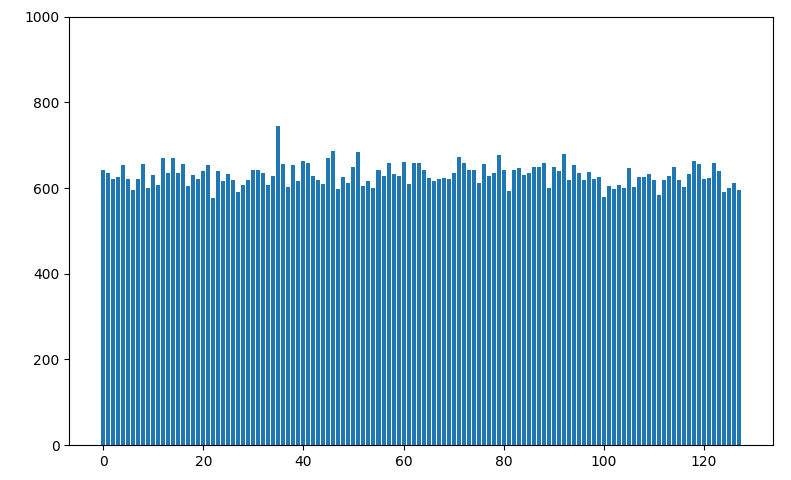
Histogram Equilization
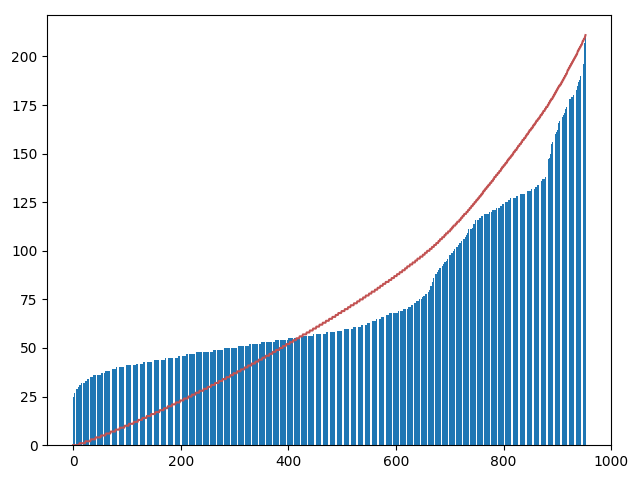
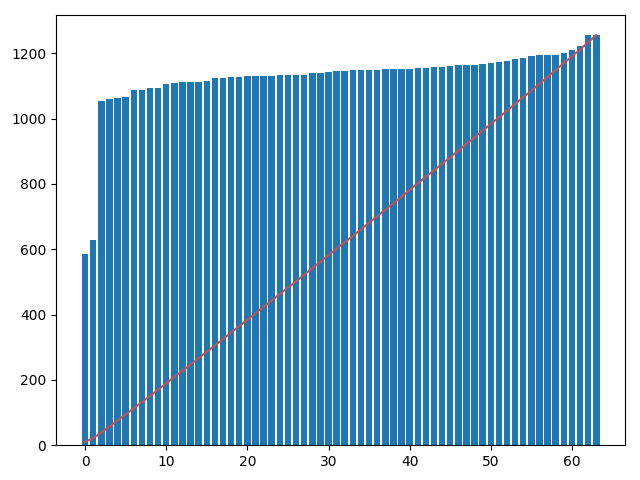
'B02 208 025'
From Histogram Equilization:
Optimization 3
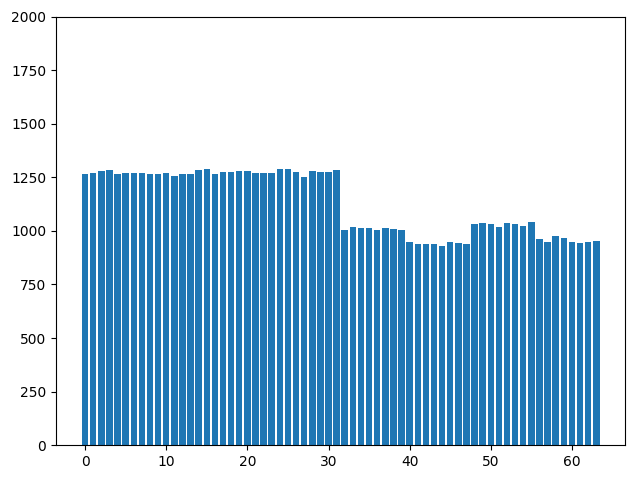
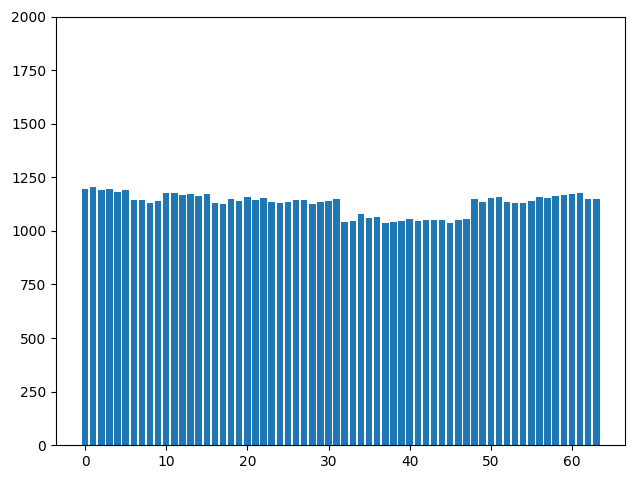
- 使用適當的桶子數
- 找到具 Uniform Distribution 的資料特徵
- 對已知分佈作 Histogram Equilization
xor8
djb2
xor8 (optimized)

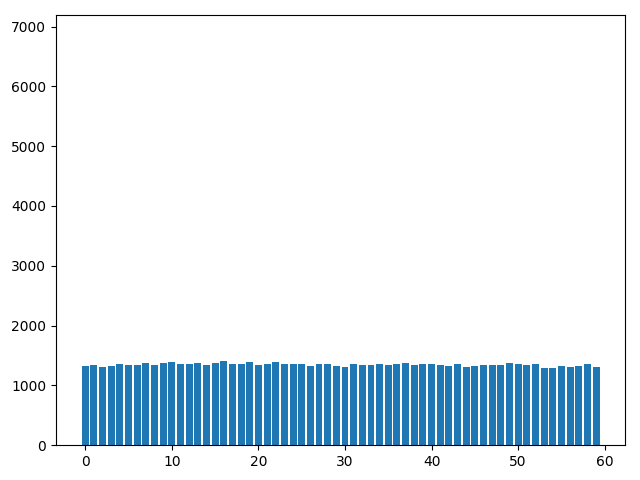
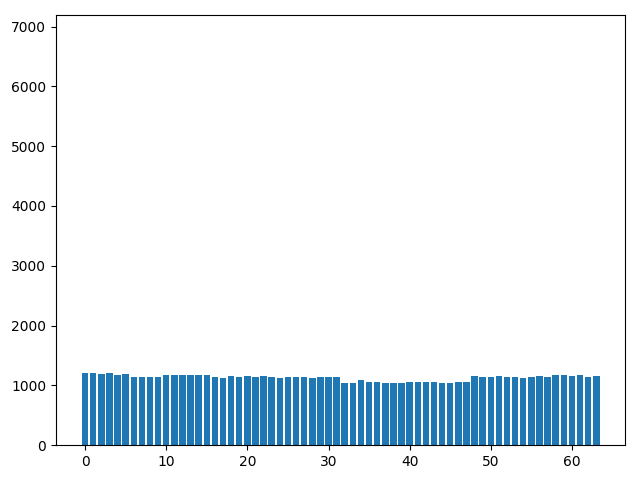
but
(156 ms ⇒ 25 ms)
Faster!
Reference
XOR8 hash function
By RedBug312
XOR8 hash function
Presentation slides of Possibility Project
- 2,079



