Upgrading FESTIM for High-Performance Computing with FEniCSx
Remi Delaporte-Mathurin, Jorgen Dokken, James Dark, Samuele Meschini
Plasma Science and Fusion Centre, MIT, Cambridge, MA, 02139, USA
Department of Numerical Analysis and Scientific Computing, Simula Research Laboratory, Oslo, Norway
5th Fusion HPC workshop, November 21-22 2024
H transport? Why do we care?
📈5 years of open-source development
Built on the FEniCS library
📑16+ publications
🧑💻23+ contributors
⭐~100 stars on GitHub
🏛️27+ institutions using the code
🧑💻5 user workshops
Component design (breeding blanket, PFCs, extraction systems...)
Experimental analysis (TDS, NRA, permeation...)
Safety studies (tritium inventory, contamination...)
Fuel cycle design (components, residence time...)
FESTIM [1]
User inputs
- Material properties
- Trap properties
- Geometry
- Boundary conditions
- Initial conditions
- ...
T
FESTIM
Outputs
- H concentration fields \(c(x,t)\)
- Temperature field \(T(x,t)\)
- surface fluxes
- inventories
- average concentration
- ...
Heat transfer model
Hydrogen transport model
3D multiphysics examples
DEMO WCLL
Permeation Against Vacuum extractor
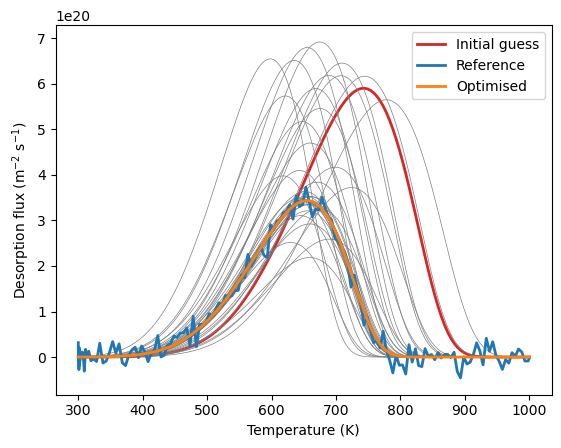
Thermo-desorption analysis
Tritium extraction system
- Permeation Against Vacuum
- Complex 3D geometry
- Coupled with fluid dynamics
- Tritium extraction from permeable membranes
Breeding Blanket modelling
- DEMO WCLL
- 3D geometry
- Multiphysics:
fluid dynamics, heat transfer, neutronics (OpenMC)
So what's the problem?
The problem: parallel scaling
100k cells
3 species
Ideal
How do we fix this?
Test case:
The solution: upgrade the finite element backend
- FESTIM is rebuilt on FEniCSx [1]
- New features and new physical models
- Better HPC performances
FEniCS problem on
45 million cells mesh [2]
FEniCSx geophysics problem [3]
Theory background
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m}) - \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k \ c_\mathrm{m} \ (n - c_{\mathrm{t}, i}) - p \ c_{\mathrm{t}, i}
Mobile H concentration
Trapped H concentration
H transport model
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m}) - \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k \ c_\mathrm{m} \ (n - c_{\mathrm{t}, i}) - p \ c_{\mathrm{t}, i}
Time derivatives
H transport model
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m}) - \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k \ c_\mathrm{m} \ (n - c_{\mathrm{t}, i}) - p \ c_{\mathrm{t}, i}
Diffusive term
H transport model
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m}) - \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k \ c_\mathrm{m} \ (n - c_{\mathrm{t}, i}) - p \ c_{\mathrm{t}, i}
Trapping term
H transport model
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m}) - \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k \ c_\mathrm{m} \ (n - c_{\mathrm{t}, i}) - p \ c_{\mathrm{t}, i}
Detrapping term
H transport model
H transport model
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m}) - \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k \ c_\mathrm{m} \ (n - c_{\mathrm{t}, i}) - p \ c_{\mathrm{t}, i}
(\frac{c_\mathrm{m}}{K_S})^- = (\frac{c_\mathrm{m}}{K_S})^+ \quad \mathrm{at \ interfaces}
This is tricky!
How are discontinuities handled in FESTIM1
Option 1: Change of variable method
\theta = \frac{c_\mathrm{m}}{K_S}
\theta^- = \theta^+ \quad \mathrm{at \ interfaces}
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m}) - \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k \ c_\mathrm{m} \ (n - c_{\mathrm{t}, i}) - p \ c_{\mathrm{t}, i}
\frac{\partial K_S \ \theta}{\partial t} = \nabla \cdot \left(D \nabla (K_S \ \theta) \right) - \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k \ K_S \ \theta \ (n - c_{\mathrm{t}, i}) - p \ c_{\mathrm{t}, i}
c_\mathrm{m} = K_S \ \theta
Solve for \( \theta \)
Reimplementing this method in FESTIM 2 shows better performances
❌If traps are not defined everywhere, then you have wasted dofs
❌Highly non-linear with dissimilar materials
3-30x
faster
Option 2: discontinuous elements everywhere
CG elements
Option 2: discontinuous elements everywhere
CG elements
DG elements
Option 2: discontinuous elements everywhere
CG elements
Duplicated degrees of freedom
❌ Not efficient!
DG elements
Option 3: Mixed domain method
Domain
Submesh 1
Submesh 2
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m})
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m})
\textcolor{#e69138}{\frac{c_\mathrm{m}}{K_S}} = \textcolor{#02506e}{\frac{c_\mathrm{m}}{K_S}}
Discontinuous Galerkin methods [1]
Option 3: Mixed domain method
✅Mixed domain can streamline multiphysics coupling
❌Some methods do not work for dissimilar materials
The mixed domain method has similar performances
3-30x
faster
- FESTIM2 is up to 30x faster than FESTIM1
-
Will improve scaling by hunting inefficiencies in FESTIM and reimplementing some functions in C++ in dolfinx
- FESTIM2 includes more physics (multi-species, chemical reactions...)
- This paves the way for:
- Streamlined multiphysics (fluid-solid problems, external solvers...)
- New interface physics (trapping, interface diffusion...)
Conclusion
👉Repository for this presentation's work: github.com/RemDelaporteMathurin/festim-benchmark
FESTIM repository: github.com/FESTIM-dev/FESTIM
Change of variable
DG everywhere
Nitsche
Penalty
Lagrange multiplier
Mixed domain
➕simple implementation
➕parameter free
➖only similar materials
➖wasted DoFs
➖only similar materials
➕simple implementation
➕can do dissimilar materials
➖penalty term \(\infty\)
➕penalty term is bounded
➖only similar materials
➕Good for multiphysics
➕No wasted DoFs
Interface discontinuities
No free lunch
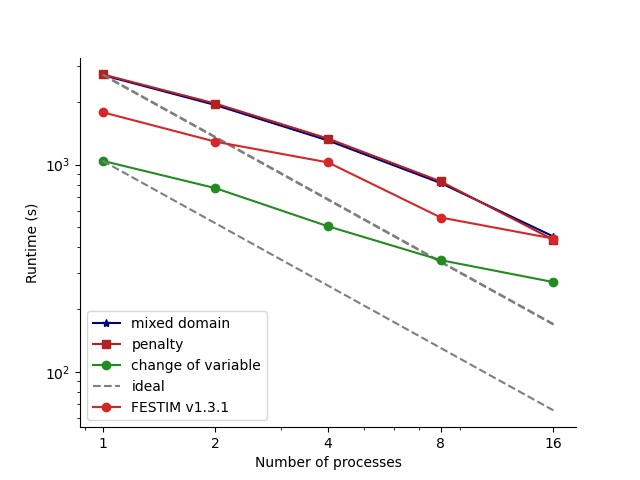
spack + proper HPC + a few optimisations cluster shows even better performances
Very large problem
- either 1 MB or an array of MBs with 2M cells
HPC fusion workshop (Nov 2024)
By Remi Delaporte-Mathurin
