Modelling helium bubble growth in tungsten
Rémi Delaporte-Mathurin
July 6, 2022
UK Atomic Energy Authority (2017)
- Tritium Breeding Blankets
- Heat transfer simulations
- Parametric optimisation
CEA French Atomic Agency (2018)
- Started the development of FESTIM
- Early work on divertor modelling
PhD CEA - LSPM (2019 - Oct 2022)
- Estimation of the tritium inventory in the ITER divertor
- Influence of helium exposure
Helium: why should we care?
Why should we care?
Why should we care?
Bubbles
Tungsten fuzz
Thermo-mechanical properties
Tritium production
Hydrogen transport
How do we model this?
Let's consider the following reactions
\mathrm{He}_x + \mathrm{He}_1 \xrightleftharpoons[]{} \mathrm{He}_{x+1}
\mathrm{He}_x\mathrm{V}_y \rightarrow \mathrm{He}_{x}\mathrm{V}_{y+1} + \mathrm{I}_1
Helium clustering (or emission)
Trap mutation
He\(_1\)
He\(_2\)
He\(_4\)
He\(_3\)
V\(_1\)He\(_7\)
V\(_1\)He\(_8\)
V\(_1\)He\(_9\)
V\(_1\)He\(_{10}\)
Our clustering scheme
Trap mutation
or
self-trapping
\mathrm{A} + \mathrm{B} \xrightleftharpoons[k^-]{k^+} \mathrm{AB}
\frac{\partial c_\mathrm{AB}}{\partial t} = -\frac{\partial c_\mathrm{A}}{\partial t} = -\frac{\partial c_\mathrm{B}}{\partial t} = k^+ c_\mathrm{A} c_\mathrm{B} - k^- c_\mathrm{AB}
k^+ = (r_A + r_B) (D_A + D_B)
k^- = \rho k^+ e^{-E_b/k_B T}
For each reaction
\frac{\partial c_i}{\partial t} = \nabla \cdot (D_i \nabla c_i) + P_i + R_i(c_1, c_2, \cdots, c_N)
3-species model:
Rate constants:
N-species model:
Diffusion coefficients
Capture radii
Diffusion
Production
Reaction
Binding energy
Issue #1: Too many equations
\( \frac{\partial c_1}{\partial t} = \nabla \cdot (D_1 \nabla c_1) + P_1 - 2 k^+_{1, 1} c_1^2 - \sum\limits_{i=2}^\infty k_{1,i}^+ c_1 c_i \)
$$ \vdots $$
\( \frac{\partial c_i}{\partial t} = \nabla \cdot (D_i \nabla c_i) - k^+_{1, i} c_1 c_i + k_{1,i-1}^+ c_1 c_{i-1} \)
$$ \vdots $$
\( \frac{\partial c_{N}}{\partial t} =\) \(- k^+_{1, N} c_1 c_{N}\) \( + k_{1,N-1}^+ c_1 c_{N-1} \)
\( \frac{\partial c_{N+1}}{\partial t} =\) \(- k^+_{1, N+1} c_1 c_{N+1}\) \( + k_{1,N}^+ c_1 c_{N} \)
\( \frac{\partial c_{N+2}}{\partial t} =\) \(- k^+_{1, N+2} c_1 c_{N+2}\) \( + k_{1,N+1}^+ c_1 c_{N+1} \)
$$ \vdots $$
💪
\( \frac{\partial c_1}{\partial t} = \nabla \cdot (D_1 \nabla c_1) + P_1 - 2 k^+_{1, 1} c_1^2 - \sum\limits_{i=2}^\infty k_{1,i}^+ c_1 c_i \)
$$ \vdots $$
\( \frac{\partial c_i}{\partial t} = \nabla \cdot (D_i \nabla c_i) - k^+_{1, i} c_1 c_i + k_{1,i-1}^+ c_1 c_{i-1} \)
$$ \vdots $$
\( \frac{\partial c_{N+1}}{\partial t} =\) \(- k^+_{1, N+1} c_1 c_{N+1}\) \( + k_{1,N}^+ c_1 c_{N} \)
\( \frac{\partial c_{N+2}}{\partial t} =\) \(- k^+_{1, N+2} c_1 c_{N+2}\) \( + k_{1,N+1}^+ c_1 c_{N+1} \)
\( \frac{\partial c_{N+3}}{\partial t} =\) \(- k^+_{1, N+3} c_1 c_{N+3}\) \( + k_{1,N+2}^+ c_1 c_{N+2} \)
$$ \vdots $$
💪
Issue #1: Too many equations
\( \frac{\partial c_1}{\partial t} = \nabla \cdot (D_1 \nabla c_1) + P_1 - 2 k^+_{1, 1} c_1^2 - \sum\limits_{i=2}^\infty k_{1,i}^+ c_1 c_i \)
$$ \vdots $$
\( \frac{\partial c_i}{\partial t} = \nabla \cdot (D_i \nabla c_i) - k^+_{1, i} c_1 c_i + k_{1,i-1}^+ c_1 c_{i-1} \)
$$ \vdots $$
\( \sum\limits_{i=N+1}^{\infty} \frac{\partial c_i}{\partial t} = k_{1,N}^+ c_1 c_{N} \)
💪
Issue #1: Too many equations
\( \frac{\partial c_1}{\partial t} = \nabla \cdot (D_1 \nabla c_1) + P_1 - 2 k^+_{1, 1} c_1^2 - \sum\limits_{i=2}^\infty k_{1,i}^+ c_1 c_i \)
$$ \vdots $$
\( \frac{\partial c_i}{\partial t} = \nabla \cdot (D_i \nabla c_i) - k^+_{1, i} c_1 c_i + k_{1,i-1}^+ c_1 c_{i-1} \)
$$ \vdots $$
\( \frac{\partial c_b}{\partial t} = k_{1,N}^+ c_1 c_{N} \)
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
💪
Issue #1: Too many equations
\( \frac{\partial c_1}{\partial t} = \nabla \cdot (D_1 \nabla c_1) + P_1 - 2 k^+_{1, 1} c_1^2 - \sum\limits_{i=2}^{N}k_{1,i}^+ c_1 c_i - \sum\limits_{i=N+1}^\infty k_{i, 1}^+c_i c_1 \)
$$ \vdots $$
\( \frac{\partial c_i}{\partial t} = \nabla \cdot (D_i \nabla c_i) - k^+_{1, i} c_1 c_i + k_{1,i-1}^+ c_1 c_{i-1} \)
$$ \vdots $$
\( \frac{\partial c_b}{\partial t} = k_{1,N}^+ c_1 c_{N} \)
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
💪
Issue #1: Too many equations
\( \frac{\partial c_1}{\partial t} = \nabla \cdot (D_1 \nabla c_1) + P_1 - 2 k^+_{1, 1} c_1^2 - \sum\limits_{i=2}^{N}k_{1,i}^+ c_1 c_i - \langle k_b^+\rangle c_1 c_b \)
$$ \vdots $$
\( \frac{\partial c_i}{\partial t} = \nabla \cdot (D_i \nabla c_i) - k^+_{1, i} c_1 c_i + k_{1,i-1}^+ c_1 c_{i-1} \)
$$ \vdots $$
\( \frac{\partial c_b}{\partial t} = k_{1,N}^+ c_1 c_{N} \)
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle k_b^+ \rangle = \left( \sum\limits_{i=N+1}^{\infty} k_ {i, 1}^+ c_i \right) / c_b\) : average clustering rate in bubbles
💪
Issue #1: Too many equations
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle k_b^+ \rangle = \left( \sum\limits_{i=N+1}^{\infty} k_ {i, 1}^+ c_i \right) / c_b\)
\( = \left(\sum\limits_{i=N+1}^{\infty} 4 \pi D_1 (r_1 + r_i) c_i\right) / c_b \)
💪
average clustering rate in bubbles
Issue #2: what's the value of \( \langle k_b^+ \rangle \)?
Issue #2: what's the value of \( \langle k_b^+ \rangle \)?
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle r_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} r_ i c_i \right) / c_b\) : average bubble radius
\( \langle k_b^+ \rangle \)\( = \left( \sum\limits_{i=N+1}^{\infty} k_ {i, 1}^+ c_i \right) / c_b\)
\( = \left(\sum\limits_{i=N+1}^{\infty} 4 \pi D_1 (r_1 + r_i) c_i\right) / c_b \)
\( =4 \pi D_1 (r_1 + \langle r_b \rangle)\)
💪
average clustering rate in bubbles
\( r_i = r_{\mathrm{He}_0\mathrm{V}_1} + \left( \frac{3}{4\pi} \frac{a_0^3}{2} n_{\mathrm{V},i} \right)^{1/3} - \left( \frac{3}{4\pi} \frac{a_0^3}{2} \right)^{1/3}\)
💪
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle k_b^+ \rangle = 4 \pi D_1 (r_1 + \langle r_b \rangle)\) : average clustering rate in bubbles
\( \langle r_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} r_ i c_i \right) / c_b\) : average bubble radius
Issue #3: what's the value of \( \langle r_b \rangle \)?
\( r_i = r_{\mathrm{He}_0\mathrm{V}_1} + \left( \frac{3}{4\pi} \frac{a_0^3}{2} \frac{i}{4} \right)^{1/3} - \left( \frac{3}{4\pi} \frac{a_0^3}{2} \right)^{1/3}\)
\( n_{\mathrm{V},i} = i/4 \) : 4 He per vacancy
💪
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle k_b^+ \rangle = 4 \pi D_1 (r_1 + \langle r_b \rangle)\) : average clustering rate in bubbles
\( \langle r_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} r_ i c_i \right) / c_b\) : average bubble radius
Issue #3: what's the value of \( \langle r_b \rangle \)?
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle k_b^+ \rangle = 4 \pi D_1 (r_1 + \langle r_b \rangle)\) : average clustering rate in bubbles
\( \langle r_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} r_ i c_i \right) / c_b\) : average bubble radius
\( \langle i_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} i c_i \right) / c_b\) : average He content in bubbles
\( n_{\mathrm{V},i} = i/4 \) : 4 He per vacancy
💪
\( \langle r_b \rangle = r_{\mathrm{He}_0\mathrm{V}_1} + \left( \frac{3}{4\pi} \frac{a_0^3}{2} \frac{\langle i_b \rangle}{4} \right)^{1/3} - \left( \frac{3}{4\pi} \frac{a_0^3}{2} \right)^{1/3}\)
\( r_i = r_{\mathrm{He}_0\mathrm{V}_1} + \left( \frac{3}{4\pi} \frac{a_0^3}{2} \frac{i}{4} \right)^{1/3} - \left( \frac{3}{4\pi} \frac{a_0^3}{2} \right)^{1/3}\)
Issue #3: what's the value of \( \langle r_b \rangle \)?
\( \langle r_b \rangle = r_{\mathrm{He}_0\mathrm{V}_1} + \left( \frac{3}{4\pi} \frac{a_0^3}{2} \frac{\langle i_b \rangle}{4} \right)^{1/3} - \left( \frac{3}{4\pi} \frac{a_0^3}{2} \right)^{1/3}\)
\( \frac{\sum\limits_{i=N+1}^{\infty} i^{1/3} c_i } { c_b} \approx \left( \sum\limits_{i=N+1}^{\infty} i c_i / c_b \right)^{1/3} = \langle i_b \rangle ^{1/3}\)
When \( c_i \) has a narrow gaussian distribution (ie. \(\sigma / \mu \ll 1\) )
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle k_b^+ \rangle = 4 \pi D_1 (r_1 + \langle r_b \rangle)\) : average clustering rate in bubbles
\( \langle i_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} i c_i \right) / c_b\) : average He content in bubbles
\( \langle i_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} i c_i \right) / c_b\)
💪
Issue #4: what's the value of \( \langle i_b \rangle \)?
\( \langle i_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} i c_i \right) / c_b\)
\( \langle i_b \rangle c_b= \sum\limits_{i=N+1}^{\infty} i c_i \)
💪
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle k_b^+ \rangle = 4 \pi D_1 (r_1 + \langle r_b \rangle)\) : average clustering rate in bubbles
\( \langle i_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} i c_i \right) / c_b\) : average He content in bubbles
Issue #4: what's the value of \( \langle i_b \rangle \)?
\( \langle i_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} i c_i \right) / c_b\)
\( \langle i_b \rangle c_b= \sum\limits_{i=N+1}^{\infty} i c_i \)
\(\frac{\partial \langle i_b \rangle c_b}{\partial t} = \sum\limits_{i=N+1}^{\infty} i \frac{\partial c_i}{\partial t}\)
💪
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle k_b^+ \rangle = 4 \pi D_1 (r_1 + \langle r_b \rangle)\) : average clustering rate in bubbles
\( \langle i_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} i c_i \right) / c_b\) : average He content in bubbles
Issue #4: what's the value of \( \langle i_b \rangle \)?
\( \langle i_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} i c_i \right) / c_b\)
\( \langle i_b \rangle c_b= \sum\limits_{i=N+1}^{\infty} i c_i \)
\(\frac{\partial \langle i_b \rangle c_b}{\partial t} = \sum\limits_{i=N+1}^{\infty} i \frac{\partial c_i}{\partial t}\)
💪
\(\frac{\partial \langle i_b \rangle c_b}{\partial t} = (N+1) k_{1, N}^+ c_1 c_N + \langle k_b^+ \rangle c_1 c_b \)
↓ trust me
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle k_b^+ \rangle = 4 \pi D_1 (r_1 + \langle r_b \rangle)\) : average clustering rate in bubbles
\( \langle i_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} i c_i \right) / c_b\) : average He content in bubbles
Issue #4: what's the value of \( \langle i_b \rangle \)?
\( \frac{\partial c_1}{\partial t} = \nabla \cdot (D_1 \nabla c_1) + P_1 - 2 k^+_{1, 1} c_1^2 - \sum\limits_{i=2}^{N-1}k_{1,i}^+ c_1 c_i - \langle k_b^+\rangle c_1 c_b \)
$$ \vdots $$
\( \frac{\partial c_i}{\partial t} = \nabla \cdot (D_i \nabla c_i) - k^+_{1, i} c_1 c_i + k_{1,i-1}^+ c_1 c_{i-1} \)
$$ \vdots $$
\( \frac{\partial c_b}{\partial t} = k_{1,N}^+ c_1 c_{N} \)
💪
\(\frac{\partial \langle i_b \rangle c_b}{\partial t} = (N+1) k_{1, N}^+ c_1 c_N + \langle k_b^+ \rangle c_1 c_b \)
\( c_b = \sum\limits_{i=N+1}^{\infty} c_i \) : bubble concentration
\( \langle k_b^+ \rangle = 4 \pi D_1 (r_1 + \langle r_b \rangle)\) : average clustering rate in bubbles
\( \langle i_b \rangle = \left( \sum\limits_{i=N+1}^{\infty} i c_i \right) / c_b\) : average He content in bubbles
Issue #4: what's the value of \( \langle i_b \rangle \)?
Assumption time!
- Only pure He clusters are mobile
- Trap-mutation from 7 He
- Grouping starts at \( i > 6 \)
- He/V ratio: 4
- No He emission from bubbles
- Pre-existing vacancies are neglected
- We don't solve for W self-interstitials
-
Diffusion coefficients from Faney et al. Nucl. Fusion (2015)
-
Dissociation energies from Becquart et al. J. Nucl. Mater. (2010)
Diffusivities and binding energies
| He1 | 0.13 | - | |
| He2 | 0.20 | 1.0 | |
| He3 | 0.25 | 1.5 | |
| He4 | 0.20 | 1.5 | |
| He5 | 0.12 | 1.6 | |
| He6 | 0.30 | 2.0 |
\( D_0 \, \mathrm{(m^2 \, s^{-1})} \)
\( E_D \, \mathrm{(eV)} \)
\( E_b \, \mathrm{(eV)} \)
2.95 \times 10^{-8}
3.24 \times 10^{-8}
2.26 \times 10^{-8}
1.68 \times 10^{-8}
5.20 \times 10^{-9}
1.20 \times 10^{-9}
He-to-Vacancy ratio
Faney et al Nucl. Fusion 2014
Rapidly negligible
The parameter \( N \) has no influence
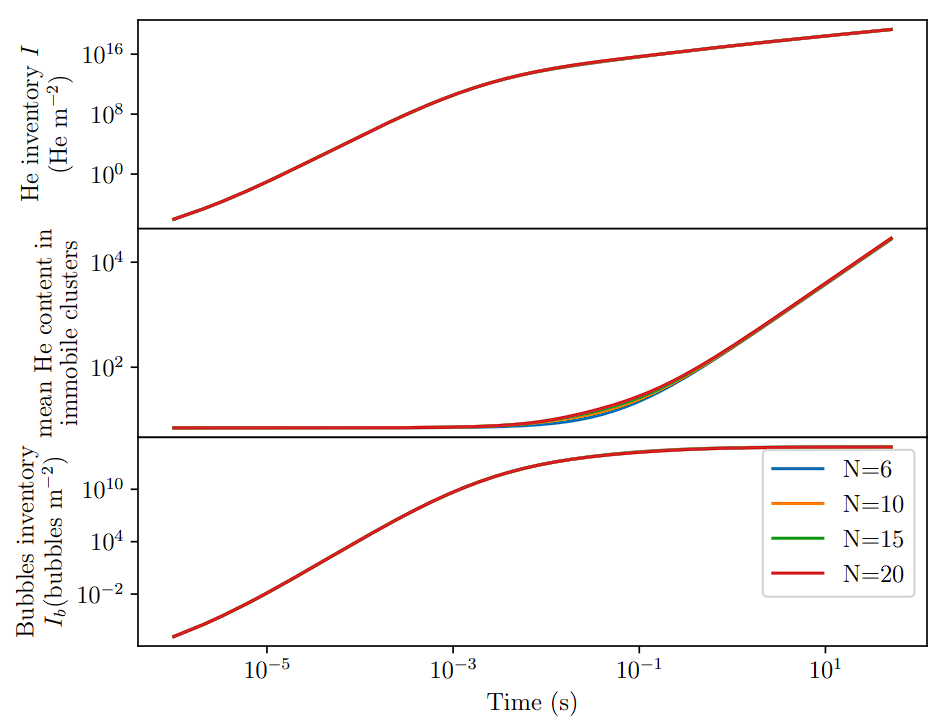
\( \frac{\partial c_1}{\partial t} = \nabla \cdot (D_1 \nabla c_1) + P_1 - 2 k^+_{1, 1} c_1^2 - \sum\limits_{i=2}^{6}k_{1,i}^+ c_1 c_i - \langle k_b^+\rangle c_1 c_b \)
$$ \vdots $$
\( \frac{\partial c_6}{\partial t} = \nabla \cdot (D_6 \nabla c_6) - k^+_{1, 6} c_1 c_6 + k_{1,5}^+ c_1 c_{5} \)
\( \frac{\partial c_b}{\partial t} = k_{1,6}^+ c_1 c_{6} \)
\(\frac{\partial \langle i_b \rangle c_b}{\partial t} = 7 k_{1, 6}^+ c_1 c_6 + \langle k_b^+ \rangle c_1 c_b \)
Our clustering scheme
average clustering rate in bubbles
\( \langle k_b^+ \rangle = 4 \pi D_1 (r_1 + \langle r_b \rangle)\)
average bubble radius
\( \langle r_b \rangle = r_{\mathrm{He}_0\mathrm{V}_1} + \left( \frac{3}{4\pi} \frac{a_0^3}{2} \frac{\langle i_b \rangle}{4} \right)^{1/3} - \left( \frac{3}{4\pi} \frac{a_0^3}{2} \right)^{1/3}\)
Only 8 equations:
Let's check our implementation...
Code comparison
Faney et al. Nucl. Fusion 2014
- 100 eV He
- Flux \( 10^{22} \mathrm{\, m^{-2} \, s^{-1}} \)
- Fluence \(5 \times 10^{25} \mathrm{\ m^{-2}} \)
30 nm
\( c_i = 0 \)
\( c_i = 0 \)
Discrepancies at high T due to different sets of dissociation energies
Dissociation energy sensitivity
Solid: +0
Dashed: + 0.5 eV
Dash-point: - 0.5 eV
Comparison with experiments
Mykola Ialovega's PhD research
Comparison with experiments
Mykola Ialovega's PhD research
Code verification & validation
✔️Results in agreement with more complex models → additional assumptions are valid
✔️The model is in qualitative agreement with experiments
Let's run a standard case
Half-slab case
- "Semi-infinite" (0.6 mm)
-
Helium source
- 100 eV
-
Gaussian distribution
- \( \mu =1.5 \mathrm{nm} \, \sigma = 1.5 \mathrm{nm} \)
- Flux \( 10^{22} \, \mathrm{m^{-2} \, s^{-1} }\)
- Temperature 1000 K
\(c_i = 0 \)
0.6 mm
Half-slab case
Can be compared to experiments!
What's the influence of exposure conditions on bubble growth?
Divertor exposure conditions
Surface temperature: \( 350 \mathrm{-} 2000 \mathrm{K}\)
Helium flux: \(10^{19} \mathrm{-} 10^{21} \mathrm{m^{-2} \, s^{-1}}\)
Parametric study
Varying temperature and particle flux
Parametric study
\( c_\mathrm{He_1 \, ideal} = \frac{\varphi_\mathrm{imp} R_p}{D_1(T)} \)
Varying temperature and particle flux
Parametric study
1 h
\( \int c_b \langle i_b \rangle dx\)
He inventory in bubbles
Parametric study
1 h
\( \int c_b \langle i_b \rangle dx\)
He inventory in bubbles
Parametric study
1 h tert
\( \bar{\langle i_b \rangle} = \frac{\int c_b \langle i_b \rangle dx}{\int c_b dx} = \frac{\mathrm{inventory}}{\mathrm{total \, bubbles}}\)
Mean helium content in bubbles
Parametric study
1 h
\( \bar{\langle i_b \rangle} = \frac{\int c_b \langle i_b \rangle dx}{\int c_b dx} = \frac{\mathrm{inventory}}{\mathrm{total \, bubbles}}\)
Mean helium content in bubbles
Parametric study
\(\int c_b dx\)
Total bubbles
1 h efef
Parametric study
\(\int c_b dx\)
Total bubbles
1 h efef
Two regimes can be identified
Two regimes can be identified
\( \langle i_b \rangle \) is low
\( \langle k_b^+ \rangle \) is low
Two regimes can be identified
Nucleation
🡺Self trapping
🡺\( c_b \) increases
\( \langle i_b \rangle \) is low
\( \langle k_b^+ \rangle \) is low
Two regimes can be identified
Nucleation
🡺Self trapping
🡺\( c_b \) increases
Growth
🡺\( \langle i_b \rangle \) increases
🡺\( \langle k_b^+ \rangle \) increases
\( \langle i_b \rangle \) is low
\( \langle k_b^+ \rangle \) is low
When \( c_b \) is large enough
Two regimes can be identified
Nucleation
🡺Self trapping
🡺\( c_b \) increases
Growth
🡺\( \langle i_b \rangle \) increases
🡺\( \langle k_b^+ \rangle \) increases
🡺Nucleation stops
\( \langle i_b \rangle \) is low
\( \langle k_b^+ \rangle \) is low
When \( c_b \) is large enough
Two regimes can be identified
\(\frac{\partial c_b}{\partial t} = k_{1, N}^+ c_1 c_N\)
\(\frac{\partial \langle i_b \rangle c_b}{\partial t} = (N+1) k_{1, N}^+ c_1 c_N + \langle k_b^+ \rangle c_1 c_b \)
\( \langle i_b \rangle \approx 7 \Leftrightarrow \langle k_b^+ \rangle \approx 0\)
\( \Leftrightarrow \frac{\partial \langle i_b \rangle c_b}{\partial t} \approx (N+1) k_{1, N}^+ c_1 c_N \)
\( \Leftrightarrow \langle i_b \rangle \frac{\partial c_b}{\partial t} + c_b \frac{\partial \langle i_b \rangle}{\partial t} \approx (N+1) k_{1, N}^+ c_1 c_N \)
\( \Leftrightarrow \frac{\partial \langle i_b \rangle}{\partial t} \propto N +1 - \langle i_b \rangle \approx 0\)
\( c_b \gg c_N \)
\(\Leftrightarrow c_N \approx 0 \)
\(\Leftrightarrow \frac{\partial c_b}{\partial t} \approx 0 \)
\( \Leftrightarrow \frac{\partial \langle i_b \rangle c_b}{\partial t} \approx \langle k_b^+ \rangle c_1 c_b \)
\( \Leftrightarrow \frac{\partial \langle i_b \rangle}{\partial t} \approx \langle k_b^+ \rangle c_1\)
Nucleation regime
Growth regime
Where to go from here?
Bursting needs to be added
Depth (nm)
Bubble radius (nm)
WIP: Collaboration with University of Tennesse, Knoxville
Influence on hydrogen transport
Coupled to the H transport code FESTIM
Reproduced TDS of deuterium in W pre-damaged with helium
Traps induced by bubbles!
Indirect sources of helium
Neutronics monoblock simulations with OpenMC
Indirect sources of helium
Tritium decay simulations with FESTIM
Neutronics monoblock simulations with OpenMC
Indirect sources of helium
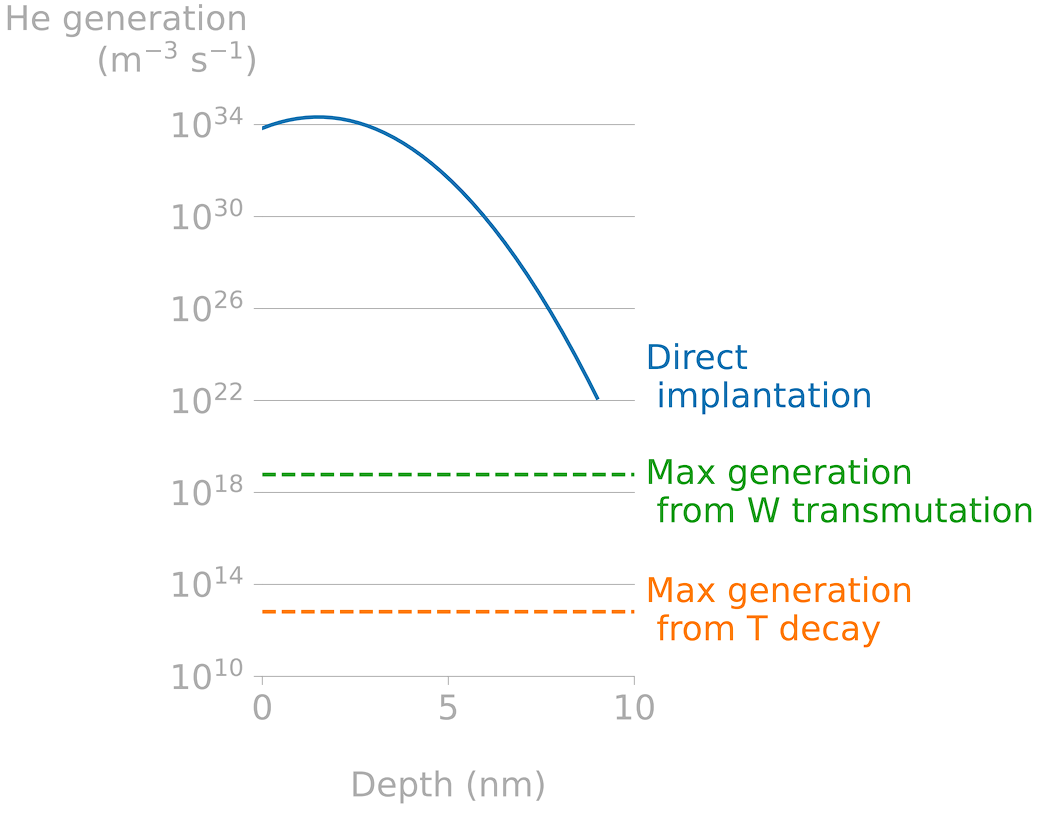
Tritium decay simulations with FESTIM
Neutronics monoblock simulations with OpenMC
Main conclusions
- The grouping technique is a powerful technique to lower the complexity of clustering schemes.
- Its implementation has been compared to published numerical results and experiments.
- Two bubble growth regimes were identified: nucleation and growth.
- The model needs to be improved to account for bubble bursting.
Thank you for your attention!
Any questions?
\mathrm{H} + \mathrm{[ ]} \xrightleftharpoons[k^-]{k^+} \mathrm{[H]}
\( k^+ \propto D = D_0 \exp{(-E_D/k_B T)}\)
\( k^- = k^-_0 \exp{(-(E_D+E_b)/k_B T)}\)
\( k^- \propto D \exp{(-E_b/k_B T)}\)
\( k^- \propto k^+ \exp{(-E_b/k_B T)}\)
K = \frac{c_A c_B}{c_{AB}} = \frac{k^+}{k^-} = \exp{(\frac{-\Delta G_0}{k_B T})}
\varphi_H = D_L(T)\nabla C_L + \frac{D_L(T) V_H}{RT}C_L \nabla P_H
\varphi_{H \, , \mathrm{diffusion \, pure}} = D_L(T)\nabla C_L
\varphi_{H \, , \mathrm{diffusion \, pure}} \ll \varphi_H
???
Wall Forum Seminar Garching
By Remi Delaporte-Mathurin
