1. BASICS

• Vector
• Units
• Addition
• Subtraction
• Scalar-vector multiplication

It's important to keep track of your units.

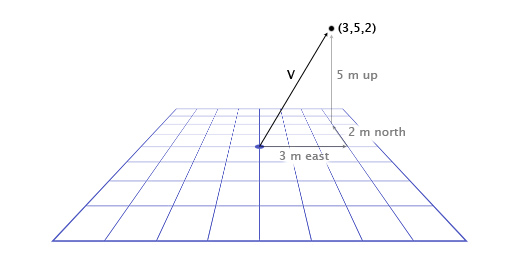
A vector by itself is just a set of numbers

it is only given meaning by its context.

V (3,5,2)

Why do we care about linear algebra?

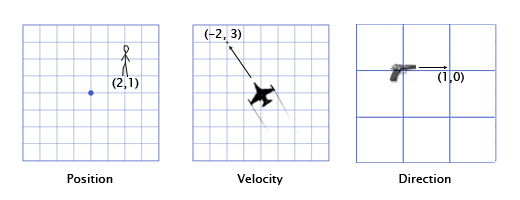
In games, vectors are used to store positions, directions, and velocities. Here are some 2-Dimensional examples

Vector addition

Why do we want to add vectors together? One of the most common applications in games for vector addition is physics integration.

Any physically-based object will likely have vectors for position, velocity, and acceleration. 

(1,2)

(1,1)

(1,-1)

(1,-2)

Here is what his jump looks like over the course of four more frames.

Mario starts at position (0,0).

As he starts the jump, his velocity is (1,2) 

Mario is moving upwards quickly, but also to the right.

 His acceleration throughout is (0,-1)

Gravity is pulling him downwards.

(1,0)

HOW IT WORKS

The game calculates the new velocity and position using physics integration (via vector addition).

Fun fact: this is the same kind of integration problem that you solve using integral calculus - we are just using an approximate brute-force approach.

Vector subtraction

(1,2)

(3,1)

(4,3)

(4,3)-(1,2) = (4-1, 3-2) = (3,1)

Vector subtraction is useful for getting a vector that points from one position to another.

Scalar-vector multiplication

For example, we can simulate basic air resistance by multiplying the player's velocity by 0.9 every frame. To do this, we just multiply each component of the vector by the scalar. If the player's velocity is (-10,0), the new velocity is:

0.9*(-10,0) = (-9,0)

Player's velocity (-10,0)

Air resistance factor 0.9

2. SOLVING VECTOR PROBLEMS

• Magnitude
• Distance
• Normalization
• Dot product
• Cross product

Length (Magnitude)

If we have a ship with velocity vector V (4,3), we might also want to know how fast it is going, in order to calculate how much the screen should shake or how much fuel it should use. To do that, we need to find the length (or magnitude) of vector V. The length of a vector is often written using || for short, so the length of V is |V|.

We can think of V as a right triangle with sides 4 and 3, and use the Pythagorean theorem to find the hypotenuse: x2 + y2 = h2. That is, the length of a vector H with components (x,y) is sqrt(x2+y2). So, to calculate the speed of our ship, we just use:

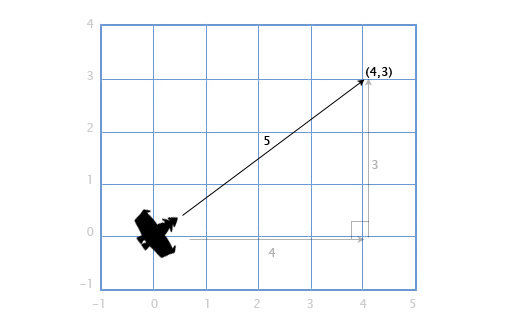
This works with 3D vectors as well -- the length of a vector with components (x,y,z) is sqrt(x^2+y^2+z^2).

Length (Magnitude)

|V| = sqrt(4^2+3^2) = sqrt(25) = 5

Distance

(1,2)

(3,3)

2.23

If the player P is at (3,3) and there is an explosion E at (1,2), we need to find the distance between them to see how much damage the player takes. This is easy to find by combining two tools we have already gone over: subtraction and length. We subtract P-E to get the vector between them, and then find the length of this vector to get the distance between them. The order doesn't matter here, |E-P| will give us the same result.

Distance = |P-E| = |(3,3)-(1,2)| = |(2,1)| = sqrt(2^2+1^2) = sqrt(5) = 2.23

Normalization

When we are dealing with directions (as opposed to positions or velocities), it is important that they have unit length (length of 1). This makes life a lot easier for us. For example, let's say there is a gun pointing in the direction of (1,0) that shoots a bullet at 20 m/s. What is the velocity of the bullet? Since the direction has length 1, we can just multiply the direction and the bullet speed to get the bullet velocity: (20,0). If the direction vector had any other length, we couldn't do this -- the bullet would be too fast or too slow.

Normalization

A vector with a length of 1 is called "normalized". So how do we normalize a vector (set its length to 1)? Easy, we divide each component by the vector's length. If we want to normalize vector V with components (3,4), we just divide each component by its length, 5, to get (3/5, 4/5). Now we can use the pythagorean theorem to prove that it has length 1:

Dot product

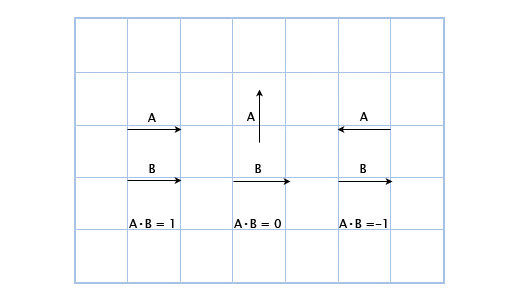
Dot product

Is he in the guard's field of view?

 We can find out by checking the sign of the dotproduct of D and V (the vector from the guard to the hero).

D

V

G

H

 Guard at position G (11,4) ,
facing the direction D (-5,0)

45° field of view

Hero sneaking by at position H (9,1)

Dot product

V = H-G = (9,1)-(11,4) = (9-11,1-4) = (-2,-3)
D•V = (-5,0)•(-2,-3) = (-5)*(-2)+(0)*(-3) = 10

Since 10 is positive, the hero is in the guard's field of view!

D

V

G

H

Dot product

We know that the dot product is related to the extent to which the vectors are pointing in the same direction, but what is the exact relation? It turns out that the exact equation for the dot product is:

AB = |A||B|cosθ

Where θ is the angle between A and B. This allows us to solve for θ if we want to find out the angle:

θ = acos([AB]/[|A||B|]).

Normalizing vectors makes our life easier! If A and B are normalized, then the equation is simply:

θ = acos(AB)

D

V

G

H

Dot product

Let's revisit the guard scenario above, except the guard's field of view is only 45. First, we get the normalized vectors for the direction the guard is facing (D'), and the direction from the guard to the hero (V'). Then, we check the angle between them. If it is greater than 22.5 (half of the field of view), then the hero is not seen.

D

V

G

H

//Initialize starting vectors
vec2 guard_pos = vec2(11,4);
vec2 guard_facing = vec2(-5,0);
vec2 hero_pos = vec2(9,1);

//Prepare normalized vectors
vec2 guard_facing_n = normalize(guard_facing);
vec2 guard_to_hero = normalize(hero_pos - guard_pos);

//Check angle
float angle = acos(dot(guard_facing_n, guard_to_hero));

Cross product

(-1,2)

(2,1)

(1,-2)

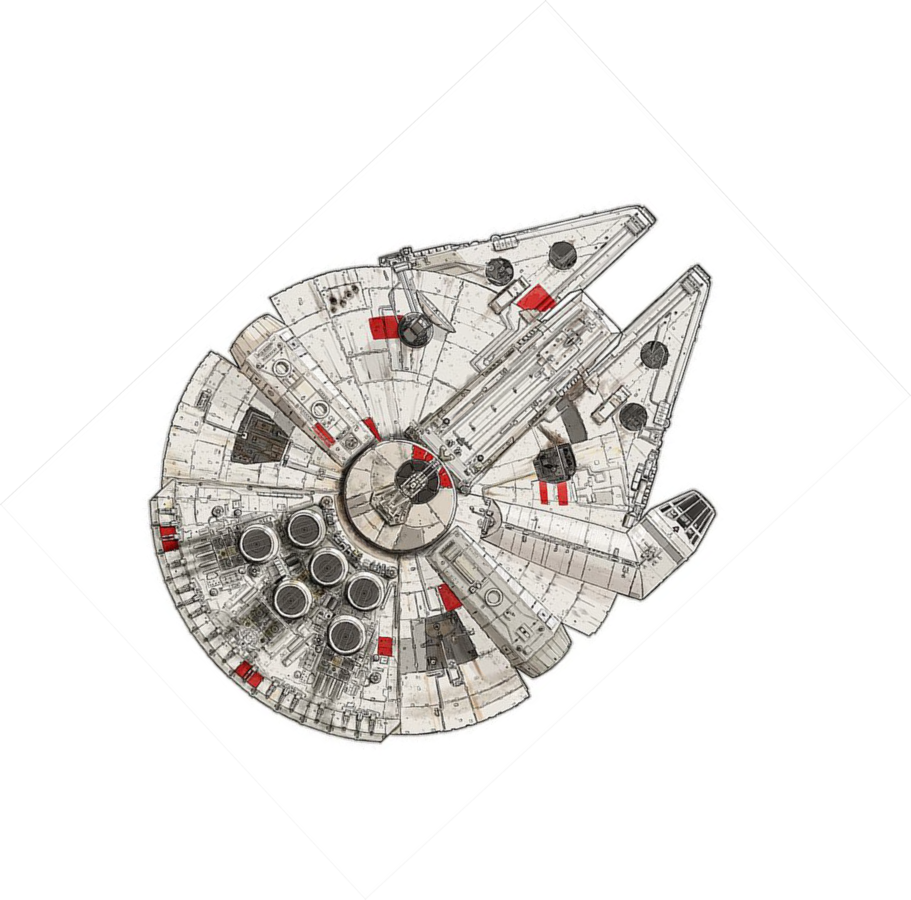
Milennium Falcon has cannons that fire to the left and right. Given that the ship is facing along the direction vector (2,1), in which directions do the cannons fire? This is easy in 2D: to rotate 90 degrees clockwise, just flip the two vector components, and then switch the sign of the second component. (a,b) becomes (b,-a). So, if the ship is facing along (2,1), the right-facing cannons fire towards (1,-2). The left-facing cannons fire in the opposite direction, so we flip both signs to get: (-1,2).

Cross product

A

S

C

So, what if we want to do this in 3D? Let's revisit our star ship. We have a vector for the direction of the antenna A, going straight up (0,1,0), and the direction of the north-north-east sector

S (1,0,2), and we want to find the direction the course C should stick out in order to avoid attack. The ship has to be perpendicular to the top antenna, and also perpendicular to the Sector S. To solve this, we can use the cross product: C = A x S.

Cross product

A

S

C

The cross product of A(a1,a2,a3)) and B(b1,b2,b3)) is:

(a2b3-a3b2, a3b1-a1b3, a1b2-a2b1)
So now we can plug in our numbers and solve our problem:

C = AxS = (0,1,0)x(1,0,2) = ([1*2-0*0], [0*1-0*2], [0*0-1*1]) = (2,0,-1)

This is pretty ugly to do by hand. For most graphics and game work I would recommend just encapsulating it in a function like the one below, and never thinking about the details again.

Cross product

A

S

C

vec3 cross(vec3 a, vec3 b) {
    vec3 result;
    result[0] = a[1] * b[2] - a[2] * b[1];
    result[1] = a[2] * b[0] - a[0] * b[2];
    result[2] = a[0] * b[1] - a[1] * b[0];
    return result;
}

Cross product

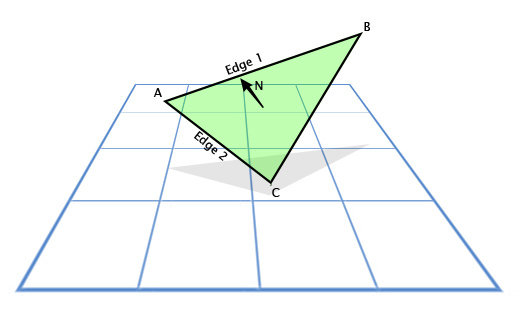
Another common use for the cross product in games is to find surface normals -- the direction that a surface is facing. For example, let's take a triangle witH vertex vectors A, B and C. How do we find the direction that the triangle is facing? It seems tricky, but we have the tools to do it now. We can use subtraction to get the direction from A to C (C-A) 'Edge 1' and A to B (B-A) 'Edge 2', and then use the cross product to find a new vector N perpendicular to both of them... the surface normal.

vec3 GetTriangleNormal(vec3 a, vec3 b, vec3 c) {
    vec3 edge1 = b-a;
    vec3 edge2 = c-a;
    vec3 normal = cross(edge1,edge2);
    return normal;
}

Cross product

Fun fact: the basic expression for lighting in games is just N•L, where N is the surface normal, and L is the normalized light direction. This is what makes surfaces bright when they face towards the light, and dark when they don't.

3. TRANSFORMATIONS

• Rotation
• Matrices

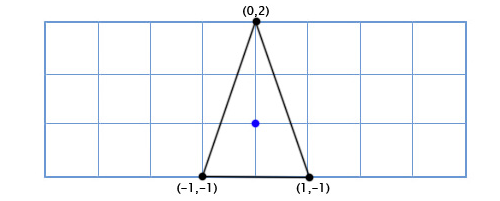
Let's say we're making an Asteroids game on really old hardware, and we want to have a simple 2D space ship that can rotate freely. The ship model looks like this

Rotation

   vec2 rotate(vec2 point, float angle){
           vec2 rotated_point;
           rotated_point.x = point.x * cos(angle) - point.y * sin(angle);
           rotated_point.y = point.x * sin(angle) + point.y * cos(angle);
           return rotated_point;
   }

Applying this to our three points gives us the following shape:

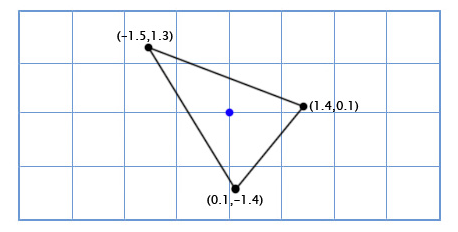
Rotation

So how do we draw it when the player rotates by an arbitrary amount, like 49 degrees counter-clockwise? Well, trigonometry we can create a function for 2D rotation that inputs a point and an angle, and outputs a rotated point:

Cosine and sine operations are pretty slow

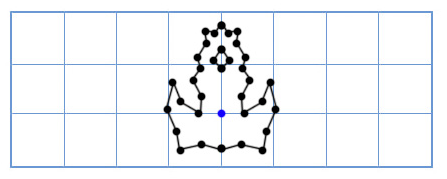
Now our old method is too slow! We don't have enough sine and cosine operations to rotate this many points.

"What if instead of rotating each point in the model, we just rotate the model's x and y axes instead?"

X

Y

X

Y

Rotation

To get the rotated x and y axes we just use the trigonometric function, if we are rotating by 49 degrees, then we get the new x-axis by rotating (1,0) by 49 degrees and we get the y-axis by rotating (0,1) by 49 degrees. Our new x-axis is (0.66, 0.75), and our new y-axis is (-0.75, 0.66).

X'

Y'

Rotation

   vec2 rotate(vec2 point, float angle){
           vec2 rotated_point;
           rotated_point.x = point.x * cos(angle) - point.y * sin(angle);
           rotated_point.y = point.x * sin(angle) + point.y * cos(angle);
           return rotated_point;
   }

x(a,b) + y(c,d)

Rotation

4. Matrices

  [a c
    b d]

When you multiply a matrix by a vector, you sum the dot product of each row of the matrix with the vector. For example, if we multiply the above matrix with the vector (x,y), we get:

(a,c)•(x,y) + (b,d)•(x,y)

x(a,b) + y(c,d)

Matrices

x(a,b) + y(c,d)

Look familiar? This is the exact same expression that we use when changing the basis vectors! This means that multiplying a 2x2 matrix with a 2D vector is the same thing as changing its basis vectors. For example, if we plug the standard basis vectors (1,0) and (0,1) into the matrix columns, we get:
[1 0
0 1]

This is the identity matrix, which has no effect, as we would expect from the neutral basis vectors we chose. If we plug in our 49-degree rotation bases, we get:

[0.66 -0.75
0.75  0.66]

Matrices

void RotateShip(float degrees){
        Matrix2x2 R = GetRotationMatrix(degrees);
        for(int i=0; i<num_points; ++i){
                rotated_point[i] = R * point[i];
        }
}

This matrix will rotate any 2D vector counter-clockwise by 49 degrees. We could write our asteroids program with a lot more elegance by using matrices like this. For example, our ship-rotation function could look like this: