Método de Newton
Robson Cruz
Gabriel Ozaki
O que é?
Um método iterativo para aproximação de raízes de uma função com valor real
x:f(x) = 0
x:f(x)=0
Considerações
- É um método que utiliza iteração;
- Embora seja eficiente, possui restrições;
- É utilizado na computação para cálculos de raízes de funções complexas
Método
Fórmula geral
x_{n+1} = {x_n} - {{f(x_n)} \over {f'(x_n)}}
xn+1=xn−f′(xn)f(xn)
x_n = aprox.\; inicial;
xn=aprox.inicial;
\Bigg\{
{
Descrição
f:[a, b] \rightarrow R
f:[a,b]→R
- Suponha que é diferenciável no intervalo com valores reais;
- Suponha que é a nossa aproximação para a raiz atual;
- A equação da reta tangente no ponto é a seguinte:
f
f
[a, b]
[a,b]
x_n
xn
x_n
xn
y = f'(x_n)(x_{n+1}-x_n)+f(x_n)
y=f′(xn)(xn+1−xn)+f(xn)
Dedução
y = 0;
y=0;
0 = f'(x_n)(x_{x+1}-x_n)+f(x_n);
0=f′(xn)(xx+1−xn)+f(xn);
-f(x_n) = f'(x_n)(x_{n+1}-x_n);
−f(xn)=f′(xn)(xn+1−xn);
{{-f(x_n)} \over {f'(x_n)}} = (x_{n+1}-x_n);
f′(xn)−f(xn)=(xn+1−xn);
x_{n+1} = x_n - {{f(x_n)} \over {f'(x_n)}}
xn+1=xn−f′(xn)f(xn)
x_2 = x_1 - {f(x_1) \over f'(x_1)}
x2=x1−f′(x1)f(x1)
x_3 = x_2 - {f(x_2) \over f'(x_2)}
x3=x2−f′(x2)f(x2)
x_1 = x_0 - {f(x_0) \over f'(x_0)}
x1=x0−f′(x0)f(x0)
Assim por diante, convergindo à raiz
Visualização
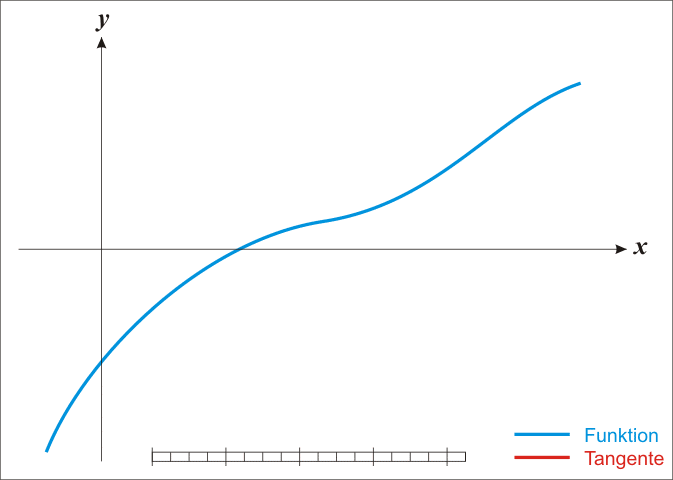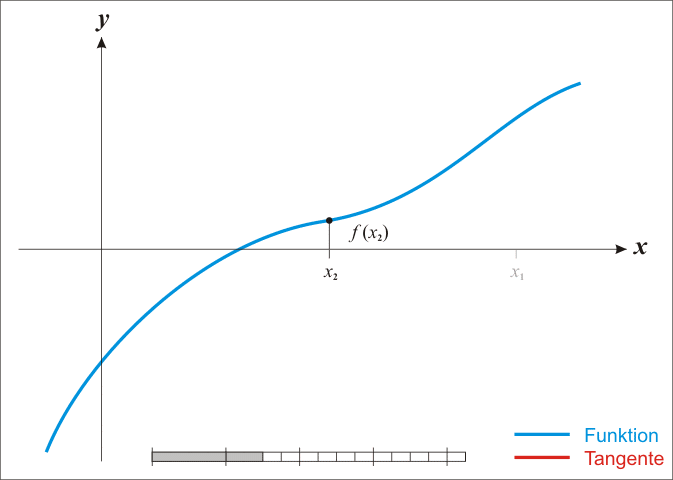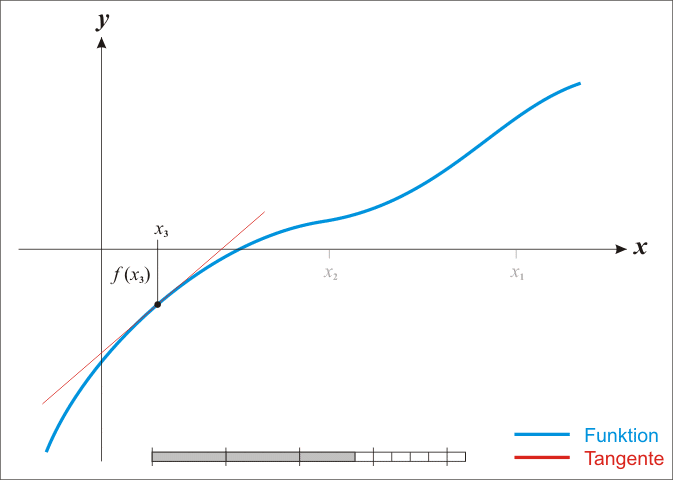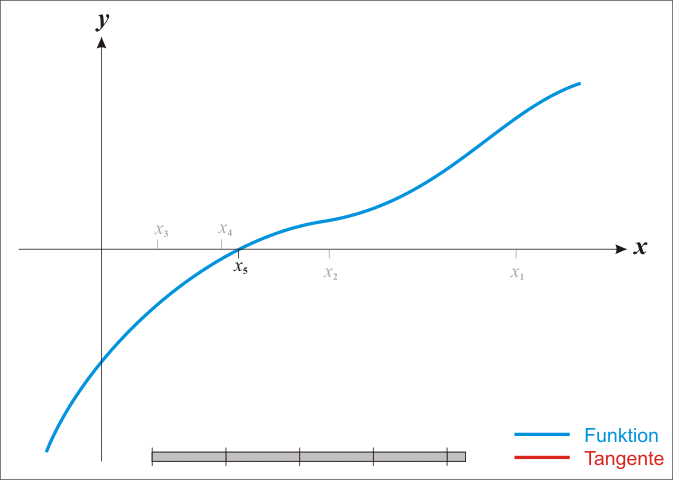
Restrições
- Casos em que a derivação é muito complexa;
- Pontos estacionários;
- Pontos iniciais ruins;
Exemplos
Exemplo 1
f(x) = x^3-9x+3
f(x)=x3−9x+3
x_0 = 3
x0=3
x_{n+1} = x_n - {f(x_n) \over f'(x_n)}
xn+1=xn−f′(xn)f(xn)
x_{1} = 3 - {3 \over 18} \approx 2.8\overline{3}
x1=3−183≈2.83
x_{2} = 2.8\overline{3} - {{2.453703 \times 10^{-1}} \over {1.508333 \times 10^{-1}}} \approx 2.817065
x2=2.83−1.508333×10−12.453703×10−1≈2.817065
x_{3} = 2.817065 - {{2.245104 \times 10^{-3}} \over {1.480757 \times 10^{-1}}} \approx 2.816914
x3=2.817065−1.480757×10−12.245104×10−3≈2.816914
Exemplo 2
f(x) = x^3-9x+3
f(x)=x3−9x+3
f'(x_0) \approx 0
f′(x0)≈0
x_0 = 1.8
x0=1.8
x_{1} = 1.8 -{-7.368 \over 0.72} = 12.0333
x1=1.8−0.72−7.368=12.0333
x_2 = 12.0333 -{1637.14 \over 425.4033} = 8.1849
x2=12.0333−425.40331637.14=8.1849
\vdots
⋮
x_9 = 2.816922 -{{1.320906 \times 10^{-4}} \over {1.480516 \times 10^{1}}} = 2.816914
x9=2.816922−1.480516×1011.320906×10−4=2.816914
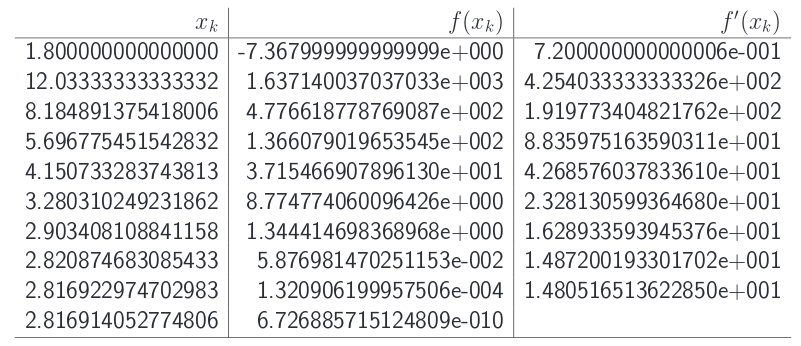
Tabela de Convergência
Exemplo 3
Cálculo da raiz de um número
x^2 = 612
x2=612
f(x) = x^2 - 612
f(x)=x2−612
f'(x) = 2x
f′(x)=2x
x_n = 10
xn=10
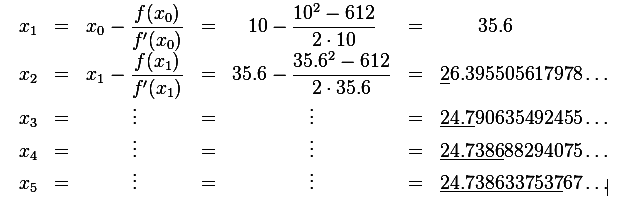
Resolução Sequencial
Os dígitos corretos foram sublinhados
Aplicações
- Minimização e maximização de problemas;
- Recíprocos de números e séries de potências;
- Resolução de equações trancedentais
Maximização e Minimização de Problemas
- O método de Newton pode ser usado para encontrar máximos e mínimos, pois a derivada nesses pontos é 0;
- Assim, podemos aplicar o método de Newton na derivada(já que a mesma é 0)
x_{n+1} = x_n - {f'(x_n) \over f''(x_n) }
xn+1=xn−f′′(xn)f′(xn)
Recíprocos de Números e Séries de Potências
f(x) = a - {1 \over x}
f(x)=a−x1
x_{n+1} = x_n - {f'(x_n) \over f'(x_n)} = x_n - {{a - {1 \over x_n}} \over {1 \over x_n^2}}
xn+1=xn−f′(xn)f′(xn)=xn−xn21a−xn1
= x_n(2 - ax_n)
=xn(2−axn)
Resolução de Equações Trancedentais
g(x) = h(x)
g(x)=h(x)
f(x) = g(x)-h(x)
f(x)=g(x)−h(x)
Com g(x) ou h(x) sendo equações trancedentais
Referências
- http://www.ime.unicamp.br/~marcia/ms211A/aulanewton.pdf
- https://en.wikipedia.org/wiki/Newton's_method
Fim
Método de Newton
By Robson Cruz
Método de Newton
- 239



