上下文嵌入以各項同性分布對於餘弦相似度計算之優勢
簡介
簡介
-
問題發現:BERT << GloVe
-
靜態詞嵌入/語境化詞嵌入的分布情況
-
各向異性/各向同性?
-
改善嵌入分布至各向同性是否成功改善效能
-
如何從理論解釋各向同性比各向異性優秀:
-
餘弦相似度的假設
-
去相關
-
問題發現:
BERT << GloVe
問題發現:
BERT << GloVe
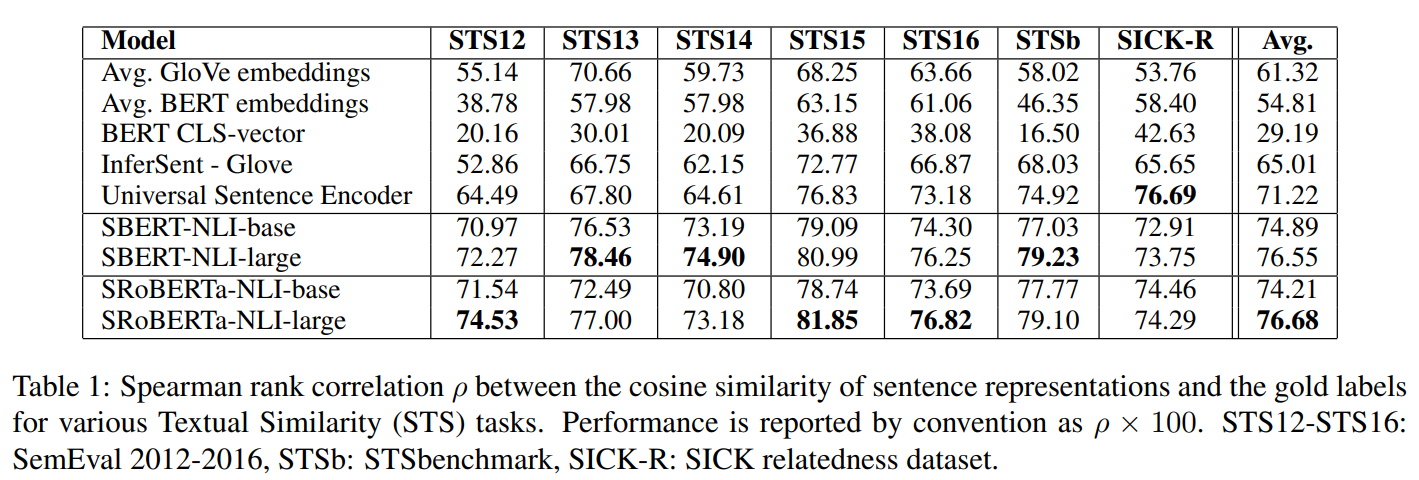
Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks (Reimers & Gurevych, EMNLP-IJCNLP 2019)問題發現:
BERT << GloVe

\rho \approx 0
x
y
\rho \approx 1
x
y
問題發現:
BERT << GloVe

\rho \approx 0
x
y
\rho \approx 1
x
y
斯皮爾曼等級相關係數
x,y 排序相同 ρ = 1
x,y 排序相反 ρ = -1
x,y 排序無關 ρ = 0
問題發現:
BERT << GloVe

問題發現:
BERT << GloVe

靜態/語境化詞嵌入
的分布情況
靜態/語境化詞嵌入
的分布情況
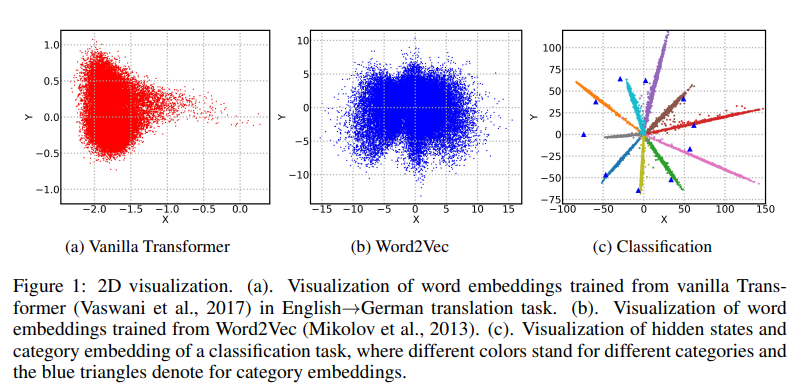
Representation Degeneration Problem in Training Natural Language Generation Models(Gao, Jun, et al., ICLR 2019)
靜態/語境化詞嵌入
的分布情況
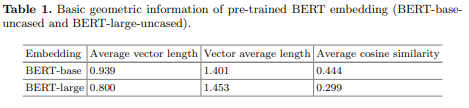

Learning to remove: Towards isotropic pre-trained BERT embedding (Liang, Yuxin, et al., Artificial Neural Networks and Machine Learning–ICANN 2021: 30th International Conference on Artificial Neural Networks)
各向同性/各向異性
各向同性/各向異性
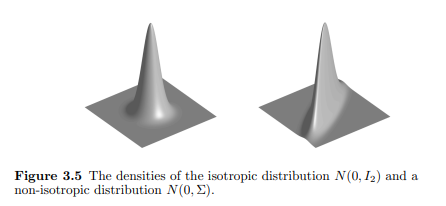
各向同性
在不同方向均勻擴展
各向異性
在不同方向不均勻擴展
Vershynin, Roman. "High-Dimensional Probability: An Introduction with Applications in Data Science. 2018." URL https://www.math.uci.edu/~rvershyn/papers/HDP-book/HDP-book.pdf (2018).各向同性/各向異性
各向同性
在不同方向均勻擴展
各向異性
在不同方向不均勻擴展
a(2,2)、b(2,-2)、c(-2,2)
a
c
b
c
a
b
各向同性/各向異性
各向同性
在不同方向均勻擴展
各向異性
在不同方向不均勻擴展
a(2,2)、b(2,-2)、c(-2,2)
\cos(a, b) = 0
\cos(a, c) = 0
\cos(a, b) < 0
\cos(a, c) > 0
各向同性/各向異性
各向同性
在不同方向均勻擴展
各向異性
在不同方向不均勻擴展
a(2,2)、b(2,-2)、c(-2,2)
\cos(a, b) = 0
\cos(a, c) = 0
\cos(a, b) < 0
\cos(a, c) > 0
餘弦相似度失真
改善嵌入分布至各向同性是否
成功改善效能
改善嵌入分布至各向同性是否
成功改善效能
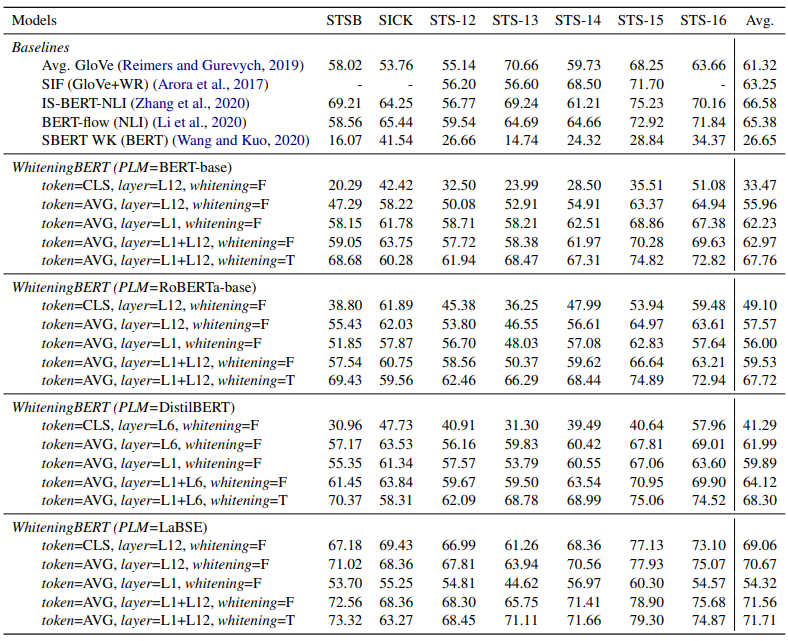


Su, Jianlin, et al. "Whitening sentence representations for better semantics and faster retrieval." arXiv preprint arXiv:2103.15316 (2021).改善嵌入分布至各向同性是否
成功改善效能
SimCSE: Simple Contrastive Learning of Sentence Embeddings (Gao et al., EMNLP 2021)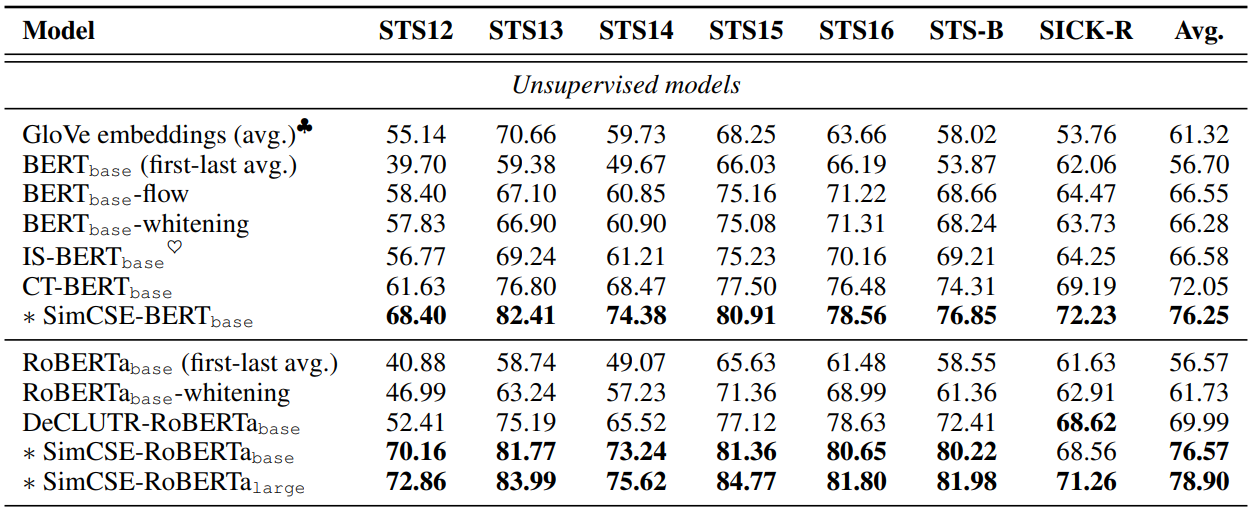






改善嵌入分布至各向同性是否
成功改善效能







如何從理論解釋各向同性比
各向異性優秀
如何從理論解釋各向同性比
各向異性優秀
1. 餘弦相似度的假設
如何從理論解釋各向同性比各向異性優秀
1. 餘弦相似度的假設
cos(x, y) = \frac{\sum^d_i x_i y_i }{\sqrt{\sum^d_i x^2_i} \sqrt{\sum^d_i y^2_i}}
只使用座標計算,而座標值依賴於所在空間的基(basis)
基不相同,計算出的餘弦值就不同
如何從理論解釋各向同性比
各向異性優秀
如何從理論解釋各向同性比
各向異性優秀
2. 去相關
如何從理論解釋各向同性比
各向異性優秀
2. 去相關

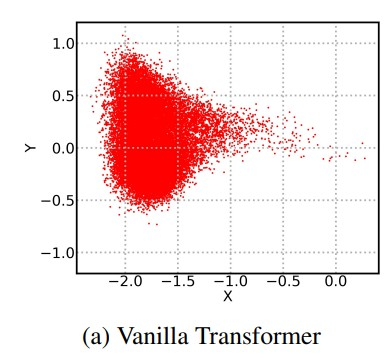
(0,0)
所有的token都有一定程度的相似
end
Recommender system with SGD
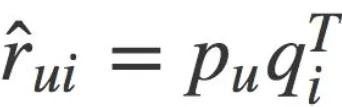
n = len(user) pu = n*k
t = len(iten)
qi = t*k
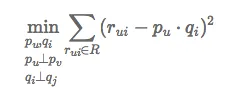
Copy of Copy of AWS
By r oger
Copy of Copy of AWS
- 1



