Fast Fourier Transform
RUSHAL\ \ VERMA
\quad 14BCS042
III^{rd}\ \ SEMESTER
Contents
-
Need of this algorithm
-
Big Idea
-
What it does
-
Wiki Definition
-
Working of the Algorithm
-
Mathematical Aspect
-
Roots of the Unity
-
Applications
-
Refrences
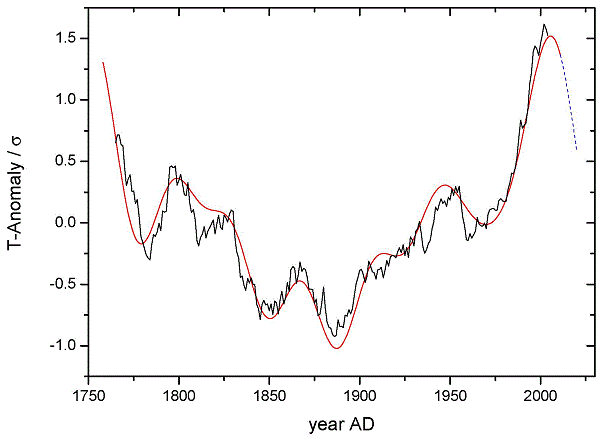
Noisy
Less Noisy
Big Idea
-
Change representation of Mathematical Objects
- Some representations have efficiency benefits over other
f(x) = 5 + 2x + x^2
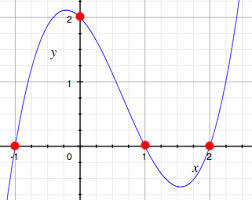
Polynomial of degree 2 denotes 3 numbers which represents the polynomial.
n-1 degree indicates n coefficients
if we have n coefficients then we are able to get a n-1 degree polynomials.
what it does
Takes input in the form of polynomial
A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}
Evaluate it into n points
A(w_0), A(w_1), A(w_2), ... , A(w_n)
What the wiki says about it!
IFFT
FFT
A(x)
Coeffiecients Form
Point-wise Form
N- Points Curve
Degree of n-1 polynomial
FFT
Input:
a_0, a_1, a_2, ... , a_{n-1}
A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}
Output:
n coefficients
Point-Wise Representation
A(w_0), A(w_1), A(w_2), ... , A(w_n)
where\ w_1, w_2, .....\ , w_n \ are\ distinct \ points.
Brute force method to evaluate A at n points
A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}
A(w_0) - \ \theta(n) \ \ operations
A(w_0),\ ... \ ,\ A(w_n) - \ \theta(n^2) \ \ operations
We\ seek\ for\ \theta(nlogn)
solve the large problem by
solving smaller problems
and combining solutions
T(n)\ =\ 2T(\frac{n}{2}) + \theta(n)
A(x)= a_0 + a_1x + a_2x^2+ ... + a_{n-1}x^{n-1}
= a_0 \ \ \ \ \ \ + a_2x^2\ \ \ \ \ \ +\ a_{n-2}x^{n-2}
+\ a_1 \ \ \ \ \ \ + a_3x^3\ \ \ \ \ \ \ \ \ +\ \ \ \ \ \ a_{n-1}x^{n-1}
A_e(y) = a_0 + a_2y + a_4 y^2 + \ ...\ +a_{n-2}^\frac{n-2}{2}
A_o(y) = a_1 + a_3y + a_5 y^2 + \ ...\ +a_{n-1}^\frac{n-1}{2}
A(x) = A_e(x^2) + xA_o(x^2)
FFT(f[i,\ .....\ ,\ n])
Evaluates degree n poly on the nth roots of UNITY
E[] = FFT (A_e)
O[] = FFT (A_o)
returns\ A[w_0\ ...\ w_n]\ using\ the\ equation
A(w_i) = A_e(w_i^2) + w_iA_o(w_i^2)
Last Remaining Issue:
w_i\ =\ \ ?
Roots of UNITY
x^n = 1
should have n no of solution and we need to find them.
e^{2\pi i} \ = \ 1
consider for j = 0,1,2,3, ...., n-1
e^{{2\pi ij/n}{}} \
[e^{2\pi i j/n}]^n = [e^{(2\pi i /n)\ . j}]^n = [e^{2\pi i}]^j = 1^j = 1
[e^{2\pi i j/n}] = w_{j,n} \ is \ a \ n^{th} \ root\ of\ unity
[e^{2\pi i j/n}] = \cos (2\pi i j/n) + i \sin (2\pi i j/n)
w_{0,n}\ , w_{1,n}\ ,w_{2,n}\ w_{3,n}\ ......\ w_{n-1,n}
w_{1,8}\ =\ e^{2\pi i(1/8)}
\ = cos({2\pi i(1/8)}) + isin({2\pi i(1/8)})
\frac{1}{\sqrt2}
i\frac{1}{\sqrt2}
+
=
Squaring the nth roots of the unity
\large{x^n}\ =\ 1
\large{x^{n/2}}\ =\ 1
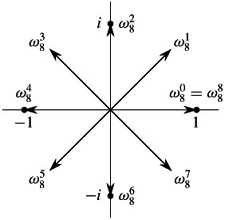
Produce the set of n/2 roots of the unity
Fact:
squaring the nth roots of the unity
results in n/2th roots of the unity
Evaluate at a root of the unity
A(x) = A_e(x^2) + xA_o(x^2)
A(w_{i,n}) = A_e(w_{i,n}^2) + w_{i,n}A_o(w_{i,n}^2)
nth root of the unity
n/2th root of the unity
n/2th root of the unity
FFT(f= a[i,..,n])
E[...] \leftarrow \ FFT(A_e)\quad \quad//eval\ A_e\ on\ n/2\ roots\ of\ the\ unity.
O[...] \leftarrow \ FFT(A_o)\quad \quad //eval\ A_o\ on\ n/2\ roots\ of\ the\ unity.
combine results using the equation:
A(w_{i,n}) = A_e(w_{i,n}^2) + w_{i,n}A_o(w_{i,n}^2)
returns n points.
Applications
Multiply two numbers in nlogn time.
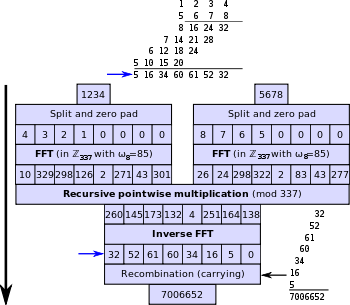
Schönhage–Strassen Algorithm
O(n\ log n\ log log \ n)
Faster than Karatsuba Multiplication Algorithm
Refrences
-
CS 4102-https://www.cs.virginia.edu/~shelat/4102/ -
https://www.youtube.com/watch?v=2V7XT_iiRRw -
http://www.cs.cmu.edu/afs/cs/academic/class/15451-s10/www/lectures/lect0423.txt -
https://en.wikipedia.org/wiki/Sch%C3%B6nhage%E2%80%93Stras sen_algorithm - https://en.wikipedia.org/wiki/Fast_Fourier_transform
THANK YOU
deck
By Rushal Verma
