Deep Learning HMC

Building Topological Samplers for Lattice QCD

Sam Foreman

May, 2021

saforem2/l2hmc-qcd

arXiv:2105.03418

Text

MCMC in Lattice QCD

Generating independent gauge configurations is a MAJOR bottleneck for LatticeQCD.

As the lattice spacing, \(a \rightarrow 0\), the MCMC updates tend to get stuck in sectors of fixed gauge topology.
- This causes the number of steps needed to adequately sample different topological sectors to increase exponentially.

Critical slowing down!

Markov Chain Monte Carlo (MCMC)

Goal: Draw independent samples from a target distribution, \(p(x)\)

x^{\prime} = x_{0} + \delta,\quad \delta\sim\mathcal{N}(0, \mathbb{1})

Starting from some initial state \(x_{0}\sim \mathcal{N}(0, \mathbb{1})\) , we generate proposal configurations \(x^{\prime}\)

Use Metropolis-Hastings acceptance criteria

x_{i+1} = \begin{cases} x^{\prime},\quad\text{with probability } A(x^{\prime}|x)\\ x,\quad\text{with probability } 1 - A(x^{\prime}|x) \end{cases}

A(x^{\prime}|x) = \min\left\{1, \frac{p(x^{\prime})}{p(x)}\left|\frac{\partial x^{\prime}}{\partial x^{T}}\right|\right\}

\(\big\{ x_{0}, x_{1}, x_{2}, \ldots, x_{m-1}, x_{m}, x_{m+1}, \ldots, x_{n-2}, x_{n-1}, x_{n} \big\}\)

1. Construct chain:

\(\big\{ x_{0}, x_{1}, x_{2}, \ldots, x_{m-1}, x_{m}, x_{m+1}, \ldots, x_{n-2}, x_{n-1}, x_{n} \big\}\)

2. Thermalize ("burn-in"):

\(\big\{ x_{0}, x_{1}, x_{2}, \ldots, x_{m-1}, x_{m}, x_{m+1}, \ldots, x_{n-2}, x_{n-1}, x_{n} \big\}\)

3. Drop correlated samples ("thinning"):

dropped configurations

Inefficient!

Issues with MCMC

Generate proposal \(x^{\prime}\):

\(x^{\prime} = x + \delta\), where \(\delta \sim \mathcal{N}(0, \mathbb{1})\)

random walk

Hamiltonian Monte Carlo (HMC)

Introduce fictitious momentum:

\(v\sim\mathcal{N}(0, 1)\)

Target distribution:

\(p(x)\propto e^{-S(x)}\)

Joint target distribution:

p(x, v) = p(x)\cdot p(v) = e^{-S(x)}\cdot e^{-\frac{1}{2}v^{T}v} = e^{-\mathcal{H(x,v)}}

The joint \((x, v)\) system obeys Hamilton's Equations:

\dot{x} = \frac{\partial\mathcal{H}}{\partial v},

\dot{v} = -\frac{\partial\mathcal{H}}{\partial x}

p(x, v) = p(x|v)p(v)

lift to phase space

v\sim \mathcal{N}(0, \mathbb{1})

\mathcal{H}=\mathrm{const}

HMC: Leapfrog Integrator

(trajectory)

Hamilton's Eqs:

\dot{x}=\frac{\partial\mathcal{H}}{\partial v}, \dot{v}=-\frac{\partial{\mathcal{H}}}{\partial x}

\mathcal{H}(x, v) = S(x) + \frac{1}{2}v^{T}v

Hamiltonian:

(x_{0}, v_{0})\rightarrow \cdots \rightarrow(x_{N_{\mathrm{LF}}}, v_{N_{\mathrm{LF}}})

\(N_{\mathrm{LF}}\) leapfrog steps:

\Longrightarrow

Leapfrog Integrator

x^{\prime} = x + \varepsilon v^{1/2}

v^{\prime} = v^{1/2} - \frac{\varepsilon}{2}\partial_{x}S(x^{\prime})

v^{1/2} = v - \frac{\varepsilon}{2}\partial_{x}S(x)

2. Full-step \(x\)-update:

3. Half-step \(v\)-update:

1. Half-step \(v\)-update:

HMC: Issues

Cannot easily traverse low-density zones.

What do we want in a good sampler?

Fast mixing
Fast burn-in

Mix across energy levels
Mix between modes

Energy levels selected randomly \(\longrightarrow\) slow mixing!

Stuck!

Leapfrog Layer

Introduce a persistent direction \(d \sim \mathcal{U}(+,-)\) (forward/backward)

Introduce a discrete index \(k \in \{1, 2, \ldots, N_{\mathrm{LF}}\}\) to denote the current leapfrog step

Let \(\xi = (x, v, \pm)\) denote a complete state, then the target distribution is given by

p(\xi) = p(x)\cdot p(v)\cdot p(d)

Each leapfrog step transforms \(\xi_{k} = (x_{k}, v_{k}, \pm) \rightarrow (x''_{k}, v''_{k} \pm) = \xi''_{k}\) by passing it through the \(k^{\mathrm{th}}\) leapfrog layer

Leapfrog Layer

where \((s_{v}^{k}, q^{k}_{v}, t^{k}_{v})\), and \((s_{x}^{k}, q^{k}_{x}, t^{k}_{x})\), are parameterized by neural networks

\(x\)-update \((d = +)\):

x^{\prime}_{k} = \Lambda^{+}_{k}(x_{k};\zeta_{x_{k}})

\zeta_{x_{k}}\equiv \big(\quad\odot x_{k}, \partial_{x}S(x_{k})\big)

\bar{m}_{t}

(\(m_{t}\)\(\odot x\)) -independent

\,\quad= x_{k}\odot\exp\left(\varepsilon^{k}_{x}s^{k}_{x}(\zeta_{x_{k}})\right) + \varepsilon^{k}_{x}\left[v^{\prime}_{k}\odot\exp\left(\varepsilon^{k}_{x}q^{k}_{x}(\zeta_{x_{k}})\right)+t^{k}_{x}(\zeta_{x_{k}})\right]

masks:

m_{t}

\bar{m}_{t}

= \mathbb{1}

Momentum (\(v_{k}\)) scaling

Gradient \(\partial_{x}S(x_{k})\) scaling

Translation

\,\quad\equiv\, v_{k}\odot \exp\left(\frac{\varepsilon^{k}_{v}}{2}s^{k}_{v}(\zeta_{v_{k}})\right) - \frac{\varepsilon^{k}_{v}}{2}\left[\partial_{x}S(x_{k})\odot\exp\left(\varepsilon^{k}_{v}q^{k}_{v}(\zeta_{v_{k}})\right) \,+\,t^{k}_{v}(\zeta_{v_{k}})\right]

\zeta_{v_{k}}\equiv \big(x_{k}, \partial_{x}S(x_{k})\big)

\(v\)-update \((d = +)\):

v^{\prime}_{k} = \Gamma^{+}_{k}(v_{k};\zeta_{v_{k}} )

\overbrace{\hspace{80px}}

\overbrace{\hspace{100px}}

\overbrace{\hspace{30px}}

(\(v\)-independent)

Each leapfrog step transforms

\xi_{k} = (x_{k}, v_{k}, \pm)\longrightarrow (x''_{k}, v''_{k}, \pm)=\xi''_{k}

by passing it through the \(k^{\mathrm{th}}\) leapfrog layer.

L2HMC: Generalized Leapfrog

Complete (generalized) update:
1. Half-step \(v\) update:
2. Full-step \(\frac{1}{2} x\) update:
3. Full-step \(\frac{1}{2} x\) update:
4. Half-step \(v\) update:

v^{\prime}_{k} = \Gamma^{\pm}(v_{k};\zeta_{v_{k}})

x^{\prime}_{k} = \hspace{14px}\odot x_{k} + \hspace{14px}\odot \Lambda^{\pm}(x_{k};\zeta_{x_{k}})

\bar{m}^{t}

m^{t}

x^{\prime\prime}_{k} = \hspace{14px}\odot \Lambda^{\pm}_{k}(x^{\prime}_{k};\zeta_{x^{\prime}_{k}}) + \hspace{14px}\odot x^{\prime}_{k}

\bar{m}^{t}

m^{t}

v^{\prime\prime}_{k} = \Gamma^{\pm}(v^{\prime}_{k};\zeta_{v^{\prime}_{k}})

Leapfrog Layer

masks:

Stack of fully-connected layers

Example: GMM \(\in\mathbb{R}^{2}\)

\(A(\xi',\xi)\) = acceptance probability

\(A(\xi'|\xi)\cdot\delta(\xi',\xi)\) = avg. distance

Note:

\(\xi'\) = proposed state

\(\xi\) = initial state

Maximize expected squared jump distance:

\mathcal{L}_{\theta}\left(\theta\right) \equiv \mathbb{E}_{p(\xi)}\left[A(\xi'|\xi)\cdot \delta(\xi',\xi)\right]

Define the squared jump distance:

\delta(\xi^{\prime}, \xi) = \|x^{\prime} - x\|^{2}_{2}

HMC

L2HMC

Training Algorithm

     construct
trajectory

Compute loss
  + backprop

 Metropolis-Hastings 
       accept/reject

     re-sample    
      momentum
   + direction

Annealing Schedule

\left\{\gamma_{t}\right\}_{t=0}^{N} = \left\{\gamma_{0}, \gamma_{1}, \ldots, \gamma_{N-1}, \gamma_{N}\right\},

\gamma_{0} < \gamma_{1} < \ldots < \gamma_{N} \equiv 1

\gamma_{t+1} - \gamma_{t} \ll 1

Introduce an annealing schedule during the training phase:

(varied slowly)

e.g. \( \{0.1, 0.2, \ldots, 0.9, 1.0\}\)

(increasing)

p_{t}(x)\propto e^{-\gamma_{t}S(x)},\quad\text{for}\quad t=0, 1,\ldots, N

Target distribution becomes:

For \(\|\gamma_{t}\| < 1\), this helps to rescale (shrink) the energy barriers between isolated modes
- Allows our sampler to explore previously inaccessible regions of the target distribution

Wilson action:

S_{\beta}(x)=\beta \sum_{P}1-\cos x_{P}

x_{P} = x_{\mu}(n) + x_{\nu}(n+\hat{\mu}) - x_{\mu}(n+\hat{\nu}) - x_{\nu}(n)

Topological charge:

continuous, differentiable

discrete, hard to work with

\left\lfloor x_{P}\right\rfloor = x_{P} - 2\pi\left\lfloor\frac{x_{P}+\pi}{2\pi}\right\rfloor

\mathcal{Q}_{\mathbb{Z}} = \frac{1}{2\pi}\sum_{P}\left\lfloor x_{P}\right\rfloor\hspace{6pt} \in\mathbb{Z}

\mathcal{Q}_{\mathbb{R}} = \frac{1}{2\pi}\sum_{P}\sin x_{P}\in\mathbb{R}

Link variables:

U_{\mu}(x) = e^{i x_{\mu}(n)} \in U(1)

x_{\mu}(n) \in [-\pi,\pi]

Lattice Gauge Theory

We maximize the expected squared charge difference:

Loss function: \(\mathcal{L}(\theta)\)

\delta \mathcal{Q}_{\mathbb{R}}^{2}(\xi',\xi) \equiv \left(\mathcal{Q}_{\mathbb{R}}(x') - \mathcal{Q}_{\mathbb{R}}(x)\right)^{2}

\mathcal{L}(\theta) = \mathbb{E}_{p(\xi)}\left[-\delta\mathcal{Q}^{2}_{\mathbb{R}}(\xi',\xi)\cdot A(\xi'|\xi)\right]

A(\xi'|\xi) = \min\left\{1, \frac{p(\xi')}{p(\xi)} \left|\frac{\partial\xi'}{\partial\xi^{T}}\right|\right\}

Results

We maximize the expected squared charge difference:

\delta \mathcal{Q}_{\mathbb{R}}^{2}(\xi',\xi) \equiv \left(\mathcal{Q}_{\mathbb{R}}(x') - \mathcal{Q}_{\mathbb{R}}(x)\right)^{2}

\mathcal{L}(\theta) = \mathbb{E}_{p(\xi)}\left[-\delta\mathcal{Q}^{2}_{\mathbb{R}}(\xi',\xi)\cdot A(\xi'|\xi)\right]

A(\xi'|\xi) = \min\left\{1, \frac{p(\xi')}{p(\xi)} \left|\frac{\partial\xi'}{\partial\xi^{T}}\right|\right\}

Interpretation

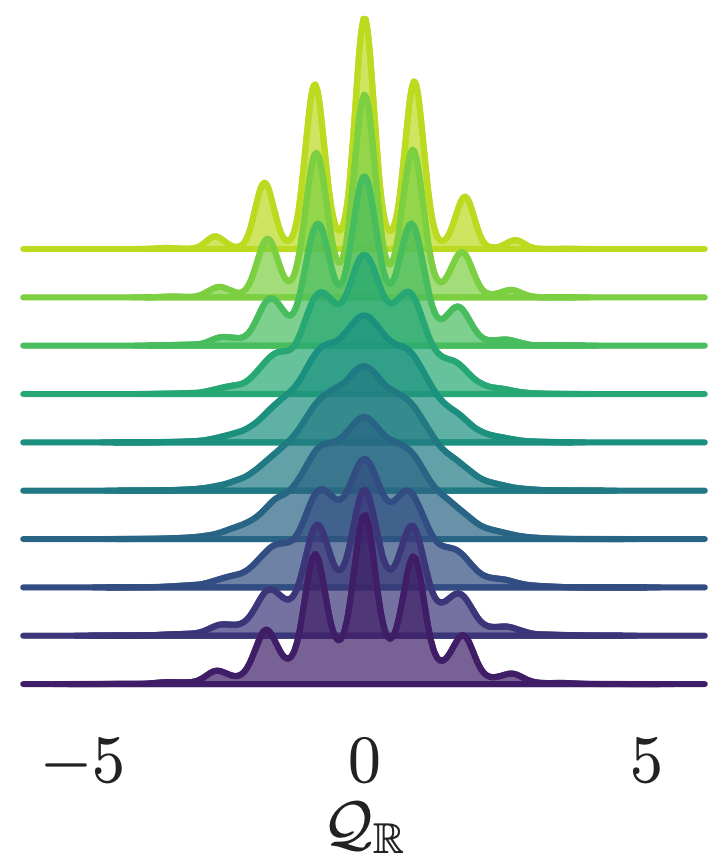
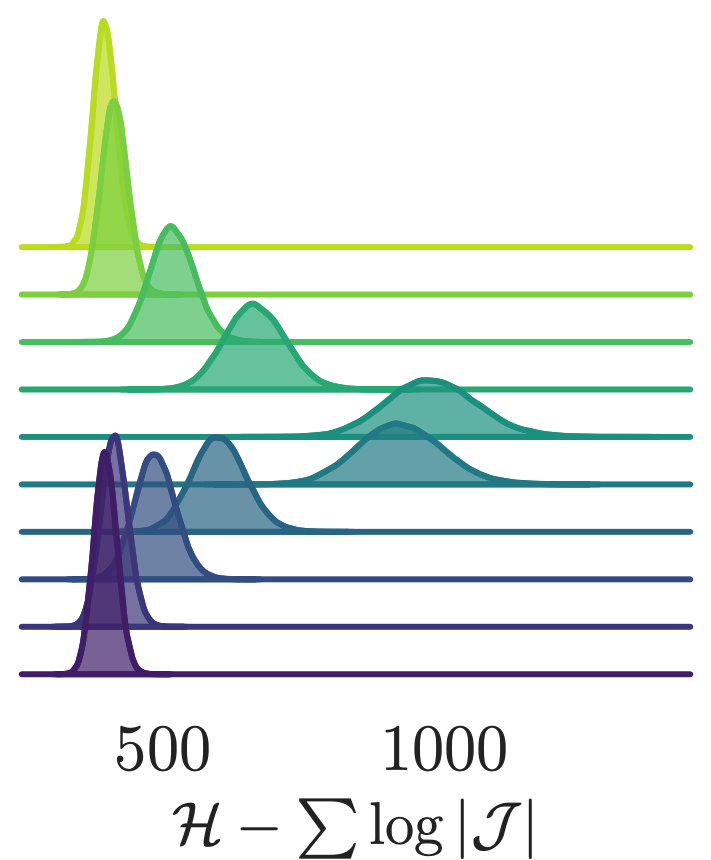
Look at how different quantities evolve over a single trajectory
- See that the sampler artificially increases the energy during the first half of the trajectory (before returning to original value)

Leapfrog step

variation in the avg plaquette

continuous topological charge

shifted energy

Text

Leapfrog step

variation in the avg plaquette

continuous topological charge

shifted energy

\langle x_{P}-x^{*}_{p}\rangle

\text{leapfrog step}

Interpretation

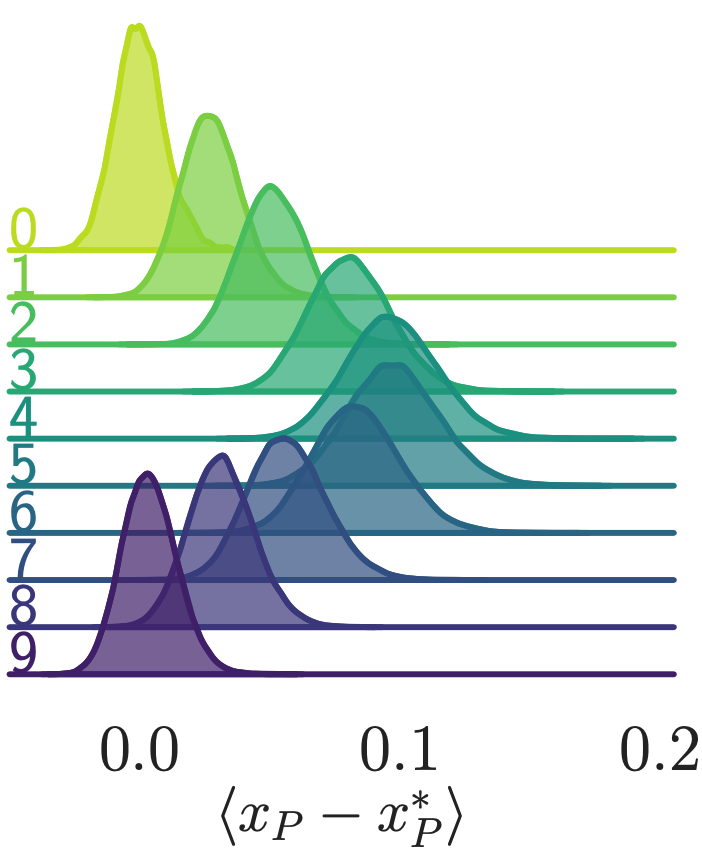
Look at how the variation in \(\langle\delta x_{P}\rangle\) varies for different values of \(\beta\)

\(\beta = 7\)

\(\simeq \beta = 3\)

\(\beta = 5\)

\(\beta = 6\)

\(\beta = 7\)

Integrated Autocorrelation Time

Want to calculate: \(\langle \mathcal{O}\rangle\propto \int \left[\mathcal{D} x\right] \mathcal{O}(x)e^{-S[x]}\)

Instead, we account for the autocorrelation, so the variance becomes: \(\sigma^{2} = \frac{\tau^{\mathcal{O}}_{int}}{N}\mathrm{Var}\left[\mathcal{O}(x)\right]\)

If we had independent configurations, we could approximate by \(\langle\mathcal{O}\rangle \simeq \frac{1}{N}\sum_{n=1}^{N} \mathcal{O}(x_{n})\longrightarrow \sigma^{2}=\frac{1}{N}\mathrm{Var}\left[\mathcal{O}(x)\right]\propto\frac{1}{N}\)