R
E
A
C
T
O

xamples
epeat
ode
pproach
ptimize
est
{Lattice Paths}

The Question
Given a square grid, how could you determine the number of possible paths from the top left of the grid to the bottom right, assuming you can only move to the right and down?
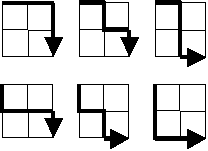
Example: a 2 by 2 grid has 6 possible paths

Approach

From any given corner it's difficult to know exactly how many possible paths there are. But we do know that the total number of paths at any given corner is equal to the sum from the right and the bottom.
NumofPossiblePaths (x,y) =
NumofPossiblePaths from the next corner to the right (x+1, y)
+ NumofPossiblePaths from the next corner to the bottom (x, y+1).
We also know that when you hit the right or bottom edge of a grid, there is only one possible path.

Same Approach, Different View
(0,0)
(1,0)
(0,1)
(2,0)
(1,1)
(0,2)
(2,1)
(2,2)
(1,1)

(1,2)
(2,2)
(2,1)
(2,1)
(1,2)
(2,2)
(2,2)
(2,2)
(2,2)
(1,2)

Possible Solution
function paths2Bottom(x, y, max){
if (x == max || y == max){
return 1;
}
return paths2Bottom(x+1, y, max) + paths2Bottom(x, y+1, max);
}- Recursive
- Only works for small grids
- Demo of it failing on big grids

Memoized Solution
var paths = {};
function memoizer(x, y, max){
if(paths[[x,y,max]]){
return paths[[x,y,max]];
}
else{
return paths[[x,y,max]] = paths2Bottom(x, y, max);
}
}
function paths2Bottom(x, y, max){
if (x == max || y == max){
return 1;
}
return memoizer(x+1, y, max) + memoizer(x, y+1, max);
}- Still Recursive
- Works on bigger grids

Conclusion
Solution on Repl.it
Source from Project Euler

Copy of Lattice Paths
By Sarah Muenzinger
Copy of Lattice Paths
Technical interview problem on lattice paths
- 1,557



