Understanding Python's DataStructure: Dictionary

Sayan Chowdhury

@chowdhury_sayan

The Dictionary

>>> d = {
...    'Fedora': 21,
...    3.1415: 'pi',
...    9 : 'Planets', 
...    (1, 4, 17): 'Django version',
...}

keys can be anything.

A dictionary is really a list

>>> # An empty dictionary is an 8-element list!
>>> d = {}

>>> # This actually creates a `hash table` 
>>> # containing `slots`

Keys are hashed to produce indexes

How the hashing is done?

Python uses the built-in hash() function.

Let's hash some keys now!

>>> def bits(n):
...    n += 2**32
...    return bin(n)[-32:]  # remove '0b'
...
>>> print bits(1)
00000000000000000000000000000001
>>> print bits(-1)
11111111111111111111111111111111

>>> for key in 'Monty', 3.1415, (1, 4, 17):
...     print bits(hash(key)), key

10011000011001101001001100000010 Monty
01101010101011010000100100000010 3.1415
11000111101010001110010110011011 (1, 4, 17)

>>> k1 = bits(hash('Monty'))
>>> k2 = bits(hash('Money'))
>>> diff = ('^ '[a==b] for a,b in zip(k1, k2))
>>> print k1; print k2; print ''.join(diff)

10011000011001101001001100000010
10011001010010110111010100010111
       ^  ^ ^^ ^^^^  ^^    ^ ^ ^

Even minor change in value can lead to drastic change in hashed value

Same value returns the same hash

for key in 3.1415, 3.1415, 3.1415:
...     print bits(hash(key)), key

01101010101011010000100100000010 3.1415
01101010101011010000100100000010 3.1415
01101010101011010000100100000010 3.1415

Now, let me show something interesting!

>>> for key in 9, 9.0, complex(9):
...     print bits(hash(key)), key

00000000000000000000000000001001 9
00000000000000000000000000001001 9.0
00000000000000000000000000001001 (9+0j)

Keys <===> Indexes

#1. Keys are hashed.

#2. To build an index, Python uses the bottom

n bits of the hash

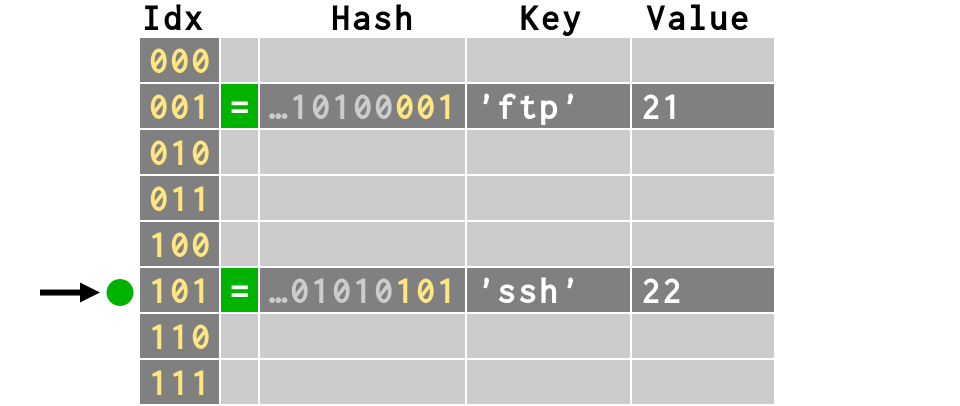
>>> d['ftp'] = 21

>>> b = bits(hash('ftp'))
>>> print b
11010010011111111001001010100001
>>> print b[-3:]  # last 3 bits = 8 combinations
001

>>> d['ssh'] = 22

>>> print bits(hash('ssh'))[-3:]
101

>>> d['ssh'] = 22

>>> print bits(hash('ssh'))[-3:]
101

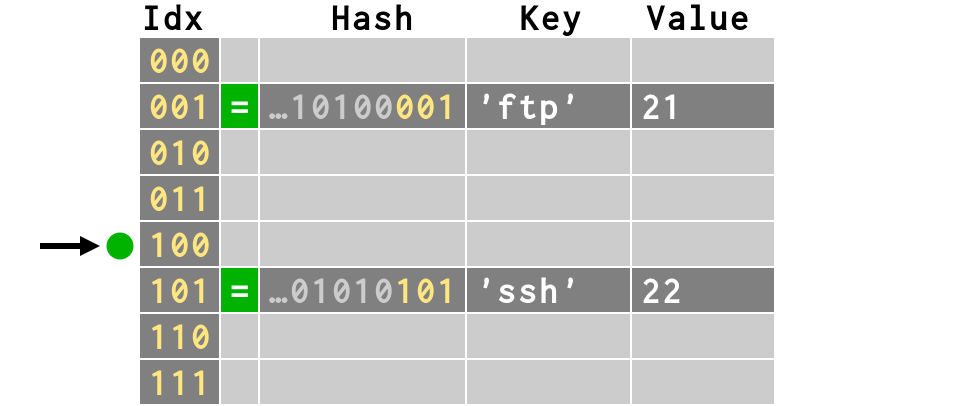
>>> d['smtp'] = 25

>>> print bits(hash('smtp'))[-3:]
100

>>> d['smtp'] = 25

>>> print bits(hash('smtp'))[-3:]
100

>>> d['time'] = 37

>>> print bits(hash('time'))[-3:]
111

>>> d['time'] = 37

>>> print bits(hash('time'))[-3:]
111

>>> d['www'] = 80

>>> print bits(hash('www'))[-3:]
010

>>> d['www'] = 80

>>> print bits(hash('www'))[-3:]
010

d = {'ftp': 21, 'ssh': 22,
     'smtp': 25, 'time': 37,
     'www': 80}

Lookup?

compute hash

get the index using `i` bits

search in the hash table

>>> print d['smtp']
25
>>> print bits(hash('smtp'))[-3:]
100

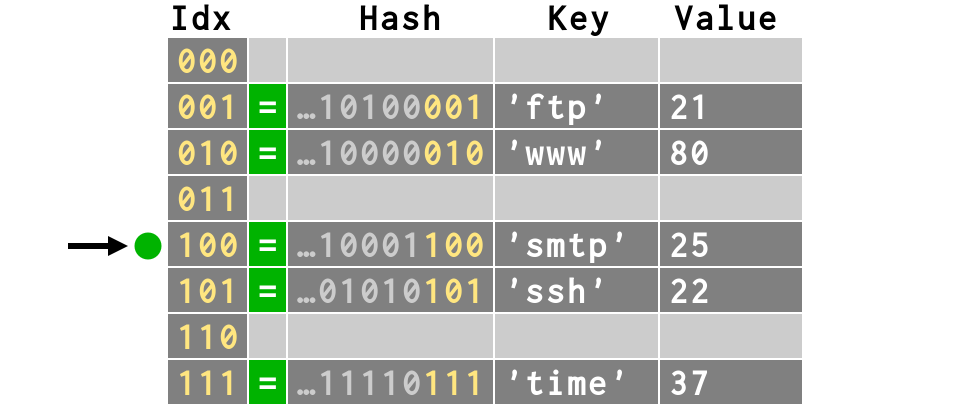
Ever noticed the crazy order of a dictionary ?

>>> # Different than our insertion order:
>>> print d
{'ftp': 21, 'www': 80, 'smtp': 25, 'ssh': 22,
 'time': 37}
>>> # But same order as in the hash table!

>>> # keys and values also in table order
>>> d.keys()
['ftp', 'www', 'smtp', 'ssh', 'time']
>>> d.values()
[21, 80, 25, 22, 37]

Collision

What happens when two keys need the same slot?

>>> # start over with a new dictionary
>>> d = {}

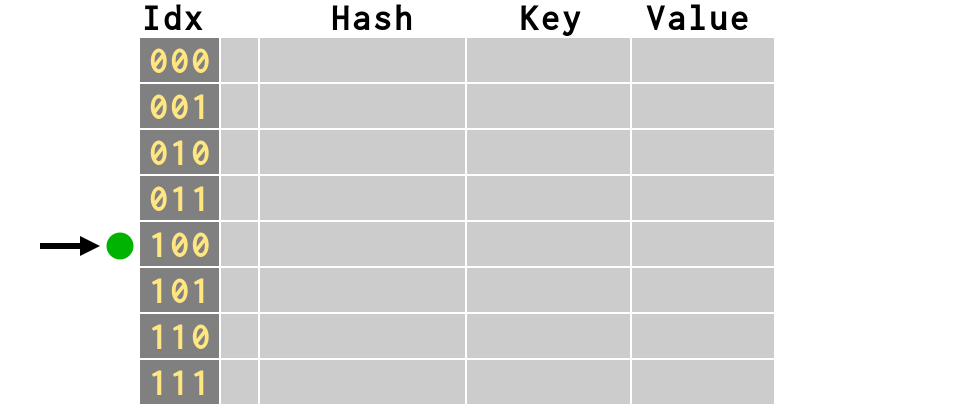
>>> # first item inserts fine
>>> d['smtp'] = 21

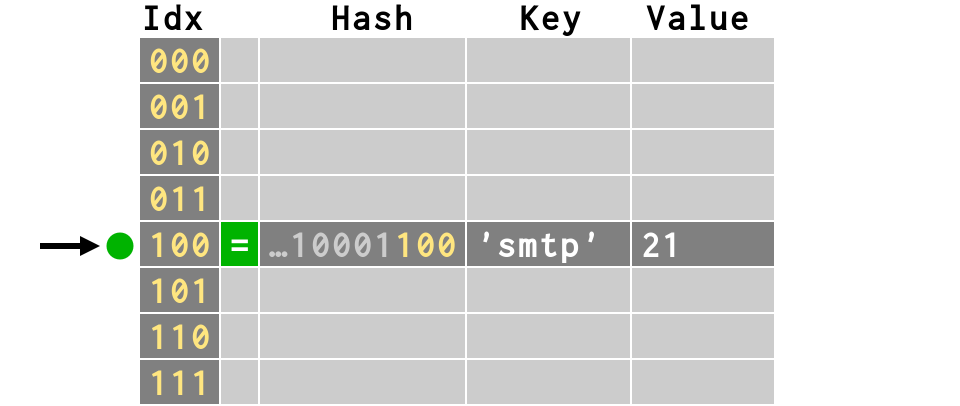
>>> # first item inserts fine
>>> d['smtp'] = 21

>>> # second item collides!
>>> d['dict'] = 2628

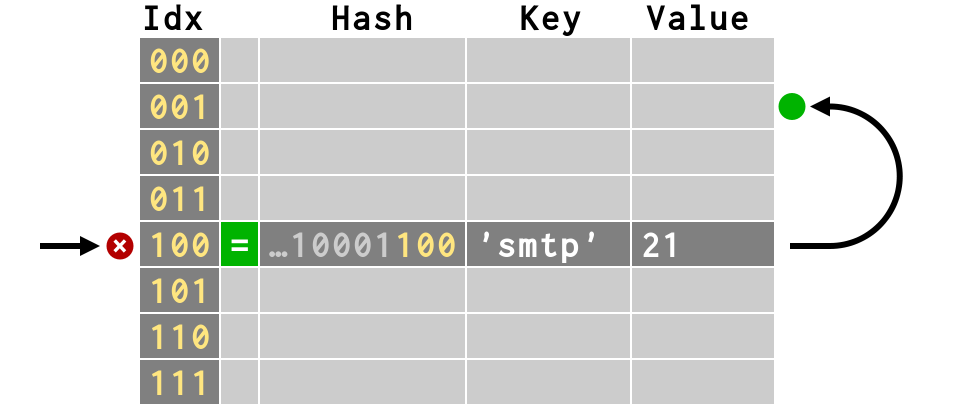
>>> # second item collides!
>>> d['dict'] = 2628

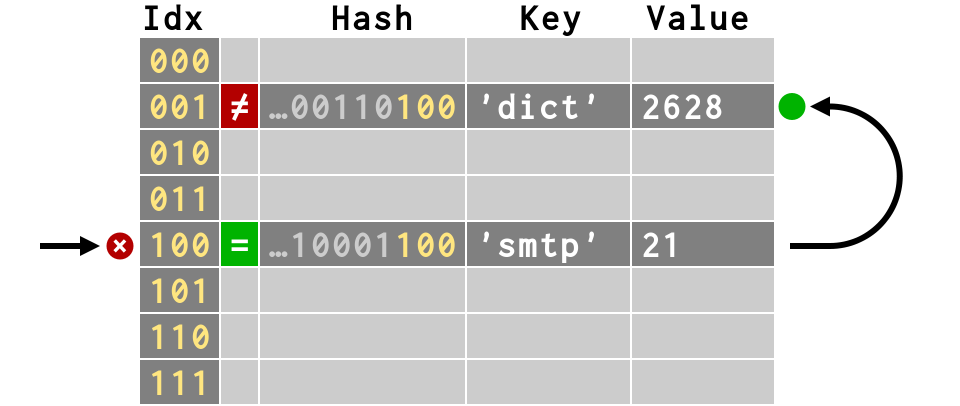
>>> # third item also finds empty slot
>>> d['svn'] = 3690

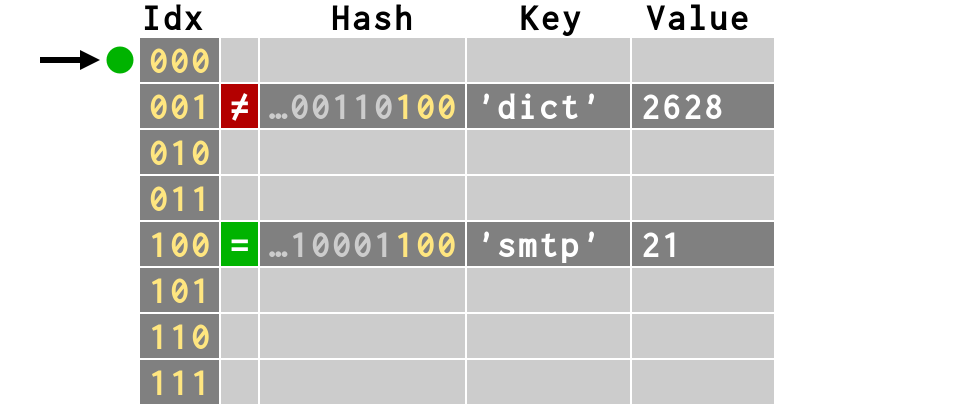
>>> # third item also finds empty slot
>>> d['svn'] = 3690

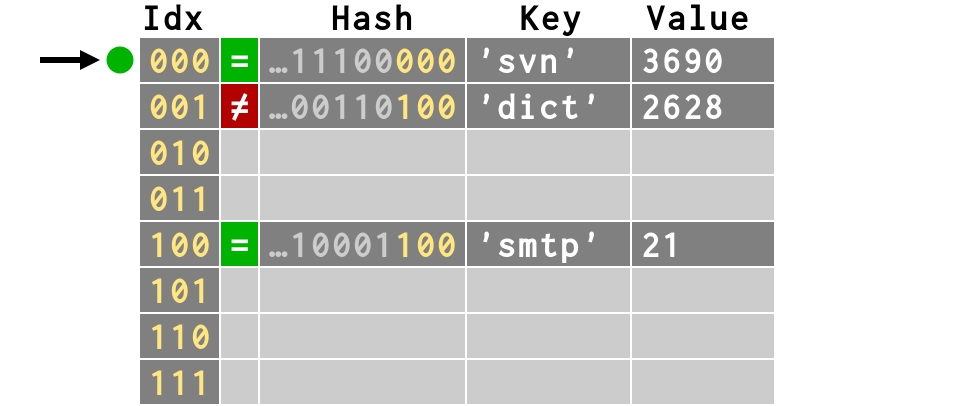
>>> # fourth item has multiple collisions
>>> d['ircd'] = 6667

>>> # fifth item collides, but less deeply
>>> d['zope'] = 9673

>>> # fifth item collides, but less deeply
>>> d['zope'] = 9673

>>> # fifth item collides, but less deeply
>>> d['zope'] = 9673

Because collisions move keys

away from their natural hash values,

key order is quite sensitive

to dictionary history

>>> d = {'smtp': 21, 'dict': 2628,
...   'svn': 3690, 'ircd': 6667, 'zope': 9673}
>>> d.keys()
['svn', 'dict', 'zope', 'smtp', 'ircd']

>>> e = {'ircd': 6667, 'zope': 9673,
...   'smtp': 21, 'dict': 2628, 'svn': 3690}
>>> e.keys()
['ircd', 'zope', 'smtp', 'svn', 'dict']

We are same yet so different!

>>> d == e
True
>>> d.keys()
['svn', 'dict', 'zope', 'smtp', 'ircd']
>>> e.keys()
['ircd', 'zope', 'smtp', 'svn', 'dict']

These dictionaries are same,

yet different by the order of keys in hash table.

>>> # Successful lookup, length 1
>>> # Compares HASHES then compares VALUES
>>> d['svn']
3690

>>> # Successful lookup, length 1
>>> # Compares HASHES then compares VALUES
>>> d['svn']
3690

>>> # Successful lookup, length 4
>>> d['ircd']
6667

>>> # Unsuccessful lookup, length 1
>>> d['nsca']
Traceback (most recent call last):
  ...
KeyError: 'nsca'

>>> # Unsuccessful lookup, length 4
>>> d['netstat']
Traceback (most recent call last):
  ...
KeyError: 'netstat'

Remember, lookups are costly !

Not all lookups are created equal.

Some finish at their first slot

Some loop over several slots

threes = {
   3: 1, 3+8: 2, 3+16: 3,
   3+24: 4,  3+32: 5
}

# Thanks to piling collisions atop each
# other, we can make lookup more expensive

timeit('d[3]', 'd=%r' % threes)    # -> 0.078
timeit('d[3+32]', 'd=%r' % threes) # -> 0.082

An interesting consequence!

what happens to lookups when we delete keys?

del d['smtp']

# Can we simply make its slot empty?

del d['smtp']

# But what would happen to d['ircd']?

When a key is deleted, its slot cannot simply

be marked as empty

Otherwise, lookups for any keys that collided would be now be impossible to find!

So we create a <dummy> key instead

>>> # Creates a <dummy> slot that
>>> # can be re-used as storage

>>> del d['smtp']

>>> # That way, we can still find d['ircd']

>>> d['ircd']
6667

>>> del d['svn'], d['dict'], d['zope']
>>> d['ircd']
6667
>>> # Still requires 4 steps!

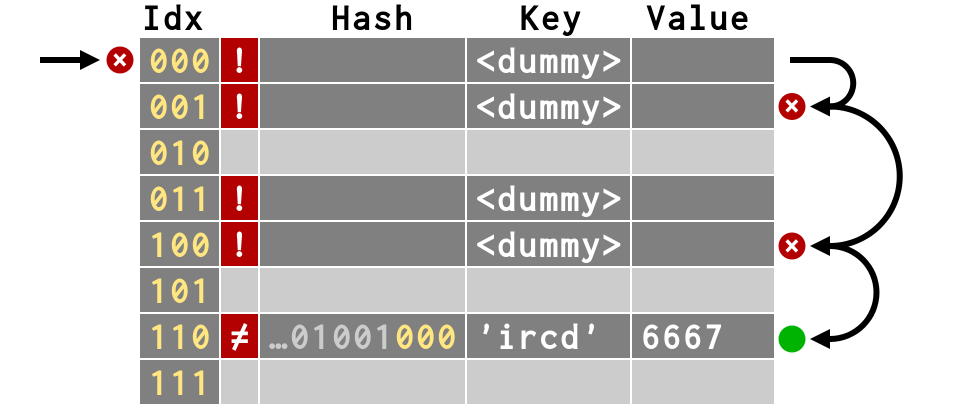
Dictionary resize when they get full

To keep collisions rare, dicts resize when only ⅔ full

>>> wordfile = open('/home/sayan/words')
>>> text = wordfile.read().decode('utf-8')
>>> words = [ w for w in text.split()
...     if w == w.lower() and len(w) < 6 ]
>>> words
[u'a', u'abaci', u'aback', u'abaft', u'abase',
 ..., u'zoom', u'zooms', u'zoos', ...]

d = {}
# Again, an empty dict has 8 slots
# Let's start filling it with keys

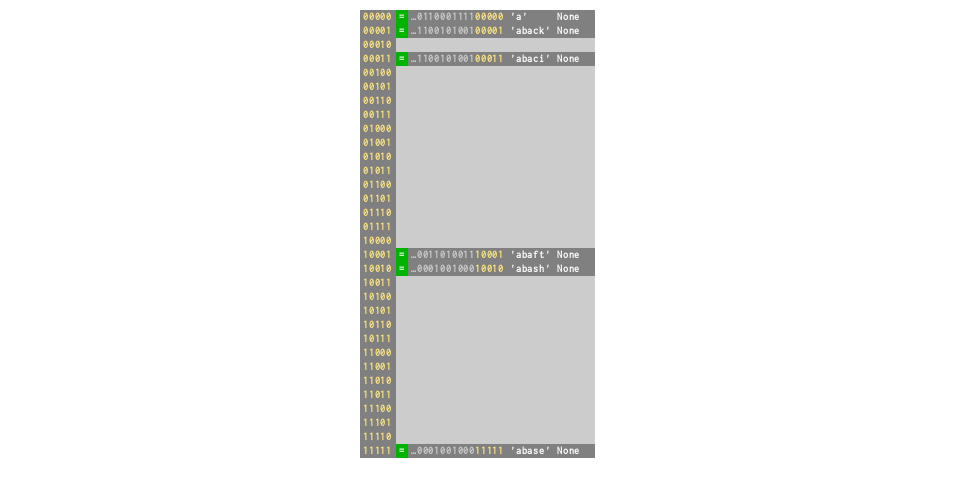
d = dict.fromkeys(words[:5])
# collision rate 40%
# but now ⅔ full — on verge of resizing!

d['abash'] = None
# Resizes ×4 to 32, collision rate drops to 0%

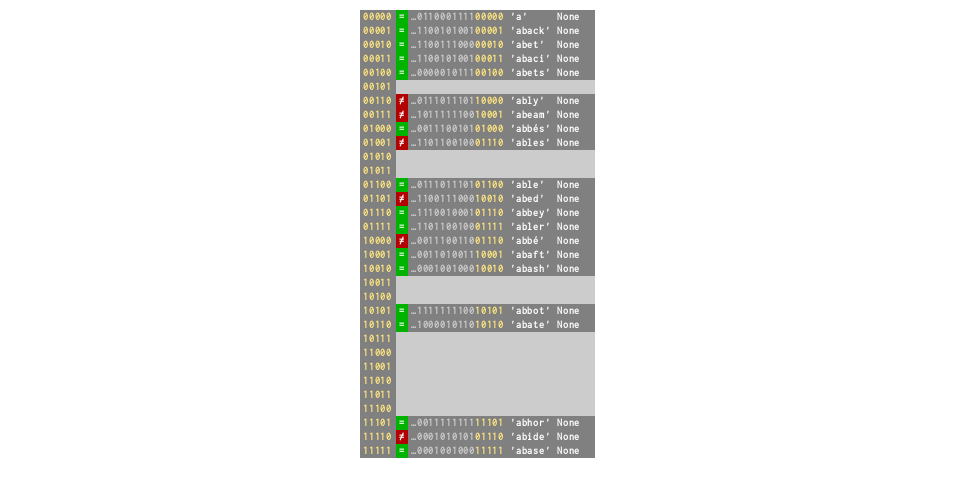
d = dict.fromkeys(words[:21])
# ⅔ full again — collision rate 29%

d['abode'] = None
# Resizes ×4 to 128, collision rate drops to 9%

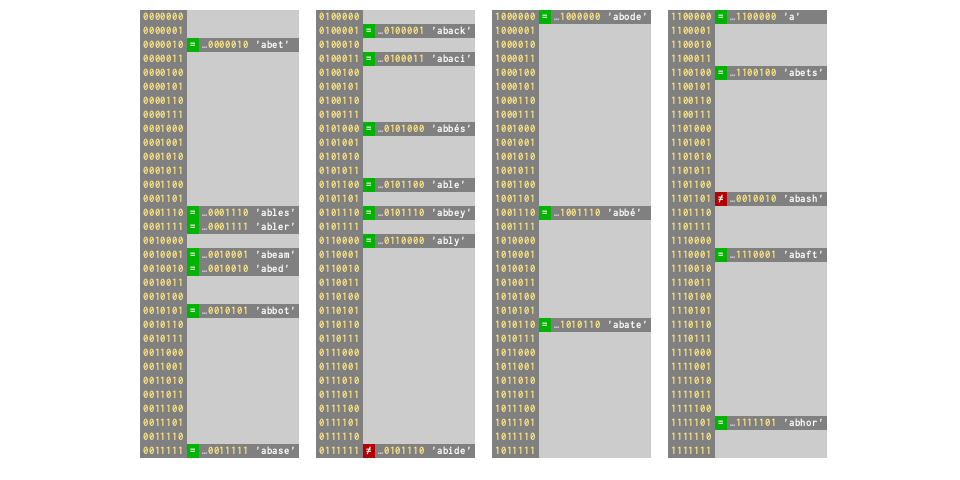
d = dict.fromkeys(words[:85])
# ⅔ full again — collision rate 33%

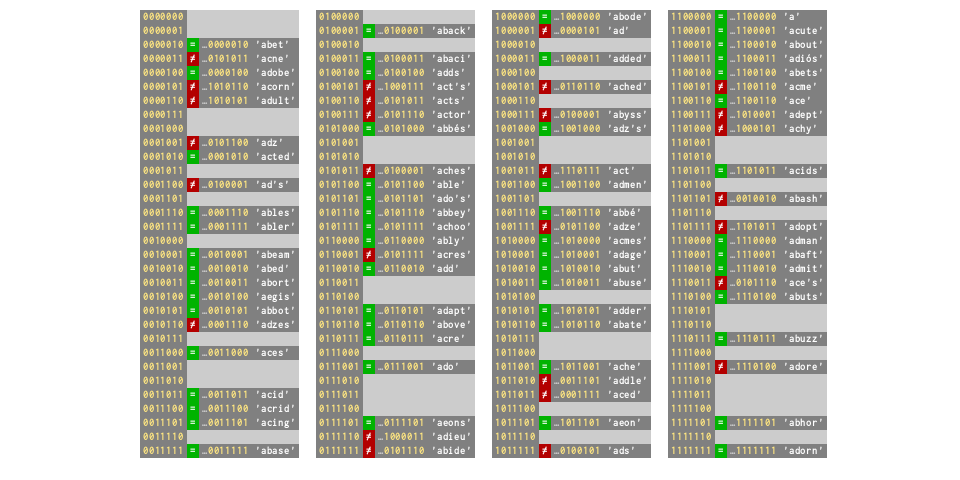
So, dictionary size increase as the keys become crowded

Average dictionary

performance is excellent

A dictionary of common words:

>>> wfile = open('/usr/sayan/words')
>>> words = wfile.read().split()[:1365]
>>> print words
['A', "A's", ..., "Backus's", 'Bacon', "Bacon's"]

>>> pmap = _dictinfo.probe_all_steps(words)

Some are lucky enough to hit in first try

>>> pmap['Ajax']
[1330]
>>> pmap['Agamemnon']
[2020]

While some of them where not that lucky enough!

>>> pmap['Aristarchus']  # requires 5 probes
[864, 1089, 801, 1108, 74]
>>> pmap['Baal']         # requires 16 probes!
[916, 1401, 250, 1359, 399, 1156, 1722, 420, 53,
 266, 1331, 512, 513, 518, 543, 668]

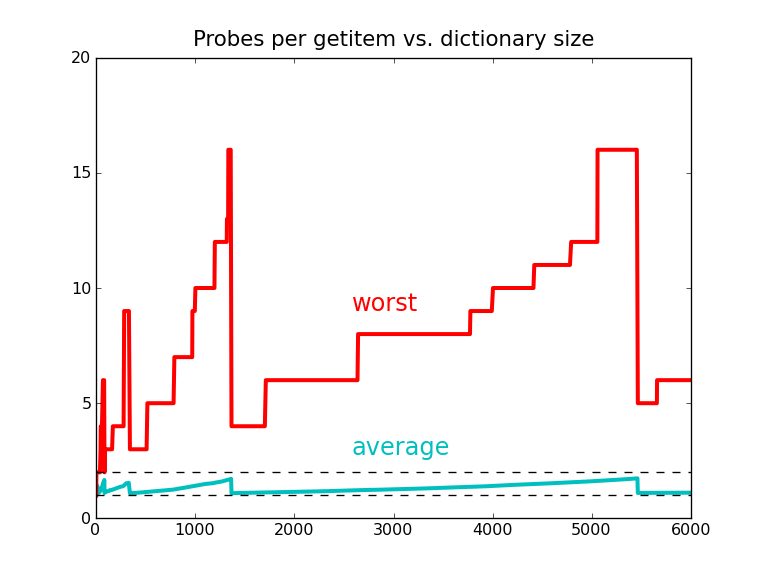
Probes sound to be slow ? right?

But they aren't !

>>> setup = "d=dict.fromkeys(%r)" % words
>>> fast = timeit("d['Ajax']", setup)
>>> slow = timeit("d['Baal']", setup)
>>> '%.1f' % (slow/fast)
'1.7'

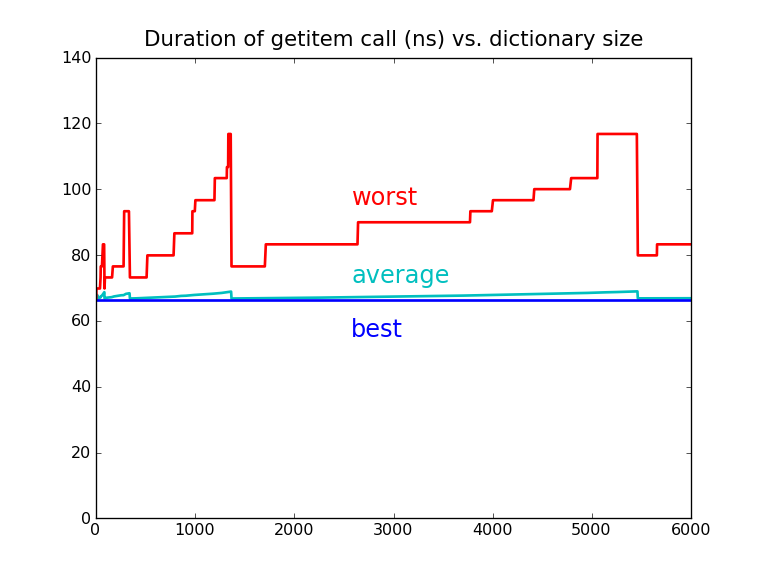
An insert can completely reorder a dictionary during resizing!

>>> d = {'Double': 1, 'double': 2, 'toil': 3,
...      'and': 4, 'trouble': 5}
>>> d.keys()
['toil', 'Double', 'and', 'trouble', 'double']
>>> d['fire'] = 6
>>> d.keys()
['and', 'fire', 'Double', 'double', 'toil',
 'trouble']

Because an insert can radically reorder a dictionary, key insertion

is prohibited during iteration

>>> d = {'Double': 1, 'double': 2, 'toil': 3,
...     'and': 4, 'trouble': 5}
>>> for key in d:
...     d['fire'] = 6
Traceback (most recent call last):
  ...
RuntimeError: dictionary changed size during
  iteration

Rules to follow!

Don't rely on the order

Don't insert while iterating

Mutable keys not allowed

Dictionaries trade space for time

Equal values should have equal hashes

regardless of their type!

>>> hash(9)
9
>>> hash(9.0)
9
>>> hash(complex(9, 0))
9

>>> dict = { 9: 'nine' }
9
>>> dict[9]
'nine'
>>> dict[9.0]
'nine'
>>> dict[complex(9)]
'nine'

References

The Mighty Dictionary by Brandon Rhodes - https://www.youtube.com/watch?v=C4Kc8xzcA68
http://svn.python.org/projects/python/trunk/Objects/dictnotes.txt
http://svn.python.org/projects/python/trunk/Objects/dictobject.c
https://gist.github.com/avances123/9497630

Understanding Python's DataStructure: Dictionary

How the hashing is done?

Lookup?

compute hash

get the index using `i` bits

search in the hash table

Ever noticed the crazy order of a dictionary ?

Collision

What happens when two keys need the same slot?

Because collisions move keys

away from their natural hash values,

key order is quite sensitive

to dictionary history

We are same yet so different!

Remember, lookups are costly !

Not all lookups are created equal.

Some finish at their first slot

Some loop over several slots

An interesting consequence!

what happens to lookups when we delete keys?

Dictionary resize when they get full

So, dictionary size increase as the keys become crowded

Average dictionary

performance is excellent

References

The End

Understanding Python Data Structure: Dictionary

Understanding Python Data Structure: Dictionary

sayanchowdhury

Understanding Python's DataStructure: Dictionary

How the hashing is done?

Lookup?

compute hash

get the index using `i` bits

search in the hash table

Ever noticed the crazy order of a dictionary ?

Collision

What happens when two keys need the same slot?

Because collisions move keys

away from their natural hash values,

key order is quite sensitive

to dictionary history

We are same yet so different!

Remember, lookups are costly !

Not all lookups are created equal.

Some finish at their first slot

Some loop over several slots

An interesting consequence!

what happens to lookups when we delete keys?

Dictionary resize when they get full

So, dictionary size increase as the keys become crowded

Average dictionary

performance is excellent

References

The End

Understanding Python Data Structure: Dictionary

More from sayanchowdhury