Sebastian Ordoñez-Soto

Universidad Nacional de Colombia

 

Internship tutor:  Sergey Barsuk

 

June 27th, 2024

 

Study and search of the \(B_{c}^{+}\rightarrow (\eta_{c}\rightarrow p\bar{p})\mu^{+}\nu_{\mu}\) decay

 IJCLab LHCb group meeting

Outline

  • Introduction
    • The \(B_{c}\) meson
    • \(B_{c}\) semileptonic decays
  • Dataset
    • Data sample
    • MC samples
  • ​Selection
    • Pre-selection
    • Charmonia optimization
  • Analysis
    • Fit models
    • Signal extraction
    • Final fit
  • Summary

S. Ordonez Soto

June 27th, 2024

S. Ordonez Soto

June 27th, 2024

Introduction

\(m_{B_{c}} = (6274.47 \pm 0.32)\) MeV

 \(\tau_{B_{c}} = (0.507 \pm 0.009) \) ps

  • Lowest-mass bound state of two heavy quarks of different flavors.

    • Discovered by the CDF collaboration in 1998.

    • Has no strong or electromagnetic decay channels.

    • Its weak decay yields a large branching fraction to final states containing a \(J/ \psi\)

  • Full decay width: \(\Gamma = \Gamma_{b} + \Gamma_{c} + \Gamma_{bc}\) 

    • \(\Gamma_{b}: \bar{b}\rightarrow \bar{c}W^{+}\), with \(c\) as  spectator (~ 20%)

    • \(\Gamma_{c}: c\rightarrow sW^{+}\), with \(\bar{b}\) as spectator  (~ 70%)

    • \(\Gamma_{bc}: c\bar{b} \rightarrow W^{+}\), weak annihilation (~ 10%)

Introducing the \(B_{c}^{+}\) meson

\longrightarrow
\longrightarrow
\longrightarrow
(c\bar{c}) l \nu_{l}
,(c\bar{c}) \pi, ...
B_{s} \pi, B_{s}l\nu_{l}, ...
D^{*}K^{+}, ...

S. Ordonez Soto

June 27th, 2024

Introduction

The decay channel

  • \(B_{c}^{+}\rightarrow \eta_{c}\mu^{+}\nu_{\mu}\) is one of the possible \(B_{c}^{+}\) semileptonic (SL) decay channels.

    • Full width determination
    • Lepton Flavor Universality test \(\rightarrow R(\eta_{c})\)

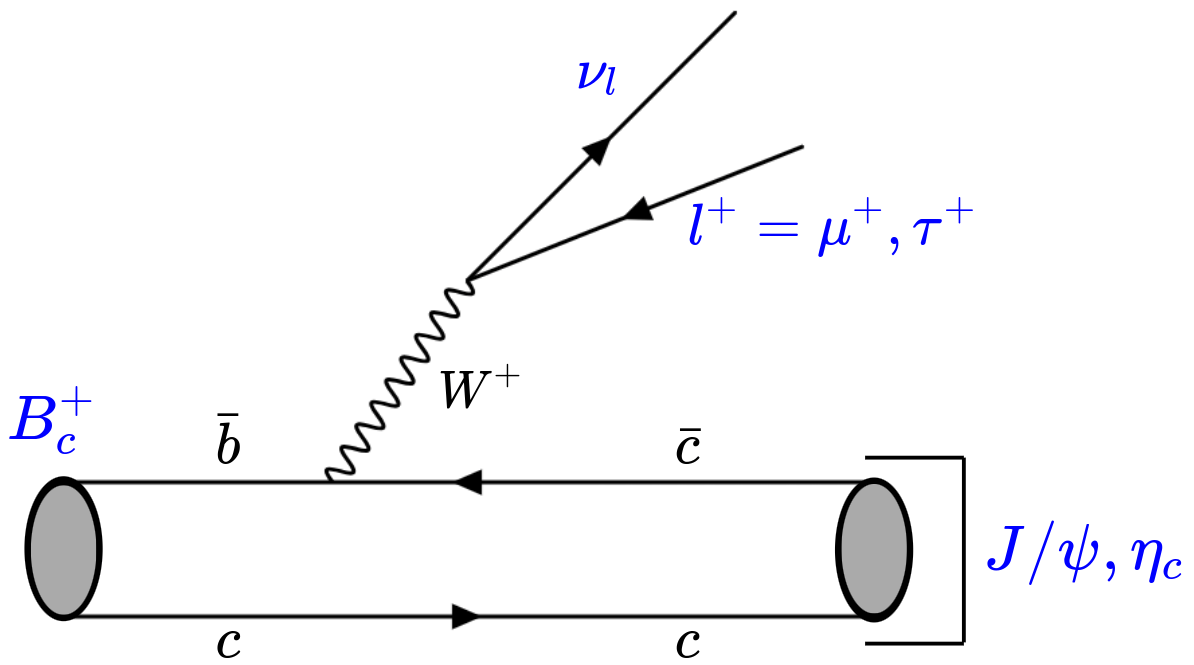
  • \(B_{c}^{+}\rightarrow J/\psi\mu^{+}\nu_{\mu}\) was already measured by LHCb \(\rightarrow R(J/\psi)\).  

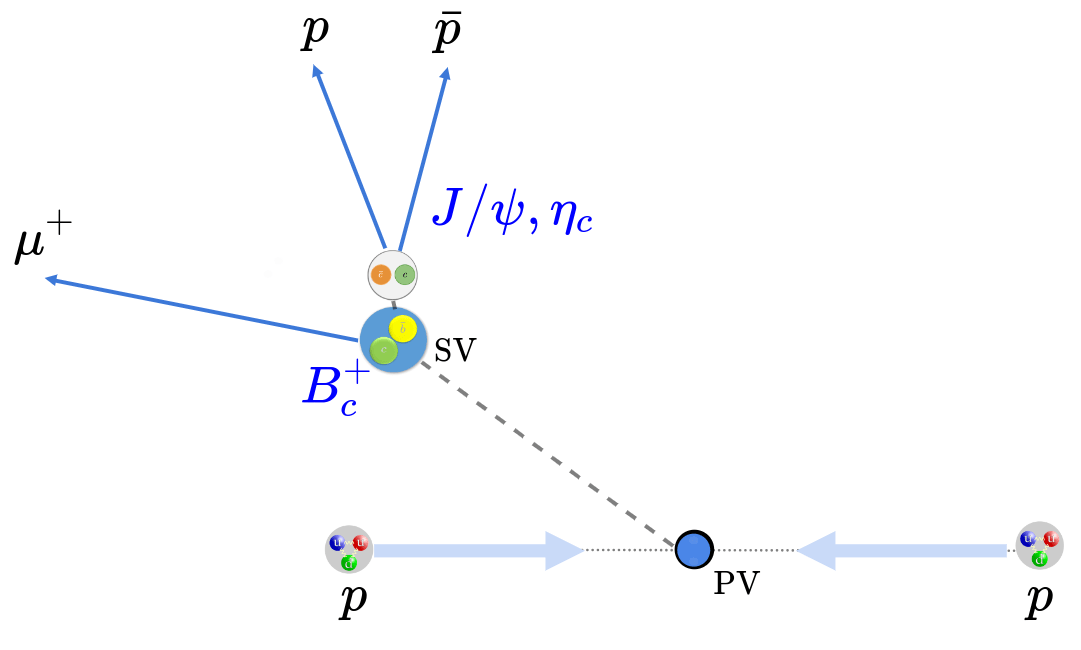
S. Ordonez Soto

June 27th, 2024

Introduction

Analysis strategy

  • The \(B_{c}^{+}\rightarrow \eta_{c}\mu^{+}\nu_{\mu}\) decay will be analyzed together with the  \(B_{c}^{+}\rightarrow J/\psi\mu^{+}\nu_{\mu}\), which is used as normalization channel.

  • The ratio \(\frac{\mathcal{B}(B_{c}^{+}\rightarrow \eta_{c}\mu^{+}\nu_{\mu})}{\mathcal{B}(B_{c}^{+}\rightarrow J/\psi\mu^{+}\nu_{\mu})}\) can be calculated as:

Measured!

See: here and here.

Calculated from MC

Yield extraction from final fit

\boxed{\frac{\mathcal{B}(B_{c}^{+}\rightarrow \eta_{c}\mu^{+}\nu_{\mu})}{\mathcal{B}(B_{c}^{+}\rightarrow J/\psi\mu^{+}\nu_{\mu})} = \frac{N_{B_{c}^{+}\rightarrow \eta_{c}\mu^{+}\nu_{\mu}}}{N_{B_{c}^{+}\rightarrow J/\psi\mu^{+}\nu_{\mu}}} \times \frac{\mathcal{B}(J/\psi \rightarrow p\bar{p})}{\mathcal{B}(\eta_{c}\rightarrow p\bar{p})} \times \frac{\epsilon_{tot}(B_{c}^{+}\rightarrow \eta_{c}\mu^{+}\nu_{\mu})}{\epsilon_{tot}(B_{c}^{+}\rightarrow J/\psi\mu^{+}\nu_{\mu})}}

  • The \(R_{\eta_{c}}\) could be calculated as:

\boxed{R_{\eta_{c}}=\frac{\mathcal{B}(B_{c}^{+}\rightarrow \eta_{c}\mu^{+}\nu_{\mu})}{\mathcal{B}(B_{c}^{+}\rightarrow J/\psi\mu^{+}\nu_{\mu})} \times \frac{\mathcal{B}(B_{c}^{+}\rightarrow J/\psi\tau^{+}\nu_{\tau})}{\mathcal{B}(B_{c}^{+}\rightarrow \eta_{c}\tau^{+}\nu_{\tau})} \times \frac{1}{R_{J/\psi}}}

S. Ordonez Soto

June 27th, 2024

Dataset

Data sample

LHCb run 2 data from proton-proton collisions, at \(\sqrt{s}=13 \text{TeV}\) and \(4 \text{fb}^{-1}\), collected from 2015 to 2017. 

  • There are two main variables for the analysis:

    • The \(p\bar{p}\) invariant mass \(M(p\bar{p})\)

    • The \(p\bar{p}\mu\) corrected mass, defined as: \(M_{CORR} = \sqrt{M^{2}(p\bar{p}\mu) + p^{2}_{\bot}} + p_{\bot}\)

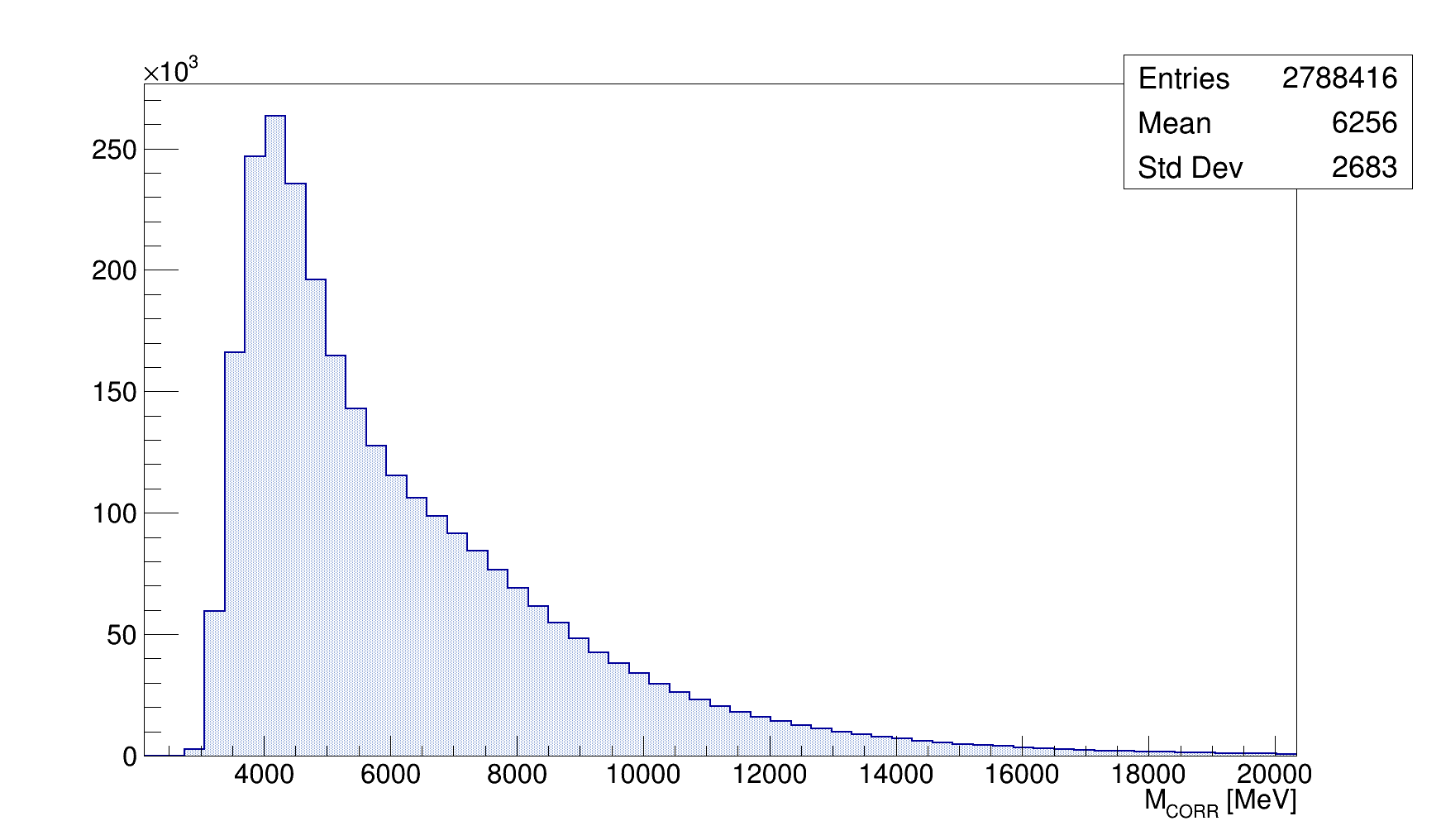
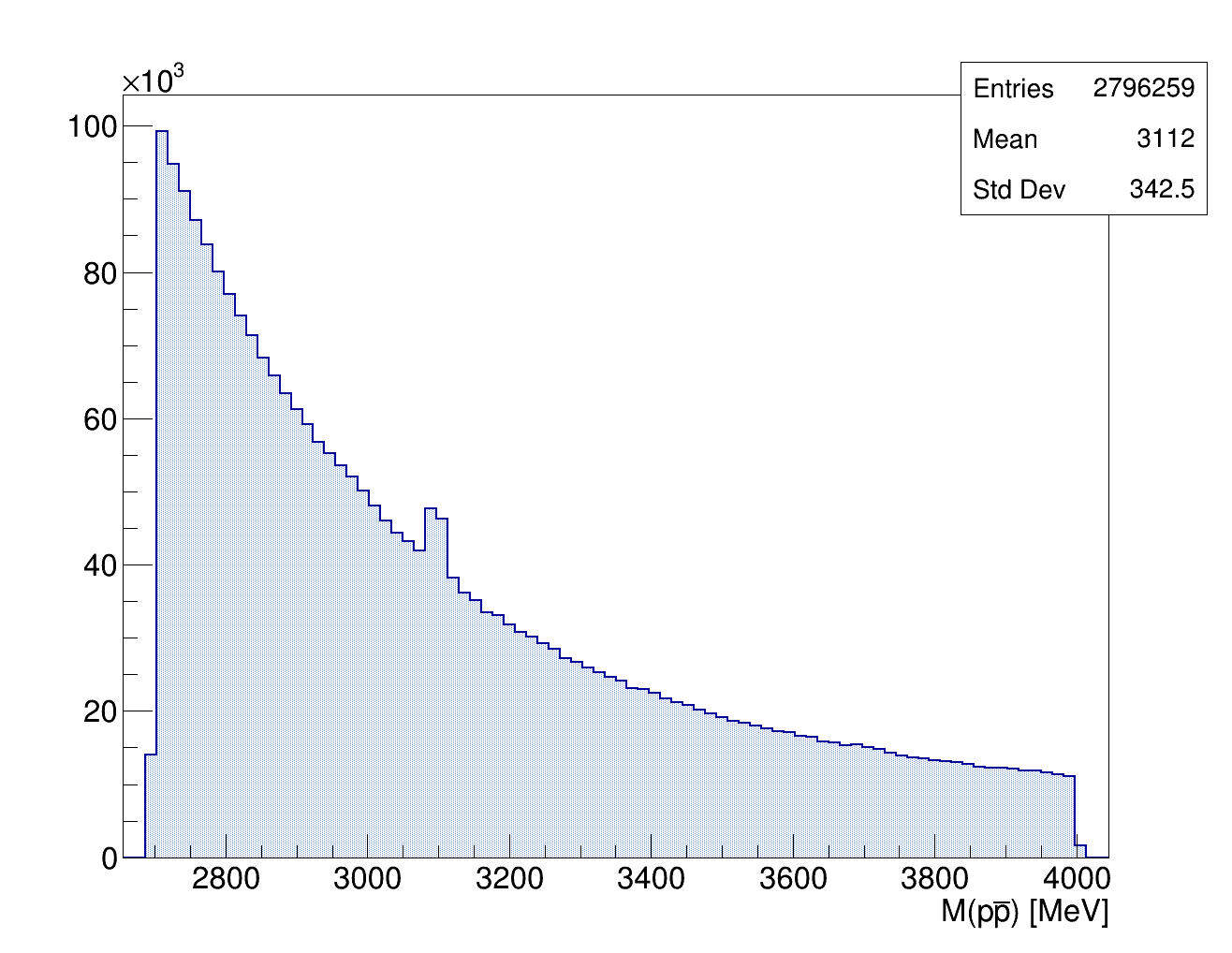
S. Ordonez Soto

June 27th, 2024

Simulation samples

There are Monte Carlo samples available for both signal and different backgrounds

Dataset

B_{c}^{+}\rightarrow (h_{c}\rightarrow \eta_{c}\gamma)\mu^{+}\nu_{\mu}
B_{c}^{+}\rightarrow \eta_{c}(\tau^{+}\rightarrow\mu^{+}\nu_{\mu}\bar{\nu}_{\tau})\nu_{\tau}
B_{c}^{+}\rightarrow (\psi(2S)\rightarrow J/\psi\pi^{+}\pi^{-})\mu^{+}\nu_{\mu}
B_{c}^{+}\rightarrow J/\psi(\tau^{+}\rightarrow\mu^{+}\nu_{\mu}\bar{\nu}_{\tau})\nu_{\tau}
B_{c}^{+}\rightarrow (\chi_{c0}\rightarrow J/\psi\gamma)\mu^{+}\nu_{\mu}
\eta_{c} \hspace{0.1cm} \text{peaking bkg.}
J/\psi \hspace{0.1cm }\text{peaking bkg.}
B_{c}^{+}\rightarrow (\chi_{c1}\rightarrow J/\psi\gamma)\mu^{+}\nu_{\mu}
B_{c}^{+}\rightarrow (\chi_{c2}\rightarrow J/\psi\gamma)\mu^{+}\nu_{\mu}
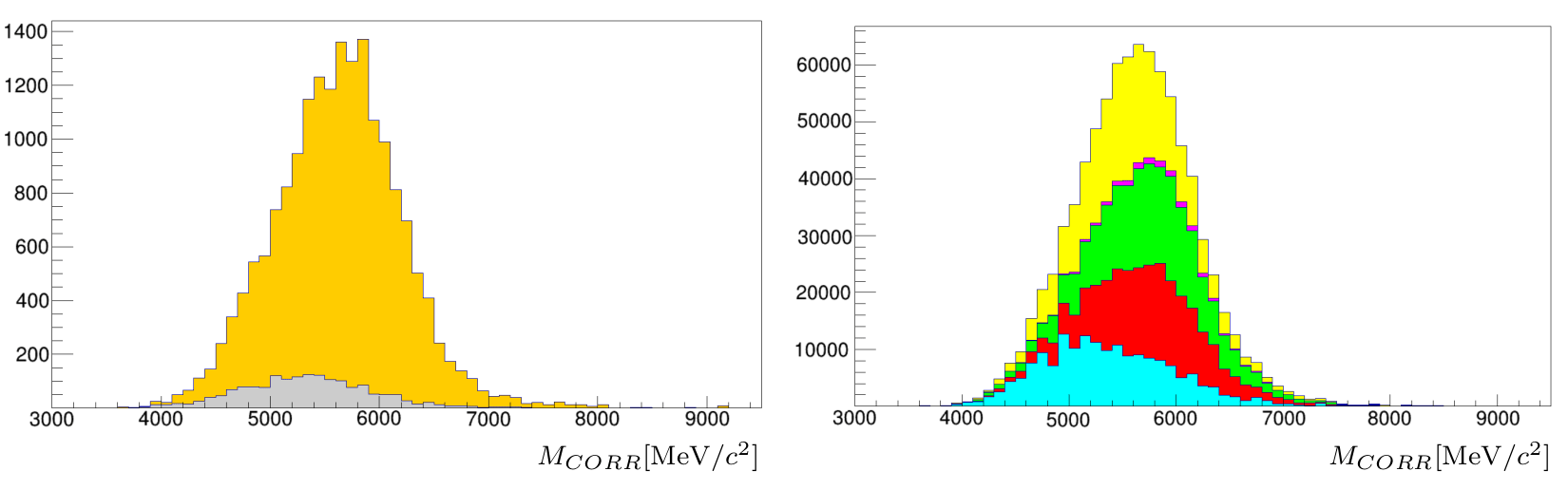
  • Signal: \(B_{c}^{+}\rightarrow (\eta_{c}\rightarrow p\bar{p})\mu^{+}\nu_{\mu}\) and \(B_{c}^{+}\rightarrow (J/\psi\rightarrow p\bar{p})\mu^{+}\nu_{\mu}\)
  • Background:

    • ​Inclusive bkg: \(b\rightarrow \eta_{c}X\) and \(b\rightarrow J/\psi X\) decays

    • Peaking bkg:

S. Ordonez Soto

June 27th, 2024

Selection

Pre-selection

Charmonia optimization

A set of selection requirements is initially applied, including: vertex quality and PID requirements

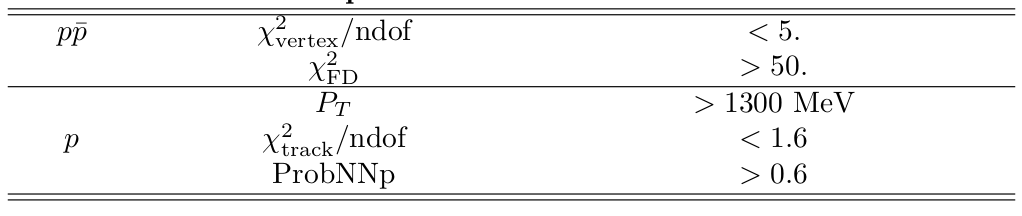
Additional cuts are added to optimize charmonia:

S. Ordonez Soto

June 27th, 2024

Analysis

Fit  models to \(M_{CORR}\) distributions

Using the MC samples the shapes of the \(M_{CORR}\) distributions for signal and background decay channels are extracted.

  • Signal: 

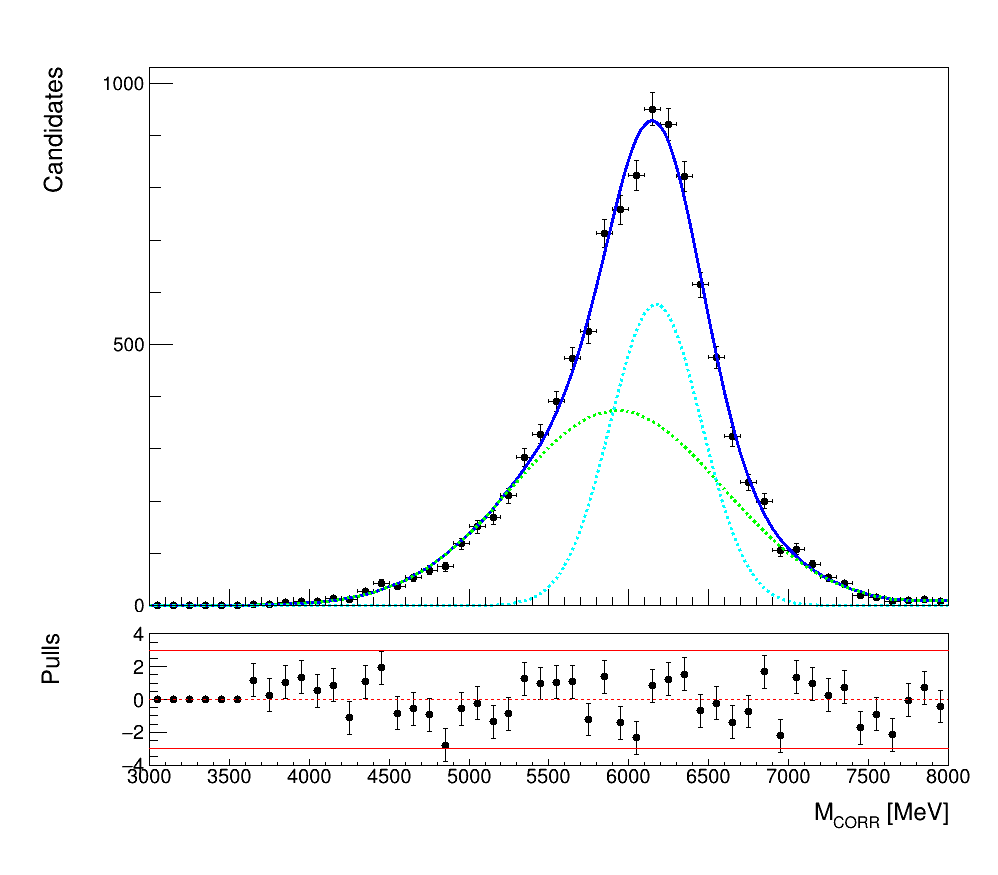
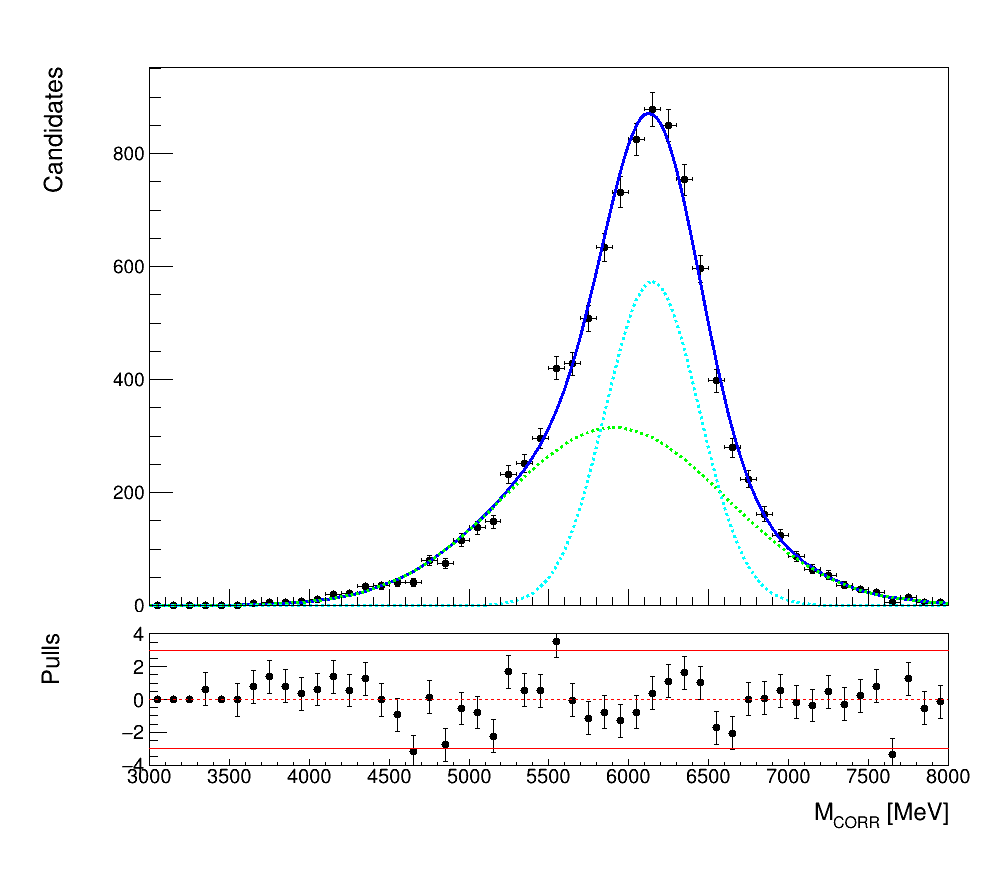
\(B_{c}^{+}\rightarrow\eta_{c}\mu^{+}\nu_{\mu}\)

\(B_{c}^{+}\rightarrow J/\psi\mu^{+}\nu_{\mu}\)

F_{excl,sig} (M_{CORR}) = f \cdot CB(M_{CORR};\mu_{1},R,\alpha,n) + (1-f) \cdot G(M_{CORR};\mu_{1}+d,\sigma_{1})

S. Ordonez Soto

June 27th, 2024

Analysis

Fit  models to \(M_{CORR}\) distributions

  • \(\eta_{c}\) peaking background: 

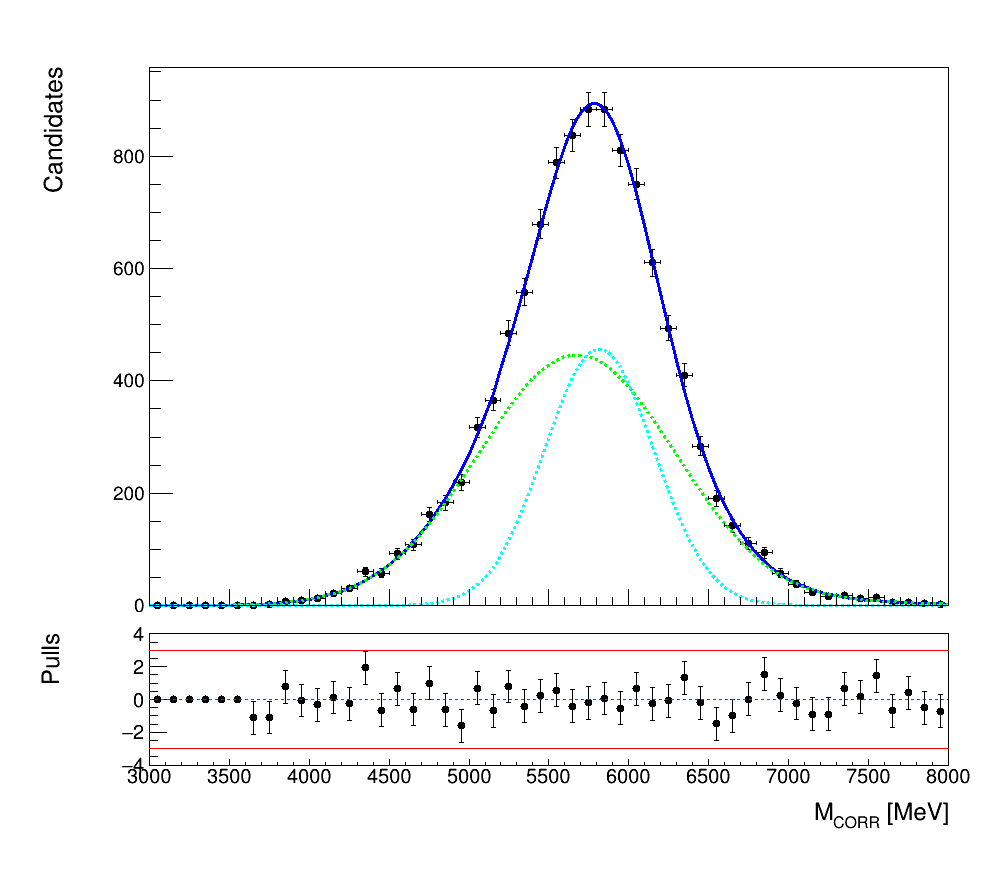
\(B_{c}\rightarrow(\chi_{0}\rightarrow J/\psi\gamma)\mu\nu_{\mu}\)

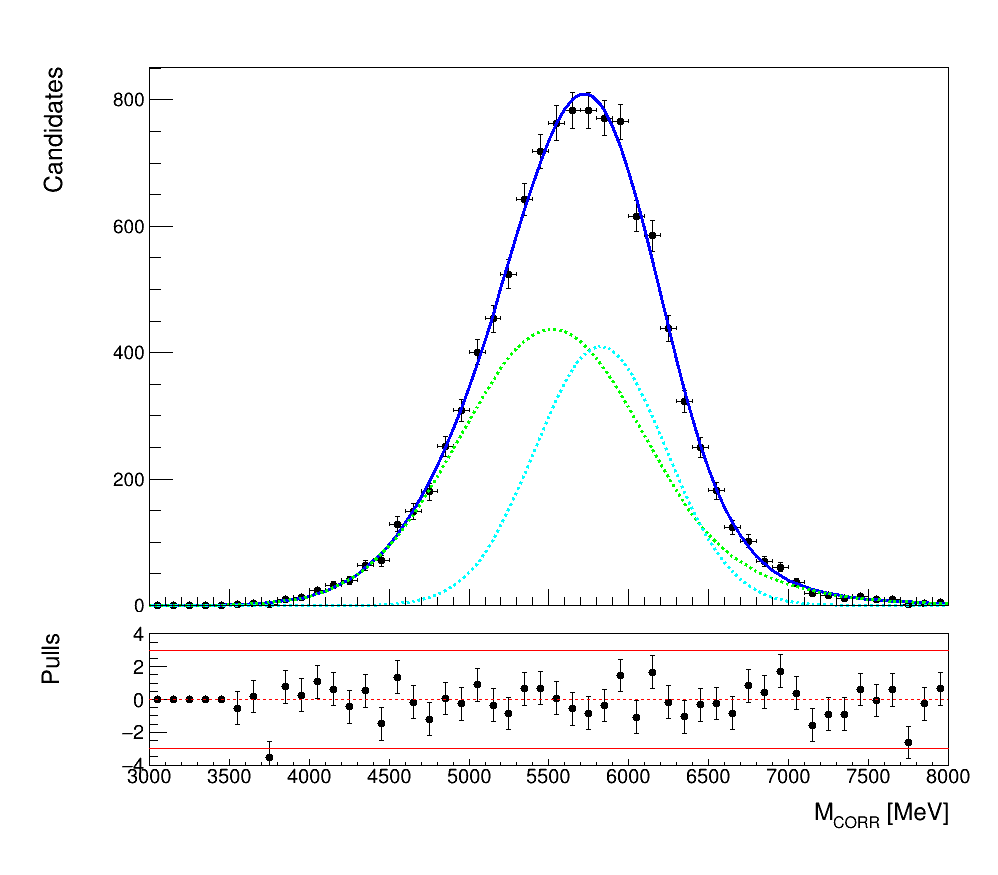
\(B_{c}\rightarrow(\chi_{1}\rightarrow J/\psi\gamma)\mu\nu_{\mu}\)

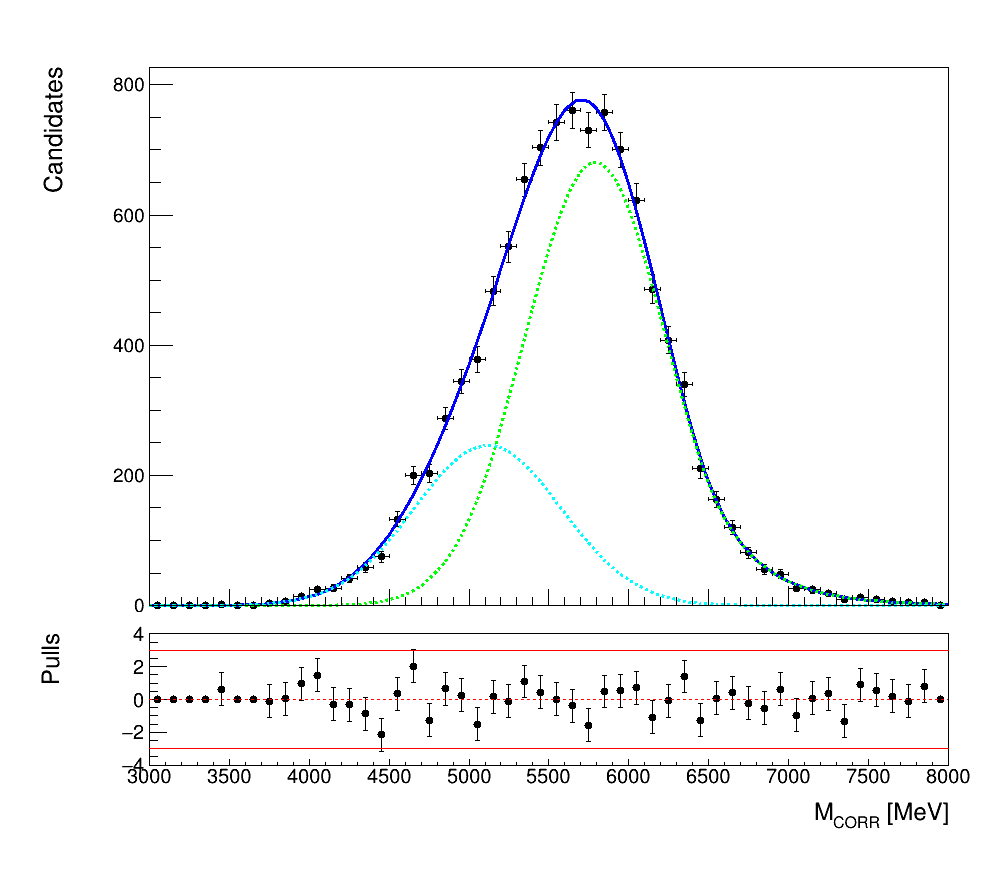
\(B_{c}\rightarrow(\chi_{2}\rightarrow J/\psi\gamma)\mu\nu_{\mu}\)

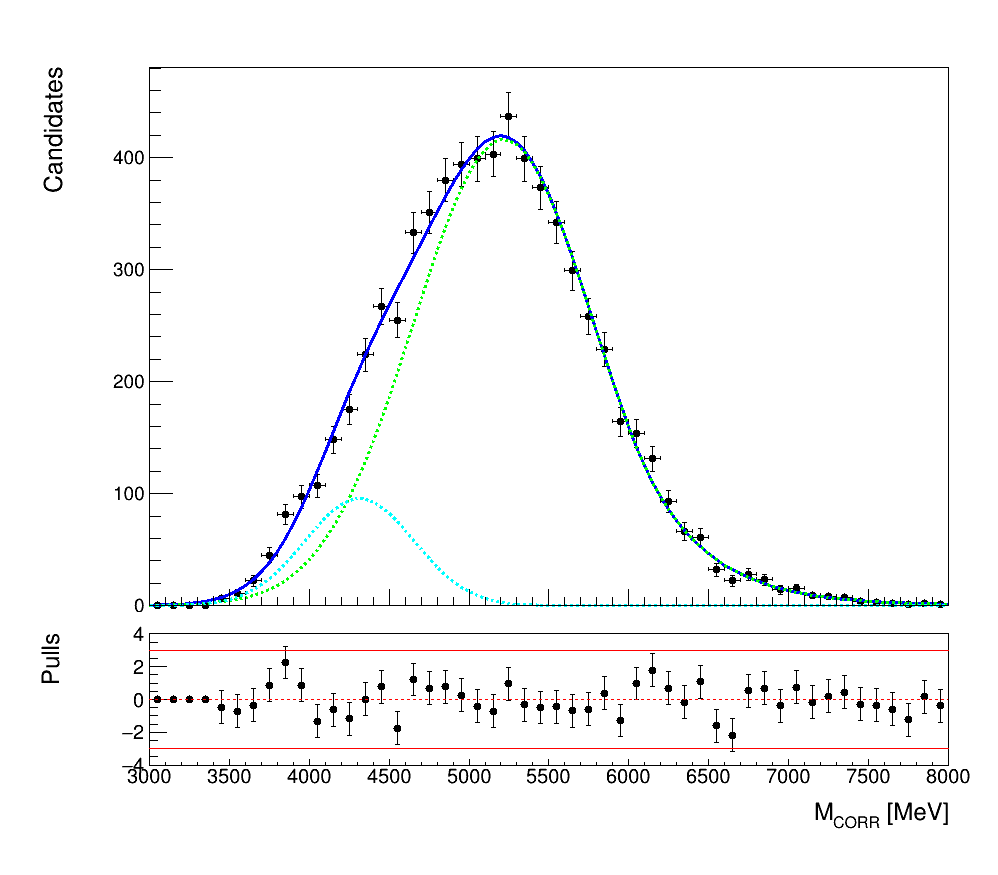
\(B_{c}\rightarrow \eta_{c}(\tau\rightarrow\mu\nu_{\mu}\bar{\nu_{\tau}})\nu_{\tau}\)

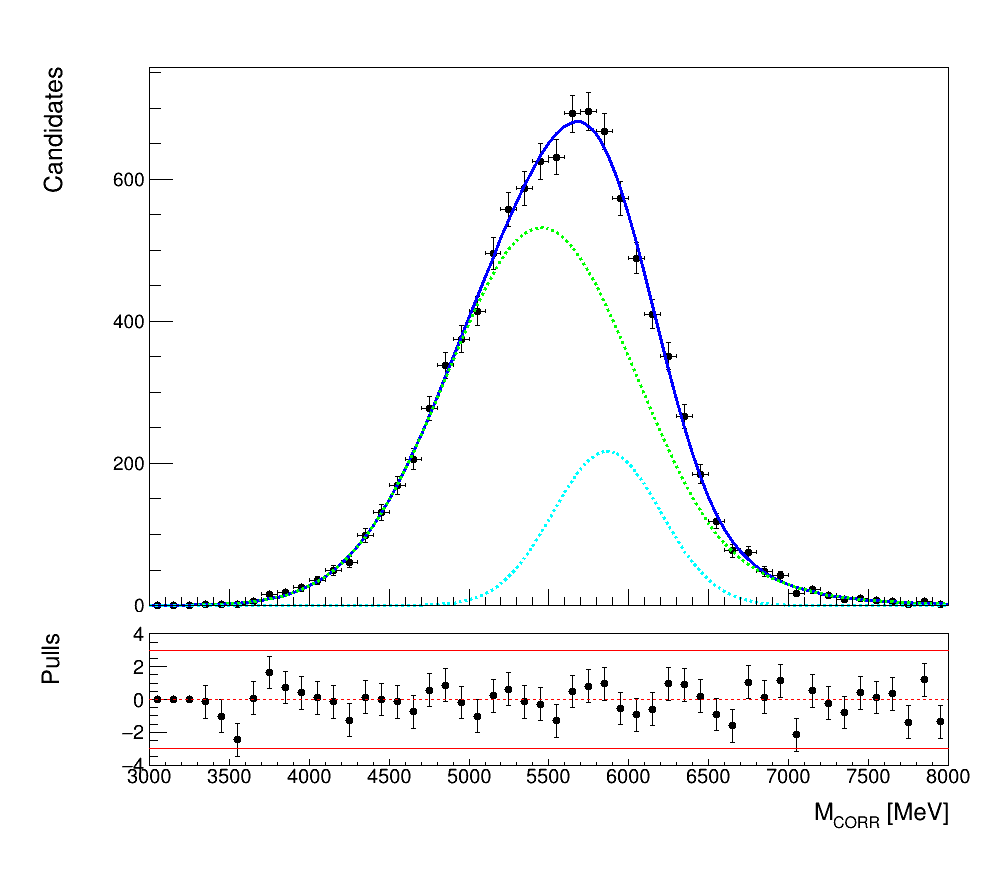
\(B_{c}\rightarrow(h_{c}\rightarrow\eta_{c}\gamma)\mu\nu_{\mu}\)

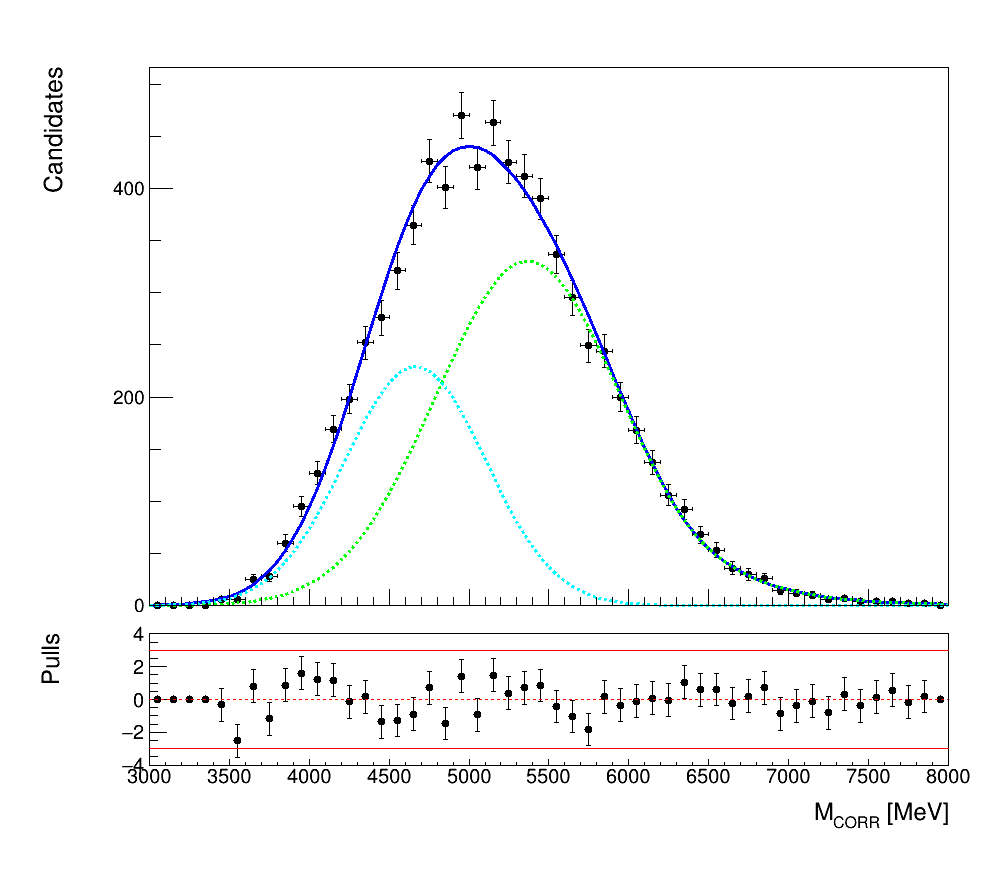
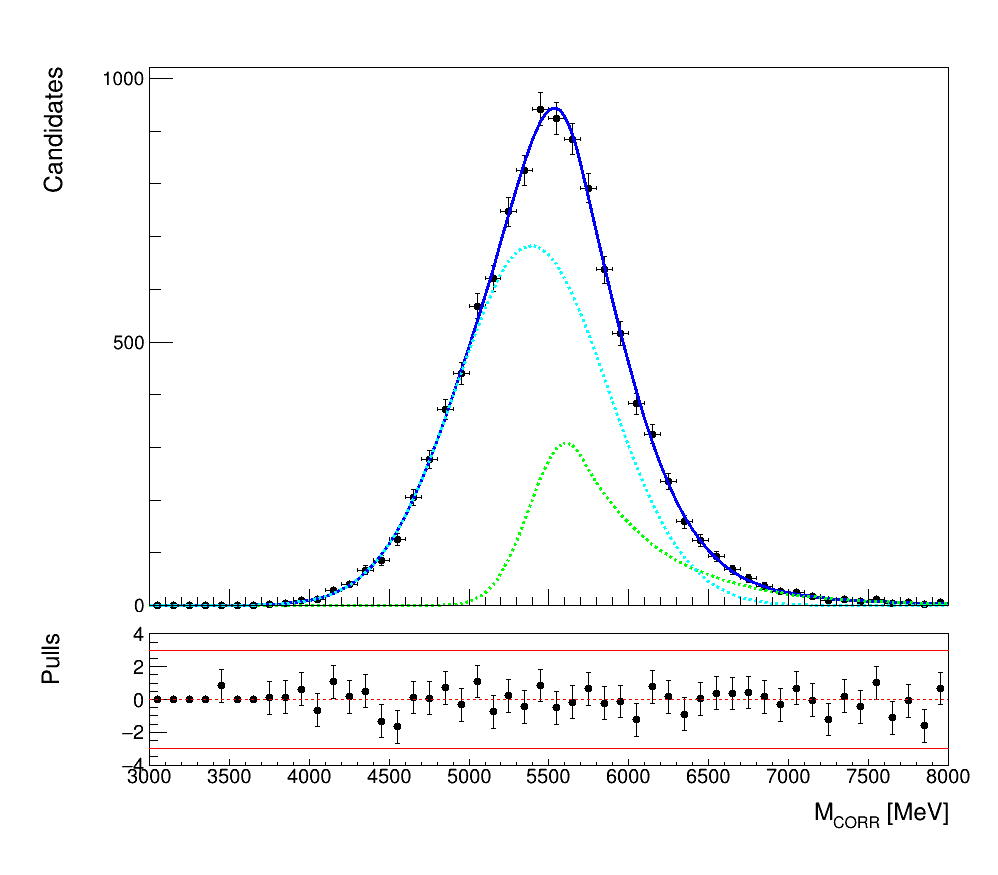
  • \(J/\psi\) peaking background: 

\(B_{c}\rightarrow J/\psi(\tau\rightarrow\mu\nu_{\mu}\bar{\nu_{\tau}})\nu_{\tau}\)

\(B_{c}\rightarrow(\psi(2S)\rightarrow J/\psi \pi\pi)\mu\nu_{\mu}\)

S. Ordonez Soto

June 27th, 2024

Analysis

Fit  models to \(M_{CORR}\) distributions

F_{incl}(M_{CORR}) = \left(1-\left(\frac{m_{0}}{M_{CORR}}\right)\right)^{p} [f\cdot G(M_{CORR};\mu,\sigma)+(1-f)e^{\alpha\cdot M_{CORR}}]
  • Inclusive background 

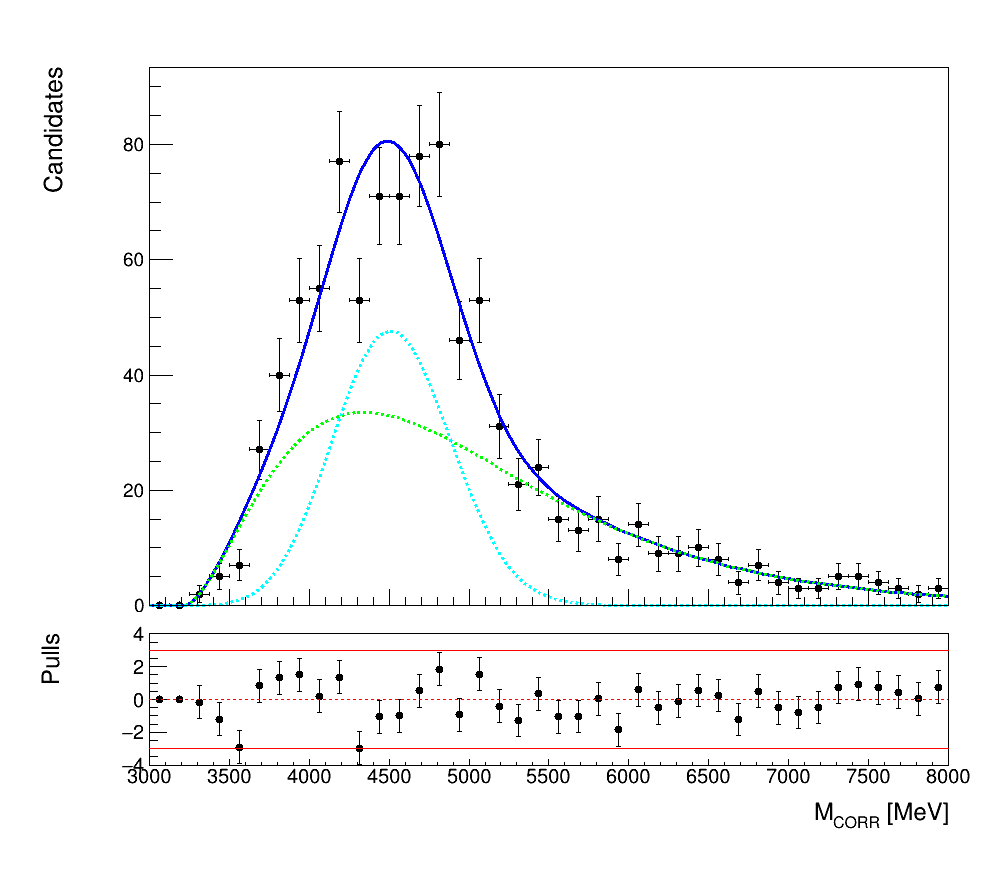
\(b\rightarrow J/\psi X\)

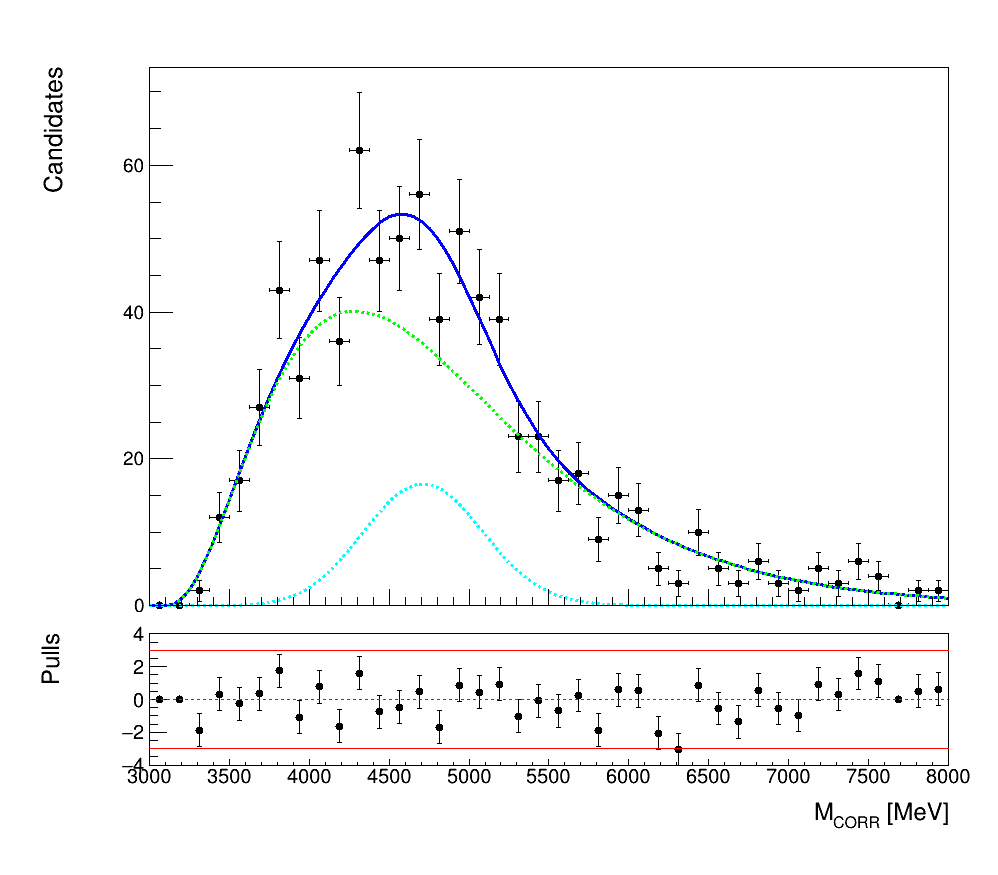
\(b\rightarrow \eta_{c} X\)

S. Ordonez Soto

June 27th, 2024

Analysis

Signal extraction

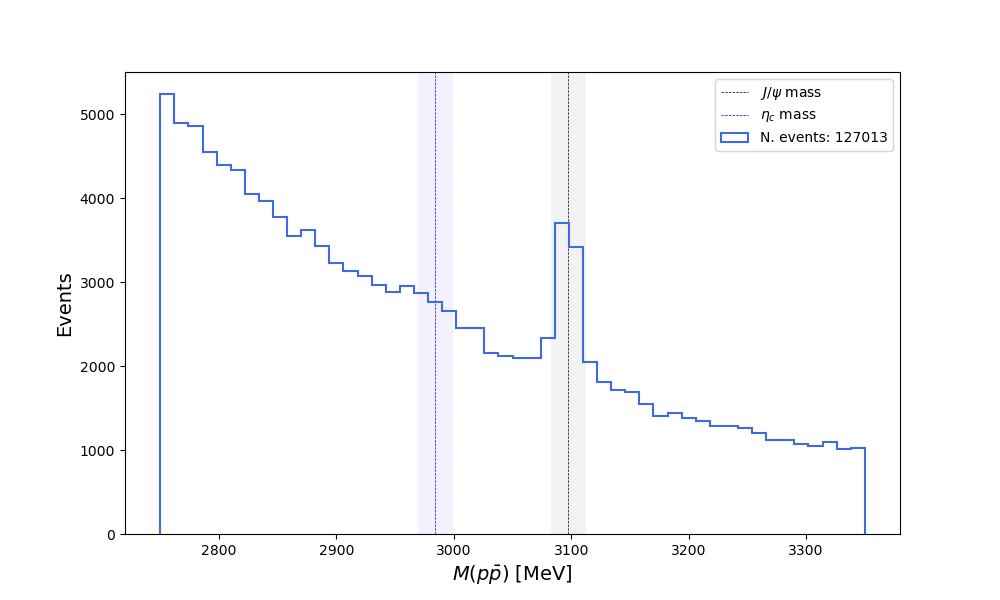
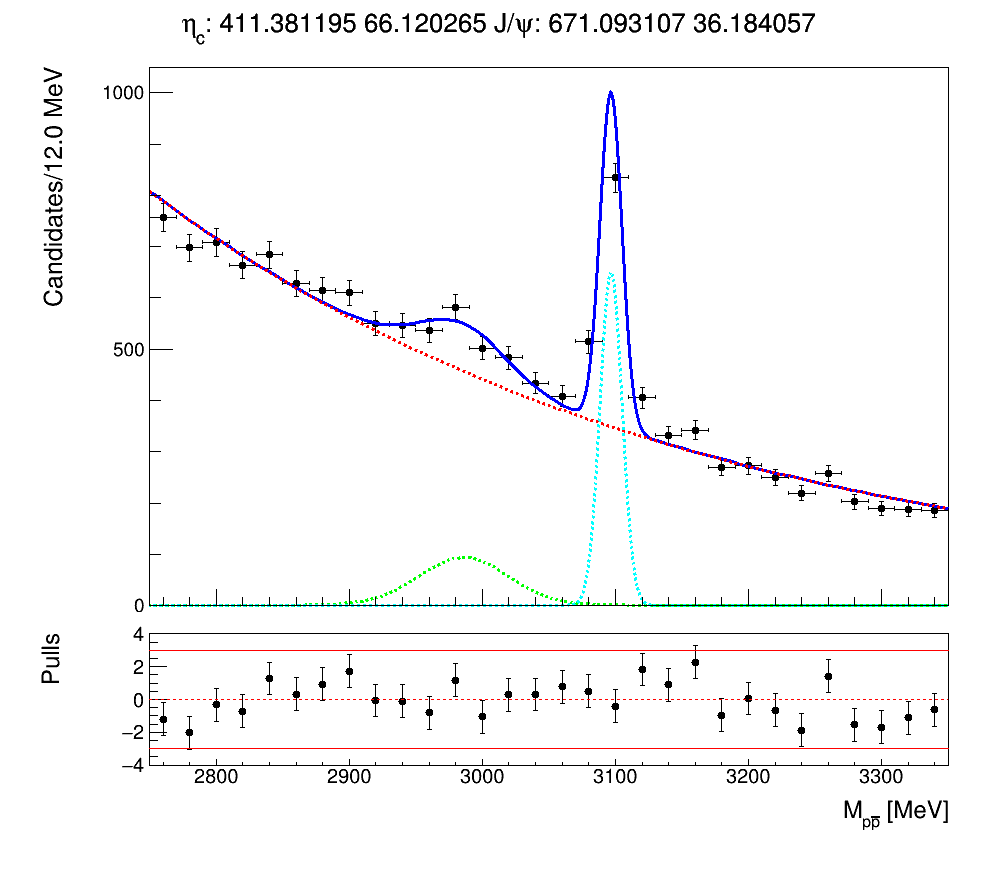
 \(\eta_{c}\) and \(J/\psi\) yields are extracted from fits to the \(M(p\bar{p})\) distribution in bins of \(M_{CORR}\)

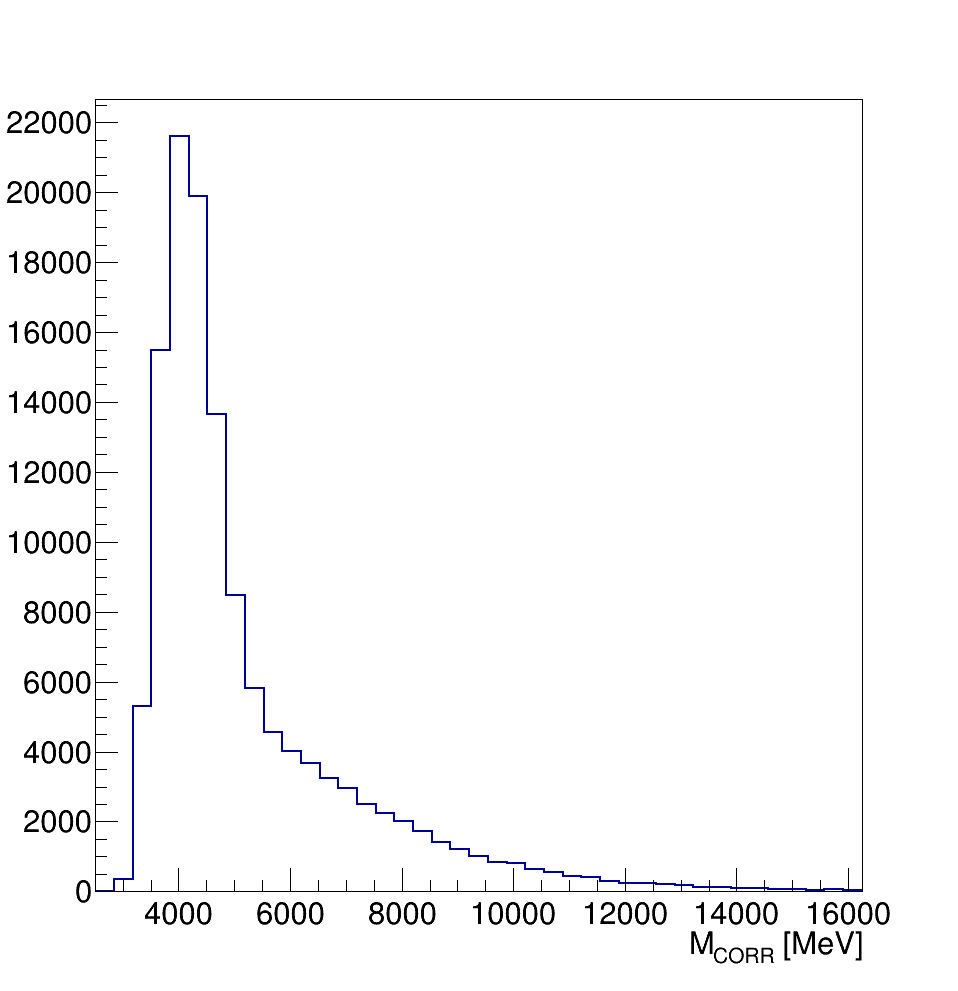
Data from this bin is extracted, and the charmonia fit model is used

S. Ordonez Soto

June 27th, 2024

Analysis

Signal extraction

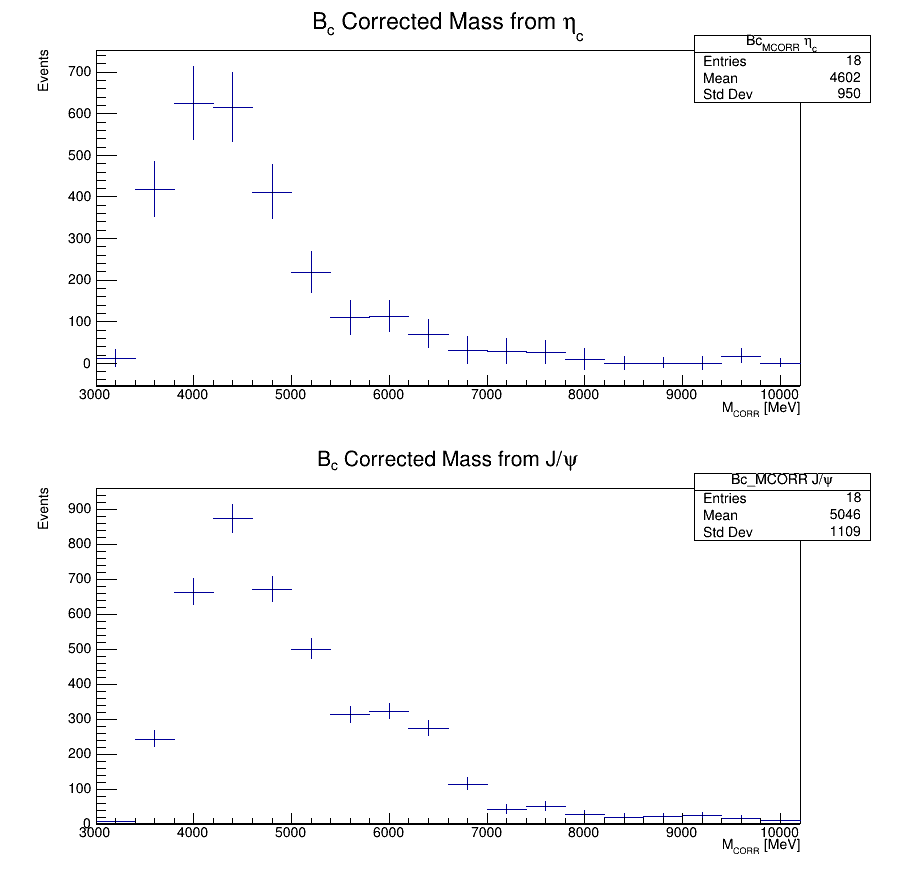
The yields from fits to the \(M(p\bar{p})\) in bins of \(M_{CORR}\) allow us to obtain the \(M_{CORR}\) distribution for true \(\eta_{c}\) and \(J/\psi\)

These true \(\eta_{c}\) and \(J/\psi\) don't necessarily come from \(B_{c}^{+}\rightarrow \eta_{c}\mu^{+}\nu_{\mu}\)

S. Ordonez Soto

June 27th, 2024

Final fit

Analysis

We use the different shapes to fit these \(M_{CORR}\) distributions and extract the two yields: \(N_{B_{c}^{+}\rightarrow \eta_{c}\mu^{+}\nu_{\mu}}\) and \(N_{B_{c}^{+}\rightarrow J/\psi\mu^{+}\nu_{\mu}}\) 

This is work in progress!

\longrightarrow \boxed{\frac{N_{B_{c}^{+}\rightarrow \eta_{c}\mu^{+}\nu_{\mu}}}{N_{B_{c}^{+}\rightarrow J/\psi\mu^{+}\nu_{\mu}}} = \boxed{?}}

S. Ordonez Soto

June 27th, 2024

Summary

  • Review of the different steps of the analysis has be done and implemented.
  • A preliminary selection was used which is subject to changes and optimization.
  • The shapes of the different signal and background contributions were determined.
  • The signal extraction procedure was successfully implemented.
  • Next steps:
    • ​The \(B_{c}^{+}\) optimization is the main next step to complete this preliminary study.
    • For next steps would be great to include 2018 data.

S. Ordonez Soto

June 27th, 2024

Thank you for your attention.

Back up

S. Ordonez Soto

June 27th, 2024

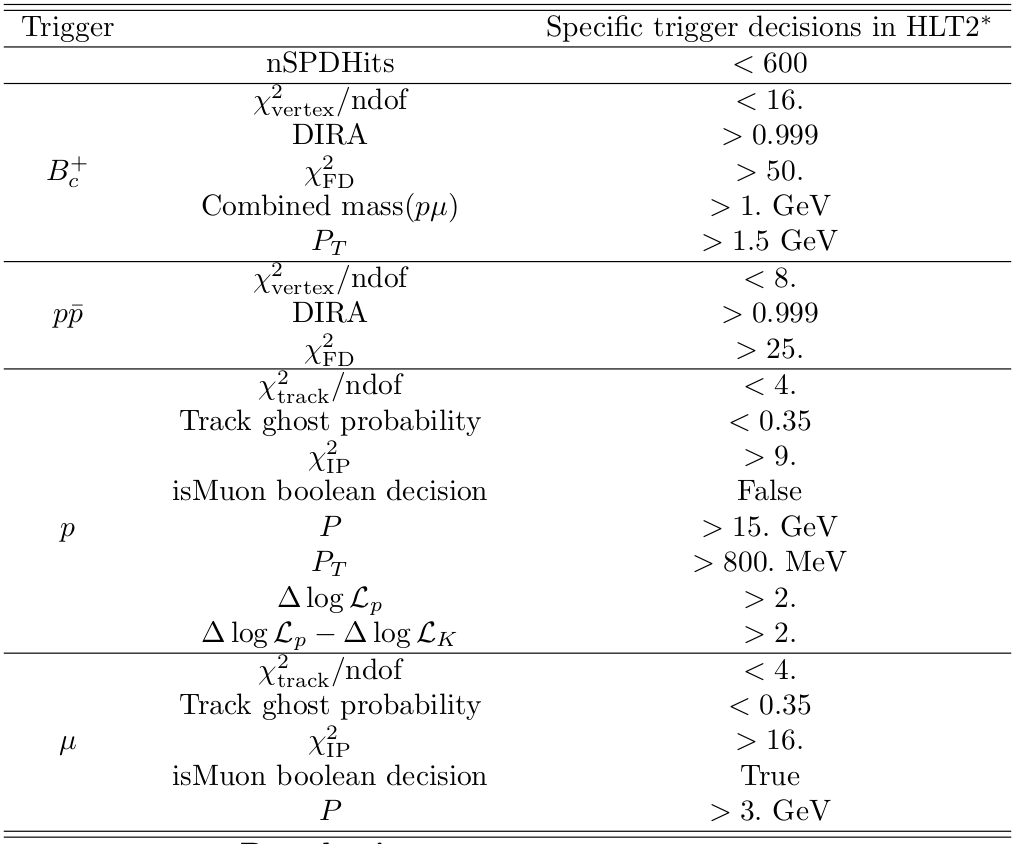
Selection

Stripping selection

S. Ordonez Soto

June 27th, 2024

Analysis

\(M_{CORR}\) resolution study

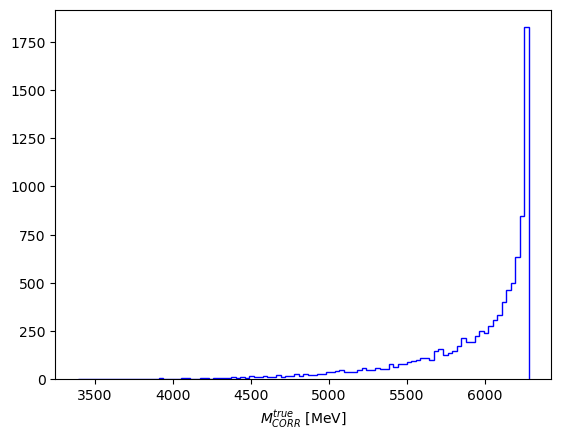
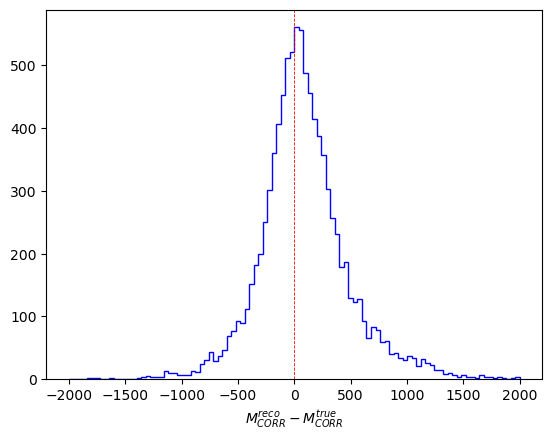
Previous to the signal extraction, it is necessary to check the resolution in the \(M_{CORR}\) using signal MC .

\boxed{\sigma = 397 \pm 3}

Efficiency ratio computation

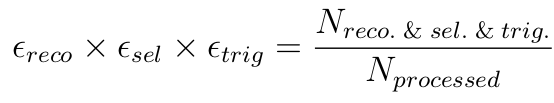
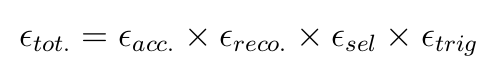
Acceptance efficiency \(\epsilon_{acc}\) from generator-level simulations. The product \(\epsilon_{reco} \times \epsilon_{sel} \times \epsilon_{trig}\) can be calculated as follows:

\(\longrightarrow N_{processed} = 1\)M events

Total efficiency

S. Ordonez Soto

June 27th, 2024

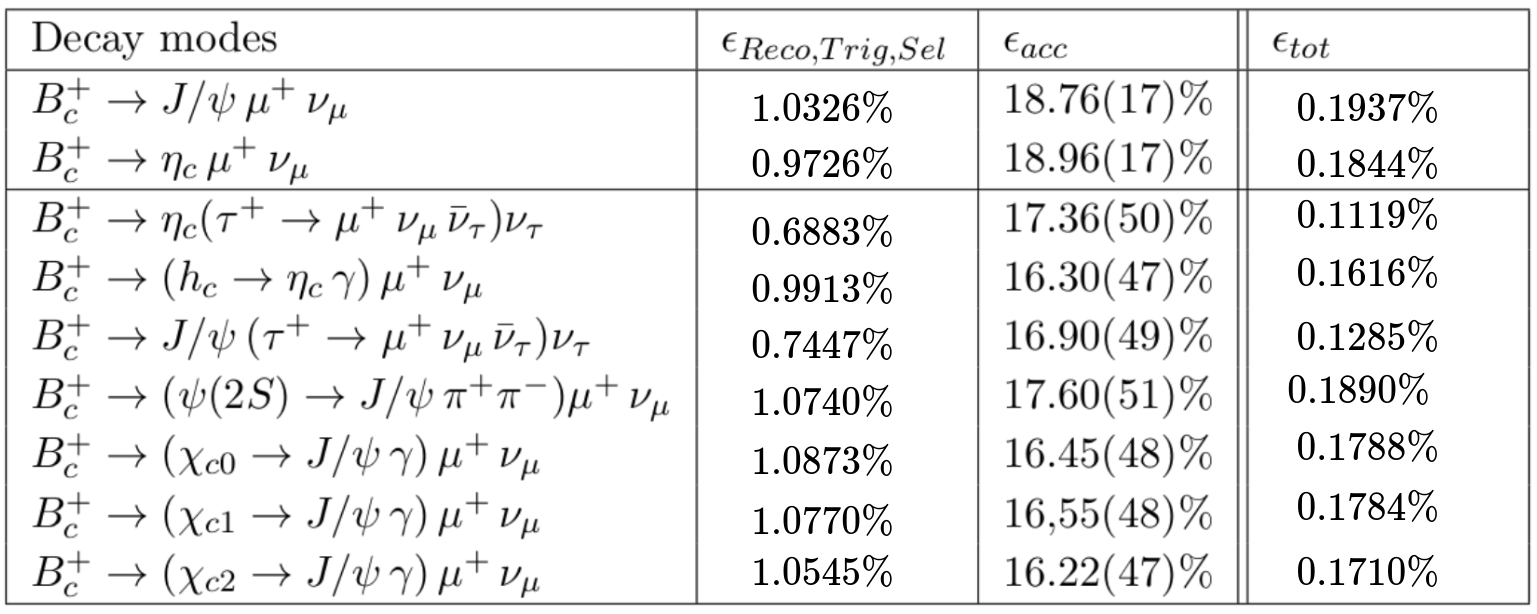
Decay modes efficiency

Efficiency ratio computation

S. Ordonez Soto

June 27th, 2024

The yields of the peaking background decays are fixed with respect to the yields of the signal with the values shown in the table:

LHCb IJCLab internship presentation: Bc2etacmunu

By Sebastian Ordoñez

LHCb IJCLab internship presentation: Bc2etacmunu

  • 230

More from Sebastian Ordoñez