Sebastian Ordoñez-Soto
LHCb@LPCA group meeting
April 2nd, 2025


Time-integrated Amplitude Analysis of the decay \(B_{s}\rightarrow K_{S}^{0}\pi^{+}\pi^{-}\) with Run I and Run II data
Outline
Sebastian Ordoñez-Soto
-
April 2nd, 2025
- Analysis strategy
- Mass fit
- Background model
- Outlook
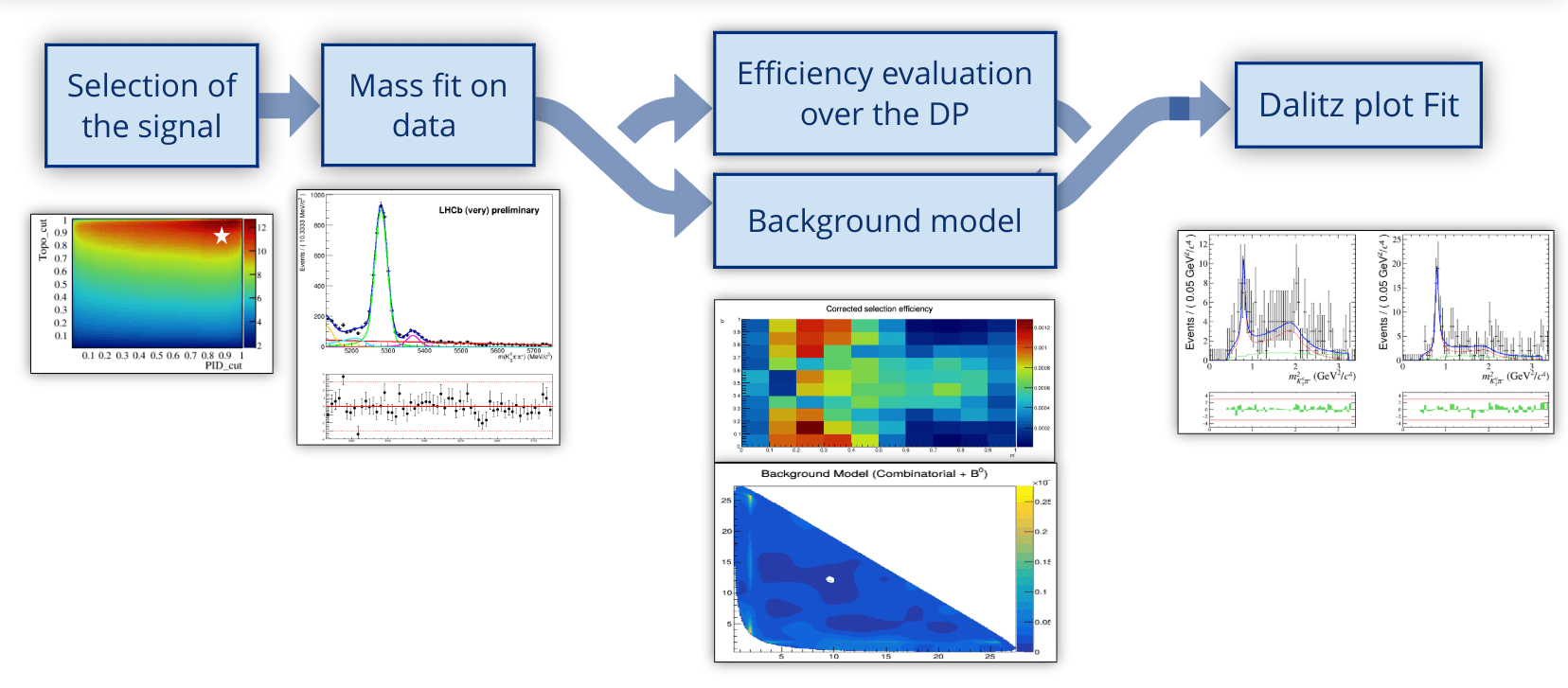
Analysis Strategy
Sebastian Ordoñez-Soto
| Selection of the signal |
| Efficiency evaluation over the DP |
| Background model |
| Dalitz plot Fit |
| Mass fit on data |
The analysis consists of mainly five stages, from the signal selection to the final Dalitz plot fit.
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
April 2nd, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Analysis Strategy

Done!
Inherited from the BF Analysis
March 24th, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Analysis Strategy


Done?
Latest "official" version is in progress
March 24th, 2025
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
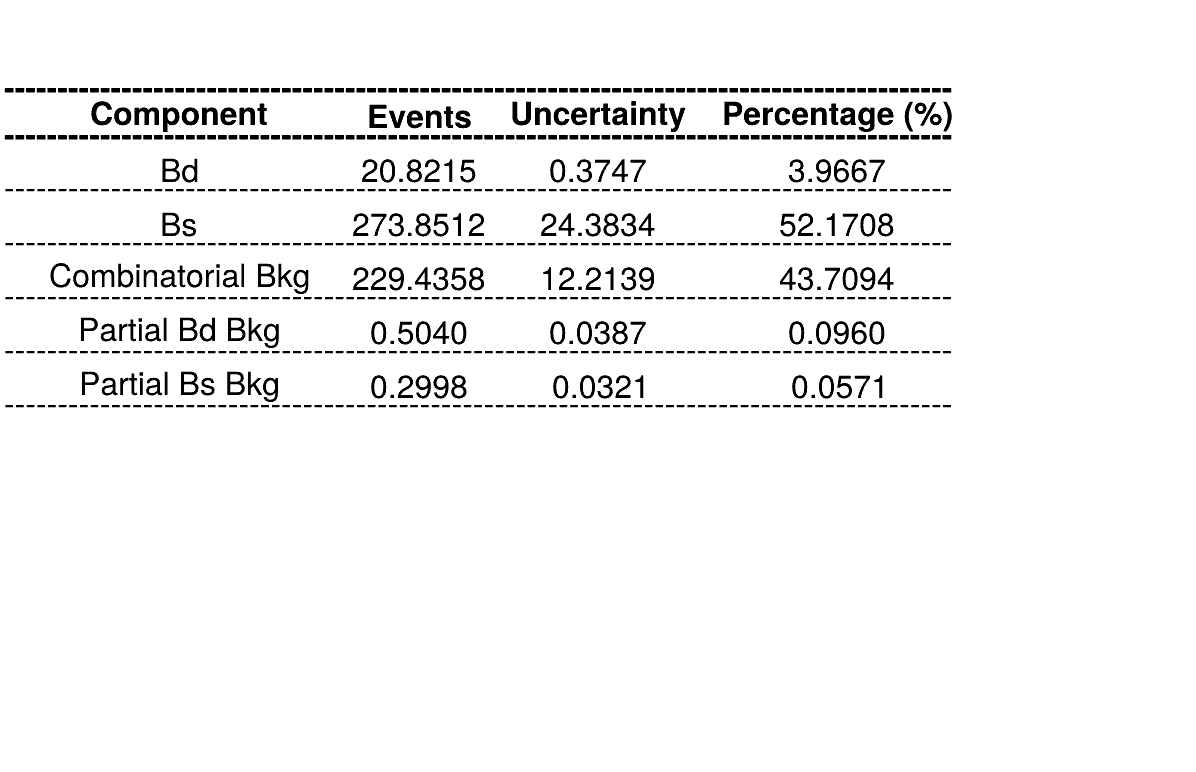
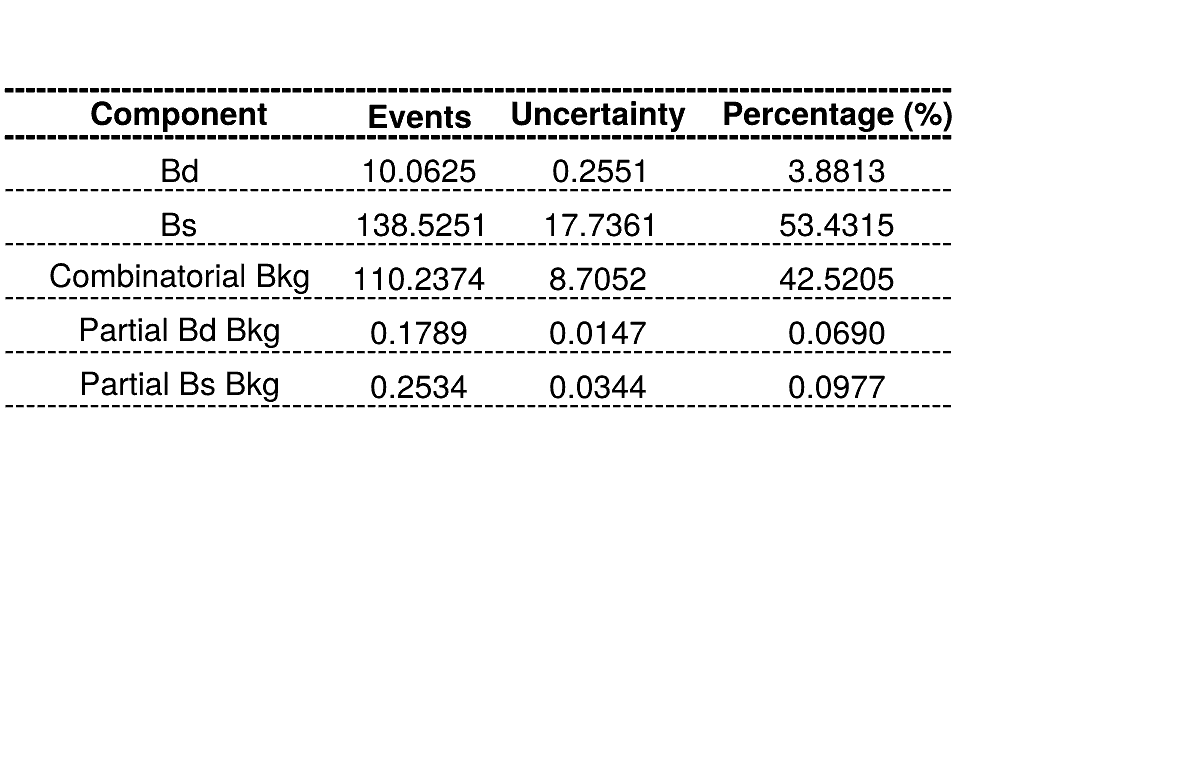
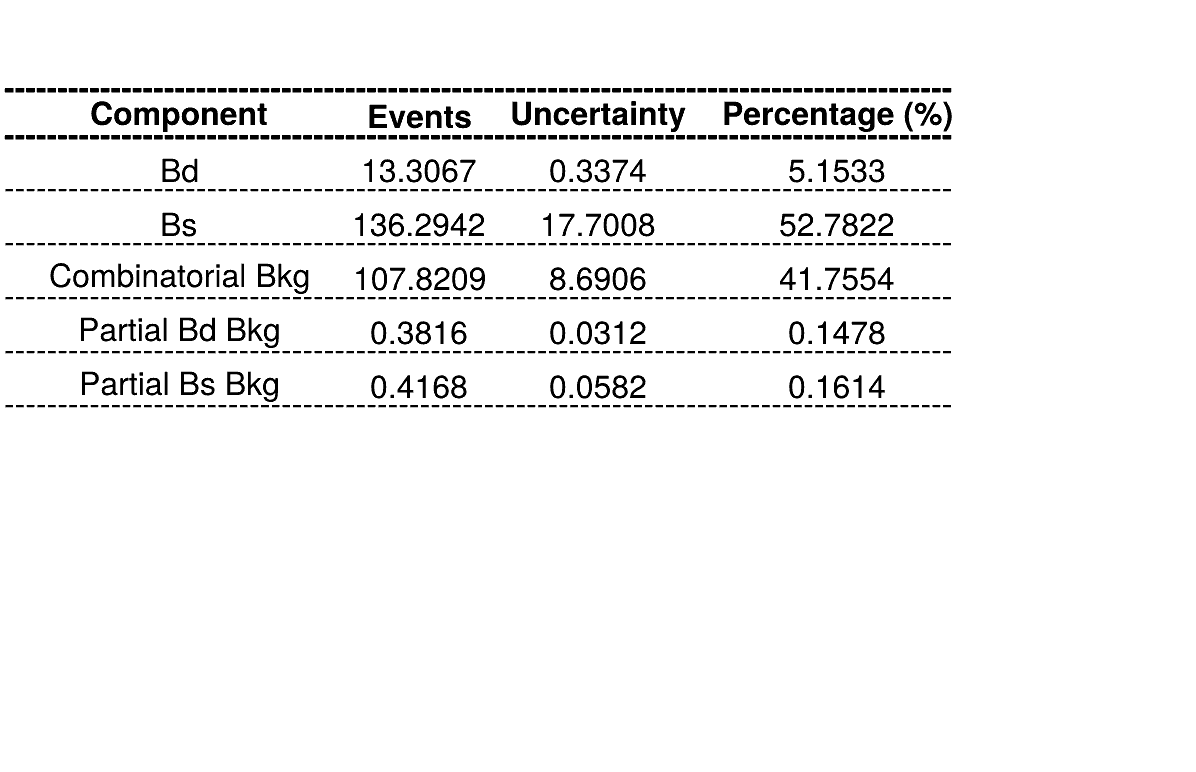
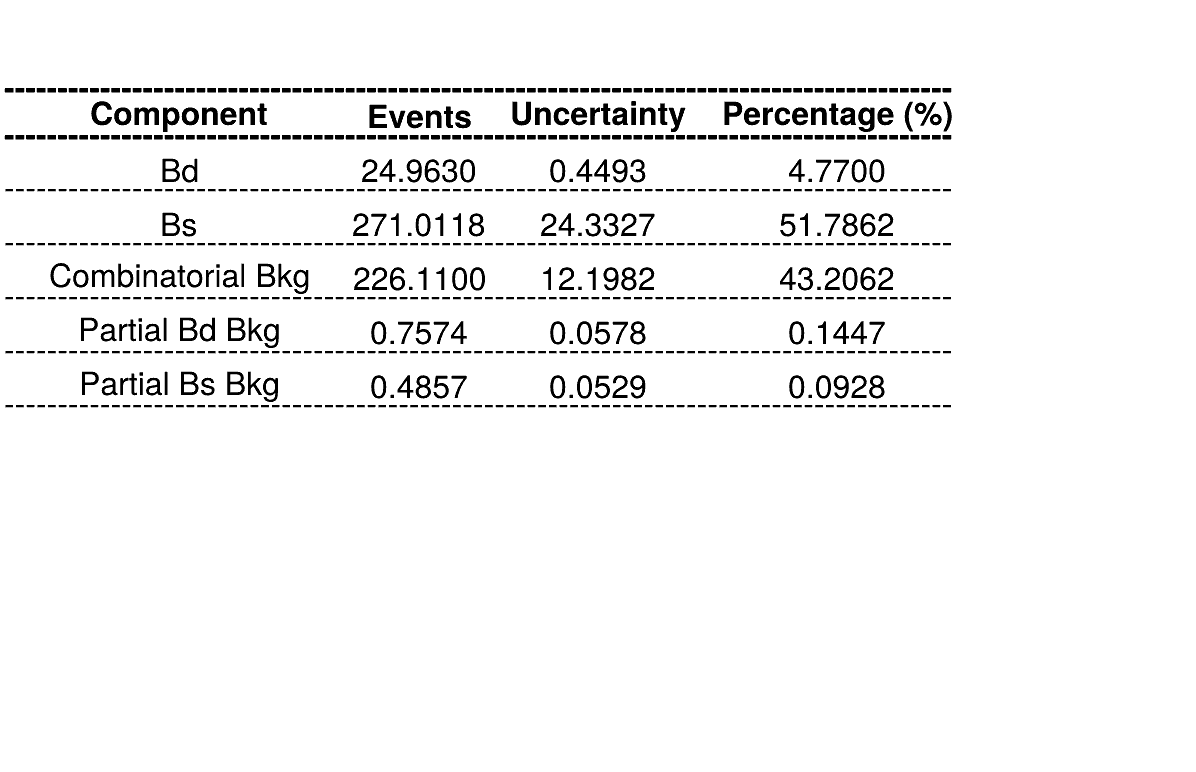
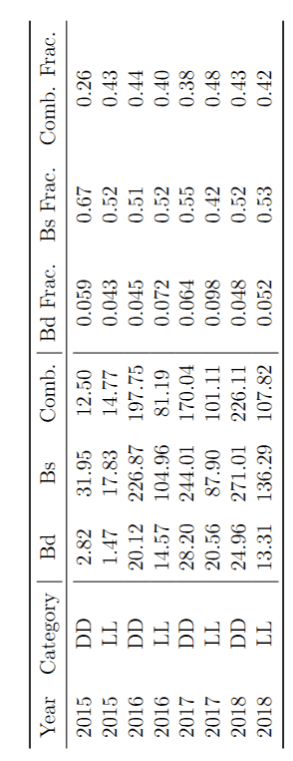
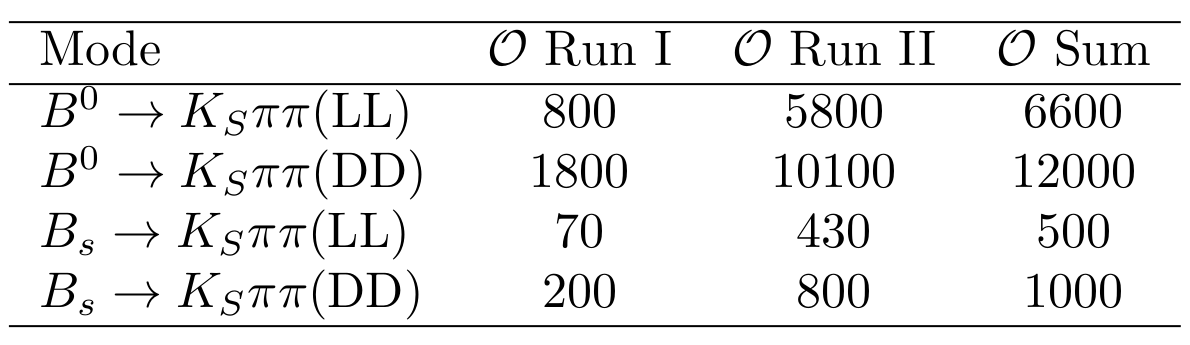
The fraction of each contribution in the \(B_{s}\) signal region are crucial for the AmAn.
- The ultimate goal is to employ the mass fit of the BF analysis.
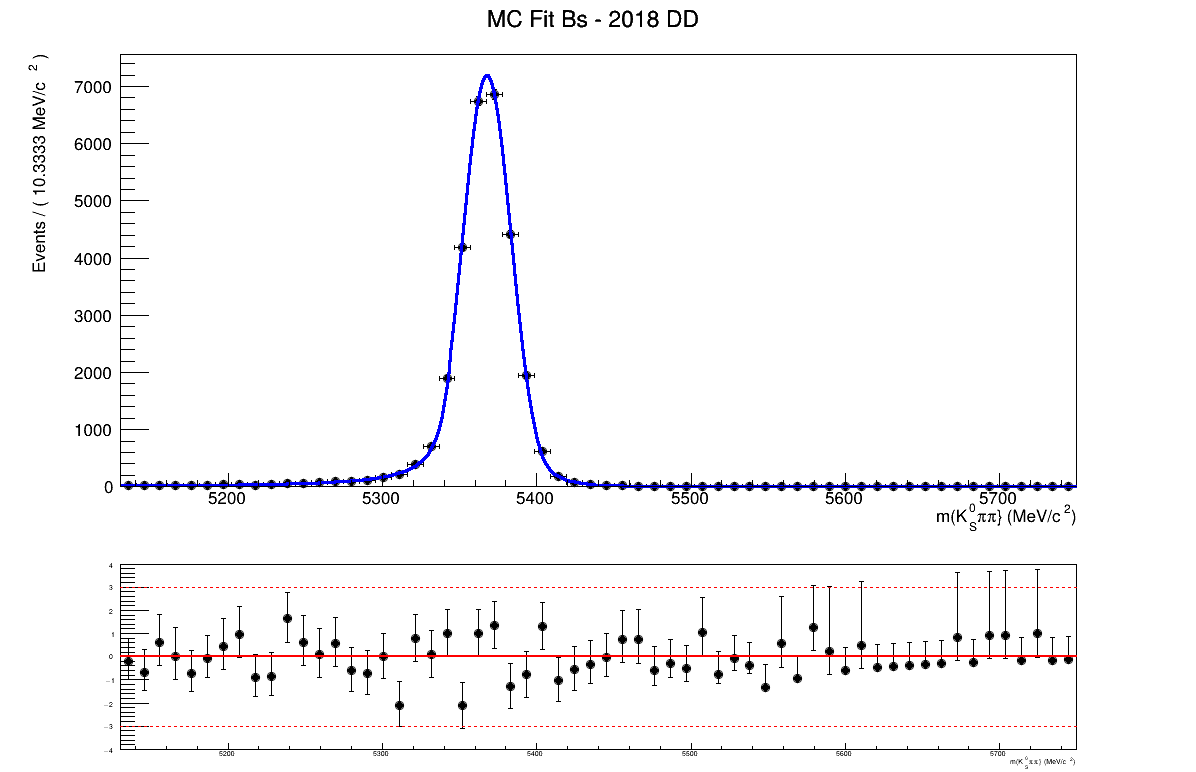
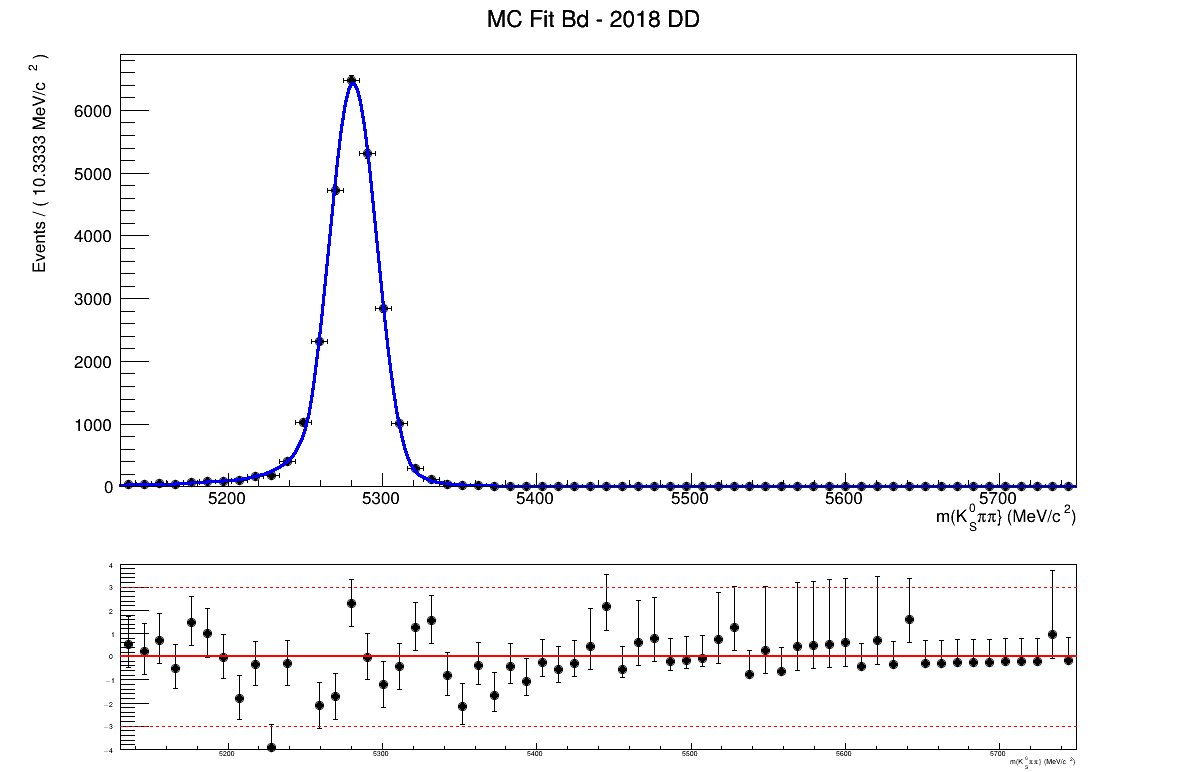
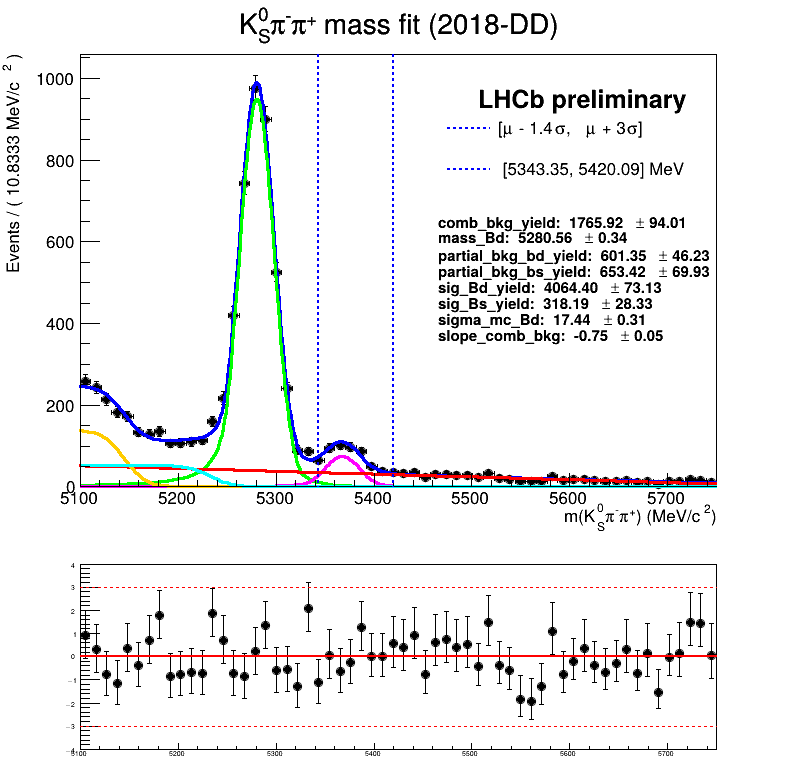
Features of the temporary homemade mass fit
- The signal MC is fitted using a Symmetric Crystal Ball PDF.
- The partial bkg MC is fitted using: Argus \(\circledast\) Symmetric Crystal Ball PDF
March 24th, 2025
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
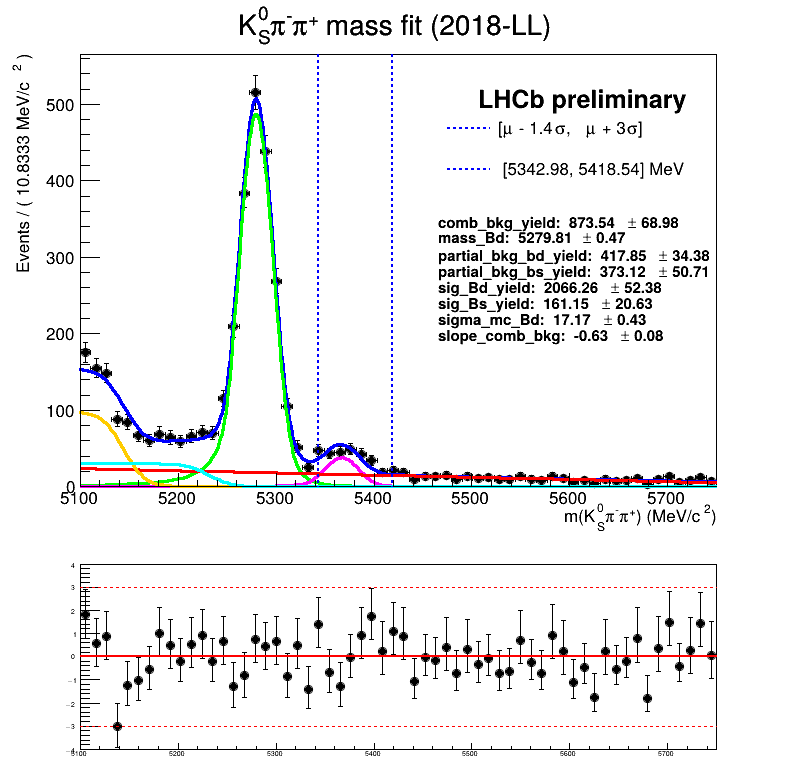
March 24th, 2025
Using Truth match MC for signal
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay

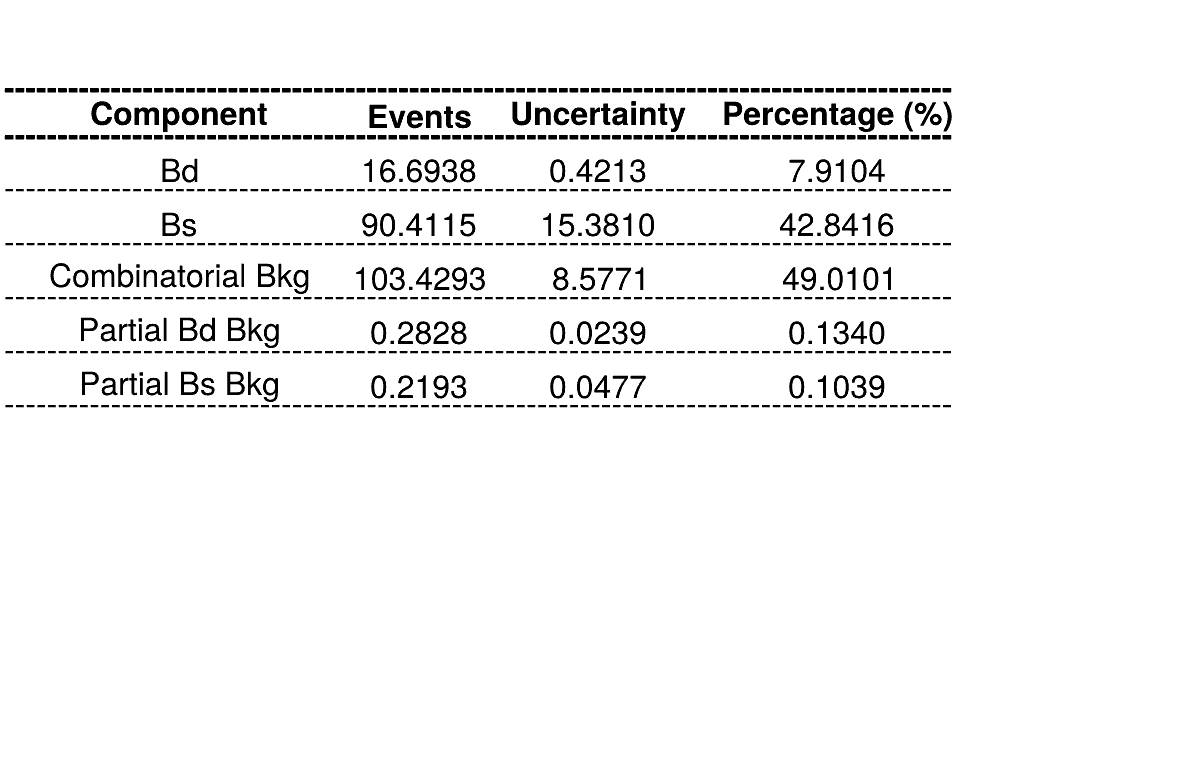
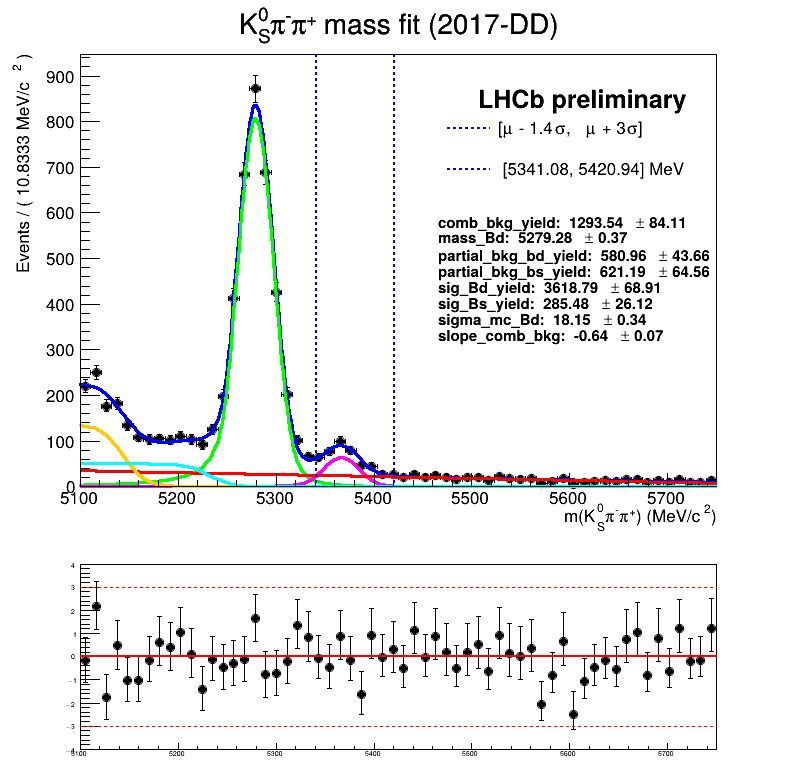
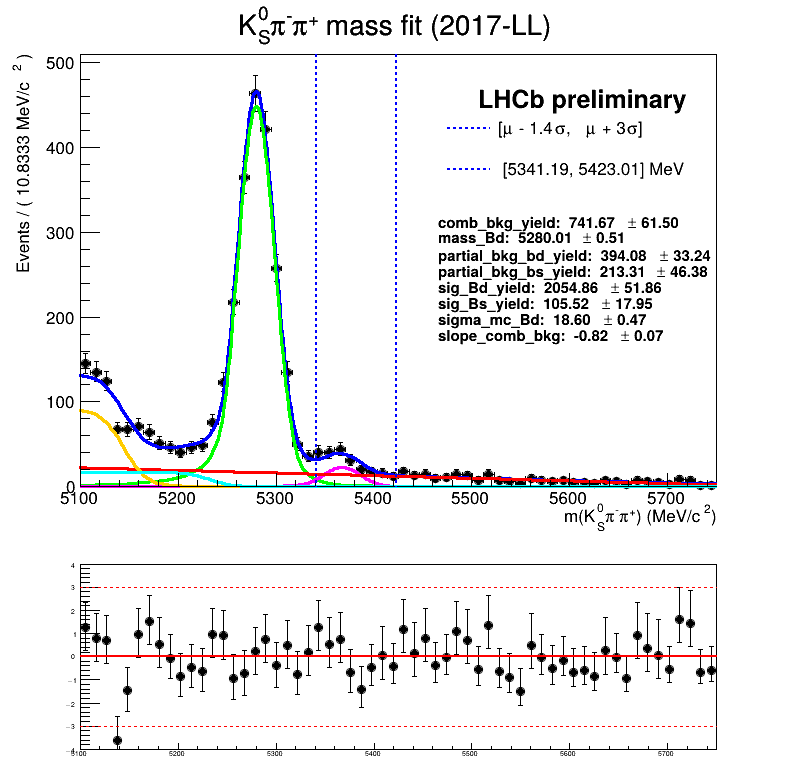
March 24th, 2025
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
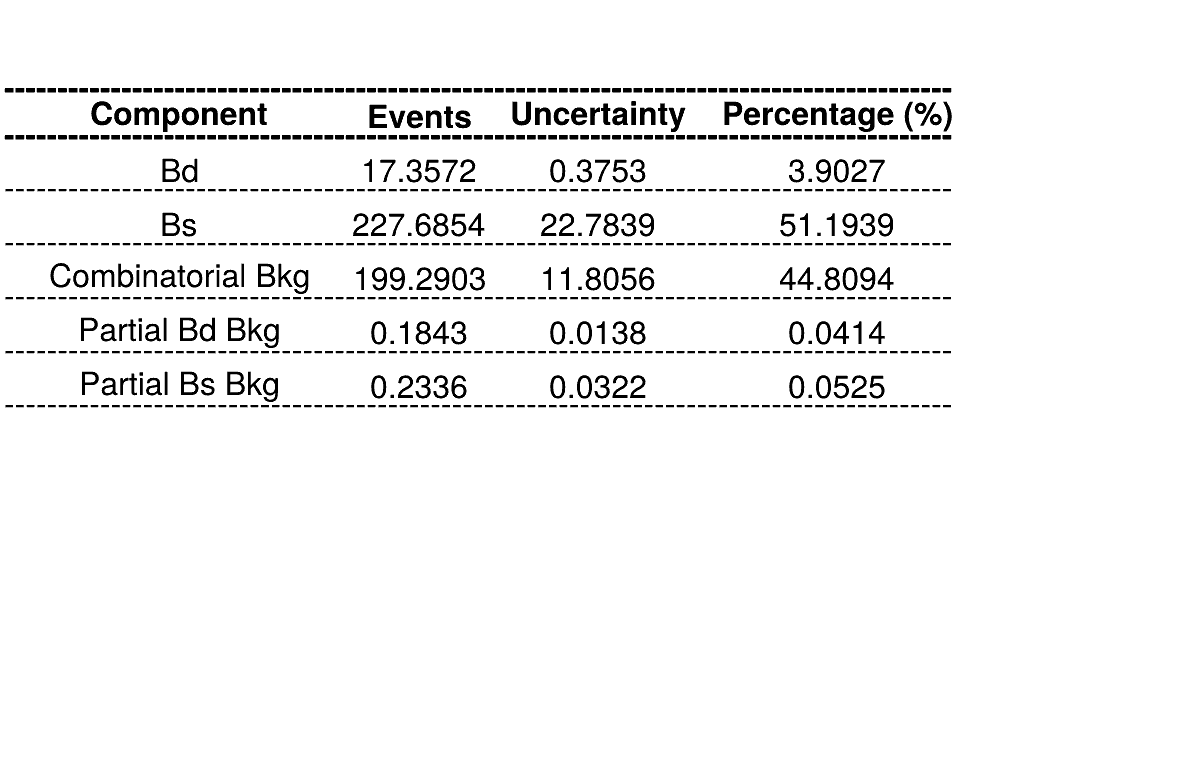
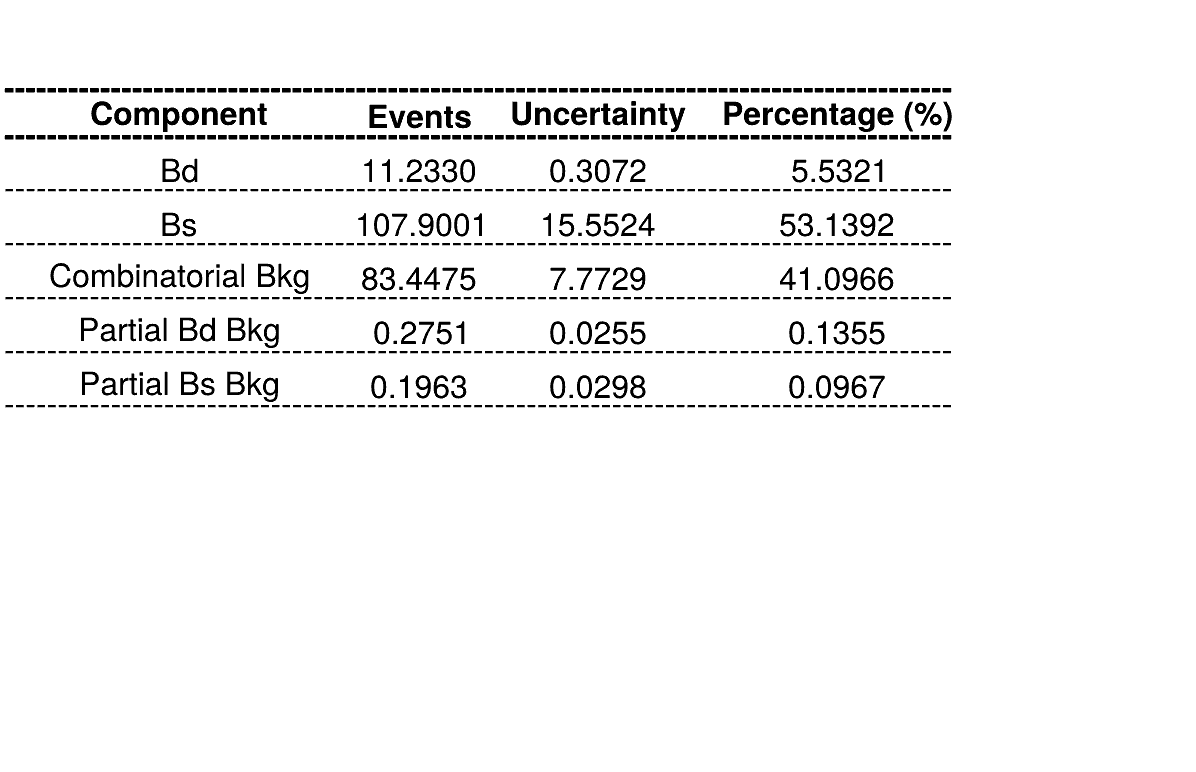
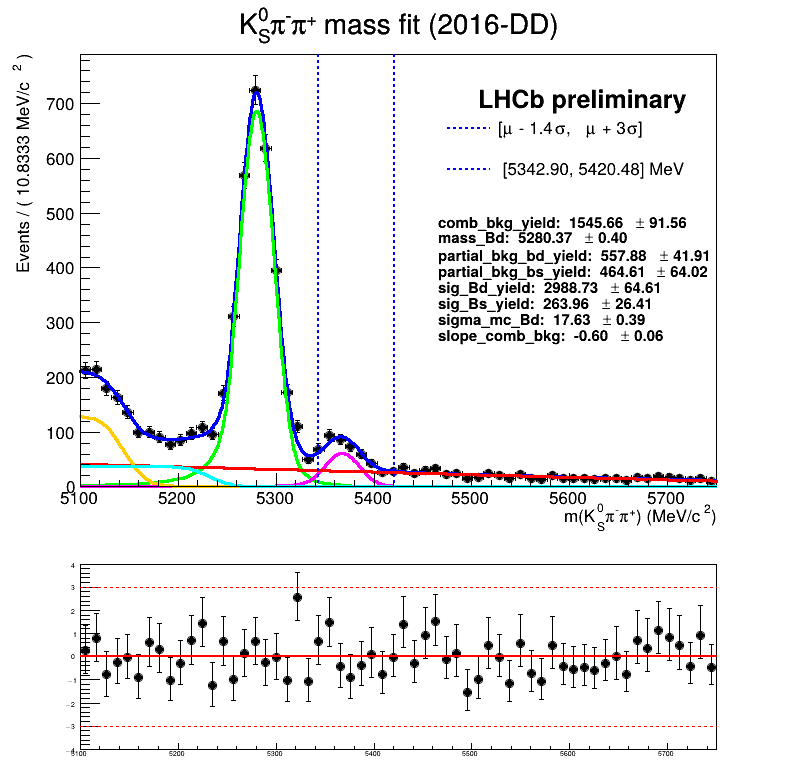
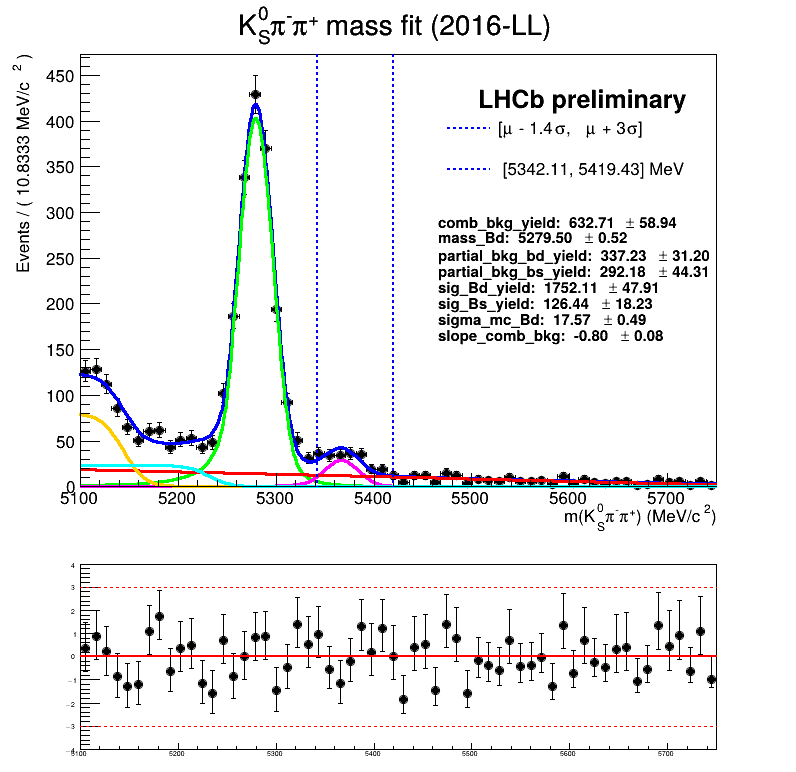
March 24th, 2025
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
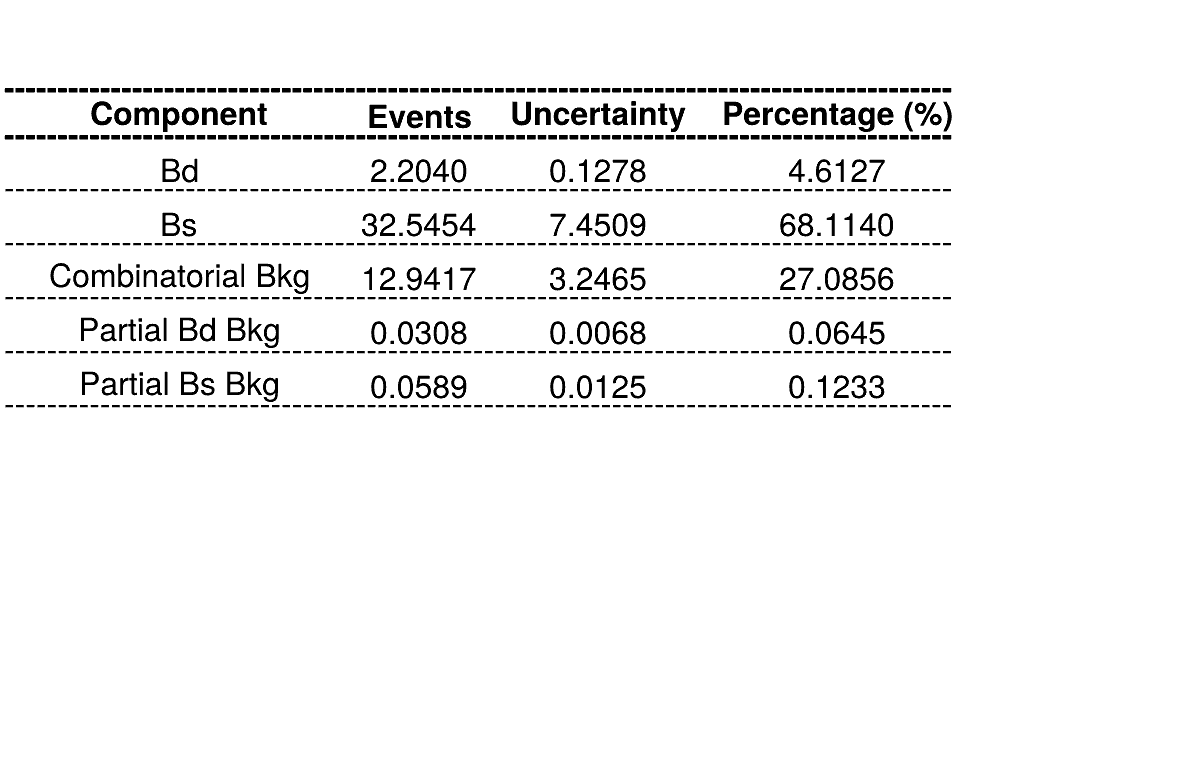
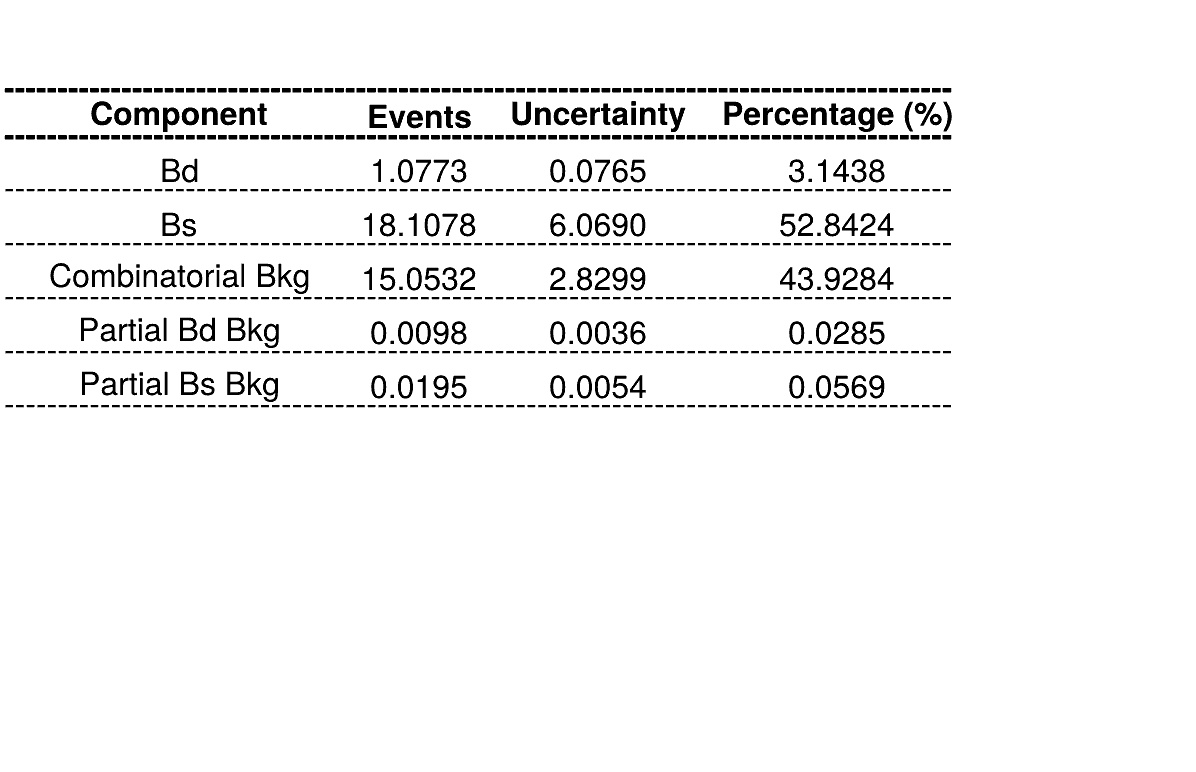
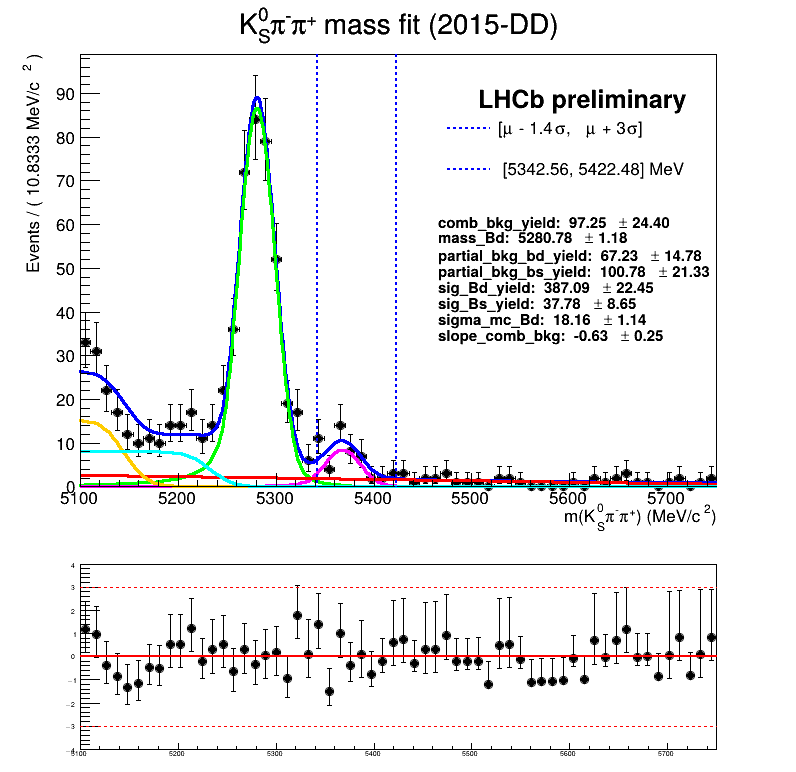
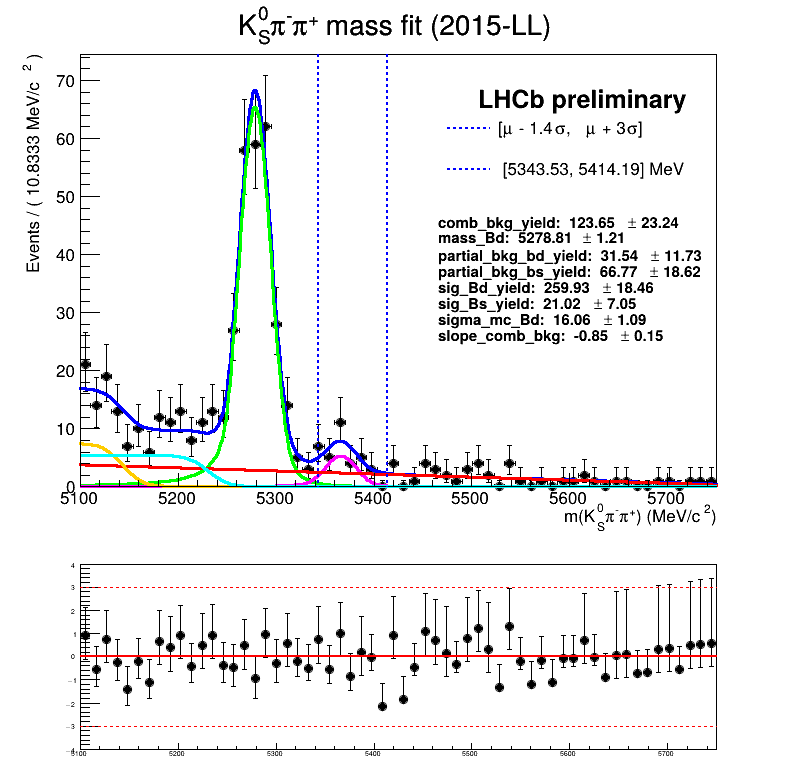
March 24th, 2025
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
March 24th, 2025
Using No Truth Match MC for signal
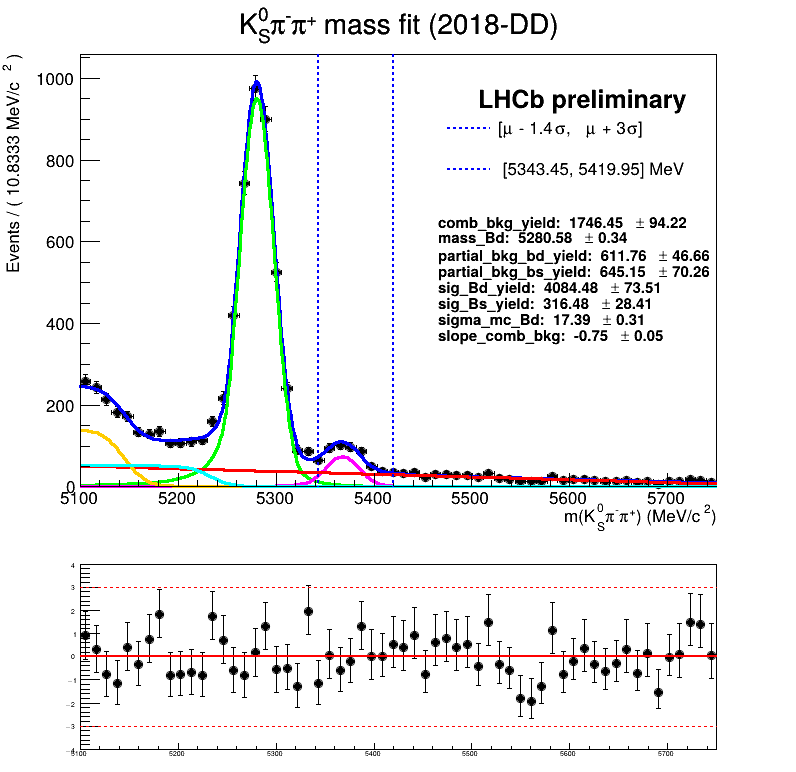
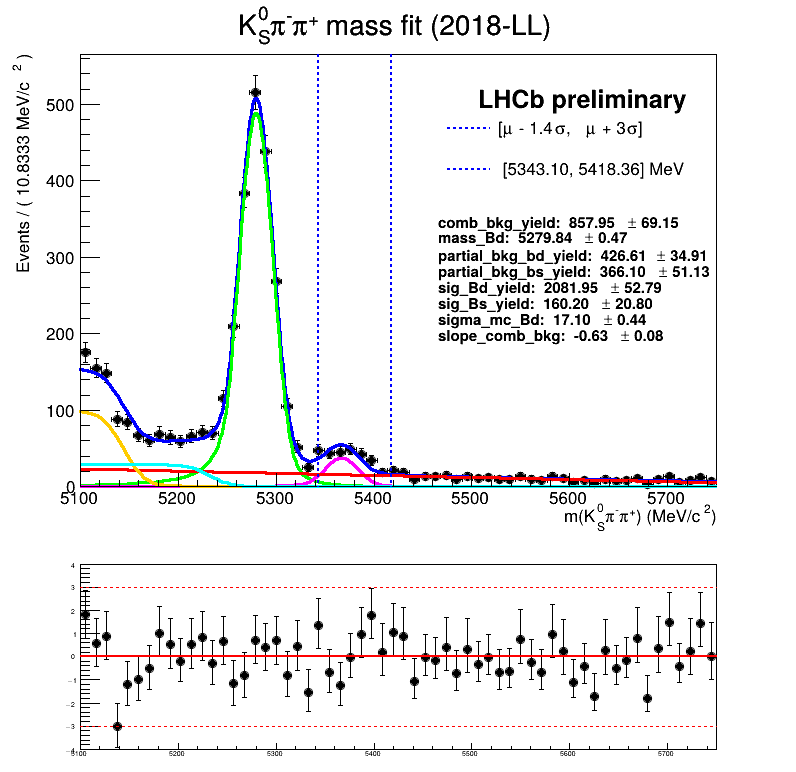
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
March 24th, 2025
Using No Truth Match MC for signal
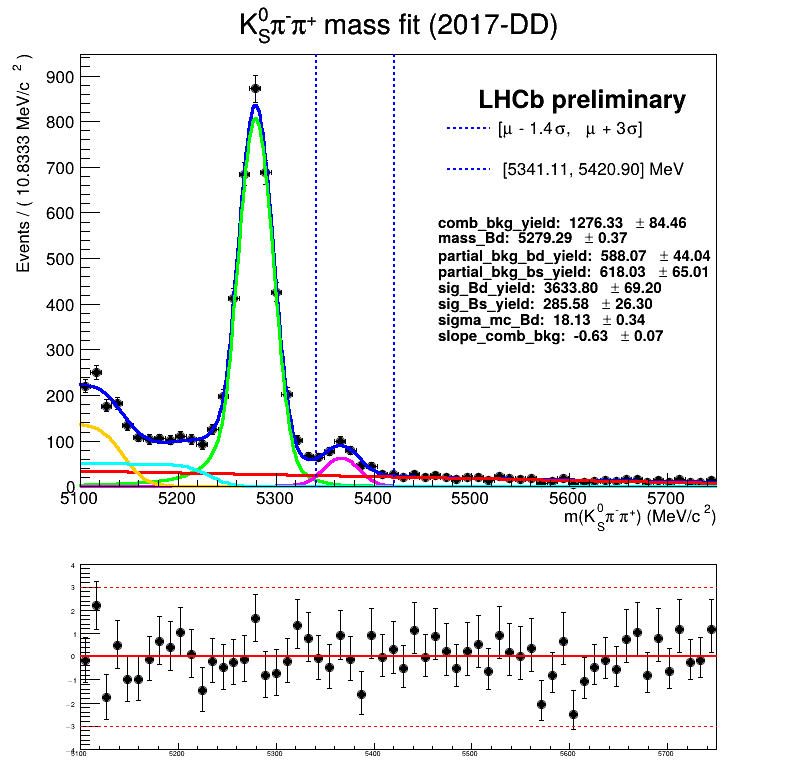
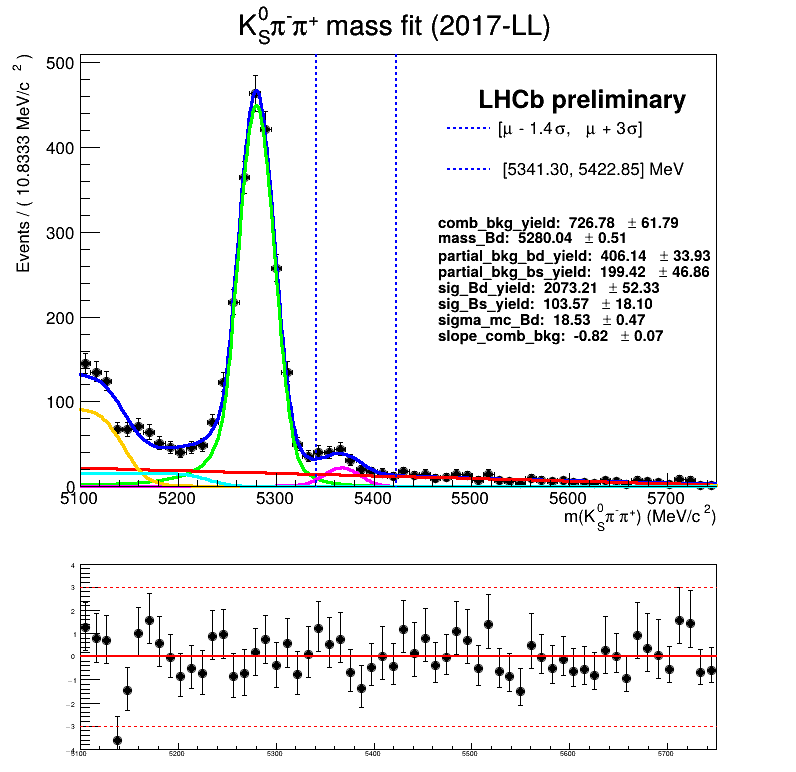
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
March 24th, 2025
Using No Truth Match MC for signal
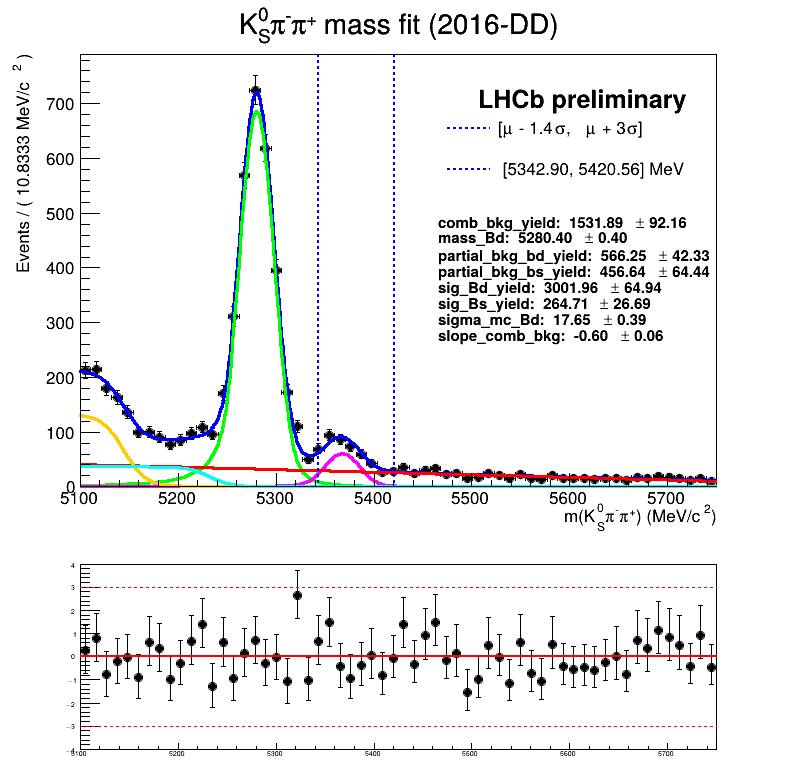
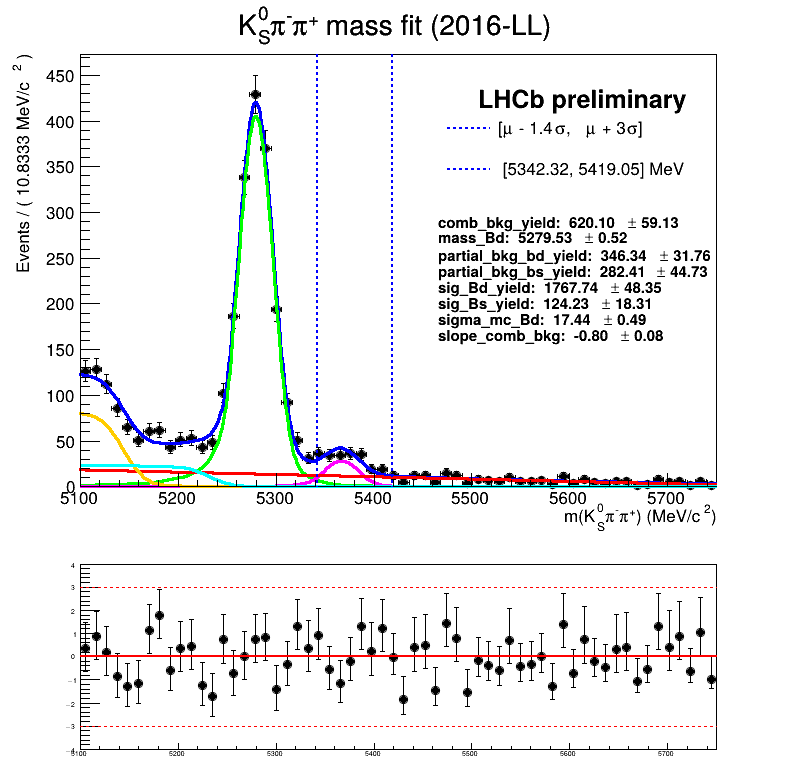
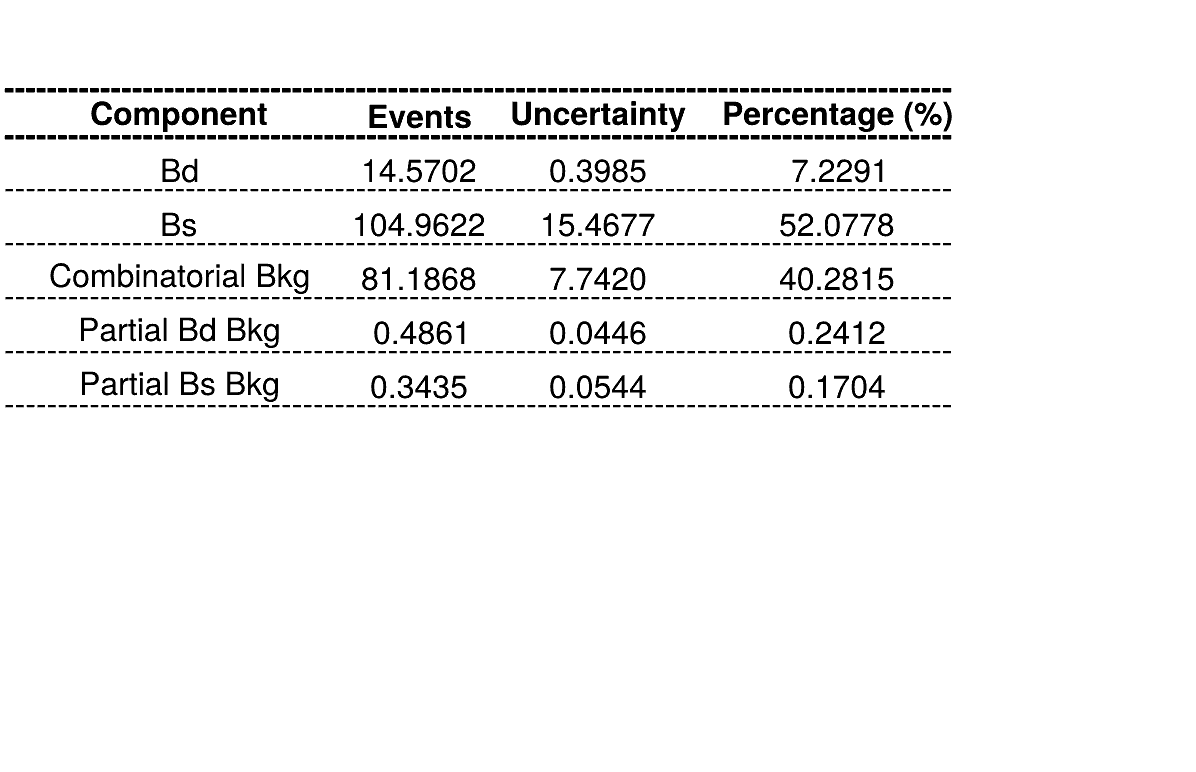
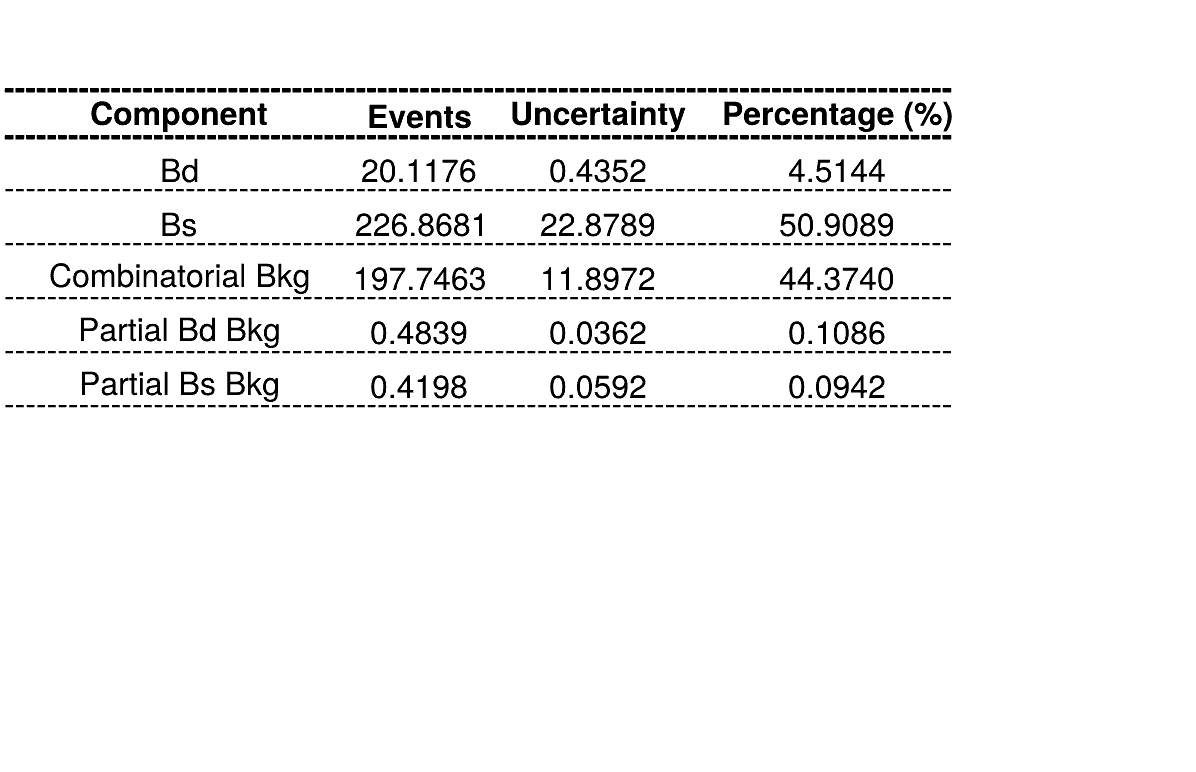
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
March 24th, 2025
Using No Truth Match MC for signal
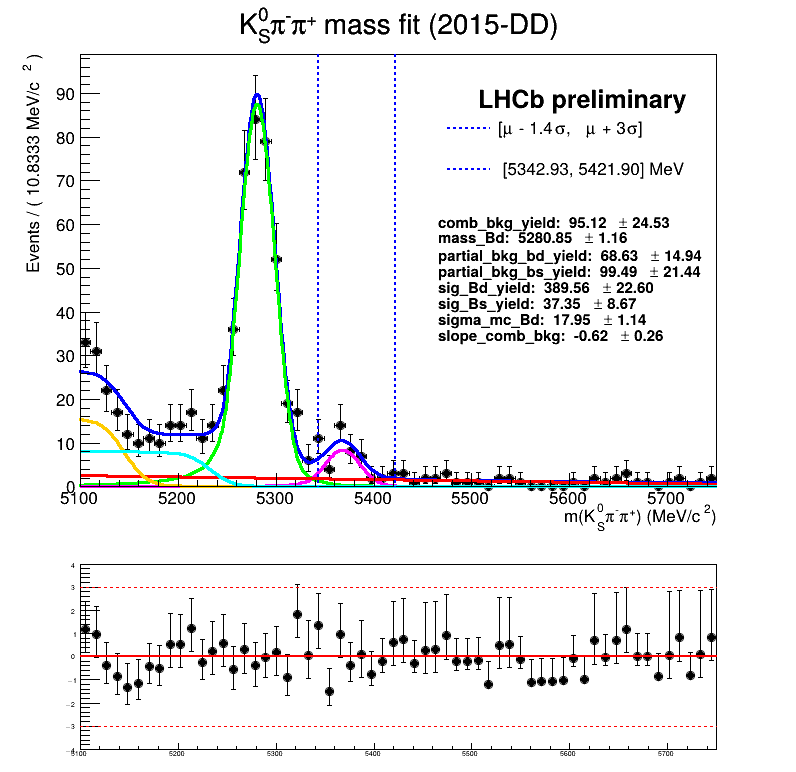
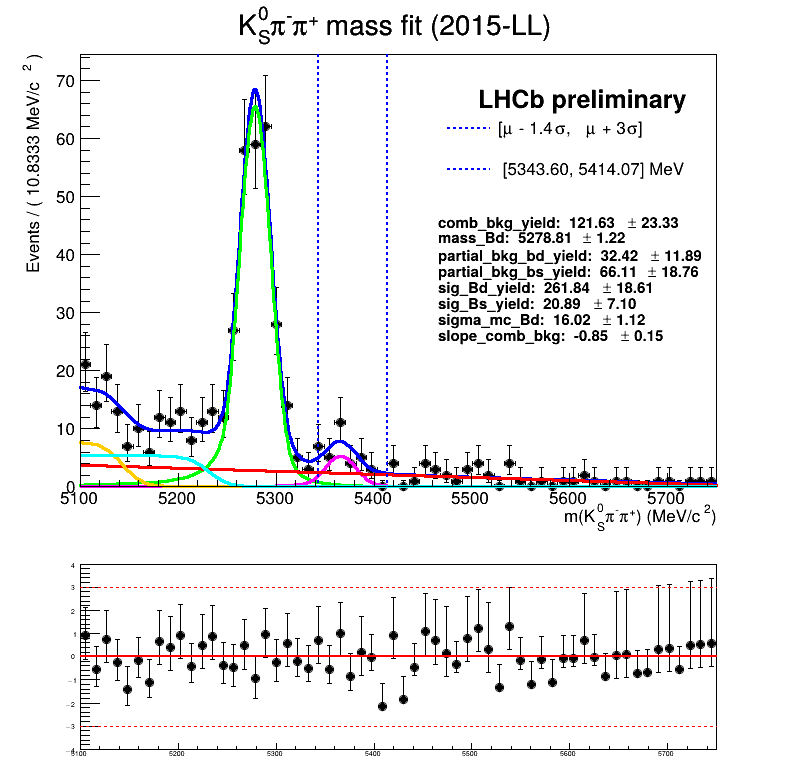
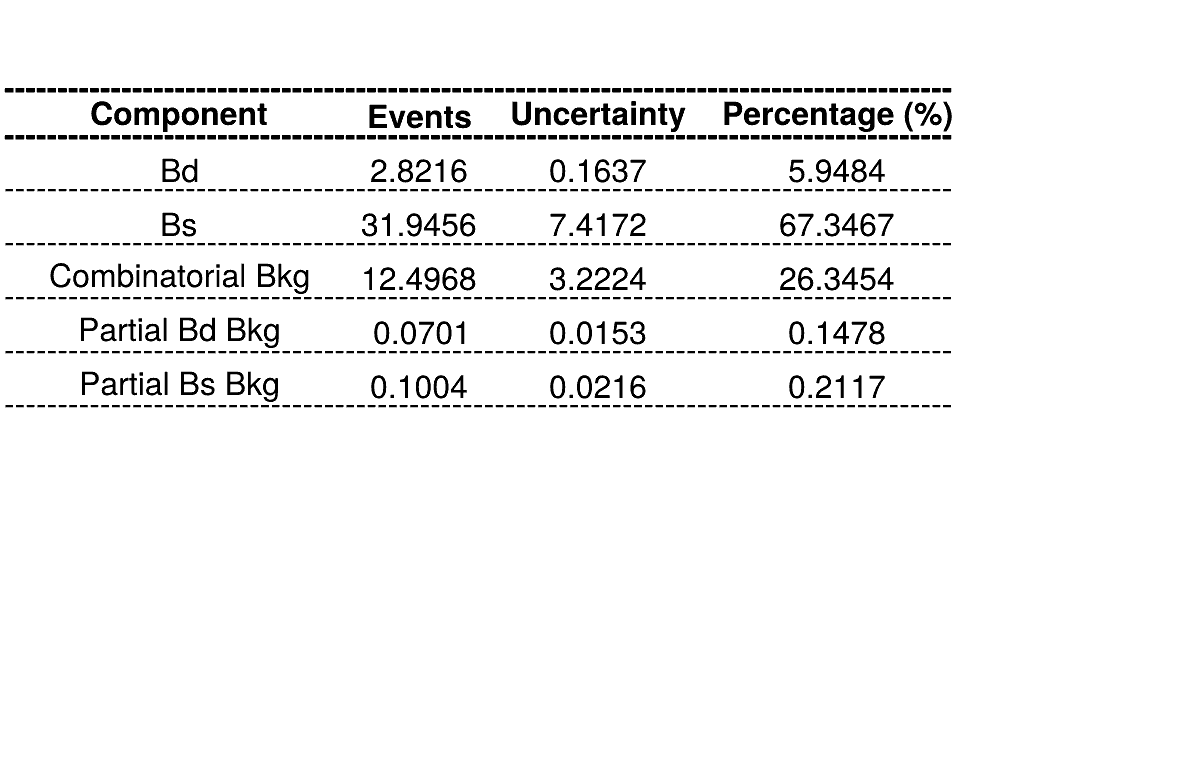
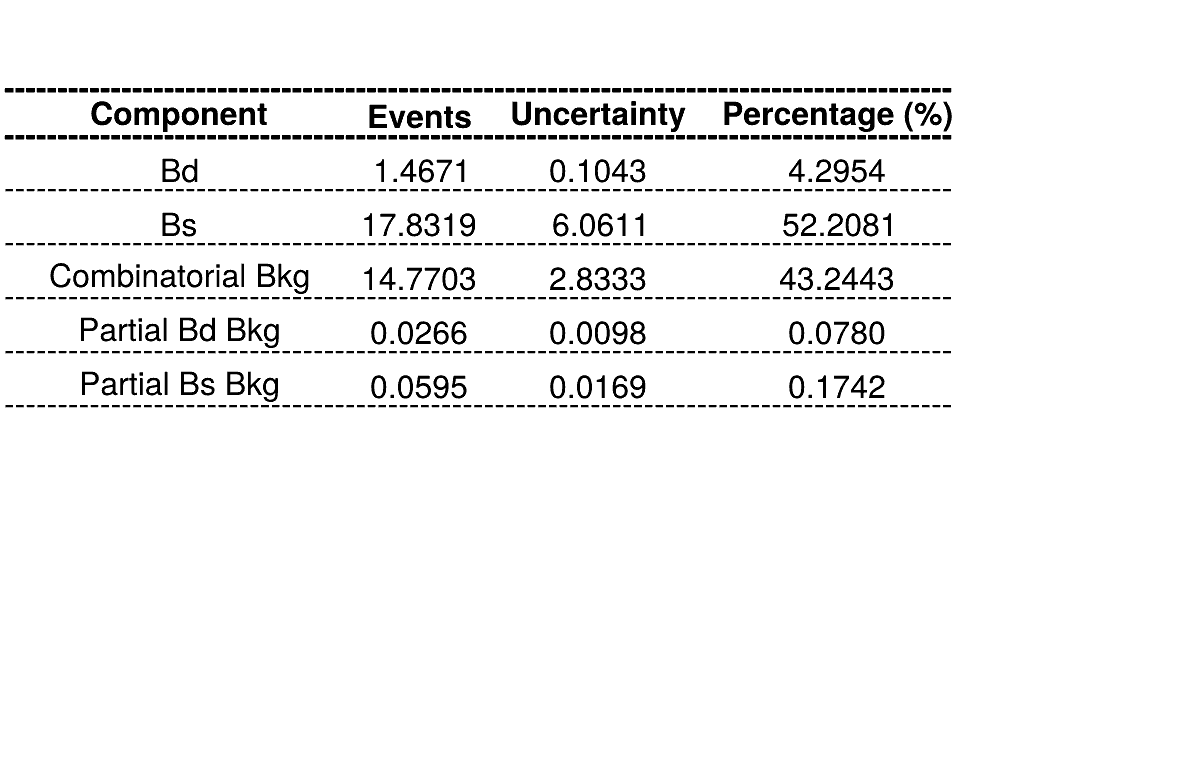
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
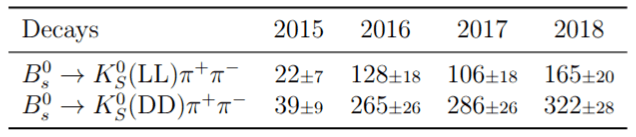
Current results from the BF analysis:
Results with the homemade fit:

March 24th, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Analysis Strategy


- Efficiency maps available, also inherited from BF analysis.
- Background model done.
Done!
Done!
Done!
March 24th, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Efficiency maps from BF analysis
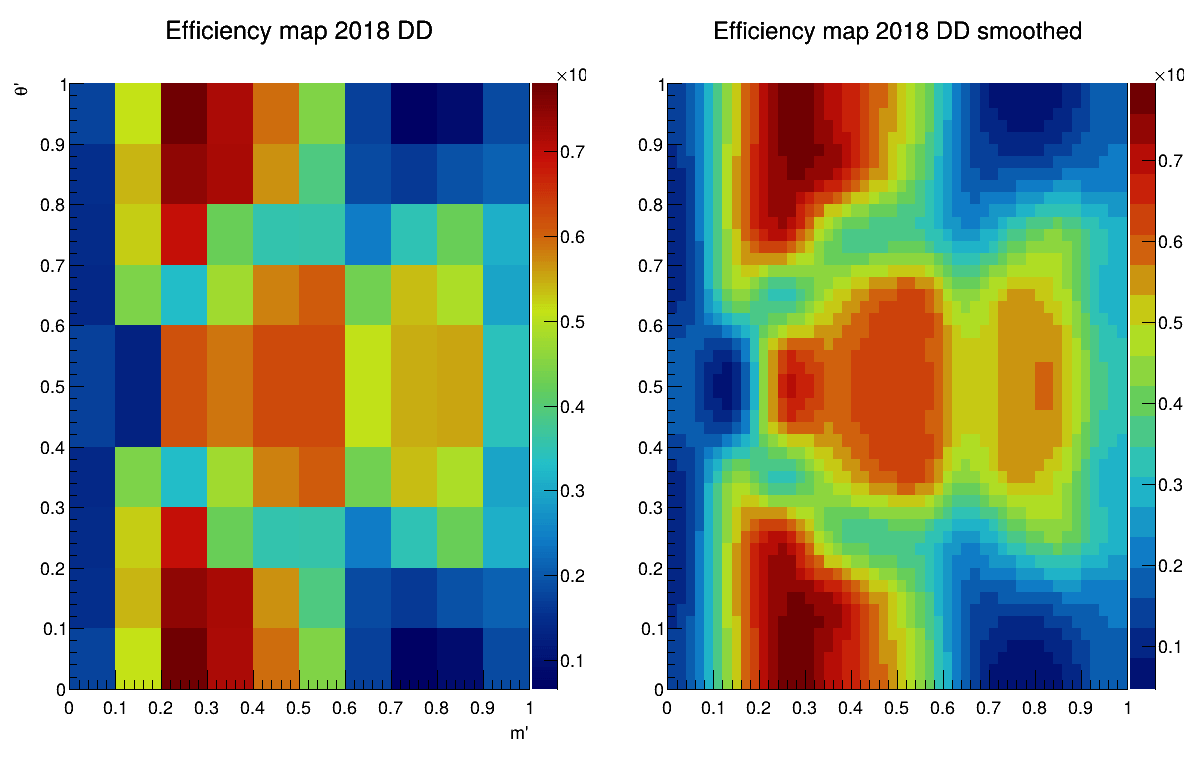
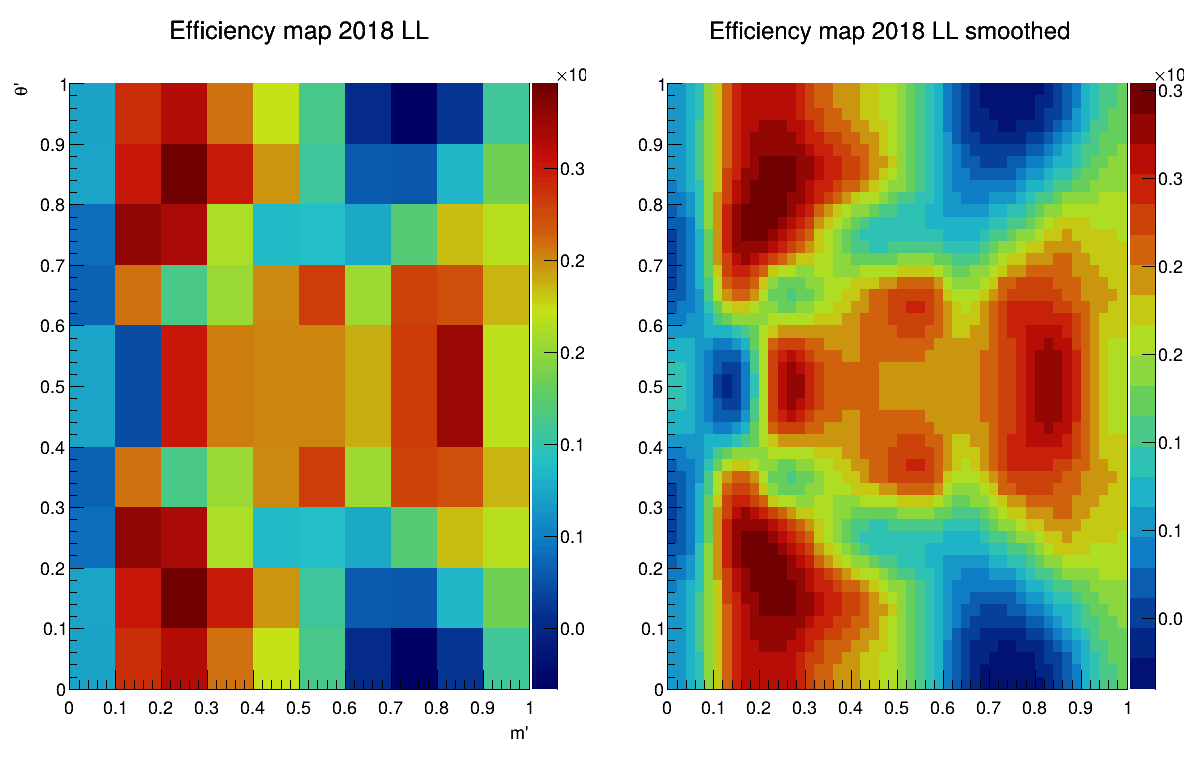
March 24th, 2025
2018-DD
2018-LL
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Efficiency maps from BF analysis
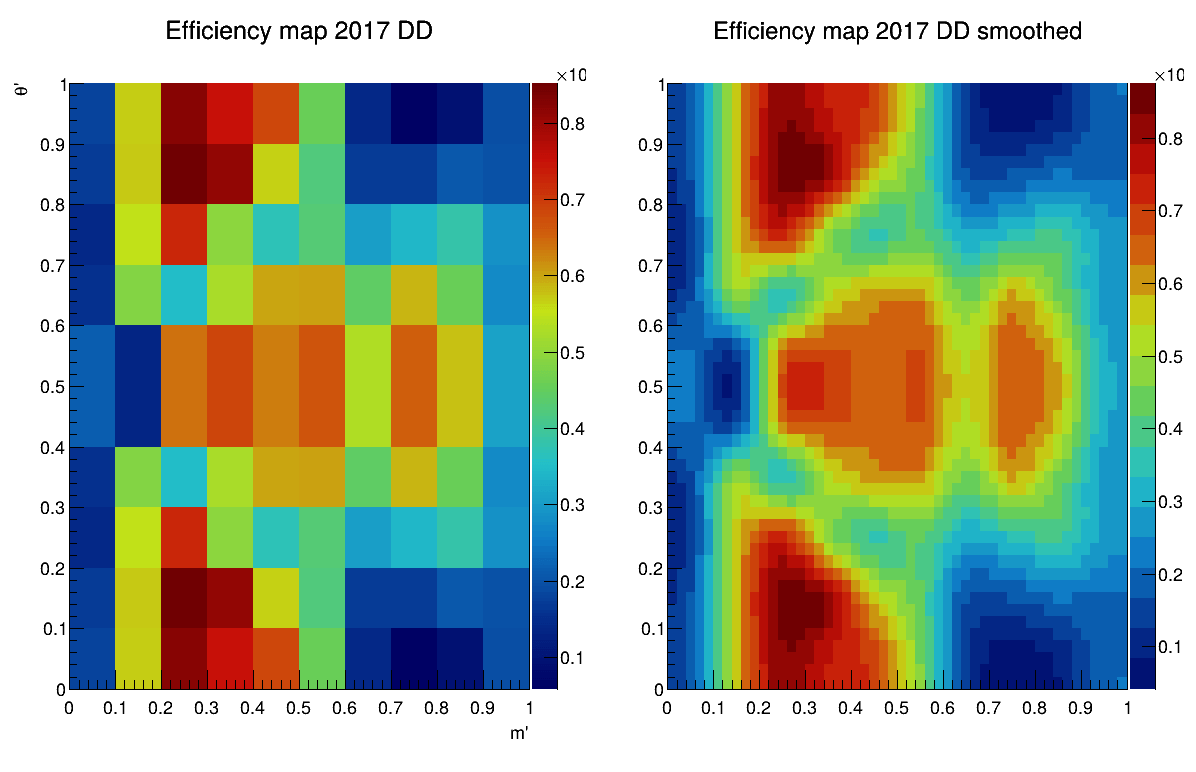
March 24th, 2025
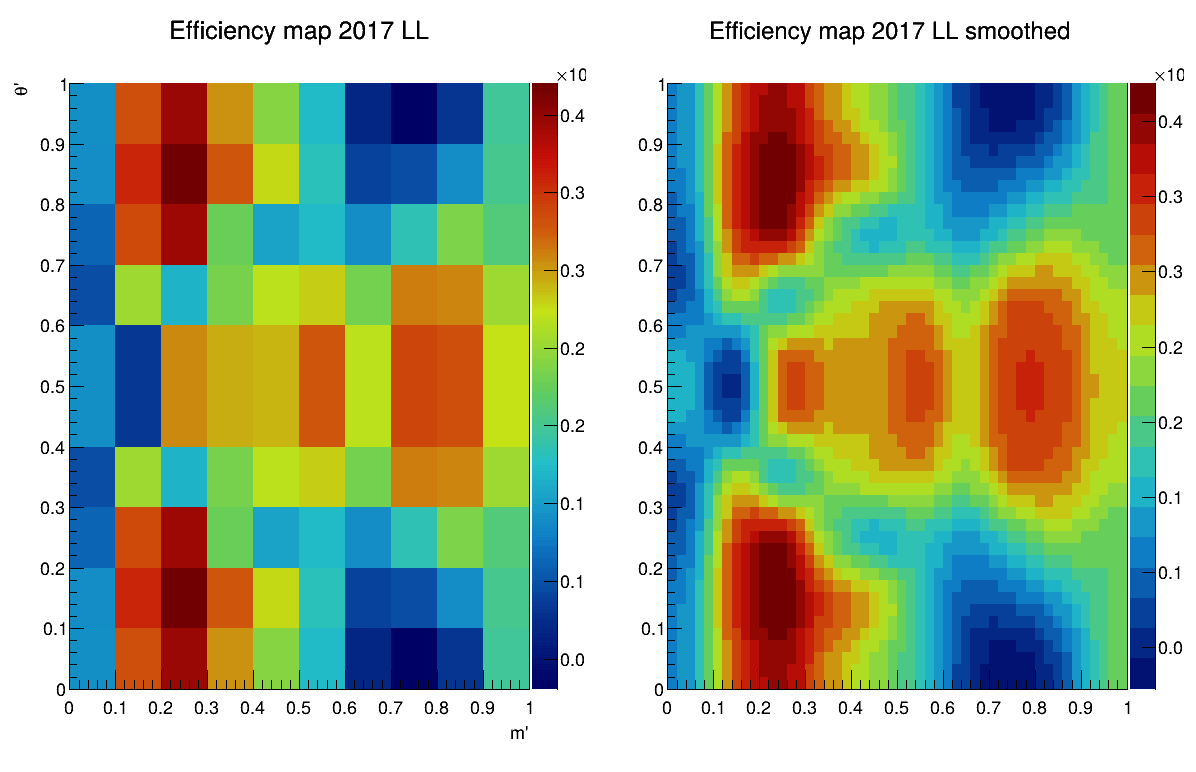
2017-DD
2017-LL
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Efficiency maps from BF analysis
March 24th, 2025
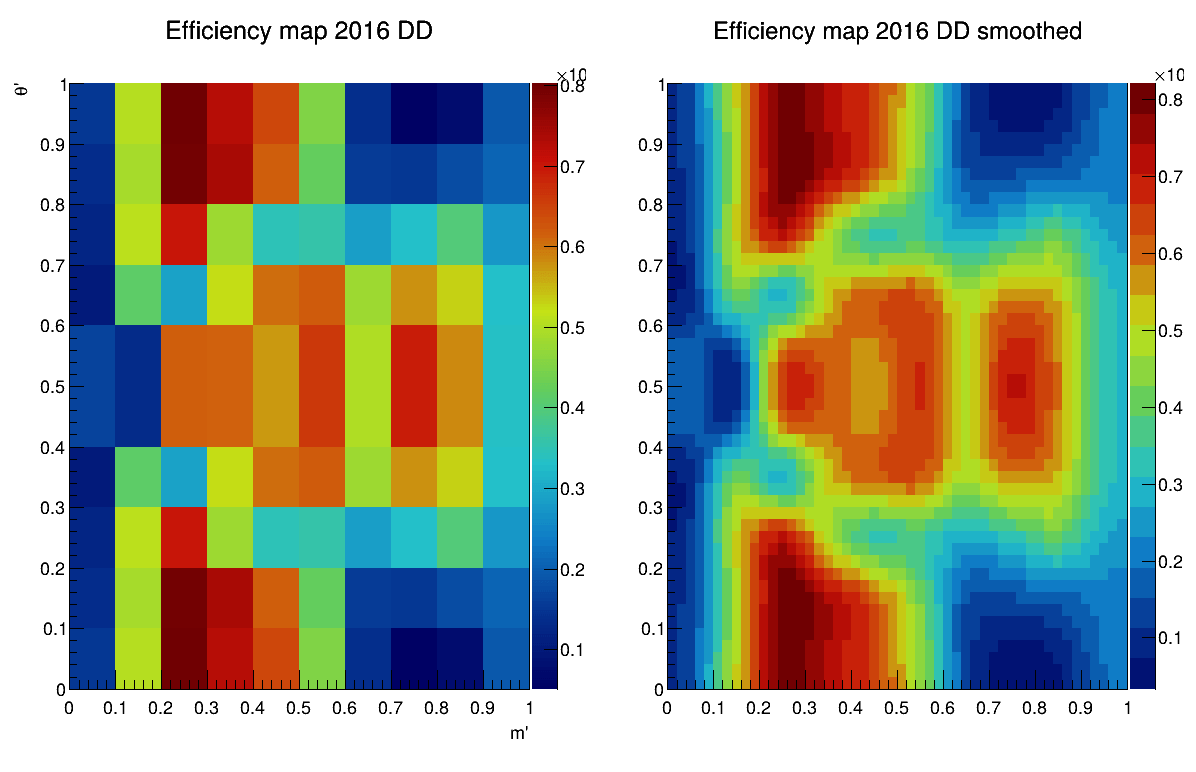
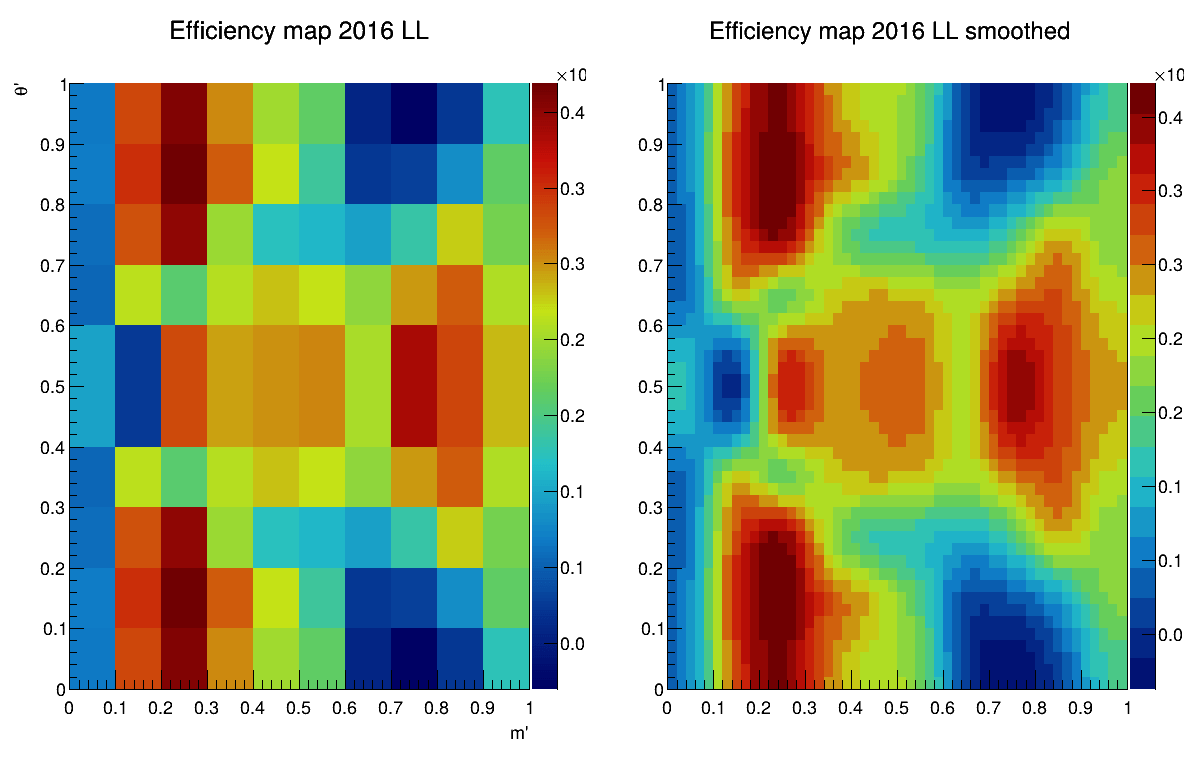
2016-DD
2016-LL
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Efficiency maps from BF analysis
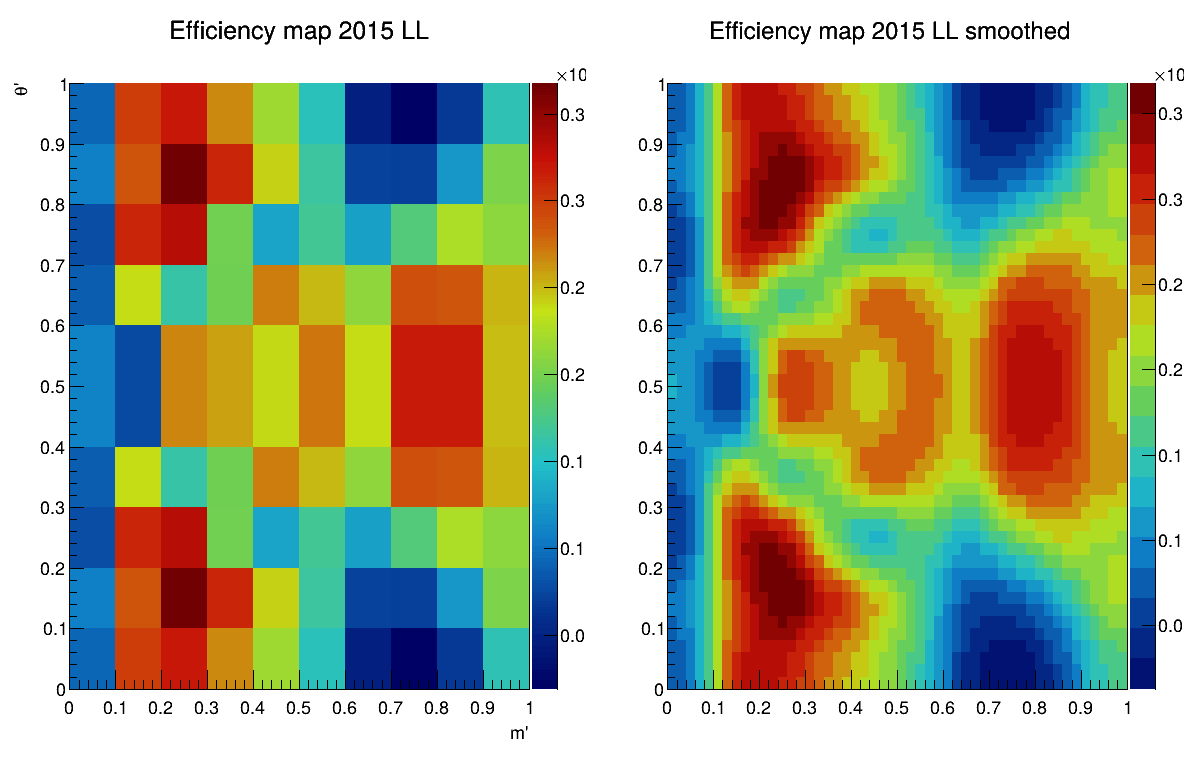
March 24th, 2025
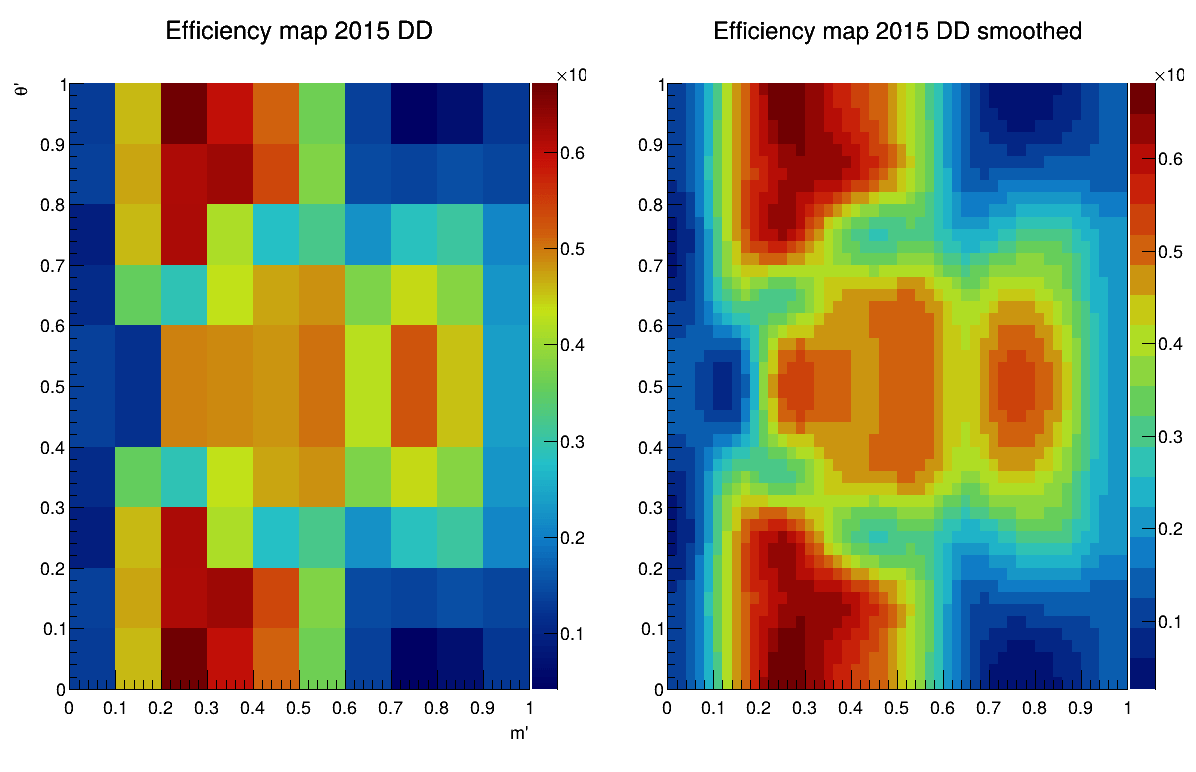
2015-DD
2015-LL
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
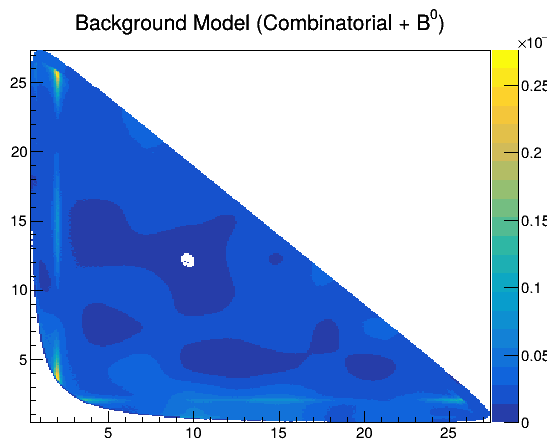
Combinatorial background model
Run 2 DD + LL categories merged
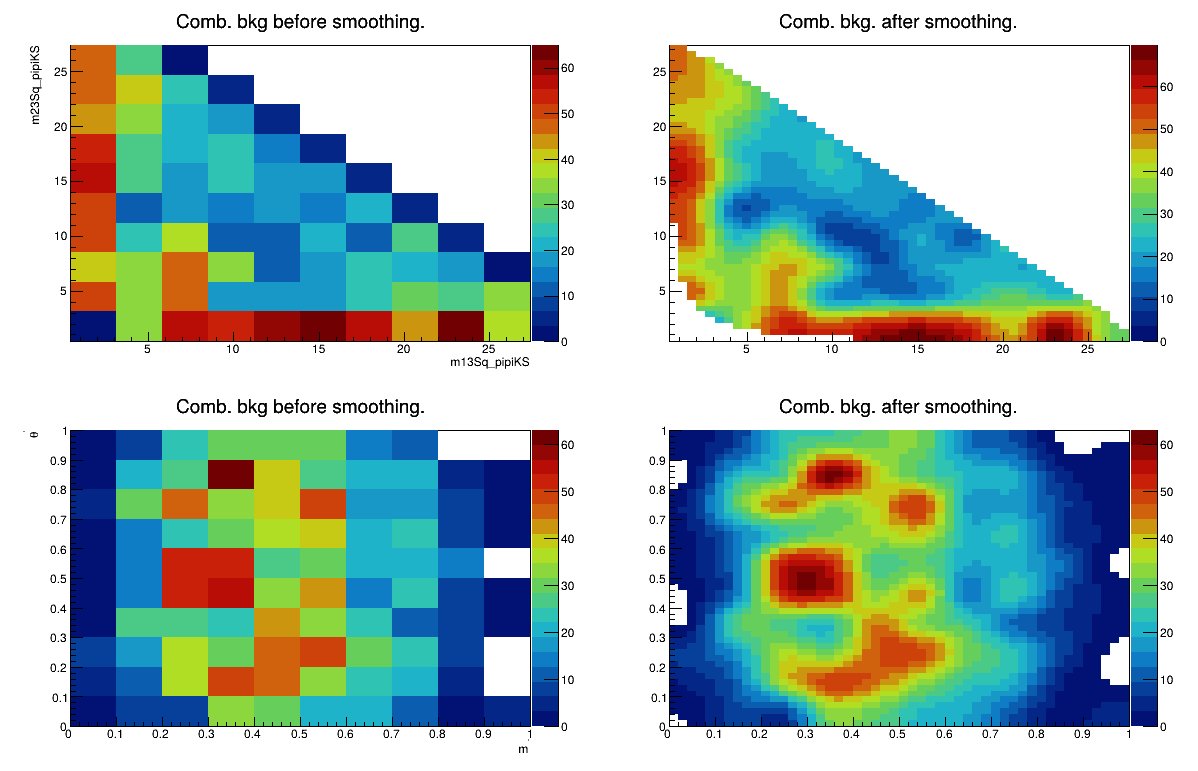
March 24th, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
\(B^{0}_{d}\) background model
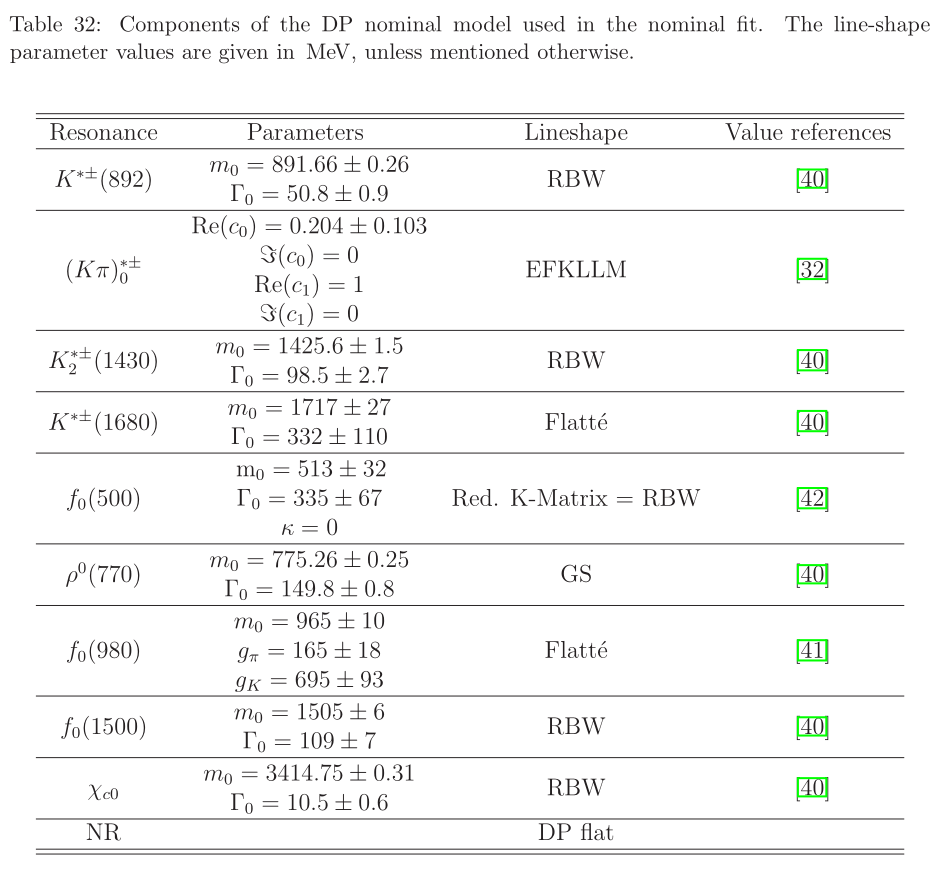
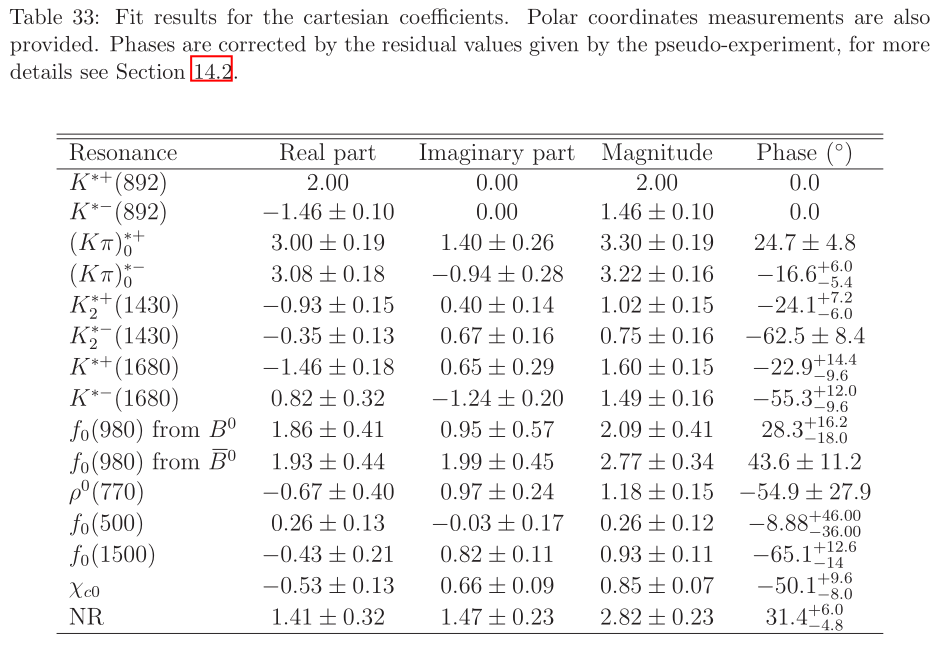
Model from \(B_{d}^{0}\rightarrow K_{S}^{0}\pi^{-}\pi^{+}\) Run I analysis
March 24th, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
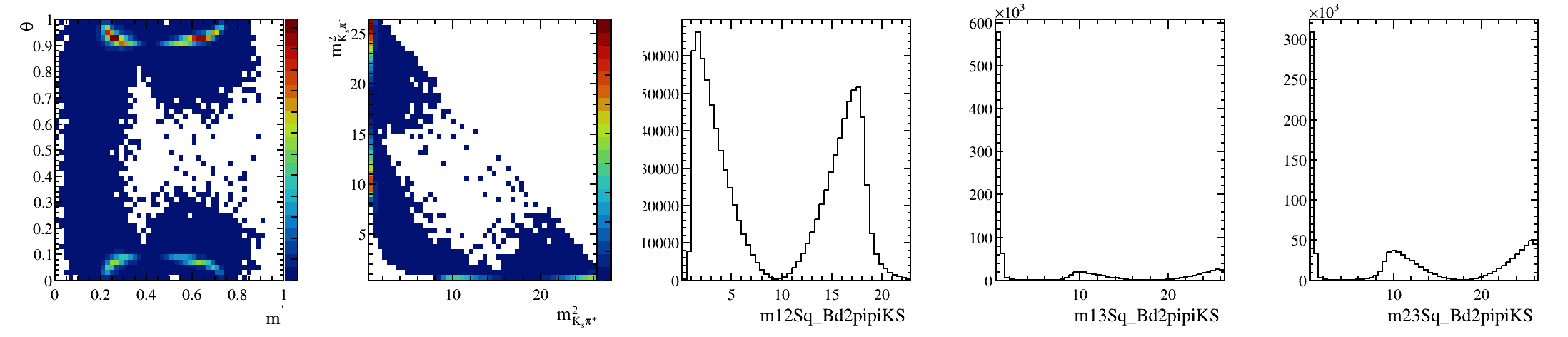
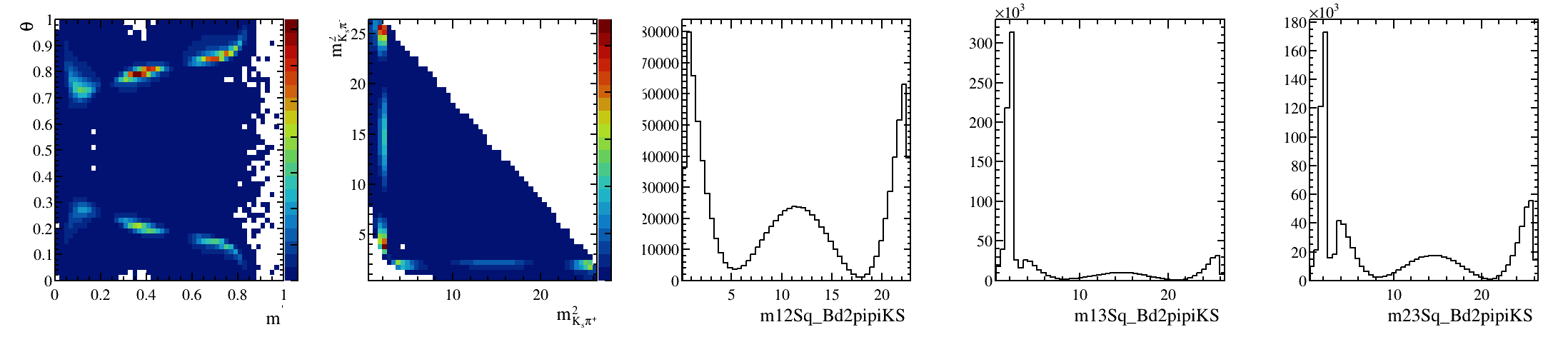
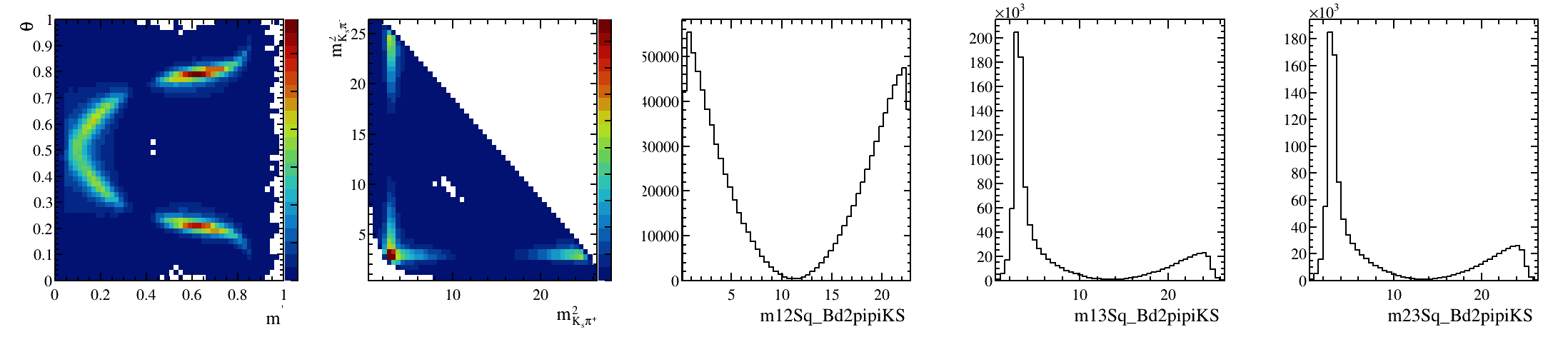
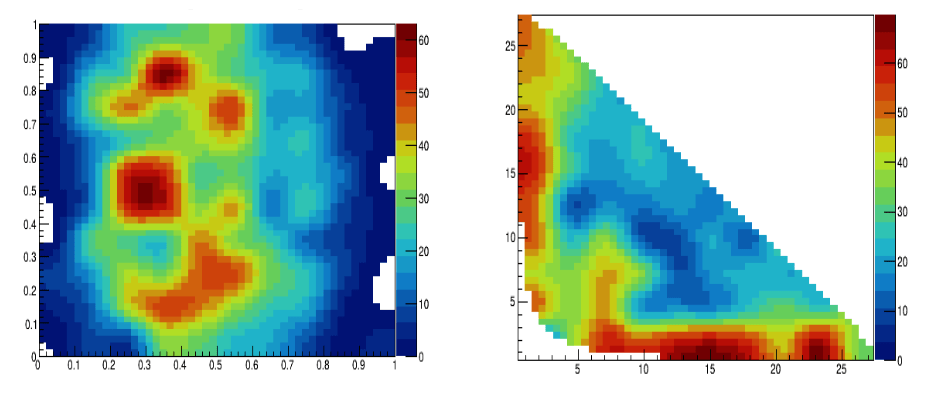
\(B^{0}_{d}\) background model: Art gallery

March 24th, 2025

Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
\(B^{0}_{d}\) background model: Art gallery

March 24th, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
\(B^{0}_{d}\) background model: Art gallery

March 24th, 2025

Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
\(B^{0}_{d}\) background model: Art gallery

March 24th, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
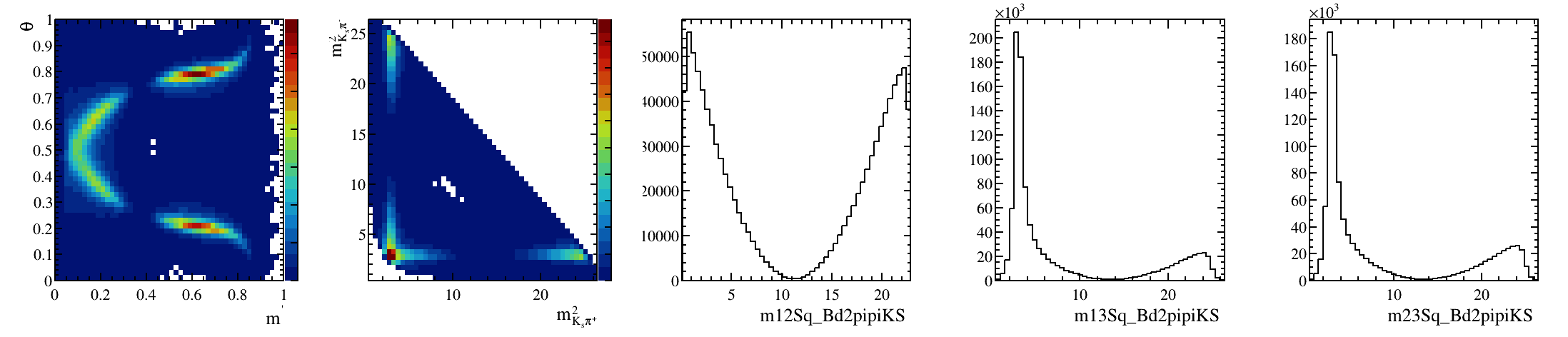
\(B^{0}_{d}\) background model: Art gallery

March 24th, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
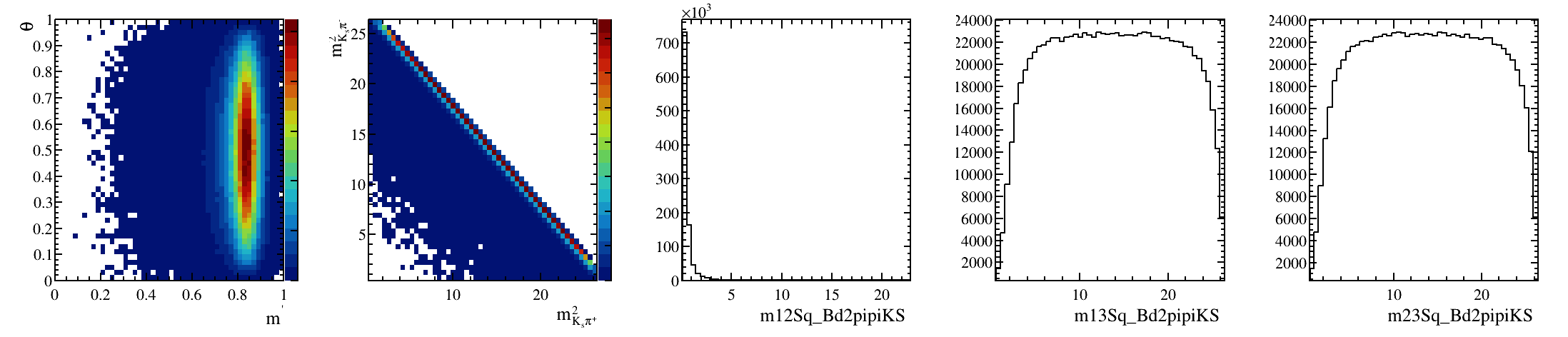
\(B^{0}_{d}\) background model: Art gallery

March 24th, 2025
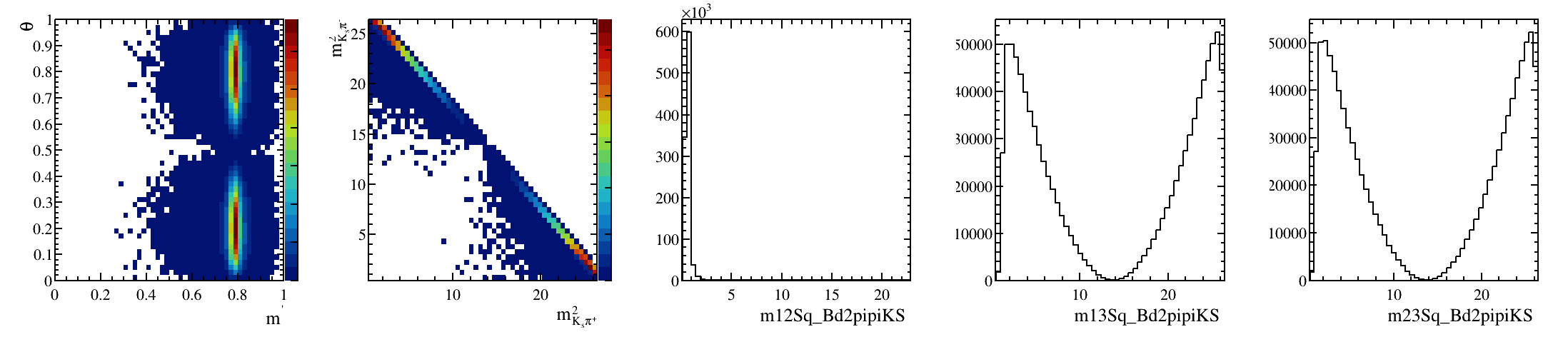
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
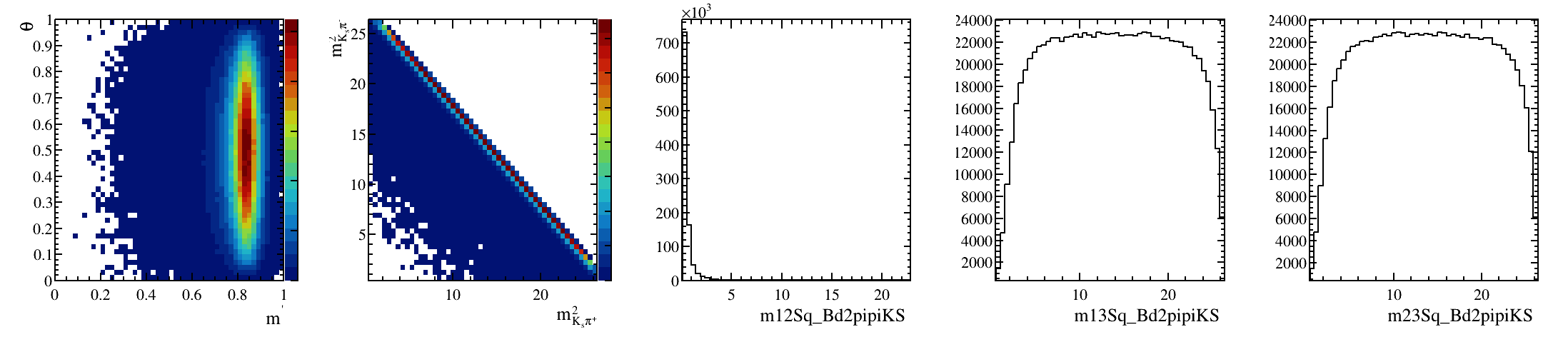
\(B^{0}_{d}\) background model: Art gallery

March 24th, 2025
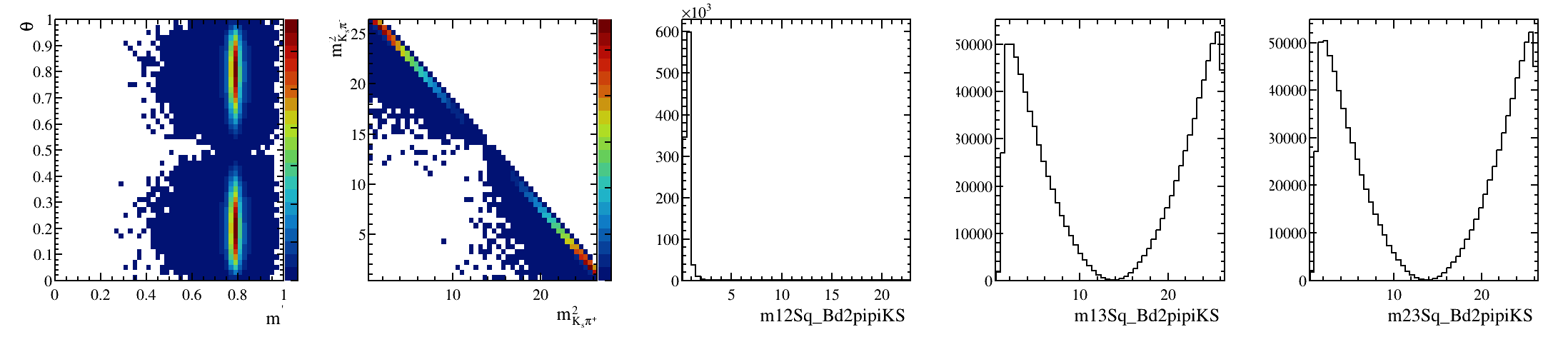
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
\(B^{0}_{d}\) background model: Art gallery

March 24th, 2025
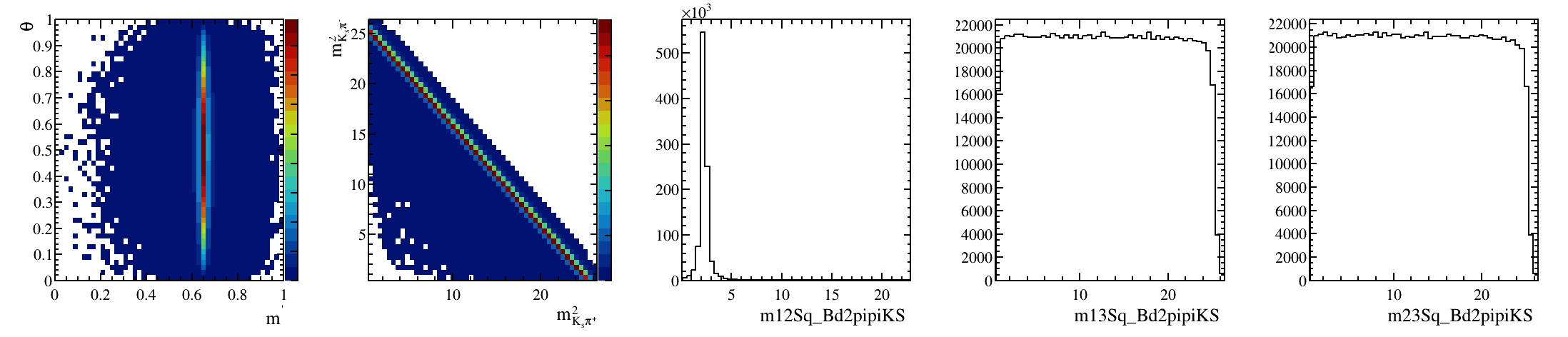
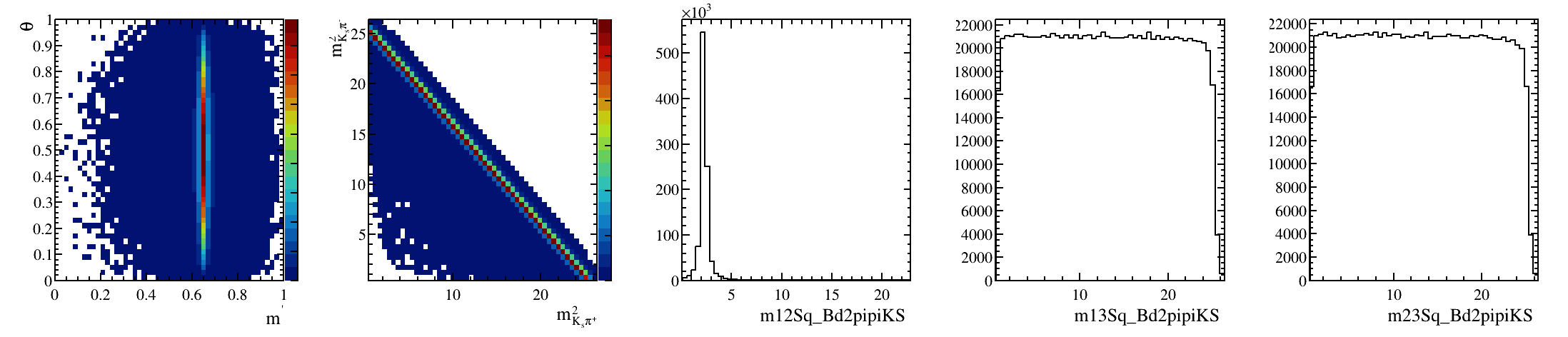
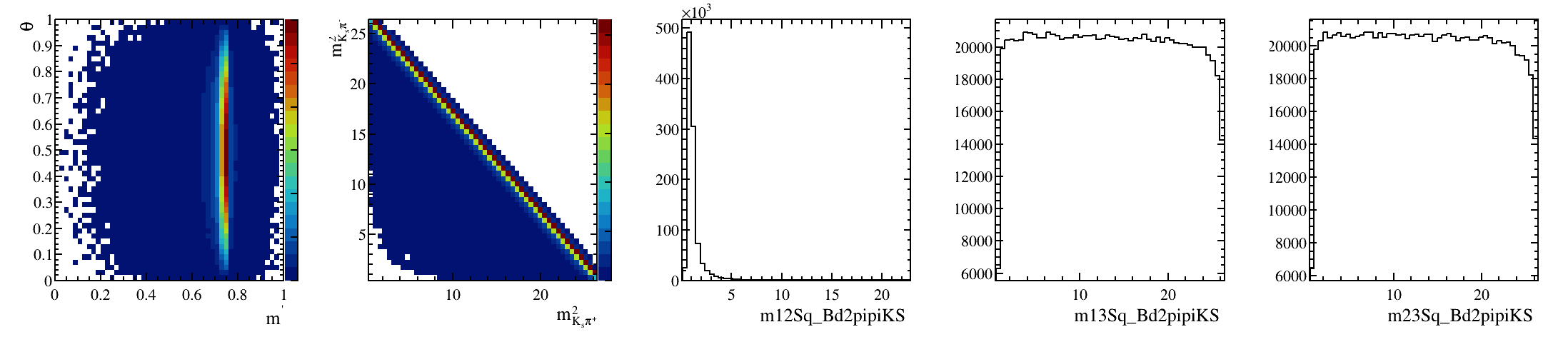
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
\(B^{0}_{d}\) background model: Art gallery

March 24th, 2025
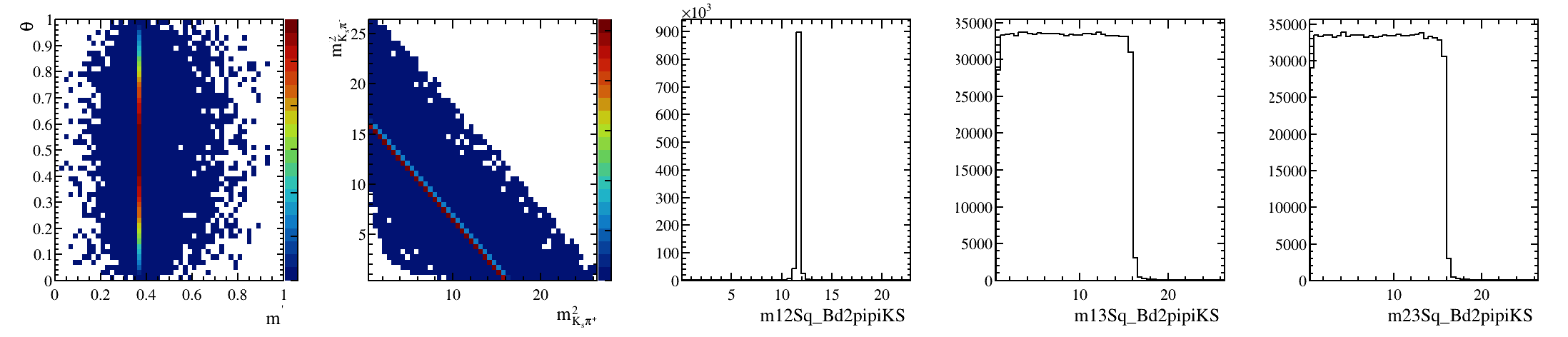
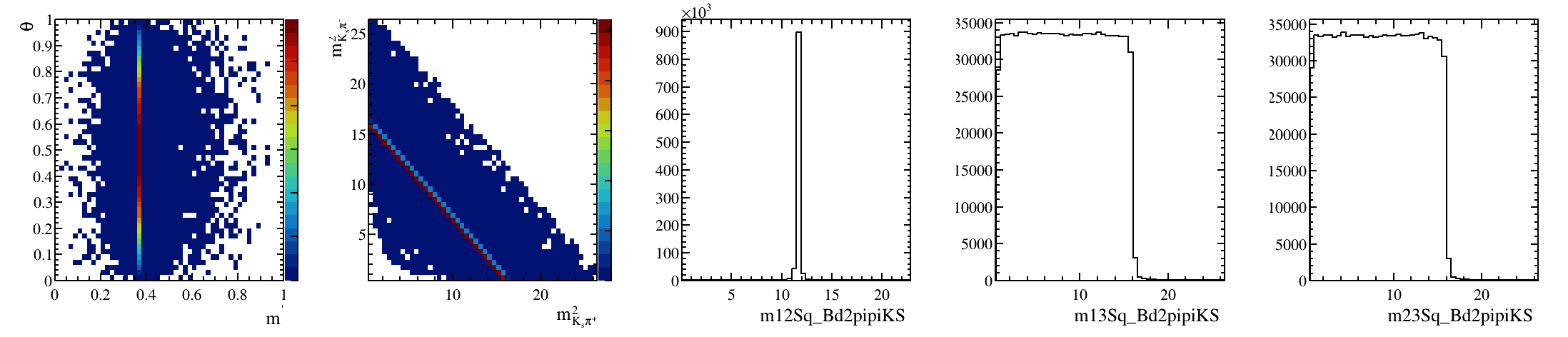
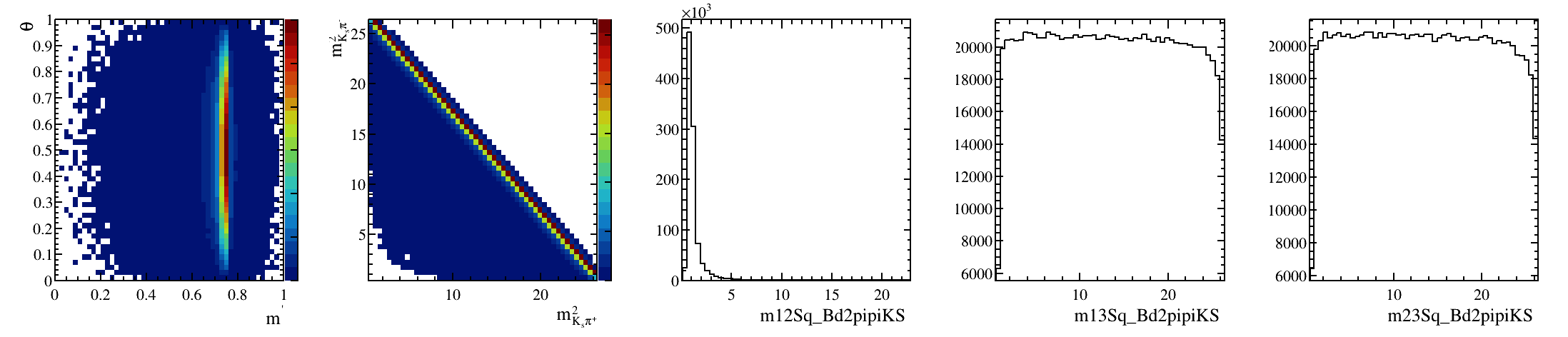
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
\(B^{0}_{d}\) background model: Art gallery

March 24th, 2025
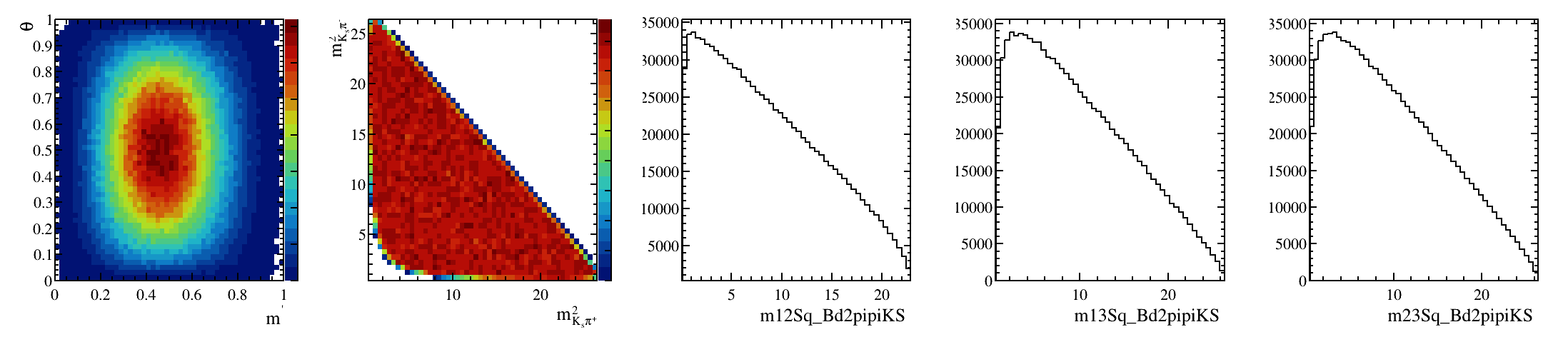
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
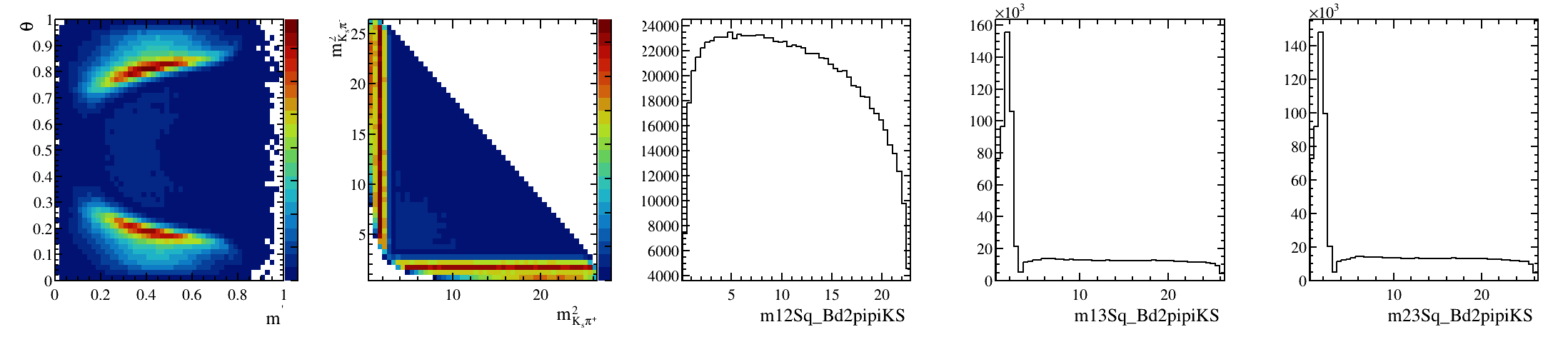
\(B^{0}_{d}\) background model
Solely physics \(\Rightarrow\) No efficiency
March 24th, 2025
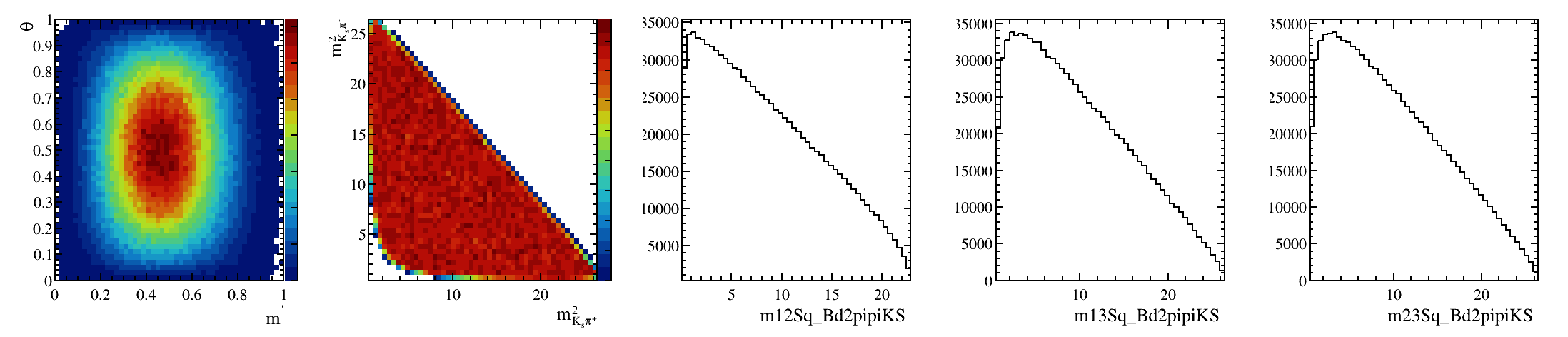
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
\(B^{0}_{d}\) background model
Solely physics \(\Rightarrow\) No efficiency


March 24th, 2025
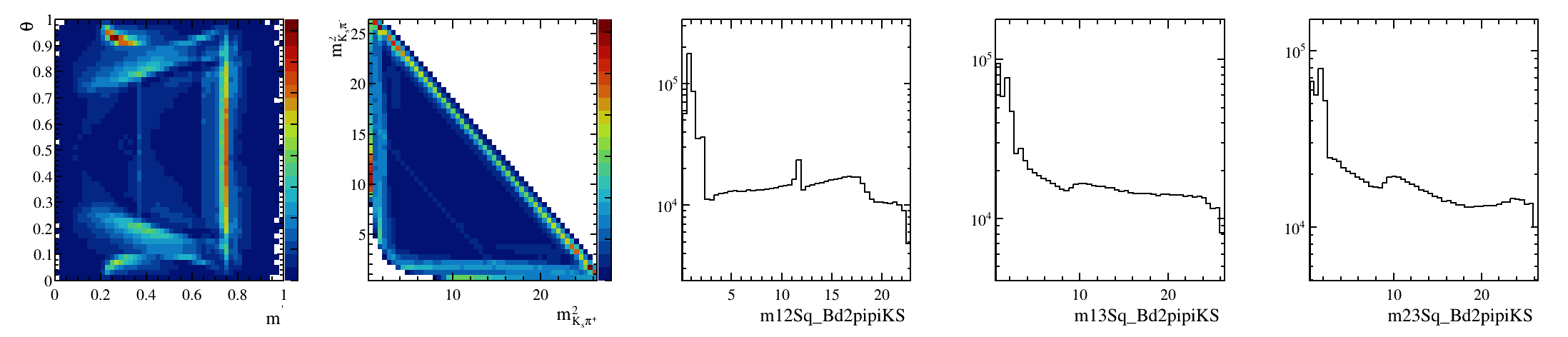
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
\(B^{0}_{d}\) background model
February 3rd, 2025
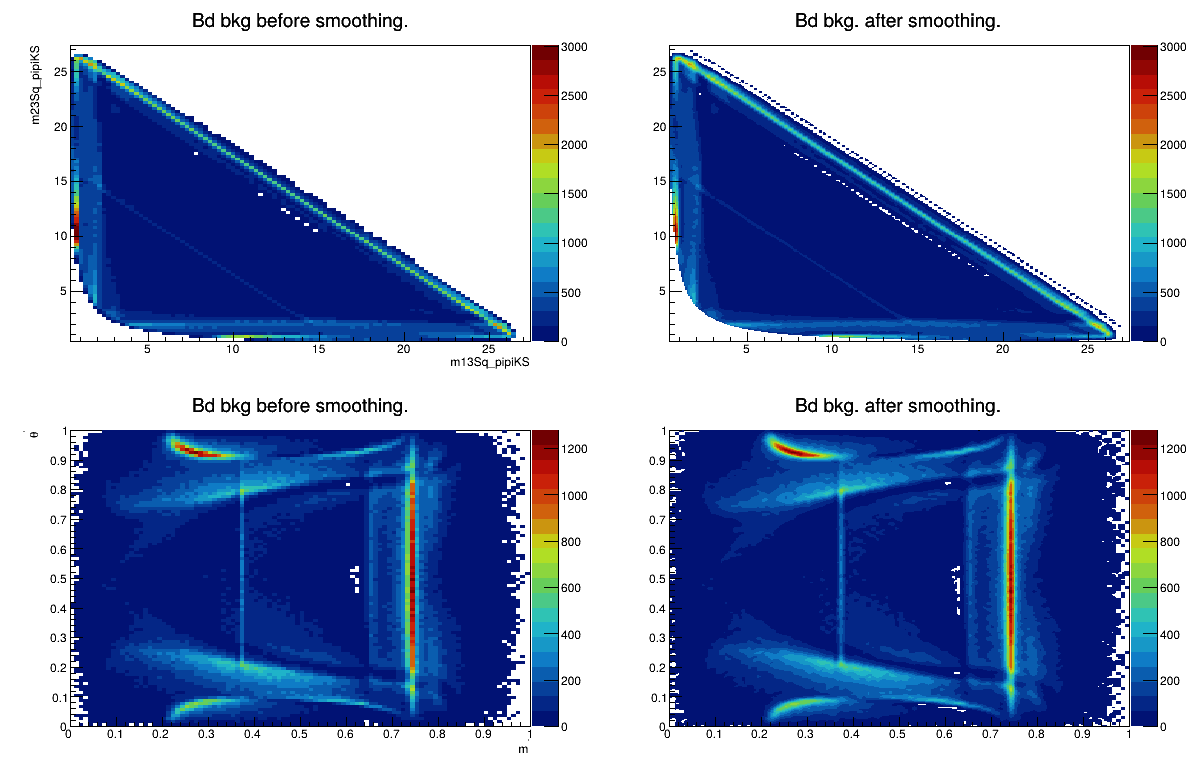
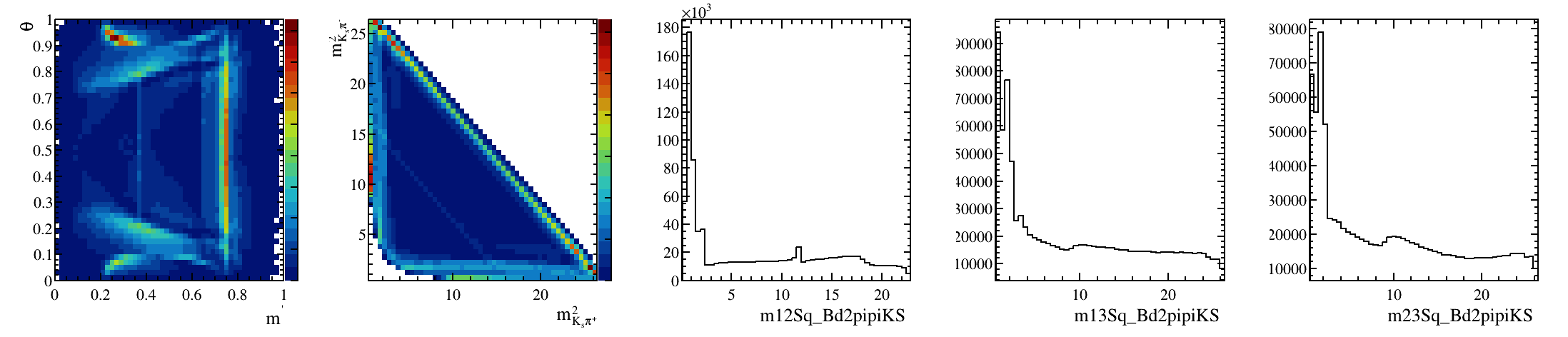
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
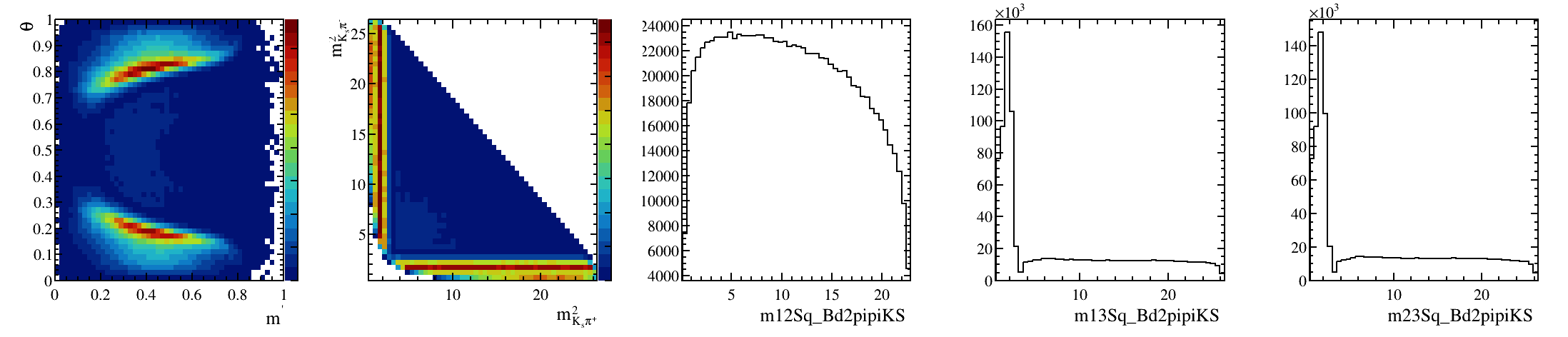
\(B^{0}_{d}\) background model
Physics + efficiency + vetoes
March 24th, 2025


2018-DD
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
\(B^{0}_{d}\) background model
Physics + efficiency + vetoes
March 24th, 2025
2018-DD
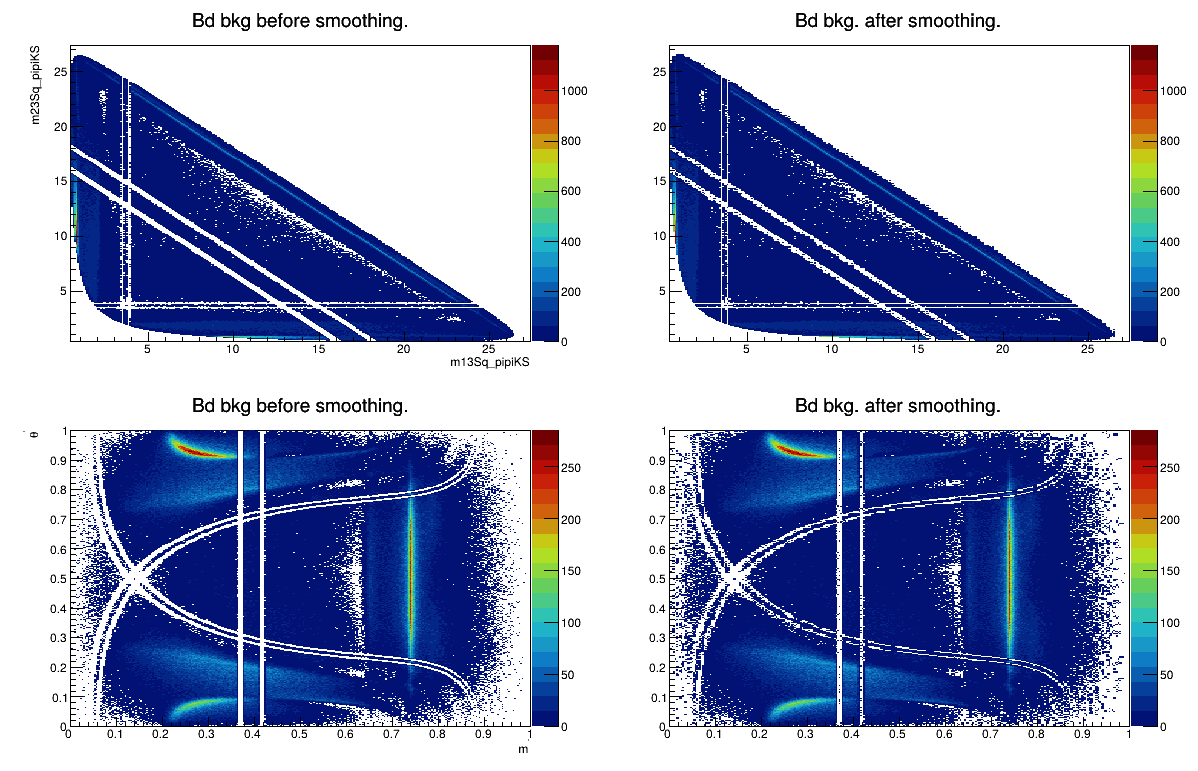
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
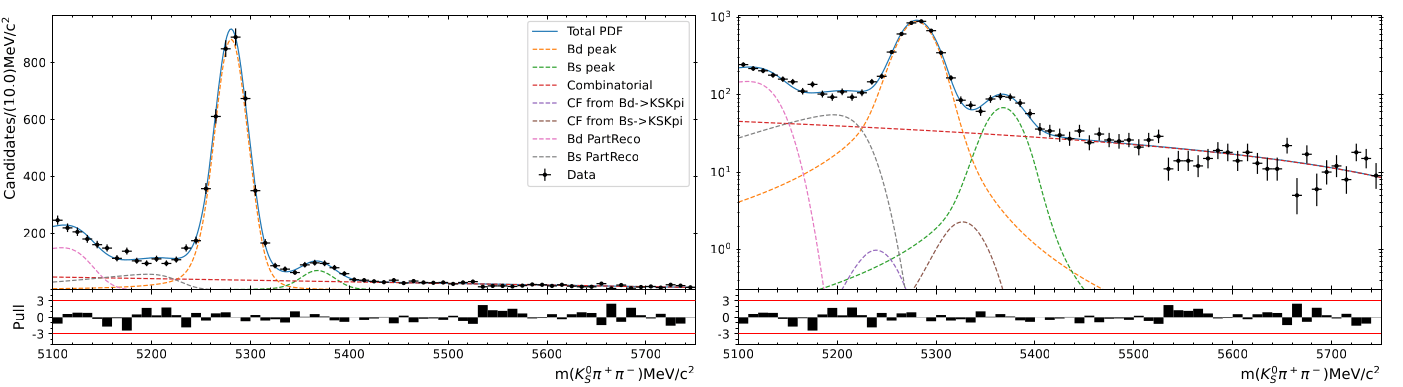
Background model
March 24th, 2025
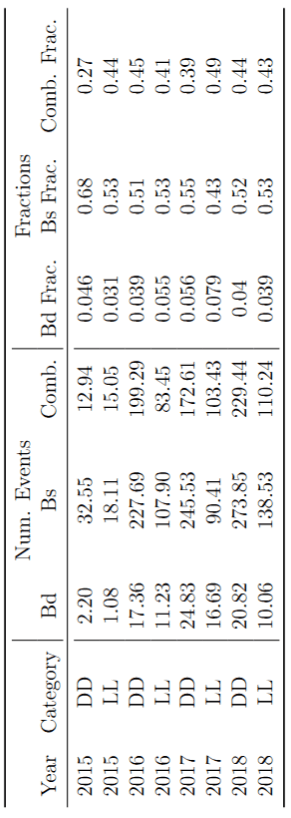
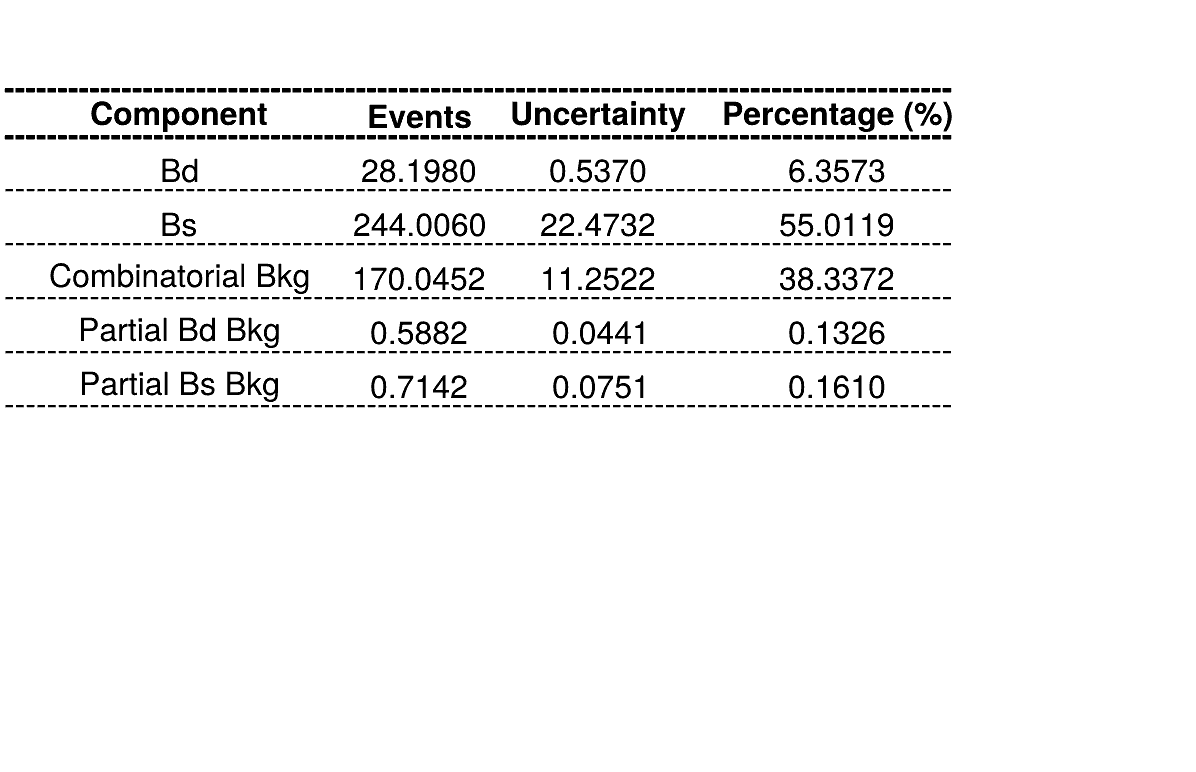
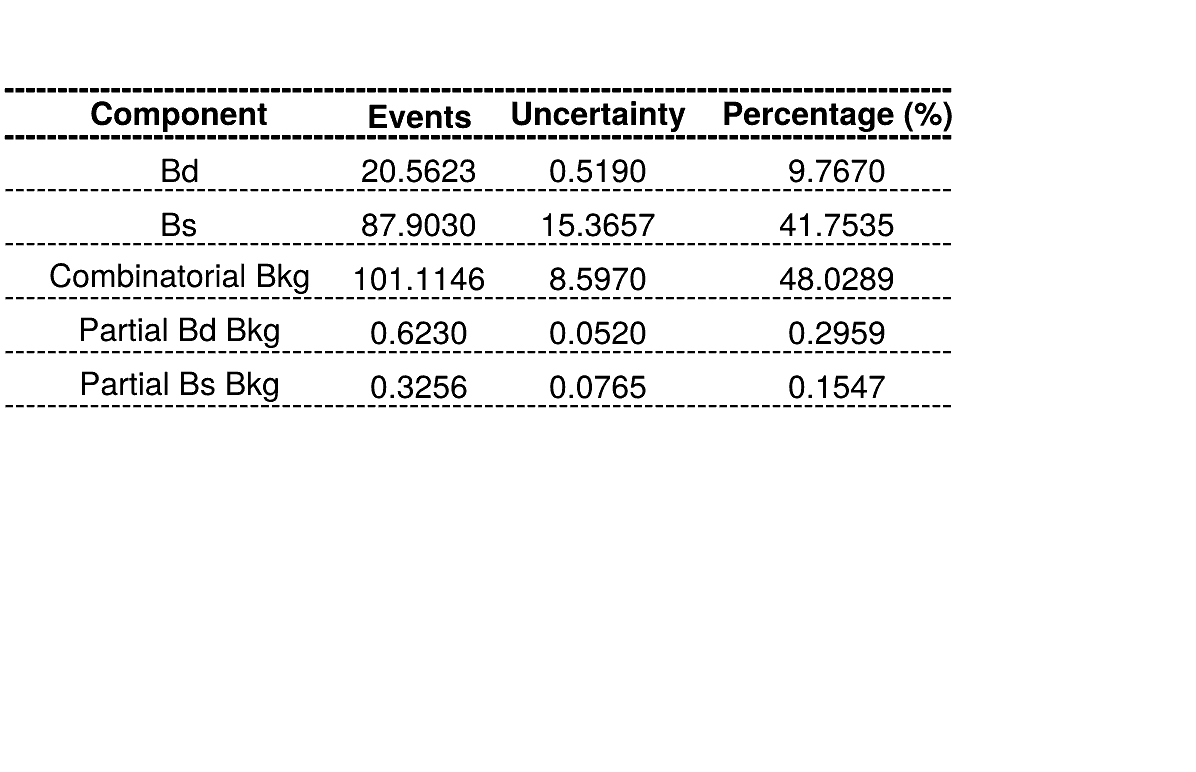
Summary of fractions for each component which are inputs for the Dalitz plot fit.
Combinatorial bkg. model
\(B_{d}^{0}\rightarrow K_{s}\pi\pi\) bkg. model
Using Truth match MC for signal
Using No Truth Match MC for signal

Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Analysis Strategy


Work in progress!
First fit with a simple (baseline) model.
Done!
April 2nd, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
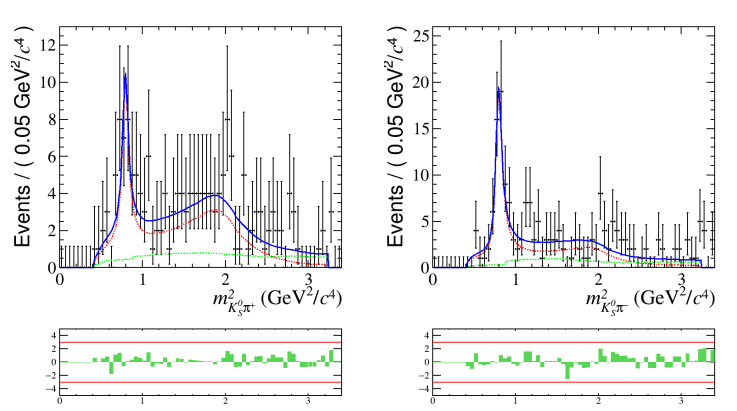
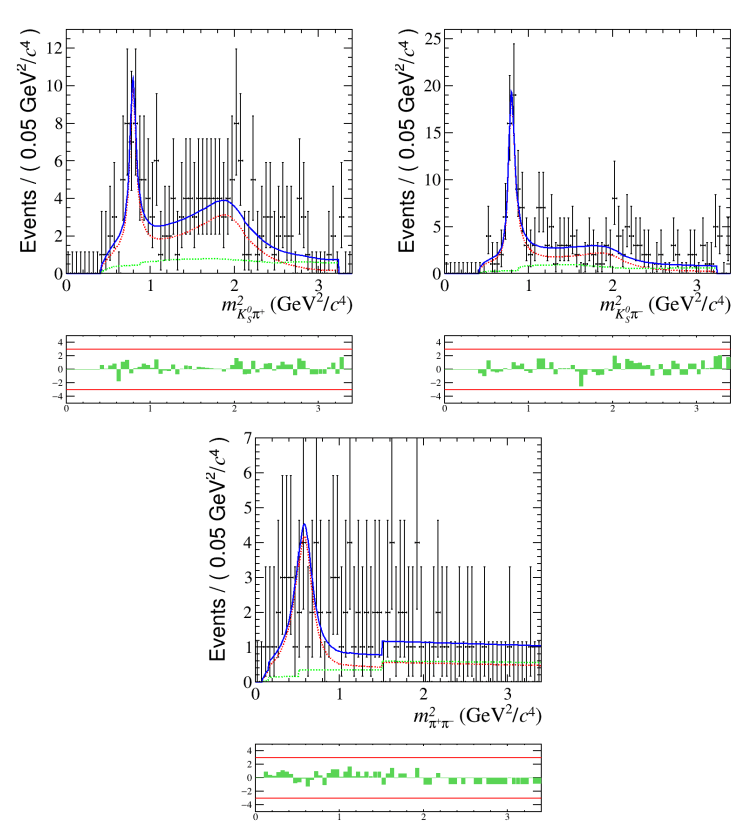
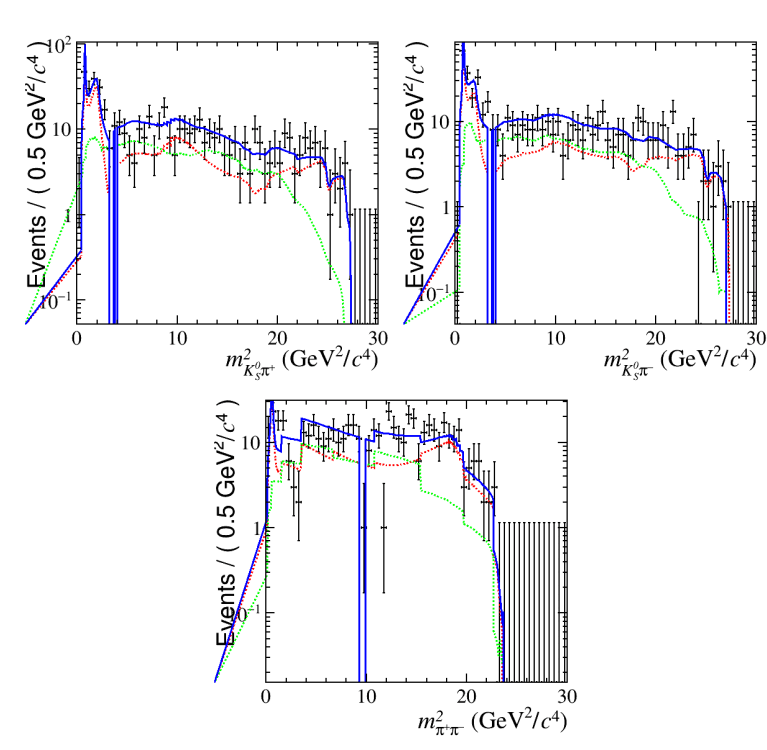
Dalitz plot Fit

Signal Model based on SM expectations
The preliminary results presented here include all the Run 2 data.
April 2nd, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Dalitz plot Fit
- Amplitudes and phases
- Raw asymmetries
April 2nd, 2025
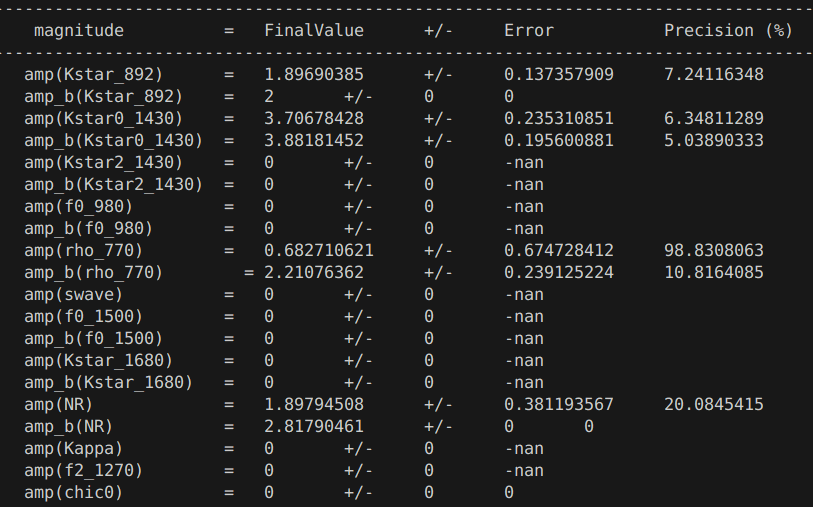
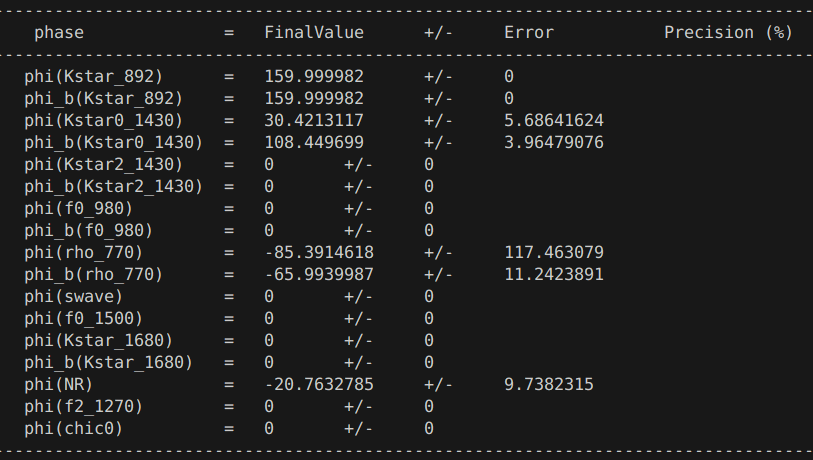
The preliminary results presented here include all the Run 2 data.

Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Dalitz plot Fit
April 2nd, 2025
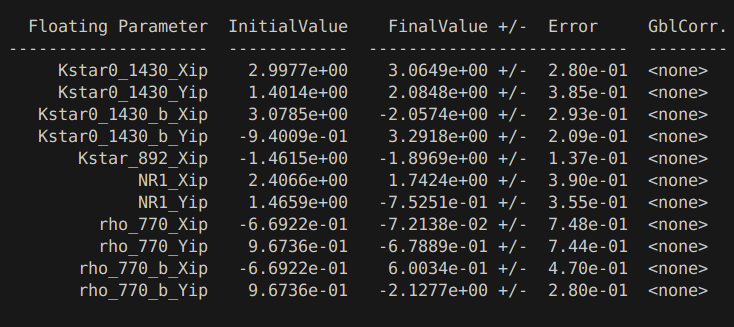
The preliminary results presented here include all the Run 2 data.
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Dalitz plot Fit
April 2nd, 2025
The preliminary results presented here include all the Run 2 data.
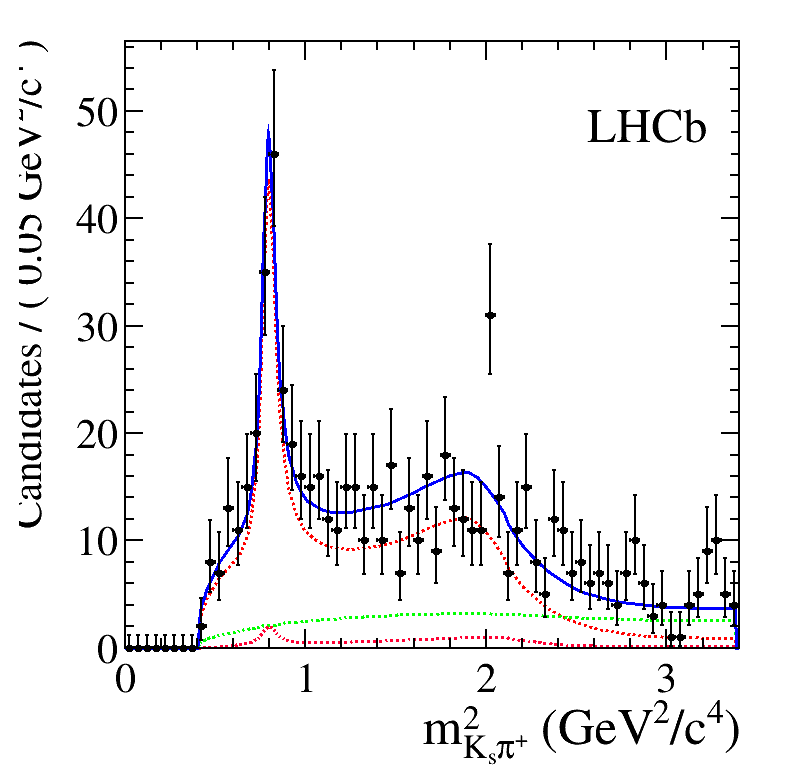

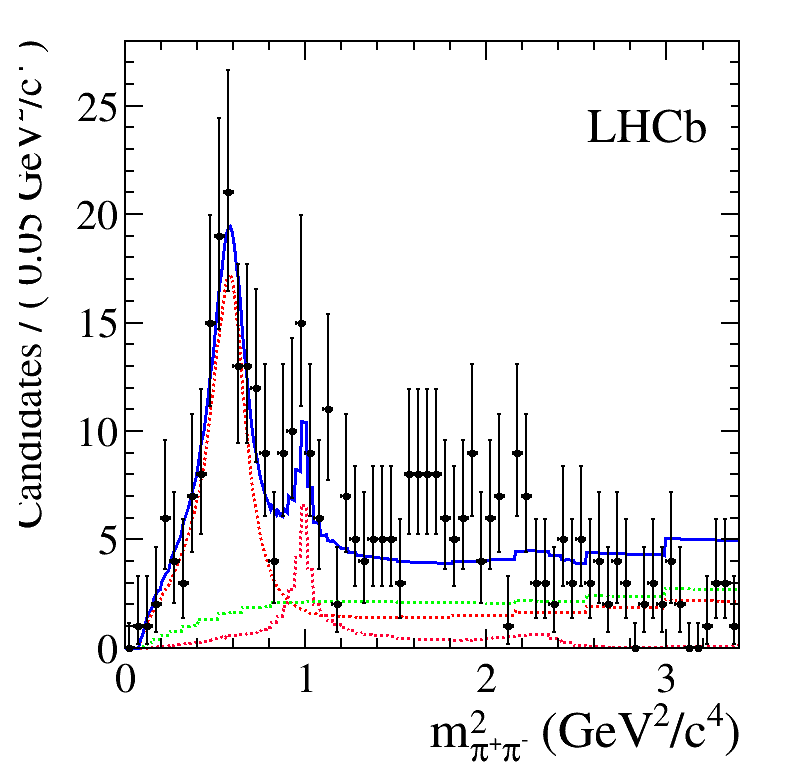
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Dalitz plot Fit
April 2nd, 2025
The preliminary results presented here include all the Run 2 data.
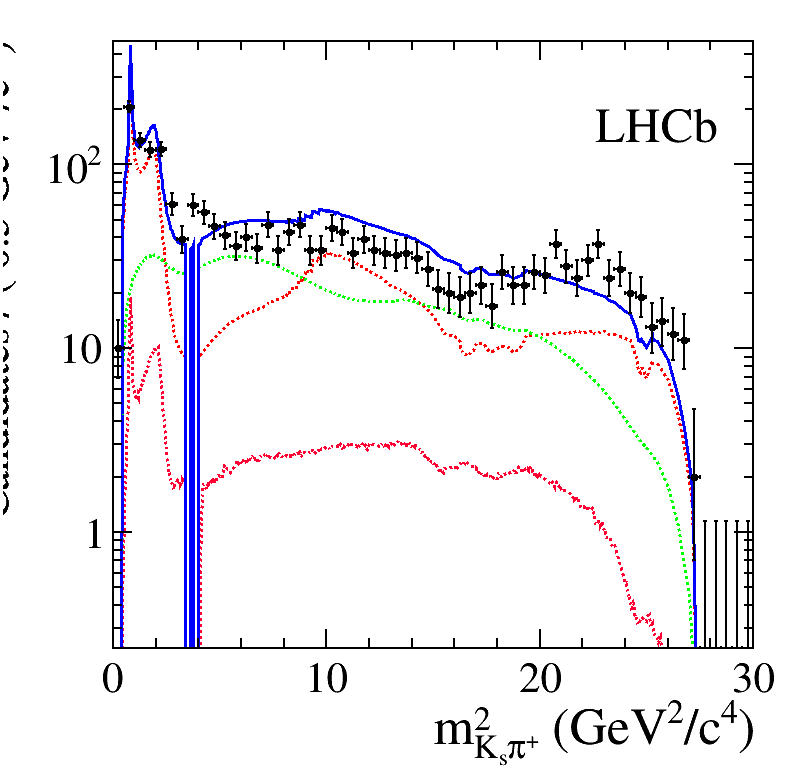
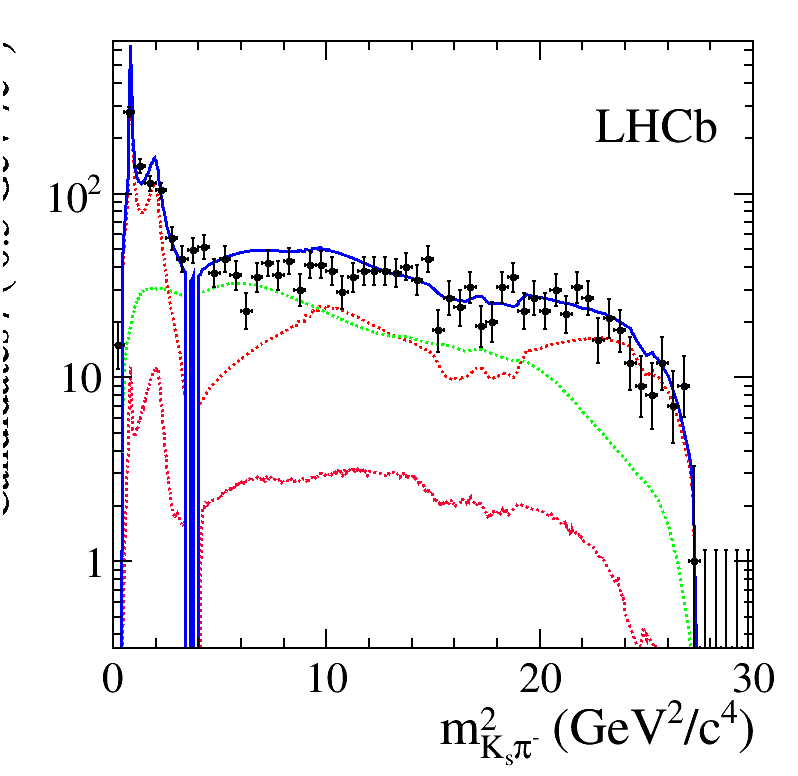
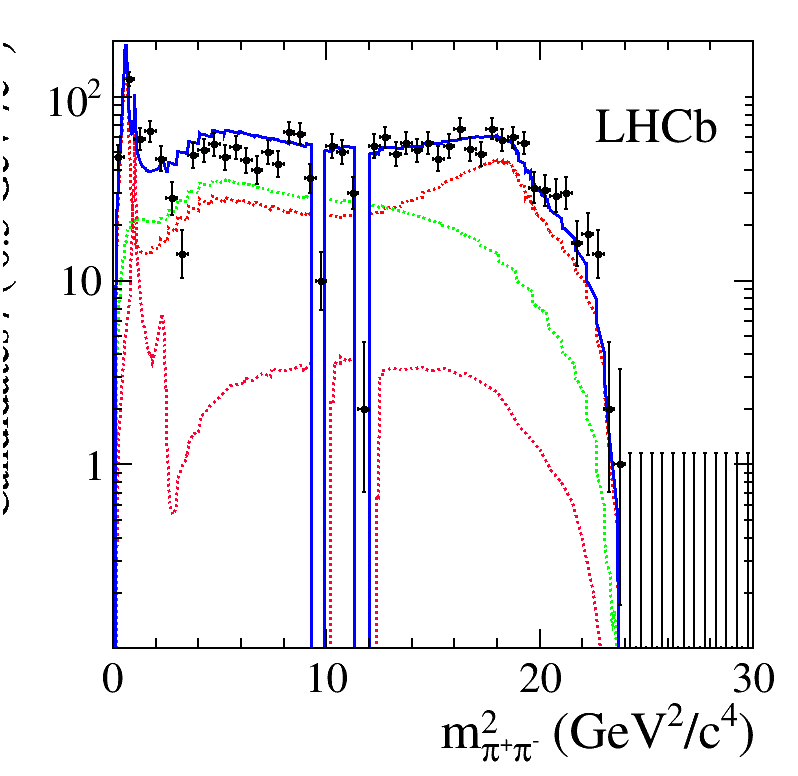
Back up
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Goodness-of-fit test
In short, this is what we do at this stage:
- We do an unbinned maximum likelihood fit of a PDF to the data.
- This fitted PDF is then used to extract the value of some observables from the data.
It is crucial to determine the level of agreement between the fit PDF and the data from a statistical argument (null-hypothesis significance test) \(\Rightarrow\) a goodness-of-fit (g.o.f).
The unbinned Point-to-Point Dissimilarity Method will be used \(\Rightarrow\) event by event
- Notation:
- \(\vec{s} = (s_{-},s_{+}) = (s_{K_{S}\pi^{-}},s_{K_{S}\pi^{+}}) \)
- \(f(\vec{s})\) and \(f_{0}(\vec{s})\): parent/true PDF of the data and test PDF, respectively.
- \(T\): test statistic (TS) \(\Rightarrow\) Larger values correspond to a worse level of agreement.
- \(H_{0}\): Null hypothesis \(\Rightarrow\) "The two samples are drawn from the same PDF".
- \(p\): \(p\)-value \(\Rightarrow\) Significance of any discrepancy between the data and the test PDF
How good are your fits? Unbinned multivariate goodness-of-fit tests in high energy physics: http://arxiv.org/abs/1006.3019
April 2nd, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Goodness-of-fit test
February 19th, 2025
In short, this is what we do at this stage:
- We do an unbinned maximum likelihood fit of a PDF to the data.
- This fitted PDF is then used to extract the value of some observables from the data.
It is crucial to determine the level of agreement between the fit PDF and the data from a statistical argument (null-hypothesis significance test) \(\Rightarrow\) a goodness-of-fit (g.o.f).
We will use the unbinned Point-to-Point Dissimilarity Method.
- Notation:
- \(\vec{s} = (s_{-},s_{+}) = (s_{K_{S}\pi^{-}},s_{K_{S}\pi^{+}}) \)
- \(f(\vec{s})\) and \(f_{0}(\vec{s})\): parent PDF of the data and test PDF, respectively.
- \(T\): test statistic (TS) \(\Rightarrow\) Larger values correspond to a worse level of agreement.
- \(p\): \(p\)-value \(\Rightarrow\) Significance of any discrepancy between the data and the test PDF
You want to know whether two sets of points in phase space come from the same underlying distribution
The p-value is the probability of getting a test statistic TTT as large or larger than the observed one, under the null hypothesis.
“If the samples really come from the same distribution, how often would I get a dissimilarity as large as the one I observed, just due to chance?”
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Point-to-Point Dissimilarity Method
Ideally, the difference between \(f\) and \(f_{0}\) could be estimated from the T statistic:
It is plausible to postulate a weighting function (WF) \(\psi(|\vec{s}-\vec{s}'|)\) which correlates the difference between the PDF's at different points, such that:
This can be approximated by:
The average kernel value between pairs of points if both are drawn from distribution fff
April 2nd, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Point-to-Point Dissimilarity Method
The distribution of \(T\) for the case \(f = f_{0}\) is not known... How do we estimate a \(p\)-value?
- Permutation sampling
- Combine all data points from both samples into a single pool \(n_{d}+n_{mc}\)
- Randomly reassign points into two new "data" and "MC" samples with sizes \(n_{d}\) and \(n_{mc}\)
- Compute the test statistic \(T_{perm}\) for each permuted pair.
- Repeat this process \(n_{perm}\) times to obtain \(\{T_{perm}^{1},...,T_{perm}^{n_{perm}}\}\)
- The \(p\)-value is the fraction of permutations where \(T_{perm} \geq T \)
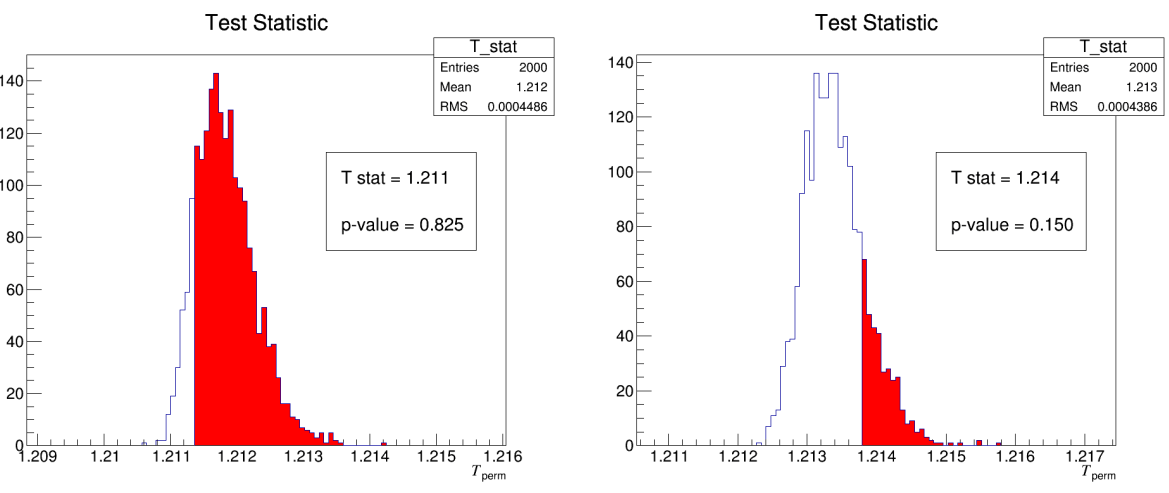
- If \(p\)-value is small:
- The observed dissimilarity is unlikely under \(H_{0}\).
- If \(p\)-value is large:
- The observed dissimilarity could happen by chance.
April 2nd, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Point-to-Point Dissimilarity Method
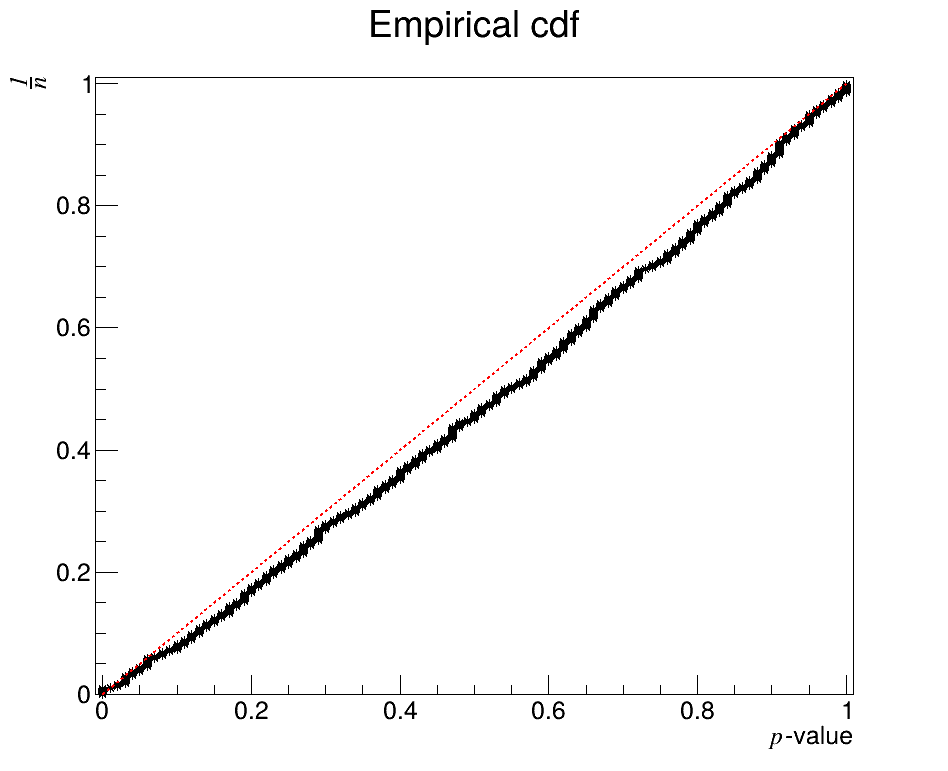
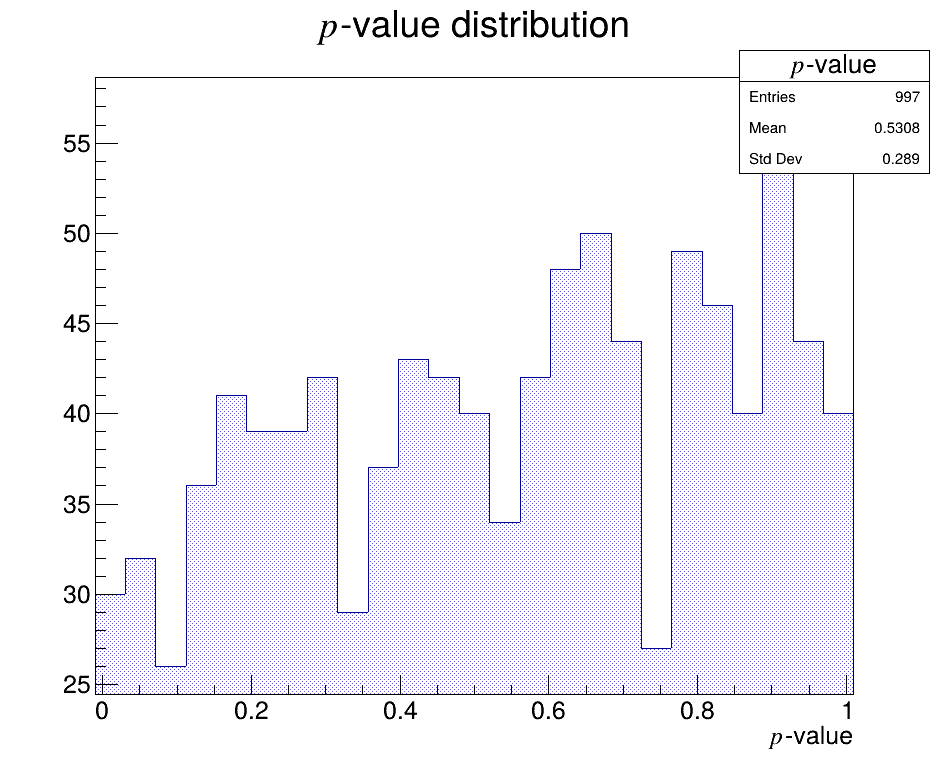
- First test of the method using the Run 1 B2KSpipi PDF
- ~1000 toys
- \(n_{d}=n_{mc} = 100\) (low statistics)
- \(n_{perm}\) = 100
- The logarithmic function is chosen as \(\psi\)
The \(p\)-value is a function of the data and MC, and is therefore itself a random variable
April 2nd, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Towards the nominal DP model
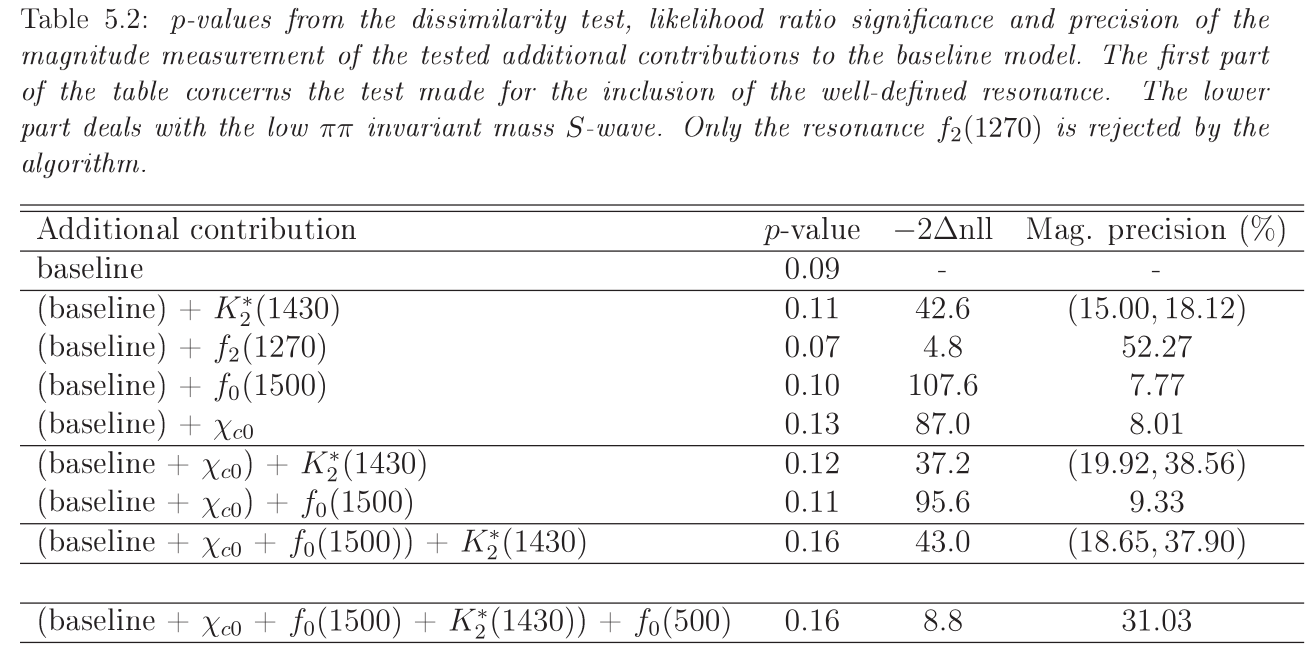
Run 1 procedure for B2KSpipi

April 2nd, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Outlook
- The installation of the (pre) Dalitz plot Fit is complete and ready for the first fits.
- First results expected in the two coming weeks.
- The Paris colleagues are working again in the BF mass fit \(\Rightarrow\) New results
- New inputs for the AmAn.
- The plan after the Bs2KsPiPi AmAn is to continue with the update of the Bd2KsPiPi AmAn.
- This will be the starter point for the TD AmAn.
February 19th, 2025
"Mass window optimization"
Mass window optimization
Analysis
Sebastian Ordoñez-Soto
January 30th, 2025
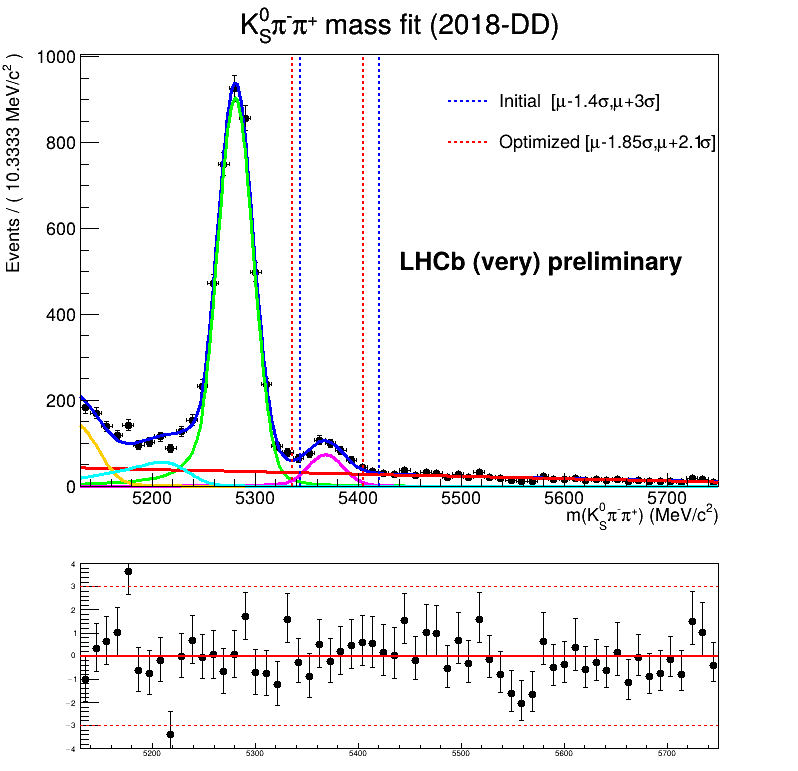
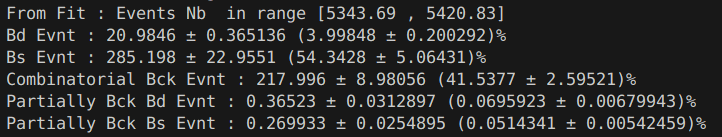
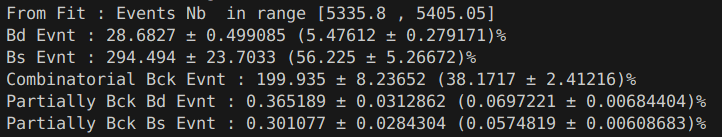
Fractions during the installation
Fractions after optimisation
Mass window optimization
Sebastian Ordoñez-Soto
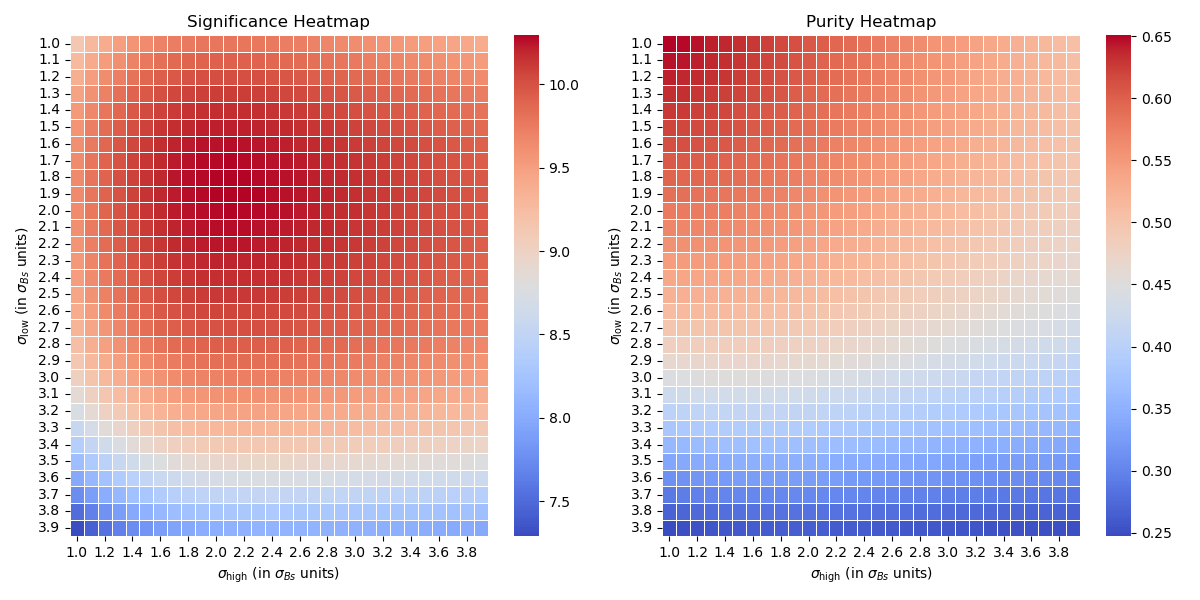
Analysis
January 30th, 2025
Mass window optimization
Sebastian Ordoñez-Soto
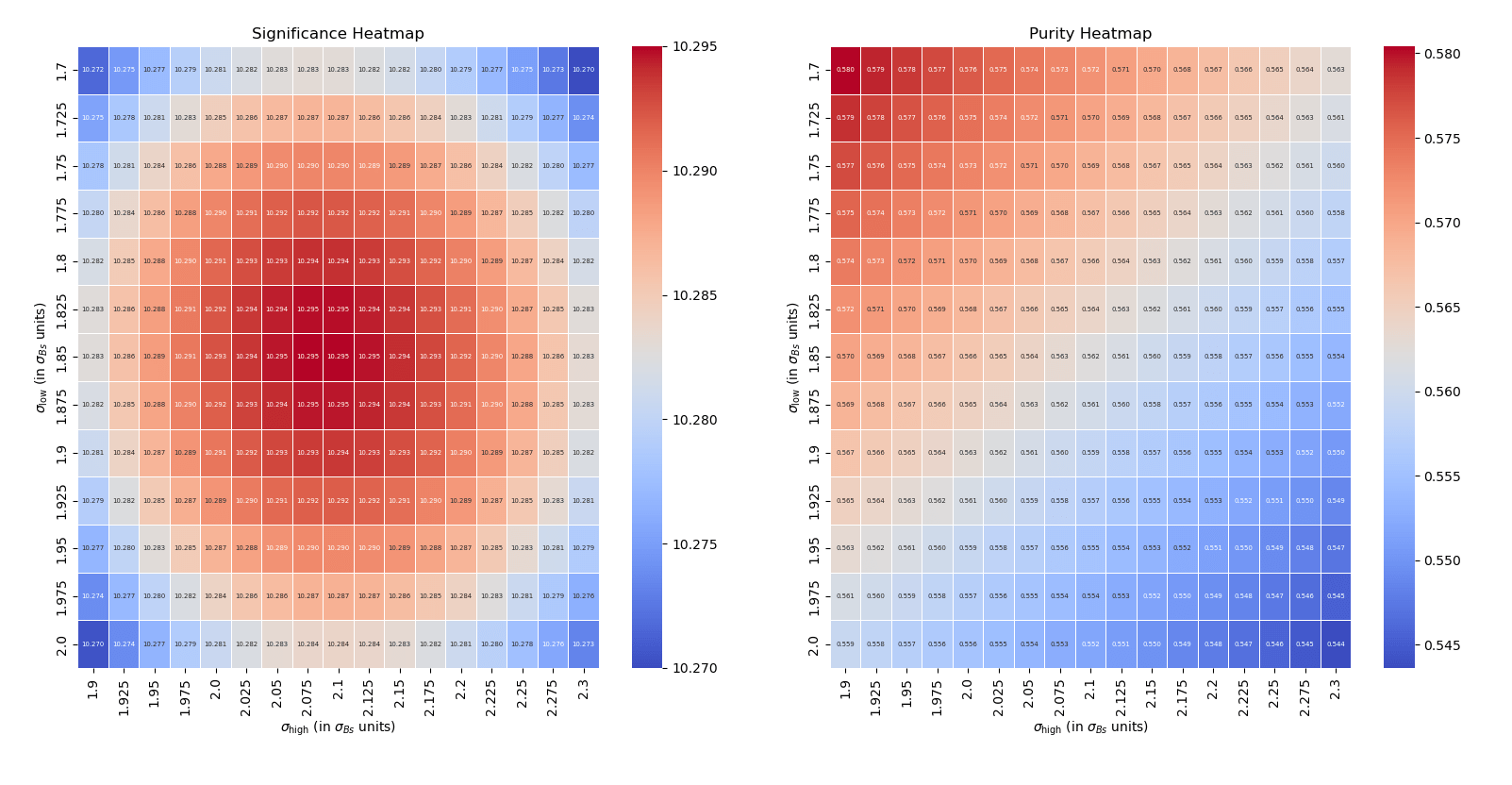
January 30th, 2025
Analysis
Home made massfit
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
February 3rd, 2025
About the fits below:
- Include an unnecessary veto, it turns out that our tuples already included them.
- I saw them in CRAFT in the scripts used during the installation of the analysis. Unfortunately, there was a wrong number in the D+ range.
- The combinatorial background slope was fixed.
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
February 3rd, 2025
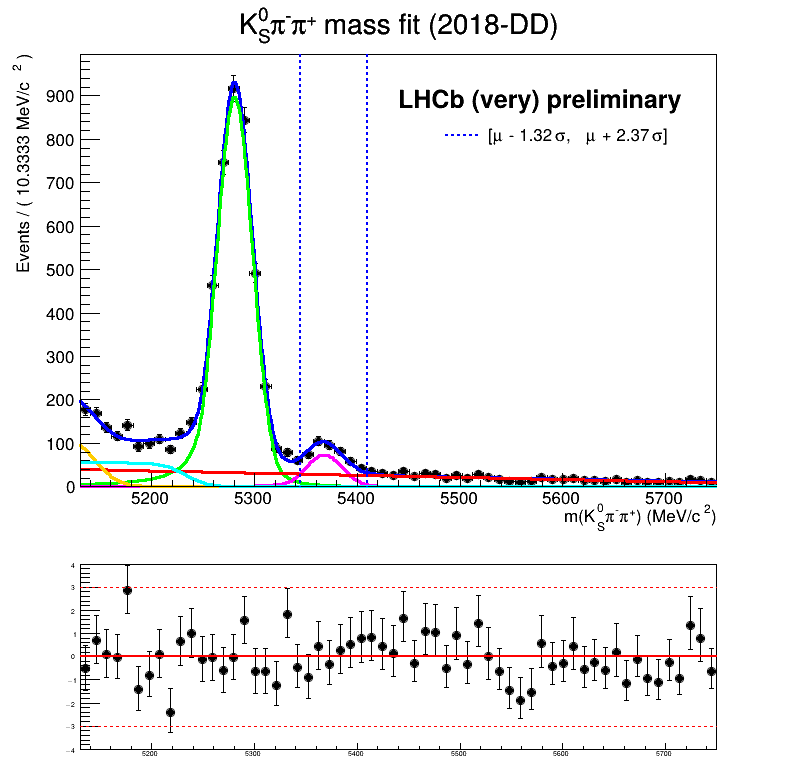
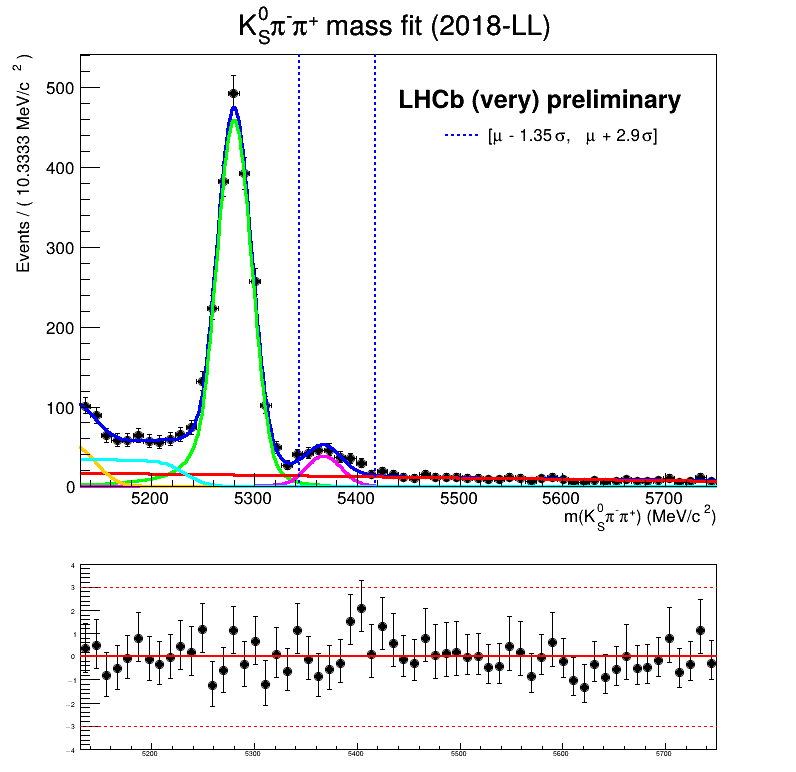
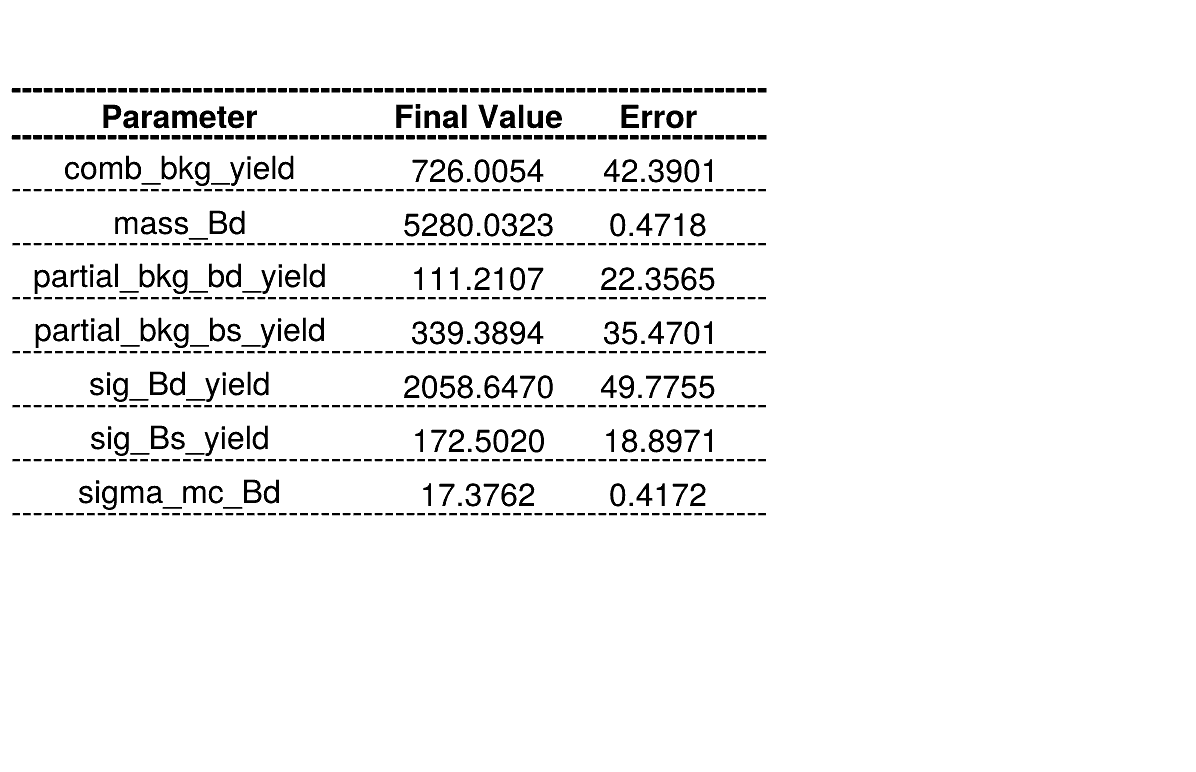
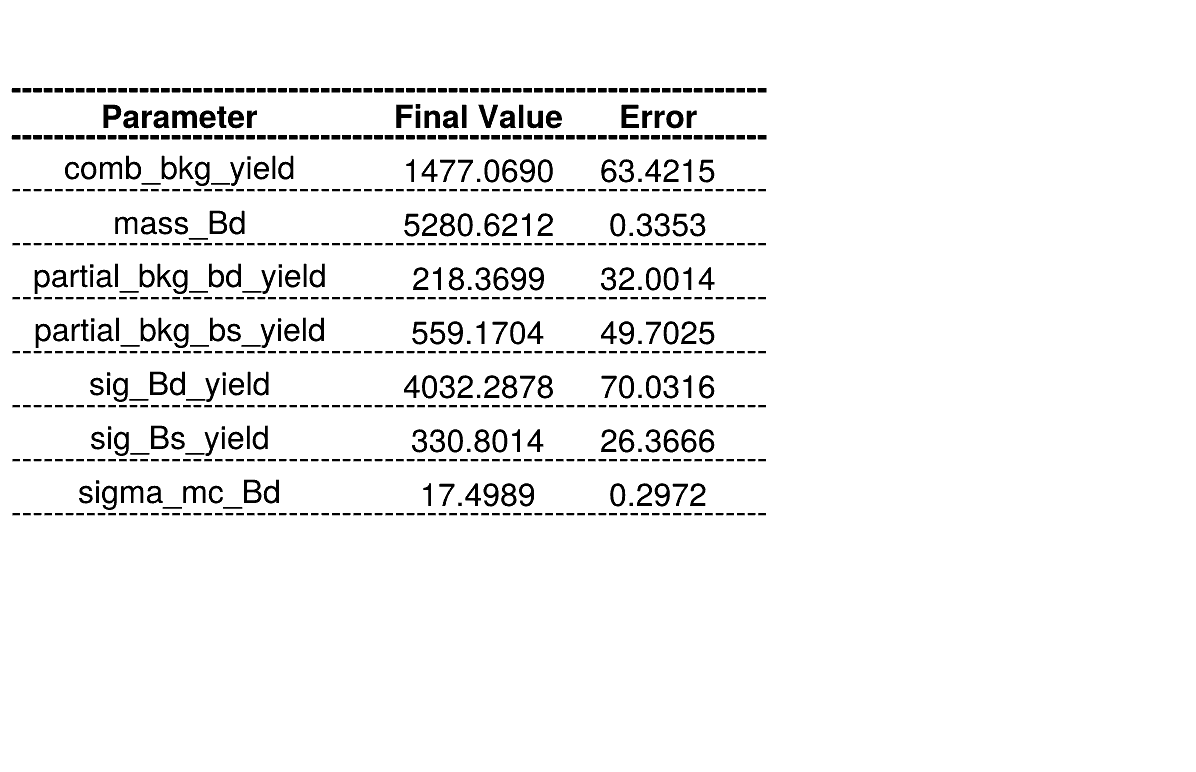
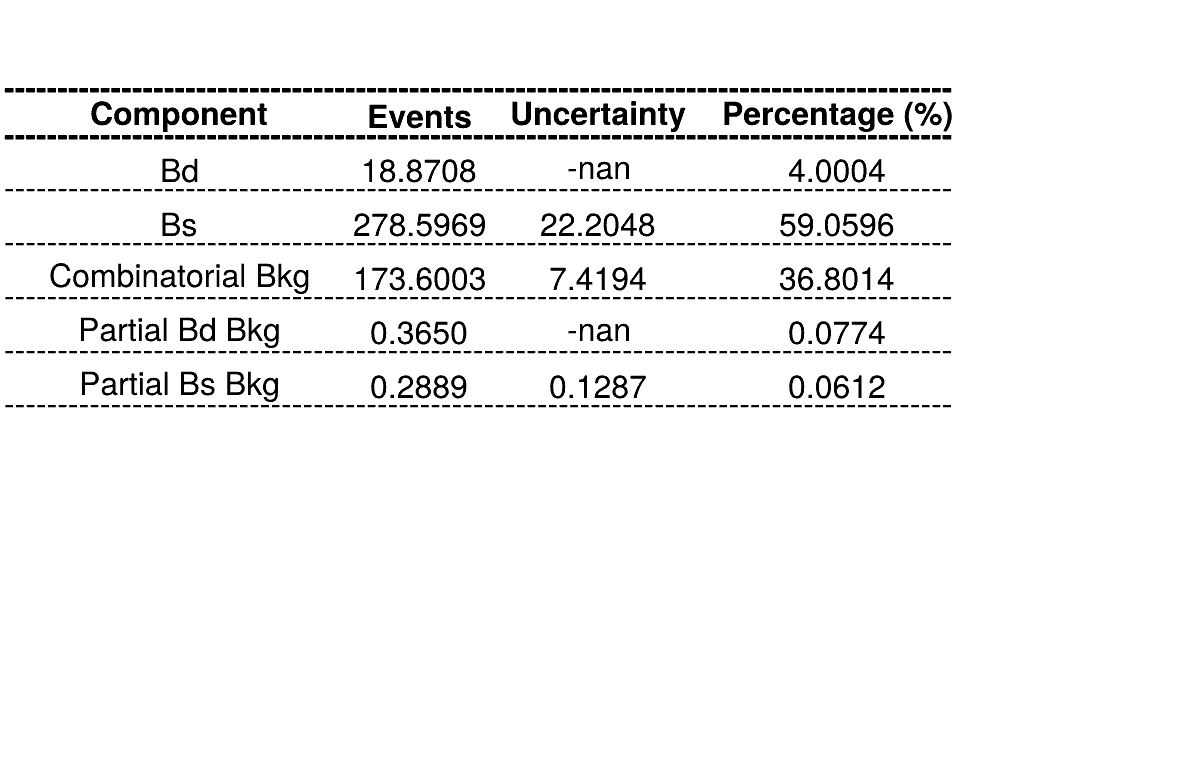
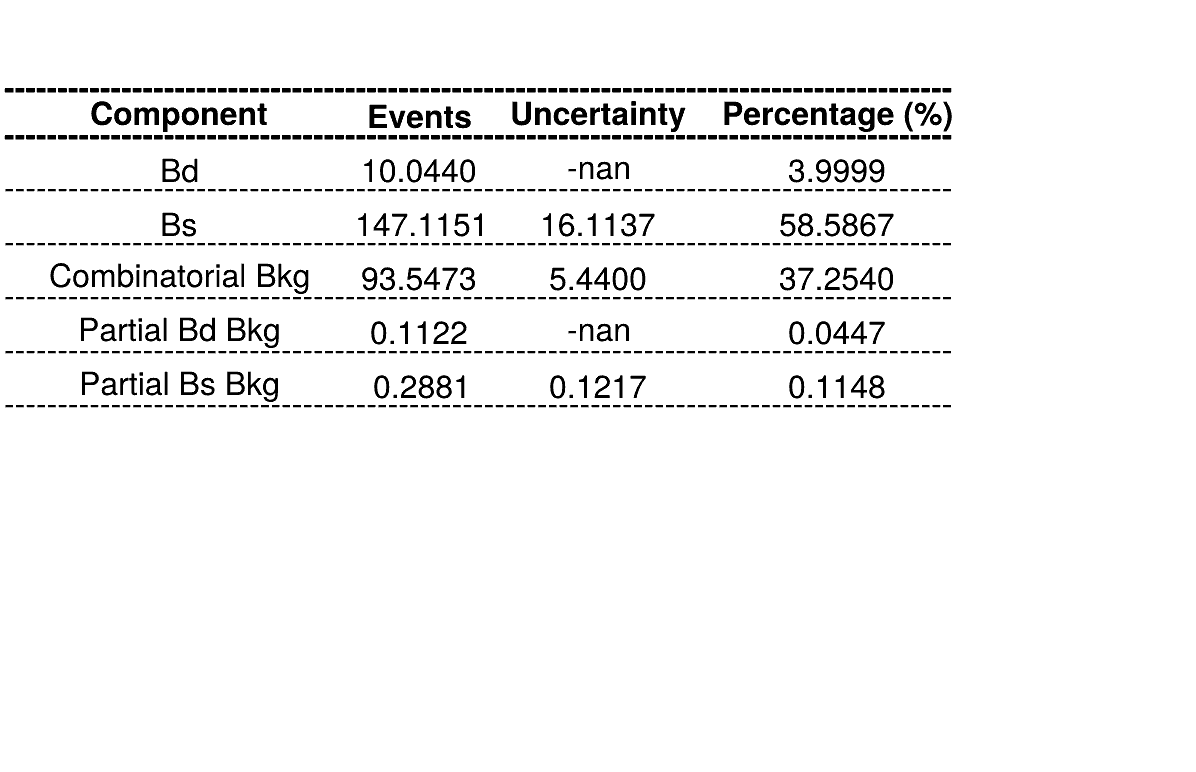
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
February 3rd, 2025
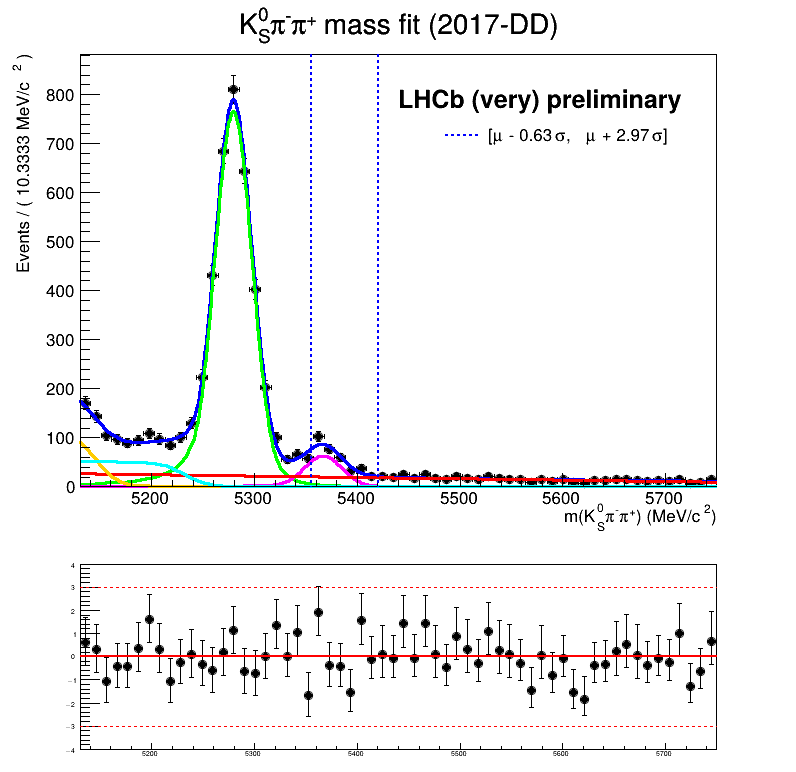
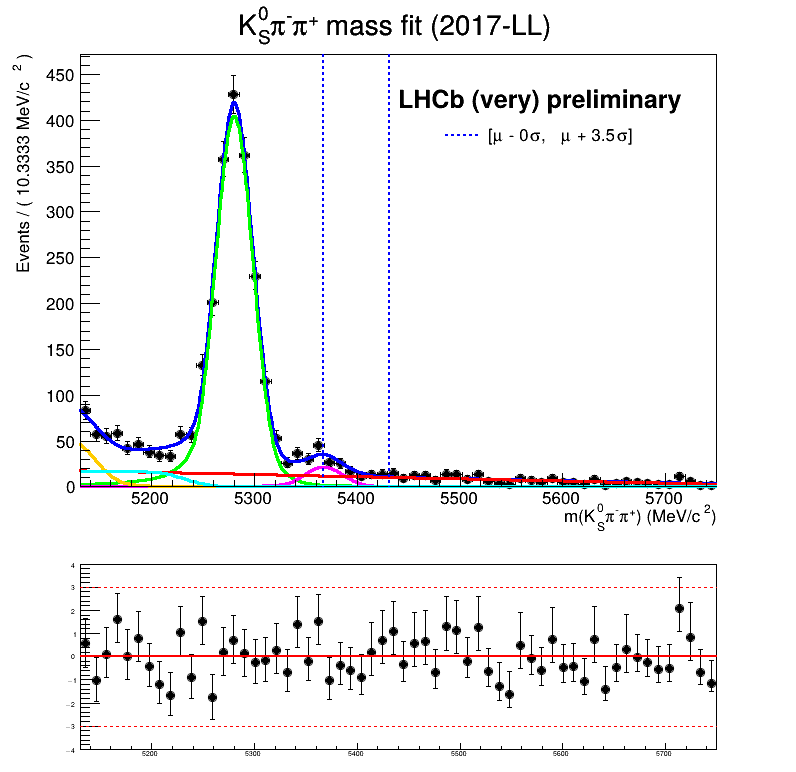
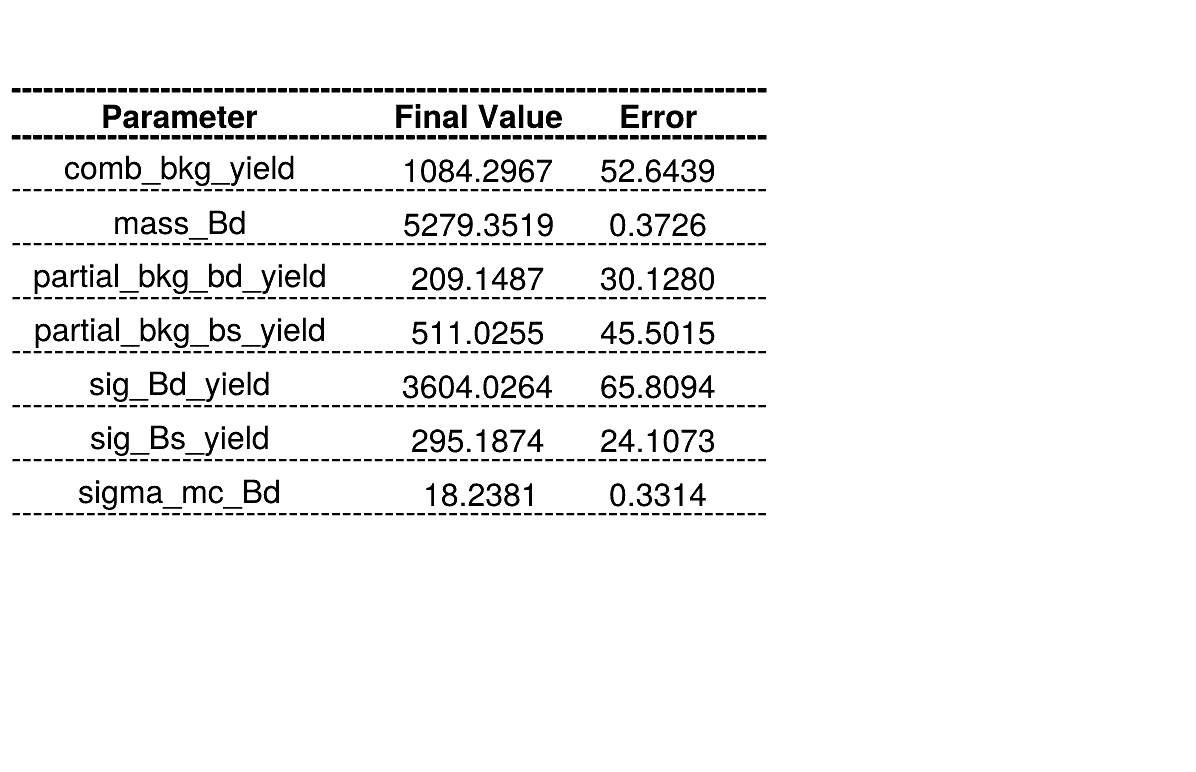
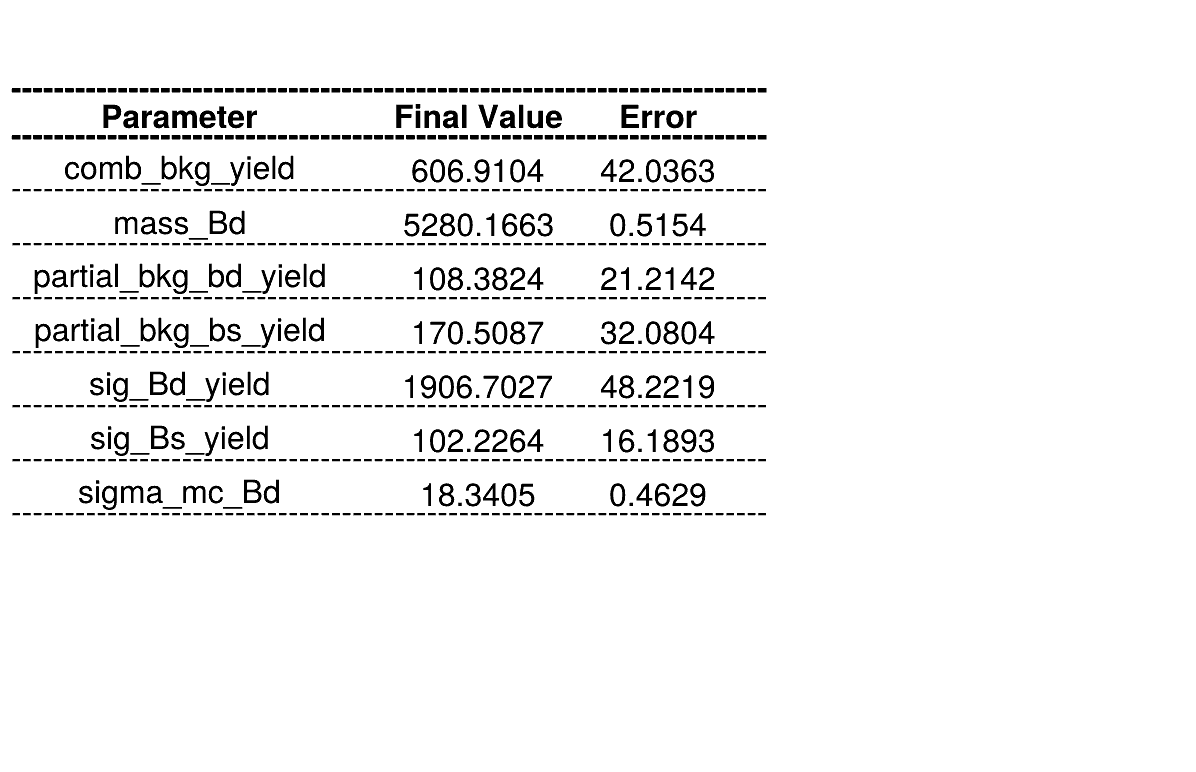
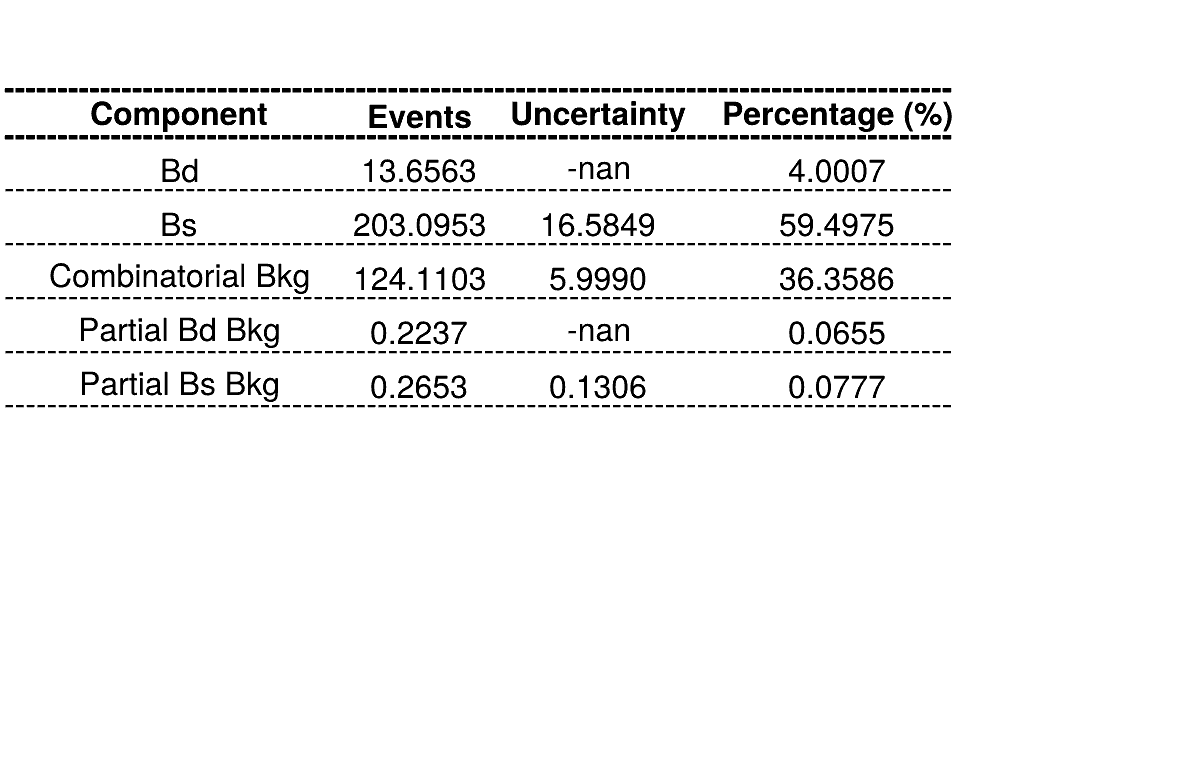
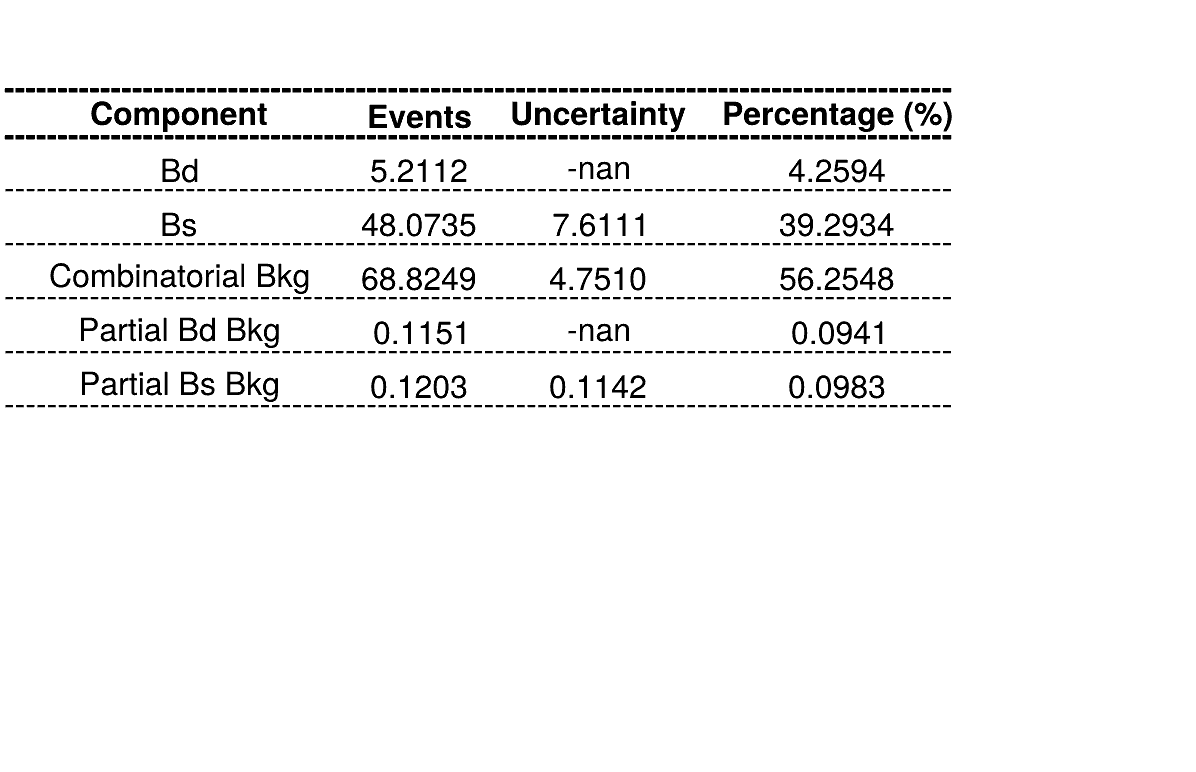
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
February 3rd, 2025
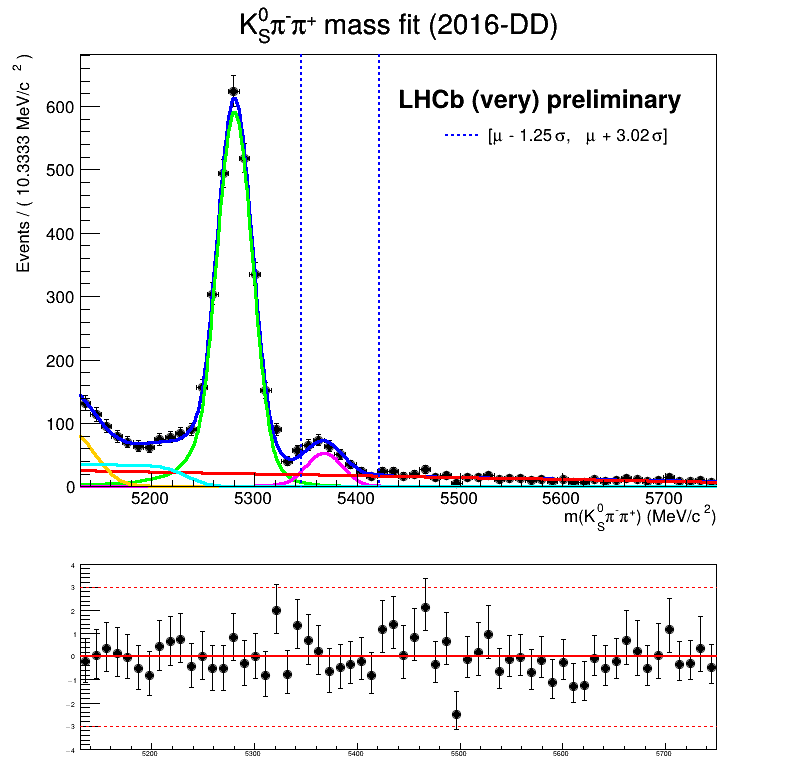
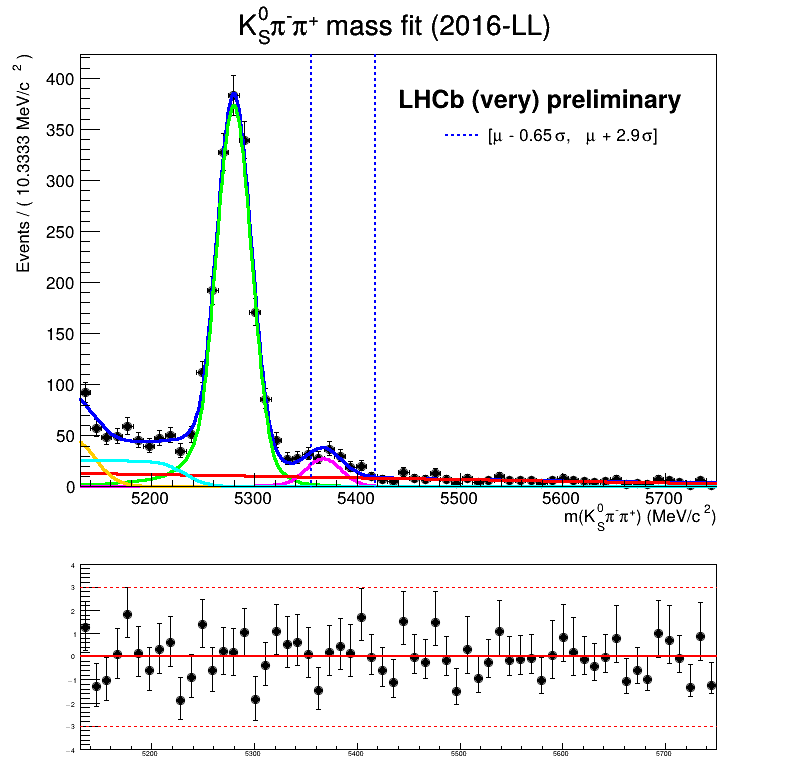
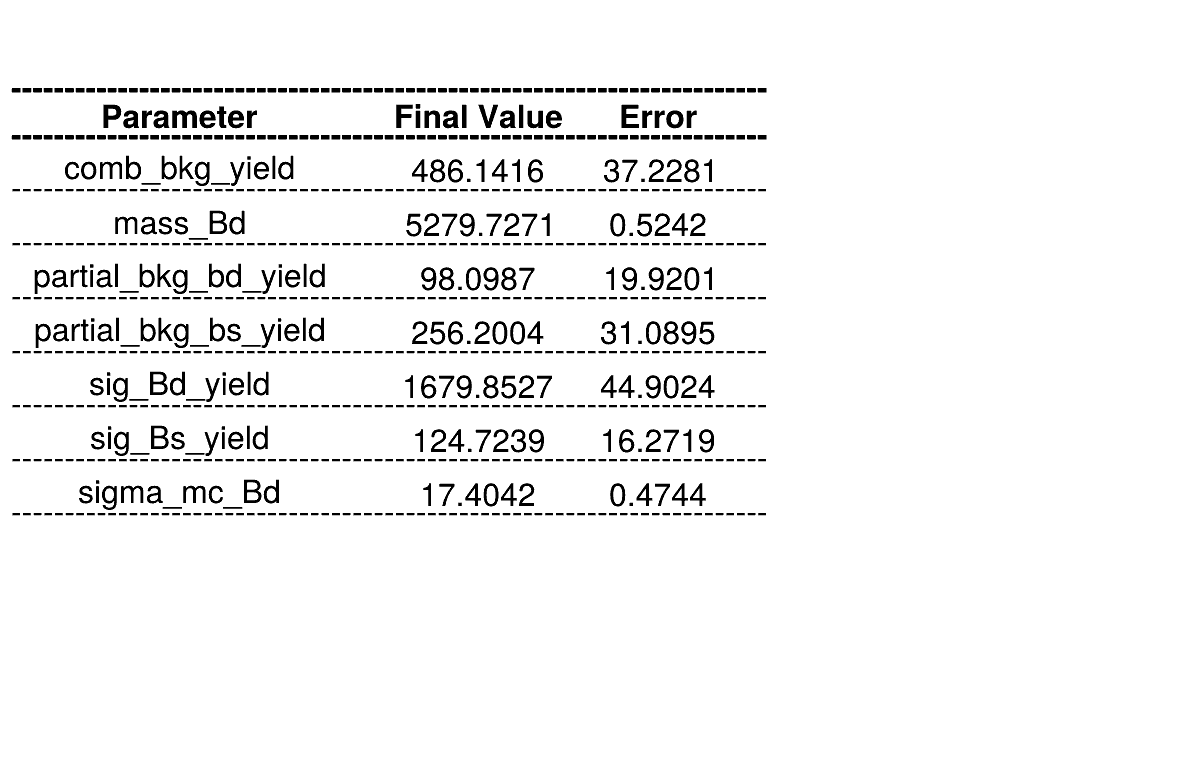
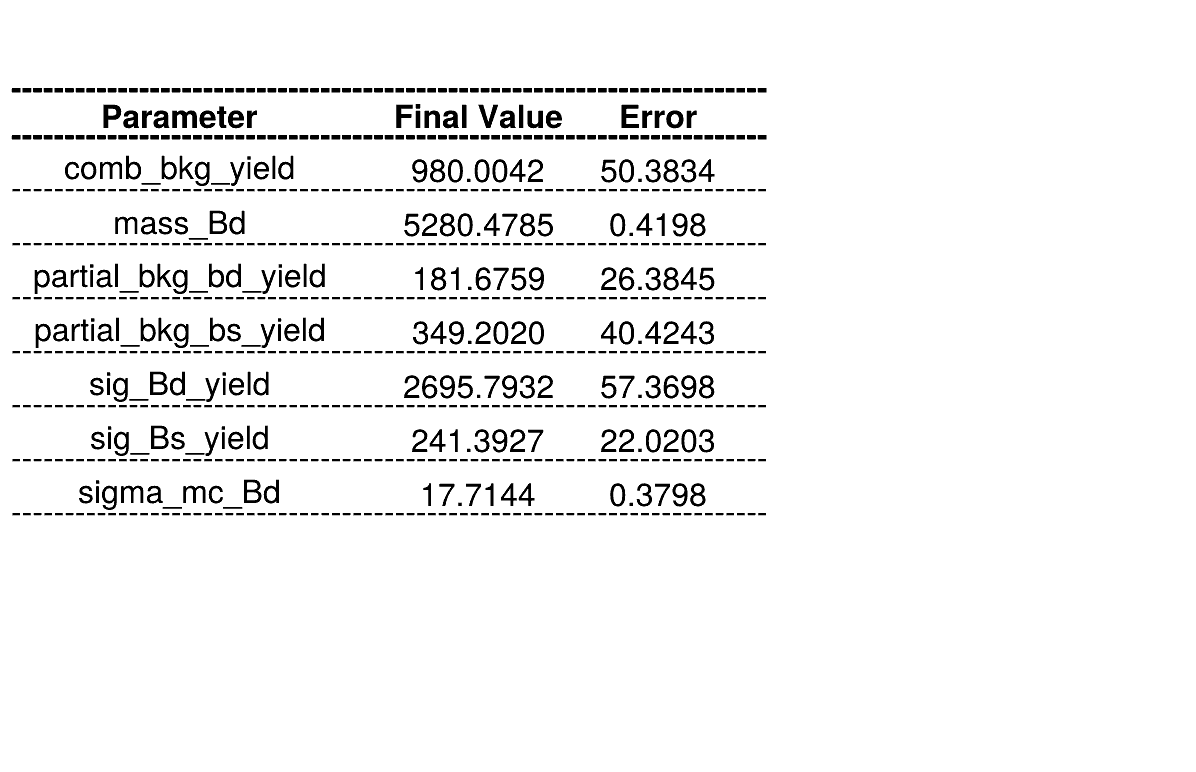
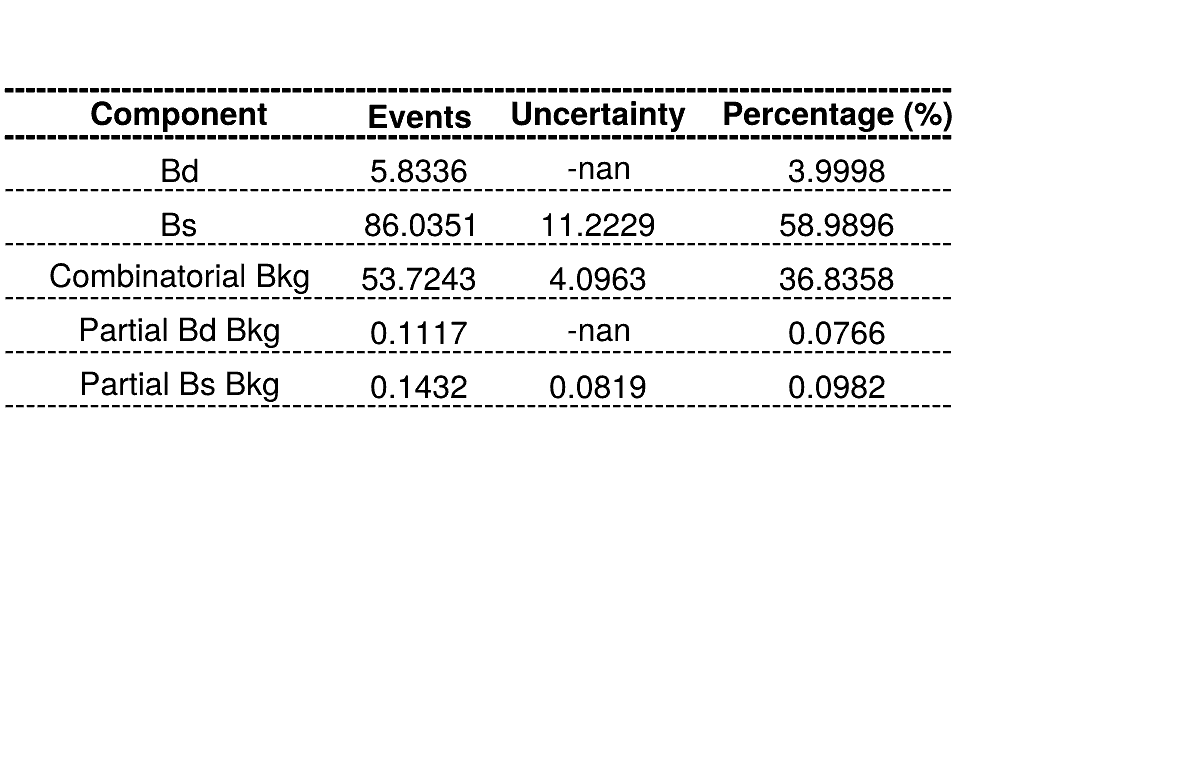
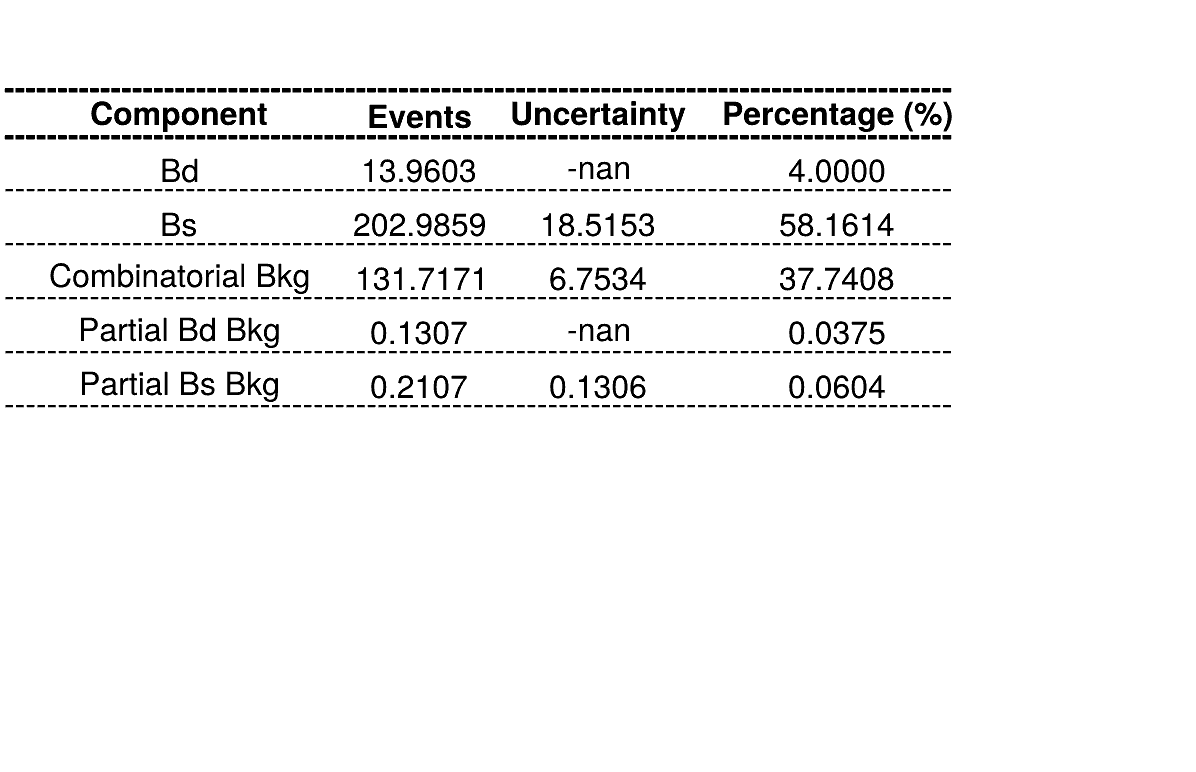
Homemade mass fit
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
February 3rd, 2025
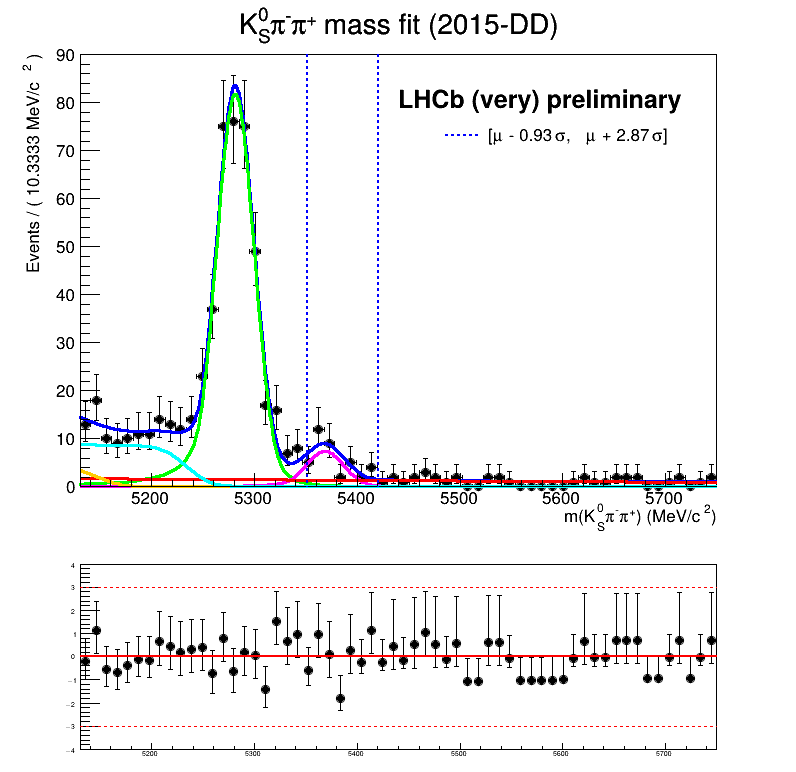

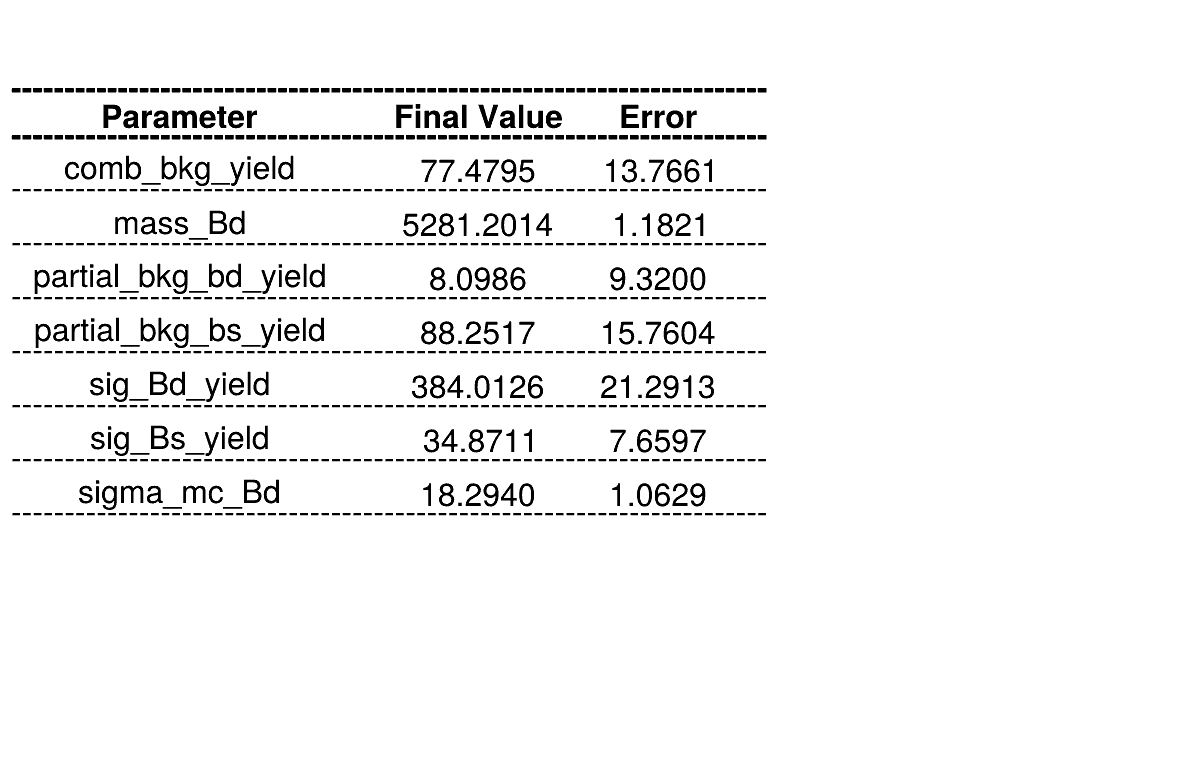

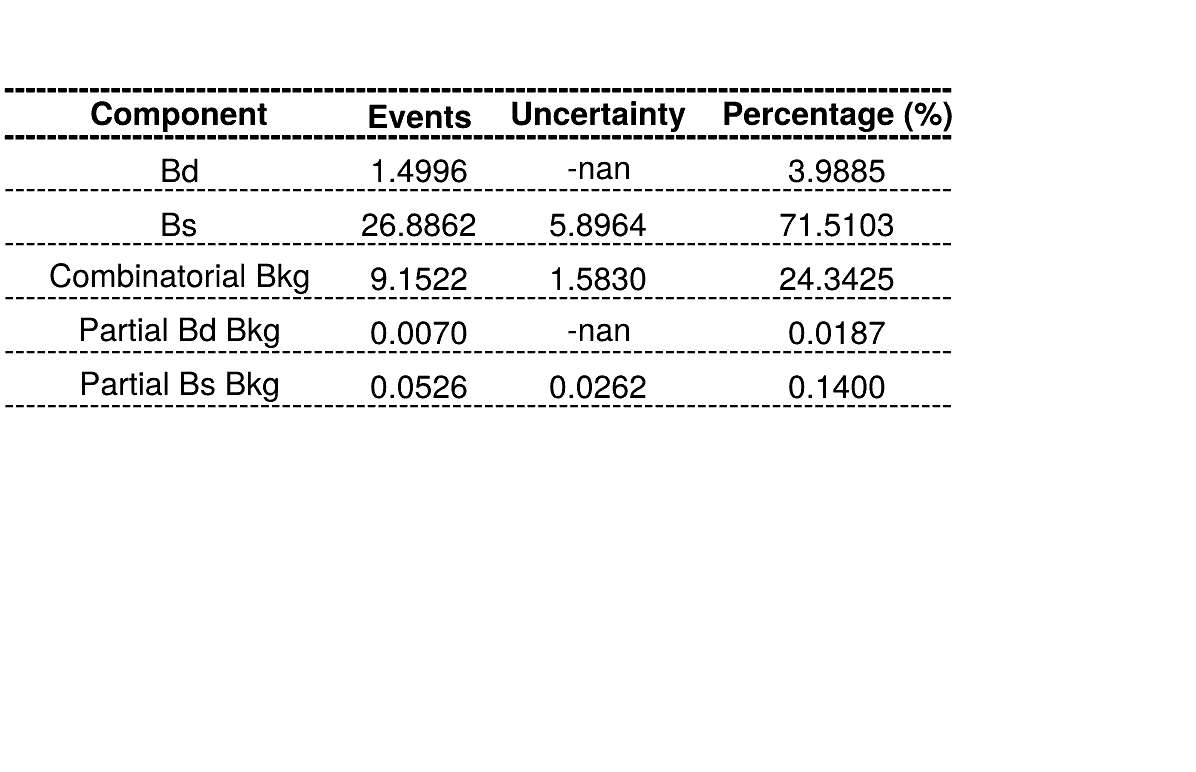

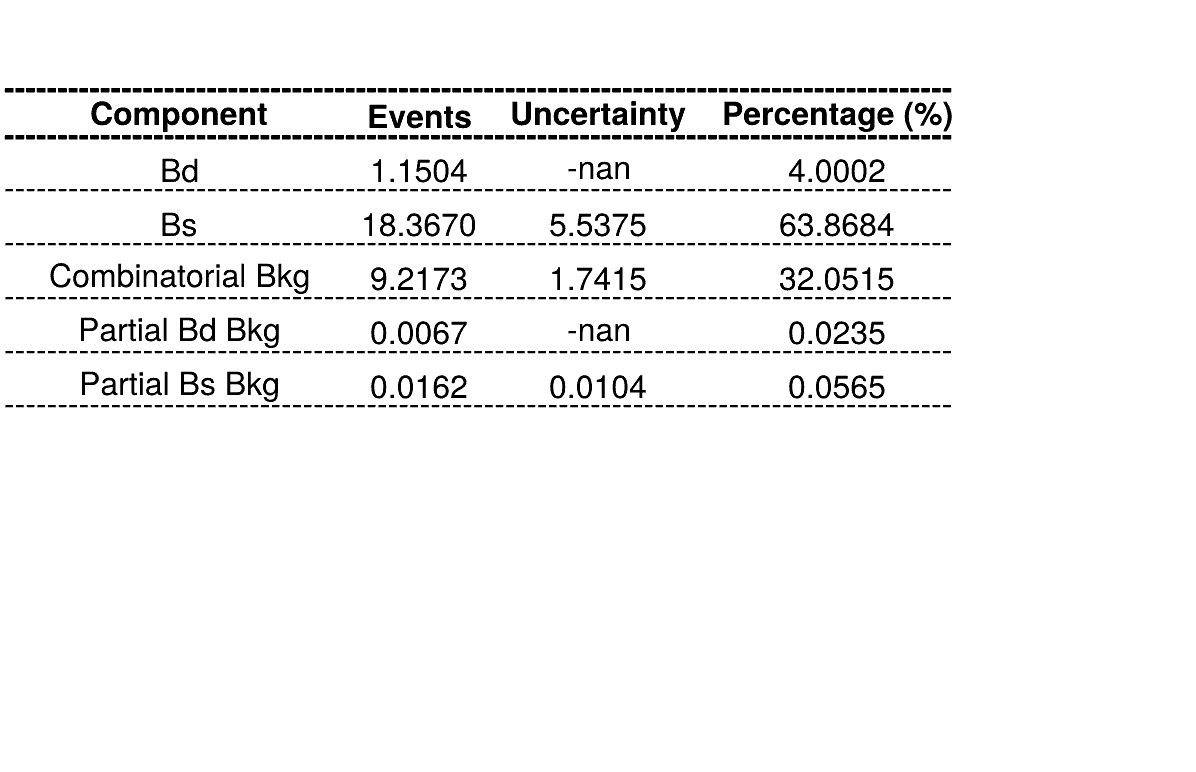
Combinatorial bkg.
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
Run 2 DD merged
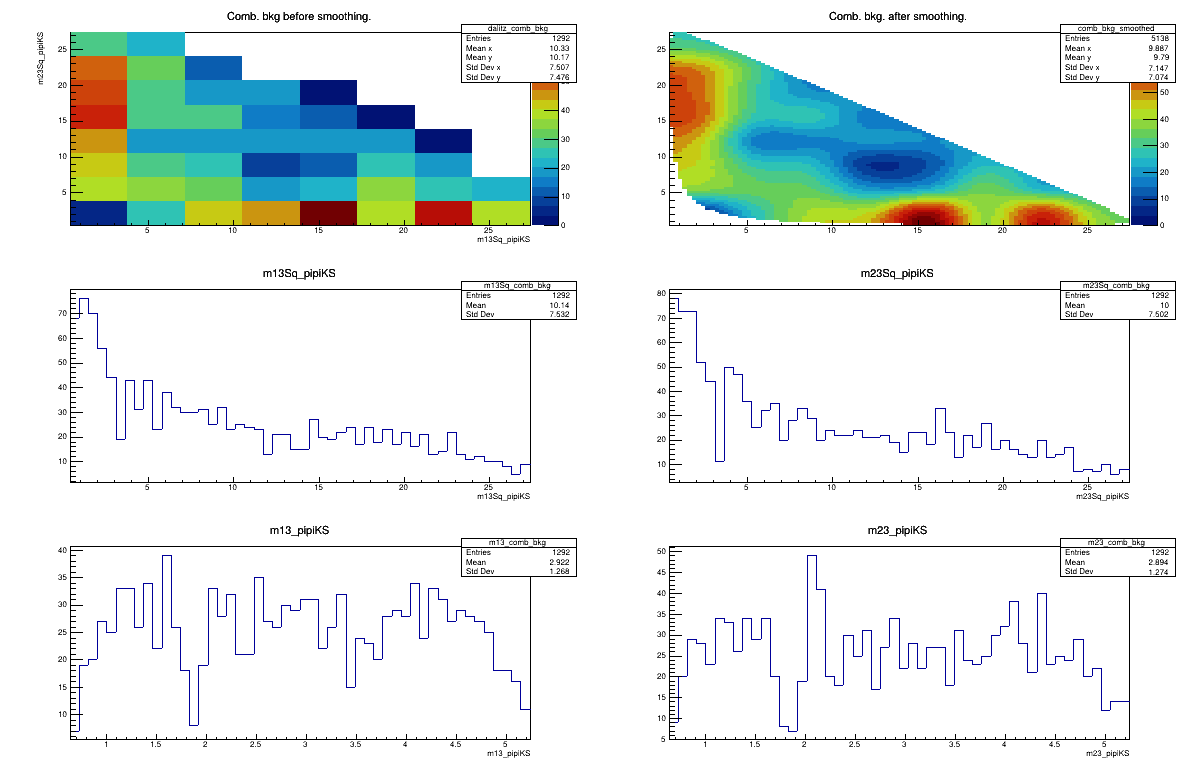
February 17th, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2018 DD
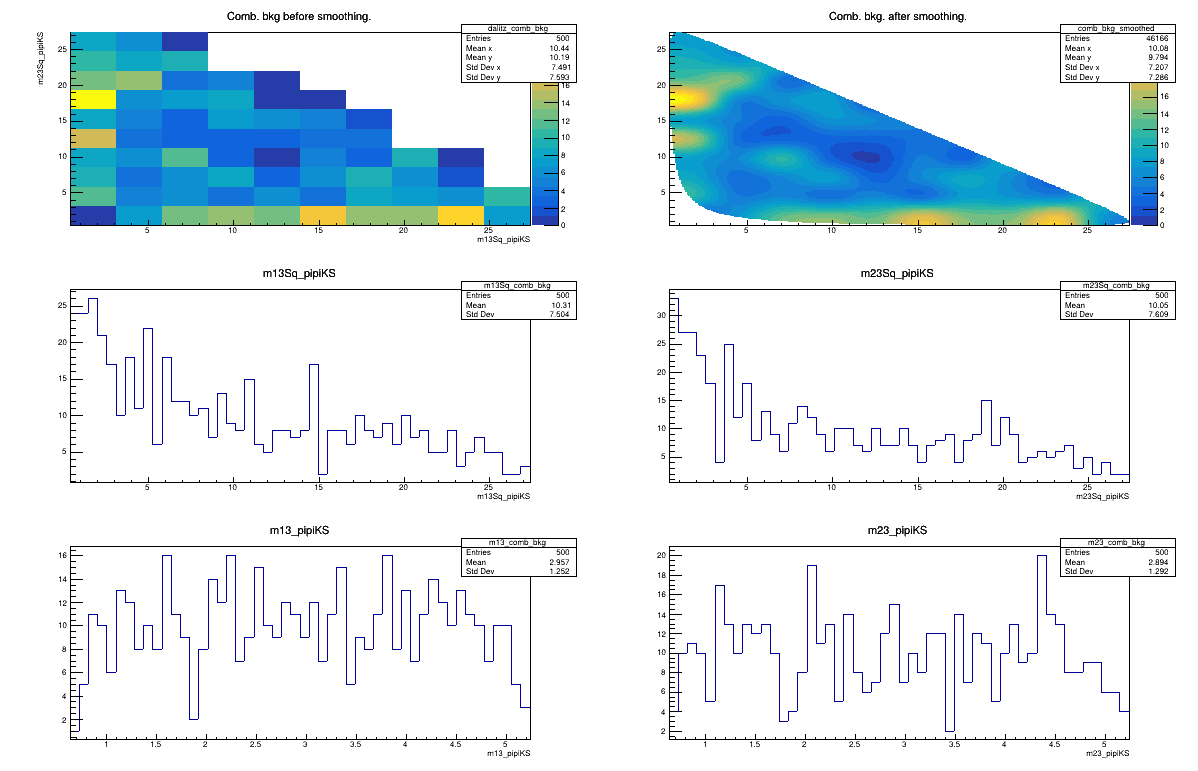
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2017 DD
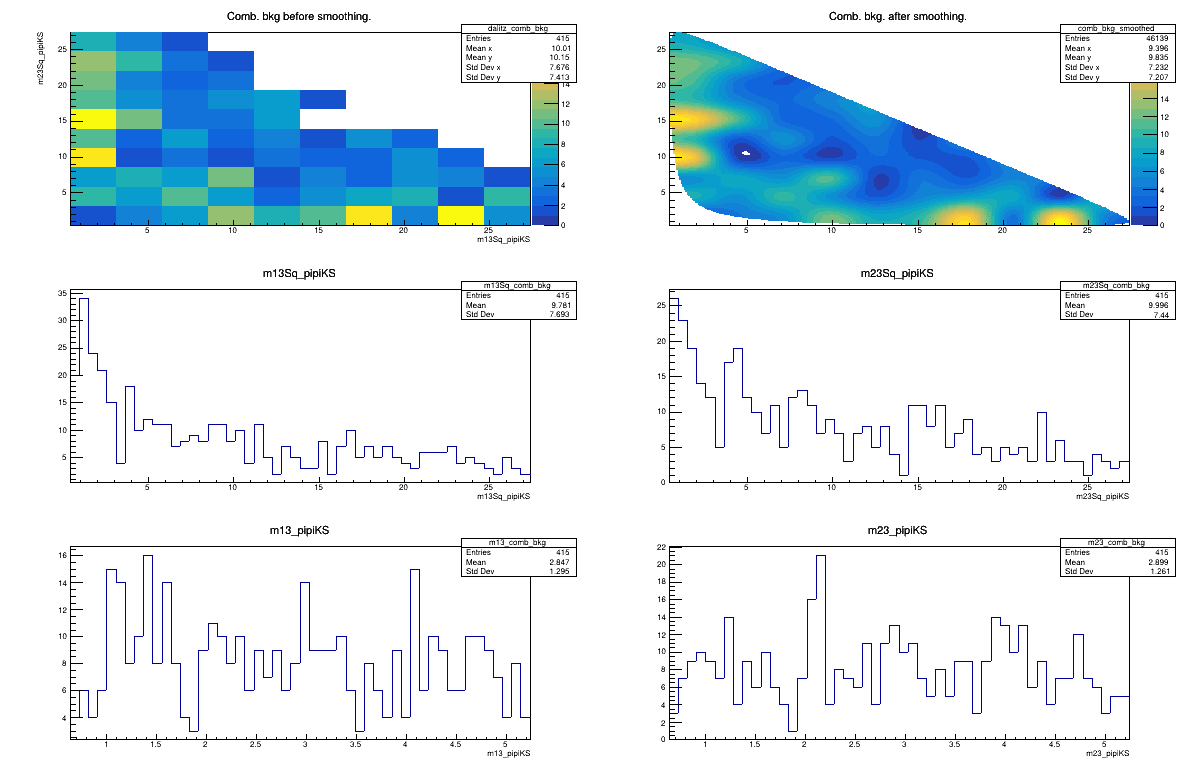
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2016 DD
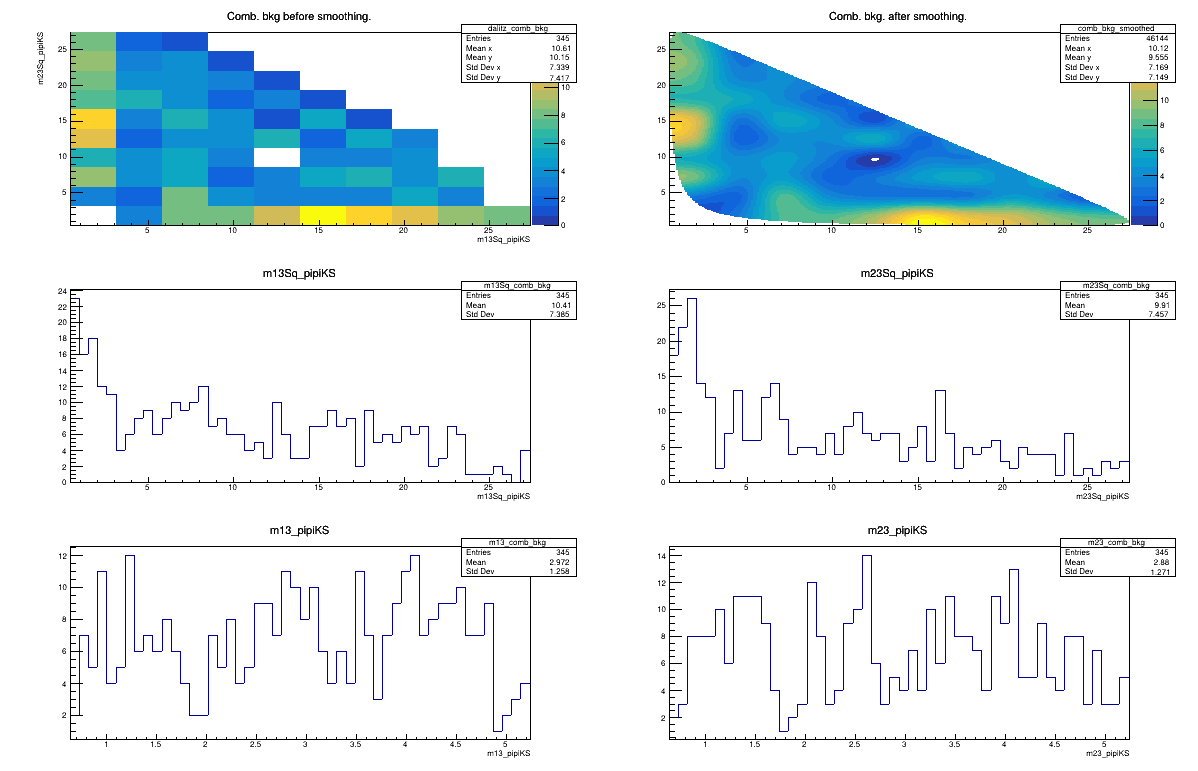
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2015 DD
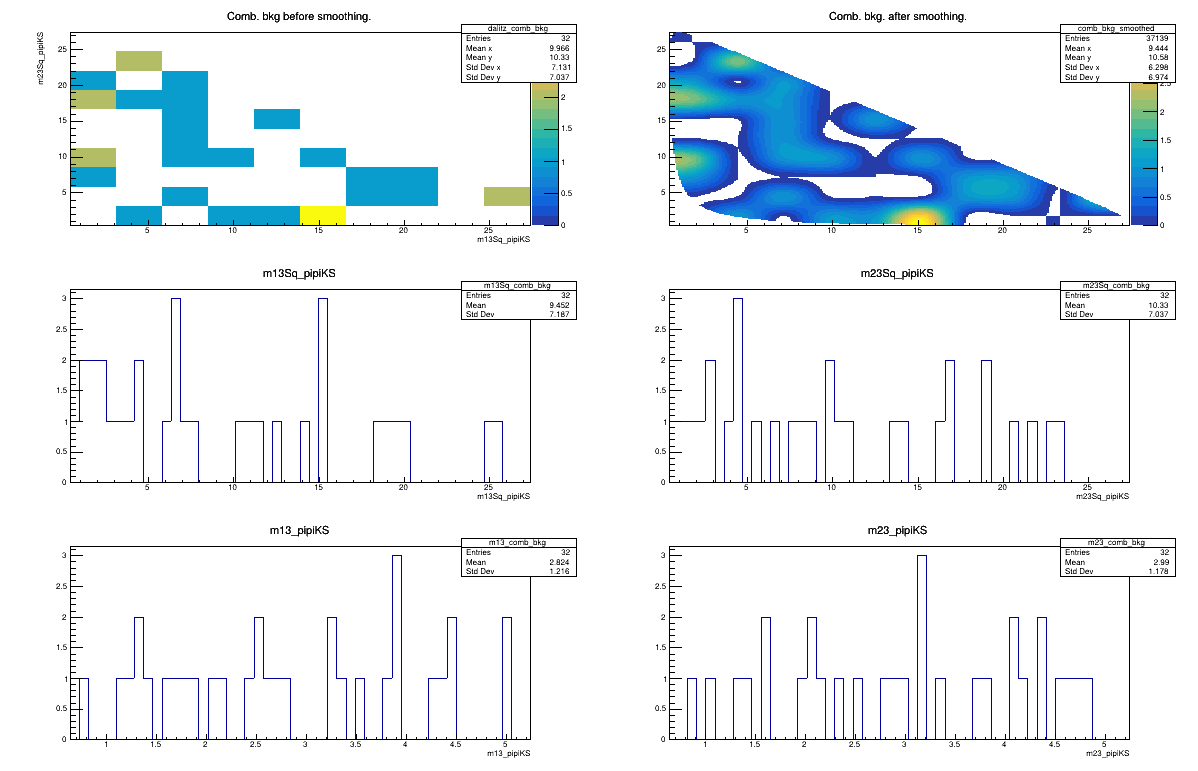
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
Run 2 LL merged
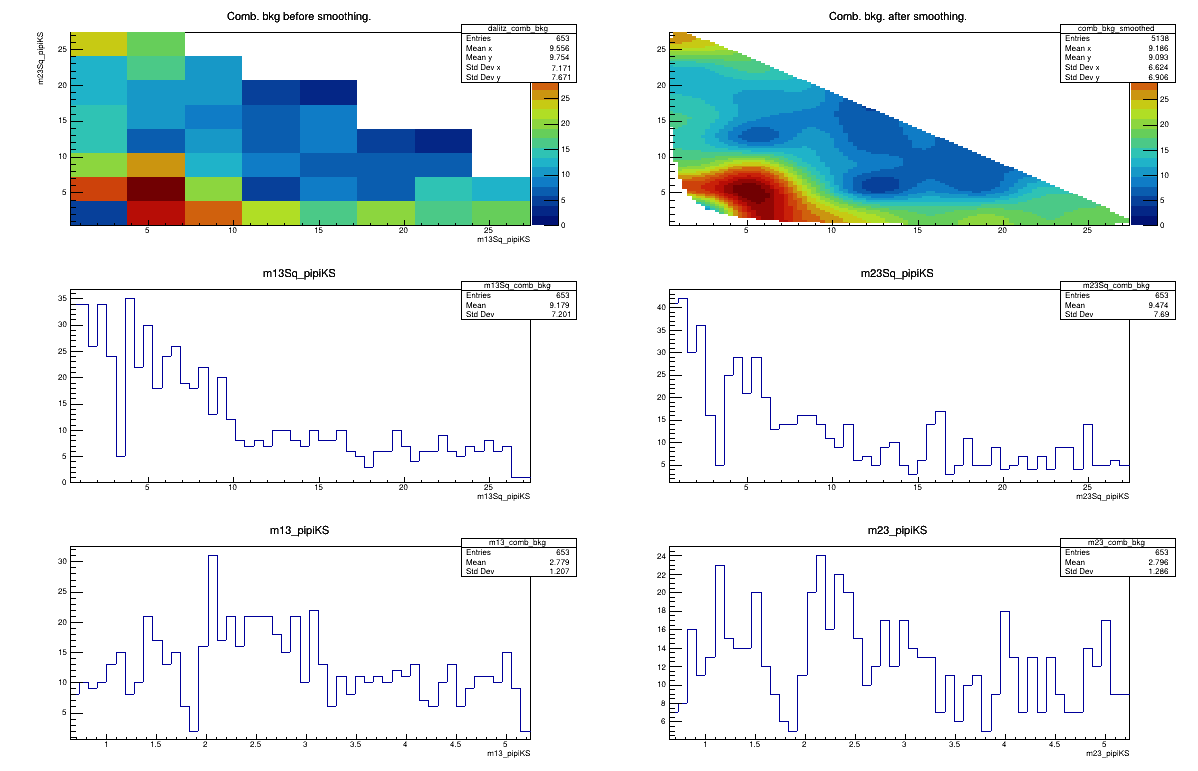
February 17th, 2025
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2018 LL
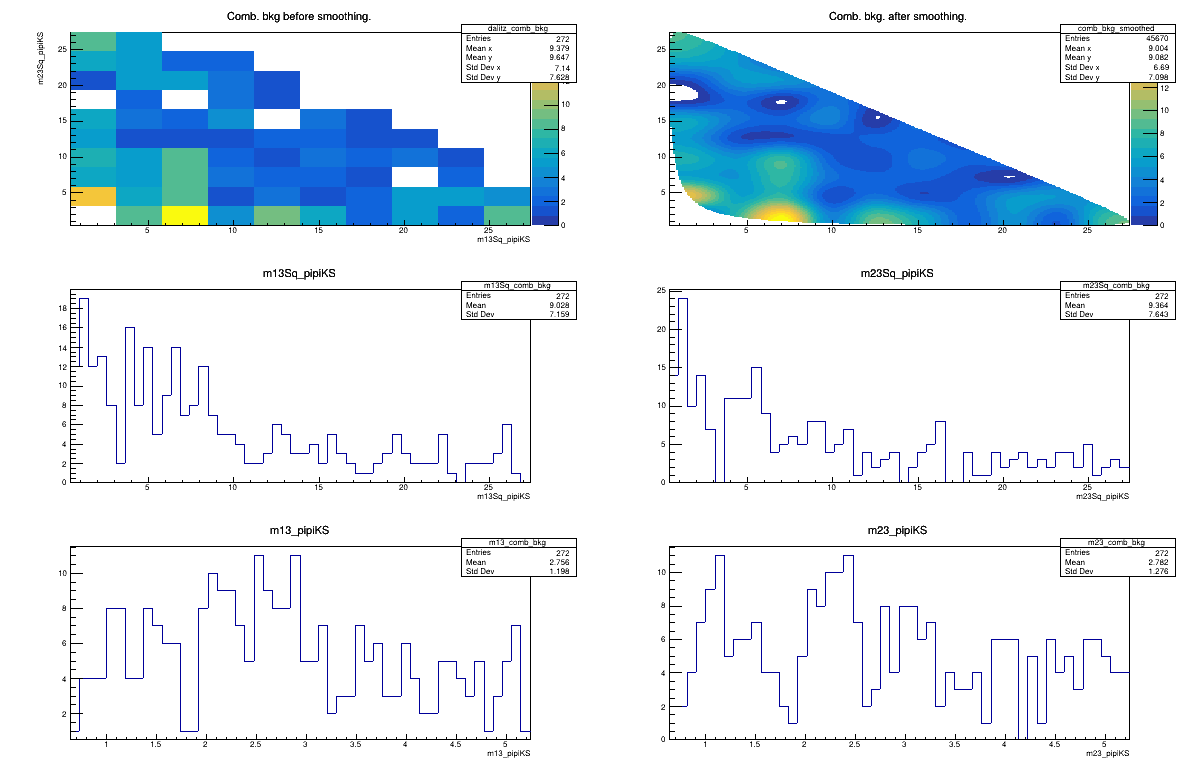
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2017 LL
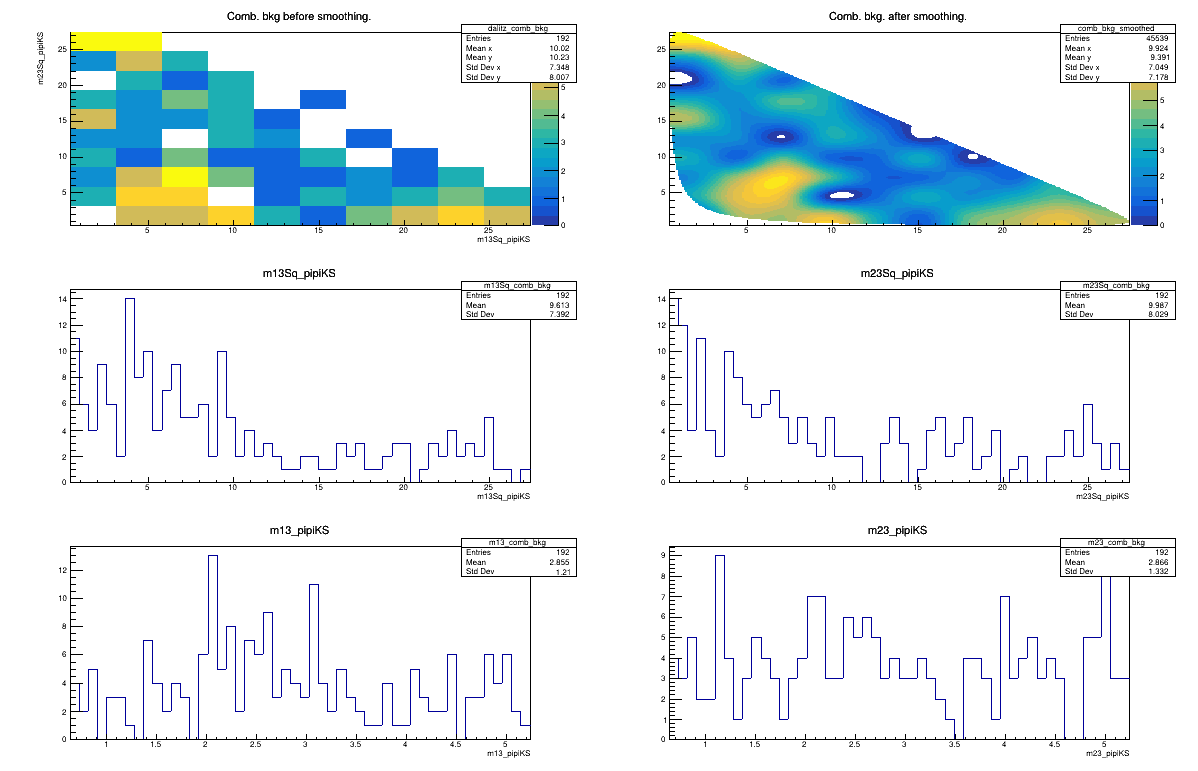
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2016 LL
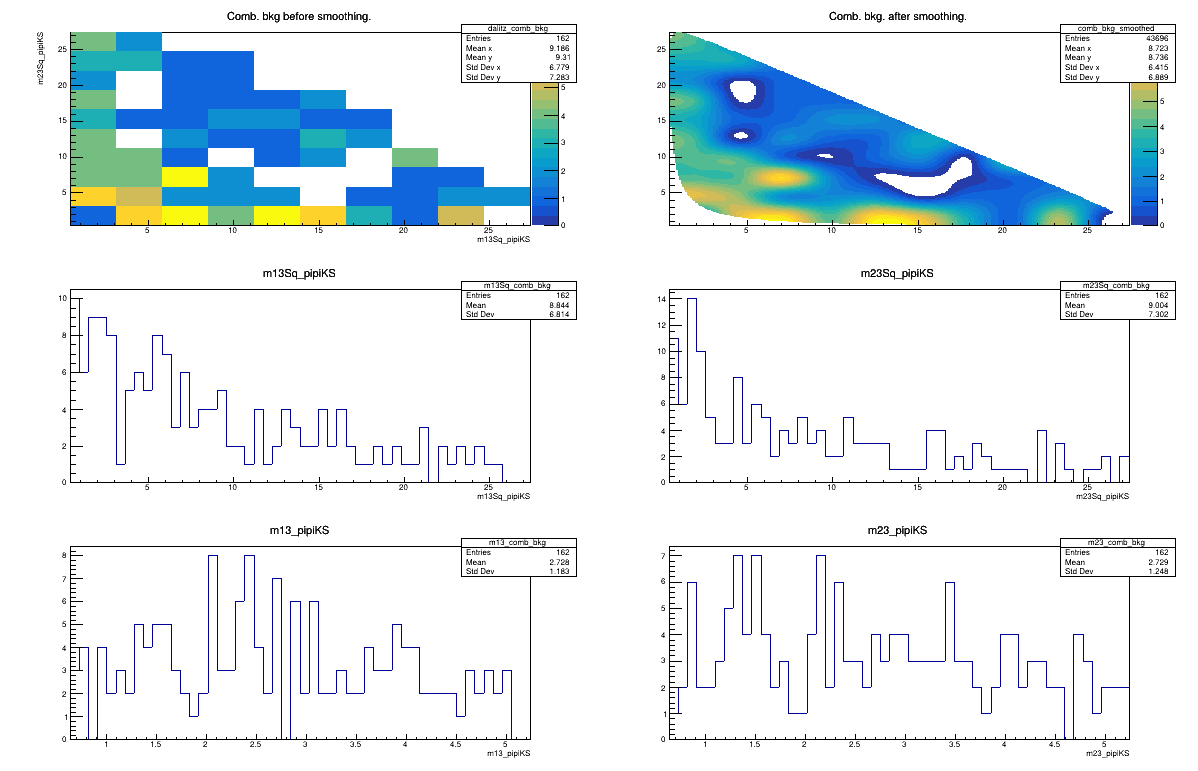
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2015 LL
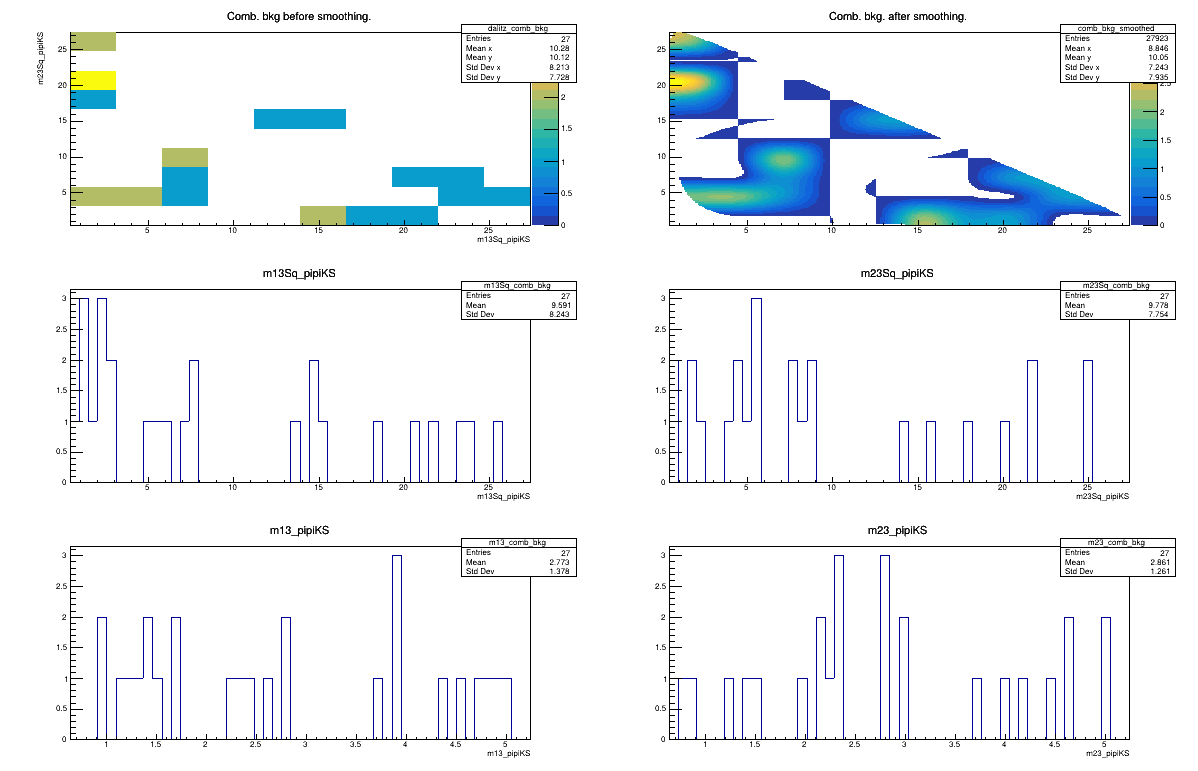
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
Run 2 DD + LL categories merged
February 19th, 2025
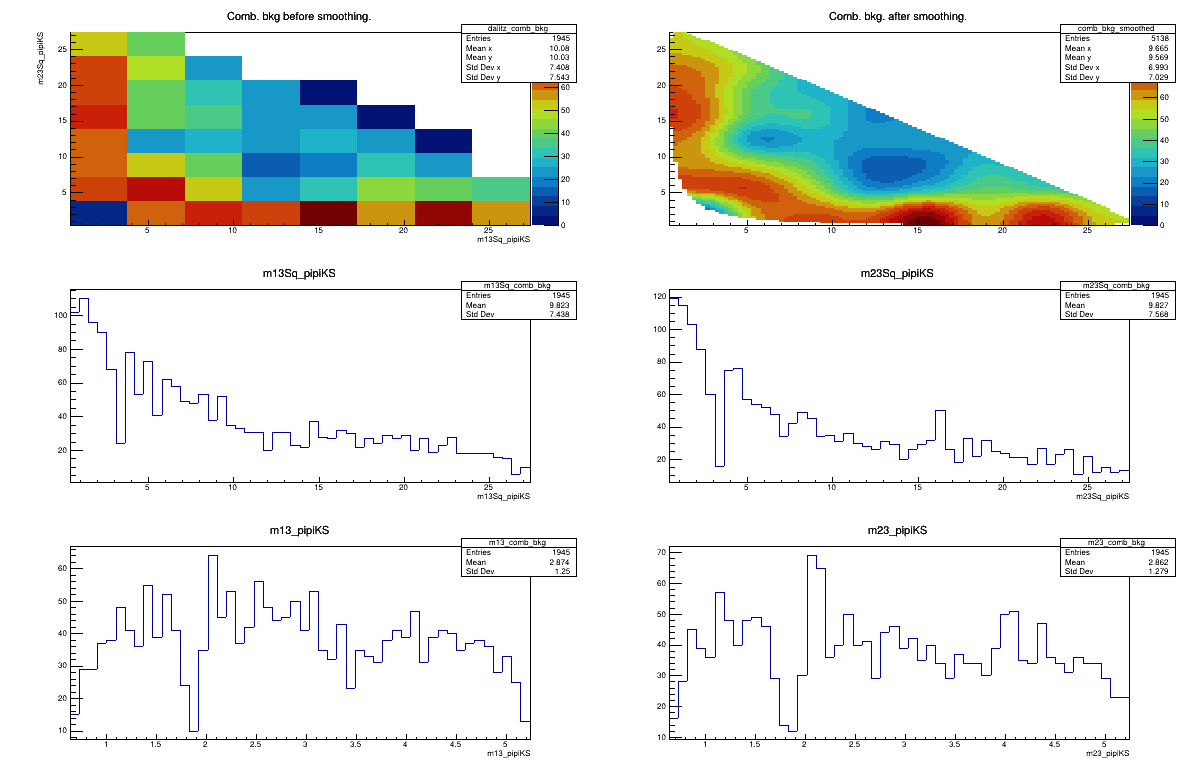
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2018 DD + LL categories merged
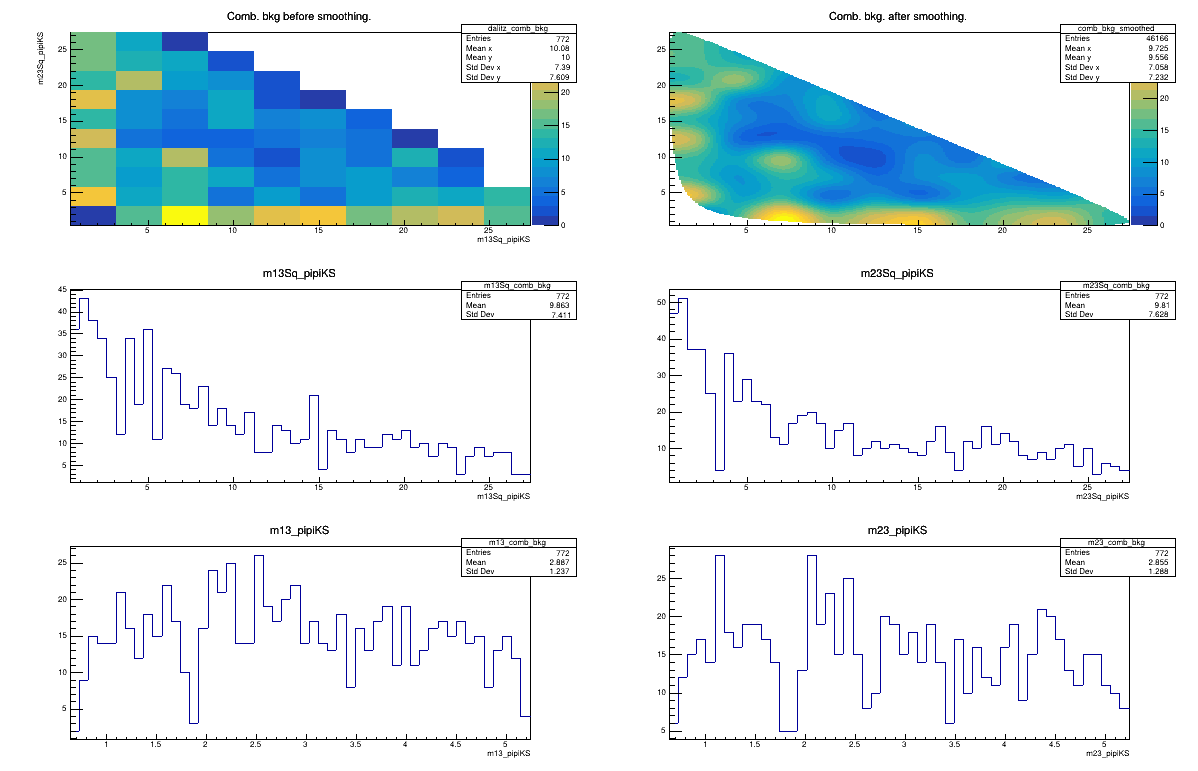
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2017 DD + LL categories merged
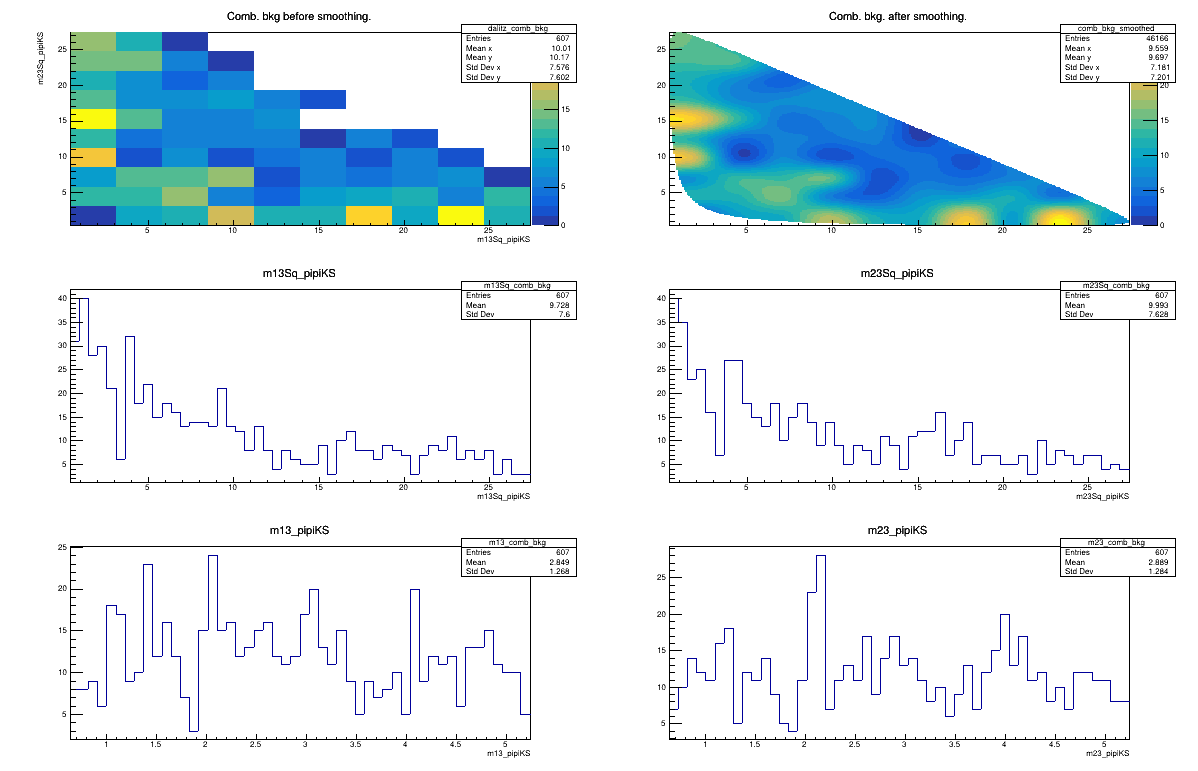
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2016 DD + LL categories merged
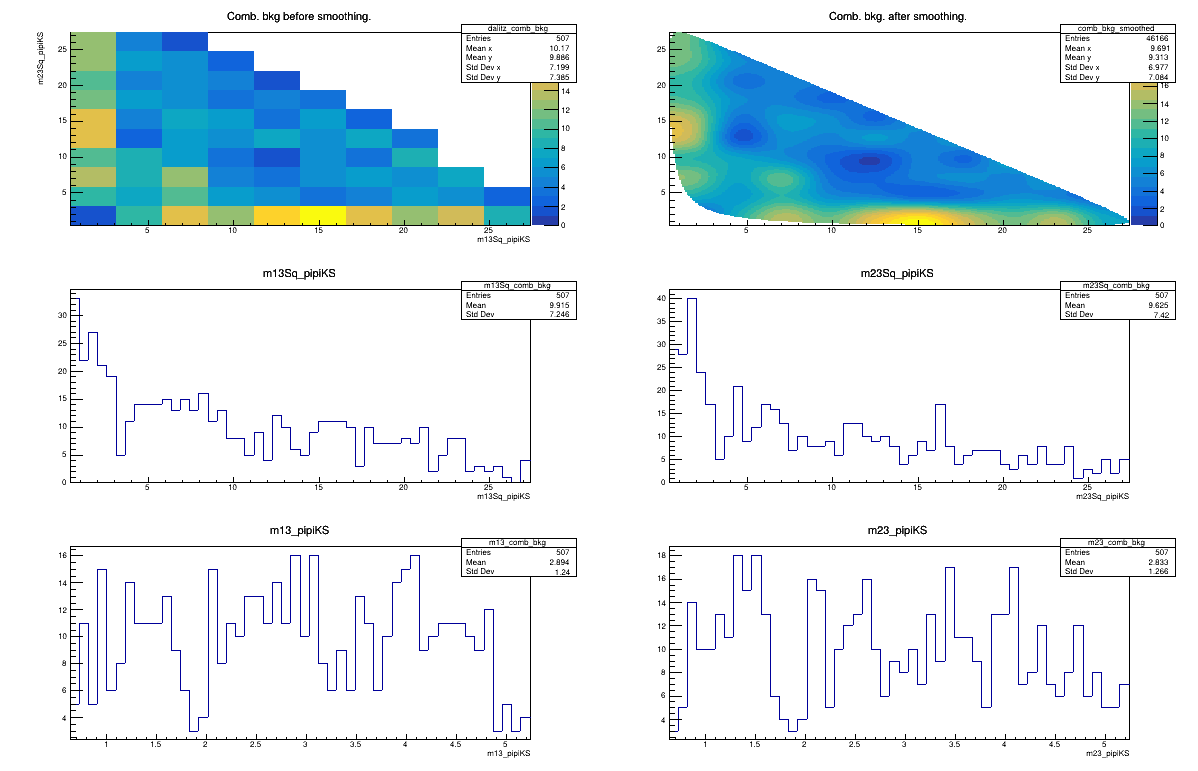
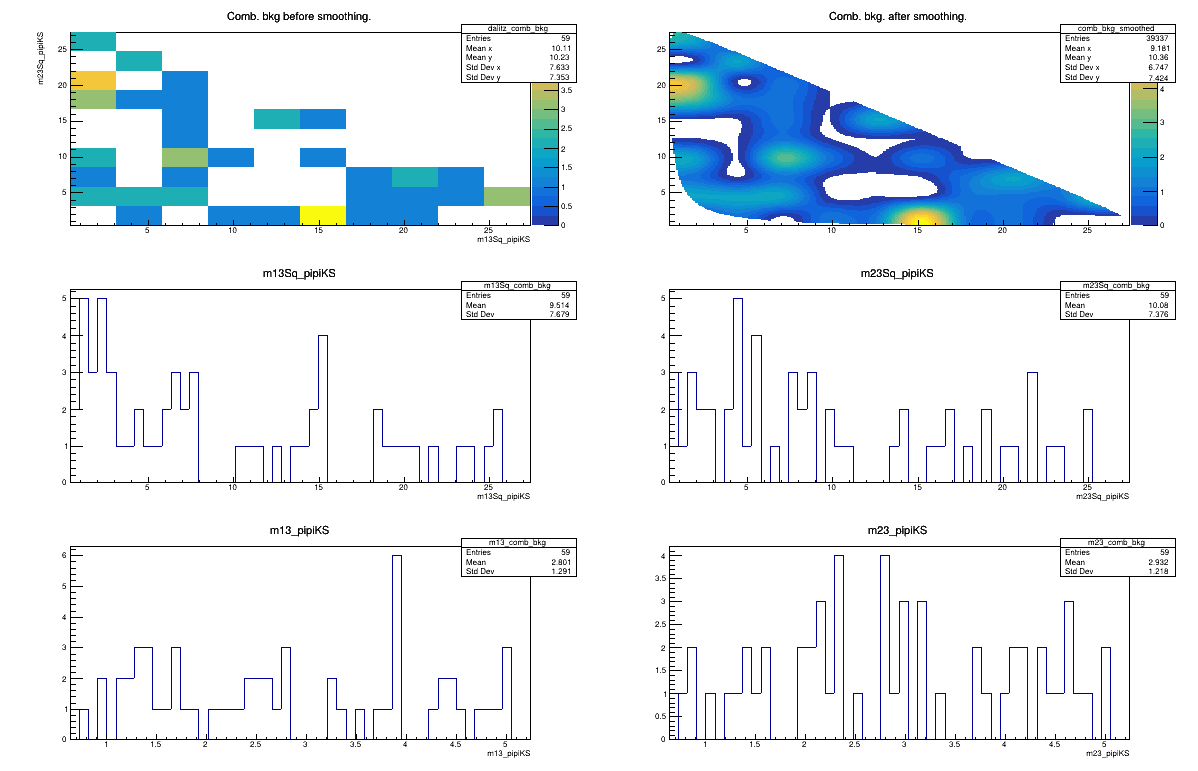
Sebastian Ordoñez-Soto
AmAn of the \(B_{s}^{0}\rightarrow K_{S}^{0} \pi^{+}\pi^{-}\) decay
Combinatorial background model
February 3rd, 2025
2015 DD + LL categories merged
Motivation
S. Ordonez-Soto
December 16th, 2024
Introduction
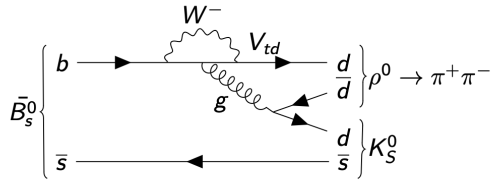
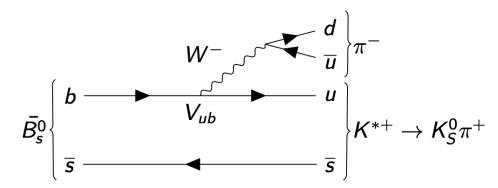
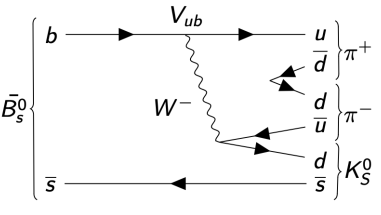
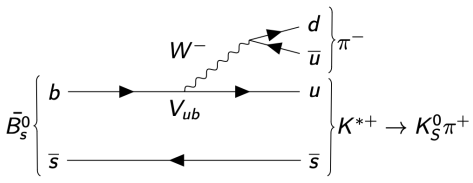
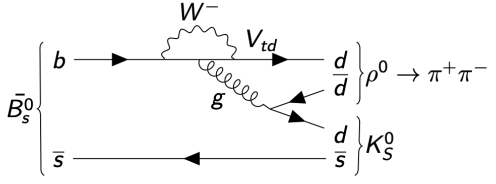
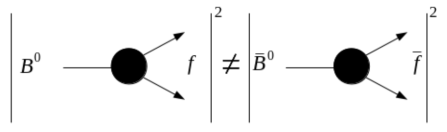
- The TI AmAn of \(B_{s}^{0}\rightarrow K_{S}^{0}\pi^{+}\pi^{-}\) aims to: Search for CP violation in decay in quasi-two-body states such as \(B_{s}\rightarrow K^{*-}\pi^{+}\) or \(B_{s}\rightarrow K_{S}^{0}\rho^{0}\)
- CP asymmetry parameter:
- \(B_{(s)}^{0}\rightarrow K_{S}^{0}hh'\) decays mostly proceed through quasi-two-body intermediate states
- Resonant states can be either flavour-specific states or CP eigenstates
- Excellent laboratories to study CP violation in decay and in interference between decay and mixing
Dalitz plot technique
S. Ordonez-Soto
December 16th, 2024
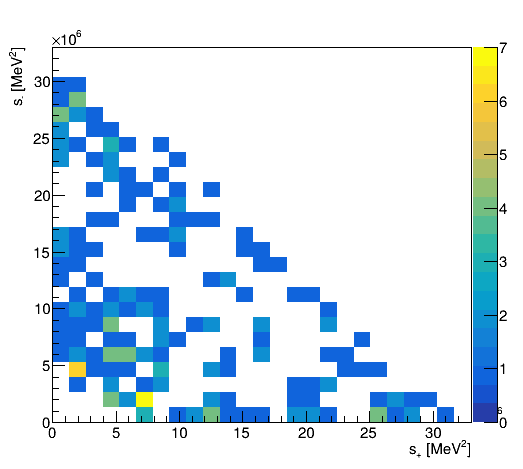
Dalitz plot analysis of \(B_{s}^{0}\rightarrow K_{S}^{0}\pi^{+}\pi^{-}\)
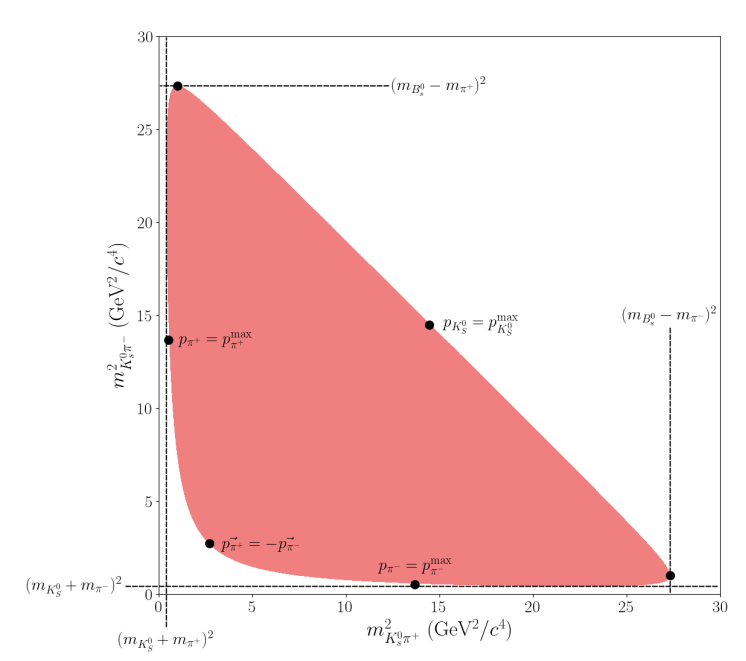
\(B_{s}\rightarrow K_{S}^{0}\pi^{-}\pi^{+}\) phase space
Using the Dalitz plot variables to describe the B0→K0π+π−B^0 \to K^0 \pi^+ \pi^-Bs2KSpipi decay, the partial decay rate is given by:
To describe the kinematic and dynamics of 3-body decays, the analysis employs the Dalitz plot formalism.
S. Ordonez-Soto
December 16th, 2024
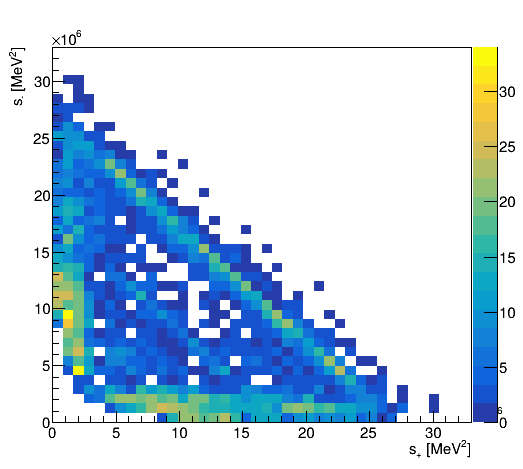
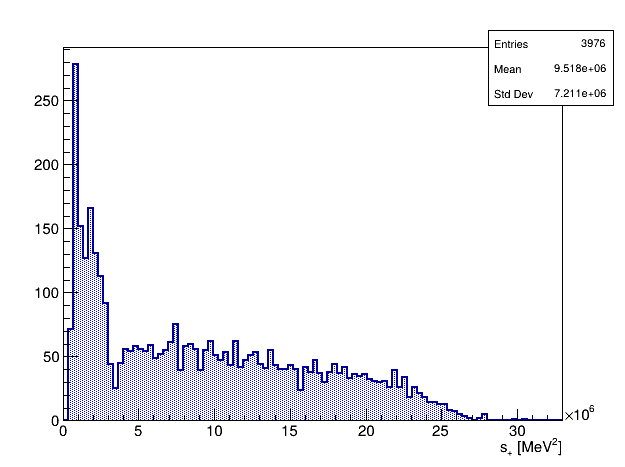
Dalitz plot analysis of \(B_{s}^{0}\rightarrow K_{S}^{0}\pi^{+}\pi^{-}\)
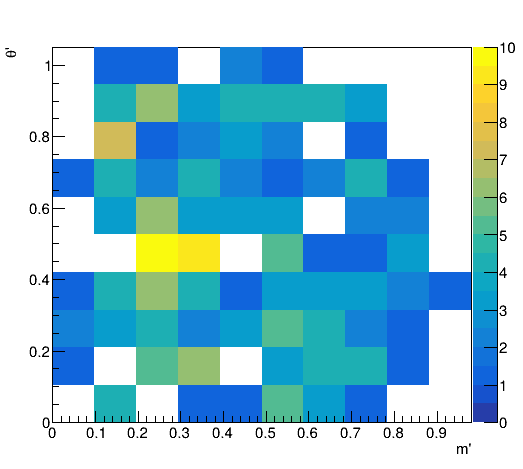
Dalitz plot technique
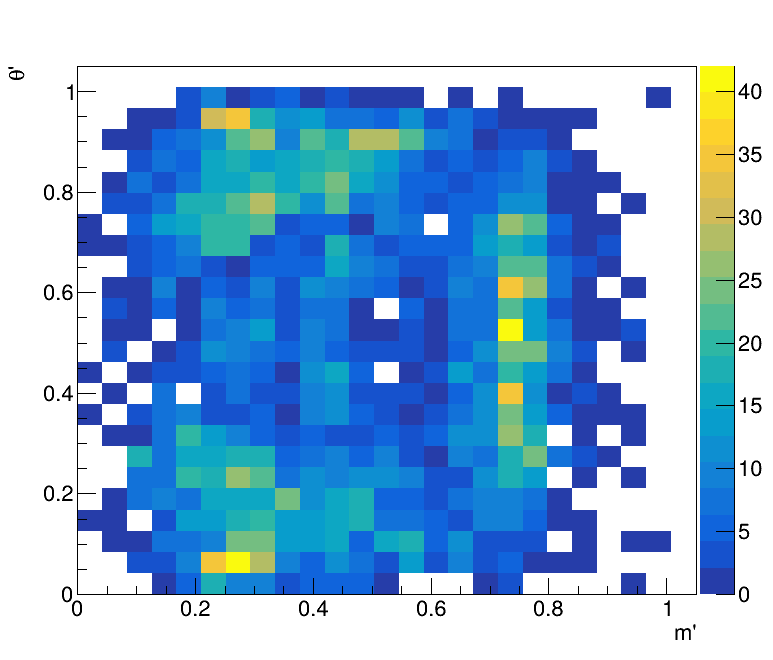
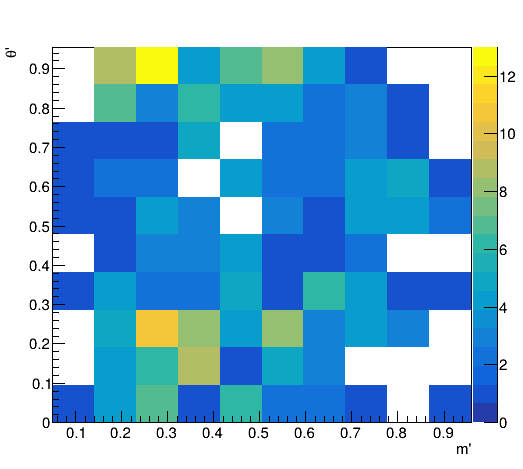
Square Dalitz plot
The boundaries of the B0→K0π+π−B^0 \to K^0 \pi^+ \pi^-DP are crucial, as most interference effects between amplitudes involving intermediate resonances occur in these regions.
S. Ordonez-Soto
December 16th, 2024
After integration over time:
Finally, with \(r_{\text{tag}}=0\) the Dalitz signal PDF becomes simply:
Dalitz plot signal PDF
Dalitz plot analysis of \(B_{s}^{0}\rightarrow K_{S}^{0}\pi^{+}\pi^{-}\)
The time and DP dependent signal PDF accounting for the transitions \(\mathcal{A}_{f} = \langle f|H_{\Delta F=1}|B_{s}^{0}\rangle\) and \(\bar{\mathcal{A}}_{f} = \langle f|H_{\Delta F=1}|\bar{B}_{s}^{0}\rangle\) reads:
Isobar model
S. Ordonez-Soto
December 16th, 2024
The total amplitude is approximated as a coherent sum of terms:
The spin-dependent dynamical function is rewritten as:
Dalitz plot analysis of \(B_{s}^{0}\rightarrow K_{S}^{0}\pi^{+}\pi^{-}\)
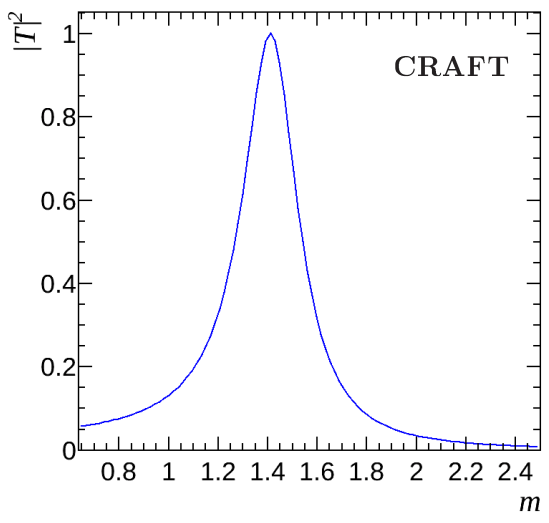
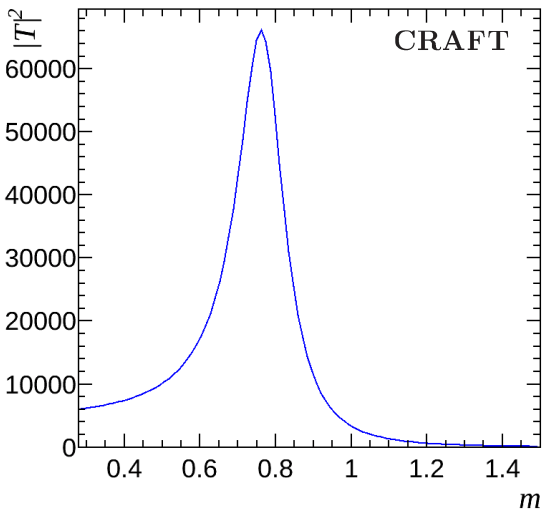
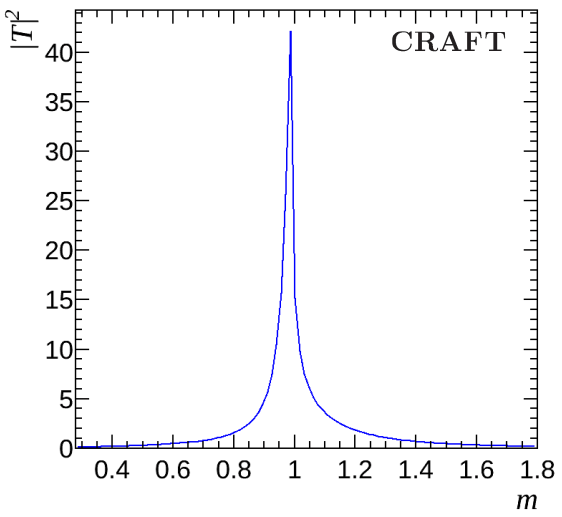
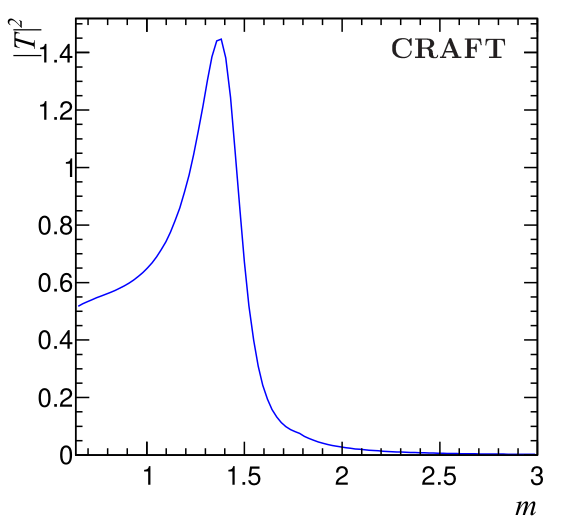
RBW
GS
Flatté
LASS
Total Dalitz plot PDF
S. Ordonez-Soto
December 16th, 2024
The signal Dalitz plot PDF in this framework is then given by:
The total Dalitz plot PDF is written as:
with \(f_{\text{sig}} + \sum_{i} f_{\text{bkg}_{i}} = 1\). Three main components of the PDF are clearly distinguished:
- Signal PDF (\(\mathcal{S}(s_{+},s_{-})\)):
- Background models (\(\mathcal{B}_{i}(s_{+},s_{-})\))
- Efficiency maps (\(\epsilon(s_{+},s_{-})\))
Dalitz plot analysis of \(B_{s}^{0}\rightarrow K_{S}^{0}\pi^{+}\pi^{-}\)
Physical observables from DP fit
S. Ordonez-Soto
December 16th, 2024
Dalitz plot analysis of \(B_{s}^{0}\rightarrow K_{S}^{0}\pi^{+}\pi^{-}\)
A fit to data allows to measure the isobar parameters, i.e., the relative magnitudes of the isobar amplitude
From there, the direct CP asymmetry for an amplitude \(j\) can be derived:
The fit fraction of a given amplitude is obtained also as result from the fit:
Steps of the Amplitude Analysis
S. Ordonez-Soto
December 16th, 2024
The analysis strategy is summarized in the following steps:
-
Fit the invariant mass spectrum \(K_{S}\pi^{+}\pi^{-}\).
- Define a signal window around \(B_{s}^{0}\) signal peak.
- Determine the fractions of each component in this signal window: \(f_{\text{sig}}\) and \(f_{\text{bkg}_{i}}\)
-
Model the distribution of the backgrounds in the Dalitz plot of \(B_{s}\rightarrow K_{S}^{0}\pi^{-}\pi^{+}\).
- Obtain a smoothed histogram with the model for each background.
-
Estimate the efficiency variation across the DP.
- Obtain a map from signal MC after the selection and with all of the corrections incorporated.
-
Fit simultaneously the different samples (with shared IM parameters for all categories).
- Define a nominal model according to SM predictions.
- Educate the final model by adding potential contributions to the baseline.
Analysis strategy
S. Ordonez-Soto
December 16th, 2024
LL
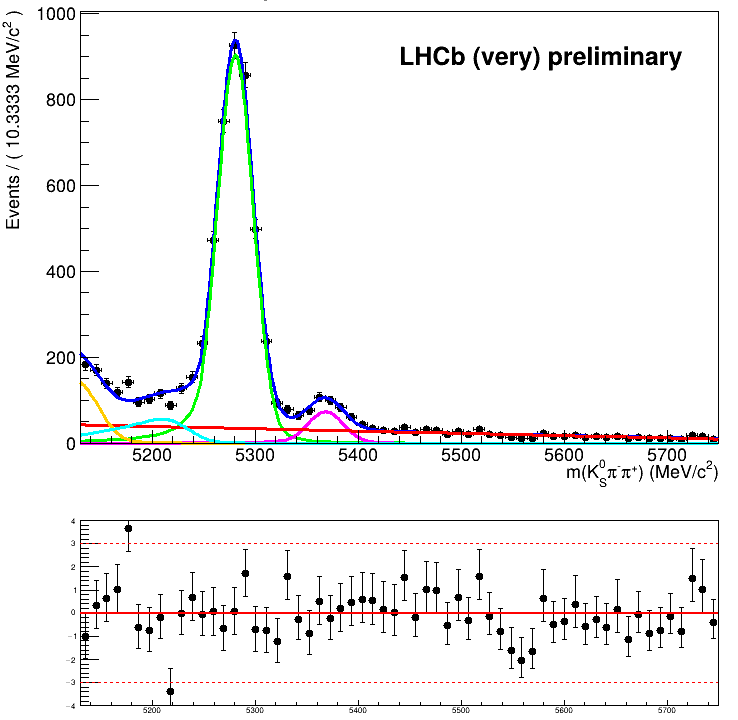
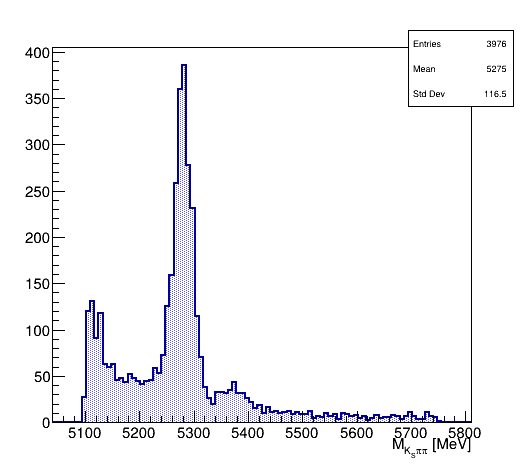
Invariant mass fit corresponding to \(B_{s}^{0}\rightarrow K_{S}^{0}\pi^{+}\pi^{-}\) 2018 data
\(K_{S}^{0}\pi^{+}\pi^{-}\) Invariant mass fit
Analysis strategy
\(B_{s}^{0}\rightarrow K_{S}^{0}\pi^{+}\pi^{-}\) Dalitz plot considering only data within the signal window
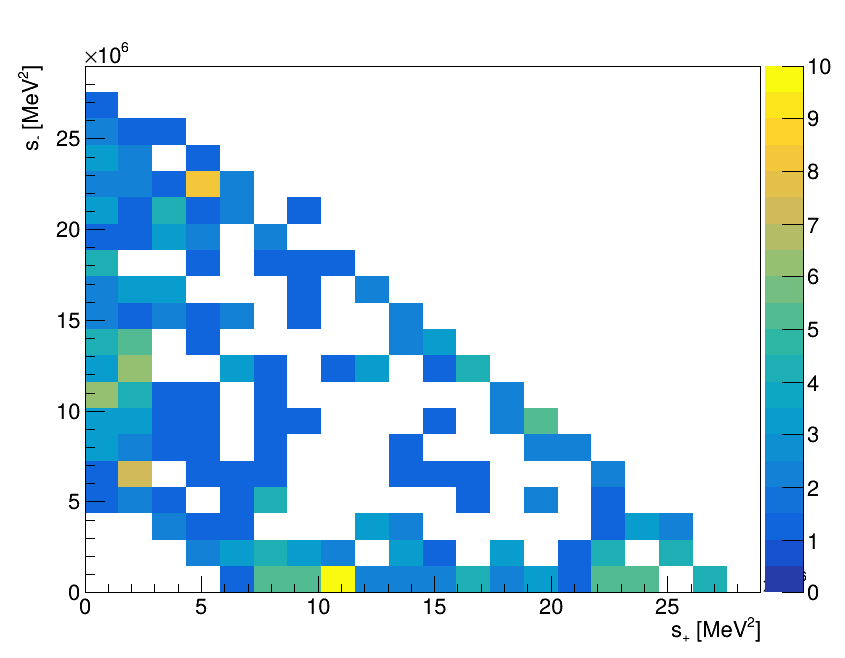
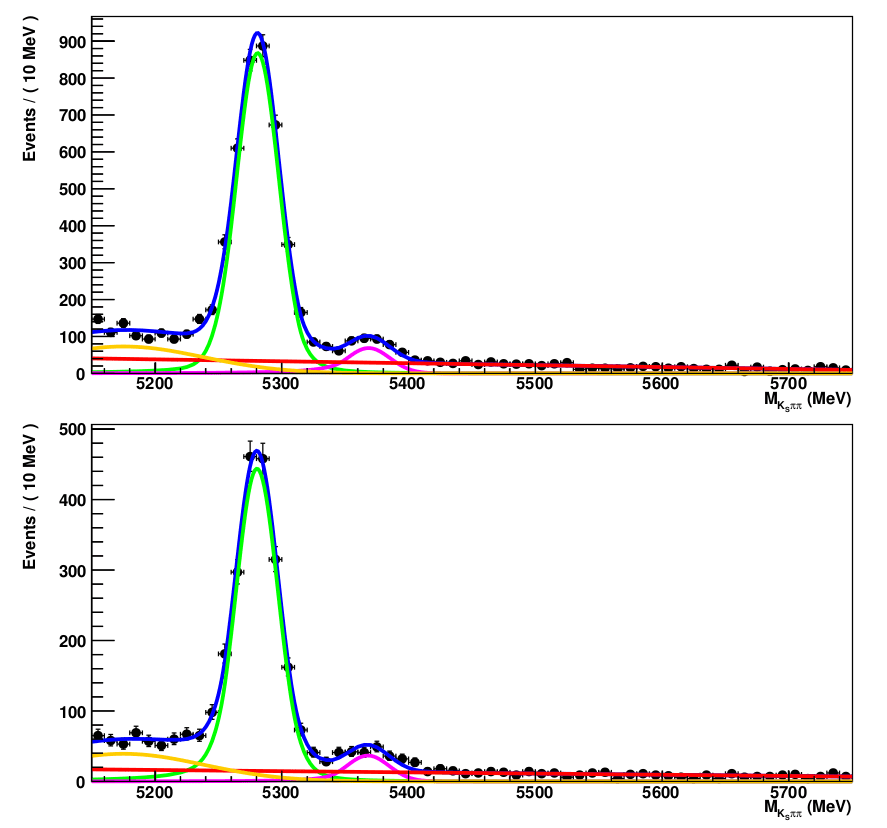
\(K_{S}^{0}\pi^{+}\pi^{-}\) Invariant mass fit
S. Ordonez-Soto
December 16th, 2024
Analysis strategy
DD
LL
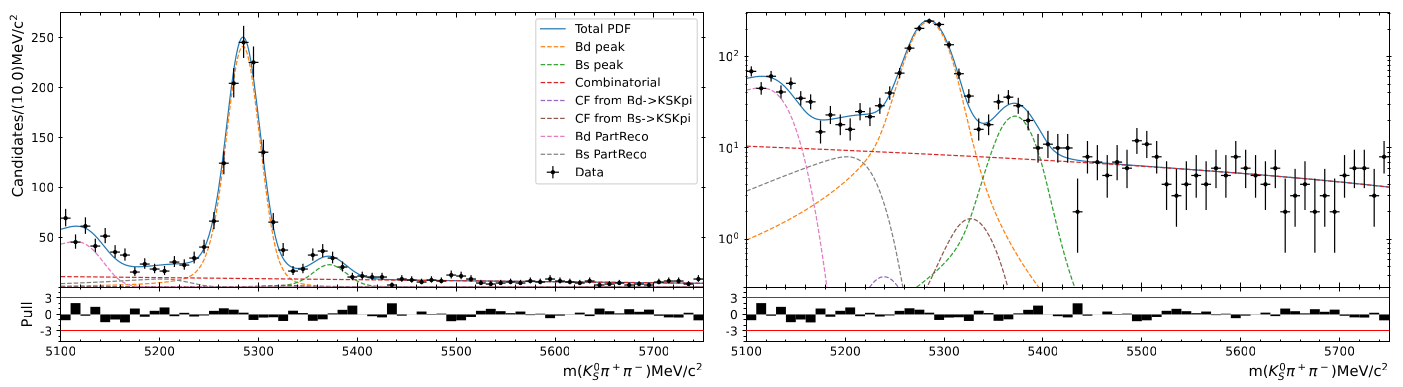
\(K_{S}^{0}\pi^{+}\pi^{-}\) Invariant mass fit
S. Ordonez-Soto
December 16th, 2024
Analysis strategy
DD
LL


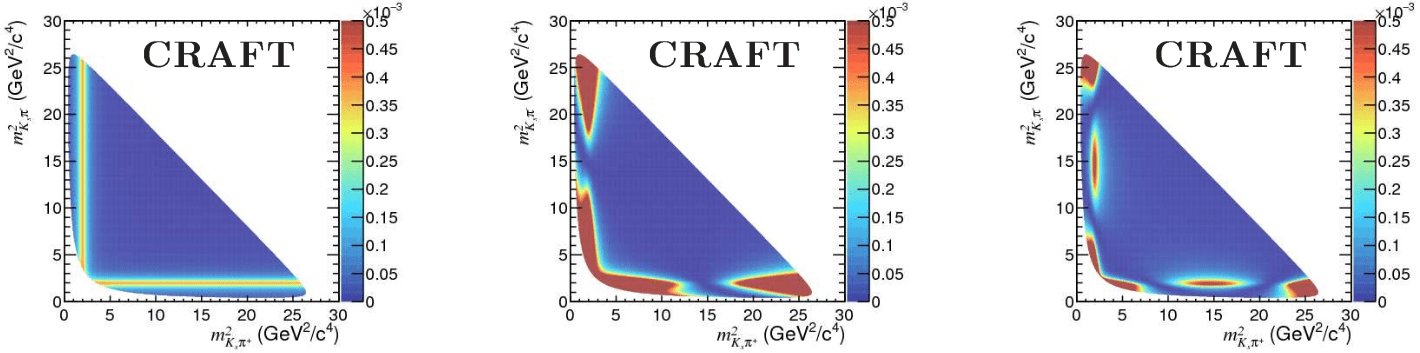
Distribution of the backgrounds
S. Ordonez-Soto
December 16th, 2024
Analysis strategy
It is clear that the most relevant source of bkg. within the signal window is the combinatorial bkg.
- This contribution can be modeled using the data from the right side-band.

One of the challenges in this analysis is the modeling of other sources of background, primarily from the B2KSpipi signal tail, which, although small, is not negligible.
Efficiency variation across the DP
S. Ordonez-Soto
December 16th, 2024
Analysis strategy
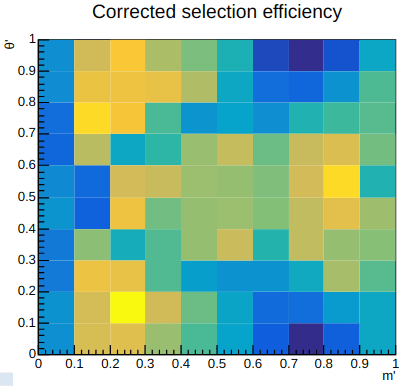
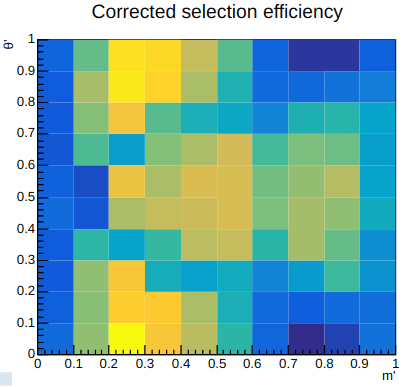
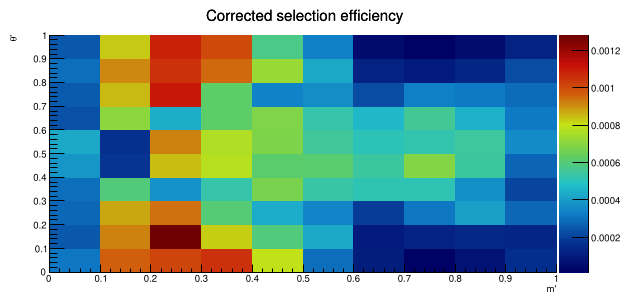
The efficiency of signal events is affected by selection cuts, geometrical acceptance, and trigger efficiency, leading to non-uniform event distribution across the Dalitz plane.
This efficiency is determined by using MC samples with appropriate corrections, e.g., PIDcorr.
LL
DD
Efficiency maps \(\epsilon(s_{+},s_{-})\) used as input for the Dalitz plot fit
Dalitz plot fit
S. Ordonez-Soto
December 16th, 2024
Analysis strategy
First attempt with signal decay model based on SM expectations, then add potential contributions and decide based on s statistical test.

Clermont Root-based Amplitude Fitter Tool
- Perform a simultaneous fit of independent samples to determine a common set of parameters by minimizing the sum of all negative log-likelihoods:
Efficiency determination
subWG Kshh
Sebastian Ordoñez-Soto
February 24th, 2025
if (dkmode == "KK") {
cut += "h1_PROBNNp" + cut_name + "< 0.5";
cut += "h2_PROBNNp" + cut_name + "< 0.5";
if (year == "2018"){
cut += "Topo_xgb > 0.95";
cut += "PID_xgb_Bs2KKKS > 0.985";
}
} else {
cut += "h1_PROBNNp" + cut_name + "< 0.9";
cut += "h2_PROBNNp" + cut_name + "< 0.9";
}
if (dkmode == "KK") {
cut += "h1_PROBNNp" + cut_name + "< 0.9";
cut += "h2_PROBNNp" + cut_name + "< 0.9";
if (year == "2018"){
cut += "Topo_xgb > 0.95";
cut += "PID_xgb_Bs2KKKS > 0.985";
}
} else {
cut += "h1_PROBNNp" + cut_name + "< 0.9";
cut += "h2_PROBNNp" + cut_name + "< 0.9";
}
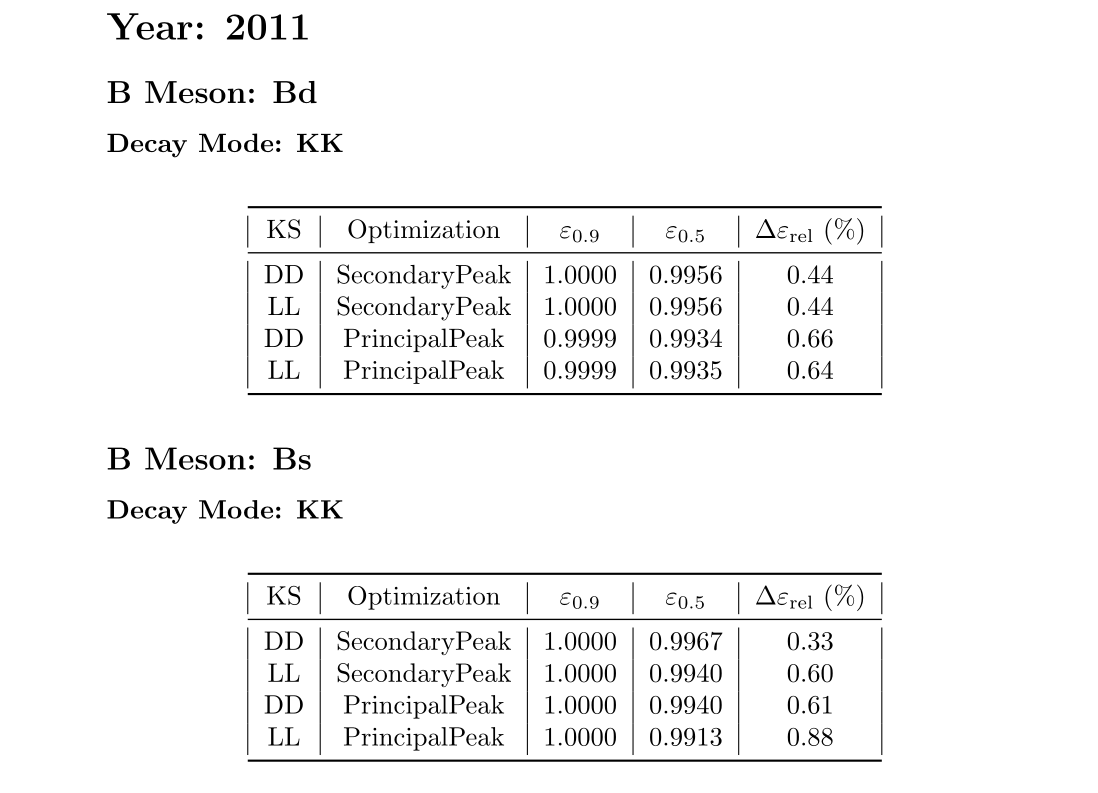
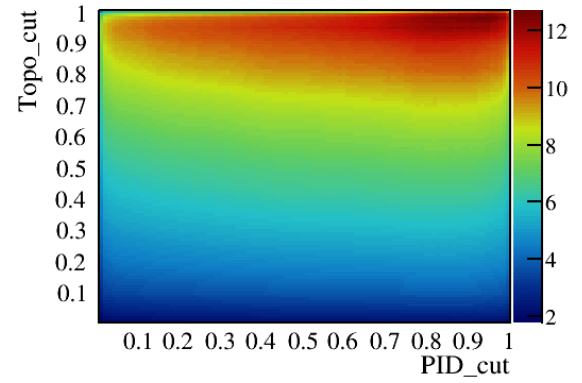
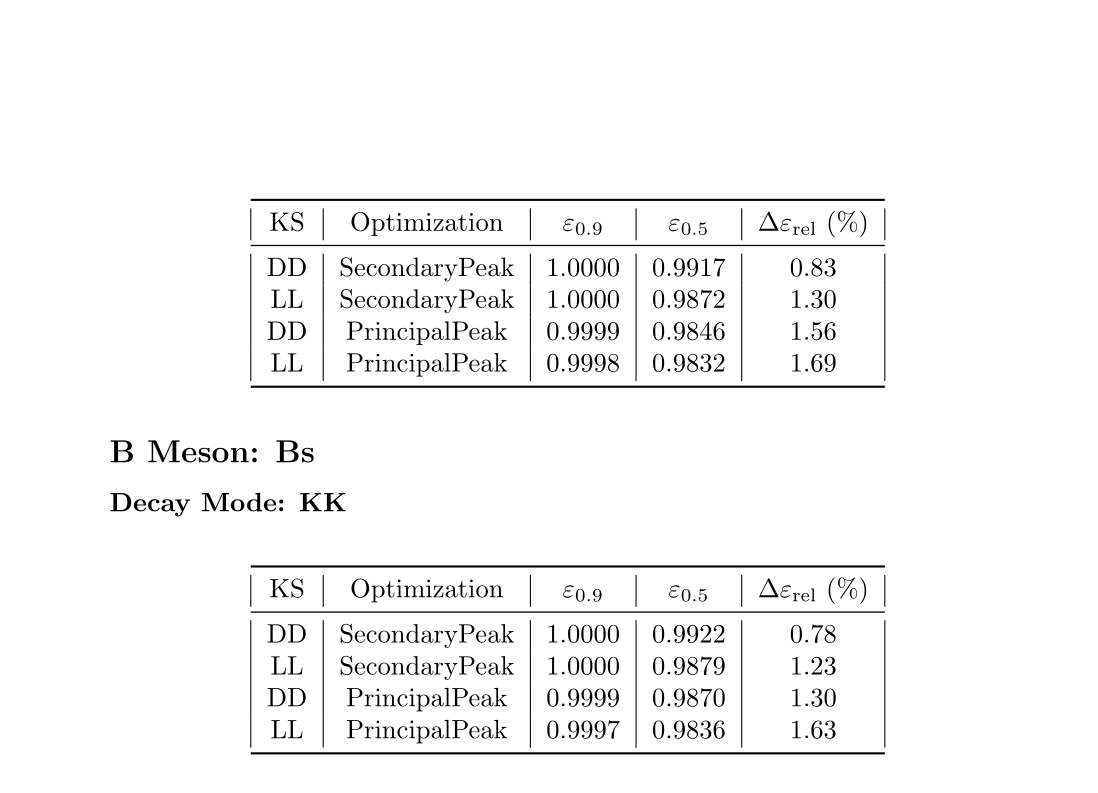
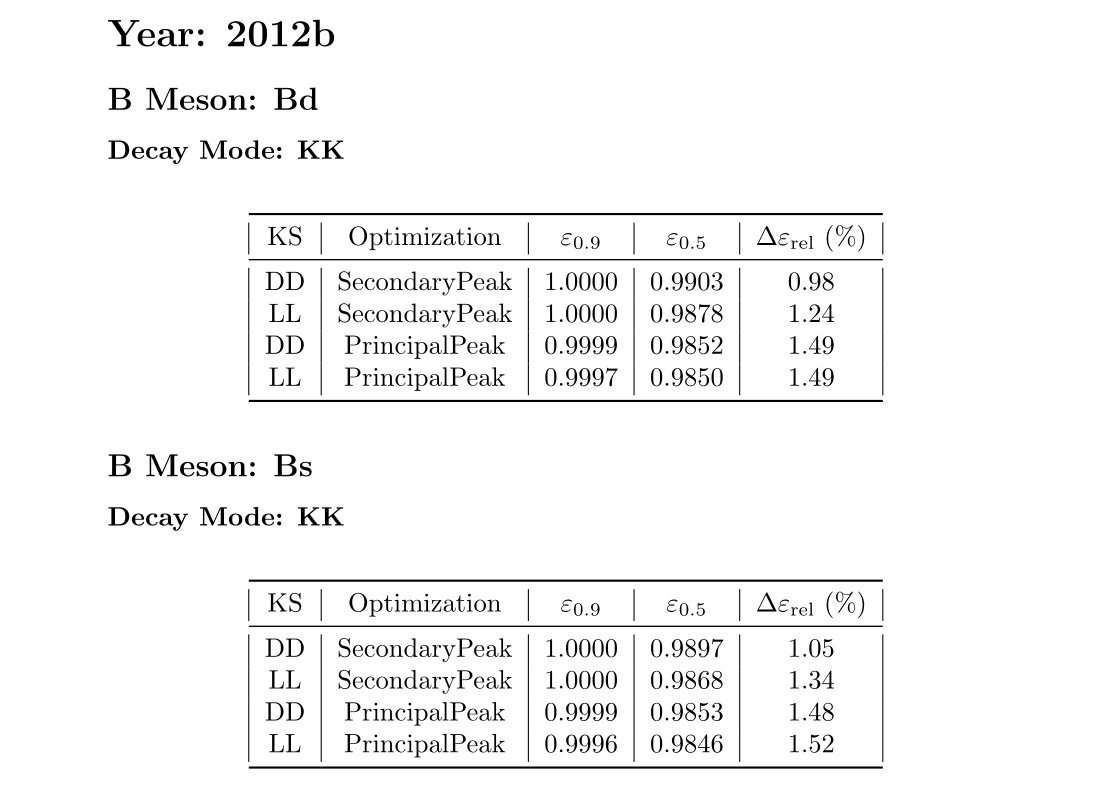
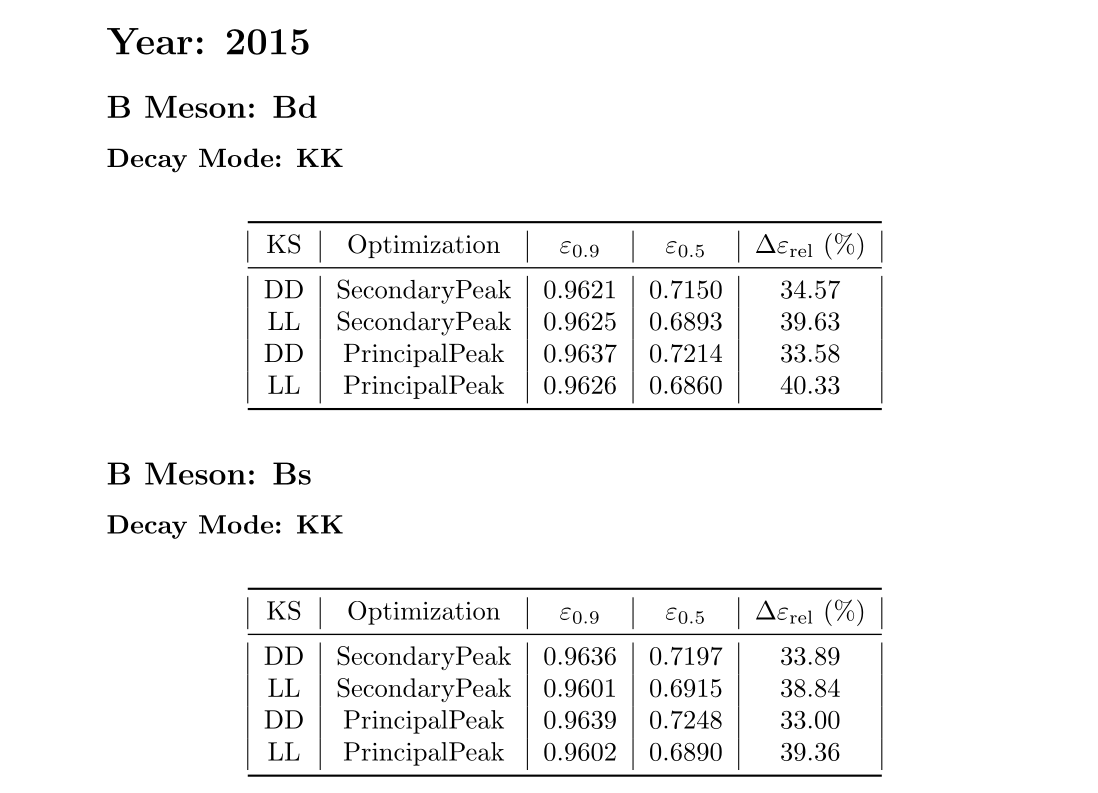
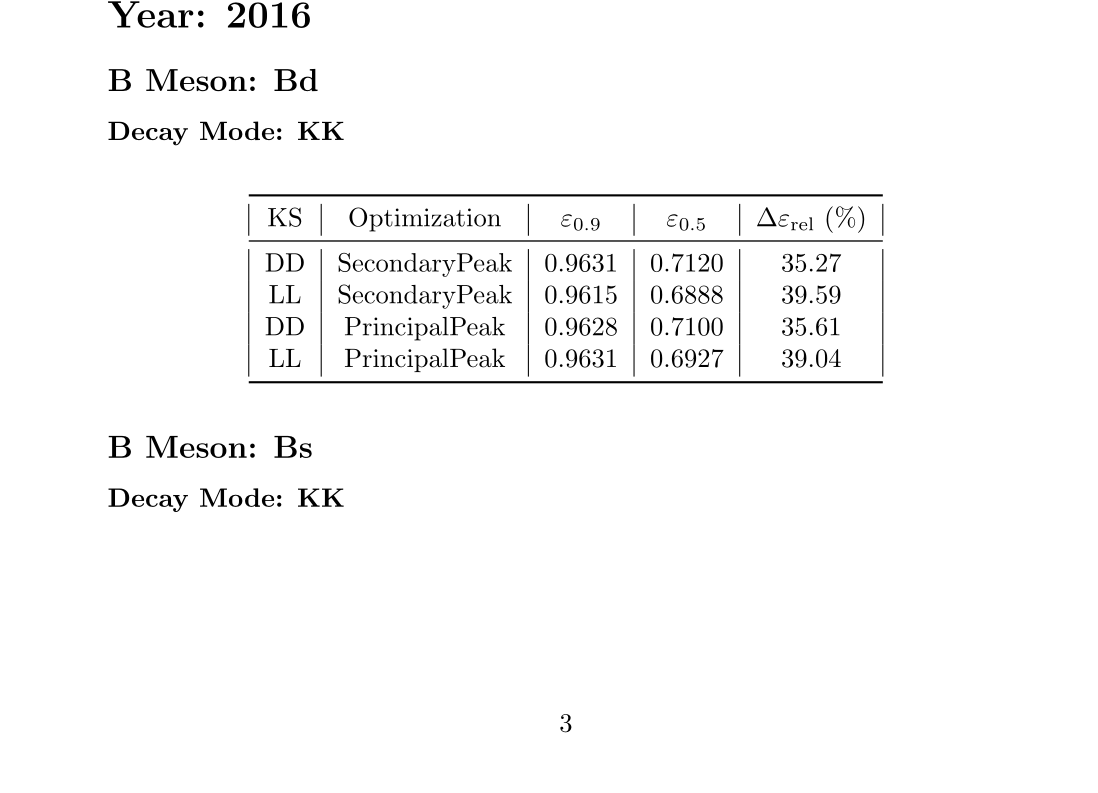
Previous selection \(\epsilon_{0.9}\)
Current selection \(\epsilon_{0.5}\)


Efficiency determination
subWG Kshh
Sebastian Ordoñez-Soto
February 24th, 2025
Efficiency determination
subWG Kshh
Sebastian Ordoñez-Soto
February 24th, 2025

Efficiency determination
subWG Kshh
Sebastian Ordoñez-Soto
February 24th, 2025
Efficiency determination
subWG Kshh
Sebastian Ordoñez-Soto
February 24th, 2025
Efficiency determination
subWG Kshh
Sebastian Ordoñez-Soto
February 24th, 2025
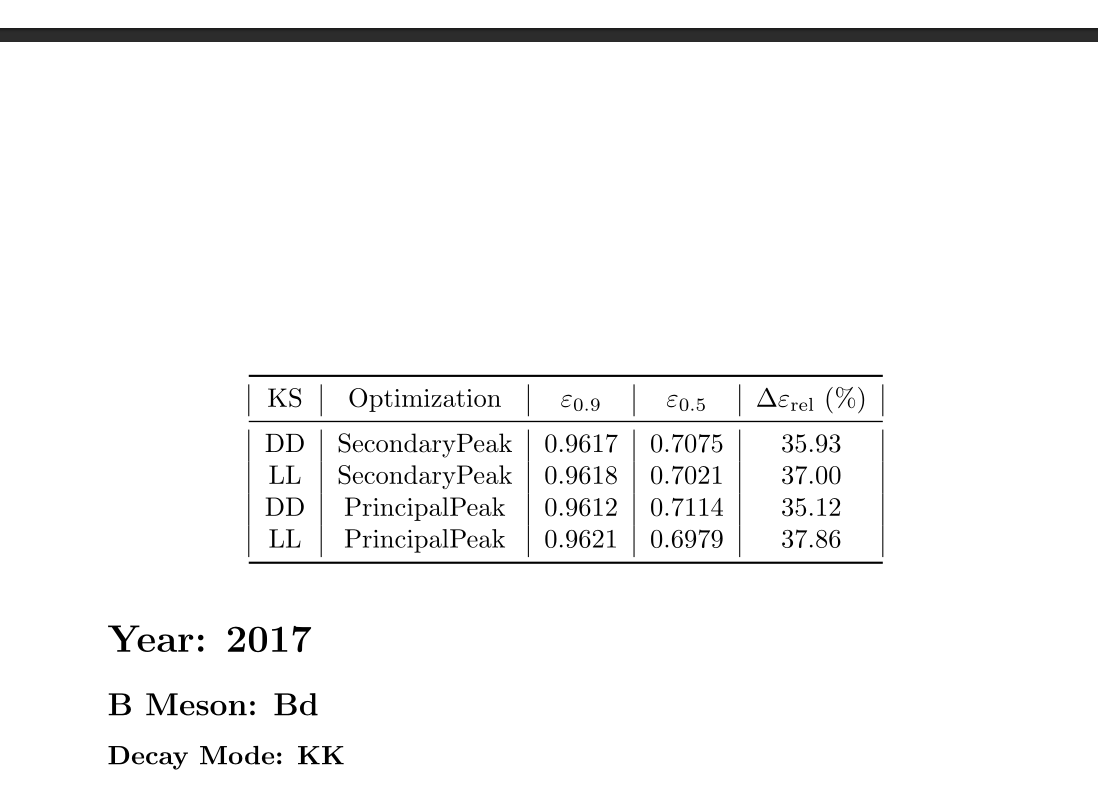
Efficiency determination
subWG Kshh
Sebastian Ordoñez-Soto
February 24th, 2025
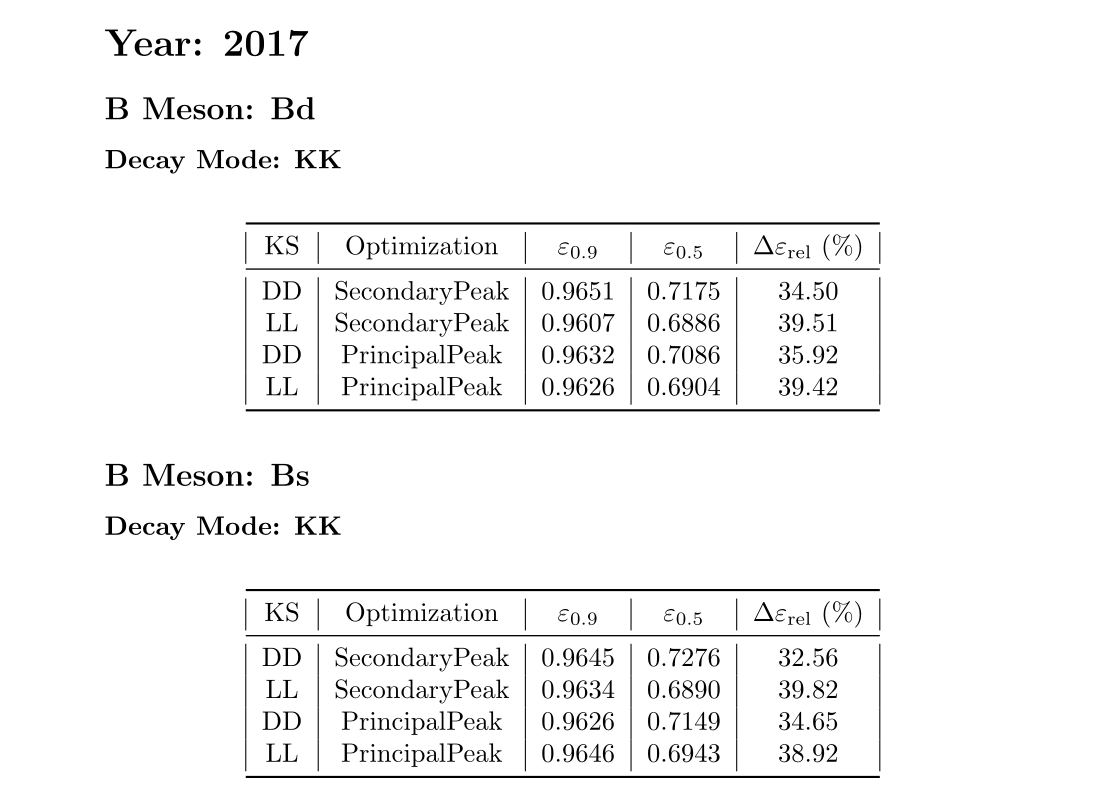
Efficiency determination
subWG Kshh
Sebastian Ordoñez-Soto
February 24th, 2025

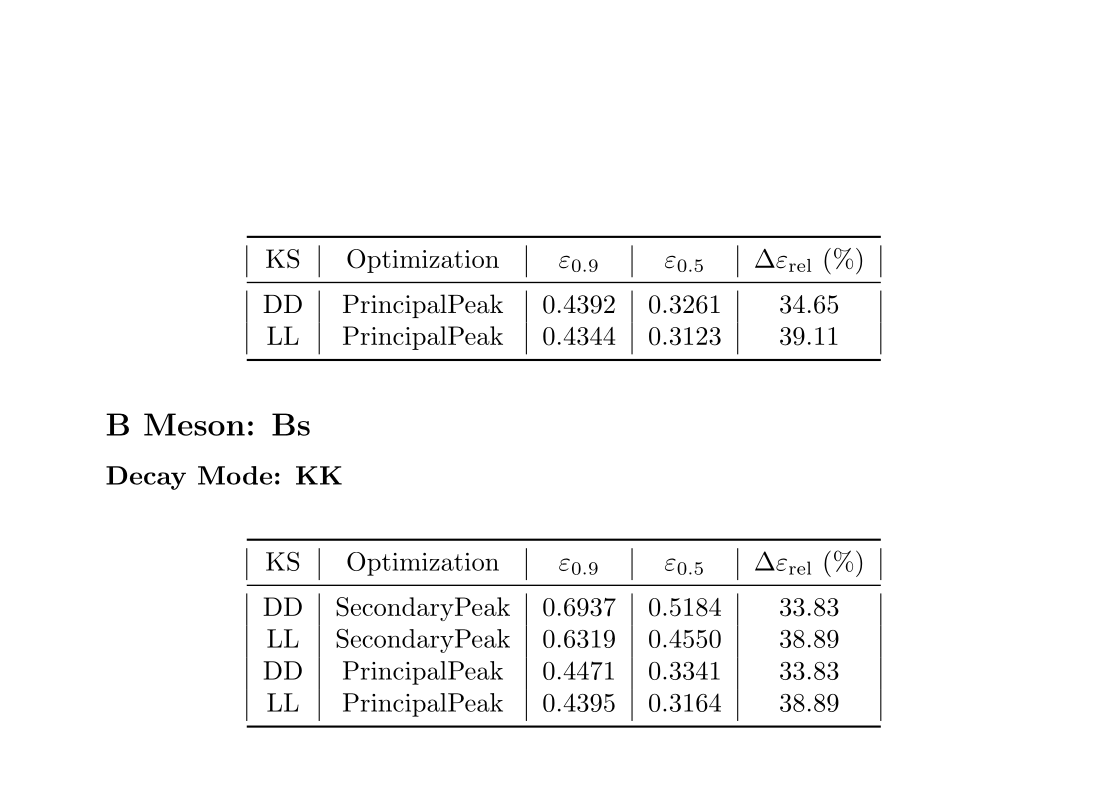
Group meeting-24/03/25
By Sebastian Ordoñez
Group meeting-24/03/25
- 167