Universidad Nacional de Colombia
Facultad de Ciencias Naturales, Departamento de Física
Bogotá, Colombia
January 2022
Sebastián Ordoñez
jsordonezs@unal.edu.co
Supervisor: Prof. Diego A. Milanés C.
Maestría en Ciencias Física - Investigación
Física Experimental de Partículas
Grupo de Partículas FENYX


A dalitz plot analysis of the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) decay using the multi-meson model
Contents
- Introduction and Justification
- State of the Art
- Research Question and Objectives
- Research Question
- General Objective
- Specific Objectives
- Methodology
- Schedule
- Resources
- References
Introduction

- Nonleptonic weak decays of charmed mesons have unique features that make them excellent laboratories to study light-quark spectroscopy.
- The decays of \(D\) mesons into three hadrons exhibit a rich resonance structure at low energies, below 2 GeV.
They are, in consequence, a valuable tool for the investigation of QCD in such poorly understood regime, in which perturbation theory is not suitable.
The \(D^{+}\) meson is the lightest known particle containing charm quarks, its mass is known to be 1869.62\(\pm\)0.20 MeV
Other approaches relying on phenomenological models are required for the description of these decays.

One widely used model is the so-called isobar model (IM), derived in the Sixties, considerably before the development of QCD.

Weak decay of charmed mesons
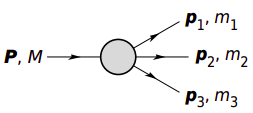
Introduction (Back up)
Justification
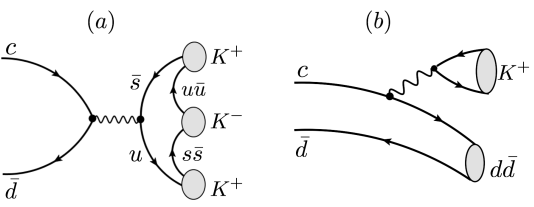
Amplitude Analysis of the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\)
- This is not a simple task considering the different types of dynamical processes implicated, namely, heavy-quark weak transitions, hadron formation and final-state interactions (FSI).
- New approaches have emerged > the multi-meson model, or Triple-M, which has been employed to describe the doubly Cabibbo-suppressed decay \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\).
This model is based on chiral effective Lagrangians and includes the main dynamical stages underlying the decay


The Triple-M also allows to determine the \(K^{+}K^{-}\) scattering amplitudes from a fit to the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) Dalitz plot.
This model is based on chiral effective Lagrangians and includes the main dynamical stages underlying the decay.
The Triple-M has already been used in a Dalitz plot fit with data from the Run 1 of the LHC, giving better results than those from the IM.

A new version of the model, in which the K-matrix approximation is removed, is available, along with data from the Run 2. A test is urgent! An advance towards the description of weak decays of \(D\) meson in a more fundamental basis could be obtained.

State of the Art
1. [2018] The first version of the Triple-M is published, after some previous related papers.
2. [2019] A full Dalitz plot analysis is performed using the first version of the Triple-M and data from the Run 1 of the LHC. The results obtained are better than those from the Isobar Model.


3. [2020] The second version of the Triple-M is published and the K-matrix approximation is removed
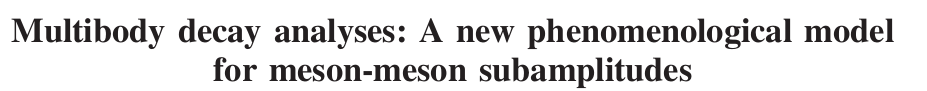

Research Question and Objectives
- Research Question
- General Objective
Analyze the implications of including the real part of the two-body propagators in the decay amplitude of the multi-meson model on a Dalitz plot analysis of the doubly Cabibbo-suppresed \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) decay , using data from the Run 2 of the LHCb experiment.
Which would be the implications of including the real part of the two-body propagators in the decay amplitude of the multi-meson model on a Dalitz plot analysis of the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) decay, using data from the Run 2 of the LHCb experiment?
Research Question and Objectives
- Specific Objectives
- Perform a toy Dalitz plot fit of the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) decay channel using the GooFit framework and the known parameters obtained with a fit using the isobar model.
- Reproduce the known results for the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) Dalitz plot fit employing the decay amplitude of the first version of the Triple-M and the GooFit framework.
- Codify the last version of the Triple-M and perform some toy Dalitz plot fits using the GooFit toolkit.
- Pre-select the \(K^{-}K^{+}K^{+}\) candidates from the trigger samples by means of the slope-difference and PID variables, in order to remove clone-tracks and cross-feeds from other decay channels, respectively.
- Match the kinematic variables of the preselected \(K^{-}K^{+}K^{+}\) simulated candidates with those of the preselected data candidates using the Gradient Boosted Reweighter algorithm.
- Reduce the combinatorial background remaining in the preselected data sample by employing a multivariate selection. The TMVA package will be used.
Introduction: Toys and fits
Selection: Data preparation and Data analysis
\(S\)-wave fit
Jan.
Mar.
Feb.
Nov.
Oct.
Sep.
Aug.
Jun.
May
Apr.
Mar.
Feb
Jan.
2022
2023
Research Question and Objectives
- Specific Objectives
7. Graph the purities obtained when different cuts are applied on the chosen classifier variable obtained from the multivariate selection.
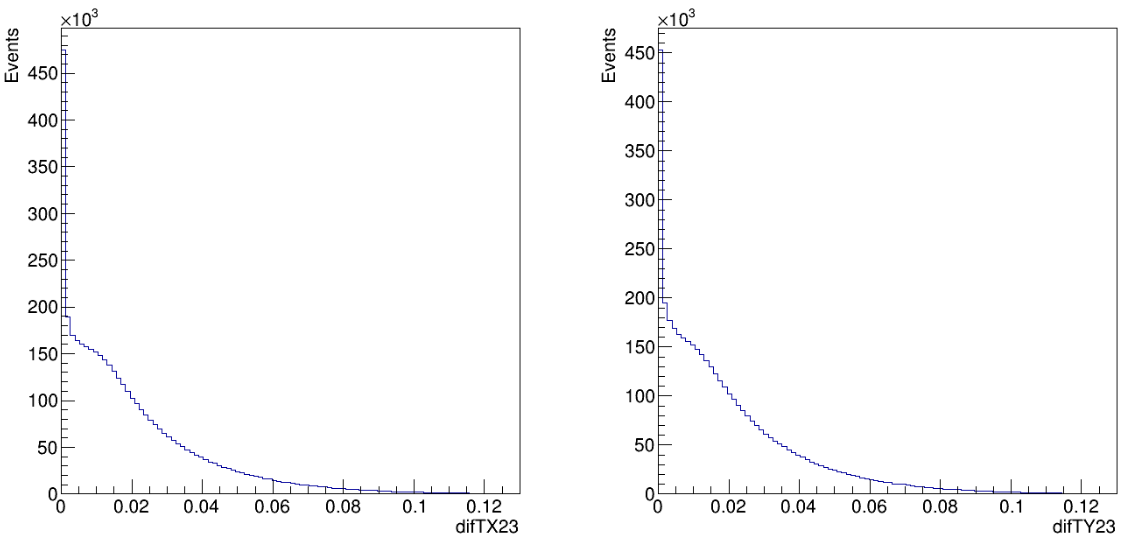
8. Make fits for the invariant mass distribution of the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) candidates using RooFit in order to determine the signal and background yields, and also to define the signal region for the Dalitz plot fit.
9. Compute a map of the total detection efficiency over the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) Dalitz plot phase space.
10. Determine the background model by inspecting the sidebands of the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) signal.
11. Perform the final Dalitz plot fit of the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) decay channel using the Triple-M formalism.
12. Study the fit results and compare them with those known for the isobar model and the first version of the Triple-M.
Methodology
A methodology proposal -including strategies, steps and tools- for each of the specific objectives presented. Here only some of them are discussed.
- Specific Objective #4



Original data Dalitz plot
Dalitz plot after a cut on the SDV
Slope difference variables (SDV)
Methodology

Methodology (Back up)
- Slope difference variables distribution
Methodology
- Specific Objective #8
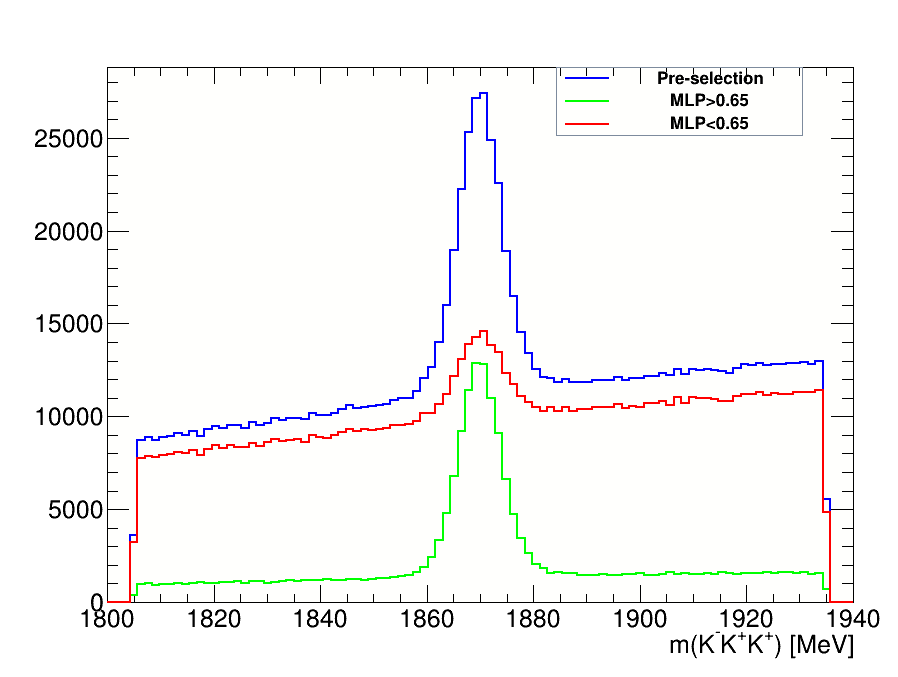

Roofit Toolkit
Methodology
- Specific Objective #8

Schedule
- Timeline
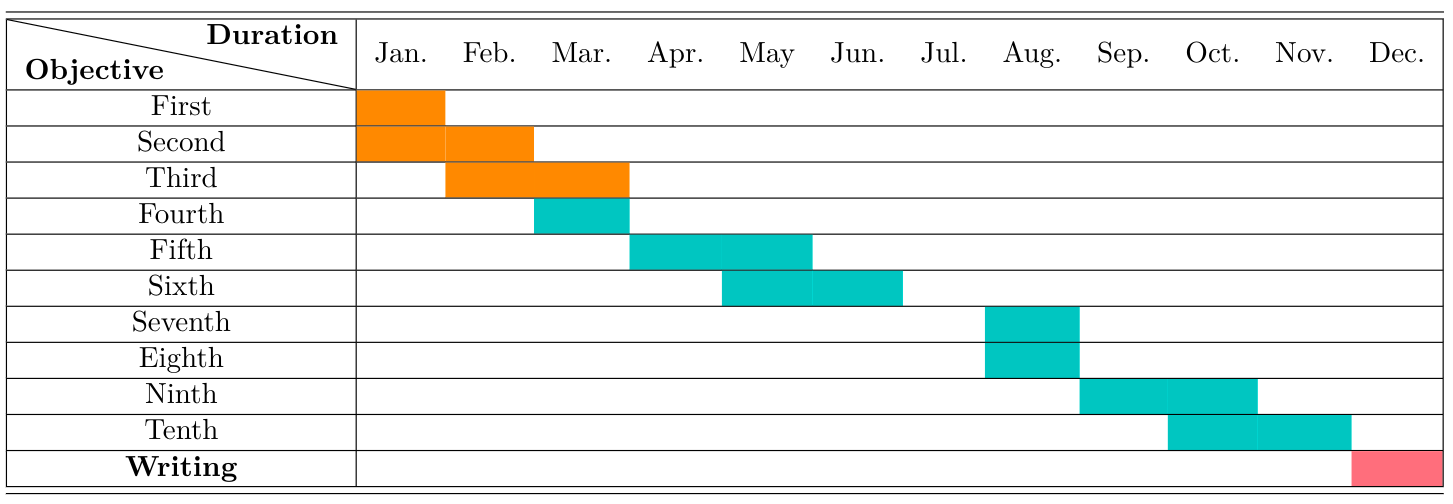

- 2022
The schedule has been splitted according to the specific objectives proposed, and for each one of them a period of one or two months has been given depending on the complexity (some of them have to developed in parallel).
Schedule
- 2023
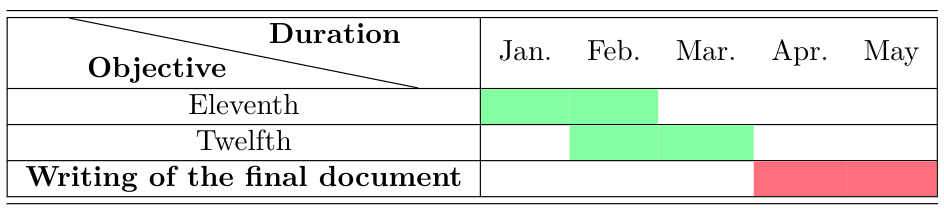
Resources
- Human resources
- Technical resources
- Master student: Time, college payment
- Supervisor: salary payment
- Collaborators: salary payment
- State-of-the-art computer > To be determined.
- Remote server > To be determined
- Data from LHCb > To be determined
- GooFit Toolkit > Free
- RooFit Toolkit > Free
- Energy
Resources and their costs are still a subject of study! > They are presented globally
References

[Seminario de Posgrados] - Proyecto de Tesis de Maestria
By Sebastian Ordoñez
[Seminario de Posgrados] - Proyecto de Tesis de Maestria
- 515



