Validation Regions for non-prompt background estimation in same charged \(W^{\pm}W^{\pm}\) scattering

Sebastian Ordoñez

jsordonezs@unal.edu.co

 

 

                                      1st of July 2021                                             

 

Outline

  • Motivation
  • Introduction
    • ​Data-driven Matrix Method
    • The LowMjj validation region
  • Trilepton validation regions
    • Evaluation
      • Statistics
      • Non-prompt composition
    • Closure Tests
      • Monte Carlo closure test
      • Data closure test
  • Conclusion and Outlook

Motivation

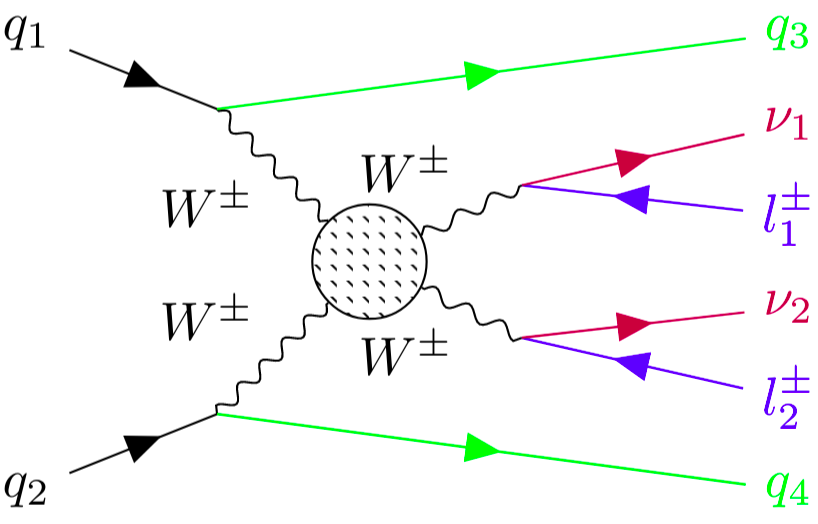
  • The production of same charged \(W^{\pm}\) is a process predicted by the Standard Model (SM) that is sensitive to the electroweak symmetry breaking (EWSB) mechanism as well as new physics BSM.
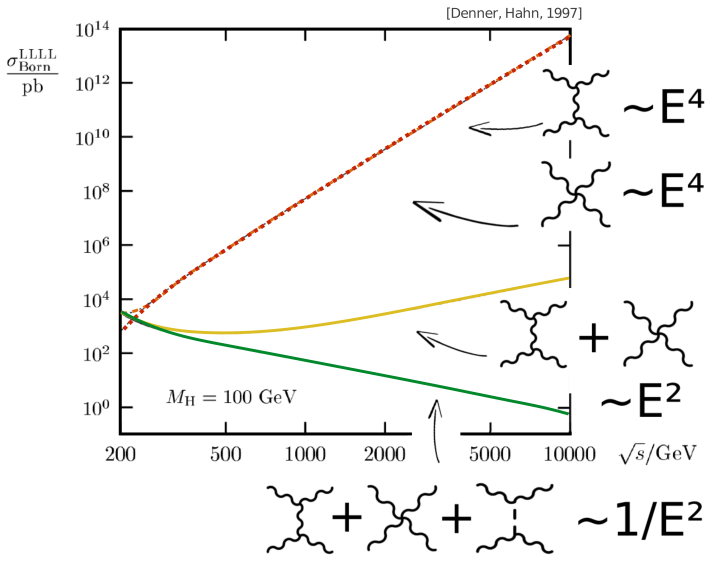
  • One of the main production mechanisms is Vector Boson Scattering: \(VV\longrightarrow VV\) with \(V=W\) or \(Z\)

Same charged \(W^{\pm}W^{\pm}\) scattering

Final state: two leptons, \(E_{T}^{miss}\), two jets.

Motivation

Event selection for the signal region

  • Drell-Yan contamination          

Motivation

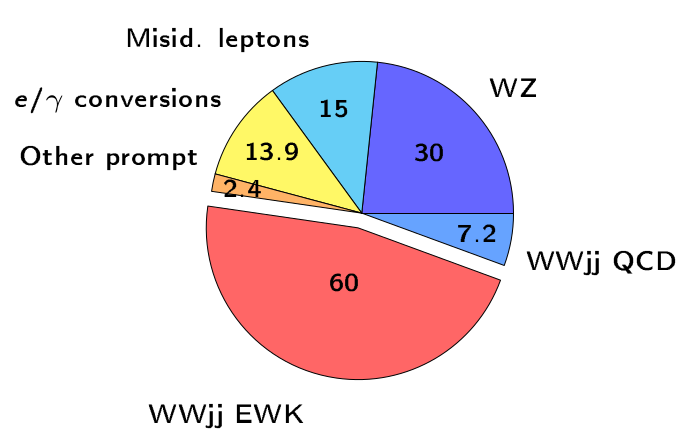
  • Misidentified leptons are the second largest background in the \(W^{\pm}W^{\pm} jj-\) EW signal region.
  • The largest experimental uncertainty comes from the data-driven estimation of the non-prompt background.

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.123.161801

Non-prompt background in the \(W^{\pm}W^{\pm} jj\)-EW analysis

Motivation

"The probability of a non-prompt lepton to be incorrectly associated with the primary vertex or a jet to fake the lepton signature is not well modelled in the Monte Carlo. " Shalu

Non-prompt background in the \(W^{\pm}W^{\pm} jj\)-EW analysis

Taken from https://arxiv.org/pdf/1906.03203.pdf

Data-driven Matrix Method

In order to calculate the non-prompt background, four lepton categories are used.

\boxed{N_{A}^{\text{non-prompt}}=(N_{N}^{\text{data CR}}-N_{N}^{\text{prompt MC}})F^{\text{data CR}}}
  • In this study the fake factor \(F\) is extracted from the dilepton control region.
  • \(F\) depends on the type and origing of the faking object.

On thruth-level:

  • Prompt leptons: Leptons originating from the hard-process, i.e., \(W\) or \(Z\) bosons.
  • Non-prompt leptons: Misidentified leptons or that stem from another source, e.g. hadron decay.

On detector-level we have:

  • Ana leptons: Leptons with kinematic and qualitative requirements such that in the signal region they are the signal for \(W^{\pm}W^{\pm}jj\)-EW.
  • Non-Ana leptons: Leptons which fail the isolation and object selection of the Ana selection.

The reducible background is calculated by using:

Data-driven Matrix Method

N_{A}^{\text{non-prompt}}
N_{N}^{\text{non-prompt}}
\text{Ana}
\text{Non-Ana}
\text{Prompt}
\text{Non-prompt}

\(F\)

\text{Object quality (detector-level)}
\text{Object origin (truth-level)}

Data-driven Matrix Method

\begin{pmatrix} N_{AA} \\ N_{NA} \\ N_{AN} \\ N_{NN} \end{pmatrix} = \begin{pmatrix} e_{1}e_{2} & e_{1}f_{2} & f_{1}e_{2} & f_{1}f_{2} \\ \bar{e}_{1}e_{2} & \bar{e}_{1}f_{2} & \bar{f}_{1}e_{2} & \bar{f}_{1}f_{2} \\ e_{1}\bar{e}_{2} & e_{1}\bar{f}_{2} & f_{1}\bar{e}_{2} & f_{1}\bar{f}_{2} \\ \bar{e}_{1}\bar{e}_{2} & \bar{e}_{1}\bar{f}_{2} & \bar{f}_{1}\bar{f}_{2} & \bar{f}_{1}\bar{f}_{2} \end{pmatrix} \begin{pmatrix} N_{PP} \\ N_{FP} \\ N_{PF} \\ N_{FF} \end{pmatrix}
\boxed{N_{AA}^{\text{non-prompt}} = (N_{NA}-\bar{e}_{1}e_{2}N_{PP})\frac{f_{1}}{\bar{f}_{1}}+(N_{AN}-e_{1}\bar{e}_{2}N_{PP})\frac{f_{2}}{\bar{f}_{2}}-(N_{NN}-\bar{e}_{1}\bar{e}_{2}N_{PP})\frac{f_{1}}{\bar{f}_{1}}\frac{f_{2}}{\bar{f}_{2}}}

Relation between the truth-level categories and the detector-level categories:

It follows that

\boxed{F_{i}=\frac{f_{i}}{\bar{f}_{i}}}

We define the fake factor as the following ratio 

Data-driven Matrix Method

Non-Analysis and Analysis selections

For a complete application of the Matrix method in the signal region we have to evaluate the \(N^{\text{non-prompt}}\) estimate in auxiliary regions, the validation regions.

Signal region

\(F\) final application

\(F\) validation

\(F\) extraction

Data-driven Matrix Method

Validation 
regions
Control region
  • My work: Evaluate the non-prompt estimate obtained by applying the fake factor extracted from the dilepton control region in two validation regions: the Trilepton muon region and the Trilepton electron region.

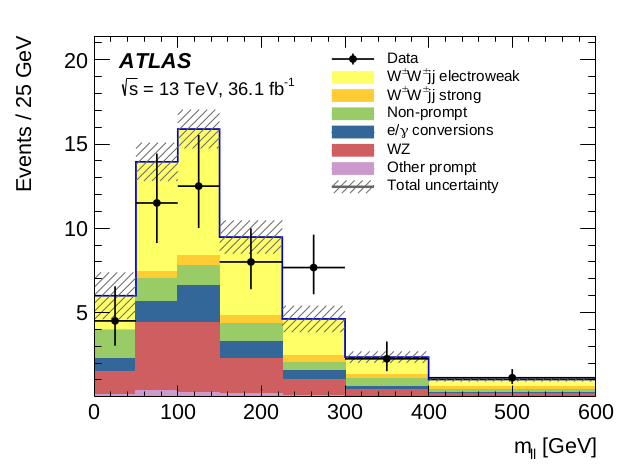
The Low Dijet Invariant Mass Validation Region

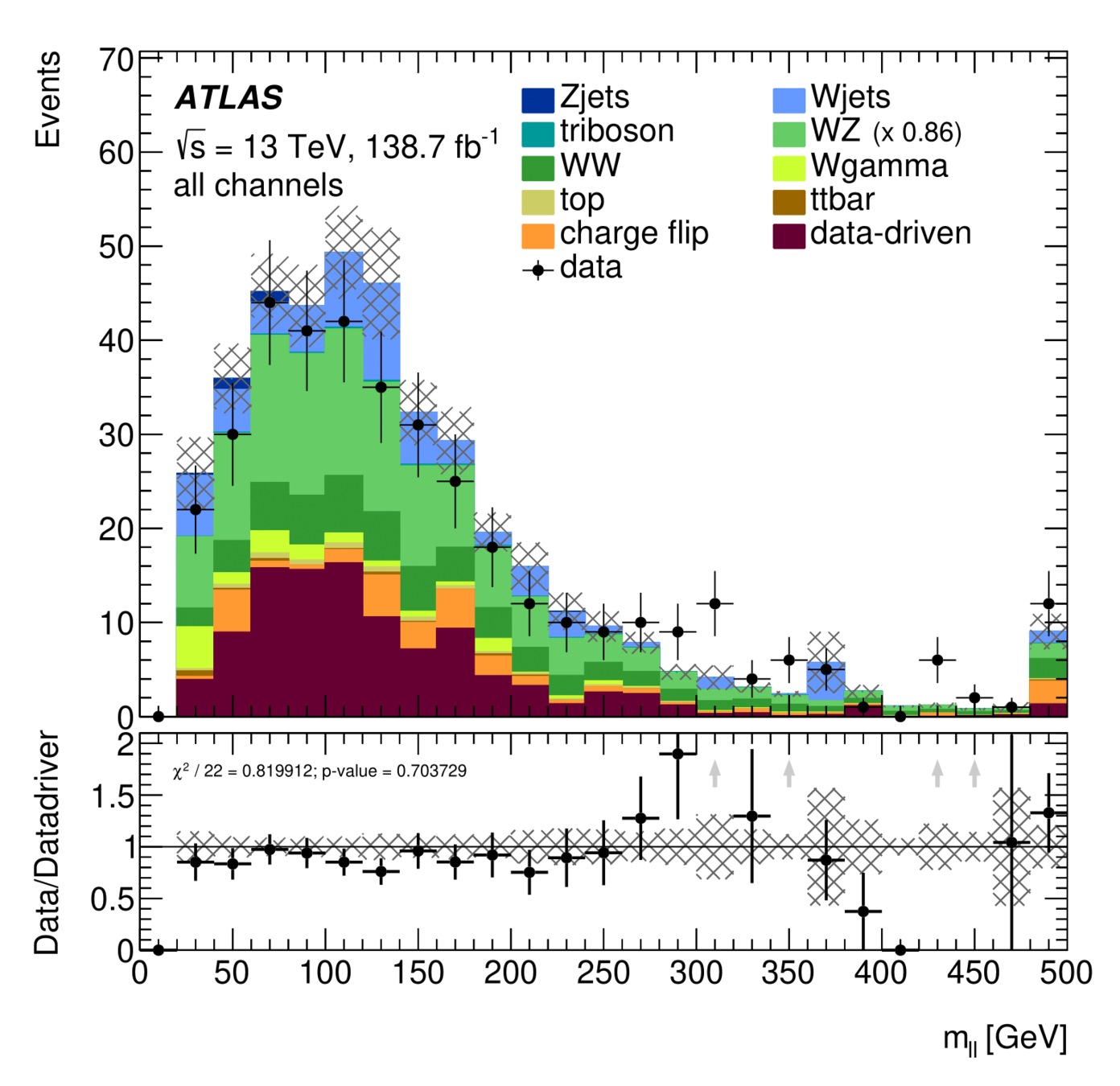
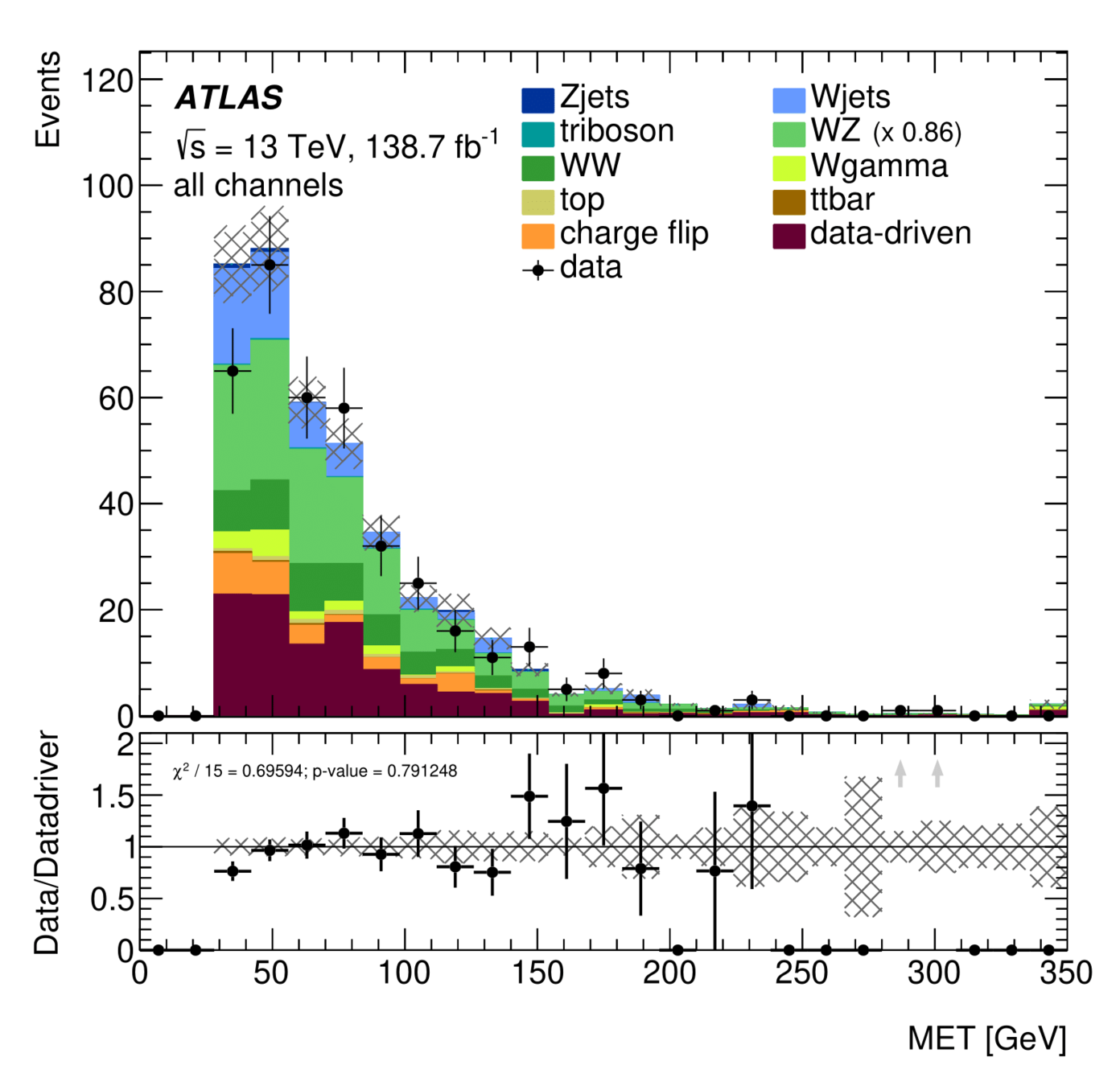
\(m_{ll}\) distribution

\(E_{T}^{miss}\) distribution

The LowMjj validation region was already used with a non-prompt contribution of about 25%. It is necessary to build new validation regions with a higher contribution. 

Trilepton muon Region

Motivation for the event selection cuts

Non-prompt muons in the signal region originate almost exclusively from \(b\) quarks coming from \(t\bar{t}\) events.

g
g
g
t
\bar{t}
W^{+}
W^{-}
e^{+}
\mu^{-}
\nu
\nu
b\longrightarrow\mu
\bar{b}
\text{non-prompt!}
  • By requiring both muons to have an identical electric charge we reject a lot of events coming from \(Z+jets\) and \(WZ\) samples.
  • Most events will originate from \(t\bar{t}\) and we get a similar composition to that of the signal region.

Trilepton muon Region Definition

A trilepton validation region for testing the modelling of non-prompt muons was built by requiring events to:

We need to guarantee that non-prompt muons have a \(p_{T}>27\) GeV in order to be able to apply the fake factor.

Preselection

Selection

Trilepton Electron Region

Motivation for the event selection cuts

Non-prompt electrons in the signal region originate primarily from light flavour jets of \(W+jets\) events. However, it is not possible to achieve that composition using a trilepton region.

g
g
g
g
q
q
W^{+}
e^{+}
\nu
q\longrightarrow e
\text{non-prompt!}
q\longrightarrow e
\text{non-prompt!}
\mu^{+}
\mu^{-}
Z

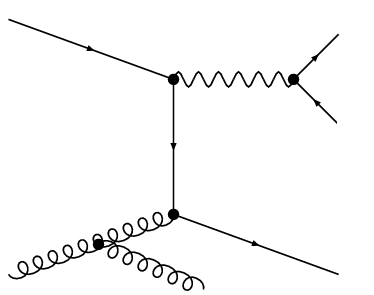
That is why we look for a similar composition coming from \(Z+jets\) events.

Trilepton electron Region Definition

Similarly, a trilepton electron validation region was bulit for testing the modelling of non-prompt electrons. We require the following cuts:

Preselection

Selection

  1. Statistic of non-prompt leptons:
    • In order to test the modelling of the non-prompt leptons and also to reduce uncertainties, one has to ensure a large number of events and a sufficient purity in non-prompt events.
  2. Composition of the non-prompt leptons:
    • Since the fake factor depends on the origin and type of the non-prompt objects, one has to guarantee an agreement in the composition of the non-prompt leptons in the signal and validation region.

Evaluation of validation regions

Criteria considered when building these validation regions:

One of the main goals of these validation regions is to improve the first point, since the LowMjj region had a contribution of only about 25% non-prompt Ana events.

Evaluation of the Trilepton muon Region

Statistic of the non-prompt muons

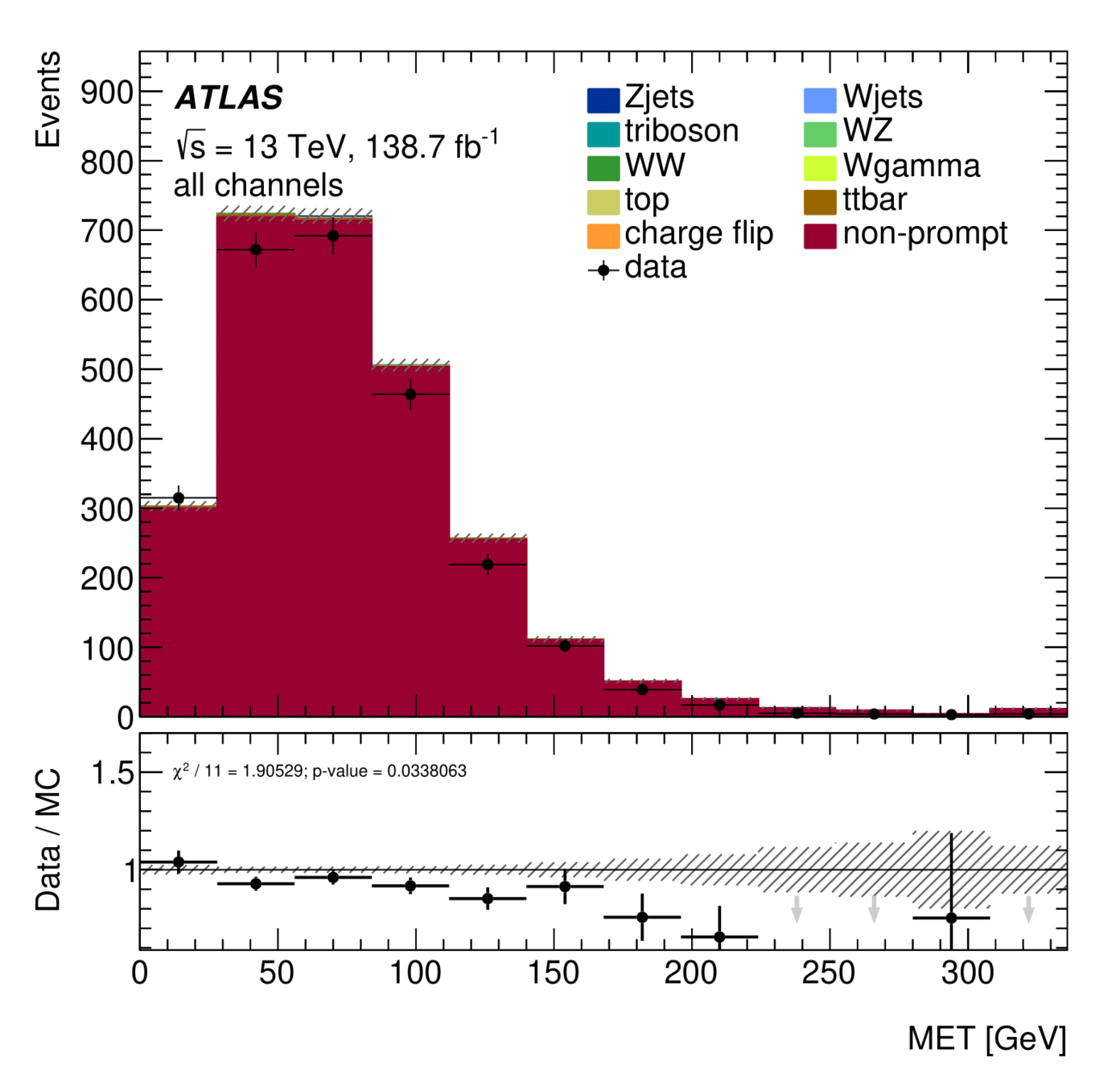
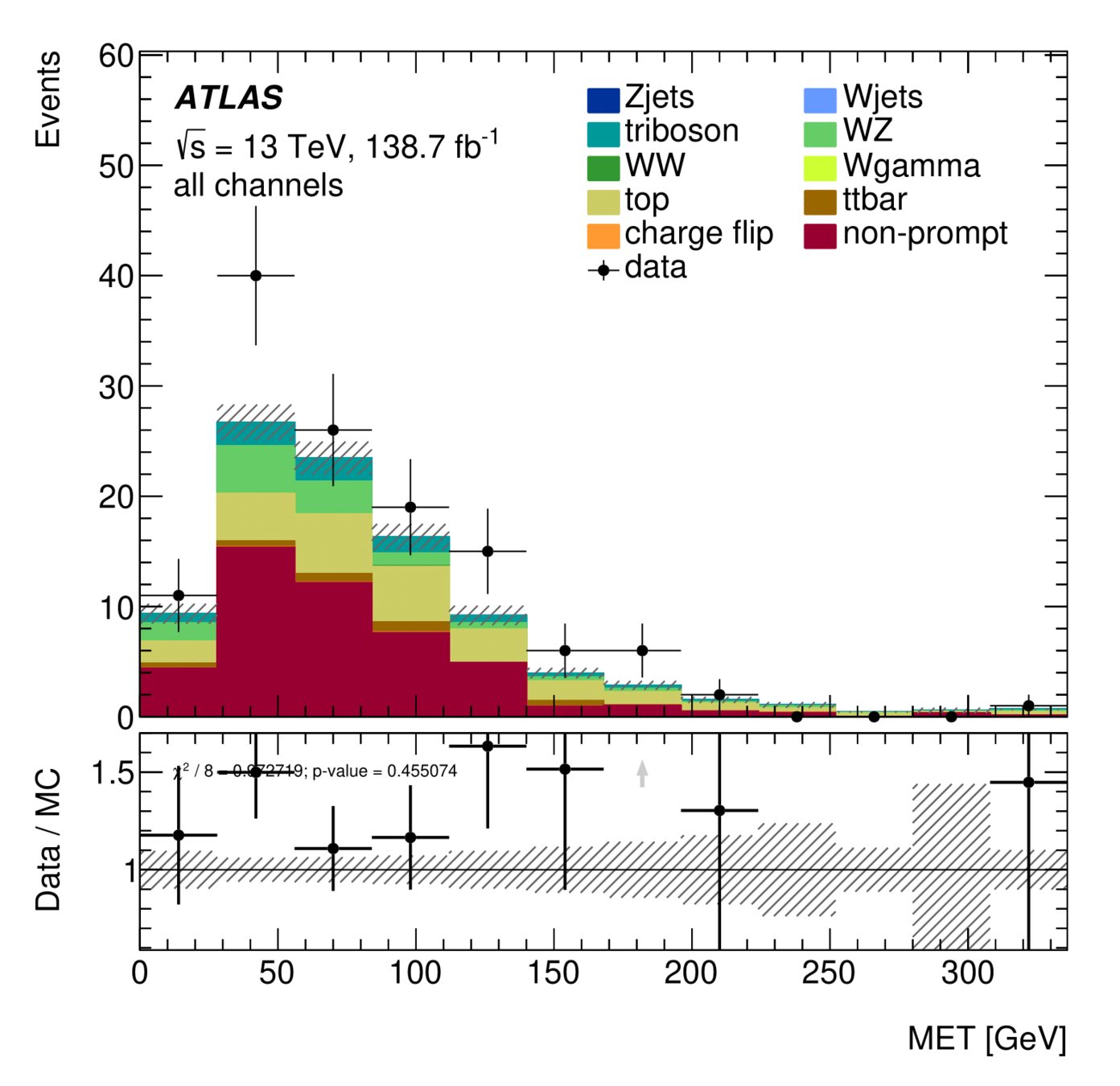
\(E_{T}^{miss}\) distribution for Non-Ana events

\(E_{T}^{miss}\) distribution for Ana events

Evaluation of the Trilepton muon Region

Statistic of the non-prompt muons

\(E_{T}^{miss}\) distribution in the Low \(m_{jj}\) region

The contribution of non-prompt muons in the Trilepton muon region is almost  50%. It was achieved a higher contribution than that of the LowMjj region.

Evaluation of the Trilepton muon Region

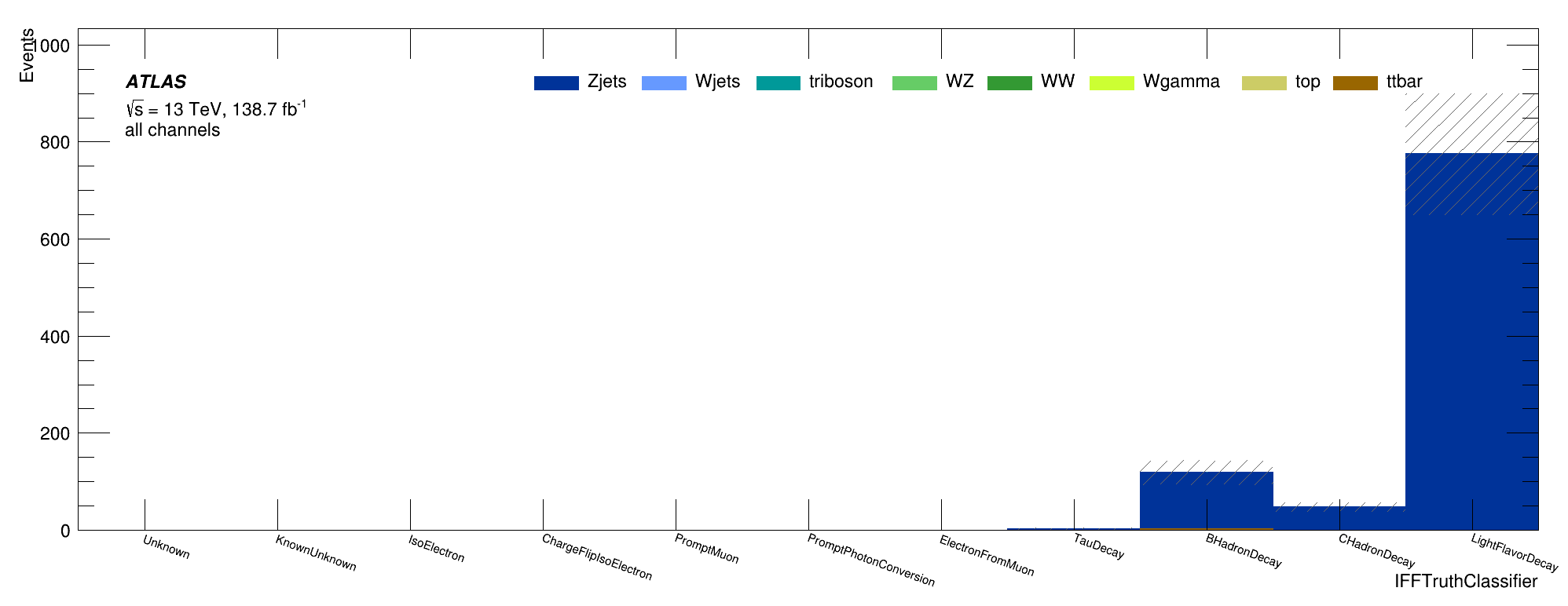
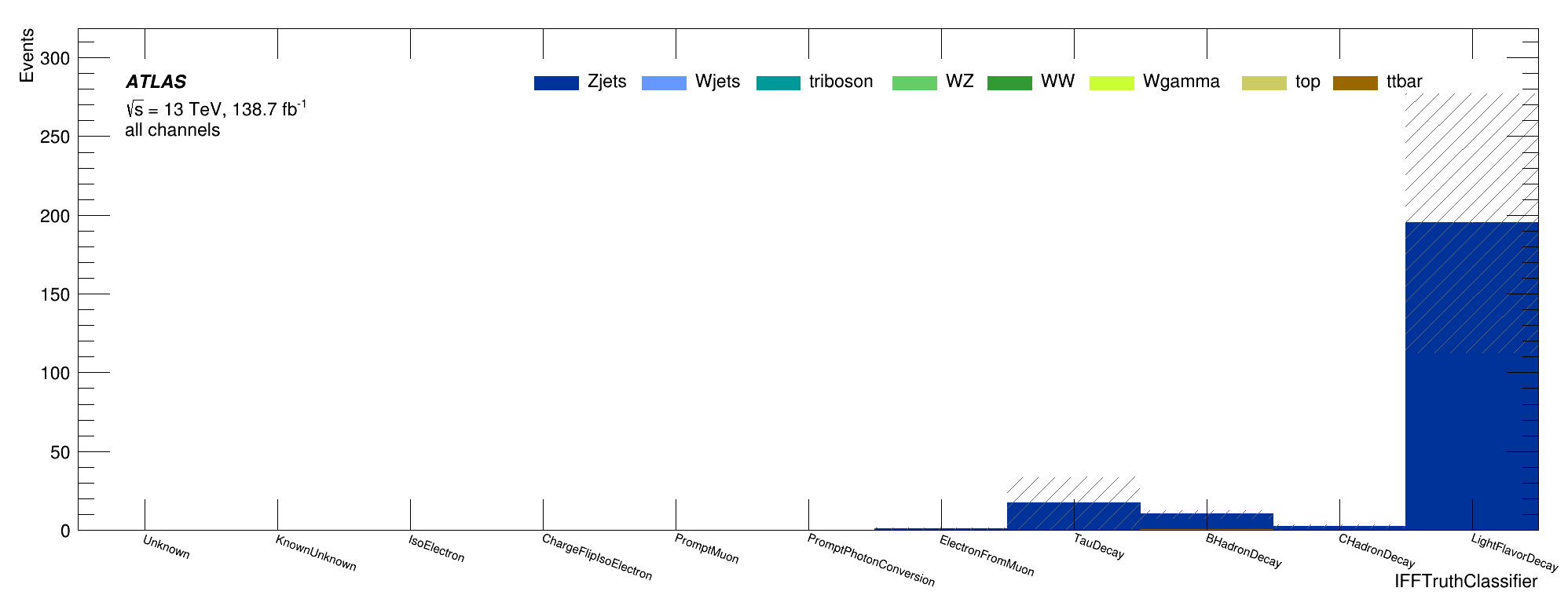
Non-prompt composition: IFFTruthClassifier

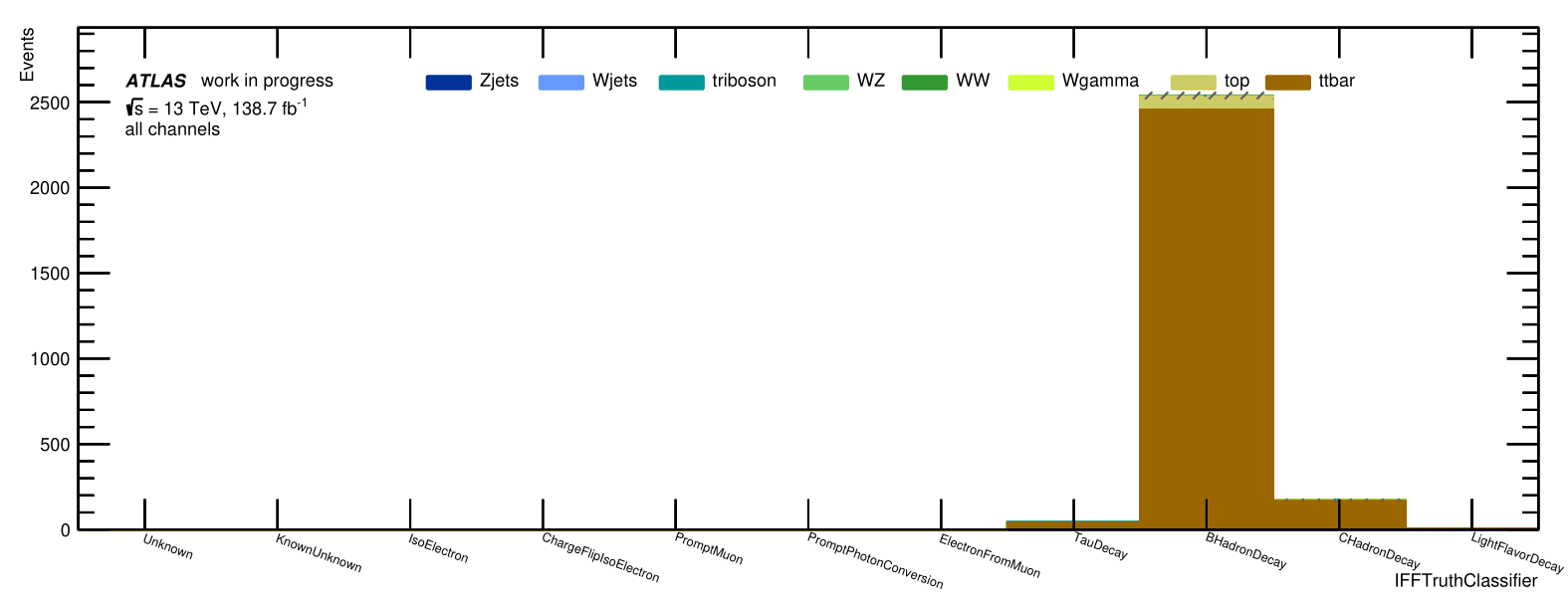
Signal Region:

All non-prompt Non-Ana muons

 

Trilepton muon

Region:

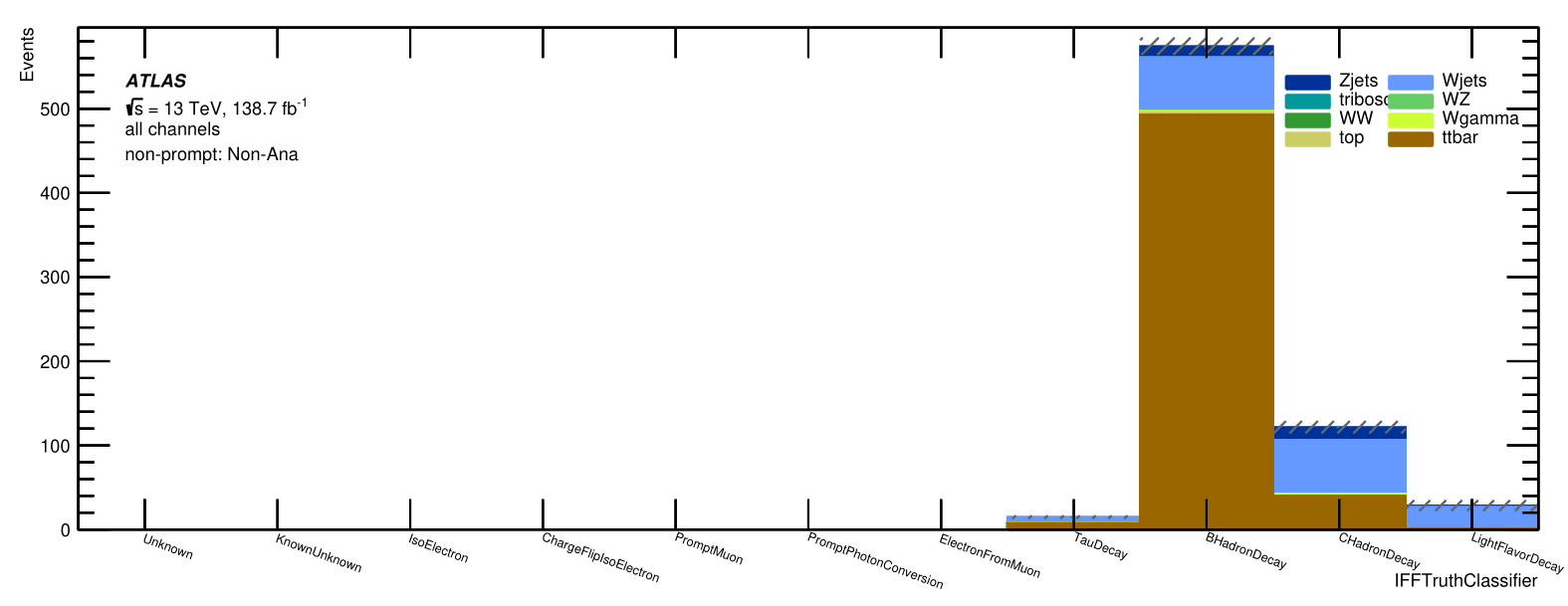
Evaluation of the Trilepton muon Region

Non-prompt composition: IFFTruthClassifier

Trilepton muon

Region:

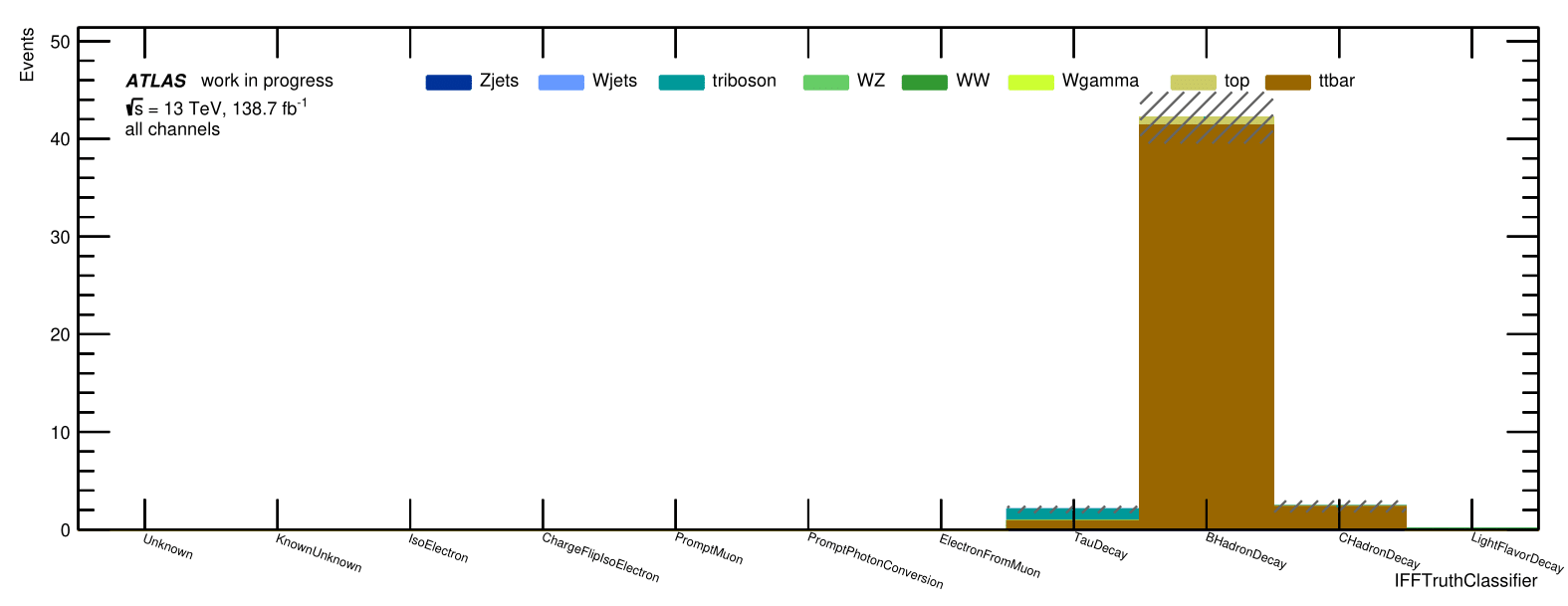
Only Non-prompt Ana muons 

Signal Region:

Evaluation of the Trilepton Electron Region

Statistic of the non-prompt electrons

\(m_{\mu\mu}\) distribution for Non-Ana events

\(m_{\mu\mu}\) distribution for Ana events

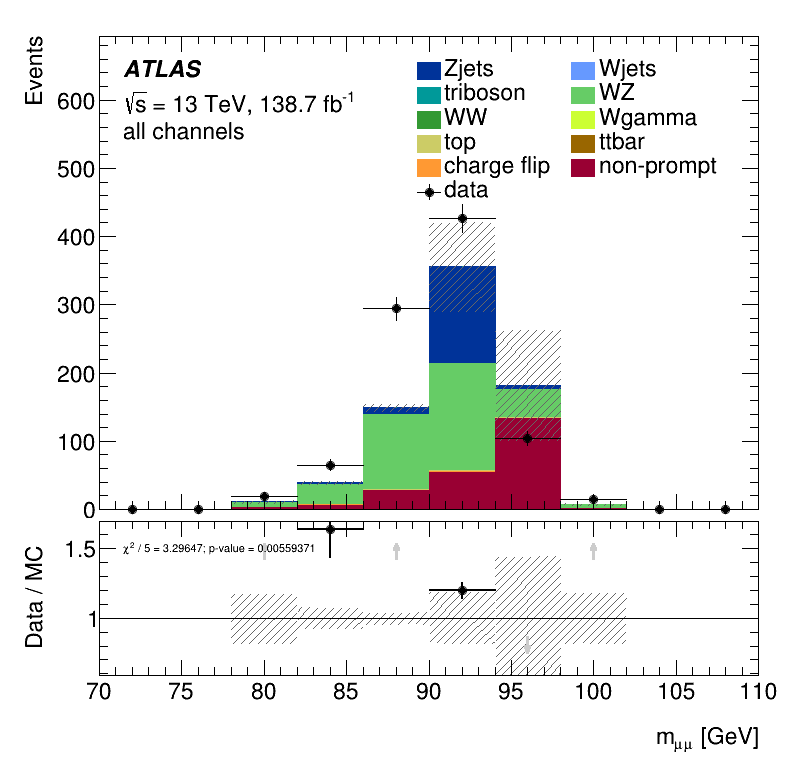
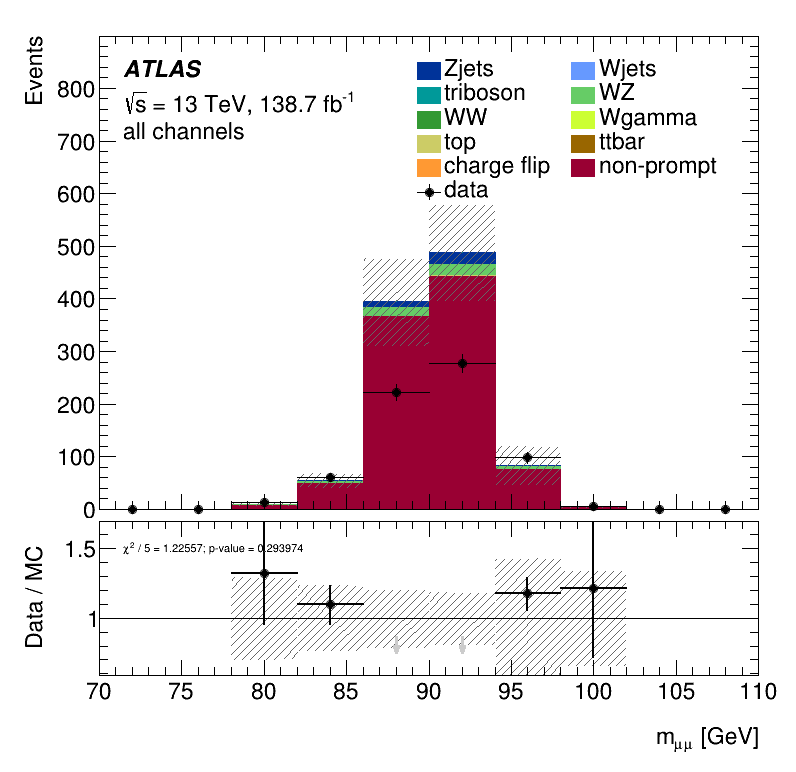
Evaluation of the Trilepton Electron Region

Statistic of the non-prompt electrons

The contribution of non-prompt Ana electrons in the Trilepton electron region is about 31%. Once again, it was achieved a higher non-prompt contribution than that of the LowMjj region.

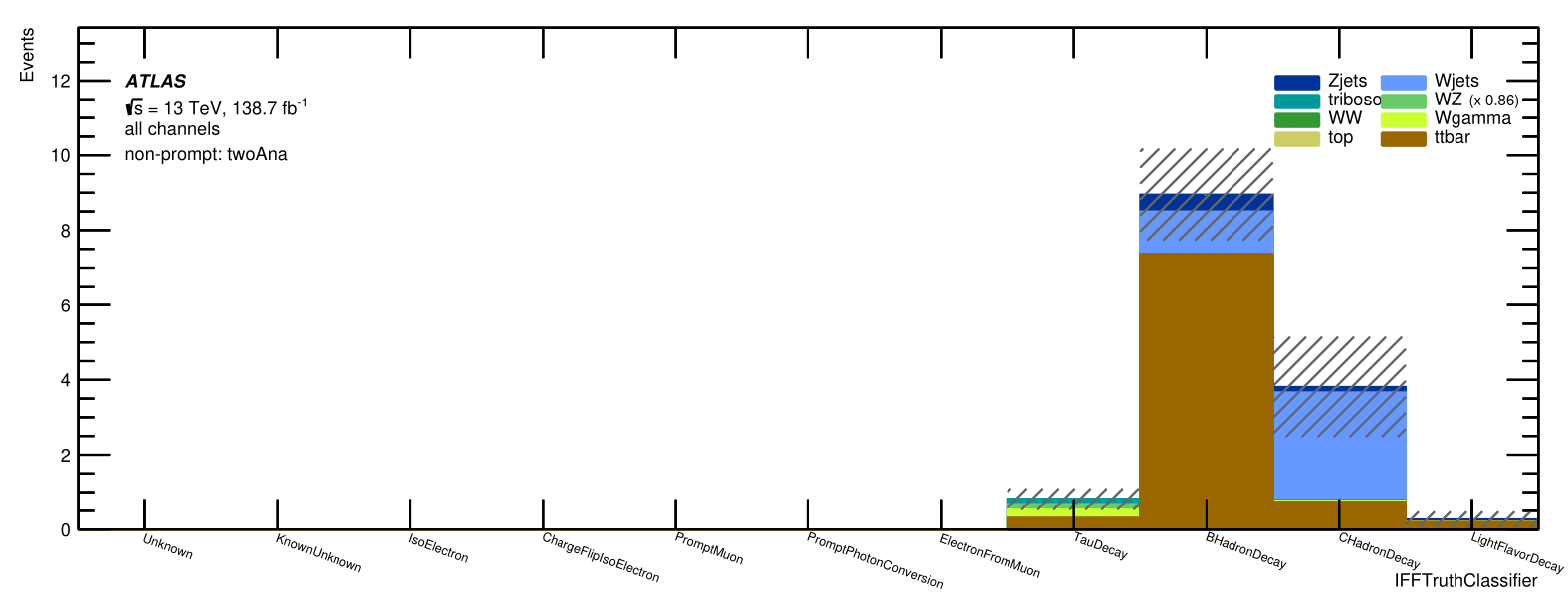
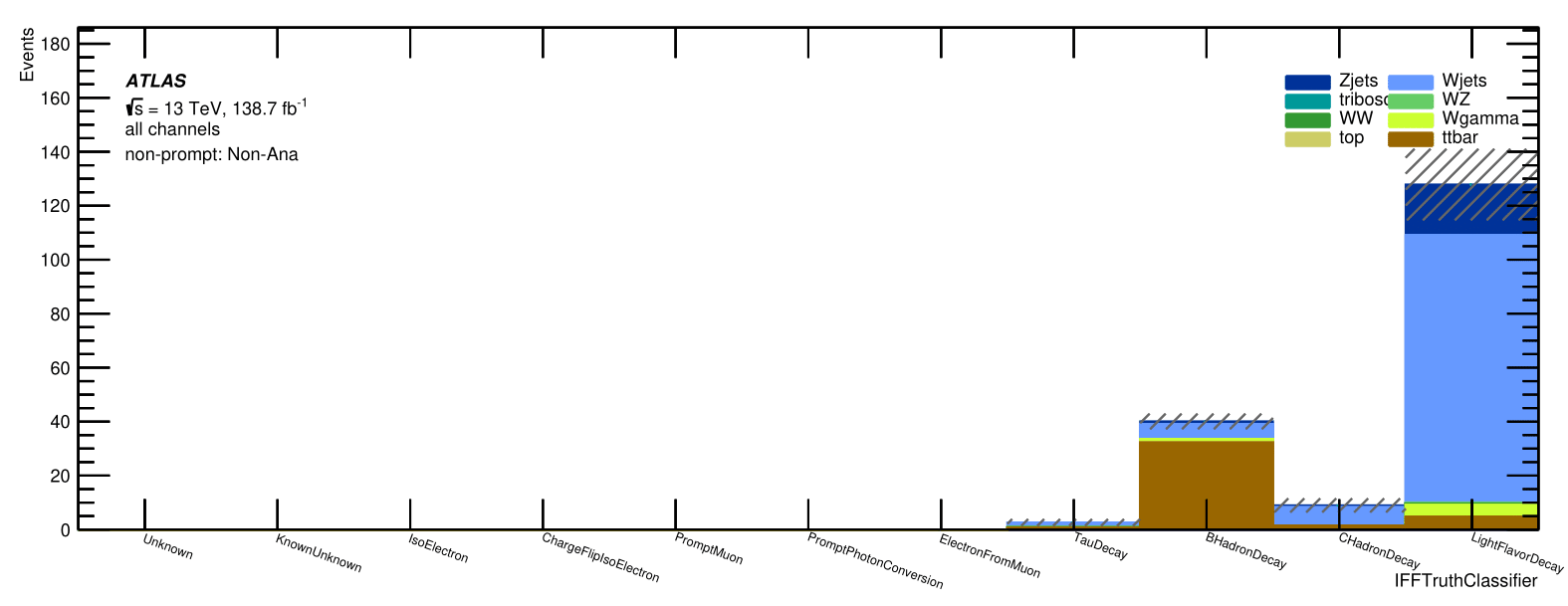
Non-prompt composition: IFFTruthClassifier

Signal Region:

All non-prompt Non-Ana electrons

 

Trilepton muon

Region:

Evaluation of the Trilepton Electron Region

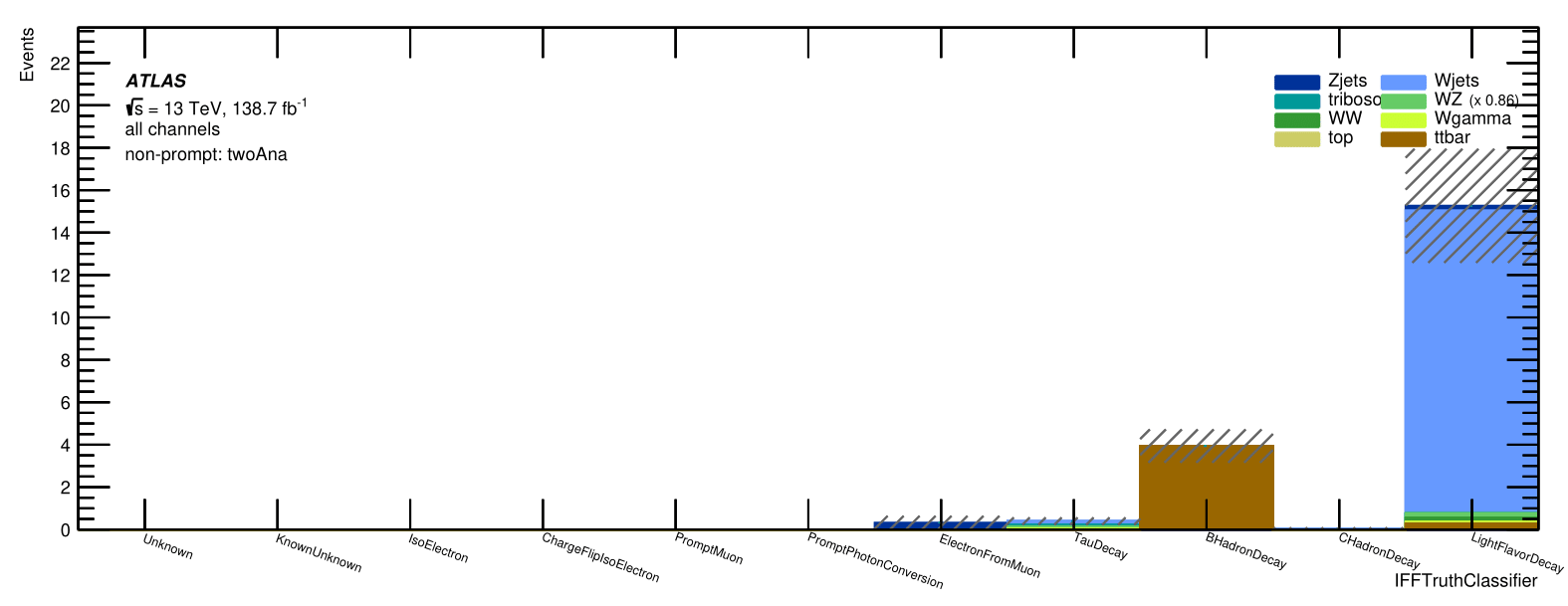
Evaluation of the Trilepton muon Region

Non-prompt composition: IFFTruthClassifier

Trilepton muon

Region:

Only Non-prompt Ana electrons 

Signal Region:

This could be a problem!

  • The fake factor is extracted from MC in control region and then applied to MC in the Validation Region.
\boxed{ N_{A}^{\text{non-prompt MC}} = N_{N}^{\text{non-prompt MC}}\cdot F^{\text{MC CR}}}

Closure Tests

Monte Carlo closure test

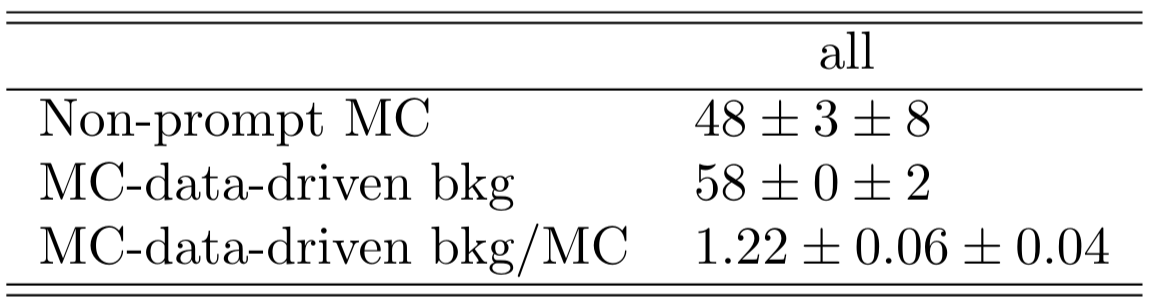
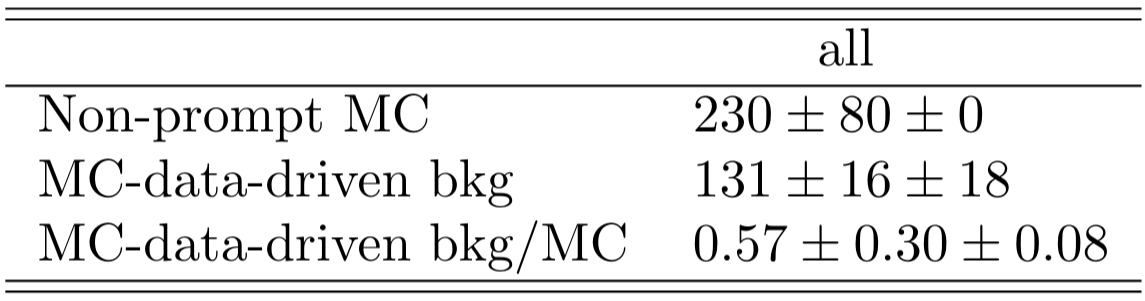
  • The \(N_{A}^{\text{non-prompt}}\) estimate given by the MC-data-driven method is compared to \(N_{A}^{\text{non-prompt}}\) which are actually non-prompt according to the MC truth level information (Non-prompt MC).

MC-data-driven

In an ideal scenario it would be expected that:

\boxed{\frac{\text{MC-datadriven}}{\text{MC}}=1}
  • The number of non-prompt events estimated by MC-data-driven in this region is singificatively above the MC events according to truth-level information.

 \(p_{T}\) distribution for non-prompt muons

  • The technical setup works. 

Results Monte Carlo closure test within the Trilepton muon region

Closure Tests

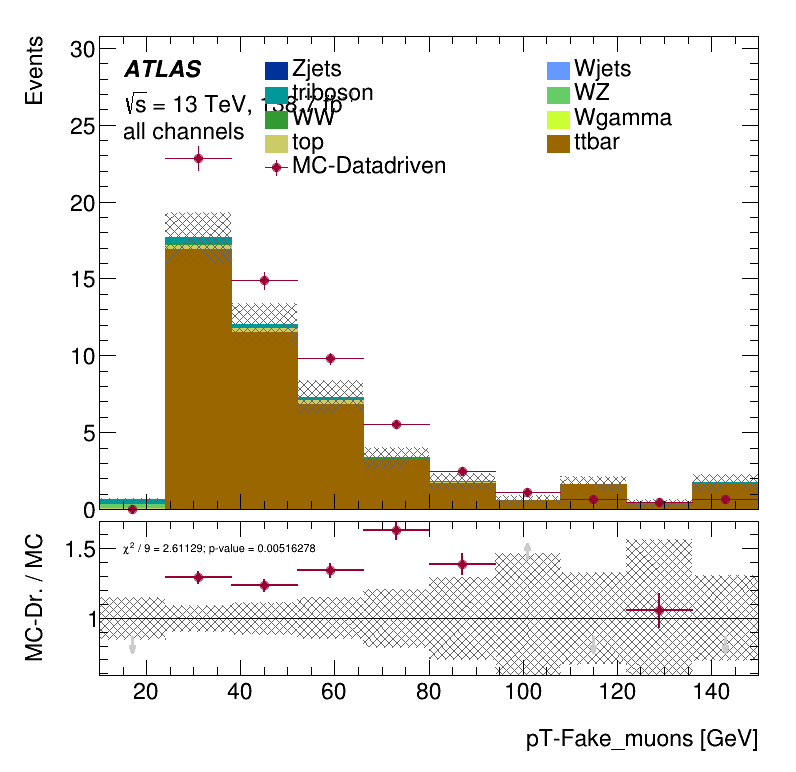
\(m_{lll}\) distribution

\(E_{T}^{miss}\) distribution

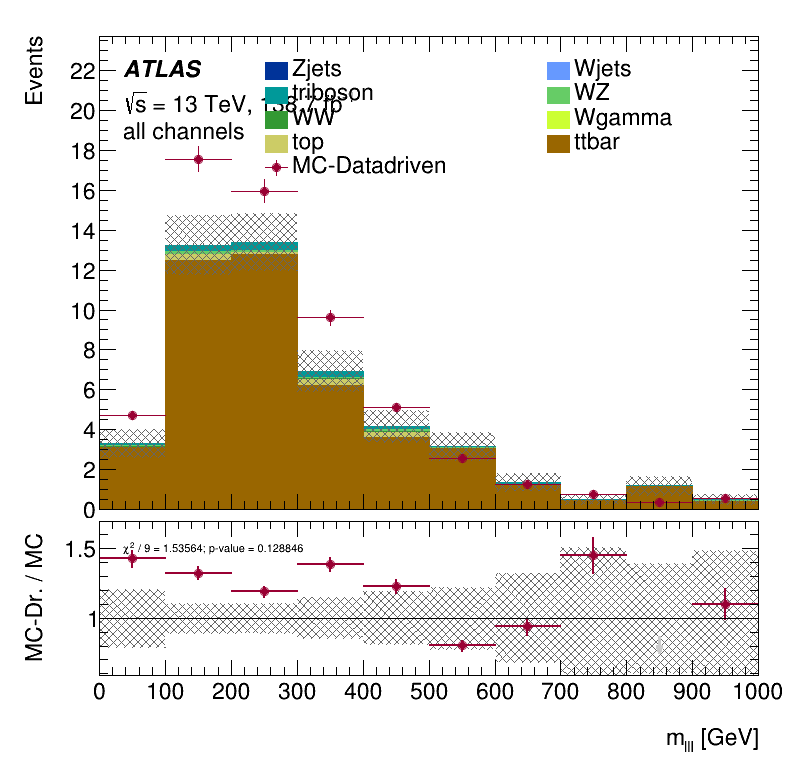
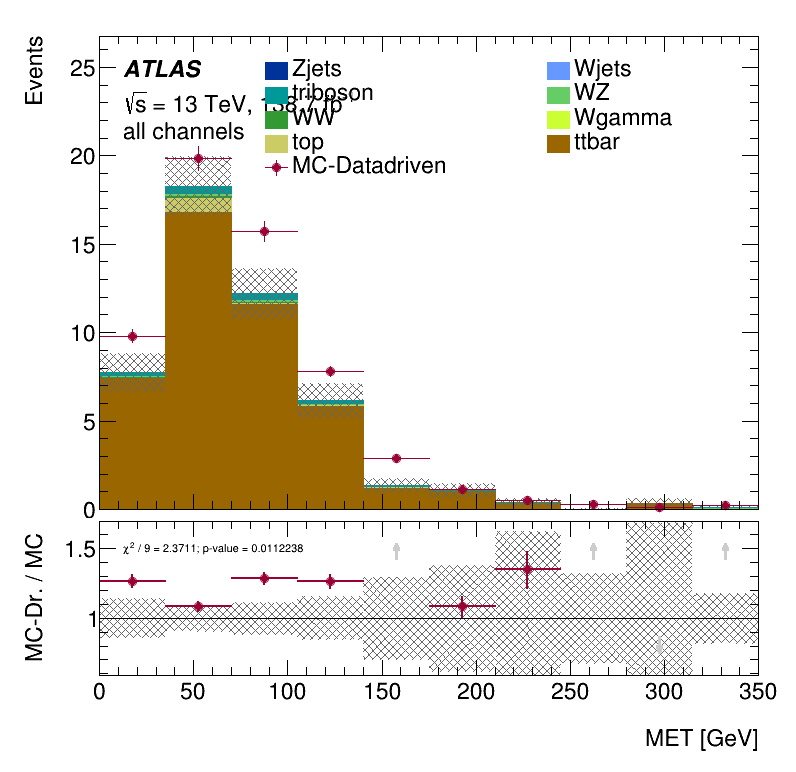
Results Monte Carlo closure test within the Trilepton muon region

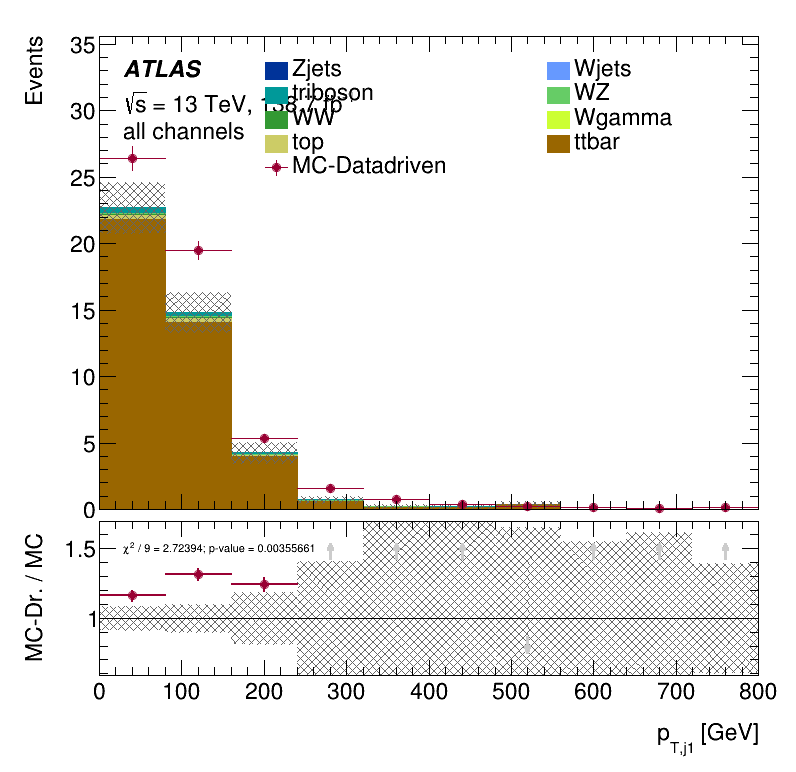
Closure Tests

\(m_{jj}\) distribution

Leading jet \(p_{T }\) distribution

Closure Tests within the trilepton muon region

Results Monte Carlo closure test

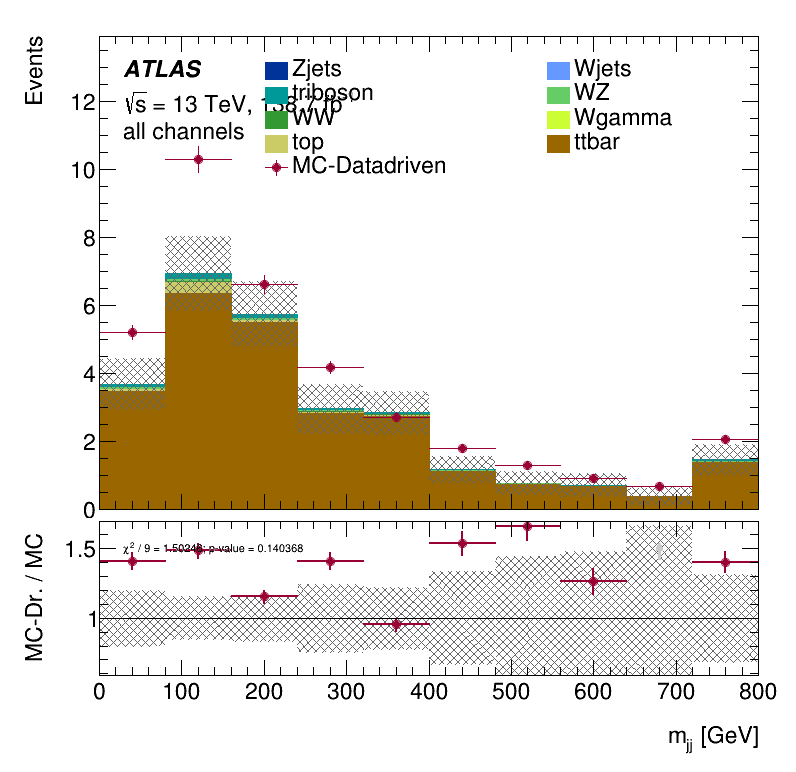
Subleading lepton \(p_{T }\) distribution

Leading lepton \(p_{T }\) distribution

Closure Tests within the trilepton muon region

Results Monte Carlo closure test

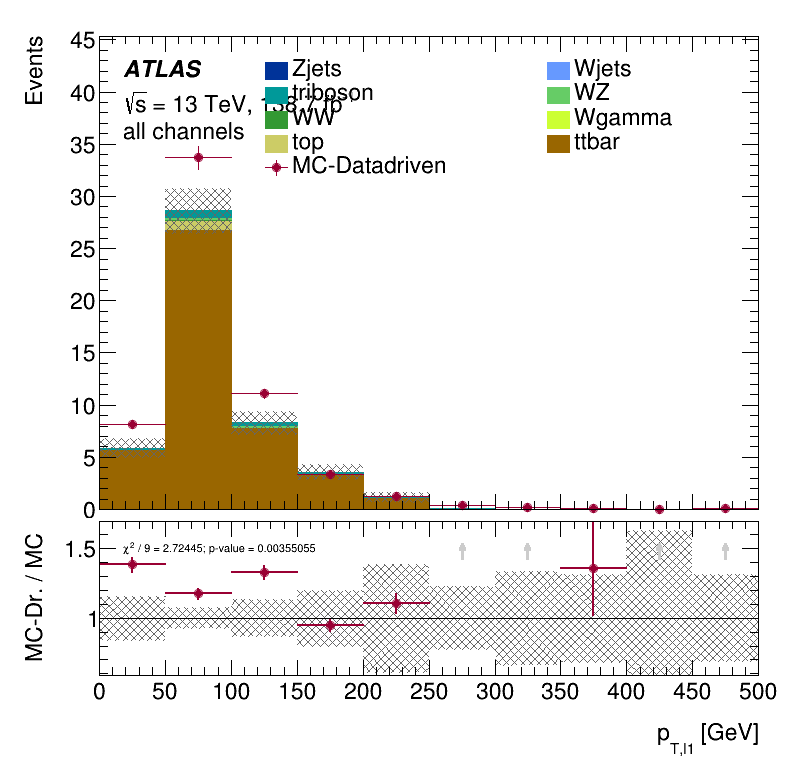
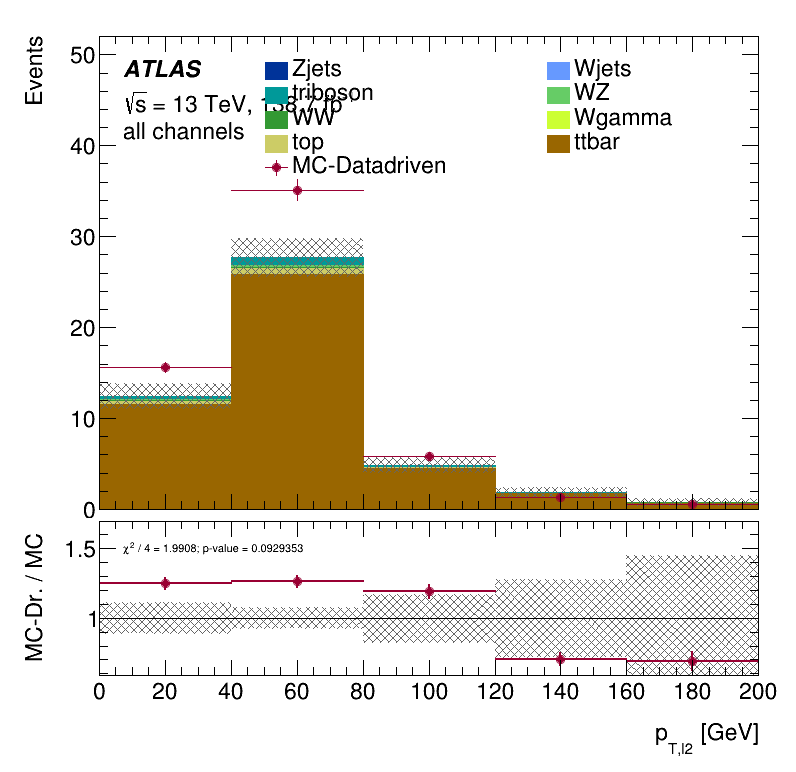
Third lepton \(p_{T }\) distribution

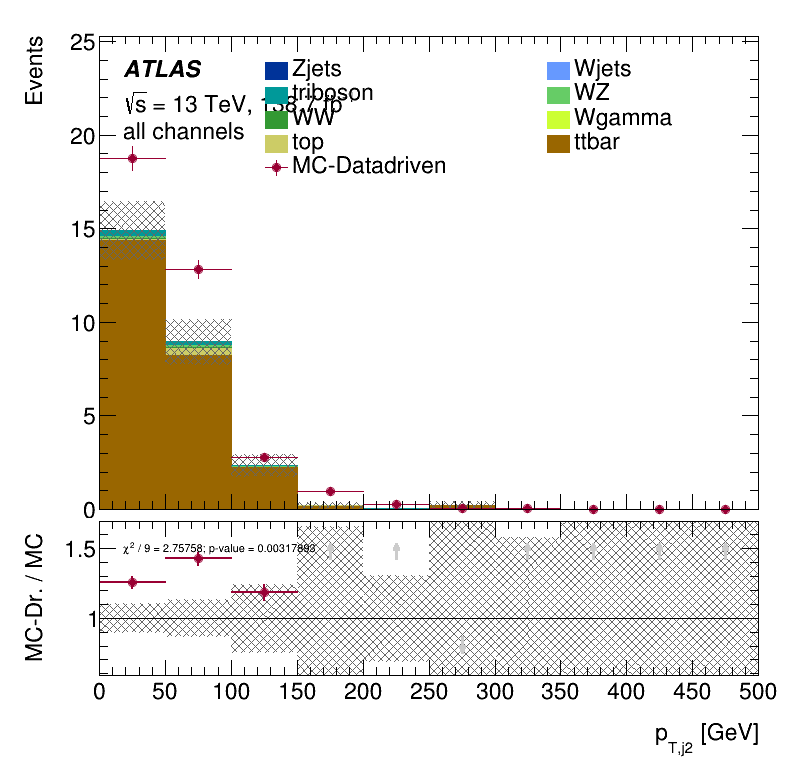
Subleading jet \(p_{T }\) distribution

Closure Tests within the trilepton muon region

Results Monte Carlo closure test

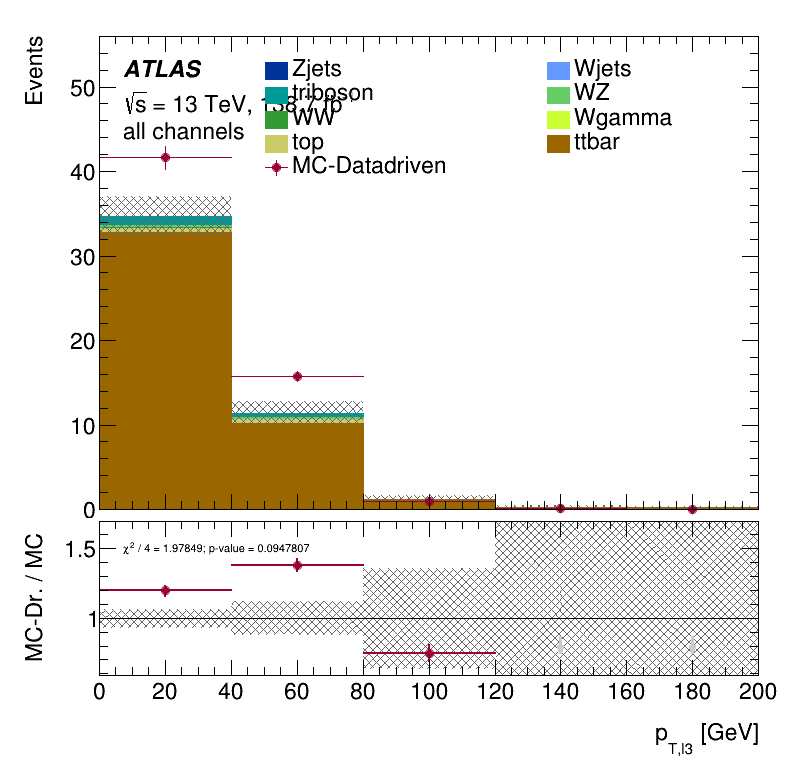
 \(p_{T}\) distribution for the  non-prompt electron

Closure Tests

Results Monte Carlo closure test within the Trilepton electron region

In this case, the number of MC-data-driven events is notably below the MC events according to truth-level information.

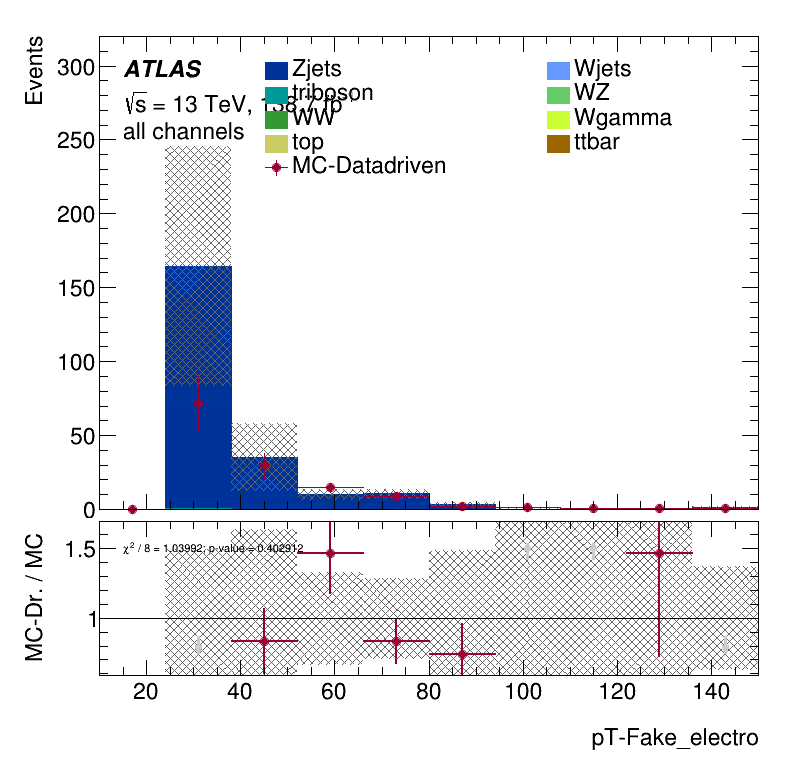
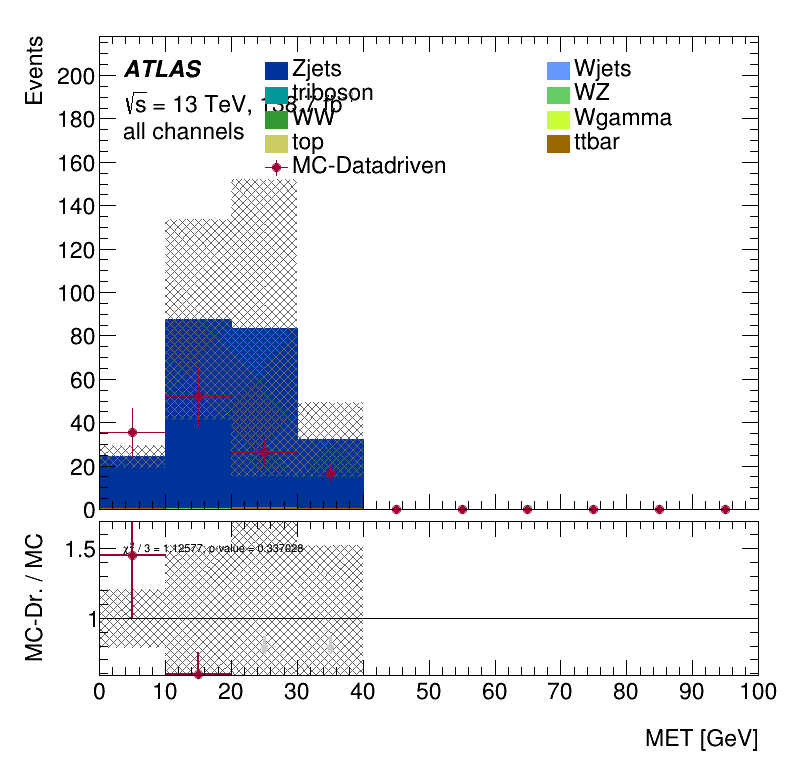
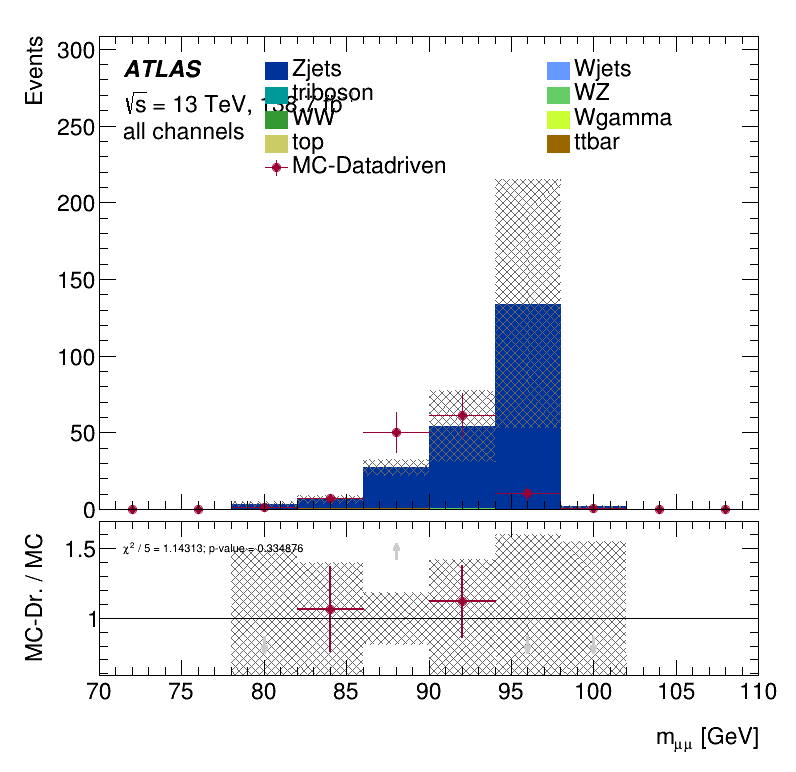
\(m_{\mu\mu}\) distribution

\(E_{T}^{miss}\) distribution

Closure Tests

Results Monte Carlo closure test within the Trilepton electron region

Closure Tests

Results Monte Carlo closure test within the Trilepton electron region

\(m_{jj}\) distribution

Leading jet \(p_{T }\) distribution

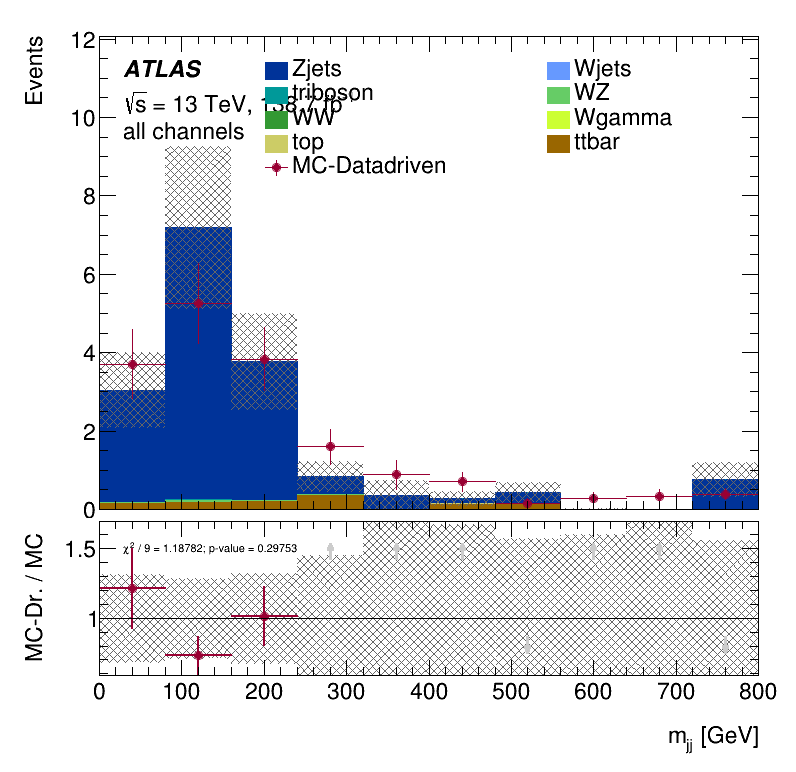
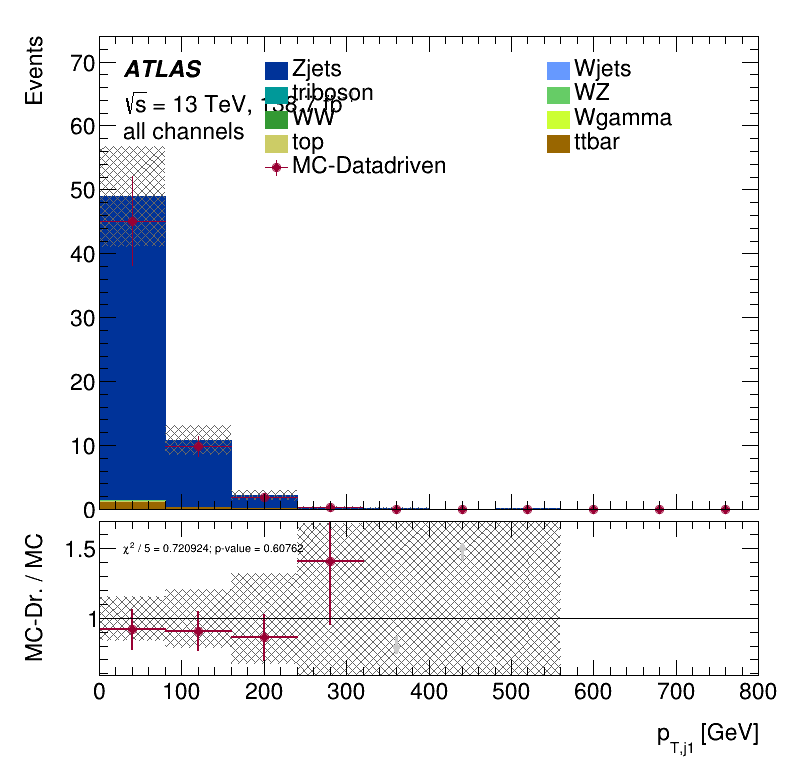
Closure Tests

Results Monte Carlo closure test within the Trilepton electron region

Leading lepton \(p_{T }\) distribution

Subleading lepton \(p_{T }\) distribution

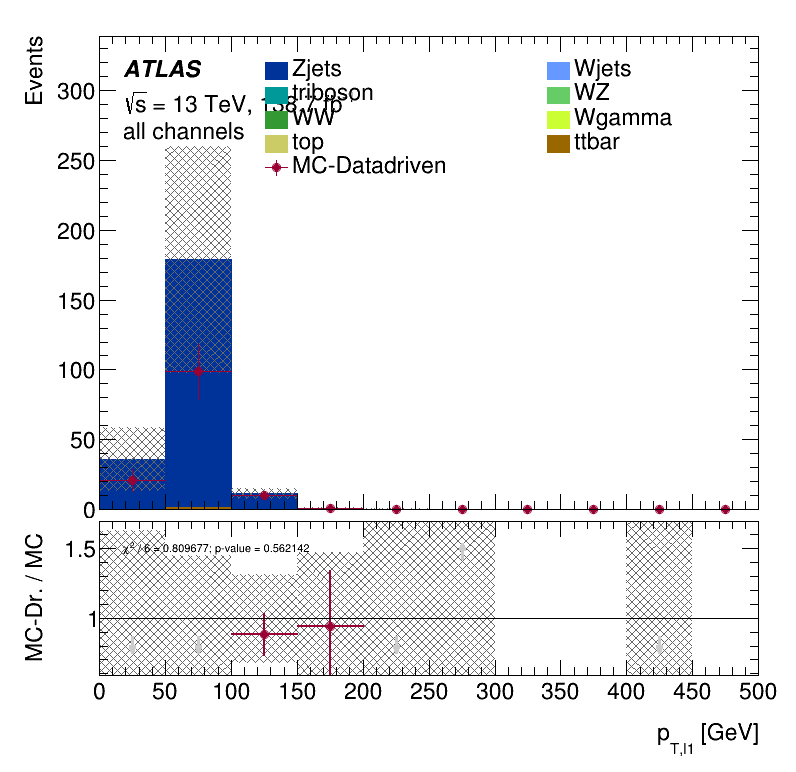
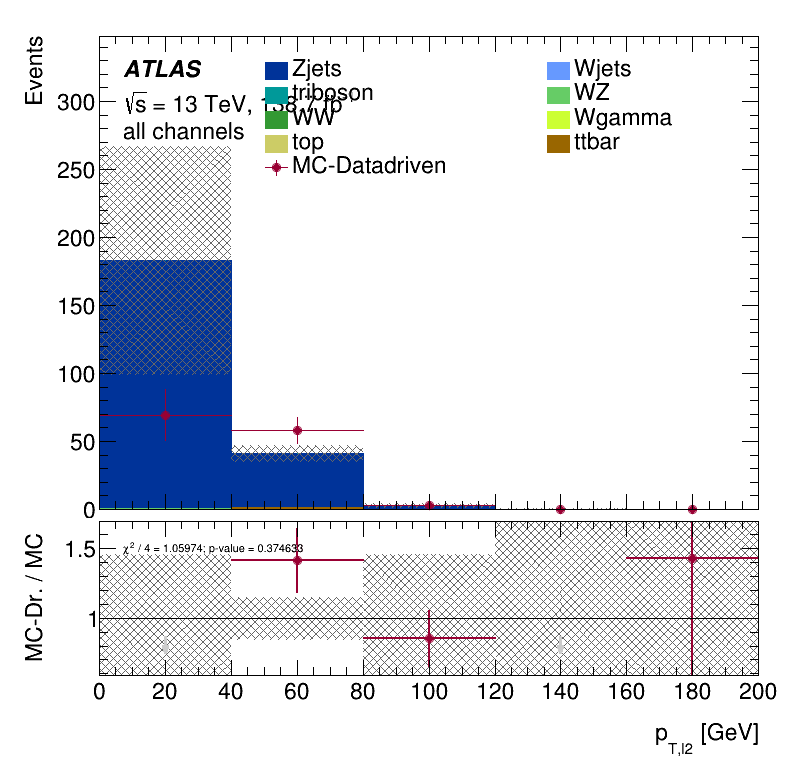
Subleading jet \(p_{T}\) distribution

Closure Tests

Results Monte Carlo closure test within the Trilepton electron region

Third lepton \(p_{T }\) distribution

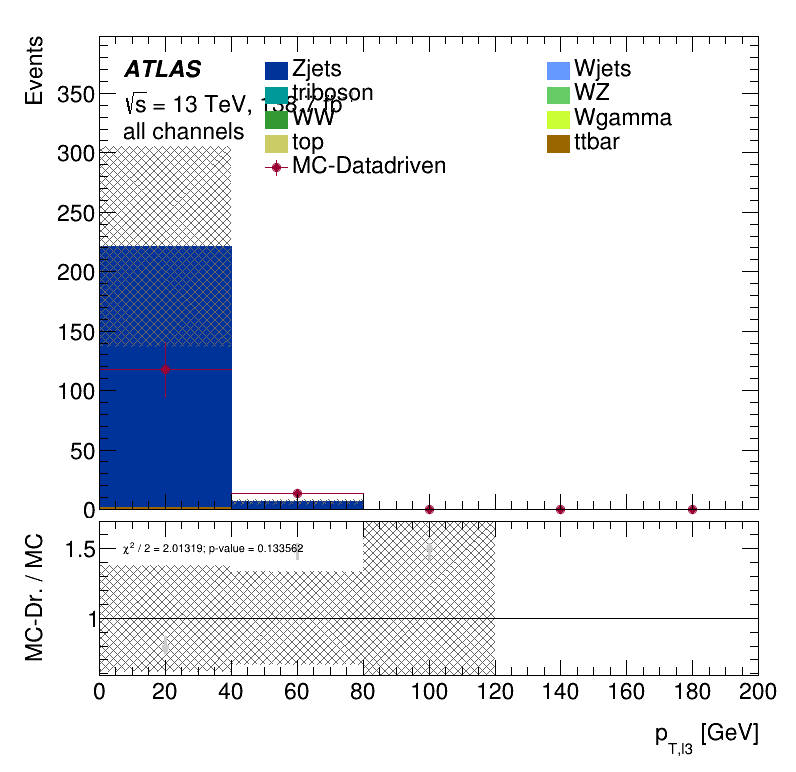
  • The fake factor is extracted from data in the control region and then applied to data in the validation region.
\boxed{ N_{A}^{\text{non-prompt}} = (N_{N}^{\text{data}}-N_{N}^{\text{prompt MC}})\cdot F^{\text{data CR}}}

Data closure test

  • It is investigated how well the collision data is modellled by the sum of the Monte Carlo predictions for the prompt background and the non-prompt background estimated by the data-driven technique.

Data-driven

\boxed{\frac{\text{Data}}{\text{Prompt MC + Charge flip MC + Data-driven bkg}}=1}

In an ideal scenario it would be expected that:

Closure Tests

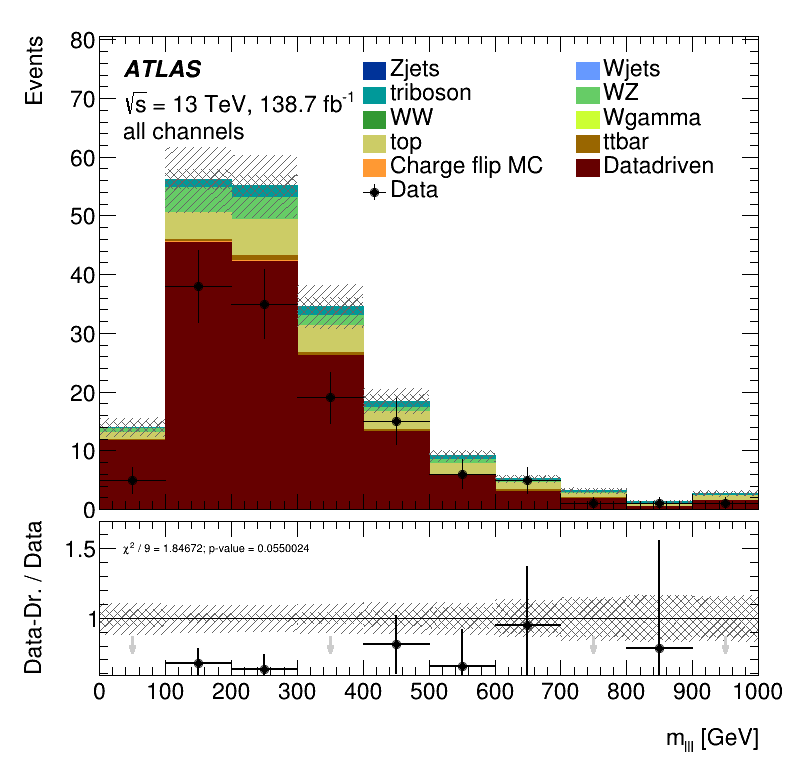
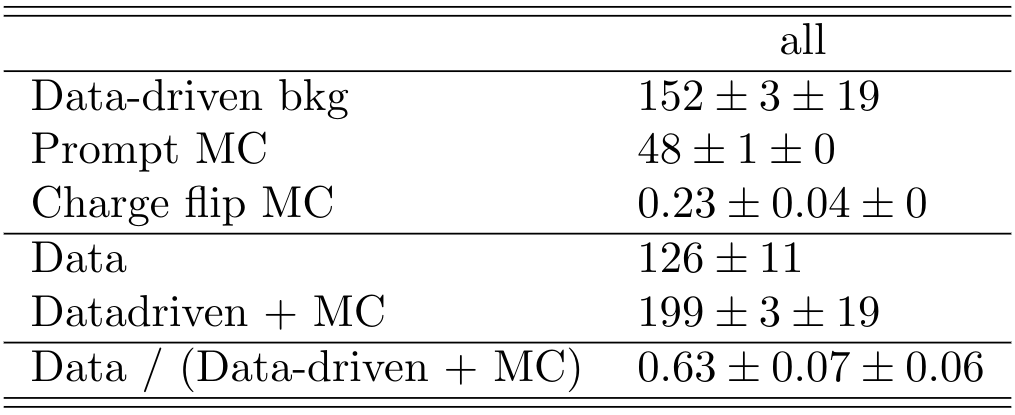
The result found in the MC closure is confirmed here. It is clear a not negligible overestimation of data by the sum of the data-driven estimated non-prompt bkg and the prompt contribution predicted by MC simulations.

\(m_{lll}\) distribution

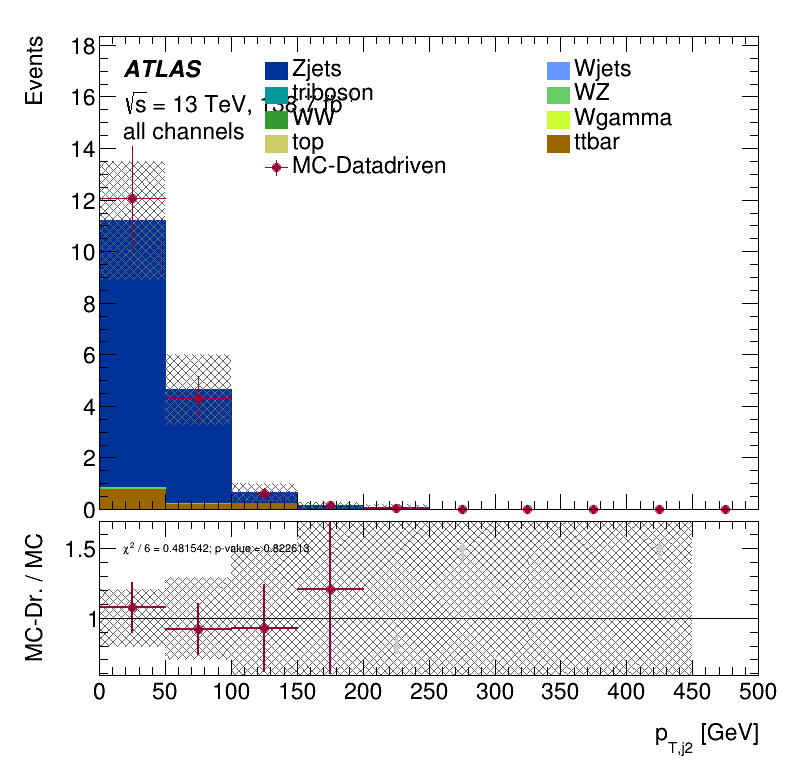
Closure Tests

Results data closure test within the Trilepton muon region

\(E_{T}^{miss}\) distribution

Leading lepton \(p_{T}\)

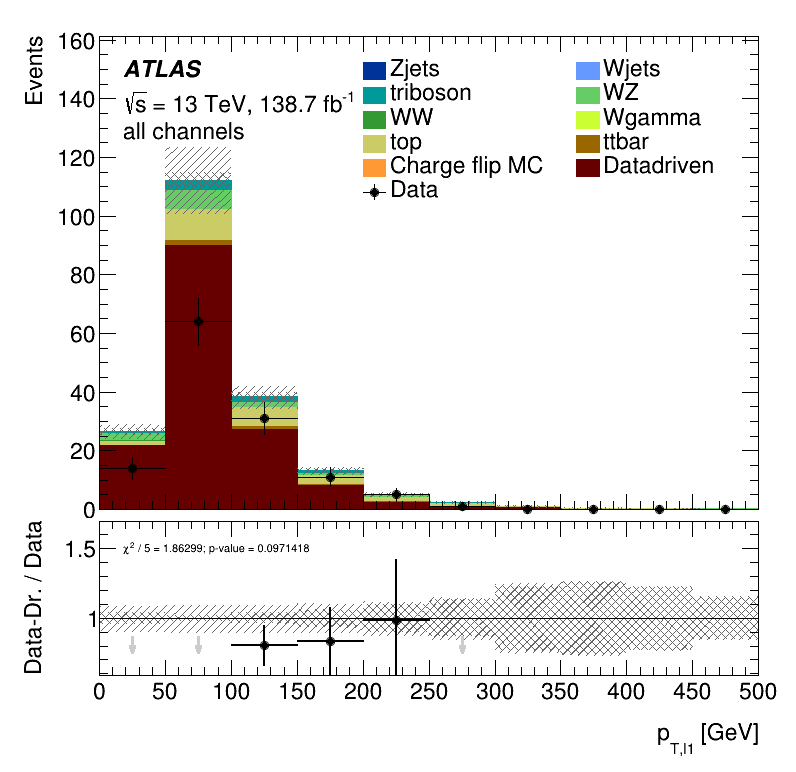
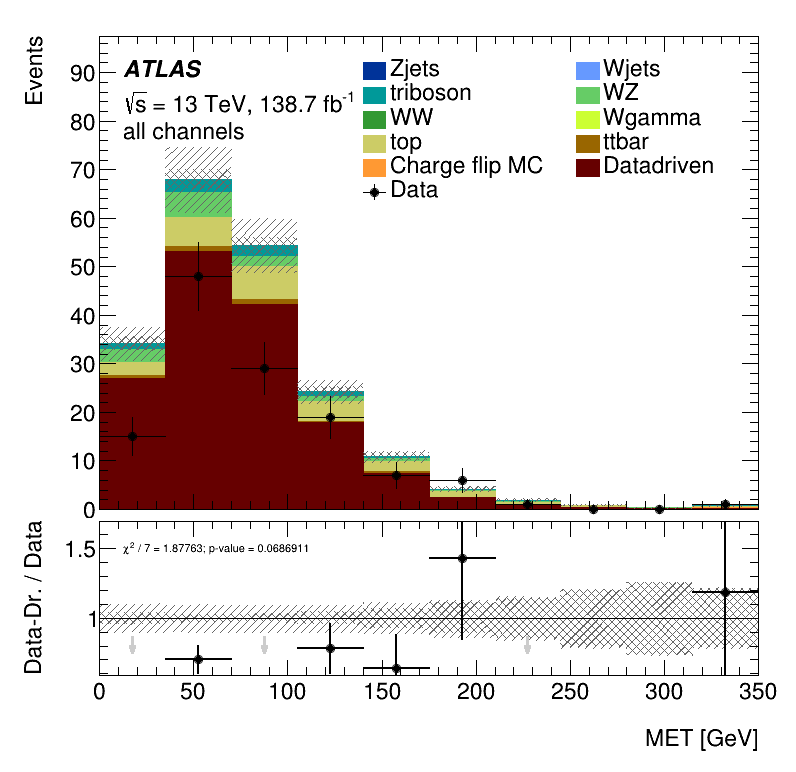
Results data closure test within the Trilepton muon region

Closure Tests

Leading jet \(p_{T}\)

Subleading jet \(p_{T}\)

Closure Tests within the trilepton muon region

Results data closure test

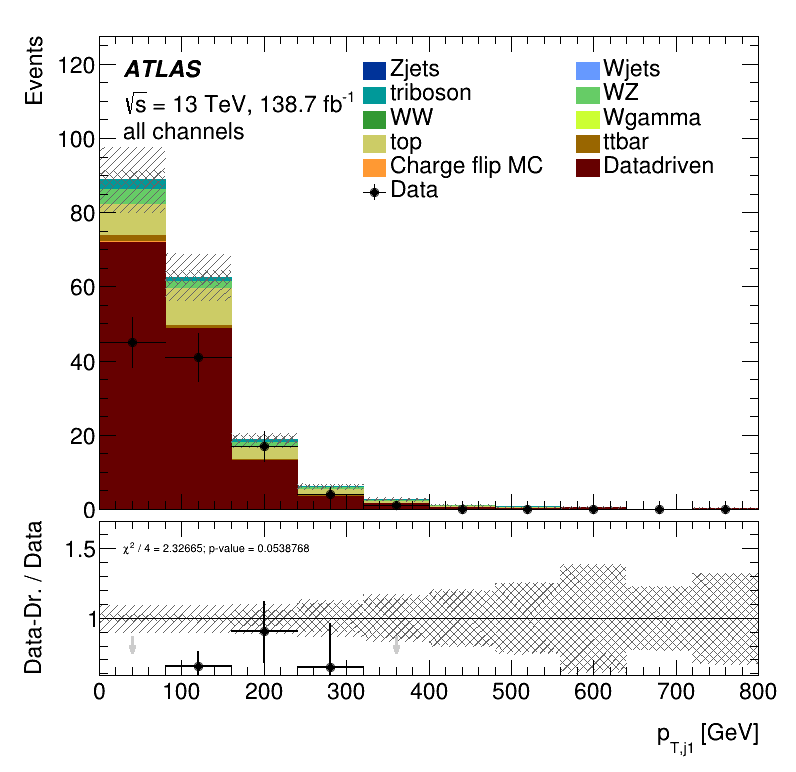
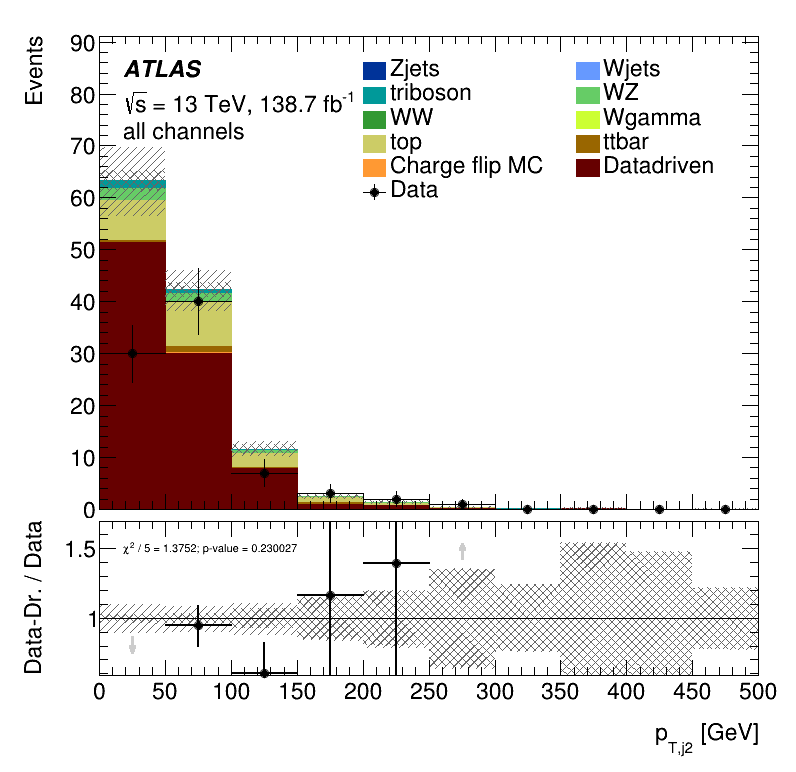
\(m_{jj}\) distribution

Subleading lepton \(p_{T}\)

Closure Tests within the trilepton muon region

Results data closure test

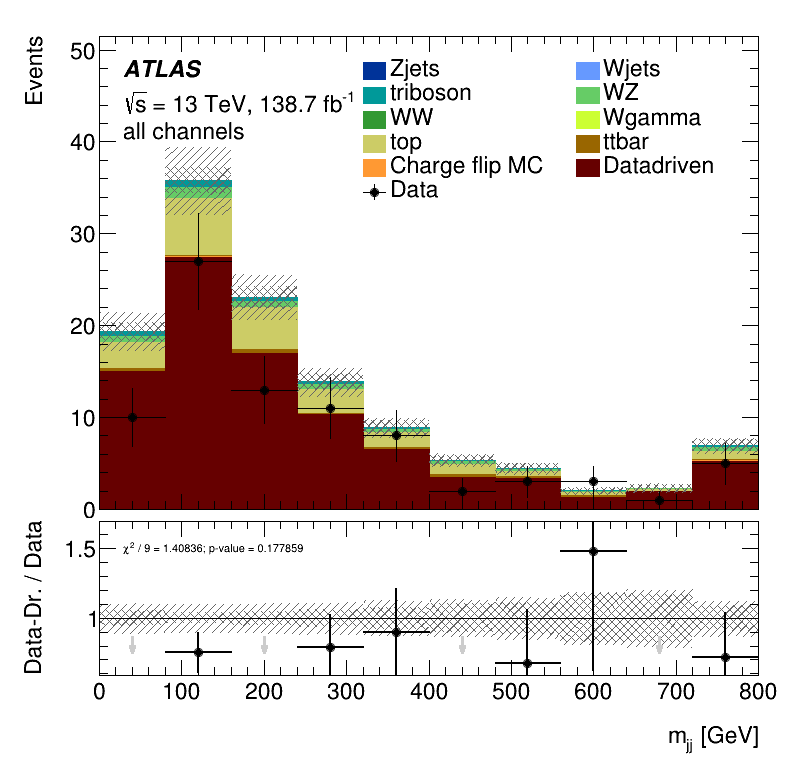
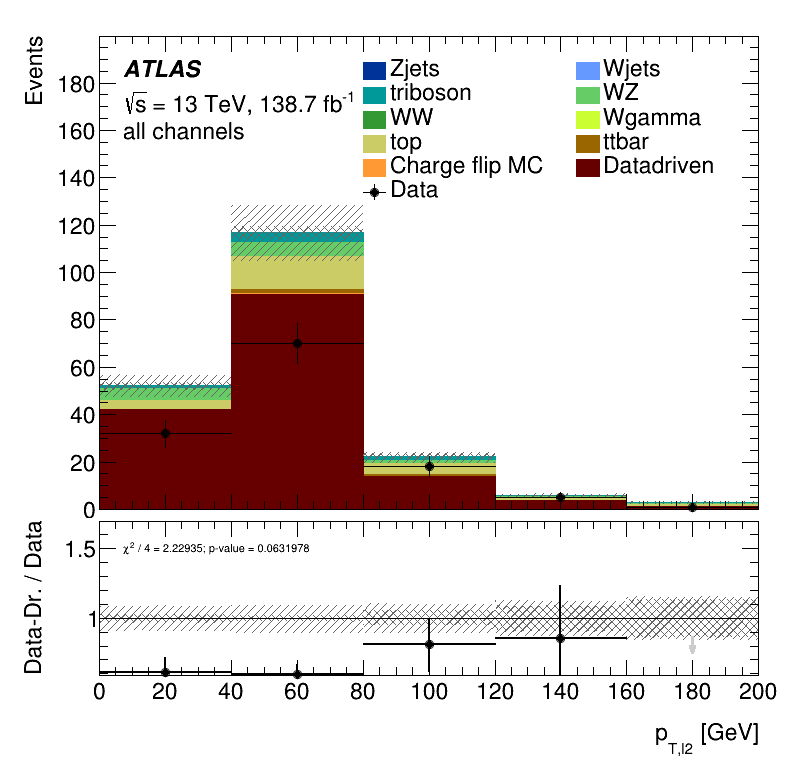
Third lepton \(p_{T}\)

Closure Tests within the trilepton muon region

Results data closure test

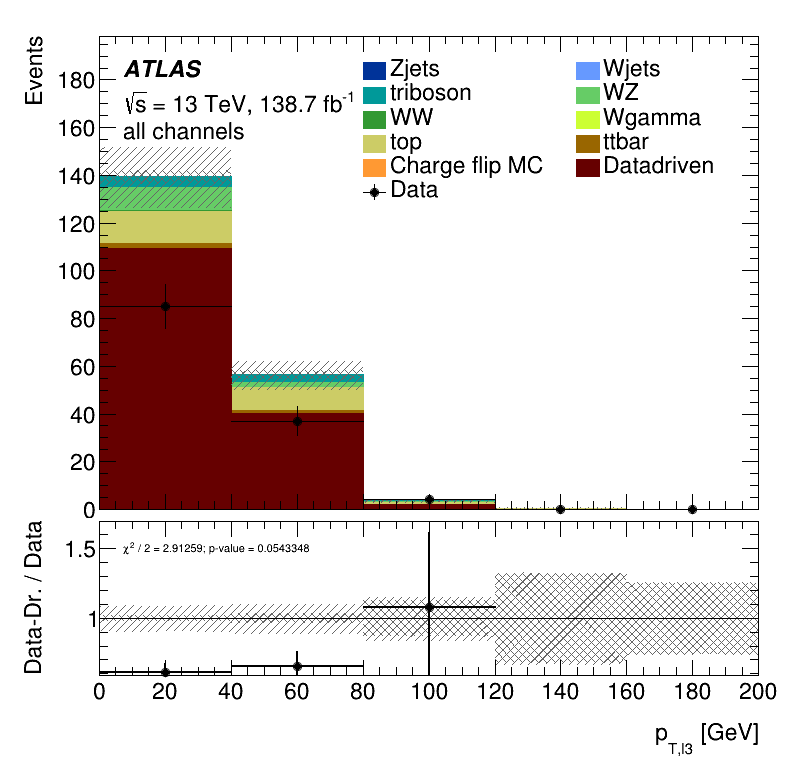
Closure Tests

Results data closure test within the Trilepton electron region

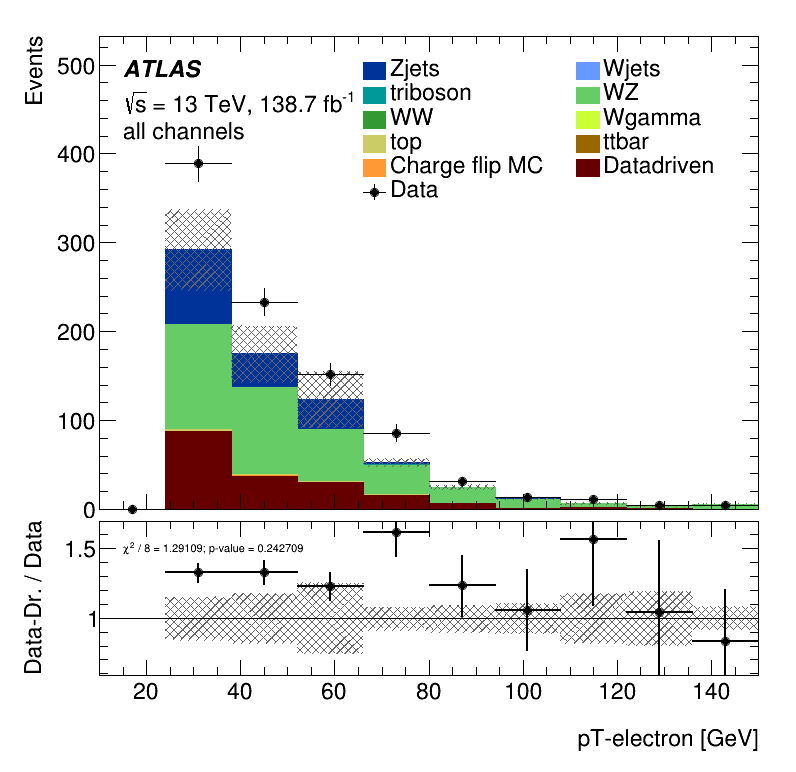
Electron \(p_{T}\) distribution

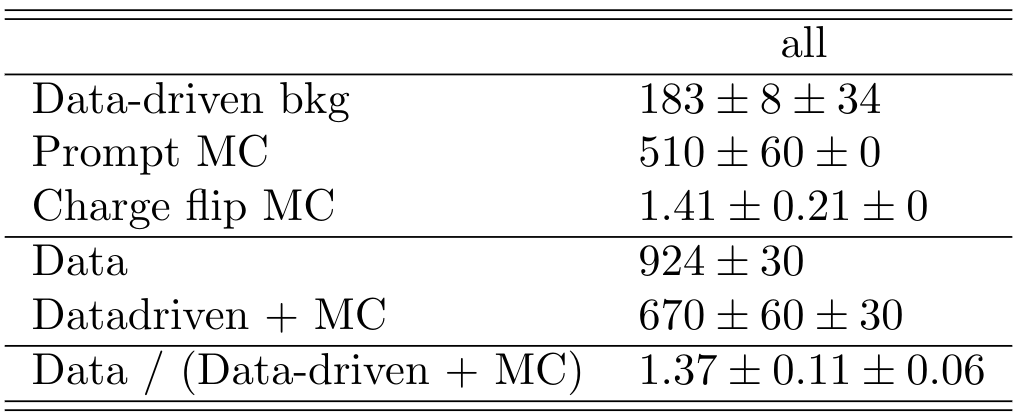
Once again the result seen in the MC closure is confirmed. It is clear a significant underestimation of the data. This underestimation is approximately a factor two in the non-prompt estimate.

Closure Tests

Results data closure test within the Trilepton electron region

\(m_{\mu\mu}\) distribution

\(E_{T}^{miss}\) distribution

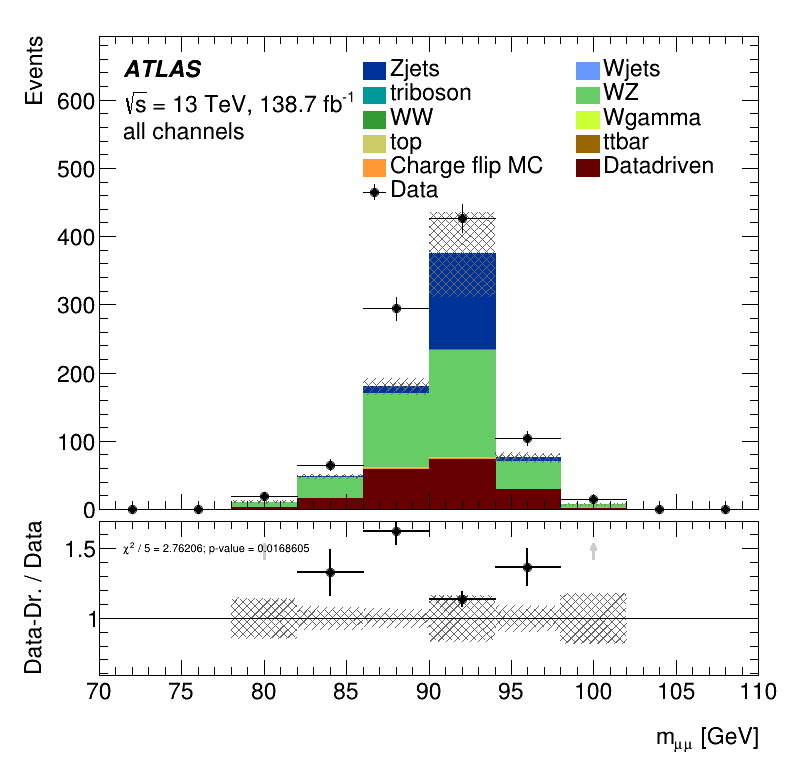
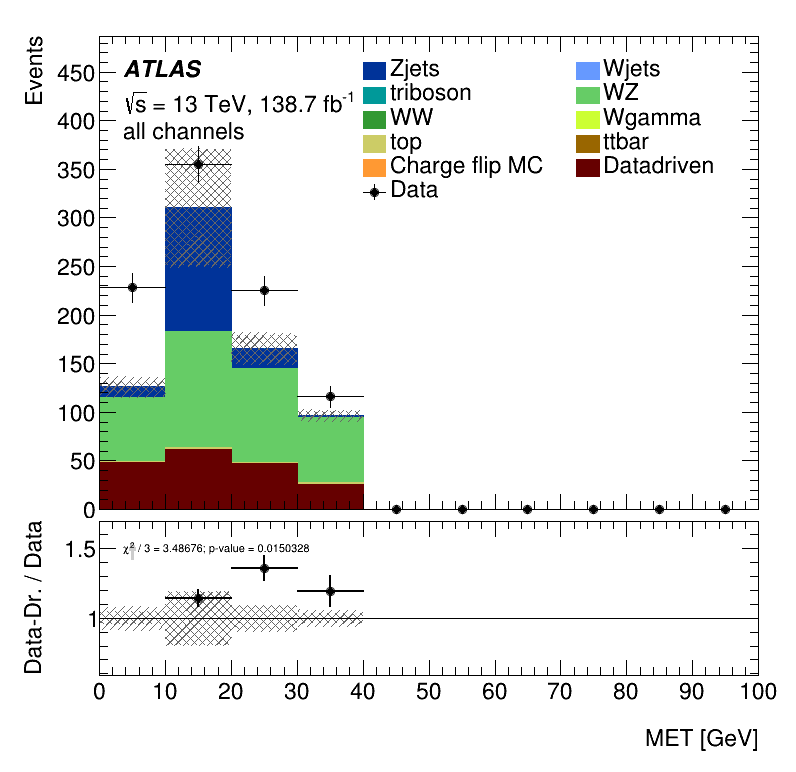
Closure Tests

Results data closure test within the Trilepton electron region

\(m_{jj}\) distribution

Leading jet \(p_{T }\) distribution

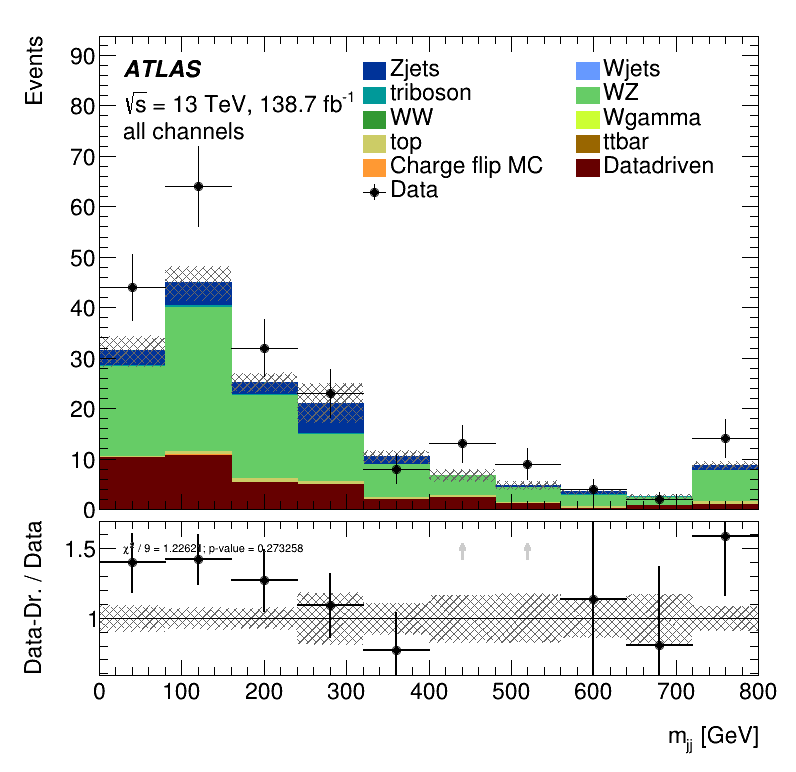
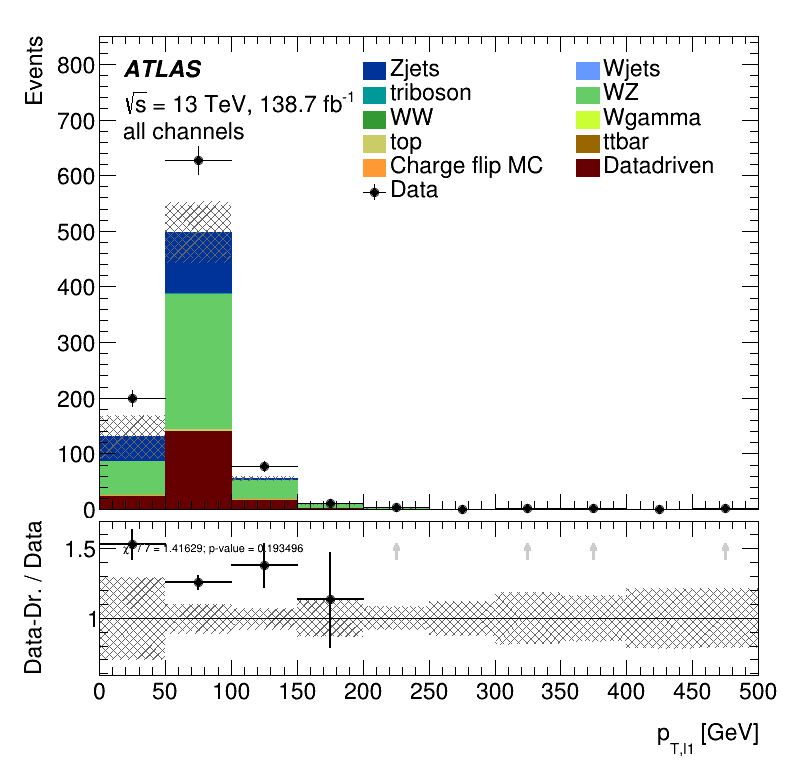
Closure Tests

Results data closure test within the Trilepton electron region

Leading lepton \(p_{T }\) distribution

Subleading lepton \(p_{T }\) distribution

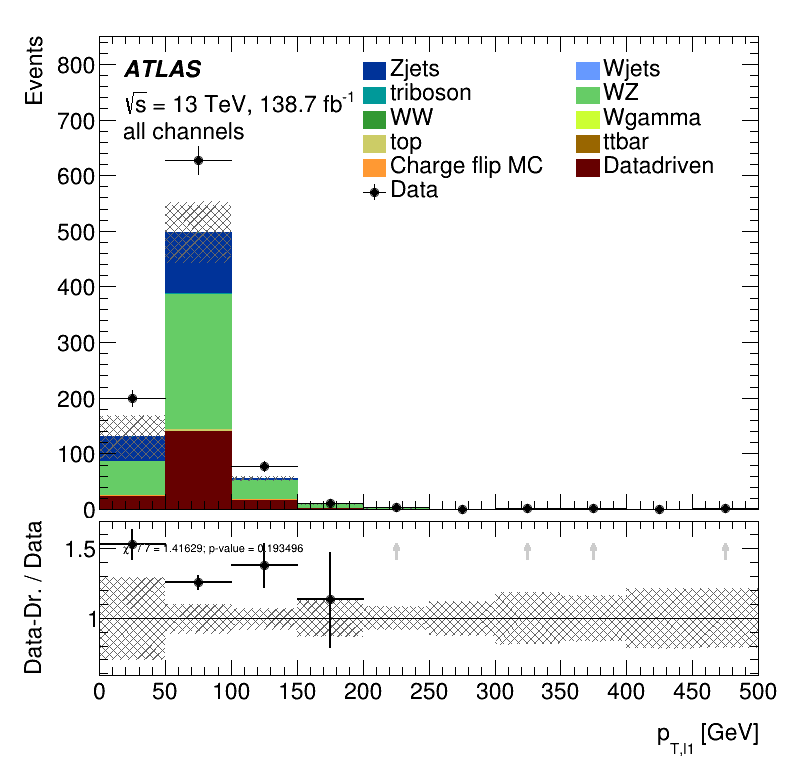
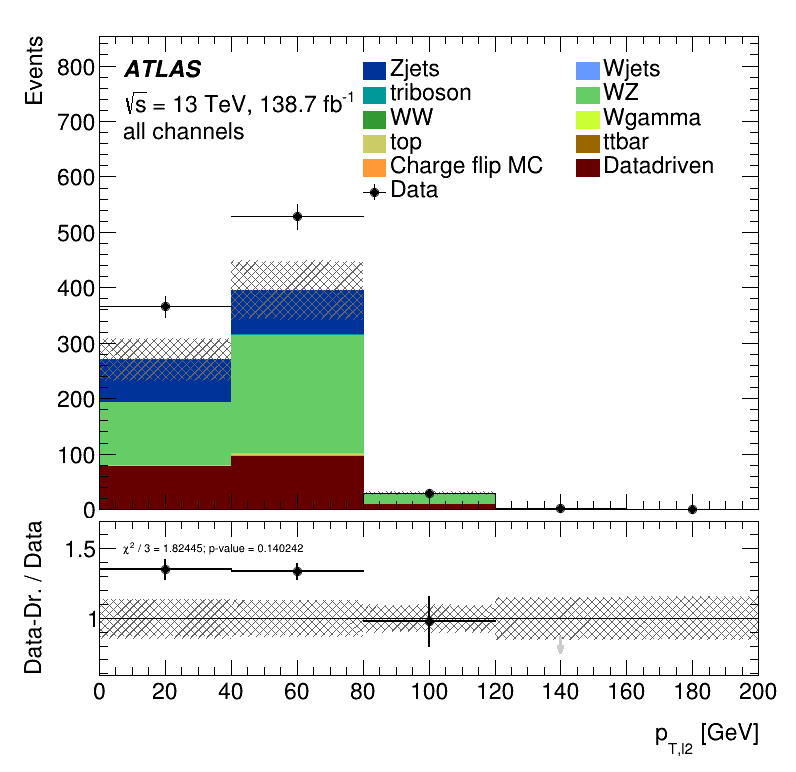
Closure Tests

Results data closure test within the Trilepton electron region

Third lepton \(p_{T }\) distribution

Subleading jet \(p_{T}\) distribution

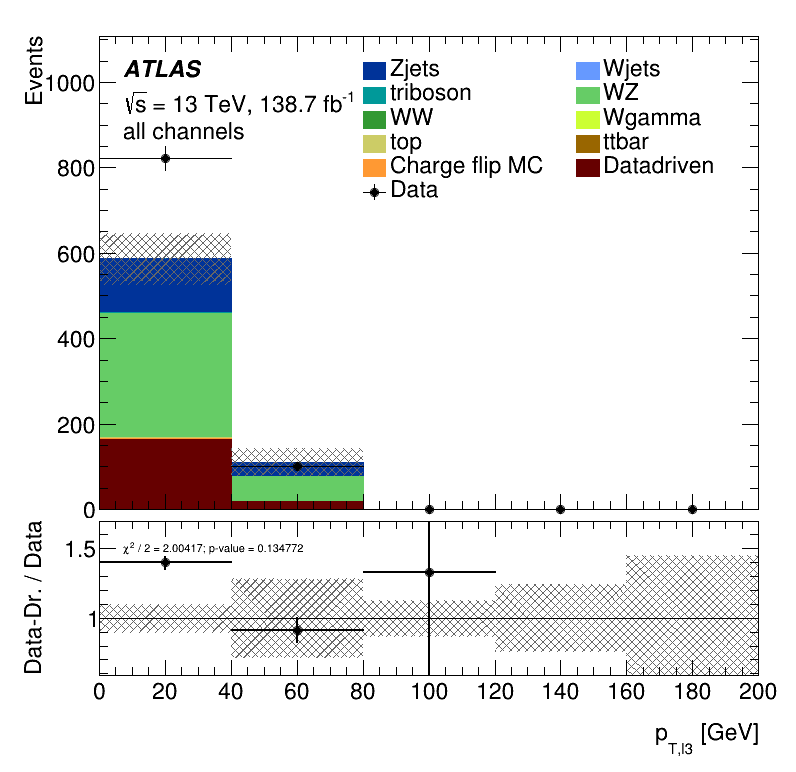
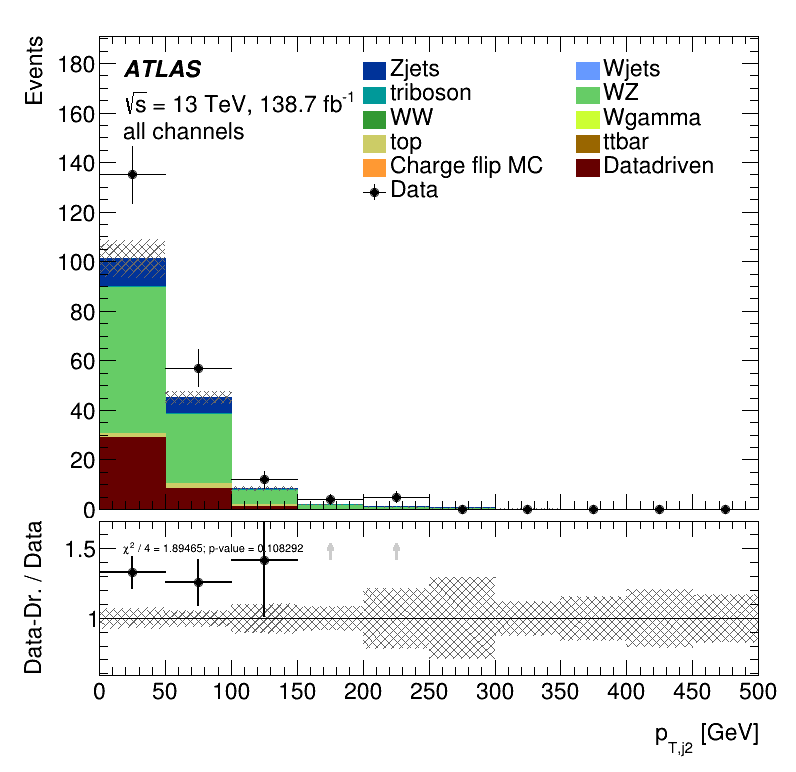
Conclusion and Outlook

  • Since they were found significant deviations with the data, it is necessary to check again the whole procedure followed  in the control region before an application in the signal region. 
  • Some of the mismodelling found could be attributed to differences between the composition of these validation regions and that of the signal region. 
  • Given that we are considering validation regions with three leptons and the fake factors are extracted from a dilepton region, it is necessary to make additional adjustments in the set up. Even so the regions have very different selections and to have a perfect modelling could be rather difficult.
  • The closure observed in the LowMjj region could be due to a compesation between the underestimation for electrons and the overestimation for muons found in the trilepton regions.

Thank you very much!

Especial thanks to Max for being such a nice supervisor!

Back up

[Dresden-VBS] Final presentation

By Sebastian Ordoñez

[Dresden-VBS] Final presentation

  • 620

More from Sebastian Ordoñez