Selection of the
\(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) candidates at the LHCb experiment
Sebastian Ordoñez
jsordonezs@unal.edu.co
Supervisors: Alberto C. dos Reis & Diego A. Milanés C.
6th Colombian Meeting on High Energy Physics
29th of November 2021
CERN Summer Student Programme 2021
Introduction
- My work: Selection of \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) candidates using a multivariate analysis (MVA). The study is based on a sample of \(pp\)-collision data, collected at a centre-of-mass energy of 13 TeV with the LHCb detector during the run 2.
- Decays of \(D\) mesons into three mesons exhibit a rich resonance structure at low energies, involving heavy-quark weak transitions, hadron formation and final-state interactions.
The \(D\) meson is the lightest known particle containing charm quarks, its mass is known to be 1869.62\(\pm\)0.20 MeV
- An additional motivation for researching three-body hadronic decays of heavy-flavoured mesons is the large and pure datasets available nowadays coming from the B-factories, LHCb, ...
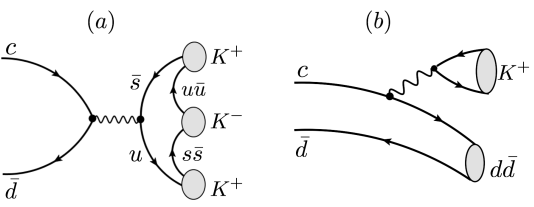
Tree-level diagram for the \(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) decay
Data Analysis
Pre-selection: Clone Tracks
\boxed{1.}
\boxed{2.}
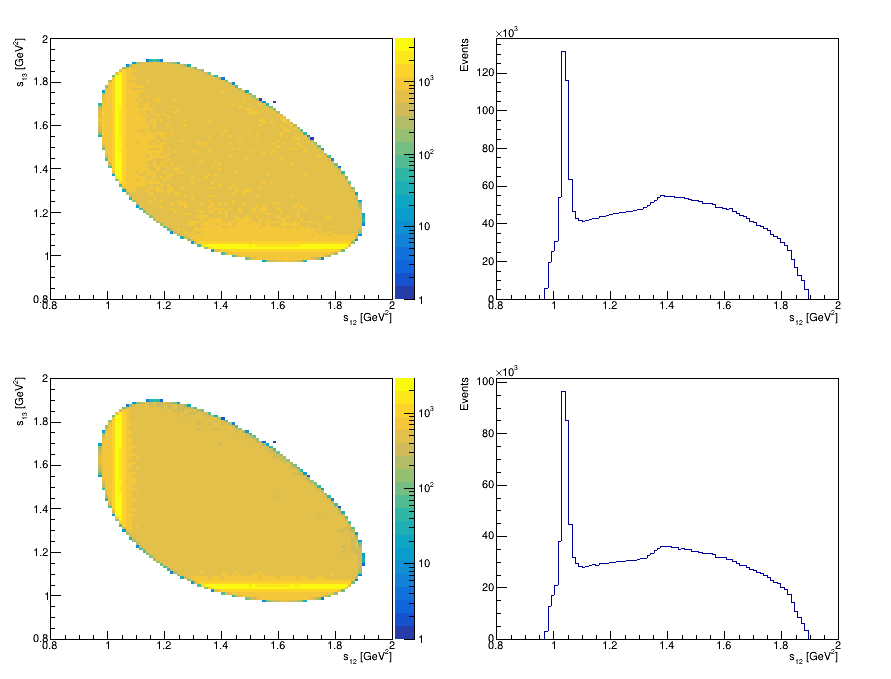
Dalitz Plot before and after cuts on the SDV
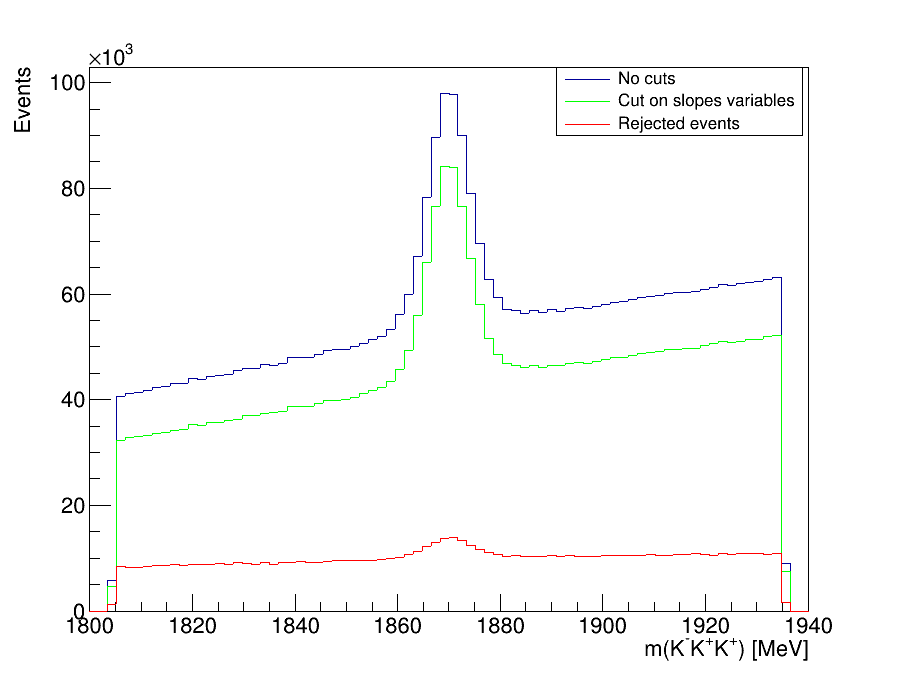
Invariant-mass spectrum of the \(K^{-}K^{+}K^{+}\) candidates
Before MVA it is necesasry to reduce the high levels of background: clone tracks and combinatorial.
\text{difTX}_{ij}=\left|\frac{p_{x_{i}}}{p_{z_{i}}}-\frac{p_{x_{j}}}{p_{z_{j}}}\right|
\text{difTY}_{ij}=\left|\frac{p_{y_{i}}}{p_{z_{i}}}-\frac{p_{y_{j}}}{p_{z_{j}}}\right|
- We use the slope difference variables (SDV):
and
Data Analysis
Pre-selection: PID
\boxed{3.}
\boxed{2.}
Invariant-mass spectrum of the \(K^{-}K^{+}K^{+}\) candidates
Dalitz Plot before and after cuts on the PID variables
- We impose requirements on PID variables in order to remove combinatorial background
- The two main sources in this channel are \(\Lambda^{+}_{c}\) decays into \(K^{-}K^{+}p\) and \(K^{-}p\pi\) final states.
Data Analysis
Multi-variate Analysis (MVA): Training-Input variables
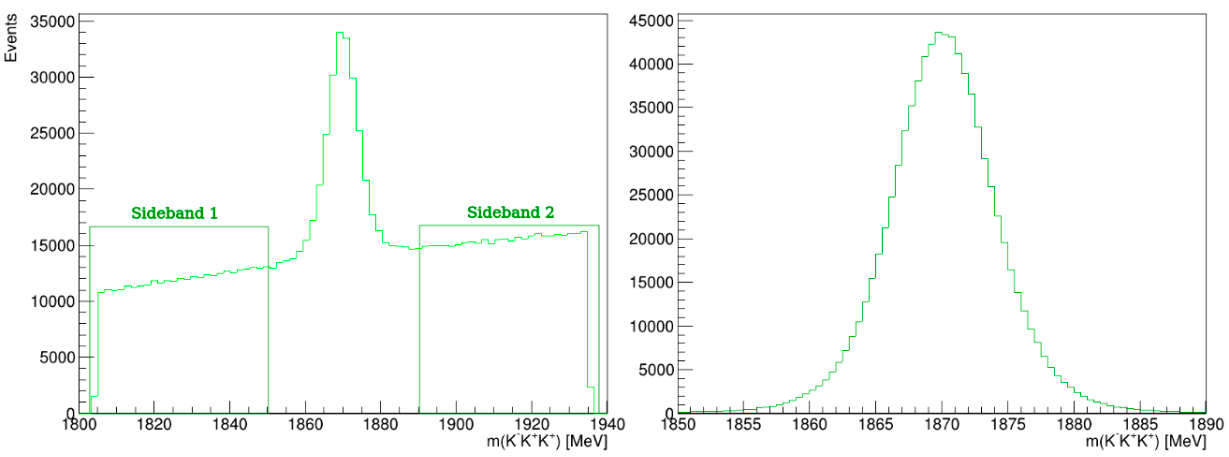
Background from data
Signal from Monte Carlo
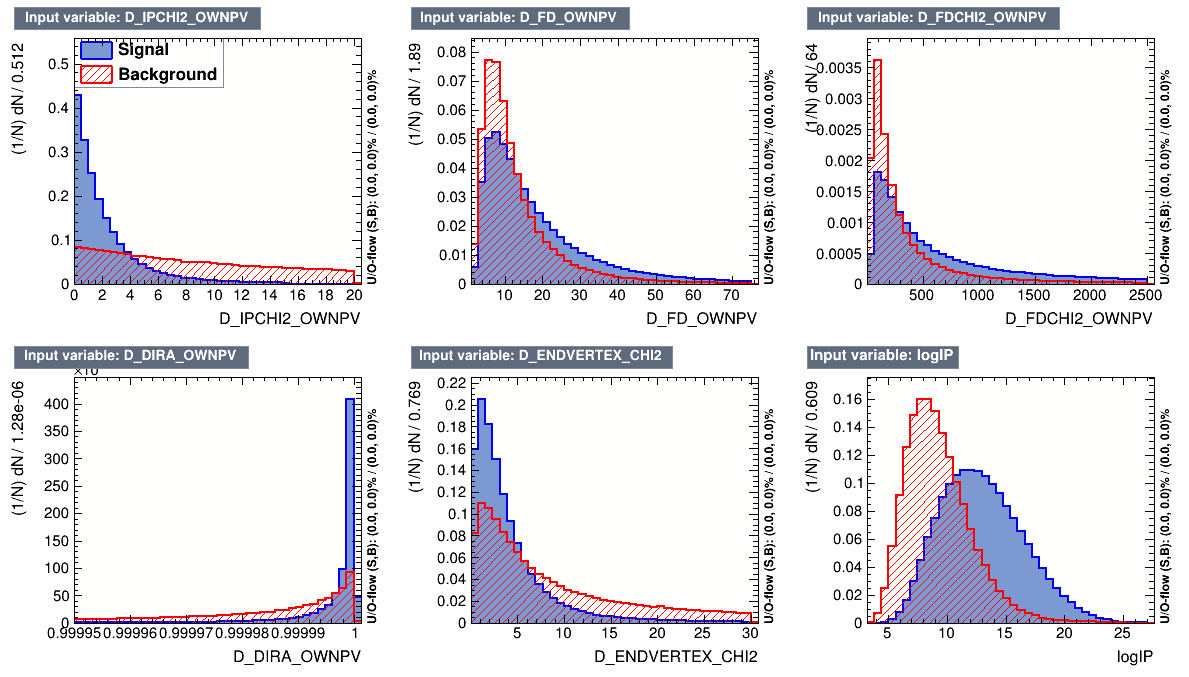
Input variables for the MVA Algorithms
- The discriminating variables chosen for the MVA methods are only related to the \(D^{+}\) candidate.
- MVA algorithm uses a set of discriminating variables for known background and signal events, with the purpose of building a new variable which provides an optimal signal-background discrimination.
Data Analysis
Multi-variate Analysis (MVA): Training-Input variables
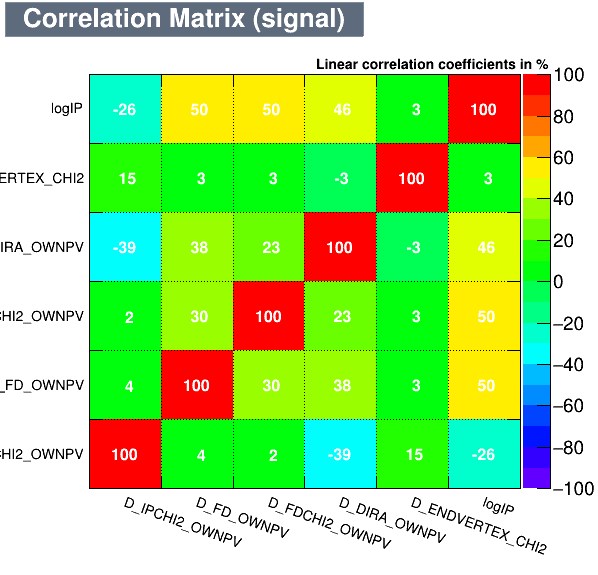
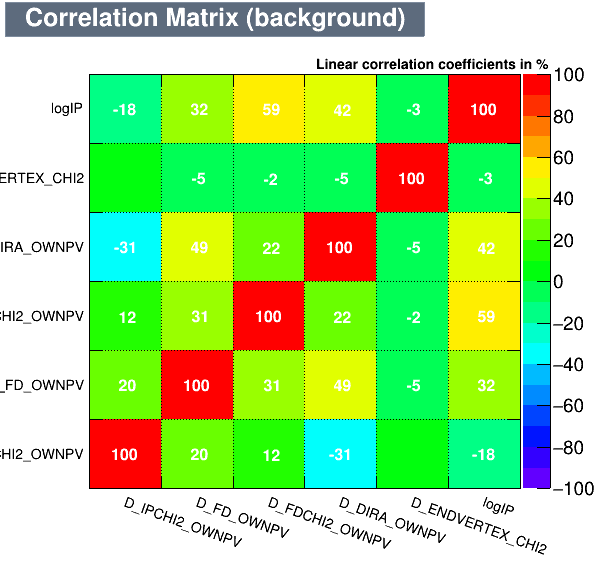
Data Analysis
Multi-variate Analysis (MVA): Training-Booking and testing
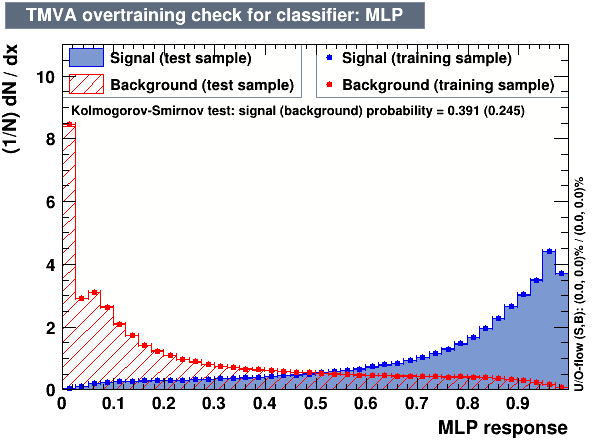
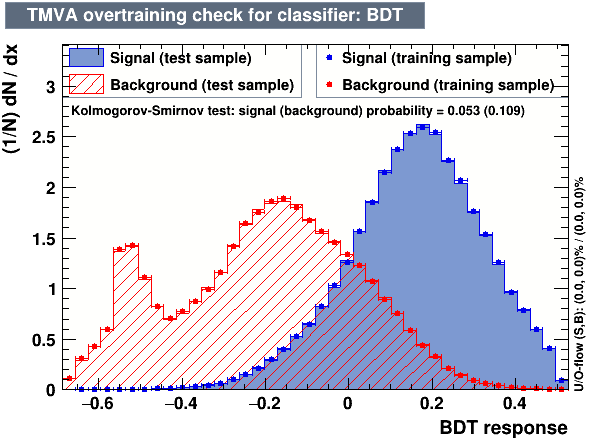
- The following algorithms were considered: Multi Layer Perceptron (MLP), Gaussian Boosted Decision Tree (BDTG), BDT, Decorrelated BDT (BDTD).
Classifier output distributions
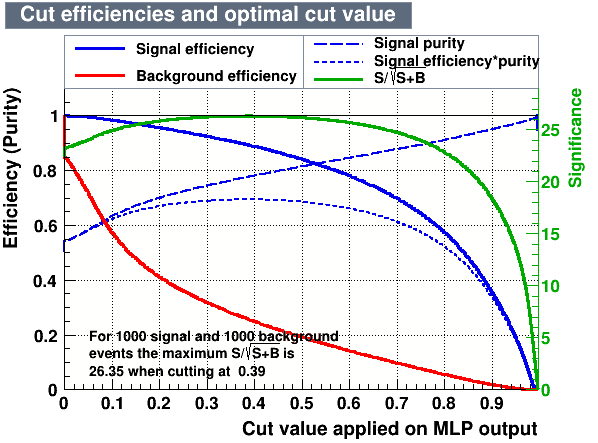
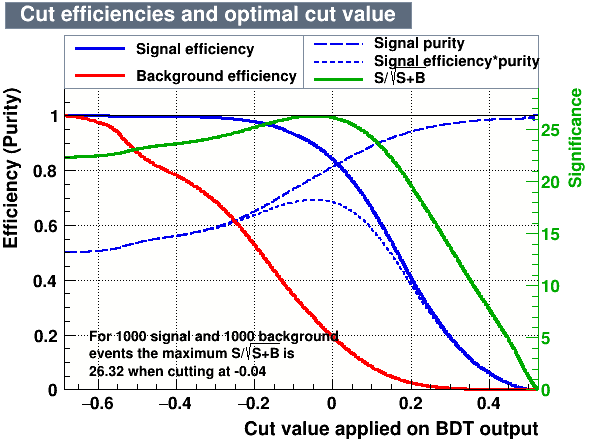
- Cutting on the value of the MVA variables, it is possible to find the one which maximises a given figure of merit, providing high signal efficiency and at the same time a significant background rejection.
Data Analysis
Multi-variate Analysis (MVA): Training-Evaluation
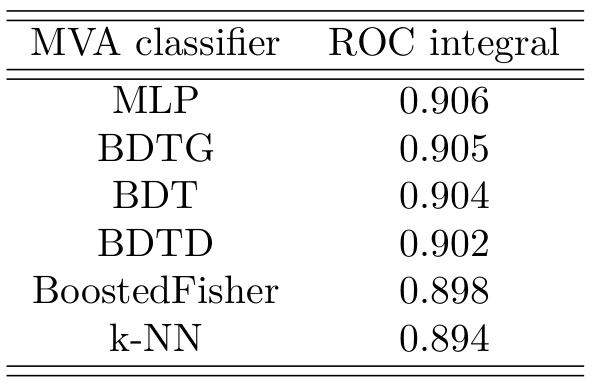
ROC curve for all the classifiers
Area under the ROC curve
- ROC curve gives a suitable performance evaluation for each classifier
Data Analysis
Multi-variate Analysis (MVA): Application
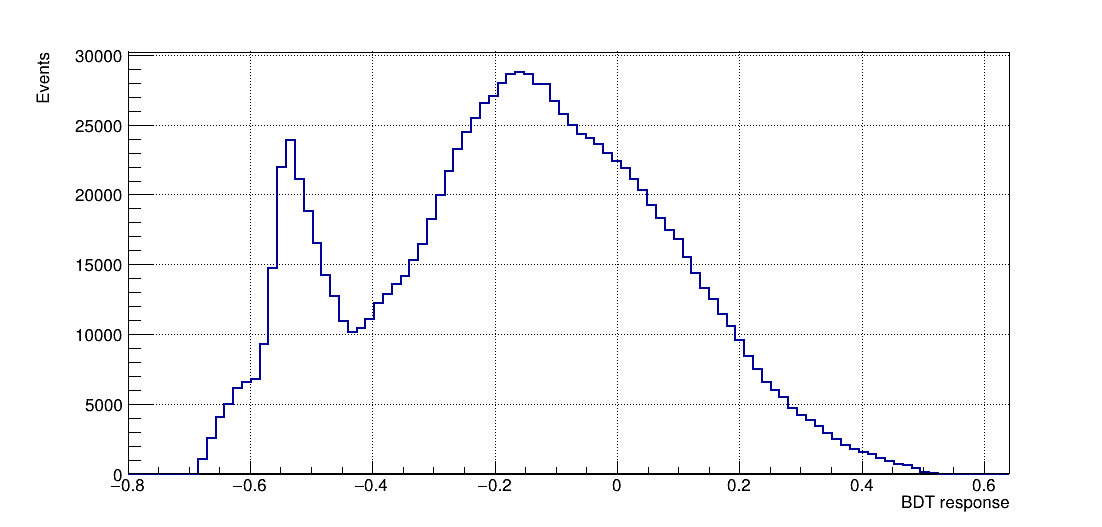
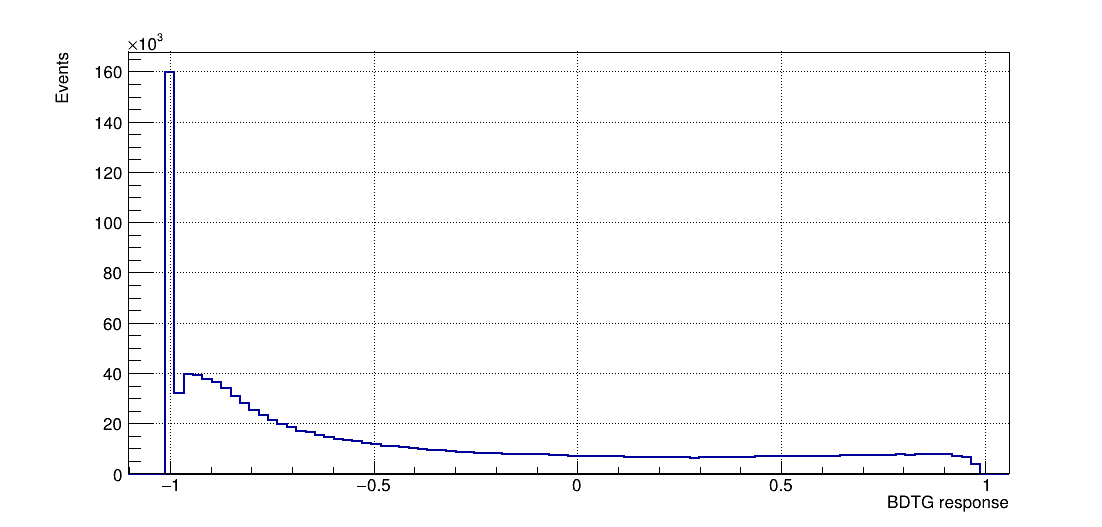
- Once the training is completed, the next phase is the application of these results to an independent data set with unknown signal and background composition.
BDTG response
BDT response
Results
Significance curves
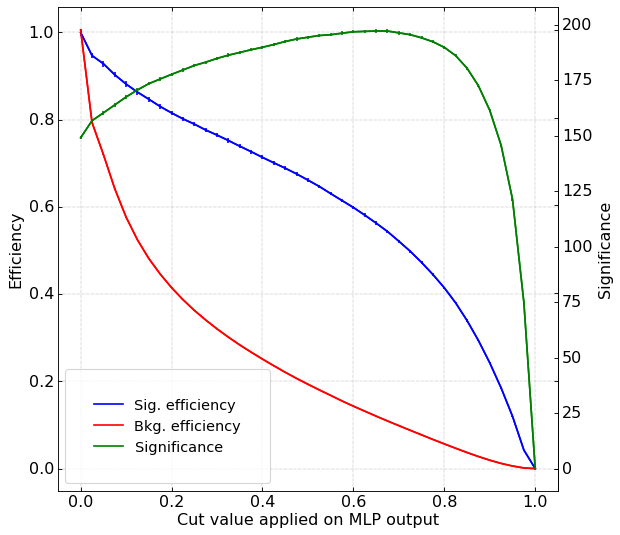
Result of applying cuts in the classifiers that showed the best signal-background discrimination performance
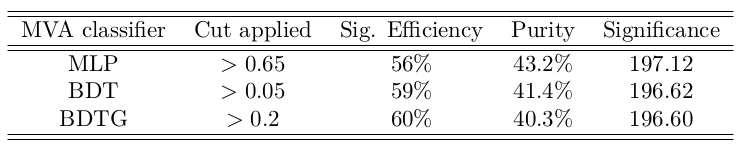
- Cut values which give the maximum signal significance
Results
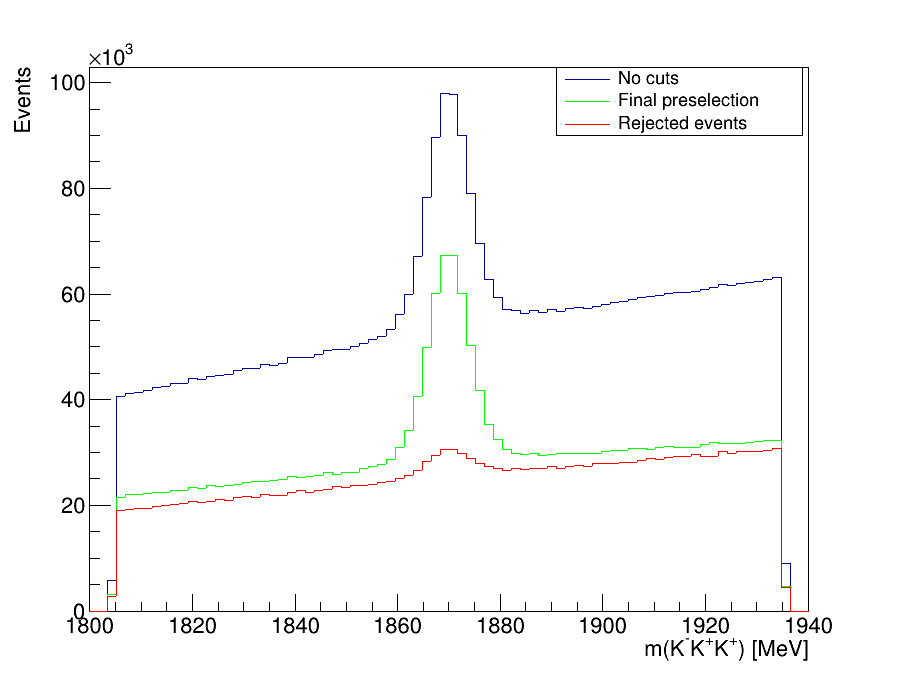
\(D^{+}\longrightarrow K^{-}K^{+}K^{+}\) invariant-mass spectrum
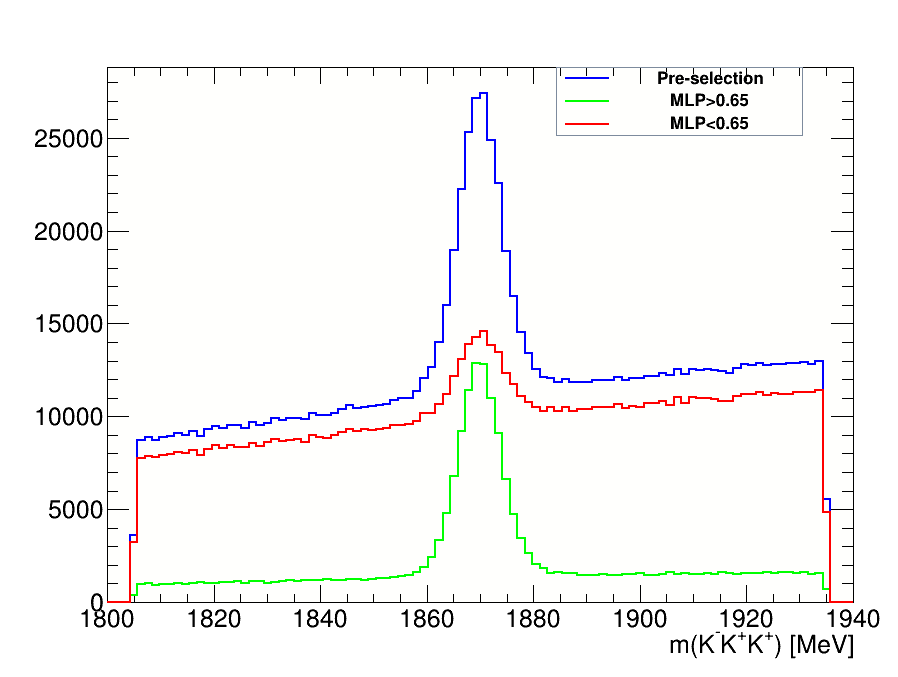
This is the final invariant-mass distribution of the \(K^{-}K^{+}K^{+}\) candidates after applying the cut on the MLP classifier, the one with the best performance.
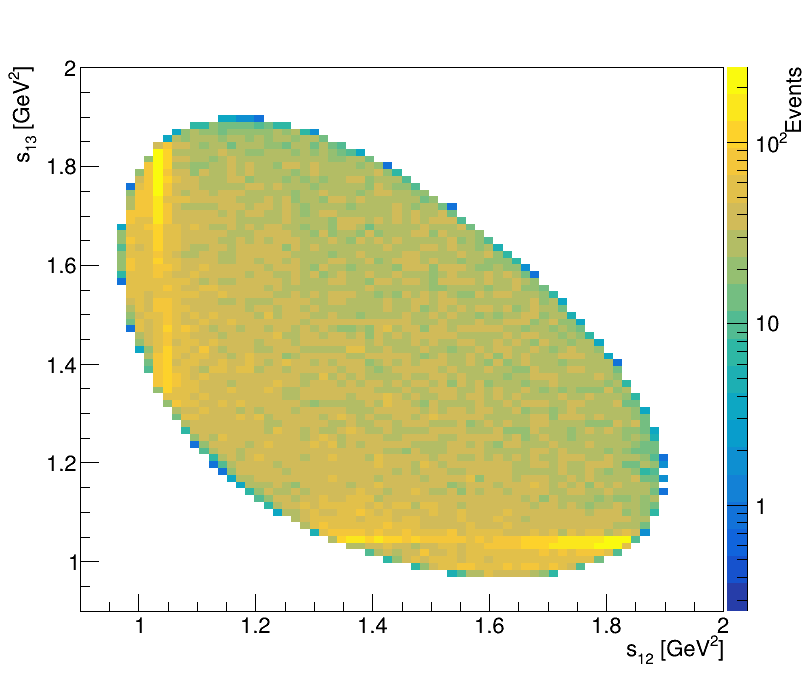
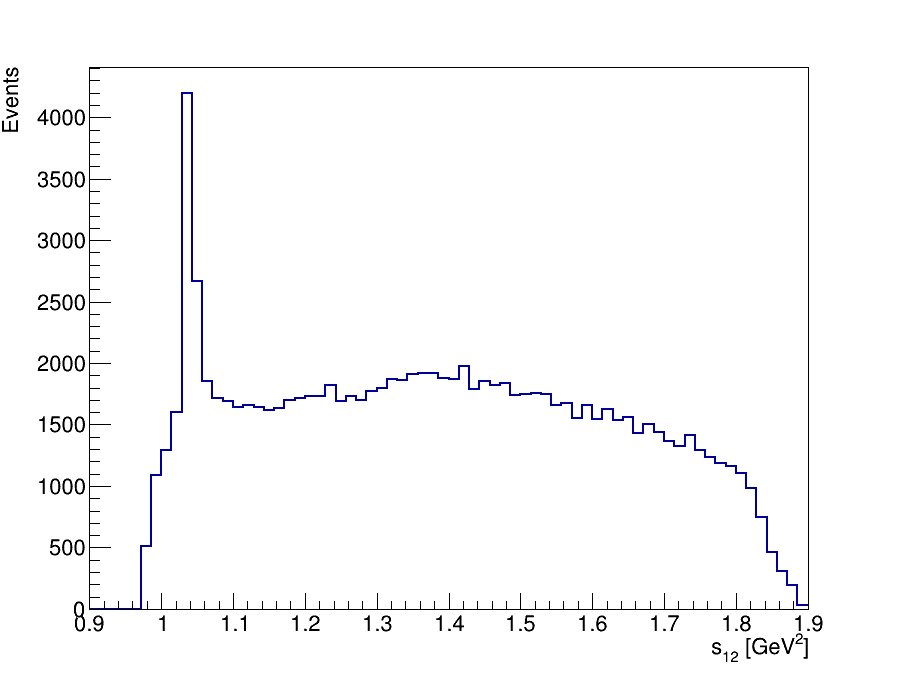
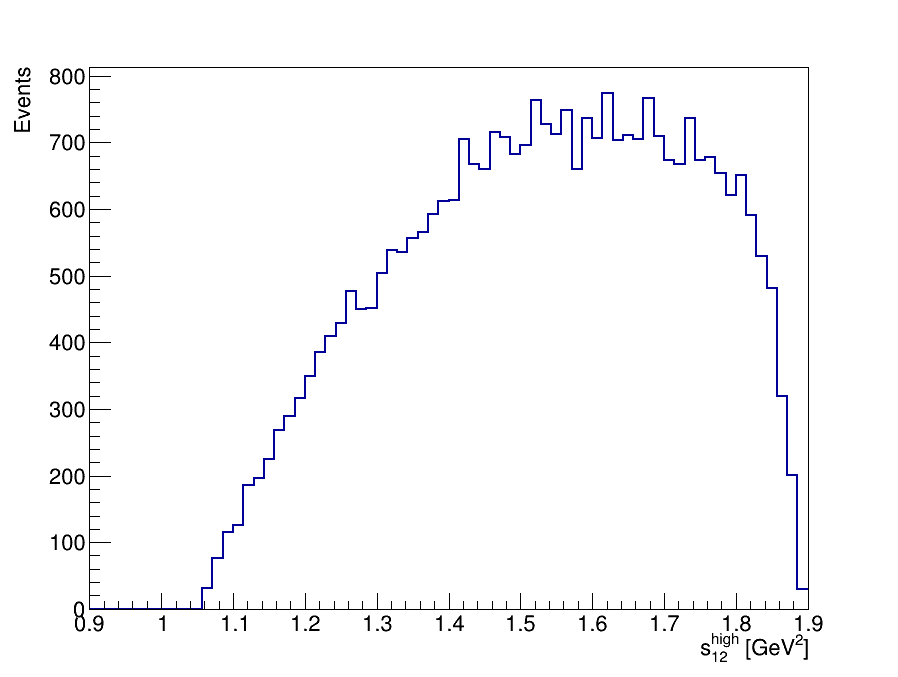
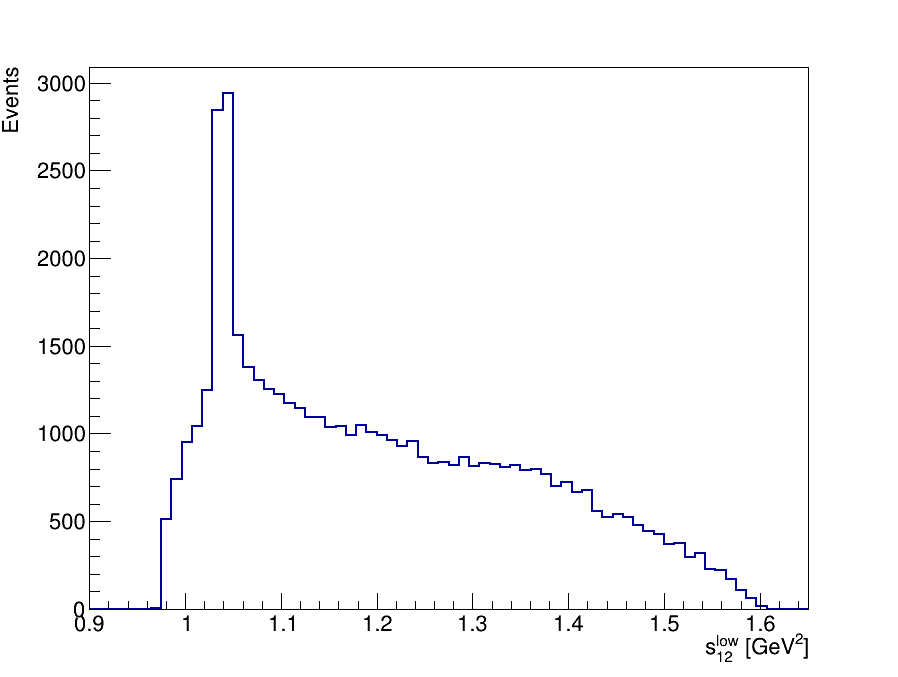
Final Dalitz Plot and Projections
Thank you!
Details and references can be found in CDS: https://cds.cern.ch/record/2781351
[ComHEP] Selection D->KKK
By Sebastian Ordoñez
