

Lecture 13: Non-parametric Models
Shen Shen
November 29, 2024
Intro to Machine Learning

Outline
- Recap: parameterized models
- Non-parametric models
- Interpretability
- Ease of use and simplicity
- Decision Tree
-
BuildTree
-
- Nearest Neighbor
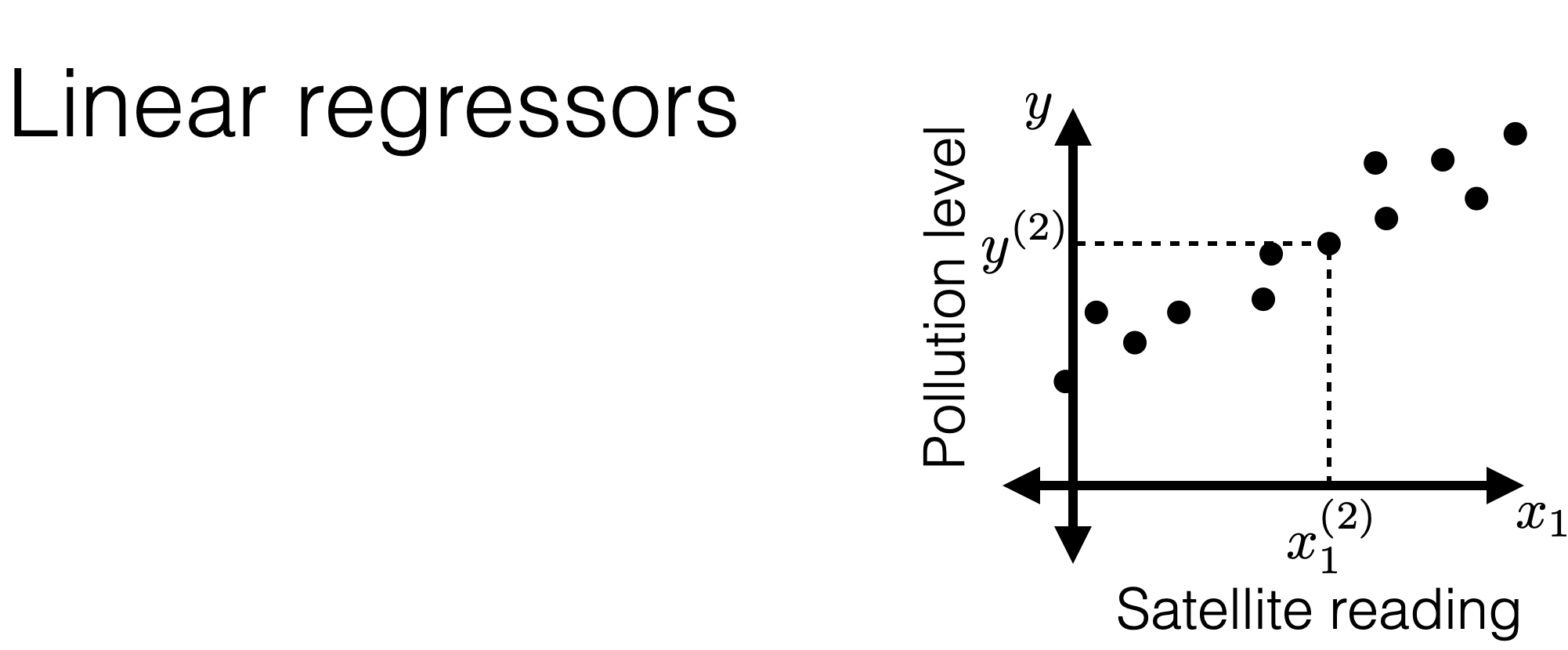

Hypothesis class \(\mathcal{H}\) : set of \(h\)
A linear regression hypothesis when \(d=1\) :
\(h\left(x ; \theta, \theta_0\right)=\theta x+\theta_0\)
A linear reg. hypothesis when \(d \geq 1\) :
\(h\left(x ; \theta, \theta_0\right)=\theta_1 x_1+\cdots+\theta_d x_d+\theta_0\)
\(=\theta^{\top} x+\theta_0\)
Recall
2 scalars
\((d+1)\) scalars
size of parameter is independent of \(n,\) the number of data points
linear combination
nonlinear activation
\(\dots\)
Forward pass: evaluate, given the current parameters,
- the model output \(g^{(i)}\) =
- the loss incurred on the current data \(\mathcal{L}(g^{(i)}, y^{(i)})\)
- the training error \(J = \frac{1}{n} \sum_{i=1}^{n}\mathcal{L}(g^{(i)}, y^{(i)})\)
loss function
Recall:
Outline
- Recap: parameterized models
-
Non-parametric models
- Interpretability
- Ease of use and simplicity
- Decision Tree
-
BuildTree
-
- Nearest Neighbor
- does not mean "no parameters"
- there are still parameters to be learned to build a hypothesis/model.
- just that, the model/hypothesis does not have a fixed parameterization.
- (e.g. even the number of parameters can change.)
Non-parametric models
- they are usually fast to implement / train and often very effective.
- often a good baseline (especially when the data doesn't involve complex structures like image or languages)
Outline
- Recap: parameterized models
- Non-parametric models
- Interpretability
- Ease of use and simplicity
-
Decision Tree
-
BuildTree
-
- Nearest Neighbor
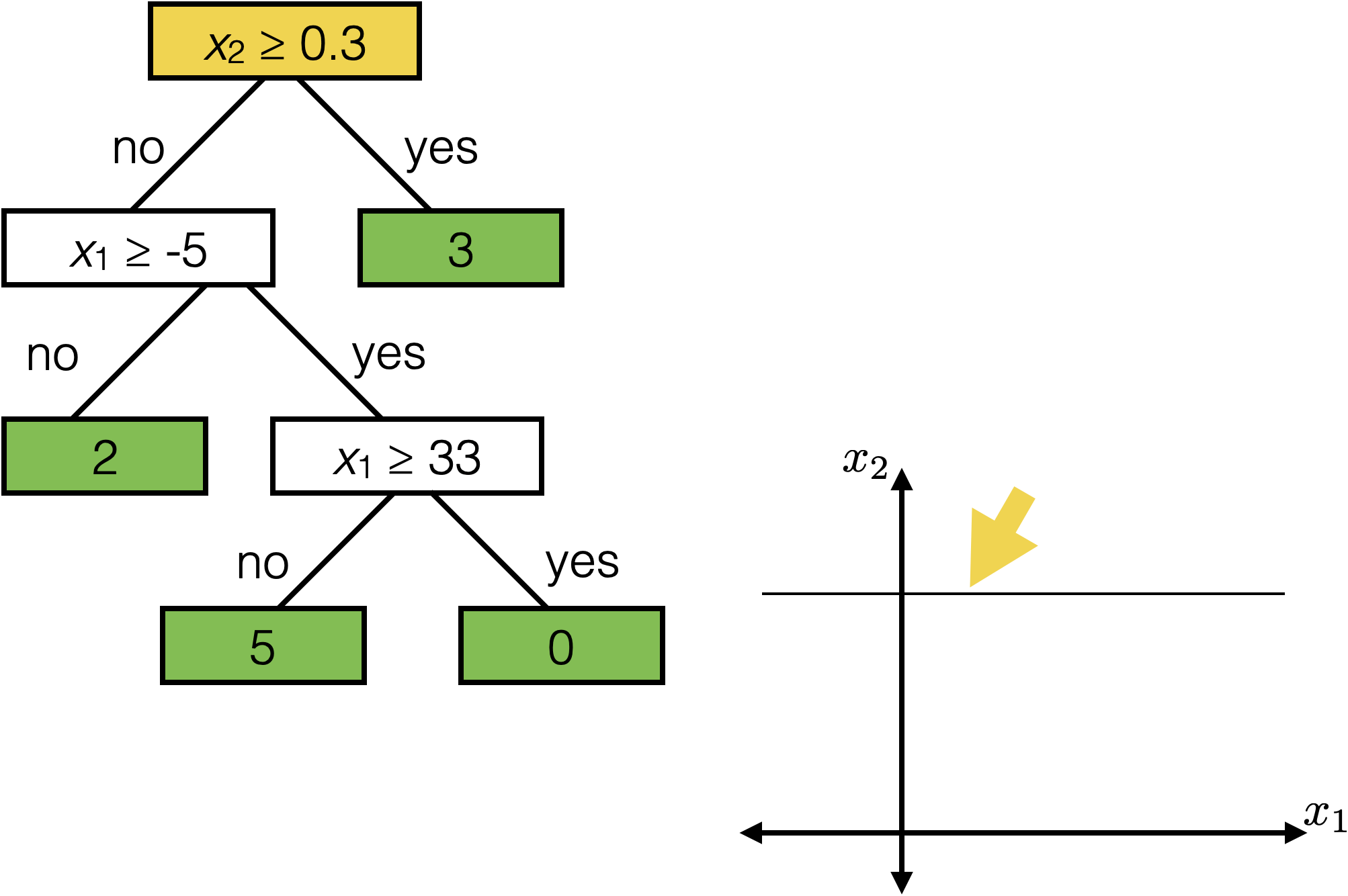
features:
- \(x_1\): temperature (deg C)
- \(x_2\): precipitation (cm/hr)
label: km run

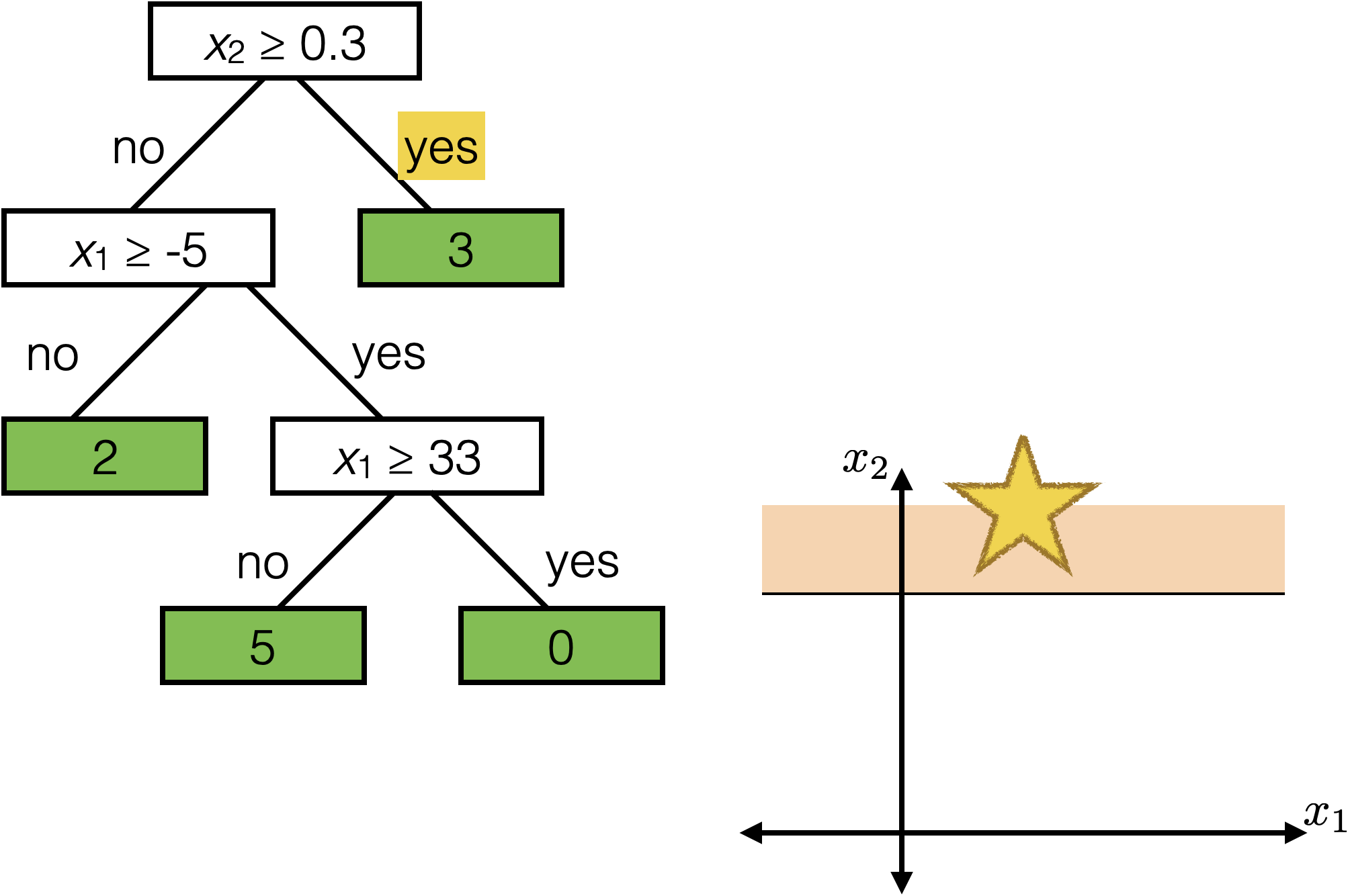
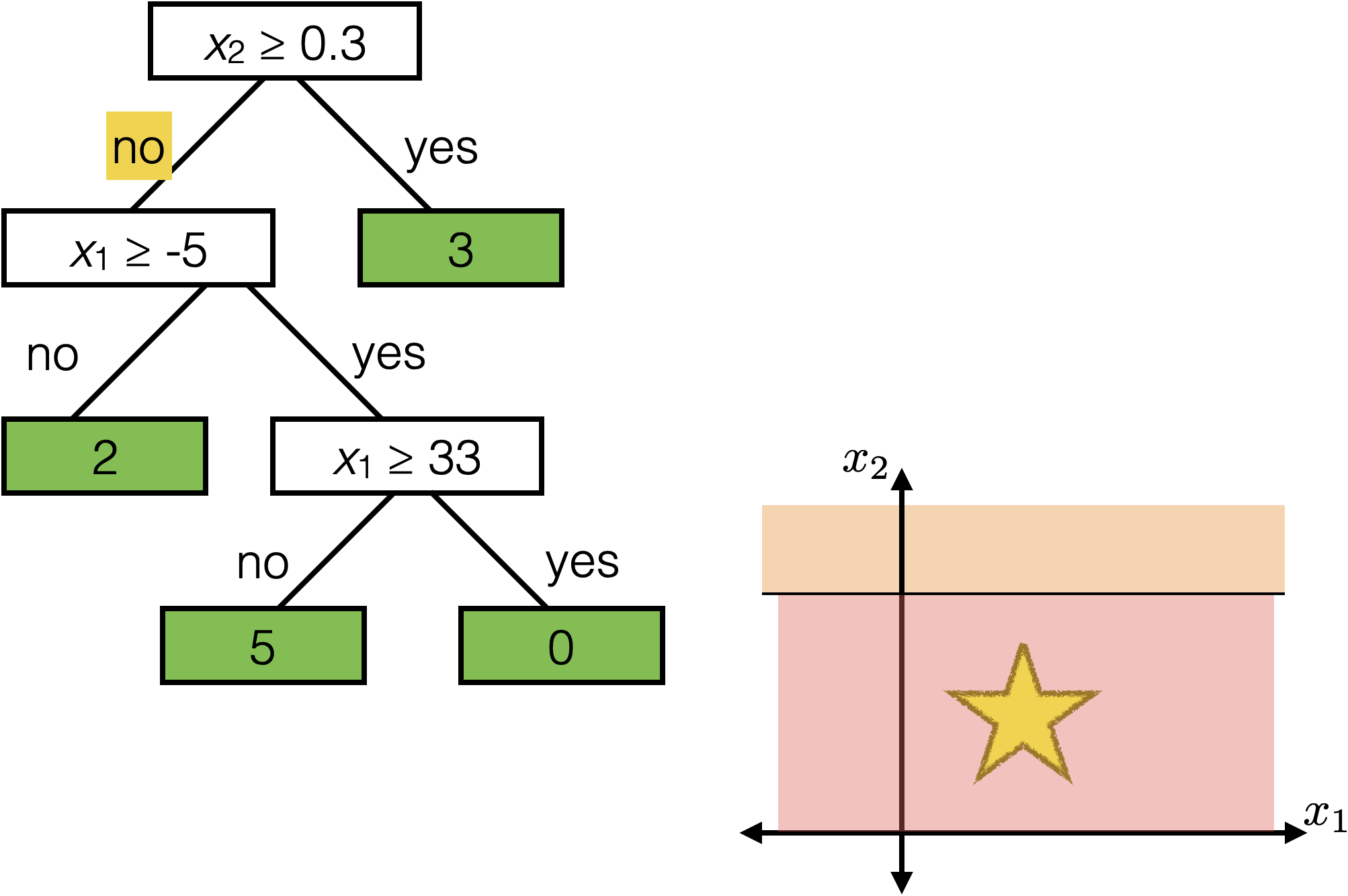

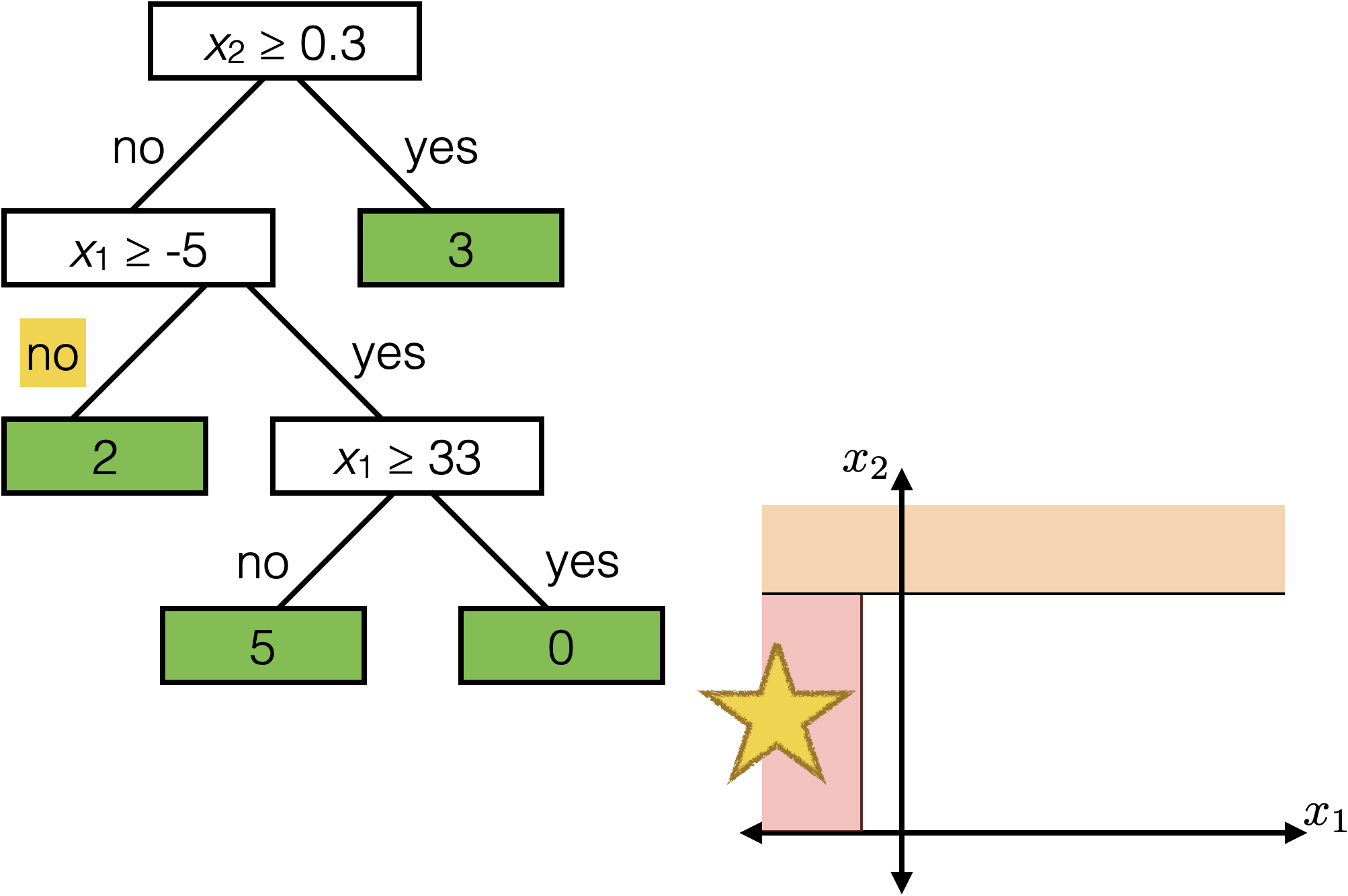
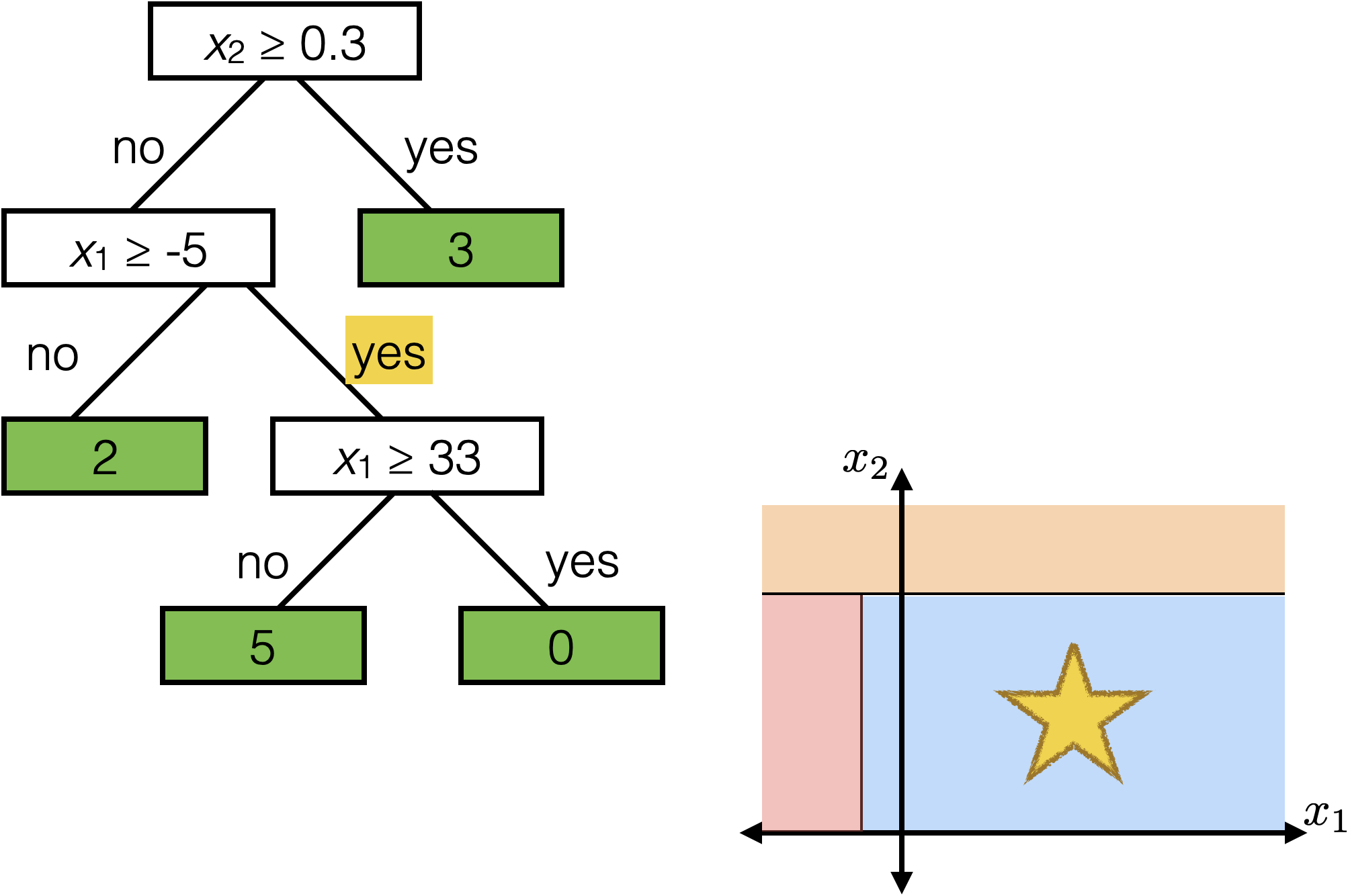
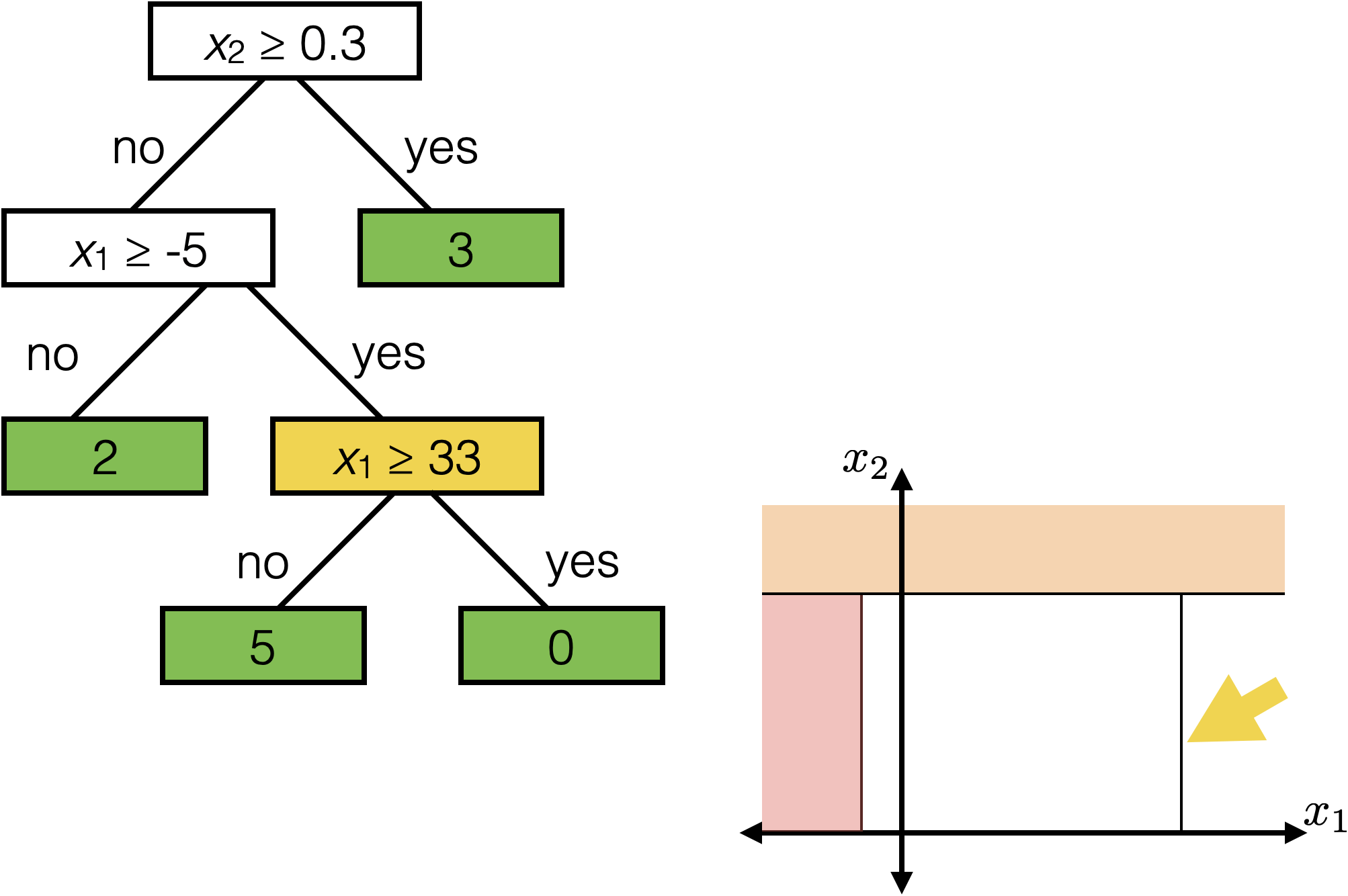
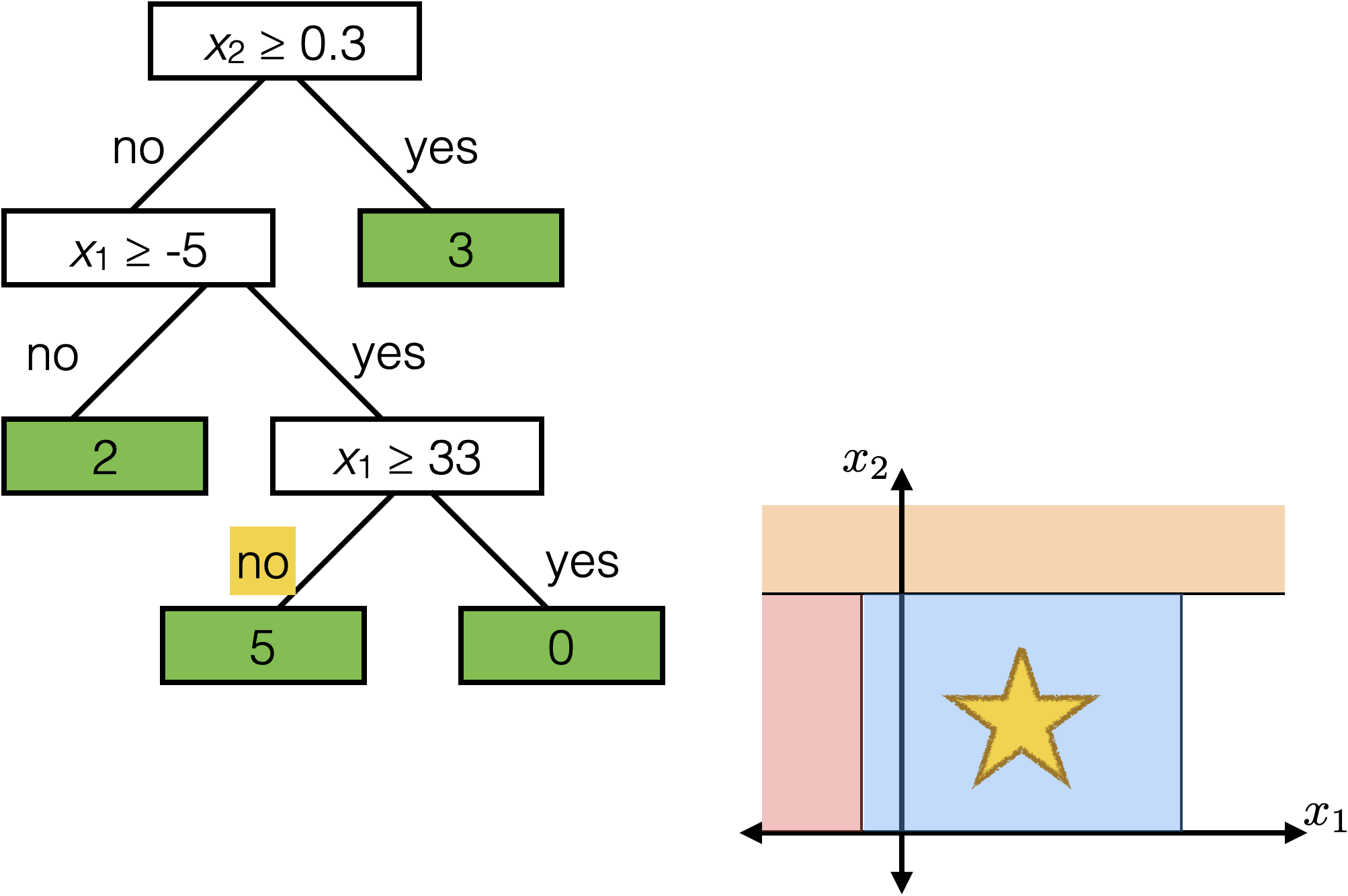
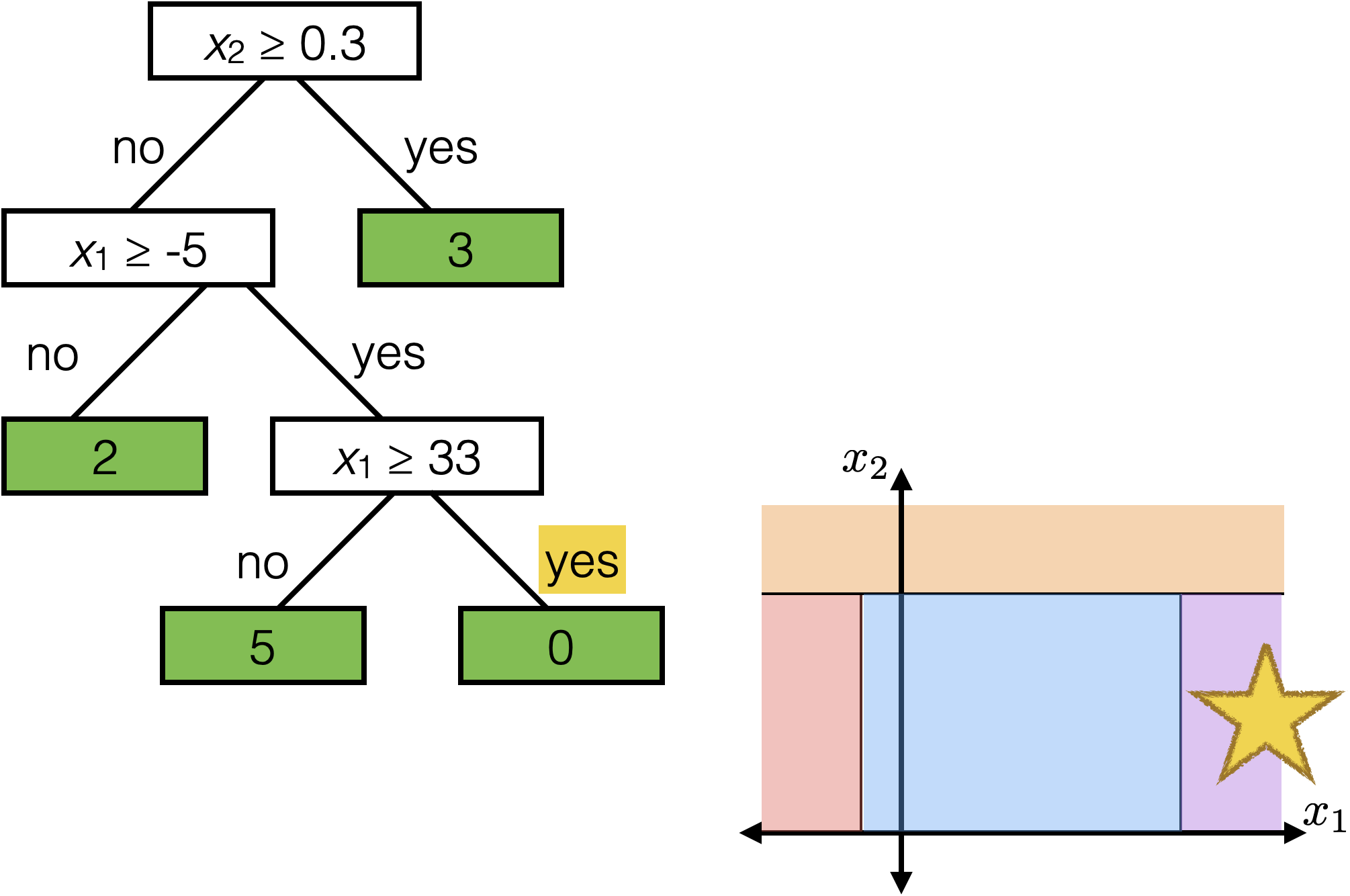
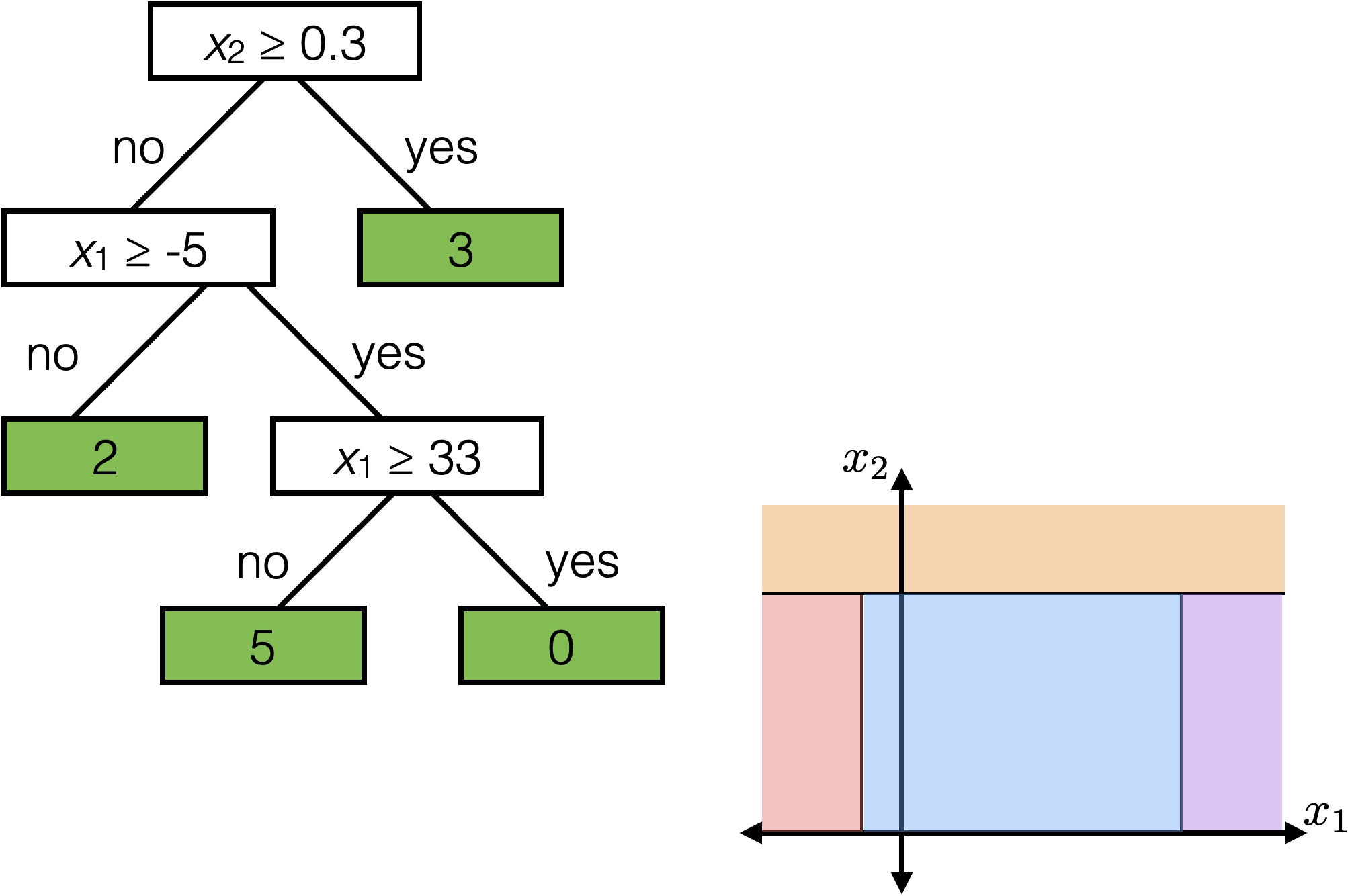
The same prediction applies to an axis-aligned ‘box’ or ‘volume’ in the feature space
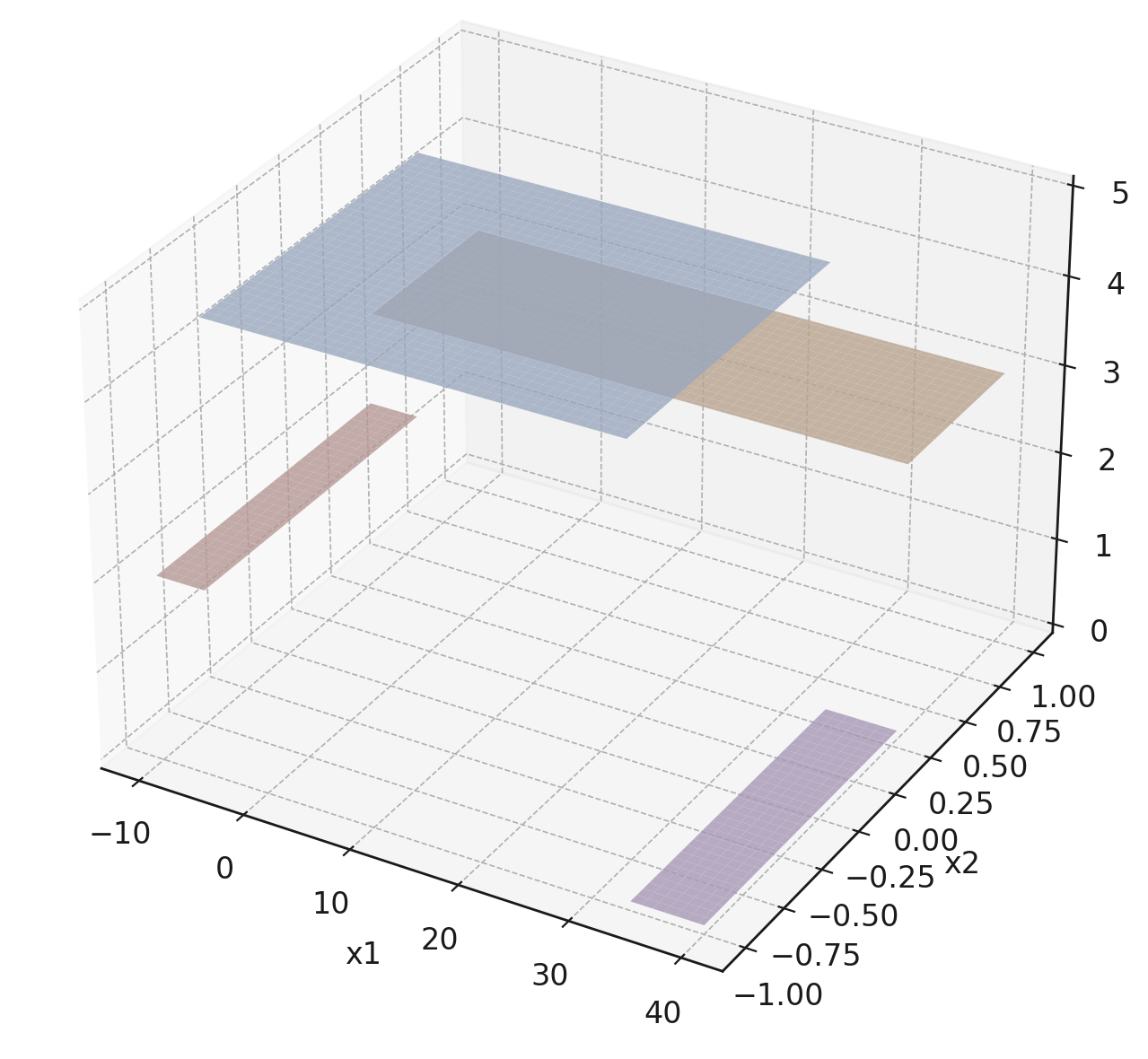
label: km run
temperature
precipitation
\(x_2 \geq 0.3\)
\(x_1 \geq -5 \)
\(x_1 \geq 33\)
2
3
0
5

temperature
precipitation
The same prediction applies to an axis-aligned ‘box’ or ‘volume’ in the feature space
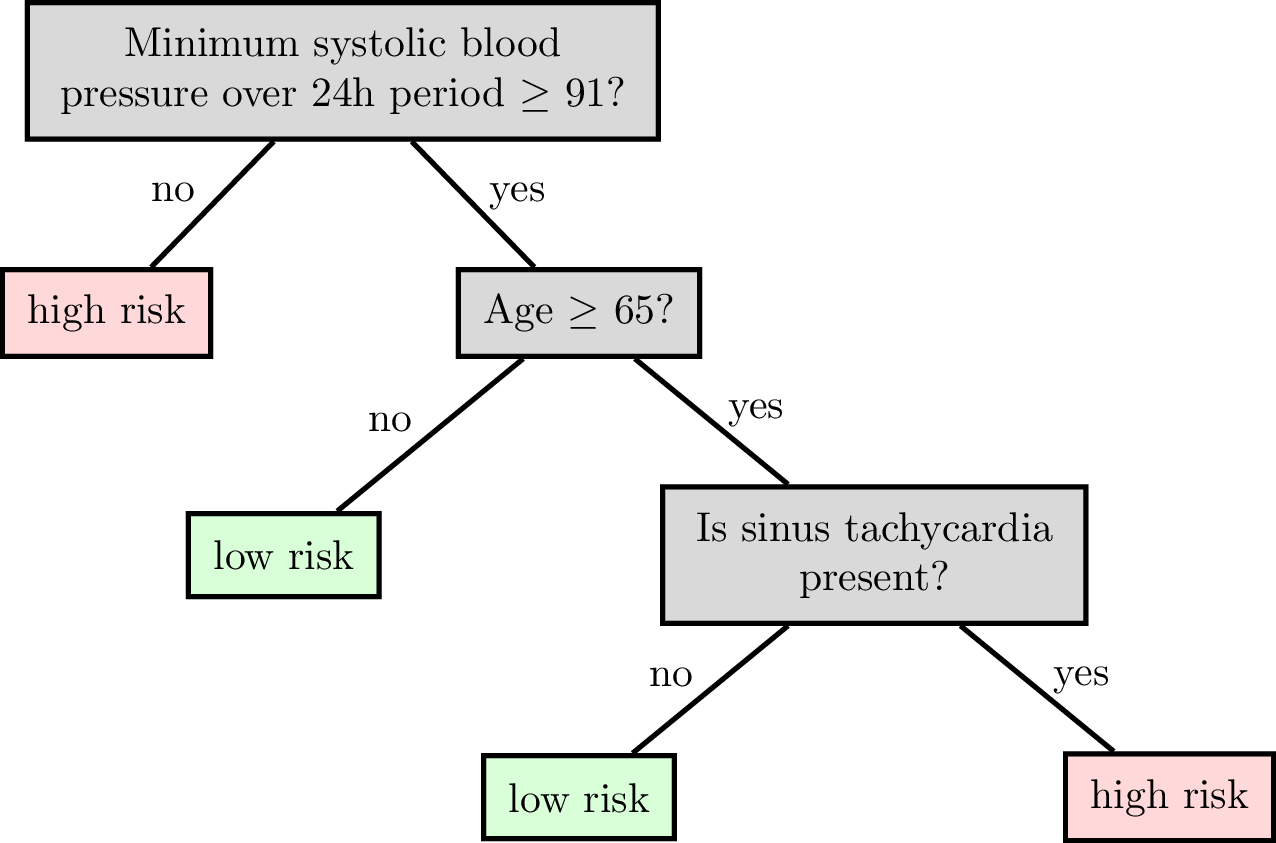
Decision tree for classification
features:
\(x_1\) : date
\(x_2\) : age
\(x_3\) : height
\(x_4\) : weight
\(x_5\) : sinus tachycardia?
\(x_6\) : min systolic bp, 24h
\(x_7\) : latest diastolic bp
labels \(y\) :
1: high risk
-1: low risk
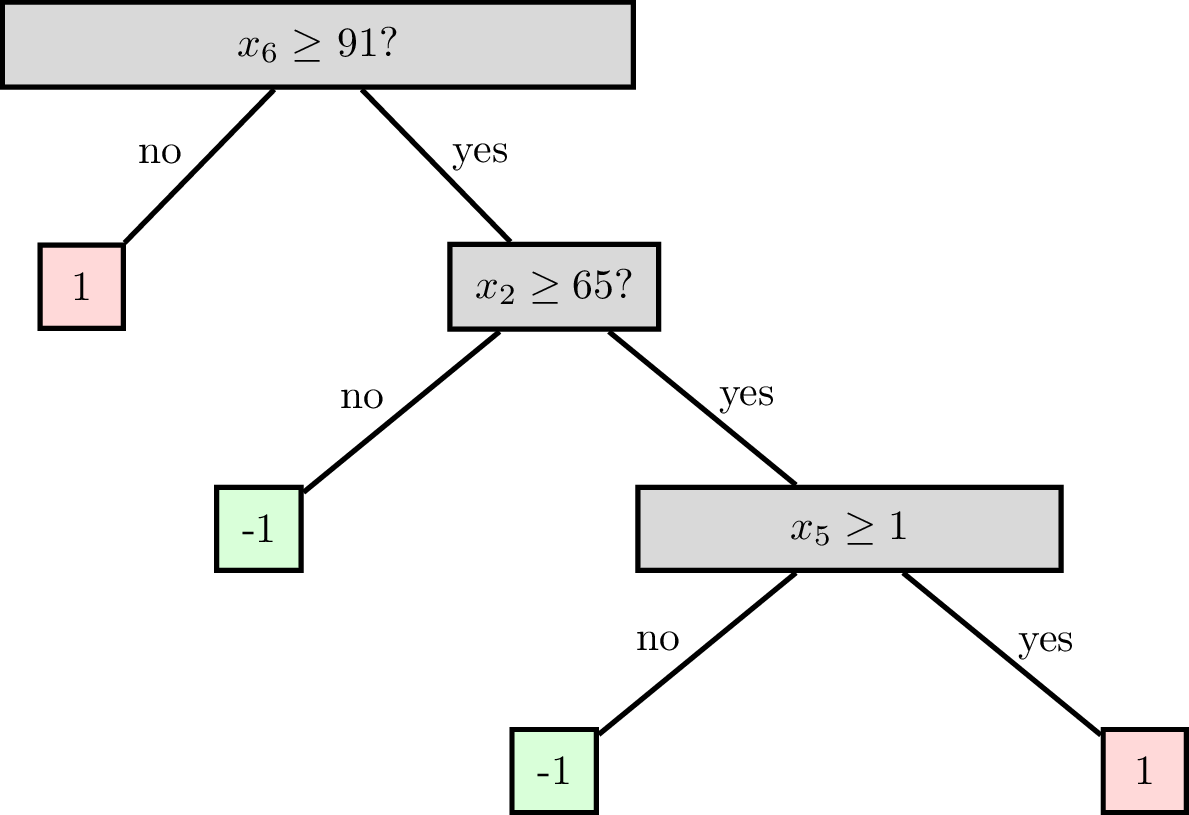
Node (root)
Leaf (terminal)
Node (internal)
Decision tree terminologies

Split dimension
Split value
A node can be specified by
Node(split dim, split value, left child, right child)
A leaf can be specified by
Leaf(leaf_value)

Outline
- Recap: parameterized models
- Non-parametric models
- Interpretability
- Ease of use and simplicity
- Decision Tree
BuildTree
- Nearest Neighbor
Set of indices.
Hyper-parameter, largest leaf size (i.e. the maximum number of training data that can "flow" into that leaf).
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k, \mathcal{D}\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k, \mathcal{D}\right)\right)\)

- Choose \(k=2\)
- \(\operatorname{BuildTree}(\{1,2,3\};2)\)
- Line 1 true
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- For this fixed \((j, s)\)
- \(I_{j, s}^{+} = \{2,3\}\)
- \(I_{j, s}^{-} = \{1\}\)
- \(\hat{y}_{j, s}^{+} = 5\)
- \(\hat{y}_{j, s}^{-} = 0\)
- \(E_{j, s} =0\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- For this fixed \((j, s)\)
- \(I_{j, s}^{+} = \{2,3\}\)
- \(I_{j, s}^{-} = \{1\}\)
- \(\hat{y}_{j, s}^{+} = 5\)
- \(\hat{y}_{j, s}^{-} = 0\)
- \(E_{j, s} =0\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- Line 2: a finite number of \((j, s)\) combo suffices (those that split in-between data points)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- Line 8: picks the "best" among these finite choices of \((j, s)\) combos (random tie-breaking).

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
Suppose line 8 sets this \((j^*,s^*)\),
say = \((j^*,s^*) = (1, 1.7)\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
Line 12 recursion
\(x_1 \geq 1.7\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
\(x_1 \geq 1.7\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
\(x_1 \geq 1.7\)
0

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
\(x_1 \geq 1.7\)
0

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
\(x_1 \geq 1.7\)
0
5
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
use
weighted average entropy
as performance metric
use majority vote as (intermediate) prediction
For classification
entropy \(H=-\sum_{\text {class }_c} \hat{P}_c (\log _2 \hat{P}_c)\)
(about 1.1)
for example: three classes

\(\hat{P}_c\)
\(H= -[\frac{4}{6} \log _2\left(\frac{4}{6}\right)+\frac{1}{6} \log _2\left(\frac{1}{6}\right)+\frac{1}{6} \log _2\left(\frac{1}{6}\right)]\)
(about 1.252)

\(\hat{P}_c\)
\(H= -[\frac{3}{6} \log _2\left(\frac{3}{6}\right)+\frac{3}{6} \log _2\left(\frac{3}{6}\right)+ 0]\)

\(\hat{P}_c\)
\(H= -[\frac{6}{6} \log _2\left(\frac{6}{6}\right)+ 0+ 0]\)
(= 0)
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

\(\frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
\(= \frac{4}{6} \cdot H\left(I_{j, s}^{-}\right)+\frac{2}{6} \cdot H\left(I_{j, s}^{+}\right)\)
fraction to the left of the split
fraction to the right of the split
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

\( \frac{4}{6} \cdot H\left(I_{j, s}^{-}\right)+\frac{2}{6} \cdot H\left(I_{j, s}^{+}\right)\)
\( -[\frac{3}{4} \log _2\left(\frac{3}{4}\right)+\frac{1}{4} \log _2\left(\frac{1}{4}\right)+0] \approx 0.811\)
\( -[\frac{1}{2} \log _2\left(\frac{1}{2}\right)+\frac{1}{2} \log _2\left(\frac{1}{2}\right)+0] = 1\)
(line 7, overall\(E_{j, s}\approx\) 0.874)
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

\( \frac{5}{6} \cdot H\left(I_{j, s}^{-}\right)+\frac{1}{6} \cdot H\left(I_{j, s}^{+}\right)\)
\( -[\frac{4}{5} \log _2\left(\frac{4}{5}\right)+\frac{1}{5} \log _2\left(\frac{1}{5}\right)+0] \approx 0.722\)
\( -[1 \log _2\left(1\right)+0+0] = 0\)
(line 7, overall \(E_{j, s}\approx\) 0.602)
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

overall \(E_{j, s}\approx\) 0.602
line 7
\(E_{j, s}\approx\) 0.874
line 8, set the better \((j, s)\)




Ensemble
- One of multiple ways to make and use an ensemble
- Bagging = Bootstrap aggregating
- Training data \(\mathcal{D}_n\)
Bagging


- Training data \(\mathcal{D}_n\)
- For \(b=1, \ldots, B\)
- Draw a new "data set" \(\tilde{\mathcal{D}}_n^{(b)}\) of size \(n\) by sampling with replacement from \(\mathcal{D}_n\)
- Train a predictor \(\hat{f}^{(b)}\) on \(\tilde{\mathcal{D}}_n^{(b)}\)
- Return
- For regression: \(\hat{f}_{\text {bag }}(x)=\frac{1}{B} \sum_{b=1}^B \hat{f}^{(b)}(x)\)
- For classification: predictor at a point is class with highest vote count at that point

Bagging
Outline
- Recap: parameterized models
- Non-parametric models
- Interpretability
- Ease of use and simplicity
- Decision Tree
-
BuildTree
-
- Nearest Neighbor
Nearest neighbor
-
Predicting (inferencing, testing):
- for a new data point \(x_{\text{new}}\) do:
- find the \(k\) points in training data nearest to \(x_{\text{new}}\)
- For classification: predict label \(\hat{y}_{\text{new}}\) for \(x_{\text{new}}\) by taking a majority vote of the \(k\) neighbors's labels \(y\)
- For regression: predict label \(\hat{y}_{\text{new}}\) for \(x_{\text{new}}\) by taking an average over the \(k\) neighbors' labels \(y\)
- find the \(k\) points in training data nearest to \(x_{\text{new}}\)
- Training: None (or rather: memorize the entire training data)
Hyper-parameter: \(k\)
Distance metric (typically Euclidean or Manhattan distance)
A tie-breaking scheme (typically at random)
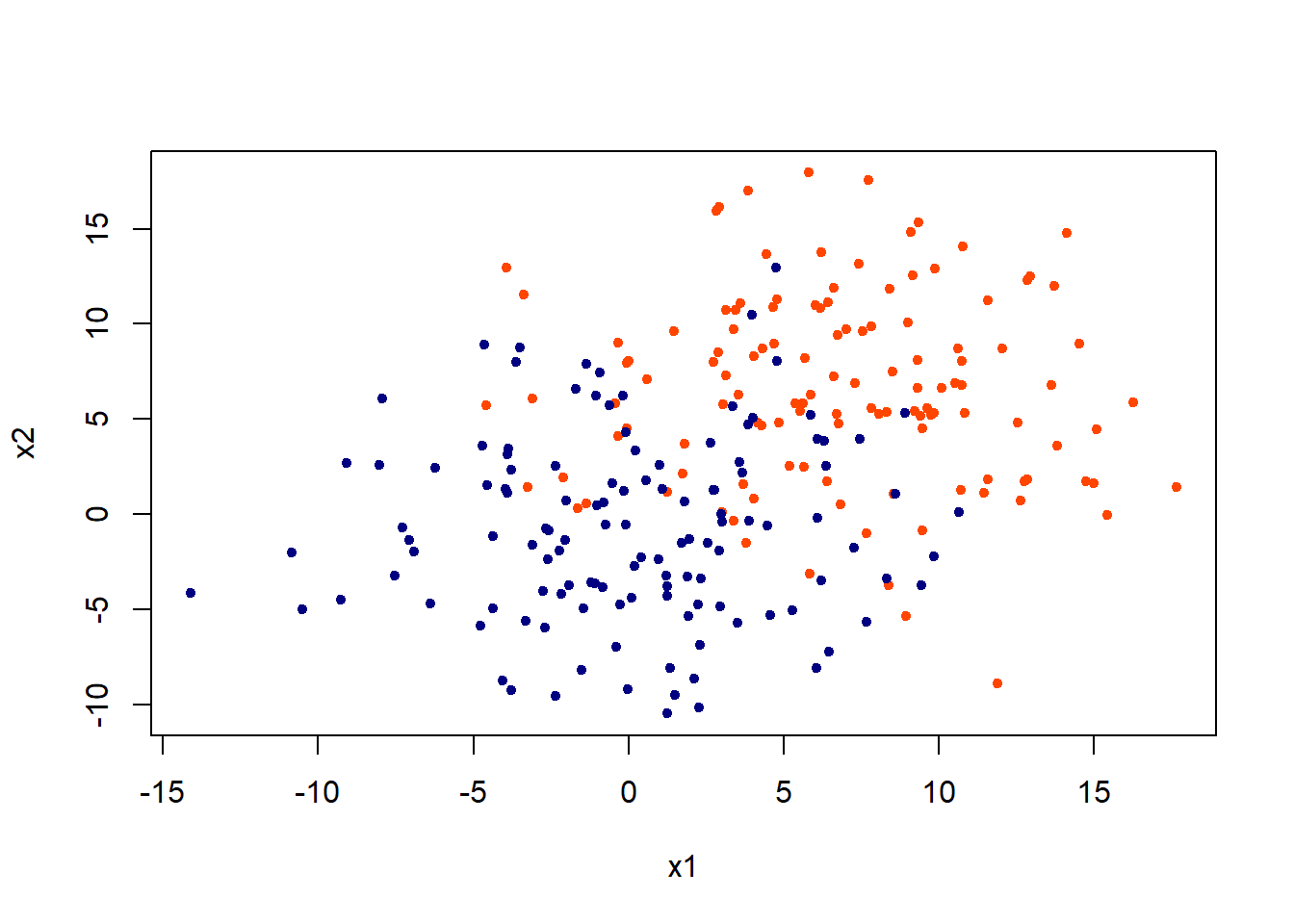
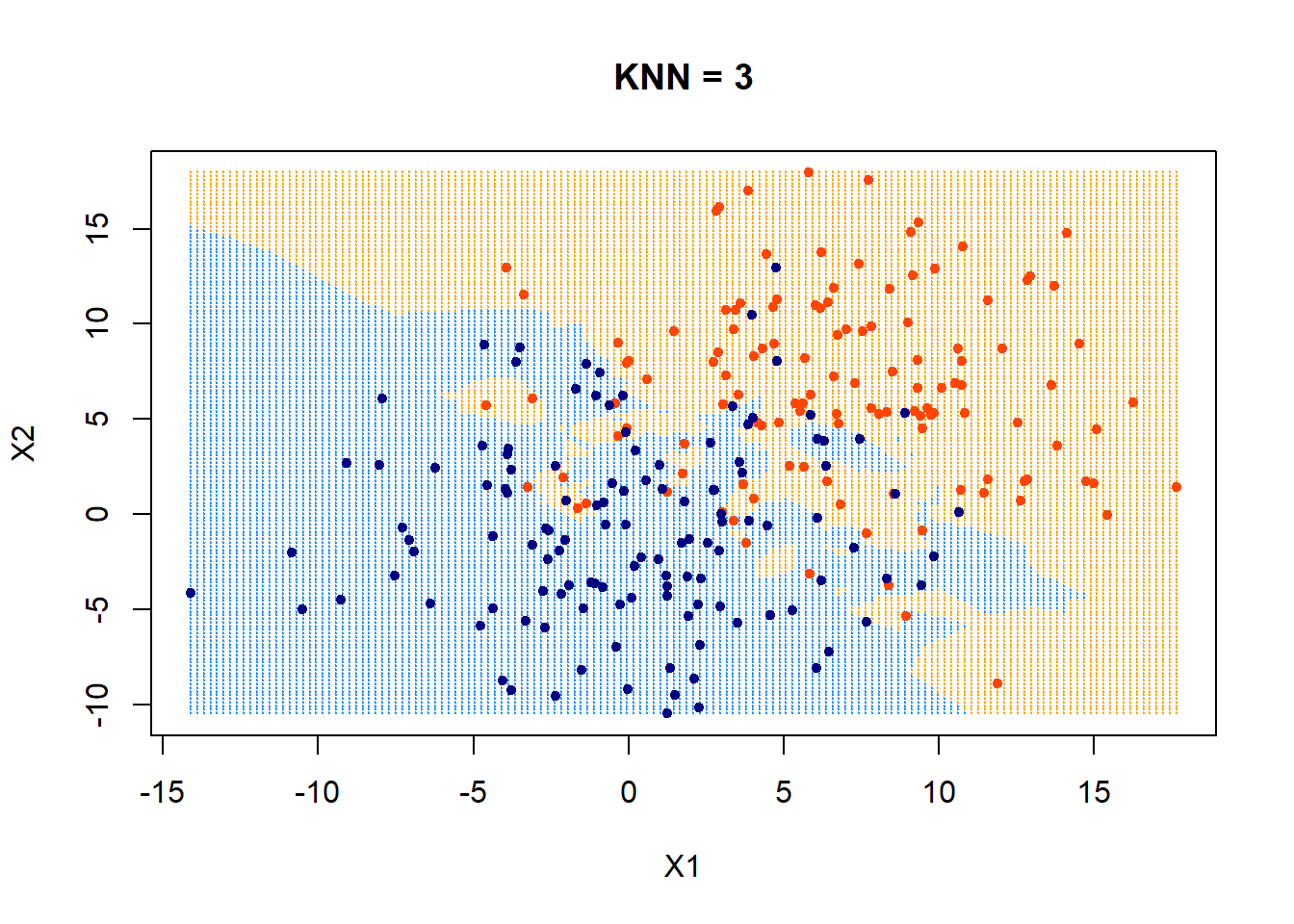
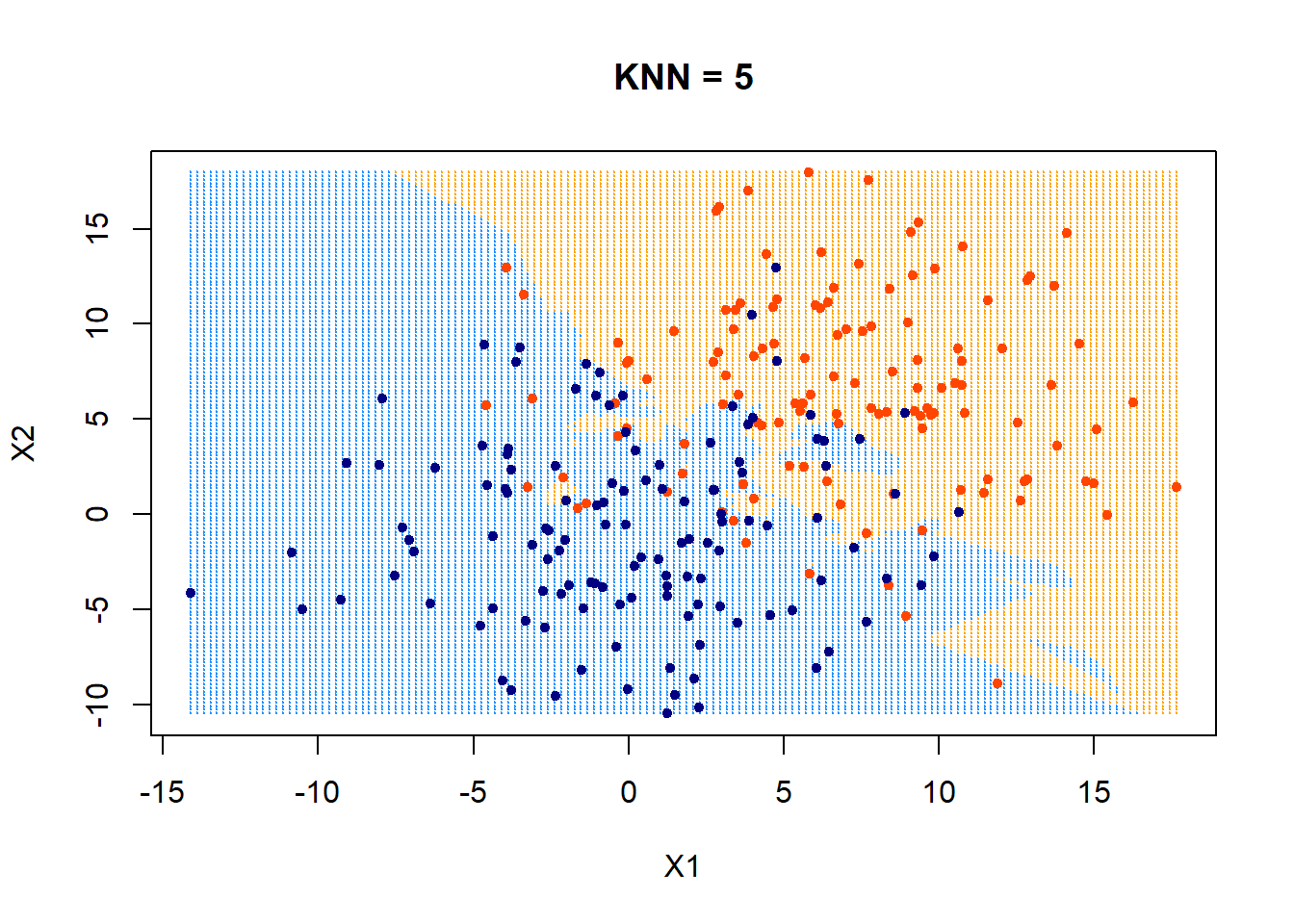
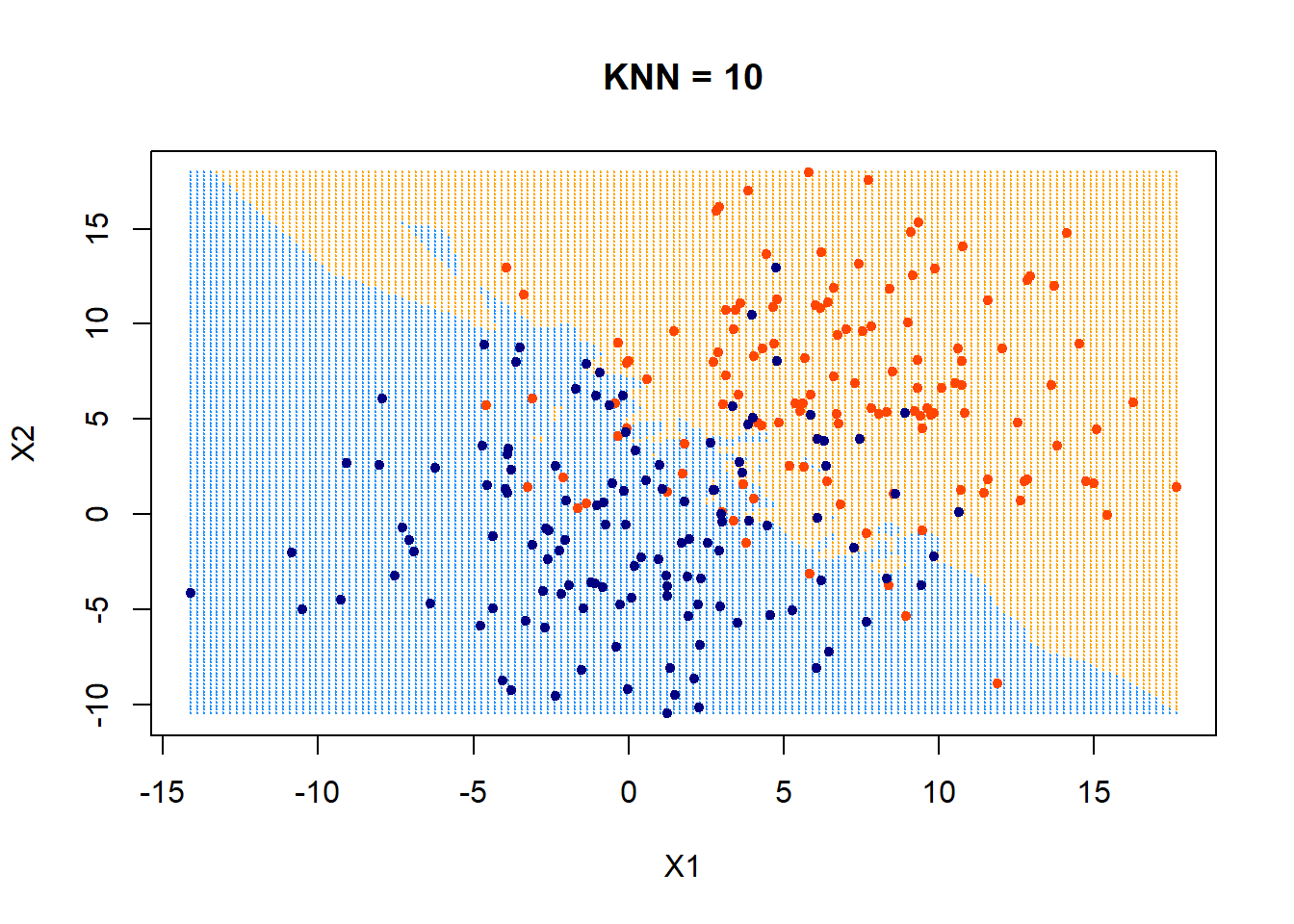
Summary
-
One really important class of ML models is called “non-parametric”.
-
Decision trees are kind of like creating a flow chart. These hypotheses are the most human-understandable of any we have worked with.We regularize by first growing trees that are very big and then “pruning” them.
-
Ensembles: sometimes it’s useful to come up with a lot of simple hypotheses and then let them “vote” to make a prediction for a new example.
-
Nearest neighbor remembers all the training data for prediction. Depends crucially on our notion of “closest” (standardize data is important). Can do fancier things (weighted kNN).Less good in high dimensions (computationally expensive).
Thanks!
We'd love to hear your thoughts.



\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)




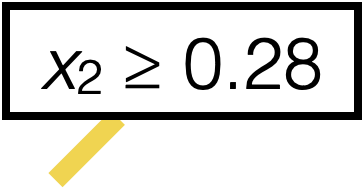
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



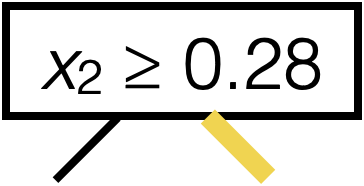
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)




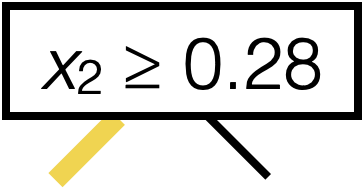
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



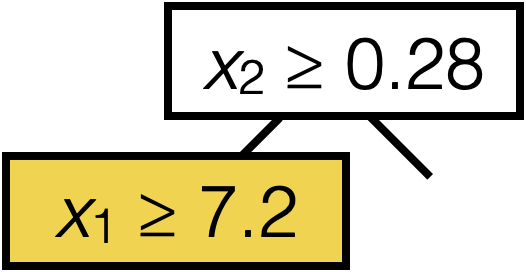

\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)


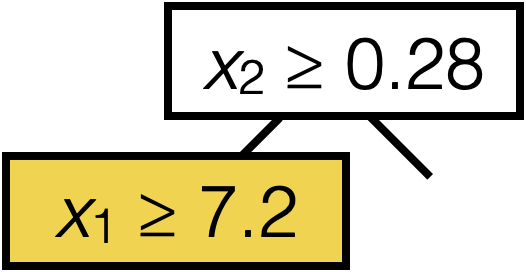

\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)




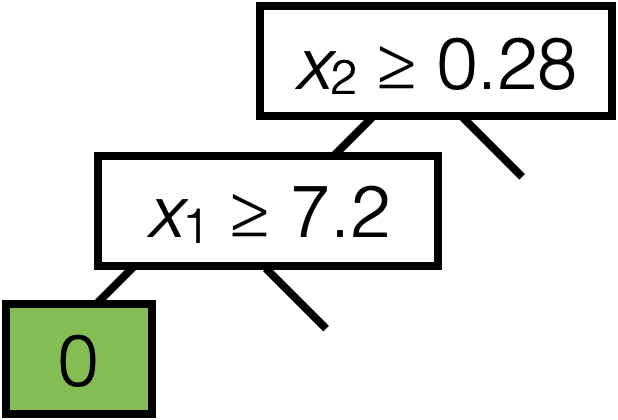
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



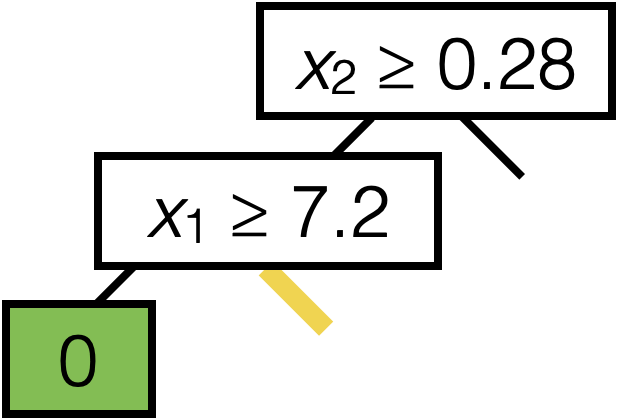
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)


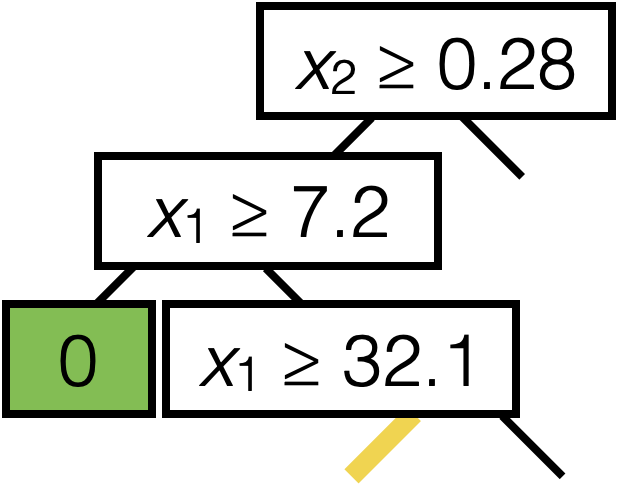

\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)


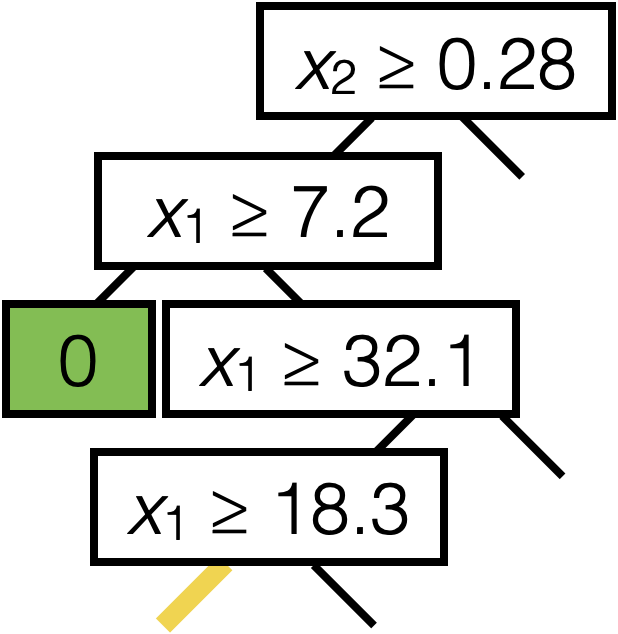

\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)




\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)






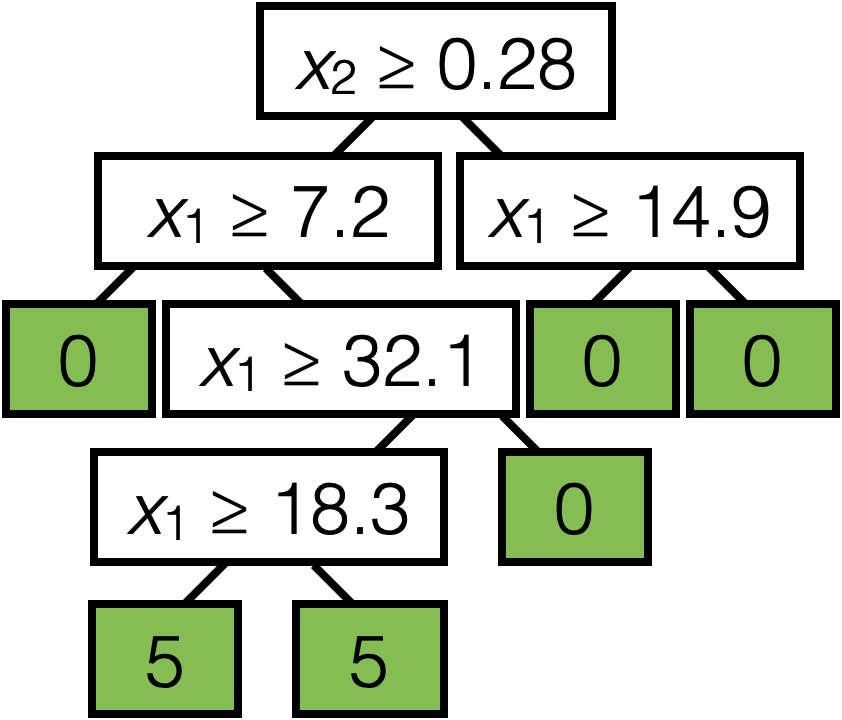

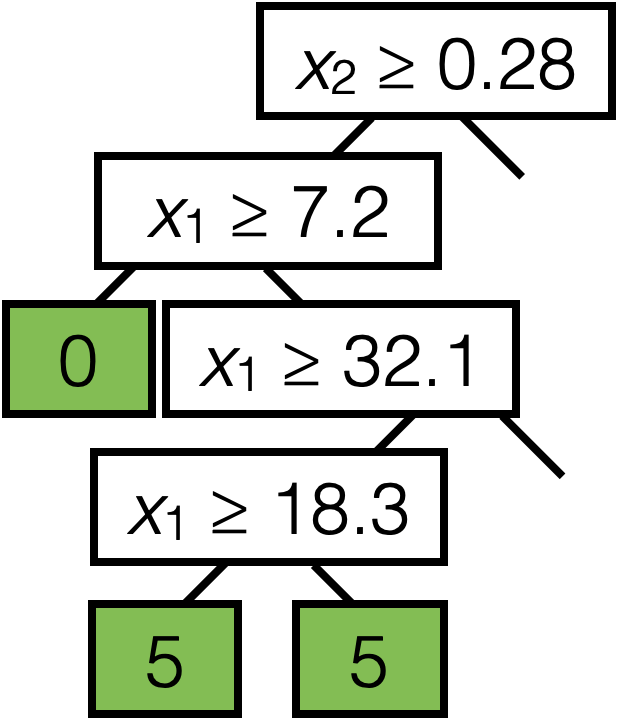
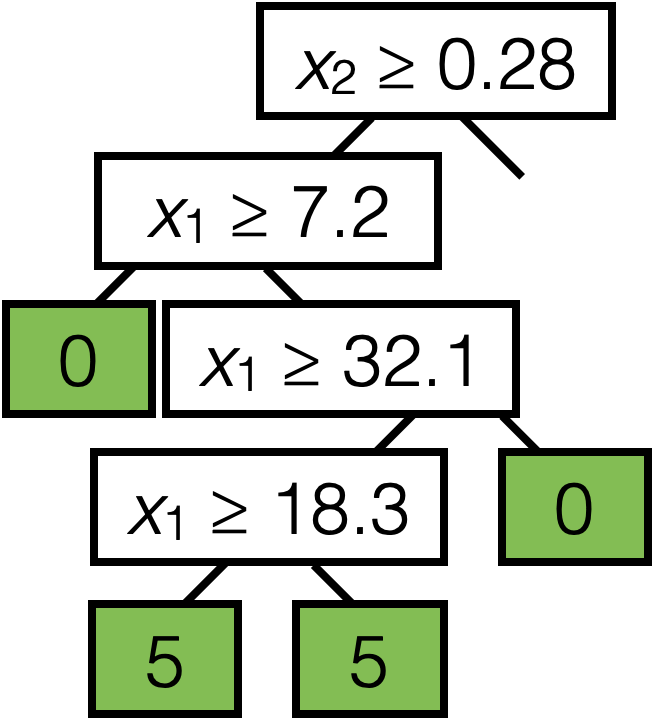
\(x_2 \geq 0.28\)
\(x_1 \geq 7.2\)
\(x_1 \geq 14.9\)
\(x_1 \geq 32.1\)
\(x_1 \geq 18.3\)
0
0
0
0
5
5
6.390 IntroML (Fall24) - Lecture 13 Non-parametric Models
By Shen Shen
6.390 IntroML (Fall24) - Lecture 13 Non-parametric Models
- 311



