Lecture 10: Markov Decision Processes
Shen Shen
April 18, 2025
11am, Room 10-250
Intro to Machine Learning
Toddler demo, Russ Tedrake thesis, 2004
(Uses vanilla policy gradient (actor-critic))
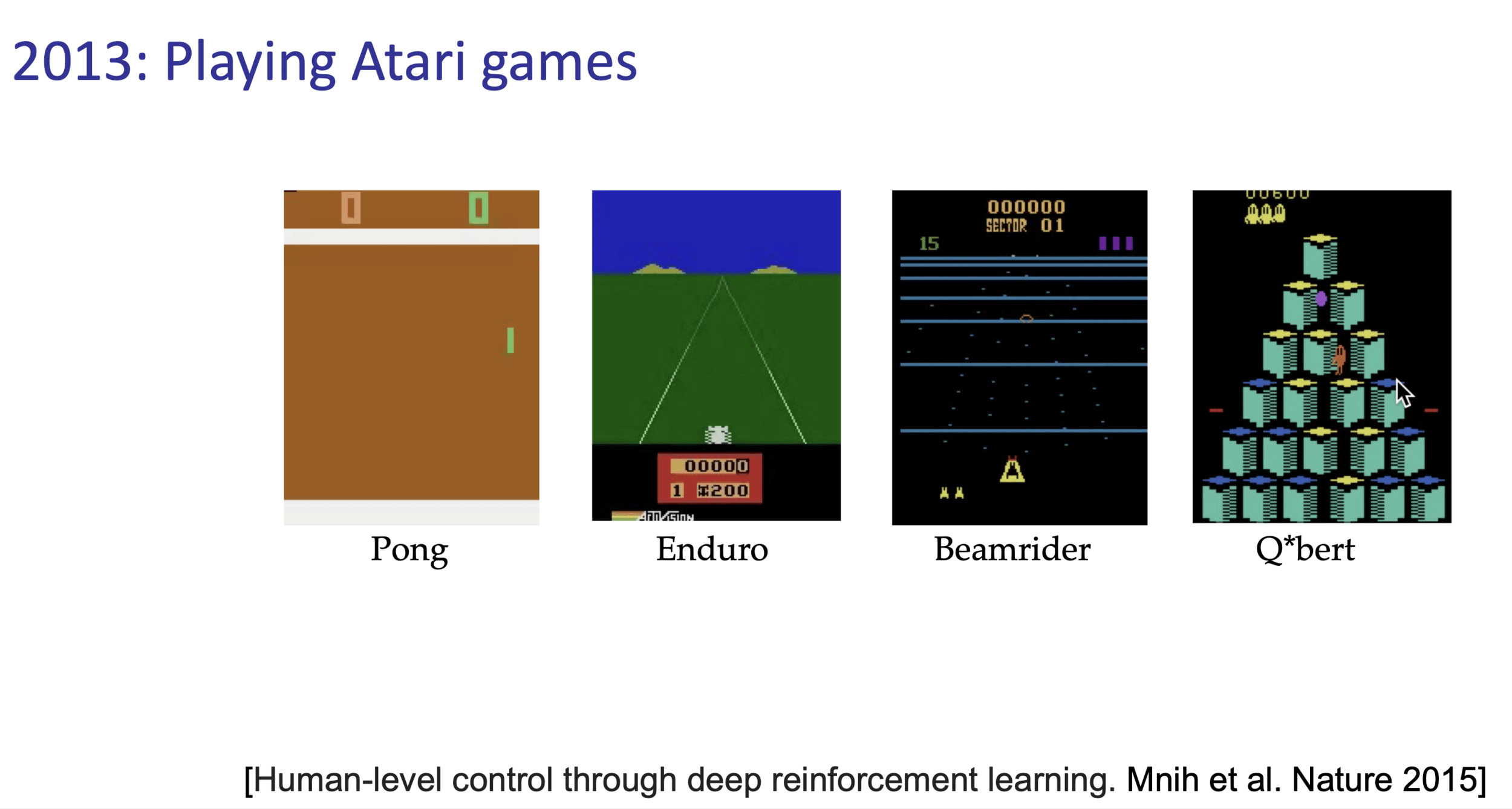
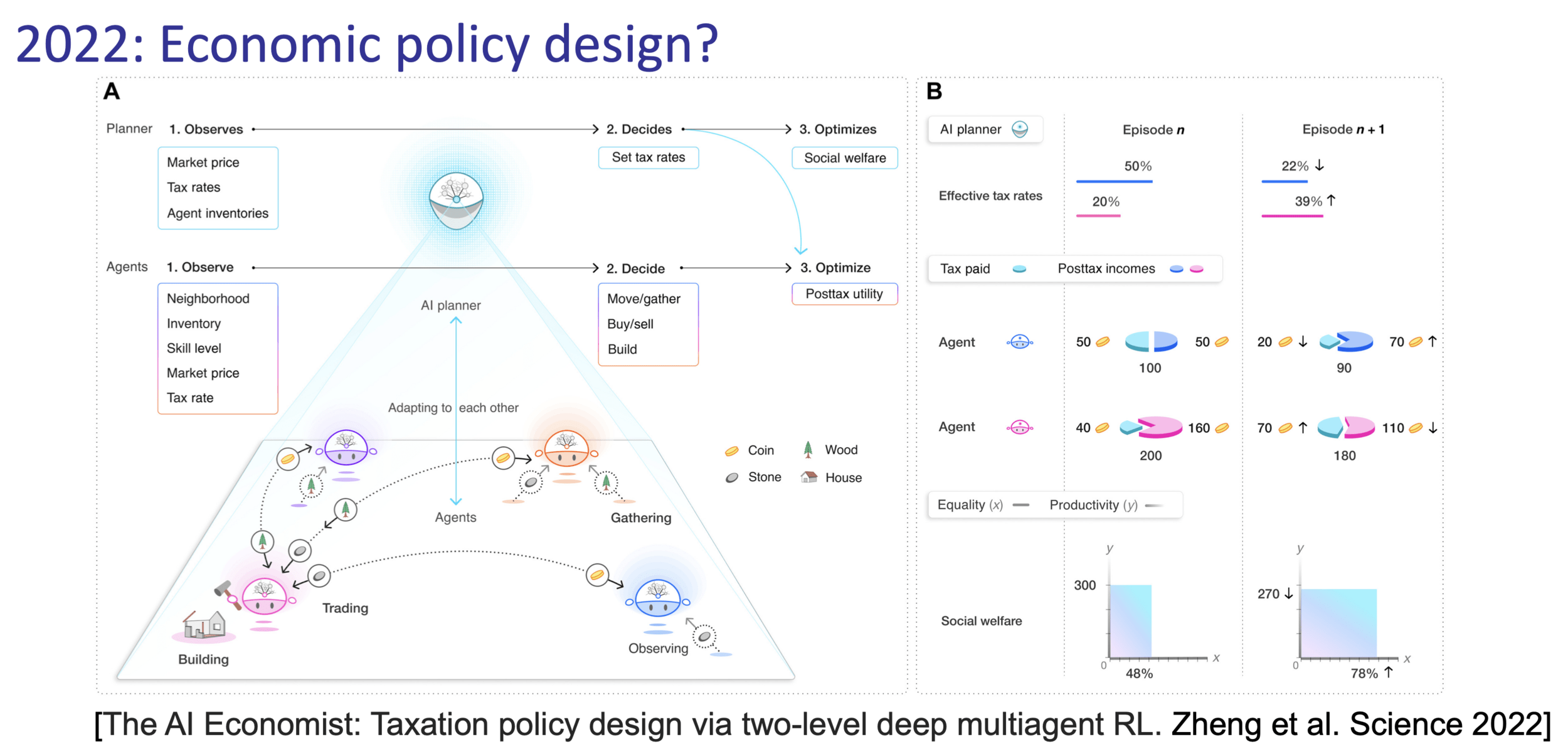
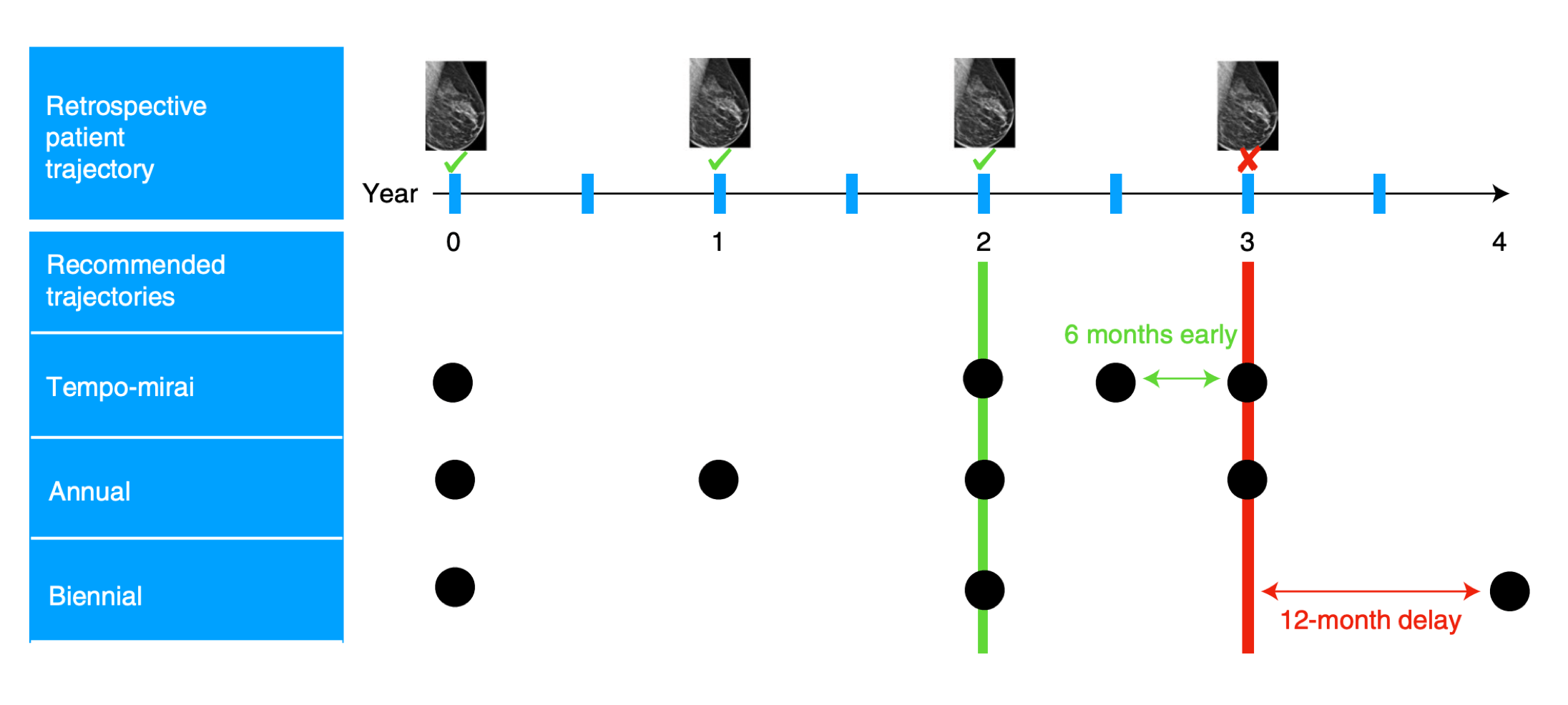
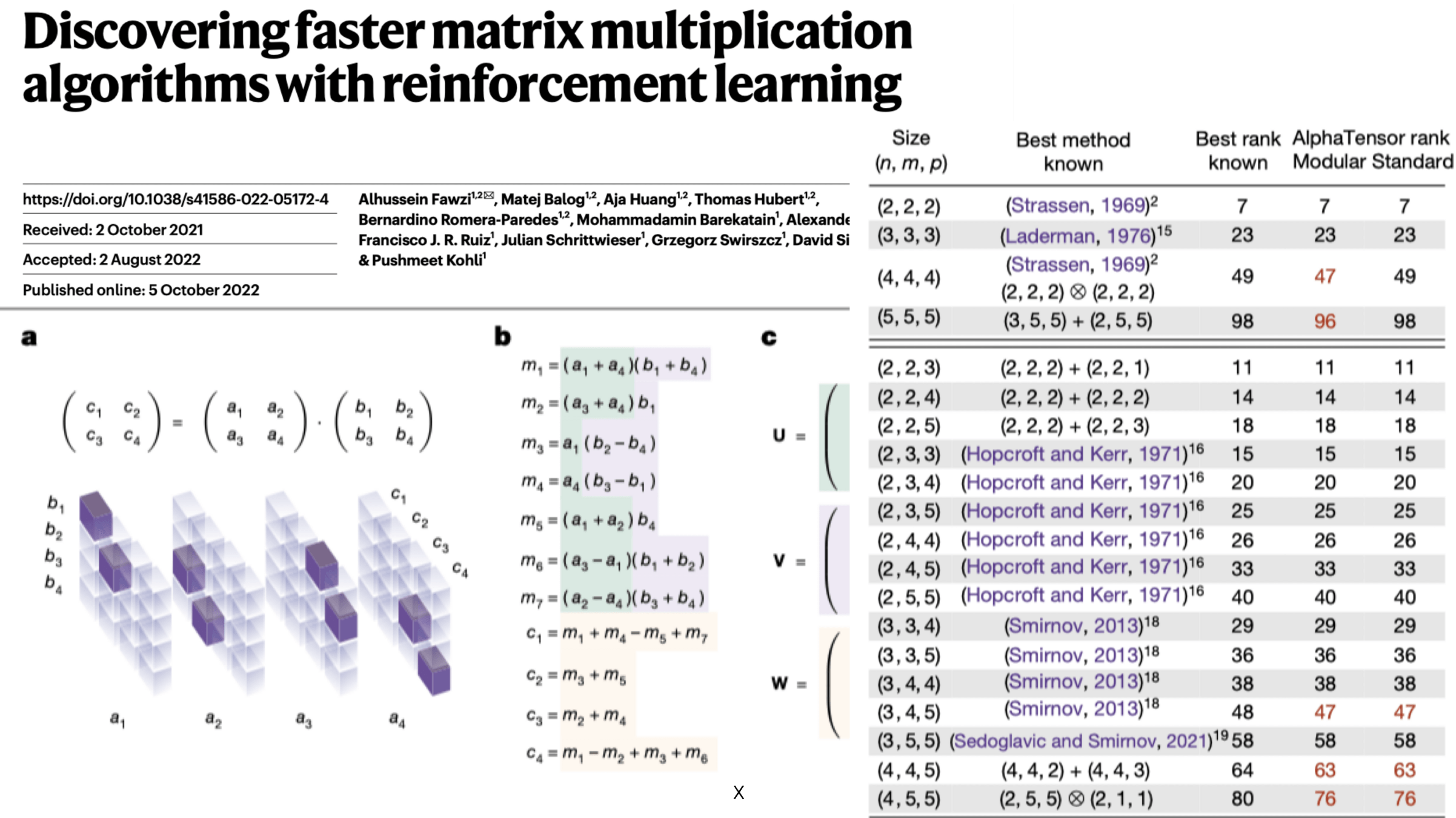
Reinforcement Learning with Human Feedback
Outline
- Markov Decision Processes Definition, terminologies, and policy
-
Policy Evaluation
-
State Value Functions \(\mathrm{V}^{\pi}\)
-
Bellman recursions and Bellman equations
-
-
Policy Optimization
-
Optimal policies \(\pi^*\)
-
Optimal action value functions: \(\mathrm{Q}^*\)
-
Value iteration
-
Outline
- Markov Decision Processes Definition, terminologies, and policy
-
Policy Evaluation
-
State Value Functions \(\mathrm{V}^{\pi}\)
-
Bellman recursions and Bellman equations
-
-
Policy Optimization
-
Optimal policies \(\pi^*\)
-
Optimal action value functions: \(\mathrm{Q}^*\)
-
Value iteration
-
Markov Decision Processes
-
Research area initiated in the 50s by Bellman, known under various names:
-
Stochastic optimal control (Control theory)
-
Stochastic shortest path (Operations research)
-
Sequential decision making under uncertainty (Economics)
-
Reinforcement learning (Artificial intelligence, Machine learning)
-
-
A rich variety of accessible and elegant theory, math, algorithms, and applications. But also, considerable variation in notations.
-
We will use the most RL-flavored notations.
- (state, action) results in a transition \(\mathrm{T}\) into a next state:
-
Normally, we get to the “intended” state;
-
E.g., in state (7), action “↑” gets to state (4)
-
-
If an action would take Mario out of the grid world, stay put;
-
E.g., in state (9), “→” gets back to state (9)
-
-
In state (6), action “↑” leads to two possibilities:
-
20% chance to (2)
-
80% chance to (3).
-
-
80\%
20\%
Running example: Mario in a grid-world
- 9 possible states \(s\)
- 4 possible actions \(a\): {Up ↑, Down ↓, Left ←, Right →}
1
1
1
1
-10
-10
-10
-10
reward of (3, \(\downarrow\))
reward of \((3,\uparrow\))
reward of \((6, \downarrow\))
reward of \((6,\rightarrow\))
- (state, action) pairs give rewards:
- in state 3, any action gives reward 1
- in state 6, any action gives reward -10
- any other (state, action) pair gives reward 0
-
discount factor: a scalar that reduces the "worth" of rewards, depending on the timing Mario gets the rewards.
- e.g., say this factor is 0.9. then, for (3, \(\leftarrow\)) pair, Mario gets a reward of 1 at the start of the game; at the 2nd time step, a discounted reward of 0.9; at the 3rd time step, it is further discounted to \((0.9)^2\), and so on.
Mario in a grid-world, cont'd
- \(\mathcal{S}\) : state space, contains all possible states \(s\).
- \(\mathcal{A}\) : action space, contains all possible actions \(a\).
Markov Decision Processes - Definition and terminologies
In 6.390,
- \(\mathcal{S}\) and \(\mathcal{A}\) are small discrete sets, unless otherwise specified.
- \(\mathcal{S}\) : state space, contains all possible states \(s\).
- \(\mathcal{A}\) : action space, contains all possible actions \(a\).
- \(\mathrm{T}\left(s, a, s^{\prime}\right)\) : the probability of transition from state \(s\) to \(s^{\prime}\) when action \(a\) is taken.
Markov Decision Processes - Definition and terminologies
80\%
20\%
\(\mathrm{T}\left(7, \uparrow, 4\right) = 1\)
\(\mathrm{T}\left(9, \rightarrow, 9\right) = 1\)
\(\mathrm{T}\left(6, \uparrow, 3\right) = 0.8\)
\(\mathrm{T}\left(6, \uparrow, 2\right) = 0.2\)
In 6.390,
- \(\mathcal{S}\) and \(\mathcal{A}\) are small discrete sets, unless otherwise specified.
- \(s^{\prime}\) and \(a^{\prime}\) are short-hand for the next-timestep
- \(\mathcal{S}\) : state space, contains all possible states \(s\).
- \(\mathcal{A}\) : action space, contains all possible actions \(a\).
- \(\mathrm{T}\left(s, a, s^{\prime}\right)\) : the probability of transition from state \(s\) to \(s^{\prime}\) when action \(a\) is taken.
- \(\mathrm{R}(s, a)\) : reward, takes in a (state, action) pair and returns a reward.
Markov Decision Processes - Definition and terminologies
reward of \((3,\uparrow\))
reward of \((6,\rightarrow\))
\(\mathrm{R}\left(3, \uparrow \right) = 1\)
\(\mathrm{R}\left(6, \rightarrow \right) = -10\)
In 6.390,
- \(\mathcal{S}\) and \(\mathcal{A}\) are small discrete sets, unless otherwise specified.
- \(s^{\prime}\) and \(a^{\prime}\) are short-hand for the next-timestep
- \(\mathrm{R}(s, a)\) is deterministic and bounded.
- \(\mathcal{S}\) : state space, contains all possible states \(s\).
- \(\mathcal{A}\) : action space, contains all possible actions \(a\).
- \(\mathrm{T}\left(s, a, s^{\prime}\right)\) : the probability of transition from state \(s\) to \(s^{\prime}\) when action \(a\) is taken.
- \(\mathrm{R}(s, a)\) : reward, takes in a (state, action) pair and returns a reward.
- \(\gamma \in [0,1]\): discount factor, a scalar.
- \(\pi{(s)}\) : policy, takes in a state and returns an action.
The goal of an MDP is to find a "good" policy.
Markov Decision Processes - Definition and terminologies
In 6.390,
- \(\mathcal{S}\) and \(\mathcal{A}\) are small discrete sets, unless otherwise specified.
- \(s^{\prime}\) and \(a^{\prime}\) are short-hand for the next-timestep
- \(\mathrm{R}(s, a)\) is deterministic and bounded.
- \(\pi(s)\) is deterministic.
- \(a_t = \pi(s_t)\)
- \(r_t = \mathrm{R}(s_t,a_t)\)
Policy \(\pi(s)\)
Transition \(\mathrm{T}\left(s, a, s^{\prime}\right)\)
Reward \(\mathrm{R}(s, a)\)
time
a trajectory (aka, an experience, or a rollout), of horizon \(h\)
\(\quad \tau=\left(s_0, a_0, r_0, s_1, a_1, r_1, \ldots s_{h-1}, a_{h-1}, r_{h-1}\right)\)
\underbrace{\hspace{4cm}}
initial state
all depends on \(\pi\)
\dots
s_2
s_3
s_4
s_5
a_2
a_3
a_4
r_2
r_3
r_4
s_0
s_1
a_0
a_1
r_0
r_1
s_{h-2}
a_{h-2}
r_{h-2}
s_{h-1}
a_{h-1}
r_{h-1}
- \(\operatorname{Pr}\left(s_t=s^{\prime} \mid s_{t-1}=s, a_{t-1}=a\right)=\mathrm{T}\left(s, a, s^{\prime}\right)\)
Policy \(\pi(s)\)
Transition \(\mathrm{T}\left(s, a, s^{\prime}\right)\)
Reward \(\mathrm{R}(s, a)\)
time
\dots
s_2
s_3
s_4
s_5
a_2
a_3
a_4
r_2
r_3
r_4
s_0
s_1
a_0
a_1
r_0
r_1
s_{h-2}
a_{h-2}
r_{h-2}
s_{h-1}
a_{h-1}
r_{h-1}
Starting in a given \(s_0\), how "good" is it to follow a policy \(\pi\) for \(h\) time steps?
\mathrm{R}(s_0, a_0)
\gamma \mathrm{R}(s_1, a_1)
\gamma^3\mathrm{R}(s_3, a_3)
\gamma^2 \mathrm{R}(s_2, a_2)
\dots
+
+
+
+
\gamma^{h-1}\mathrm{R}(s_{h-1}, a_{h-1})
+
One idea:
Policy \(\pi(s)\)
Transition \(\mathrm{T}\left(s, a, s^{\prime}\right)\)
Reward \(\mathrm{R}(s, a)\)
time
\dots
s_2
s_3
s_4
s_5
a_2
a_3
a_4
r_2
r_3
r_4
s_0
s_1
a_0
a_1
r_0
r_1
s_{h-2}
a_{h-2}
r_{h-2}
s_{h-1}
a_{h-1}
r_{h-1}
Starting in a given \(s_0\), how "good" is it to follow a policy \(\pi\) for \(h\) time steps?
But in
Mario game:
80\%
20\%
??
\mathrm{R}(s_0, a_0)
\gamma \mathrm{R}(s_1, a_1)
\gamma^3\mathrm{R}(s_3, a_3)
\gamma^2 \mathrm{R}(s_2, a_2)
\dots
+
+
+
+
\gamma^{h-1}\mathrm{R}(s_{h-1}, a_{h-1})
+
One idea:
-10
\uparrow
6
if start at \(s_0=6\) and policy \(\pi(s) =\uparrow, \forall s\), i.e., always up
\mathrm{R}(s_0, a_0)
\gamma \mathrm{R}(s_1, a_1)
\gamma^3\mathrm{R}(s_3, a_3)
\gamma^2 \mathrm{R}(s_2, a_2)
\dots
+
+
+
+
\gamma^{h-1}\mathrm{R}(s_{h-1}, a_{h-1})
+
\mathbb{E}[
]
in 390, this expectation is only w.r.t. the transition probabilities \(\mathrm{T}\left(s, a, s^{\prime}\right)\)
\( h\) terms
\underbrace{\hspace{7.6cm}}
Policy \(\pi(s)\)
Transition \(\mathrm{T}\left(s, a, s^{\prime}\right)\)
Reward \(\mathrm{R}(s, a)\)
time
\dots
s_2
s_3
s_4
s_5
a_2
a_3
a_4
r_2
r_3
r_4
s_0
s_1
a_0
a_1
r_0
r_1
s_{h-2}
a_{h-2}
r_{h-2}
s_{h-1}
a_{h-1}
r_{h-1}
Starting in a given \(s_0\), how "good" is it to follow a policy \(\pi\) for \(h\) time steps?
Outline
- Markov Decision Processes Definition, terminologies, and policy
-
Policy Evaluation
-
State Value Functions \(\mathrm{V}^{\pi}\)
-
Bellman recursions and Bellman equations
-
-
Policy Optimization
-
Optimal policies \(\pi^*\)
-
Optimal action value functions: \(\mathrm{Q}^*\)
-
Value iteration
-
Definition: For a given policy \(\pi(s),\) the state value functions
\(\mathrm{V}_h^\pi(s):=\mathbb{E}\left[\sum_{t=0}^{h-1} \gamma^t \mathrm{R}\left(s_t, \pi\left(s_t\right)\right) \mid s_0=s, \pi\right], \forall s, h\)
- value functions \(\mathrm{V}_h^\pi(s)\): the expected sum of discounted rewards, starting in state \(s,\) and follow policy \(\pi\) for \(h\) steps.
- horizon-0 values defined as 0.
- value is long-term, reward is short-term (one-time).
\mathrm{R}(s_0, a_0)
\gamma \mathrm{R}(s_1, a_1)
\gamma^3\mathrm{R}(s_3, a_3)
\gamma^2 \mathrm{R}(s_2, a_2)
\dots
+
+
+
+
\gamma^{h-1}\mathrm{R}(s_{h-1}, a_{h-1})
+
\mathbb{E}[
]
expanded form
\mathbb{E}[
]
\( h\) terms
\underbrace{\hspace{4cm}}
evaluate the "\(\pi(s) = \uparrow\), for all \(s,\) i.e. the always \(\uparrow\)" policy
\mathrm{R}(s_0, a_0)
\gamma \mathrm{R}(s_1, a_1)
\gamma^2 \mathrm{R}(s_2, a_2)
\dots
+
+
+
horizon \(h\) = 0: no step left
\mathrm{V}^{\uparrow}_0(s) = 0
horizon \(h\) = 1: receive the rewards
\mathrm{V}^{\uparrow}_1(s) = \mathrm{R}(s, \uparrow)
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
-10
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
0
0
\mathrm{R}(1, \uparrow) + \gamma \mathrm{R}(1, \uparrow)
0
\mathrm{R}(2, \uparrow) + \gamma \mathrm{R}(2, \uparrow)
1.9
\mathrm{R}(3, \uparrow) + \gamma \mathrm{R}(3, \uparrow)
0
\mathrm{R}(4, \uparrow) + \gamma \mathrm{R}(1, \uparrow)
= 1 + 0.9 *(1) = 1.9
\mathrm{R}(5, \uparrow) + \gamma \mathrm{R}(2, \uparrow)
\mathrm{V}^{\uparrow}_2(s) =
horizon \(h = 2:\)
\mathbb{E}[
]
\mathrm{R}(s_0, a_0)
\gamma\mathrm{R}(s_1, a_1)
+
\( 2\) terms inside
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
-9
0
0
-9.28
\mathrm{R}(6, \uparrow) + \gamma [.2 \mathrm{R}(2, \uparrow) + .8 \mathrm{R}(3, \uparrow)]
\mathrm{R}(8, \uparrow) + \gamma \mathrm{R}(5, \uparrow)
\mathrm{R}(7, \uparrow) + \gamma \mathrm{R}(4, \uparrow)
\mathrm{R}(9, \uparrow) + \gamma \mathrm{R}(6, \uparrow)
= -10 + 0.9*(0.2*0+0.8*1)
= -9.28
?
= 0 + 0.9*(-10)
action \(\uparrow\)
\mathrm{R}(6, \uparrow)
20\%
80\%
action \(\uparrow\)
\mathrm{R}(2, \uparrow)
\gamma
action \(\uparrow\)
\mathrm{R}(3, \uparrow)
\gamma
\mathbb{E}[
]
\mathrm{R}(s_0, a_0)
\gamma\mathrm{R}(s_1, a_1)
+
\( 2\) terms inside
\mathrm{V}^{\uparrow}_2(s) =
0
0
1.9
0
0
horizon \(h = 2:\)
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
V^{\uparrow}_3(6)
action \(\uparrow\)
action \(\uparrow\)
action \(\uparrow\)
action \(\uparrow\)
action \(\uparrow\)
20\%
80\%
80\%
\mathrm{R}(6, \uparrow)
\gamma \mathrm{R}(2, \uparrow)
20\%
+
+
\gamma \mathrm{R}(2, \uparrow)
\gamma^2 \mathrm{R}(2, \uparrow)
\gamma \mathrm{R}(3, \uparrow)
\mathrm{R}(s_0, a_0)
\gamma \mathrm{R}(s_1, a_1)
+
\mathbb{E}[
]
\gamma^2 \mathrm{R}(s_2, a_2)
+
\mathrm{R}(6, \uparrow)
\gamma^2\mathrm{R}(3, \uparrow)
\gamma^2 \mathrm{R}(2, \uparrow)
\gamma \mathrm{R}(3, \uparrow)
20\%
+
80\%
\gamma^2\mathrm{R}(3, \uparrow)
+
=
horizon \(h = 3:\)
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
\mathrm{R}(6, \uparrow)
\gamma \mathrm{R}(2, \uparrow)
20\%
+
+
\gamma^2 \mathrm{R}(2, \uparrow)
\gamma \mathrm{R}(3, \uparrow)
80\%
+
\gamma^2\mathrm{R}(3, \uparrow)
=
+
[
]
]
[
=
+
\left[\mathrm{R}(3, \uparrow) + \gamma \mathrm{R}(3, \uparrow)\right]
\gamma
+
80\%
\mathrm{R}(6, \uparrow)
\left[\mathrm{R}(2, \uparrow) + \gamma \mathrm{R}(2, \uparrow)\right]
\gamma
20\%
=
80\%
\gamma
20\%
+
V^{\uparrow}_2(2)
\gamma
+
\mathrm{R}(6, \uparrow)
\mathrm{V}^{\uparrow}_2(3)
\mathrm{V}_h^\pi(s)=\mathrm{R}\left(s, \pi(s)\right)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right)
the immediate reward for taking the policy-prescribed action \(\pi(s)\) in state \(s\).
horizon-\(h\) value in state \(s\): the expected sum of discounted rewards, starting in state \(s\) and following policy \(\pi\) for \(h\) steps.
\mathrm{V}^{\uparrow}_3(6)
=
80\%
\gamma
20\%
+
\mathrm{V}^{\uparrow}_2(2)
\gamma
+
\mathrm{R}(6, \uparrow)
\mathrm{V}^{\uparrow}_2(3)
\((h-1)\) horizon future values at a next state \(s^{\prime}\)
sum up future values weighted by the probability of getting to that next state \(s^{\prime}\)
discounted by \(\gamma\)
\mathrm{V}_h^\pi(s)=\mathrm{R}\left(s, \pi(s)\right)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right), \forall s
Bellman Recursion
\mathrm{V}^{\uparrow}_2(s)
\mathrm{V}^{\uparrow}_3(s)
\mathrm{V}^{\uparrow}_4(s)
\mathrm{V}^{\uparrow}_5(s)
\mathrm{V}^{\uparrow}_6(s)
-7.048 = -10 +.9[.2*0+0.8*4.10]
\mathrm{V}^{\uparrow}_{61}(s)
\mathrm{V}^{\uparrow}_{62}(s)
\dots
\mathrm{V}^{\uparrow}_1(s) = \mathrm{R}(s,\uparrow)
\mathrm{V}^{\uparrow}_{6}(6) = \mathrm{R}(6, \uparrow) + \gamma [.2 \mathrm{V}^{\uparrow}_{5}(2) + .8\times \mathrm{V}^{\uparrow}_{5}(3)]
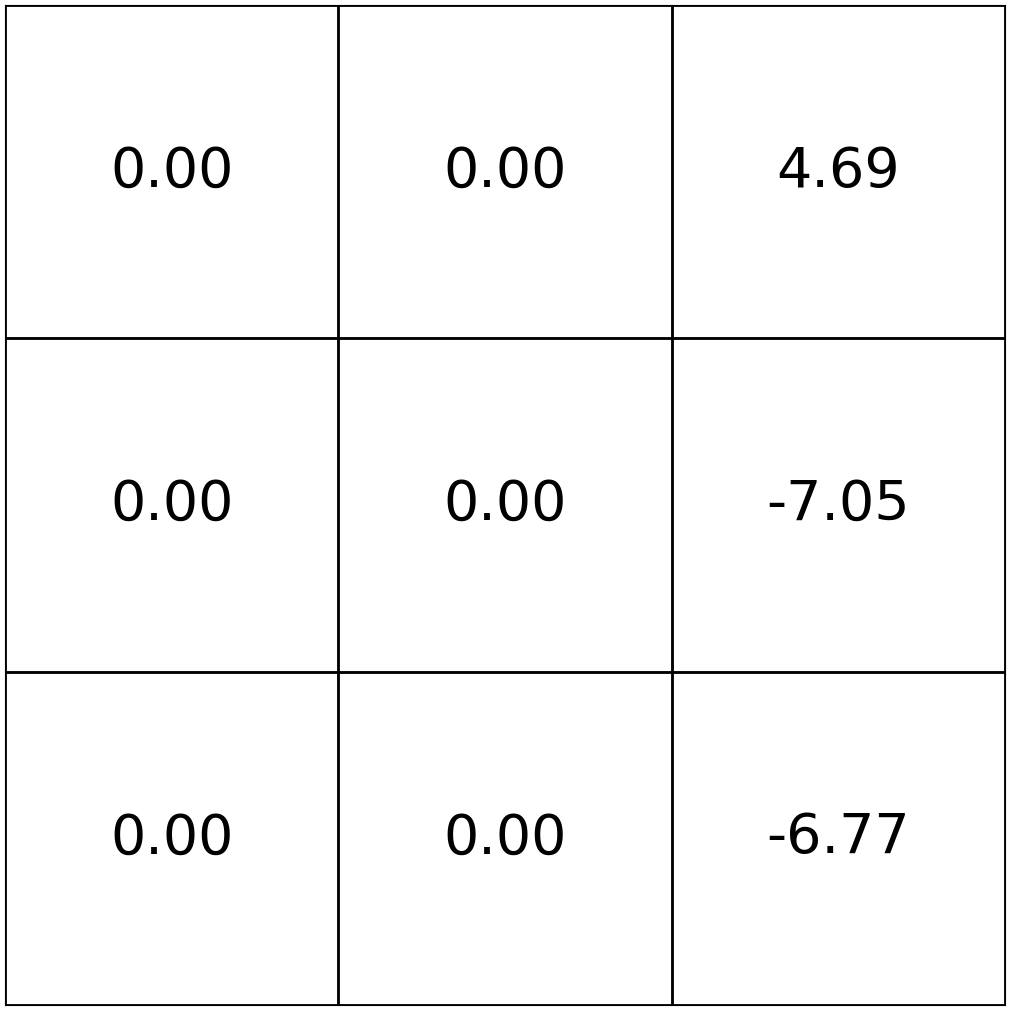
approaches infinity
\mathrm{V}^\pi_{\infty}(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}^\pi_{\infty}\left(s^{\prime}\right), \forall s
\(|\mathcal{S}|\) many linear equations, one equation for each state
typically \(\gamma <1\) in MDP definition, motivated to make \(\mathrm{V}^{\pi}_{\infty}(s):=\mathbb{E}\left[\sum_{t=0}^{\infty} \gamma^t \mathrm{R}\left(s_t, \pi\left(s_t\right)\right) \mid s_0=s, \pi\right]\) finite.
Bellman Equations
If the horizon \(h\) goes to infinity
\mathrm{V}_h^\pi(s)=\mathrm{R}\left(s, \pi(s)\right)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right), \forall s
Bellman Recursion
\mathrm{V}^{\uparrow}_{\infty}(s)
-2.8 = \mathrm{V}^{\uparrow}_{\infty}(6) = \mathrm{R}(6, \uparrow) + \gamma [.2 \mathrm{V}^{\uparrow}_{\infty}(2) + .8\times \mathrm{V}^{\uparrow}_{\infty}(3)]
= -10 + .9 [.2 \times 0 + .8 * 10]
10 = \mathrm{V}^{\uparrow}_{\infty}(3) = \mathrm{R}(3, \uparrow) + \gamma [\mathrm{V}^{\uparrow}_{\infty}(3)] = 1 + .9 \times 10
-2.52 = \mathrm{V}^{\uparrow}_{\infty}(9) = \mathrm{R}(9, \uparrow) + \gamma [\mathrm{V}^{\uparrow}_{\infty}(6)] = 0 + .9 \times (-2.8)
finite-horizon Bellman recursions
infinite-horizon Bellman equations
\mathrm{V}^\pi_{\infty}(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}^\pi_{\infty}\left(s^{\prime}\right), \forall s
\mathrm{V}_{h}^\pi(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right), \forall s
Recall: For a given policy \(\pi(s),\) the (state) value functions
\(\mathrm{V}_h^\pi(s):=\mathbb{E}\left[\sum_{t=0}^{h-1} \gamma^t \mathrm{R}\left(s_t, \pi\left(s_t\right)\right) \mid s_0=s, \pi\right], \forall s, h\)
\pi(s)
\mathrm{V}^{\pi}_{h}(s)
MDP
Policy evaluation
Quick summary
1. By summing \(h\) terms:
2. By leveraging structure:
Outline
- Markov Decision Processes Definition, terminologies, and policy
-
Policy Evaluation
-
State Value Functions \(\mathrm{V}^{\pi}\)
-
Bellman recursions and Bellman equations
-
-
Policy Optimization
-
Optimal policies \(\pi^*\)
-
Optimal action value functions: \(\mathrm{Q}^*\)
-
Value iteration
-
- An MDP has a unique optimal value \(\mathrm{V}_h^{*}({s})\).
- Optimal policy \(\pi^*\) might not be unique (think, e.g. symmetric world).
- For finite \(h\), optimal policy \(\pi^*_h\) depends on how many time steps left.
- When \(h \rightarrow \infty\), time no longer matters, i.e., there exists a stationary \(\pi^*\).
- Under optimal policy, recursion holds too
Optimal policy \(\pi^*\)
Definition: for a given MDP and a fixed horizon \(h\) (possibly infinite), \(\pi^*\) is an optimal policy if \(\mathrm{V}_h^{\pi^*}({s}) = \mathrm{V}_h^{*}({s})\geqslant \mathrm{V}_h^\pi({s})\) for all \(s \in \mathcal{S}\) and for all possible policy \(\pi\).
\mathrm{V}_{h}^{{*}}(s)= \mathrm{R}(s, \pi^*(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi^*(s), s^{\prime}\right) \mathrm{V}_{h-1}^{{*}}\left(s^{\prime}\right), \forall s, h
- One idea: enumerate over all \(\pi\), do policy evaluation, compare \(V^\pi,\) get \(\mathrm{V}^{*}(s)\)
- tedious, and even with \(\mathrm{V}^{*}(s)\)... not super clear how to act
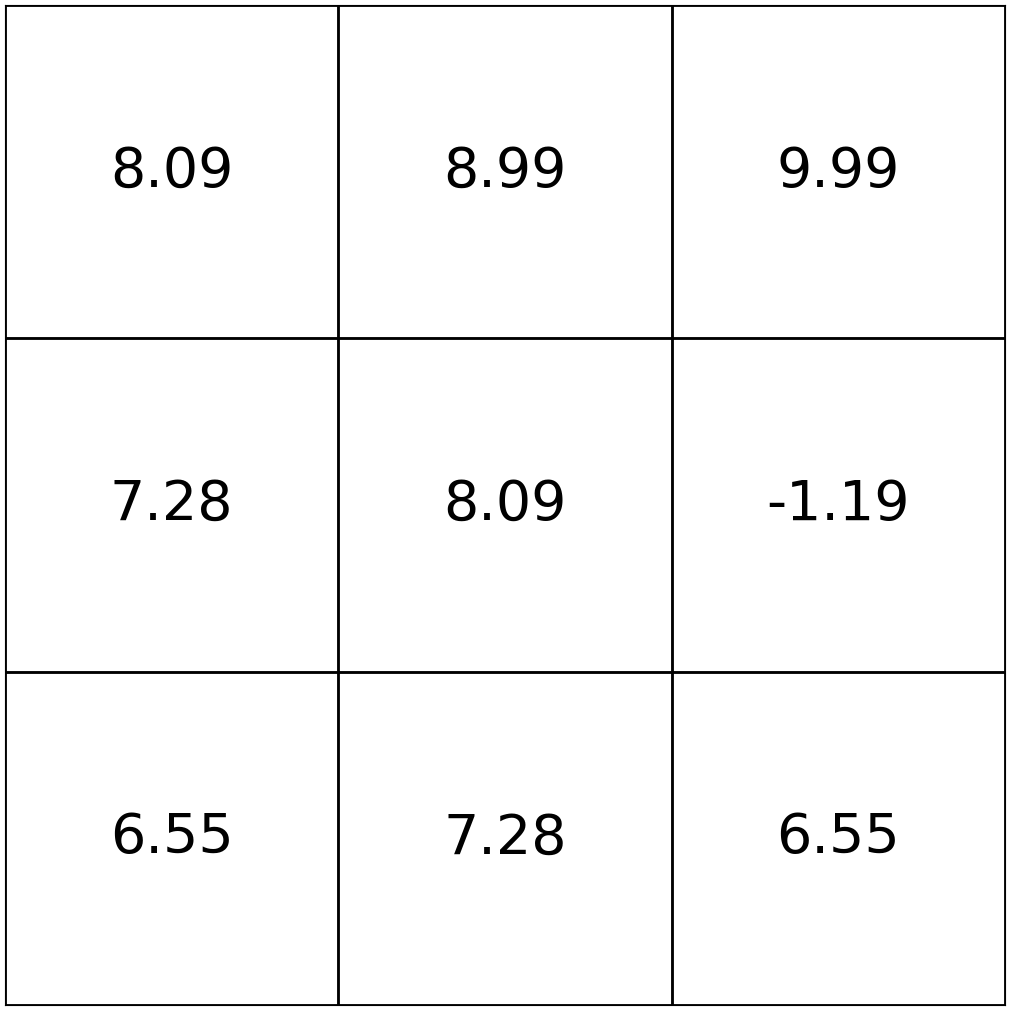
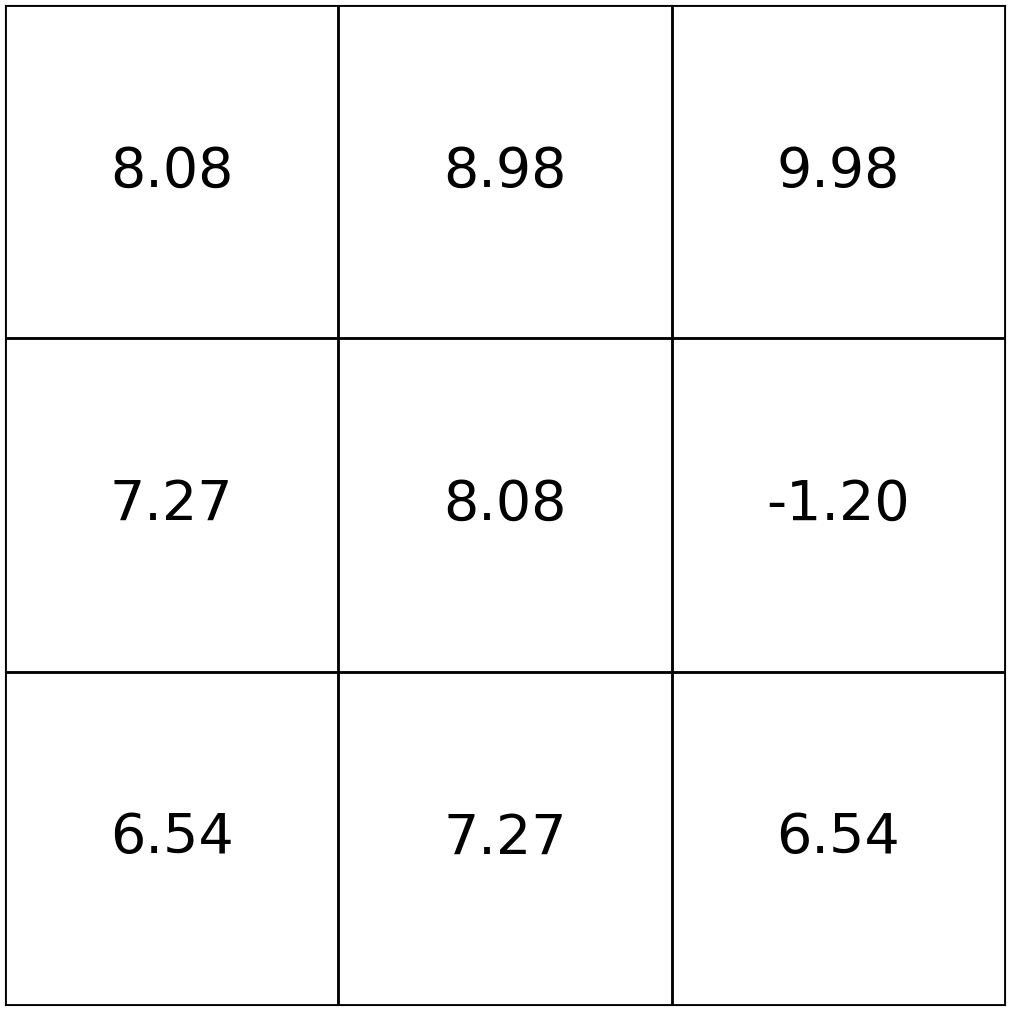
How to search for an optimal policy \(\pi^*\)?
\mathrm{V}_{h}^{{*}}(s)= \mathrm{R}(s, \pi^*(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi^*(s), s^{\prime}\right) \mathrm{V}_{h-1}^{{*}}\left(s^{\prime}\right), \forall s, h
Definition: for a given MDP and a fixed horizon \(h\) (possibly infinite), \(\pi^*\) is an optimal policy if \(\mathrm{V}_h^{\pi^*}({s}) = \mathrm{V}_h^{*}({s})\geqslant \mathrm{V}_h^\pi({s})\) for all \(s \in \mathcal{S}\) and for all possible policy \(\pi\).
\mathrm{V}^{*}_{\infty}(s)
\mathrm{V}^{*}_{62}(s)
\mathrm{V}^{*}_{61}(s)
\dots
Outline
- Markov Decision Processes Definition, terminologies, and policy
-
Policy Evaluation
-
State Value Functions \(\mathrm{V}^{\pi}\)
-
Bellman recursions and Bellman equations
-
-
Policy Optimization
-
Optimal policies \(\pi^*\)
-
Optimal action value functions: \(\mathrm{Q}^*\)
-
Value iteration
-
Optimal state-action value functions \(\mathrm{Q}^*_h(s, a)\)
\(\mathrm{Q}^*_h(s, a)\): the expected sum of discounted rewards for
- starting in state \(s\),
- take action \(a\), for one step
- act optimally there afterwards for the remaining \((h-1)\) steps
\mathrm{Q}^*_h (s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} \mathrm{Q}^*_{h-1}\left(s^{\prime}, a^{\prime}\right), \forall s, a, h
recursively finding \(\mathrm{Q}^*_h(s, a)\)
\(\mathrm{Q}^*_h(s, a)\): the expected sum of discounted rewards for
- starting in state \(s\),
- take action \(a\), for one step
- act optimally there afterwards for the remaining \((h-1)\) steps
1
2
9
8
7
5
4
3
6
80\%
20\%
Recall:
\(\gamma = 0.9\)
1
1
1
1
-10
-10
-10
-10
States and one special transition:
\(\mathrm{R}(s,a)\)
\mathrm{Q}^*_0(s, a)
\mathrm{Q}^*_1(s, a)
=\mathrm{R}(s, a)
\mathrm{Q}^*_2(s, a)
Let's consider \(\mathrm{Q}^*_2(3, \rightarrow)\)
- receive \(\mathrm{R}(3,\rightarrow)\)
\( = 1 + .9 \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(3, a^{\prime}\right)\)
- next state \(s'\) = 3, act optimally for the remaining one timestep
- receive \(\max _{a^{\prime}} \mathrm{Q}^*_{1}\left(3, a^{\prime}\right)\)
\( = 1.9\)
1.9
Recall:
\(\gamma = 0.9\)
States and one special transition:
- starting in state \(s\),
- take action \(a\), for one step
- act optimally there afterwards for the remaining \((h-1)\) steps
\(\mathrm{Q}^*_2(3, \rightarrow) = \mathrm{R}(3,\rightarrow) + \gamma \max _{a^{\prime}} \mathrm{Q}^*_{1}\left(3, a^{\prime}\right)\)
\mathrm{Q}^*_1(s, a)
=\mathrm{R}(s, a)
80\%
20\%
\(\mathrm{Q}^*_h(s, a)\): the value for
Let's consider \(\mathrm{Q}^*_2(3, \uparrow)\)
- receive \(\mathrm{R}(3,\uparrow)\)
\( = 1 + .9 \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(3, a^{\prime}\right)\)
- next state \(s'\) = 3, act optimally for the remaining one timestep
- receive \(\max _{a^{\prime}} \mathrm{Q}^*_{1}\left(3, a^{\prime}\right)\)
\( = 1.9\)
1.9
1
2
9
8
7
5
4
3
6
80\%
20\%
Recall:
\(\gamma = 0.9\)
States and one special transition:
- starting in state \(s\),
- take action \(a\), for one step
- act optimally there afterwards for the remaining \((h-1)\) steps
\(\mathrm{Q}^*_2(3, \uparrow) = \mathrm{R}(3,\uparrow) + \gamma \max _{a^{\prime}} \mathrm{Q}^*_{1}\left(3, a^{\prime}\right)\)
1.9
=\mathrm{R}(s, a)
\mathrm{Q}^*_1(s, a)
\mathrm{Q}^*_2(s, a)
\(\mathrm{Q}^*_h(s, a)\): the value for
Let's consider \(\mathrm{Q}_2^*(3, \leftarrow)\)
- receive \(\mathrm{R}(3,\leftarrow)\)
\( = 1 + .9 \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)\)
- next state \(s'\) = 2, act optimally for the remaining one timestep
- receive \(\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)\)
\( = 1\)
1
1
2
9
8
7
5
4
3
6
80\%
20\%
Recall:
\(\gamma = 0.9\)
States and one special transition:
- starting in state \(s\),
- take action \(a\), for one step
- act optimally there afterwards for the remaining \((h-1)\) steps
\(\mathrm{Q}_2^*(3, \leftarrow) = \mathrm{R}(3,\leftarrow) + \gamma \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)\)
1.9
1.9
\(\mathrm{Q}^*_h(s, a)\): the value for
\mathrm{Q}^*_2(s, a)
\mathrm{Q}^*_1(s, a)
=\mathrm{R}(s, a)
Let's consider \(\mathrm{Q}^*_2(3, \downarrow)\)
- receive \(\mathrm{R}(3,\downarrow)\)
\( = 1 + .9 \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(6, a^{\prime}\right)\)
- next state \(s'\) = 6, act optimally for the remaining one timestep
- receive \(\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(6, a^{\prime}\right)\)
\( = -8\)
-8
1
2
9
8
7
5
4
3
6
80\%
20\%
Recall:
\(\gamma = 0.9\)
States and one special transition:
- starting in state \(s\),
- take action \(a\), for one step
- act optimally there afterwards for the remaining \((h-1)\) steps
\(\mathrm{Q}_2^*(3, \downarrow) = \mathrm{R}(3,\downarrow) + \gamma \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)\)
1
1.9
1.9
\(\mathrm{Q}^*_h(s, a)\): the value for
\mathrm{Q}^*_2(s, a)
\mathrm{Q}^*_1(s, a)
=\mathrm{R}(s, a)
1
2
9
8
7
5
4
3
6
80\%
20\%
Recall:
\(\gamma = 0.9\)
States and one special transition:
- act optimally for one more timestep, at the next state \(s^{\prime}\)
- 20% chance, \(s'\) = 2, act optimally, receive \(\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)\)
- 80% chance, \(s'\) = 3, act optimally, receive \(\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(3, a^{\prime}\right)\)
-9.28
\(= -10 + .9 [.2 \times 0+ .8 \times 1] = -9.28\)
- receive \(\mathrm{R}(6,\uparrow)\)
- starting in state \(s\),
- take action \(a\), for one step
- act optimally there afterwards for the remaining \((h-1)\) steps
Let's consider \(\mathrm{Q}_2^*(6, \uparrow) \)
-8
1
1.9
1.9
\(=\mathrm{R}(6,\uparrow) + \gamma[.2 \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)+ .8\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(3, a^{\prime}\right)] \)
\(\mathrm{Q}^*_h(s, a)\): the value for
\mathrm{Q}^*_2(s, a)
\mathrm{Q}^*_1(s, a)
=\mathrm{R}(s, a)
1.9
1.9
1
-8
-9.28
\(\mathrm{Q}_2^*(6, \uparrow) =\mathrm{R}(6,\uparrow) + \gamma[.2 \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)+ .8\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(3, a^{\prime}\right)] \)
\mathrm{Q}^*_h (s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} \mathrm{Q}^*_{h-1}\left(s^{\prime}, a^{\prime}\right), \forall s,a,h
in general
1
2
9
8
7
5
4
3
6
80\%
20\%
Recall:
\(\gamma = 0.9\)
States and one special transition:
- starting in state \(s\),
- take action \(a\), for one step
- act optimally there afterwards for the remaining \((h-1)\) steps
\mathrm{Q}_1^*(s, a)
=\mathrm{R}(s, a)
\mathrm{Q}_2^*(s, a)
\(\mathrm{Q}^*_h(s, a)\): the value for
1.9
1.9
1
-8
-9.28
1
2
9
8
7
5
4
3
6
80\%
20\%
Recall:
\(\gamma = 0.9\)
States and one special transition:
- starting in state \(s\),
- take action \(a\), for one step
- act optimally there afterwards for the remaining \((h-1)\) steps
\mathrm{Q}_1^*(s, a)
=\mathrm{R}(s, a)
\mathrm{Q}_2^*(s, a)
\pi_h^*(s)=\arg \max _a \mathrm{Q}^*_h(s, a), \forall s, h
what's the optimal action in state 3, with horizon 2, given by \(\pi_2^*(3)=?\)
in general
either up or right
\(\mathrm{Q}^*_h(s, a)\): the value for
Outline
- Markov Decision Processes Definition, terminologies, and policy
-
Policy Evaluation
-
State Value Functions \(\mathrm{V}^{\pi}\)
-
Bellman recursions and Bellman equations
-
-
Policy Optimization
-
Optimal policies \(\pi^*\)
-
Optimal action value functions: \(\mathrm{Q}^*\)
-
Value iteration
-
Given the recursion
\mathrm{Q}^*_{\infty}(s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} \mathrm{Q}^*_{\infty}\left(s^{\prime}, a^{\prime}\right)
- for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
- \(\mathrm{Q}_{\text {old }}(\mathrm{s}, \mathrm{a})=0\)
- while True:
- for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
- \(\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\)
- if \(\max _{s, a}\left|Q_{\text {old }}(s, a)-Q_{\text {new }}(s, a)\right|<\epsilon:\)
- return \(\mathrm{Q}_{\text {new }}\)
- \(\mathrm{Q}_{\text {old }} \leftarrow \mathrm{Q}_{\text {new }}\)
\mathrm{Q}^*_h (s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} \mathrm{Q}^*_{h-1}\left(s^{\prime}, a^{\prime}\right)
we can have an infinite horizon equation
Value Iteration
if run this block \(h\) times and break, then the returns are exactly \(\mathrm{Q}^*_h\)
\{
\(\mathrm{Q}^*_{\infty}(s, a)\)
\(\mathrm{V}\) values vs. \(\mathrm{Q}\) values
- \(\mathrm{V}\) is defined over state space; \(\mathrm{Q}\) is defined over (state, action) space.
- \(\mathrm{V}_h^*({s})\) can be derived from \(\mathrm{Q}^*_h(s,a):\), and vise versa.
- \(\mathrm{Q}^*\) is easier to read "optimal actions" from.
- We care more about \(\mathrm{V}^{\pi}\) and \(\mathrm{Q}^*\)
\(\mathrm{V}_{h}^*(s)=\max_{a}\left[\mathrm{Q}^*_{h}(s, a)\right]\)
\mathrm{V}^{\uparrow}_{61}(s)
\mathrm{V}^{\uparrow}_{62}(s)
\mathrm{V}^{\uparrow}_{\infty}(s)
\mathrm{V}^{*}_{61}(s)
\mathrm{V}^{*}_{62}(s)
\mathrm{V}^{*}_{\infty}(s)
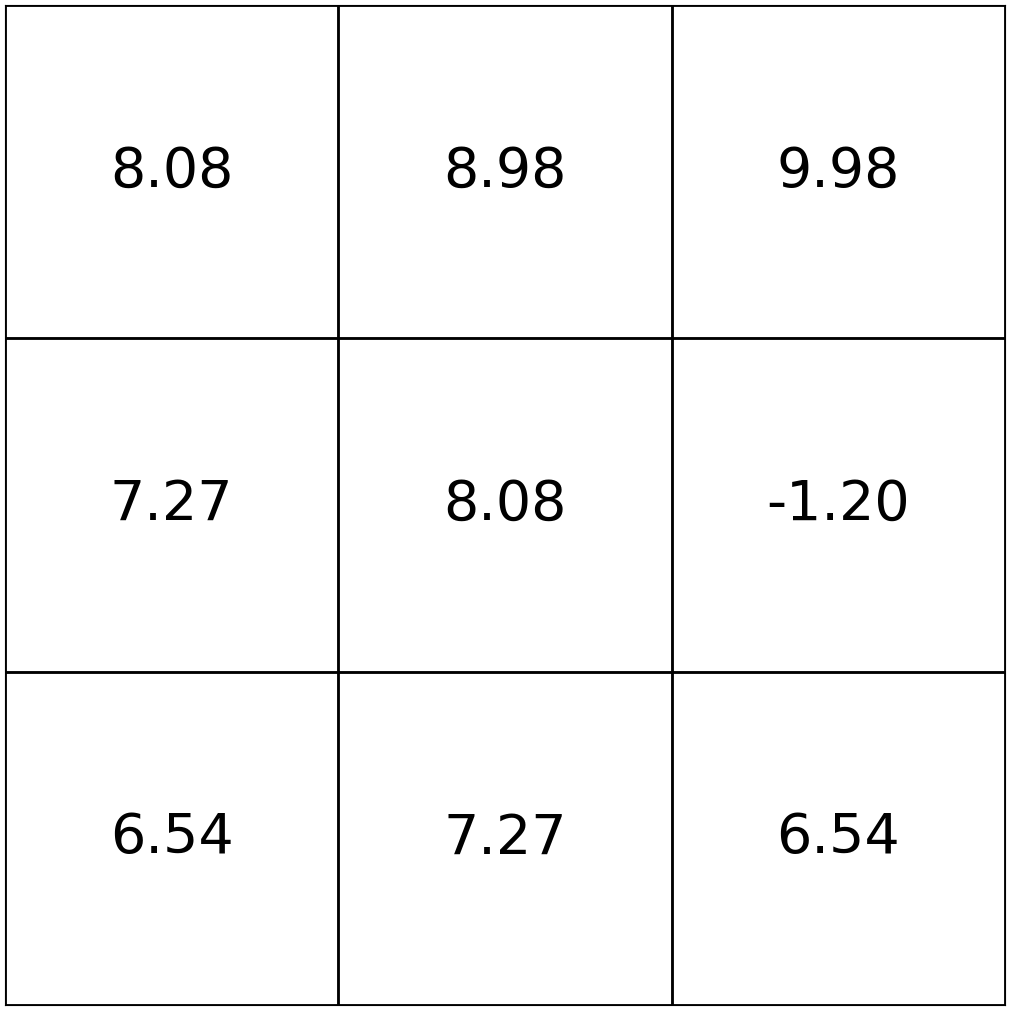
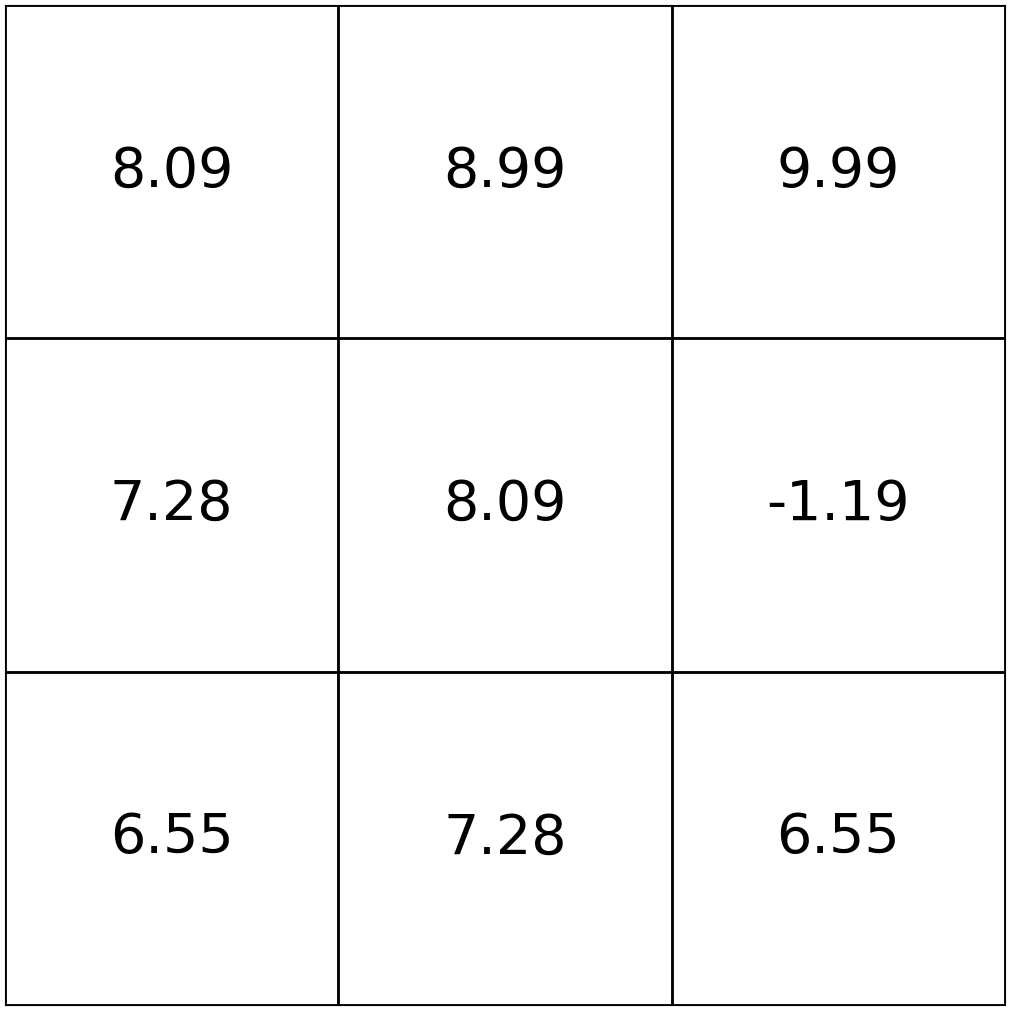
\(\mathrm{\pi}_{h}^*(s)=\arg\max_{a}\left[\mathrm{Q}^*_{h}(s, a)\right]\)
\mathrm{Q}^{*}_{61}(s,a)
\mathrm{Q}^{*}_{62}(s,a)
\mathrm{Q}^{*}_{\infty}(s,a)
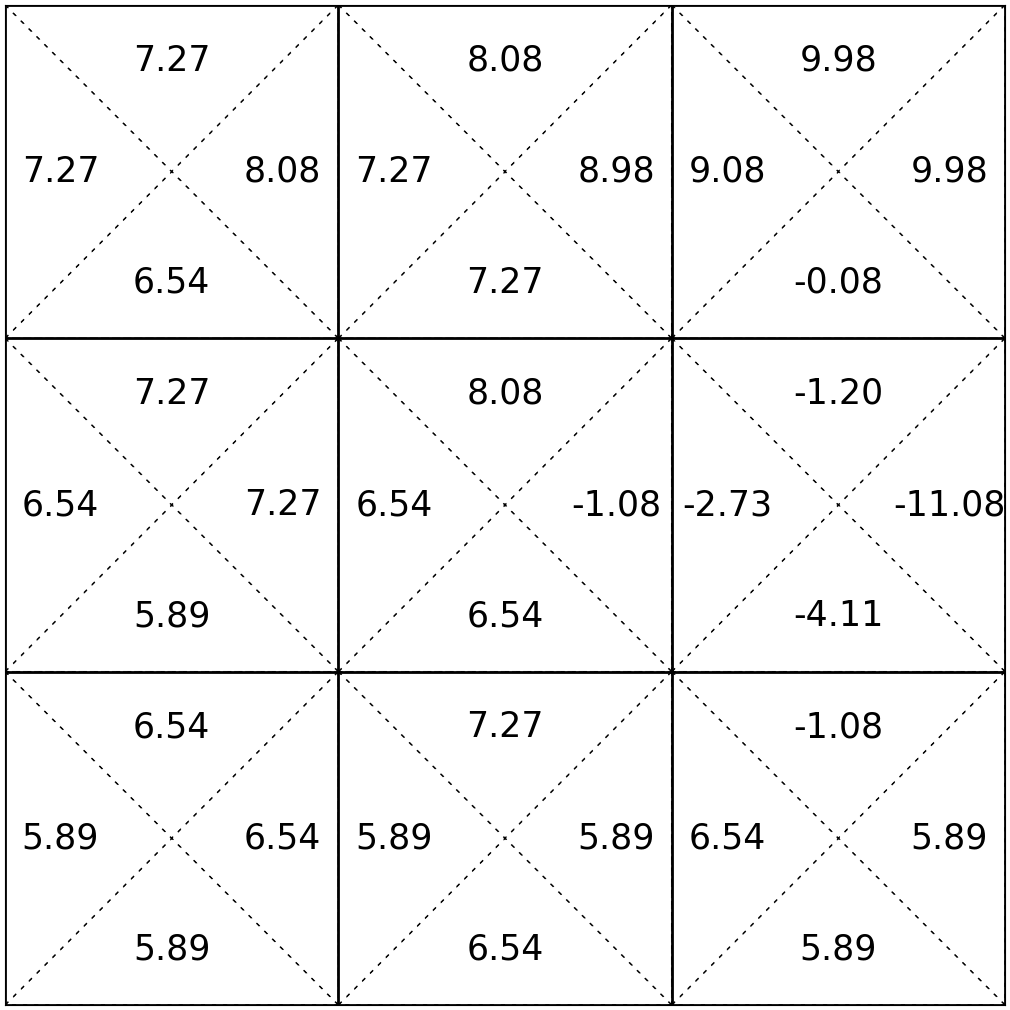
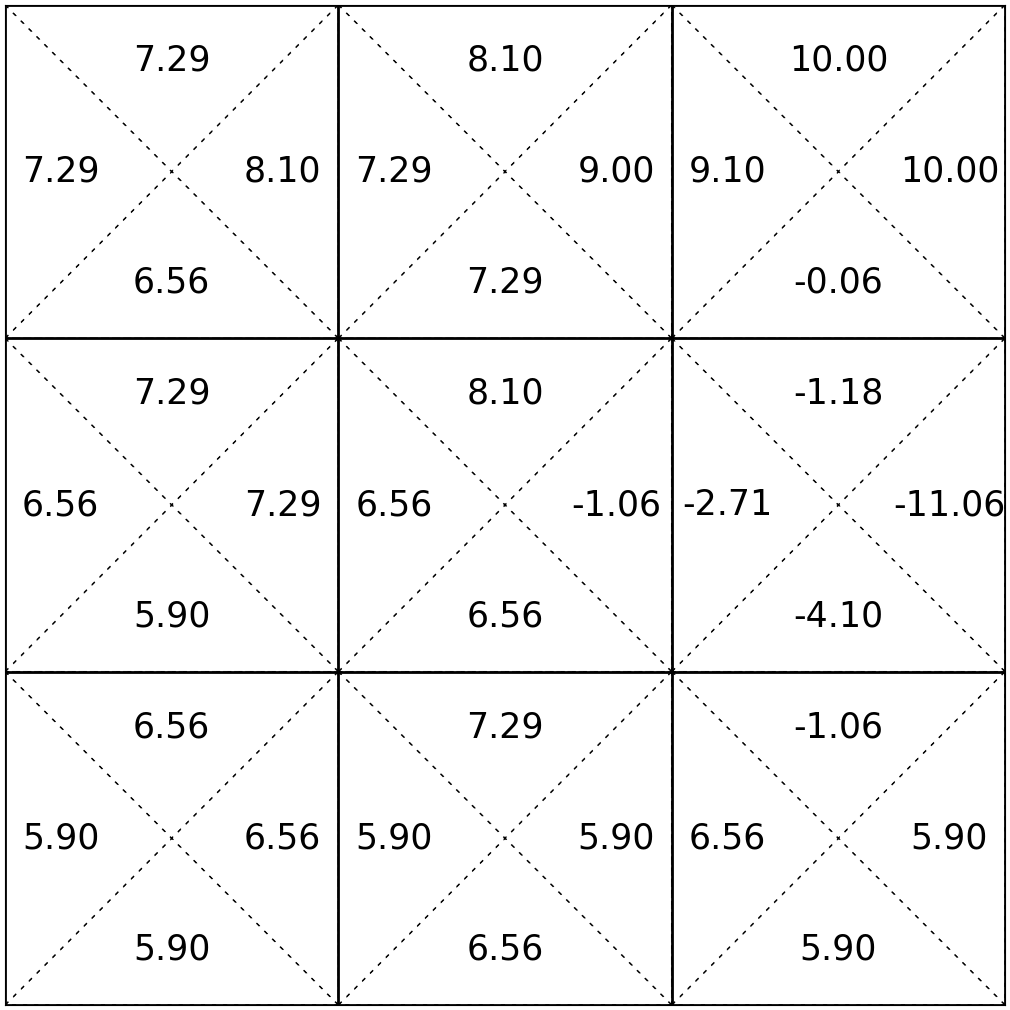
Summary
- Markov decision processes (MDP) is nice mathematical framework for making sequential decisions. It's the foundation to reinforcement learning.
- An MDP is defined by a five-tuple, and the goal is to find an optimal policy that leads to high expected cumulative discounted rewards.
- To evaluate how good a given policy \(\pi, \) we can calculate \(\mathrm{V}^{\pi}(s)\) via
- the summation over rewards definition
- Bellman recursion for finite horizon, equation for infinite horizon
- To find an optimal policy, we can recursively find \(\mathrm{Q}^*(s,a)\) via the value iteration algorithm, and then act greedily w.r.t. the \(\mathrm{Q}^*\) values.
Thanks!
We'd love to hear your thoughts.
6.390 IntroML (Spring25) - Lecture 10 Markov Decision Processes
By Shen Shen
