https://introml.mit.edu/

Lecture 2: Linear Regression and Regularization

 

Shen Shen

Feb 7, 2025

11am, Room 10-250

Intro to Machine Learning

Optimization + first-principle physics

DARPA Robotics Competition

2015

Outline

  • Recap: Supervised Learning Setup, Terminology
  • Ordinary Least Square Regression
    • Problem Formulation
    • Closed-form Solution (when well-defined)
    • When closed-form solution is not well-defined
      • Mathematically, Practically, Visually
  • Regularization and Ridge Regression
  • Hyperparameter and Cross-validation

Outline

  • Recap: Supervised Learning Setup, Terminology
  • Ordinary Least Square Regression
    • Problem Formulation
    • Closed-form Solution (when well-defined)
    • When closed-form solution is not well-defined
      • Mathematically, Practically, Visually
  • Regularization and Ridge Regression
  • Hyperparameter and Cross-validation
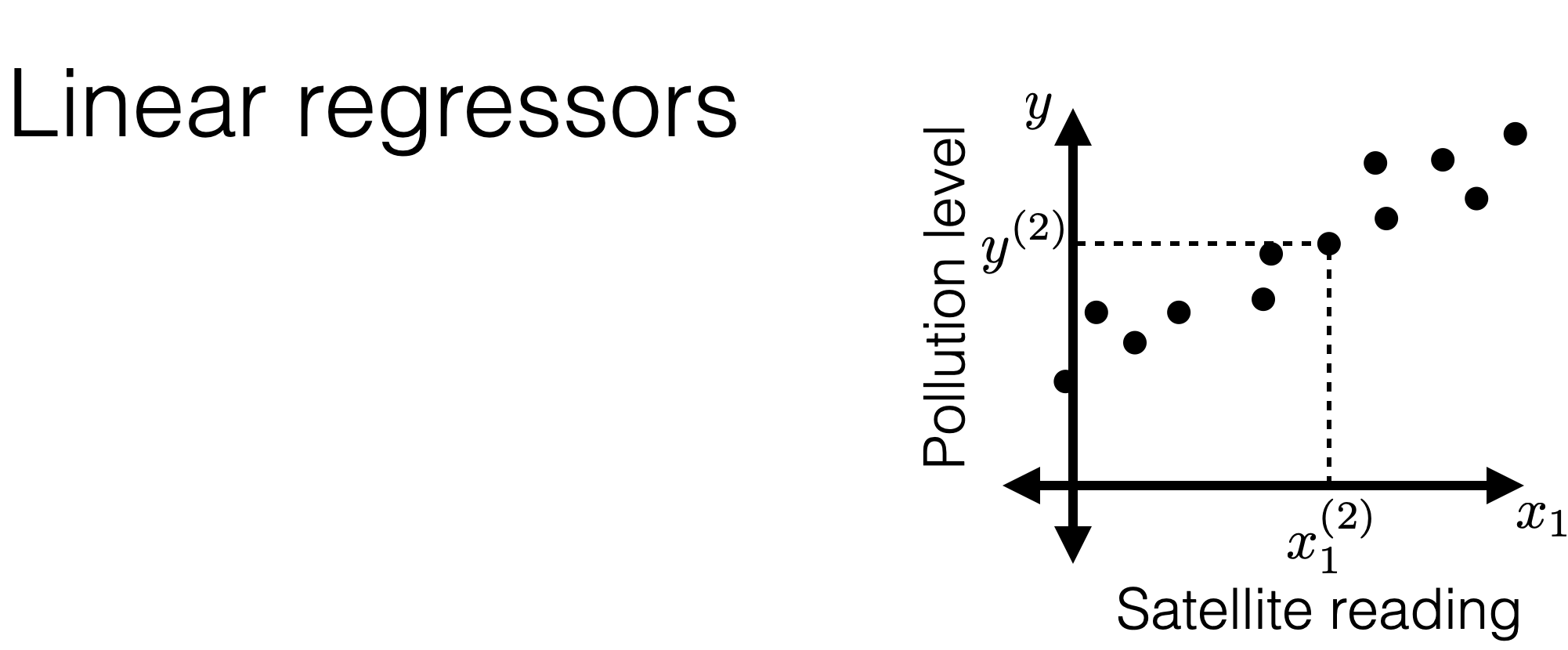
Recall: pollution prediction example

Training data:

\(\begin{bmatrix} x_1^{(1)} \\[4pt] x_2^{(1)} \\[4pt] \vdots \\[4pt] x_d^{(1)} \end{bmatrix}  \in \mathbb{R}^d\)

label

feature vector

\(y^{(1)} \in \mathbb{R}\)

\(\mathcal{D}_\text{train}\)

\(\left\{\left(x^{(1)}, y^{(1)}\right), \dots, \left(x^{(n)}, y^{(n)}\right)\right\}\)

pollution

temperature \(x_1\)

\(y\)

temperature \(x_1\)

population \(x_2\)

pollution

\(y\)

\(n = 5 ,\\ d = 1\)

\(n = 5 ,\\ d = 2\)

\boxed{h}

Supervised Learning

Algorithm

\rightarrow
\downarrow
y
x
\downarrow

\( \mathbb{R}^d \)

\( \mathbb{R}\)

\(\mathcal{D}_\text{train}\)

\rightarrow

\(\left\{\left(x^{(1)}, y^{(1)}\right), \dots, \left(x^{(n)}, y^{(n)}\right)\right\}\)

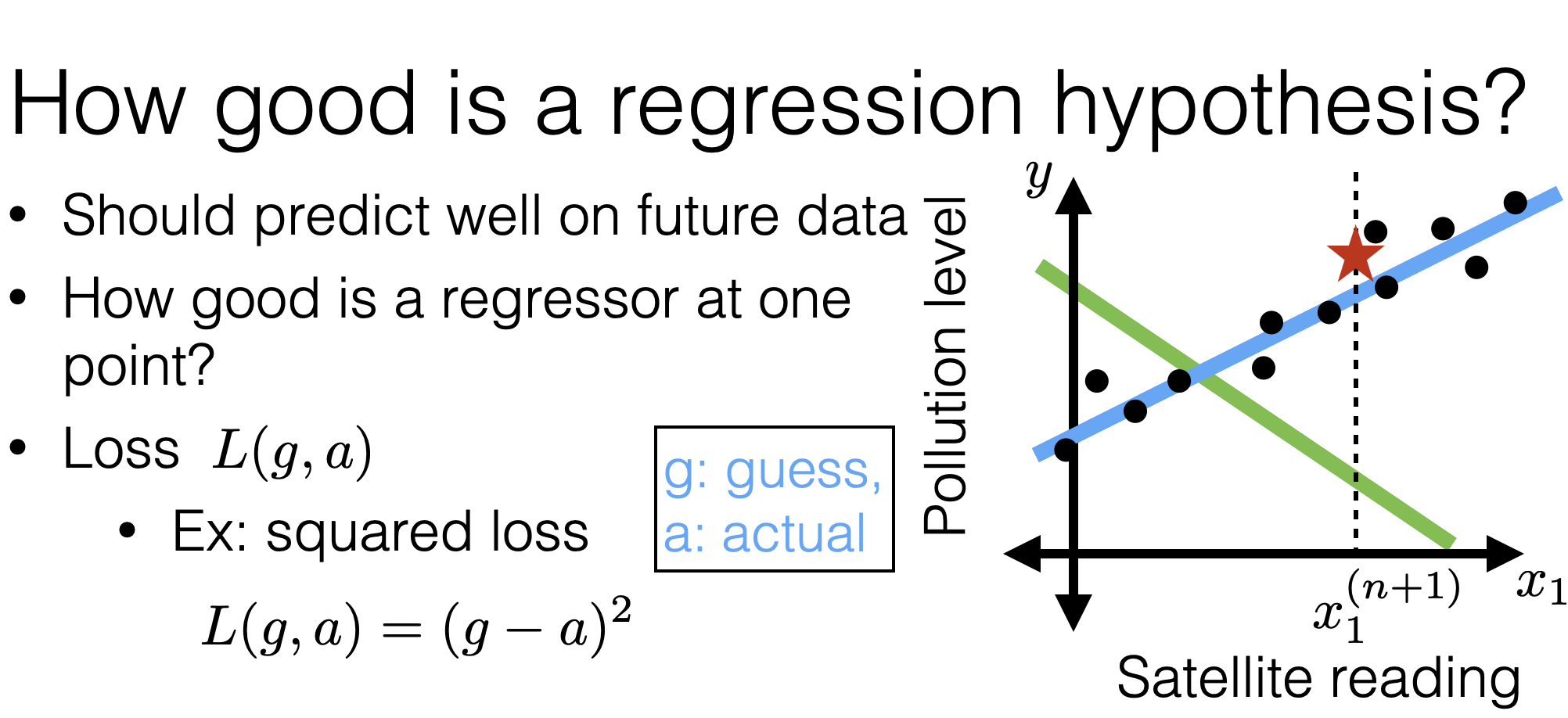
What do we want? A good way to label new features

For example, \(h\) : For any \(x, h(x)=1,000,000,\) valid but is it any good?

hypothesis

set of \(h\) (or specifically for today, the set of hyperplanes)

A linear regression hypothesis :

\(h\left(x ; \theta, \theta_0\right)=\theta^T x+\theta_0\)

\( = \left[\begin{array}{lllll} \theta_1 & \theta_2 & \cdots & \theta_d\end{array}\right]\) \(\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_d\end{array}\right] + \theta_0\) 

parameters

data

Hypothesis class \(\mathcal{H}:\)

\(\mathcal{E}_{\text {test }}(h)=\frac{1}{n^{\prime}} \sum_{i=n+1}^{n+n^{\prime}} \mathcal{L}\left(h\left(x^{(i)}\right), y^{(i)}\right)\)

\(\mathcal{E}_{\text {train }}(h)=\frac{1}{n} \sum_{i=1}^n \mathcal{L}\left(h\left(x^{(i)} \right), y^{(i)}\right)\)

  • Test error
  • Training error 

\(n'\) new points

  • Squared loss

\(\mathcal{L}\left(h\left(x^{(i)}\right), y^{(i)}\right) =(h\left(x^{(i)}\right) - y^{(i)} )^2\)

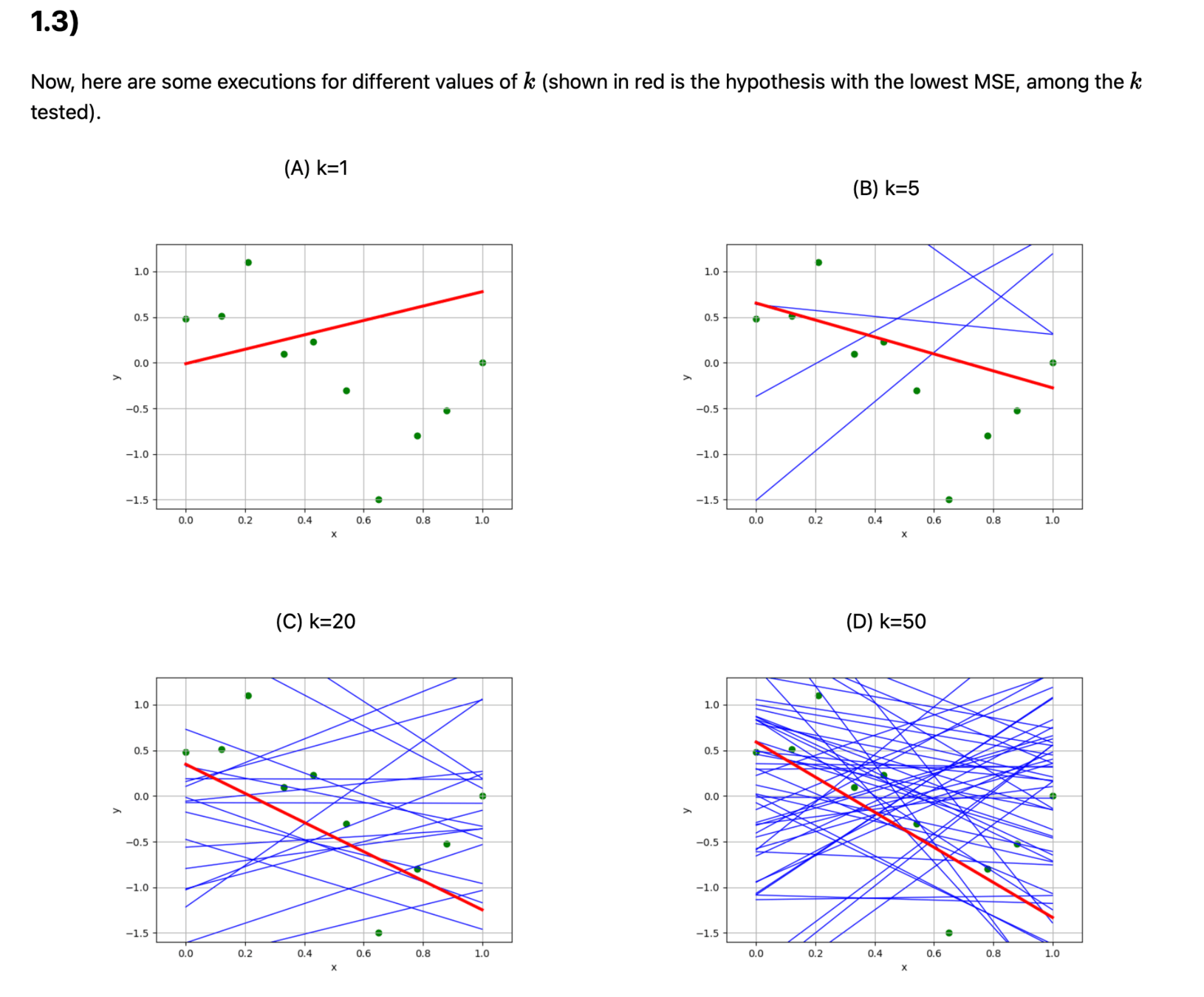
Recall lab1
def random_regress(X, Y, k):
    n, d = X.shape

    # generate k random hypotheses
    ths = np.random.randn(d, k)
    th0s = np.random.randn(1, k)

    # compute the mean squared error of each hypothesis on the data set
    errors = lin_reg_err(X, Y, ths, th0s)

    # Find the index of the hypotheses with the lowest error
    i = np.argmin(errors)

    # return the theta and theta0 parameters that define that hypothesis
    theta, theta0 = ths[:,i:i+1], th0s[:,i:i+1]
    return (theta, theta0), errors[i]

Outline

  • Recap: Supervised Learning Setup, Terminology
  • Ordinary Least Square Regression
    • Problem Formulation
    • Closed-form Solution (when well-defined)
    • When closed-form solution is not well-defined
      • Mathematically, Practically, Visually
  • Regularization and Ridge Regression
  • Hyperparameter and Cross-validationa

Linear regression: the analytical way

  • How about we just consider all hypotheses in our class and choose the one with lowest training error?
  • We’ll see: not typically straightforward
  • But for linear regression with square loss: can do it!
  • In fact, sometimes, just by plugging in an equation!

Append a "fake" feature of \(1\) 

\(h\left(x ; \theta, \theta_0\right)=\theta^T x+\theta_0\)

\( = \left[\begin{array}{lllll} \theta_1 & \theta_2 & \cdots & \theta_d\end{array}\right]\) \(\left[\begin{array}{l}x_1 \\ x_2 \\ \vdots \\ x_d\end{array}\right] + \theta_0\) 

Don't want to deal with \(\theta_0\)

\( = \left[\begin{array}{lllll} \theta_1 & \theta_2 & \cdots & \theta_d & \theta_0\end{array}\right]\) \(\left[\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_d \\ 1\end{array}\right] \) 

\( = \theta_{\mathrm{aug}}^T x_{\mathrm{aug}}\) 

"center" the data

Don't want to deal with \(\theta_0\)

\Rightarrow

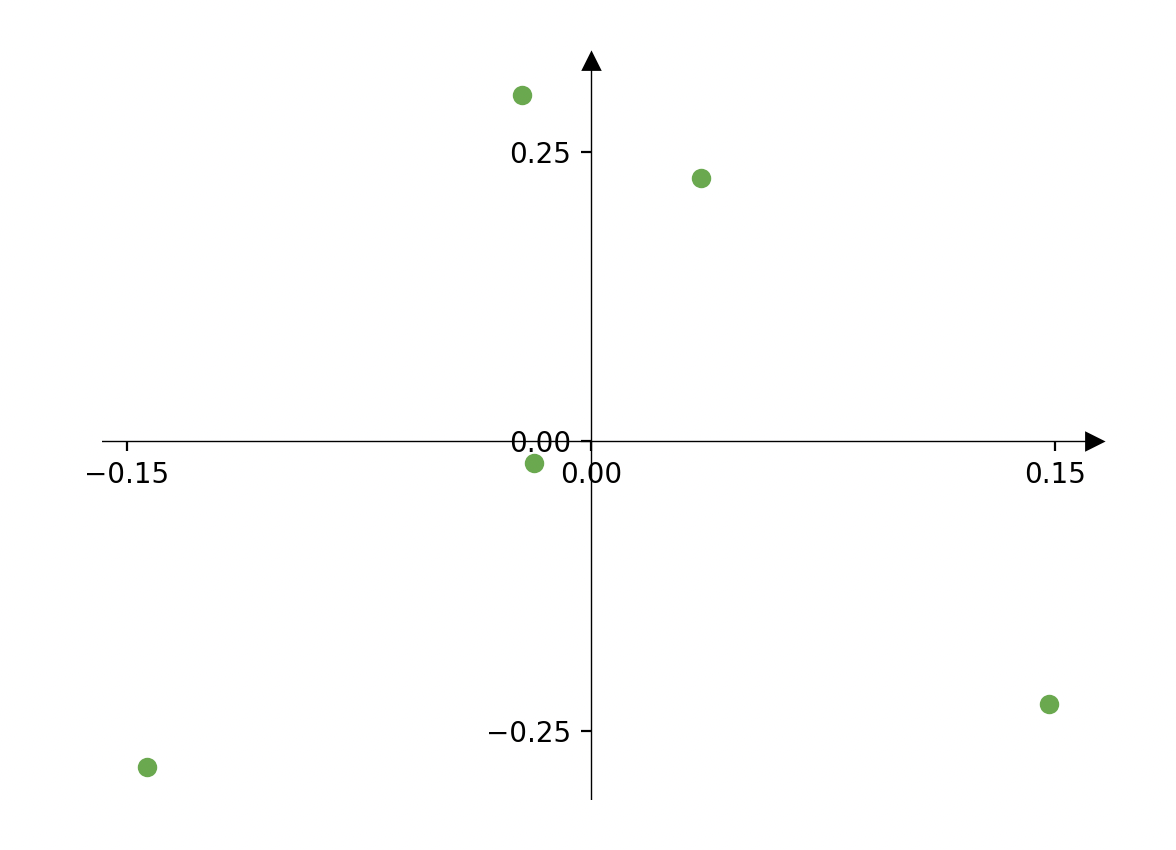
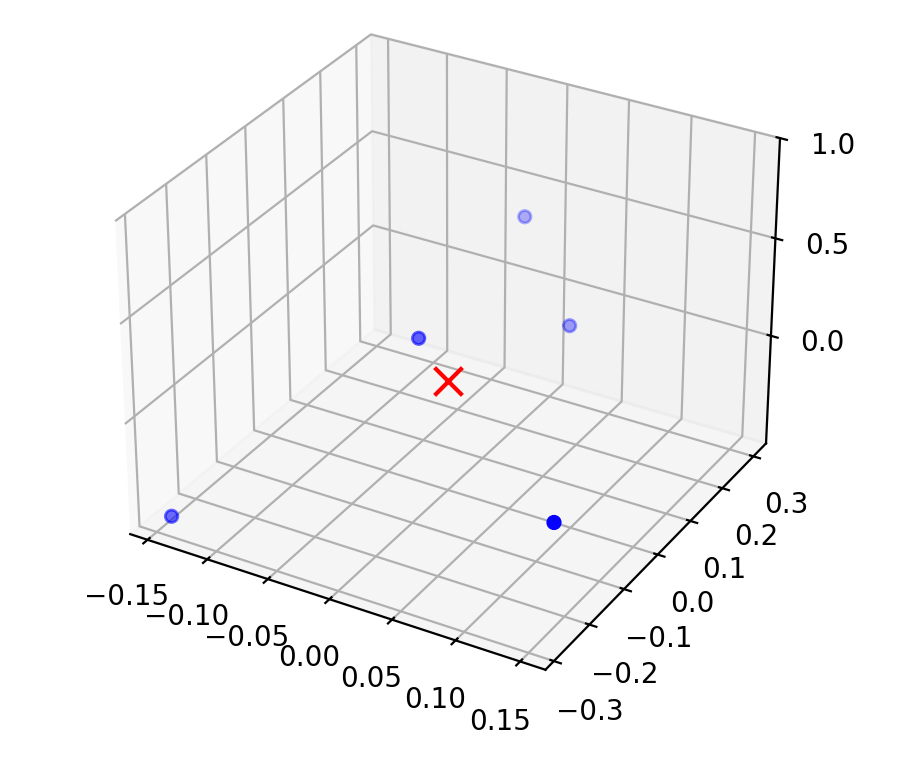
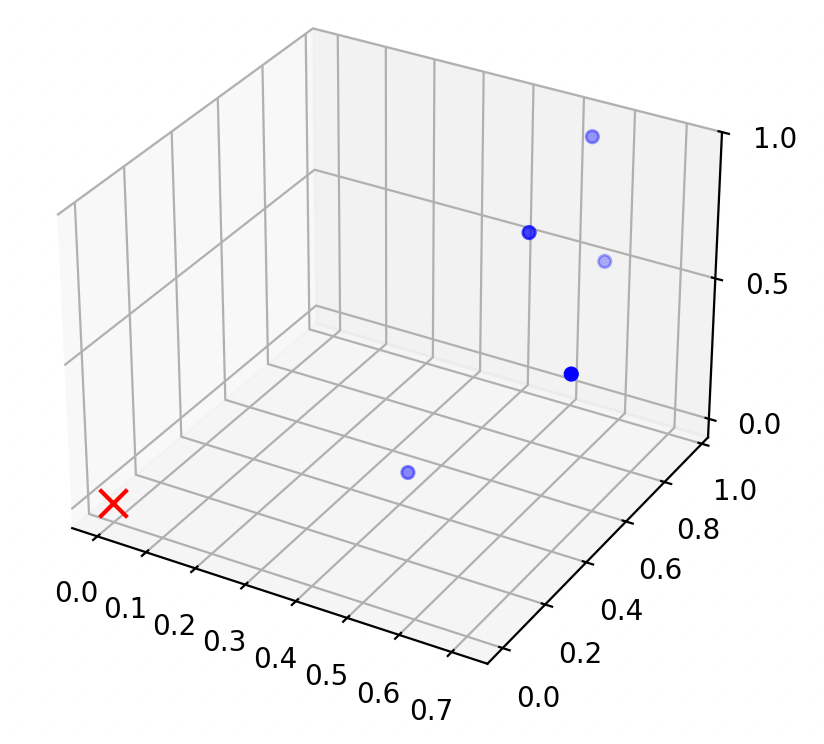
"center" the data

\Rightarrow

temperature \(x_1\)

population \(x_2\)

pollution

\(y\)

temperature \(x_1\)

population \(x_2\)

pollution

\(y\)

center the data

Temperature Population Pollution
Chicago 90 45 7.2
New York 20 32 9.5
Boston 35 100 8.4
Temperature Population Pollution
Chicago 41.66 -14 -1.66
New York -28.33 -27 1.133
Boston -13.33 41 0.033
\Rightarrow

Assemble

X = \begin{bmatrix}x_1^{(1)} & \dots & x_d^{(1)}\\\vdots & \ddots & \vdots\\x_1^{(n)} & \dots & x_d^{(n)}\end{bmatrix}
Y = \begin{bmatrix}y^{(1)}\\\vdots\\y^{(n)}\end{bmatrix}
Temperature Population Pollution
Chicago 41.66 -14 -1.66
New York -28.33 -27 1.133
Boston -13.33 41 0.033

Now the training error:  

Assemble

X = \begin{bmatrix}x_1^{(1)} & \dots & x_d^{(1)}\\\vdots & \ddots & \vdots\\x_1^{(n)} & \dots & x_d^{(n)}\end{bmatrix}
Y = \begin{bmatrix}y^{(1)}\\\vdots\\y^{(n)}\end{bmatrix}

\[=\frac{1}{n}({X} \theta-{Y})^{\top}({X} \theta-{Y})\]

\[ J(\theta) = \frac{1}{n} \sum_{i=1}^n\left({x^{(i)}}^{\top}\theta -y^{(i)}\right)^2\]

Outline

  • Recap: Supervised Learning Setup, Terminology
  • Ordinary Least Square Regression
    • Problem Formulation
    • Closed-form Solution (when well-defined)
    • When closed-form solution is not well-defined
      • Mathematically, Practically, Visually
  • Regularization and Ridge Regression
  • Hyperparameter and Cross-validationa
  • Goal: find \(\theta\) to minimize \(J(\theta)\)
  • Q: What kind of function is \(J(\theta)\)? 
  • A: Quadratic function
  • Q: What does \(J(\theta)\) look like?
  • A: Typically, looks like a "bowl"

🥰

\[ J(\theta)  =\frac{1}{n}({X} \theta-{Y})^{\top}({X} \theta-{Y})\]

Objective function (training error)

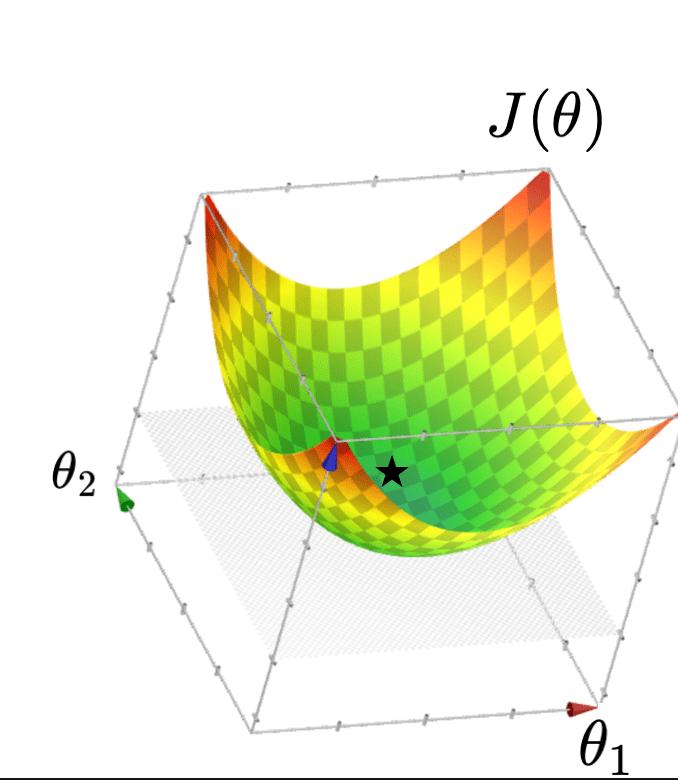
  • Typically, \(J(\theta)=\frac{1}{n}({X} \theta-{Y})^{\top}({X} \theta-{Y})\) "curves up" and is unique minimized at a point if gradient at that point is zero

Set the gradient \(\nabla_\theta J\stackrel{\text { set }}{=} 0\)

  • When \(\theta^*\) is well defined, it's indeed guaranteed to be the unique minimizer of  \(J(\theta\))

\(\nabla_\theta J=\left[\begin{array}{c}\partial J / \partial \theta_1 \\ \vdots \\ \partial J / \partial \theta_d\end{array}\right]\)

= \(\frac{2}{n}\left(X^T X \theta-X^T Y\right)\)

\Rightarrow

\(\theta^*=\left({X}^{\top} {X}\right)^{-1} {X}^{\top} {Y}\)

Outline

  • Recap: Supervised Learning Setup, Terminology
  • Ordinary Least Square Regression
    • Problem Formulation
    • Closed-form Solution (when well-defined)
    • When closed-form solution is not well-defined
      • Mathematically, Practically, Visually
  • Regularization and Ridge Regression
  • Hyperparameter and Cross-validationa
  • \(\theta^*=\left({X}^{\top} {X}\right)^{-1} {X}^{\top} {Y}\) is only well-defined if \(\left({X}^{\top} {X}\right)\) is invertible
  • and \(\left({X}^{\top} {X}\right)\) is invertible if and only if \({X}\) is full column rank

https://github.com/kenjihiranabe/The-Art-of-Linear-Algebra

https://www.3blue1brown.com/topics/linear-algebra

a. either when \(n\)<\(d\) , or

b. columns (features) in \( {X} \) have linear dependency

So, we will be in trouble if \({X}\) is not full column rank, which happens:

Case Example Objective Function Looks Like Optimal Parameters
2a. less data than features




 
2b. linearly
dependent features




 

infinitely many optimal parameters

(that define optimal hyperplanes)

temperature \(x_1\)

population \(x_2\)

pollution

\(y\)

temperature ( °F) \(x_1\)

temperature (°C) \(x_2\)

pollution

\(y\)

Quick Summary:
  • This 👈  formula is not well-defined

1. Typically, \(X\) is full column rank

🥺

🥰

  • \(\theta^*=\left({X}^{\top} {X}\right)^{-1} {X}^{\top} {Y}\)
  • \(J(\theta)\) looks like a bowl

a. either when \(n\)<\(d\) , or

b. columns (features) in \( {X} \) have linear dependency

2. When \(X\) is not full column rank

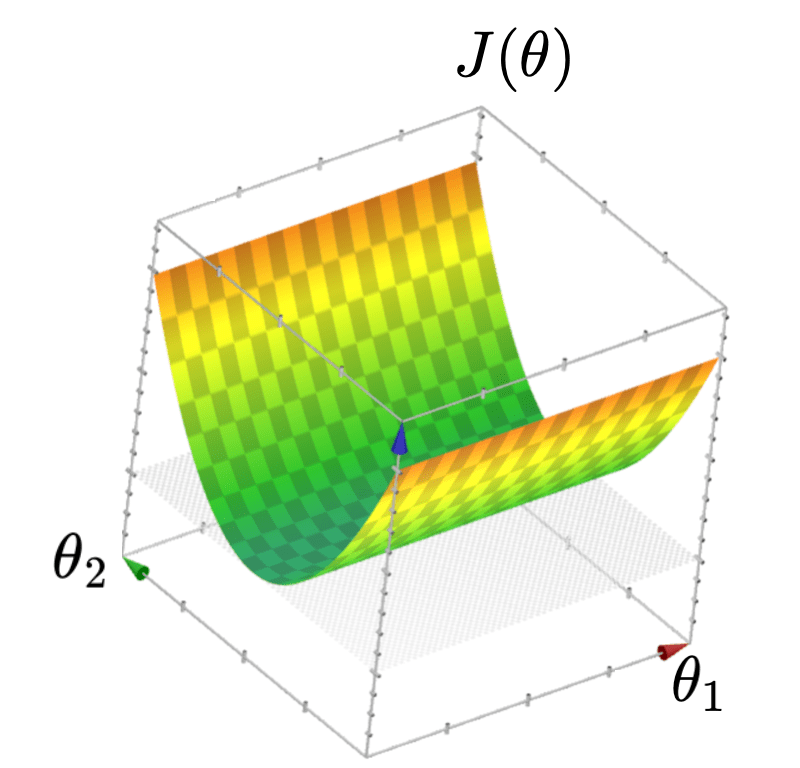
  • \(J(\theta)\) looks like a half-pipe
  • Infinitely many optimal hyperplanes
  • \(\theta^*\) gives the unique optimal hyperplane 

Outline

  • Recap: Supervised Learning Setup, Terminology
  • Ordinary Least Square Regression
    • Problem Formulation
    • Closed-form Solution (when well-defined)
    • When closed-form solution is not well-defined
      • Mathematically, Practically, Visually
  • Regularization and Ridge Regression
  • Hyperparameter and Cross-validation

🥰

🥺

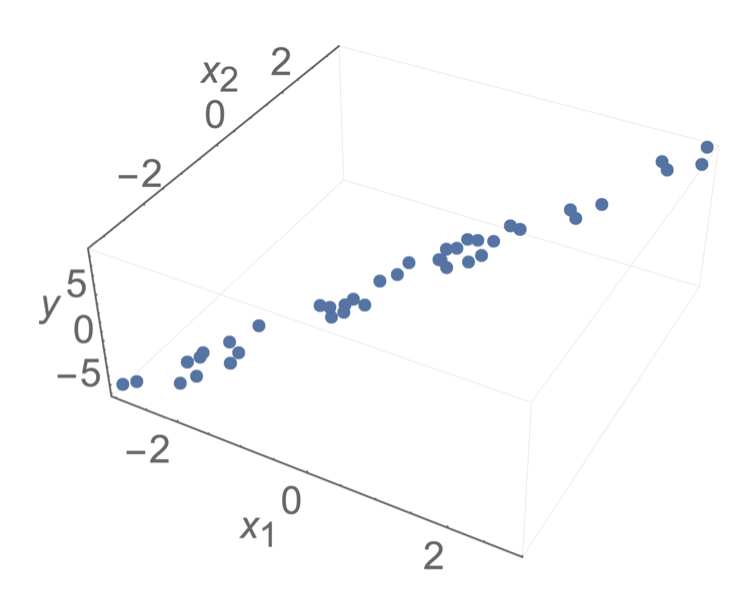
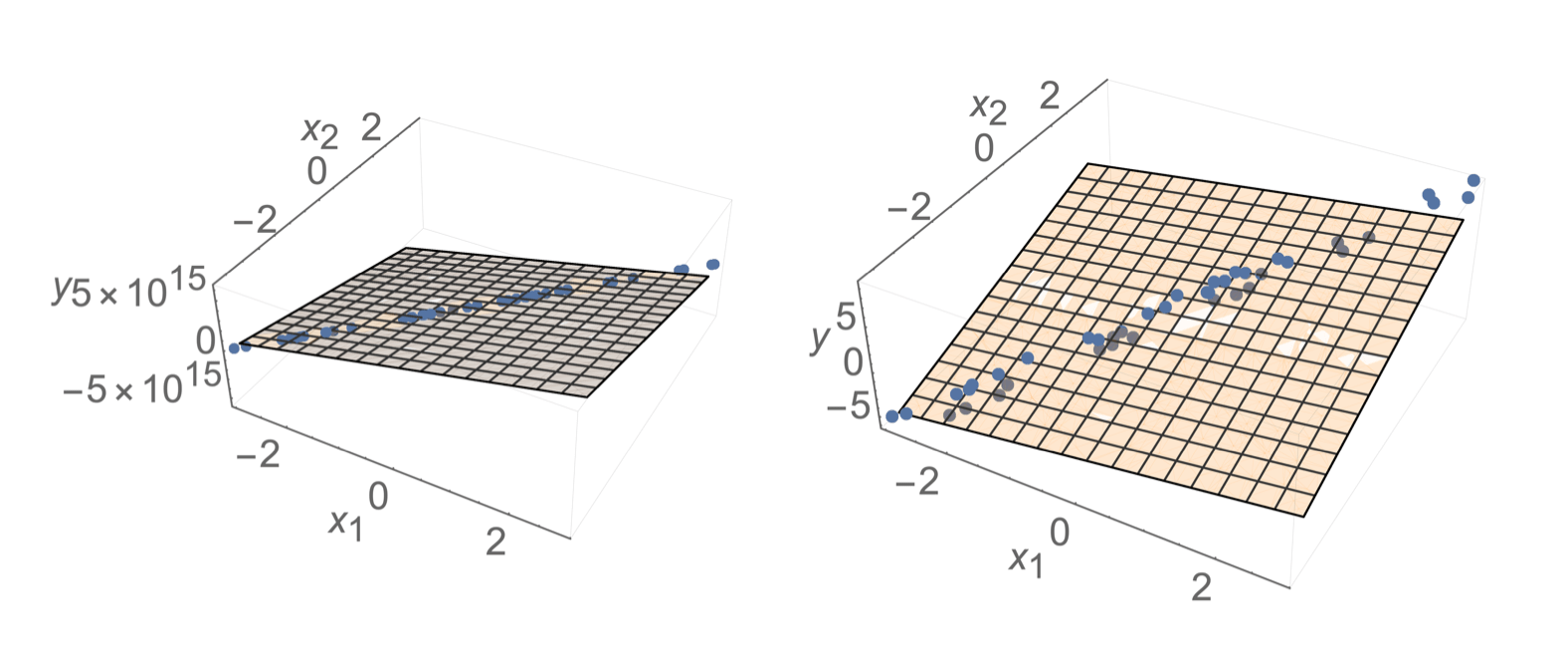
  • Sometimes, noise can resolve the invertibility issue
  • How to choose among hyperplanes?
  • but still lead to undesirable results
  • Prefer \(\theta\) with small magnitude (less sensitive prediction when \(x\) changes slightly)

Ridge Regression

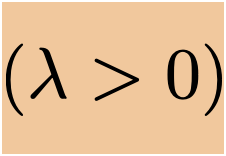
  • Add a square penalty on the magnitude
  • \(J_{\text {ridge }}(\theta)=\frac{1}{n}({X} \theta-{Y})^{\top}({X} \theta-{Y})+\lambda\|\theta\|^2\)
  • \(\lambda \) is a so-called "hyperparameter"
  • Setting \(\nabla_\theta J_{\text {ridge }}(\theta)=0\) we get \(\theta^*=\left({X}^{\top} {X}+n \lambda I\right)^{-1} {X}^{\top} {Y}\)
  • (\(\theta^*\) (here) always exists, and is always the unique optimal parameters.)
  • (see recitation/hw for discussion about the offset.)

Outline

  • Recap: Supervised Learning Setup, Terminology
  • Ordinary Least Square Regression
    • Problem Formulation
    • Closed-form Solution (when well-defined)
    • When closed-form solution is not well-defined
      • Mathematically, Practically, Visually
  • Regularization and Ridge Regression
  • Hyperparameter and Cross-validation

Cross-validation

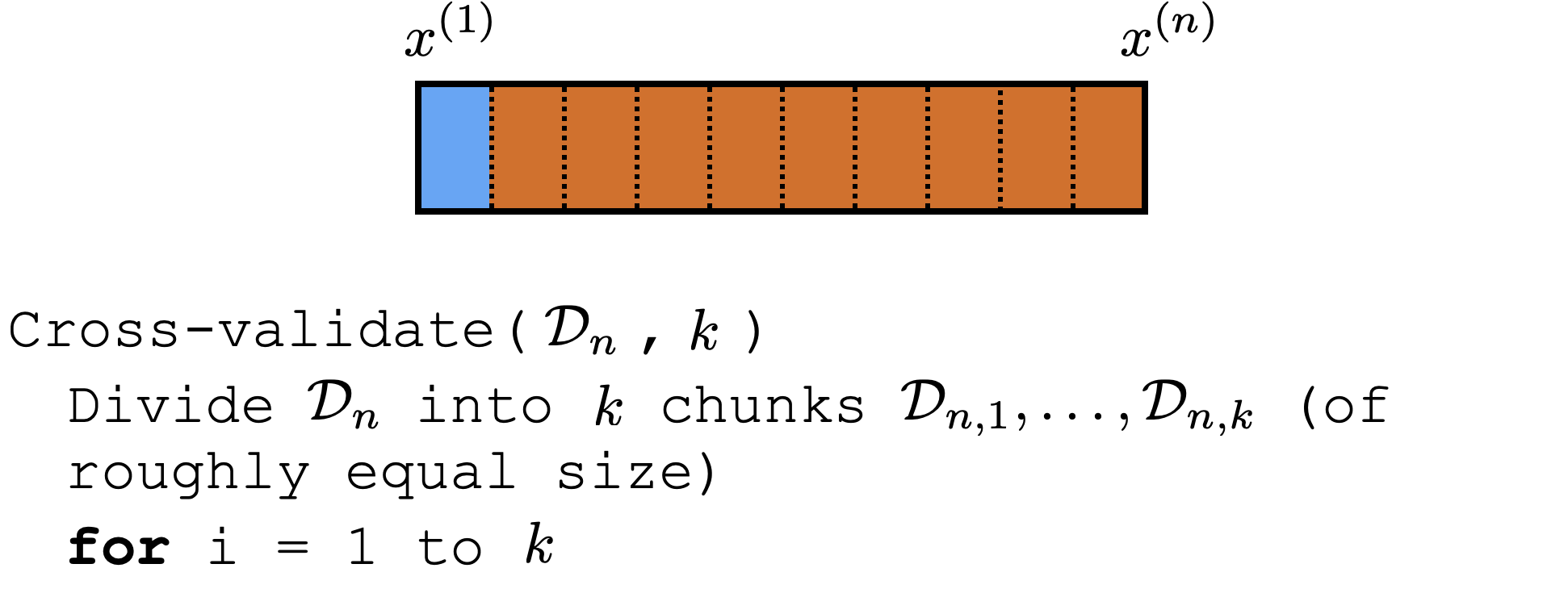
Cross-validation

Cross-validation

\dots

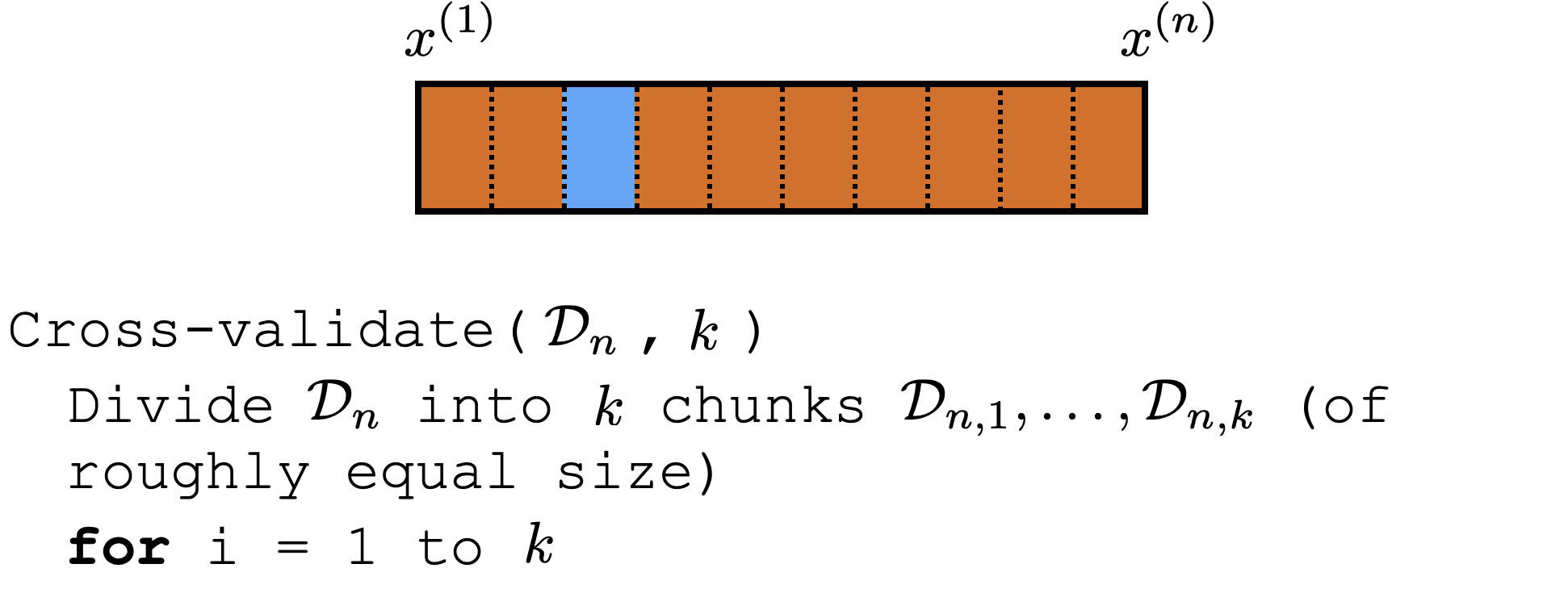
Cross-validation

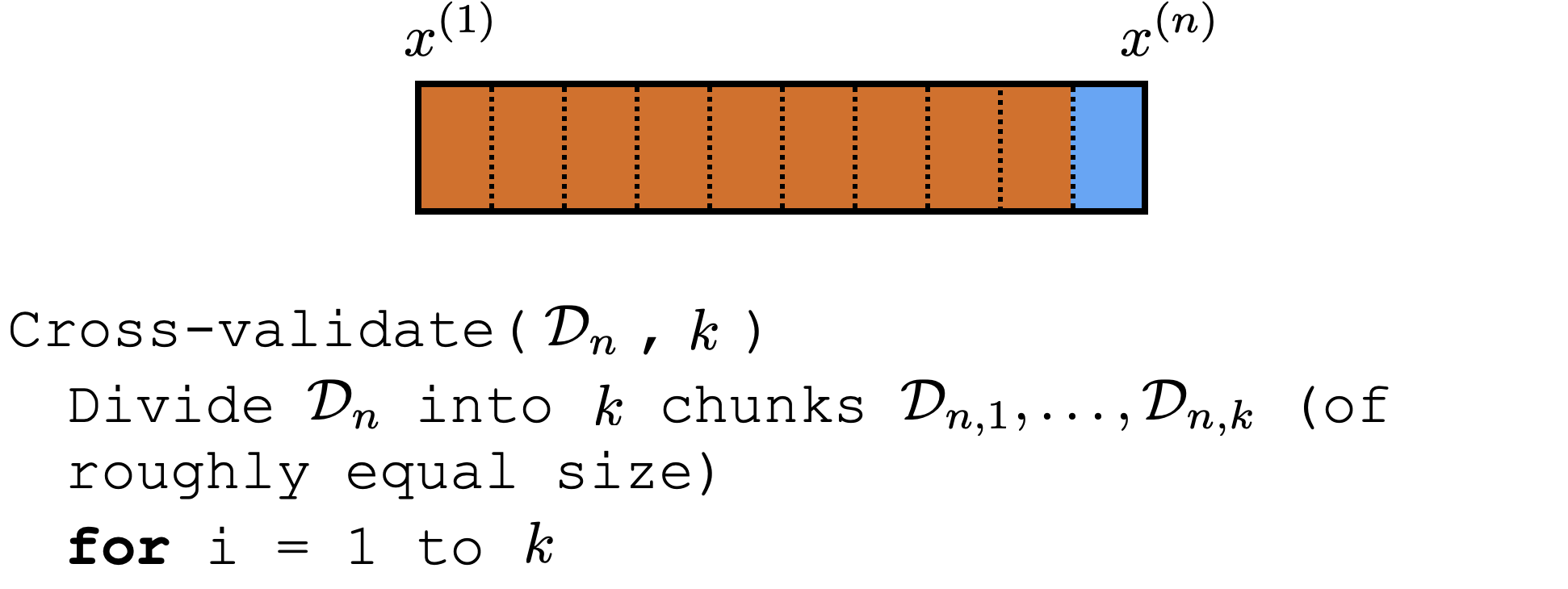
Cross-validation

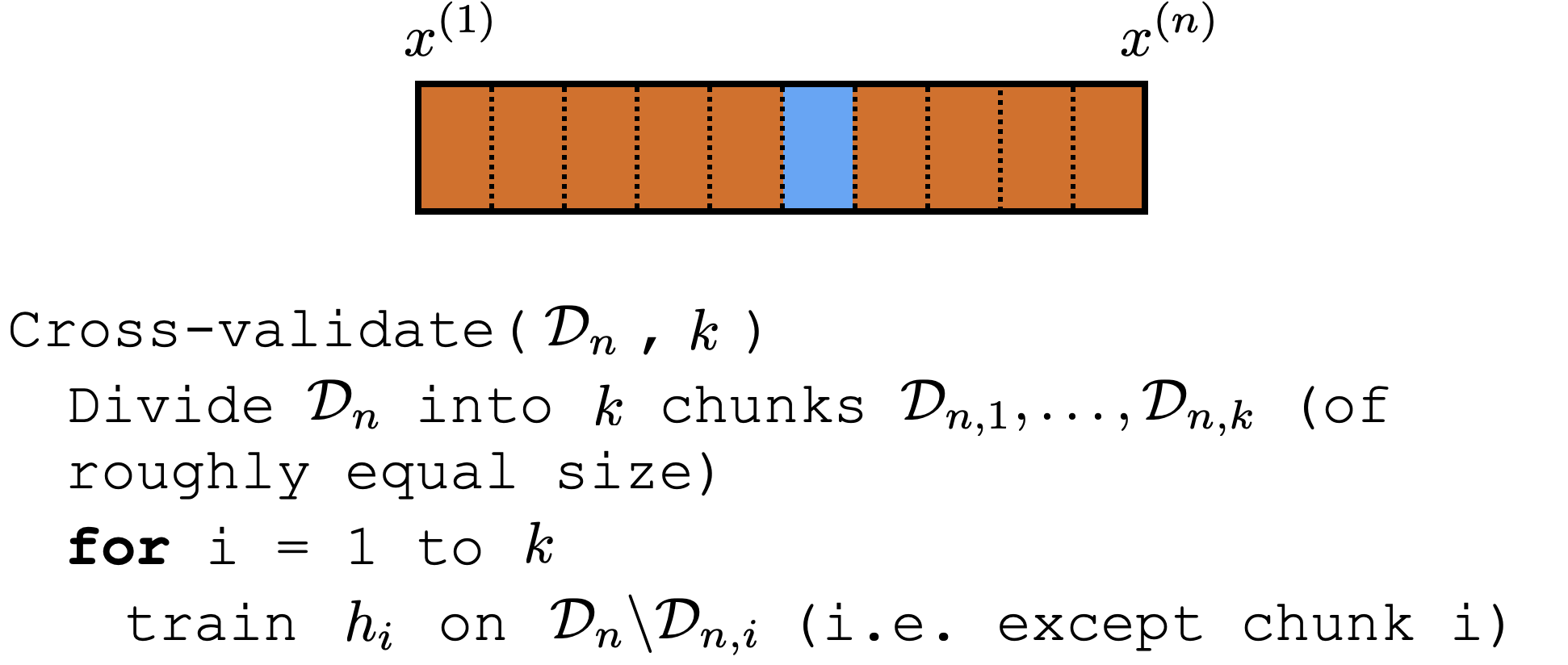
Cross-validation

Cross-validation

Comments on (cross)-validation

  • good idea to shuffle data first

  • a way to "reuse" data

  • it's not to evaluate a hypothesis

  • rather, it's to evaluate learning algorithm (e.g. hypothesis class choice, hyperparameters)

  • Could e.g. have an outer loop for picking good hyperparameter or hypothesis class

Thanks!

We'd love to hear your thoughts.

Lyrics sync

prompt engineered by 

Lyrics:

Melody and Vocal:

Video Production:

Image Prep:

  • Recall: training error: \[\frac{1}{n} \sum_{i=1}^n L\left(h\left(x^{(i)}\right), y^{(i)}\right)\]
  • With squared loss:                          \[\frac{1}{n} \sum_{i=1}^n\left(h\left(x^{(i)}\right)-y^{(i)}\right)^2\]
  • Using linear hypothesis (with extra "1" feature):                       \[\frac{1}{n} \sum_{i=1}^n\left(\theta^{\top} x^{(i)}-y^{(i)}\right)^2\]
  • With given data, the error only depends on \(\theta\), so let's call the error \(J(\theta)\)
Recall week1 intro

What do we want to learn:

  • A hypothesis (or more concretely, a set of parameters) 
  • that's "good"

What do we have:

  • Some data
  • Some ideas about the structure of the problem
Recall week1 intro

What do we want to learn:

  • A hypothesis (or more concretely, a set of parameters) 
  • that's "good"

What do we have:

  • Some data
  • Some ideas about the structure of the problem

With \(\lambda \uparrow\) , typically tend to structural error  \(\uparrow\)  but estimation error  \( \downarrow\)

Minimizing training error doesn't always gives us a hypothesis that performs well on unseen data -- one of the central struggles ML has

Very roughly, broken into two camps:

 

 

 

structural error (due to model class)

estimation error (due to e.g. not enough data)

  • hypothesis class isn't rich enough
  • bad hyperparameter
  • unreasonable loss function
  • "garbage in garbage out"
  • training data doesn't represent test data
  •  

Summary

  • For the OLS, we can find the optimizer analytically via basic calculus!  Take the gradient and set it to zero. (General optimization needs more than gradient info; suffices in OLS)
  • Two scenarios when closed-form formula not well-defined. Need to be careful about understanding the consequences.
  • Ill-conditioned, When there are many possible solutions, we need to indicate our preference somehow.
  • Regularization is a way to construct a new optimization problem.
    Regularization can help battle overfitting (sensitive model).
  • Least-squares regularization leads to the ridge-regression formulation.  Good news: we can still solve it analytically!
    Validation/cross-validation are a way to choose regularization hyper parameters. Hyperparameters and how to pick them; cross-validation.
Temperature Population Pollution
Chicago 90 45 7.2
New York 20 32 9.5
Boston 35 100 8.4

\[ J(\theta) = \frac{1}{n} \sum_{i=1}^n\left({x^{(i)}}^{\top}\theta -y^{(i)}\right)^2\]

6.390 IntroML (Spring25) - Lecture 2 Linear Regression and Regularization

By Shen Shen

6.390 IntroML (Spring25) - Lecture 2 Linear Regression and Regularization

  • 367

More from Shen Shen

  • 6.390 IntroML (Spring25) - Lecture 12 Non-parametric Models
    Shen Shen
    141
  • 6.C011/C511 - ML for CS (Spring25) - Lecture 9 EECS Case Studies & Integration
    Shen Shen
    129
  • 6.C011/C511 - ML for CS (Spring25) - Lecture 8 Domain Shift, Adaptation, and Robustness
    Shen Shen
    137