Policy Gradient Derivation

• We overload notation:
• Let \(\tau\) denote a state-action sequence: \(\tau=s_0, a_0, s_1, a_1, \ldots\)
• Let \(R(\tau)\) denote the sum of discounted rewards on \(\tau: R(\tau)=\sum_t \gamma^t R\left(s_t, a_t\right)\)
• W.l.o.g. assume \(R(\tau)\) is deterministic in \(\tau\)
• Let \(P(\tau ; \theta)\) denote the probability of trajectory \(\tau\) induced by \(\pi_\theta\)
• Let \(U(\theta)\) denote the objective: \(U(\theta)=\mathbb{E}\left[\sum_t \gamma^t R\left(s_t, a_t\right) \mid \pi_\theta\right]\)
• Our goal is to find \[\theta: \max _\theta U(\theta)=\max _\theta \sum_\tau P(\tau ; \theta) R(\tau)\]

Recap

Policy Gradient Derivation

Recap

Policy Gradient Derivation

\(=\sum_\tau P(\tau ; \theta) \nabla_\theta \log P(\tau ; \theta) R(\tau)\)

Recap

Policy Gradient Derivation

\(=\sum_\tau P(\tau ; \theta) \nabla_\theta \log P(\tau ; \theta) R(\tau)\)

Approximate with the empirical (Monte-Carlo) estimate for \(m\) sample traj. under policy \(\pi_\theta\)

\(\nabla_\theta U(\theta) \approx \hat{g}=\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right) R\left(\tau^{(i)}\right)\)

Recap

Policy Gradient Derivation

\(\nabla_\theta U(\theta) \approx \hat{g}=\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right) R\left(\tau^{(i)}\right)\)

Recap

Policy Gradient Derivation

\(=\sum_{t=0} \underbrace{\nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right)}_{\text {no transition model required}}\)

\(\nabla_\theta \log P(\tau ; \theta)\)

\(\nabla_\theta U(\theta) \approx \hat{g}=\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right) R\left(\tau^{(i)}\right)\)

The following expression provides us with an unbiased estimate of the gradient, and we can compute it without access to the transition model:

where 

Recap

\(=\sum_\tau P(\tau ; \theta) R(\tau)\)

\(\approx \hat{g} = \frac{1}{m}\sum_{i=1}^{m}\left(\sum_{t=0}\nabla_\theta \log \pi_\theta(a_t^{(i)}\mid s_t^{(i)})\right)R(\tau^{(i)})\)

This policy gradient estimator typically has high variance, due to:

• Trajectory-Level Monte Carlo Sampling
  • Single-trajectory randomness:  The gradient estimator \(\hat{g}\) depends on averaging the returns from a finite set of \(m\) trajectories.
  • Each trajectory \(\tau^{(i)}\) is sampled from the policy \(\pi_\theta\), making it inherently stochastic and subject to large fluctuations.

\(=\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right) R\left(\tau^{(i)}\right)\)

\(\nabla_\theta U(\theta)\) 

\(=\sum_\tau P(\tau ; \theta) R(\tau)\)

\(\nabla_\theta U(\theta) \approx \hat{g} = \frac{1}{m}\sum_{i=1}^{m}\left(\sum_{t=0}\nabla_\theta \log \pi_\theta(a_t^{(i)}\mid s_t^{(i)})\right)R(\tau^{(i)})\)

This policy gradient estimator typically has high variance, due to:

• High Variance of Return \(R(\tau^{(i)})\)
  • Cumulative rewards:   The return \(R(\tau^{(i)})\) is the sum of all rewards along the trajectory. A slight variation in early steps can produce large differences in total returns.
  • Sparse or delayed rewards:  When rewards are sparse or rare, returns can fluctuate drastically—some trajectories yield high rewards, others yield zero.

\(=\sum_\tau P(\tau ; \theta) R(\tau)\)

\(\nabla_\theta U(\theta) \approx \hat{g} = \frac{1}{m}\sum_{i=1}^{m}\left(\sum_{t=0}\nabla_\theta \log \pi_\theta(a_t^{(i)}\mid s_t^{(i)})\right)R(\tau^{(i)})\)

This policy gradient estimator typically has high variance, due to:

• Noisy Gradient via \(\nabla_\theta \log \pi_\theta(a_t \mid s_t)\)
  • Log probability gradients:  The term \(\nabla_\theta \log \pi_\theta(a_t^{(i)} \mid s_t^{(i)})\) can fluctuate significantly, as small parameter changes affect action probabilities greatly, especially with neural-network policies.
  • Multiplicative variance amplification:  Since the return \(R(\tau^{(i)})\) multiplies this gradient, any small variance in the log-policy gradients is amplified by large or variable returns.

\(=\sum_\tau P(\tau ; \theta) R(\tau)\)

\(\nabla_\theta U(\theta) \approx \hat{g} = \frac{1}{m}\sum_{i=1}^{m}\left(\sum_{t=0}\nabla_\theta \log \pi_\theta(a_t^{(i)}\mid s_t^{(i)})\right)R(\tau^{(i)})\)

This policy gradient estimator typically has high variance, due to:

•  Credit Assignment Problem
  • Long-horizon dependencies:  Rewards received late in a trajectory affect all preceding time-step gradient updates equally, regardless of which actions truly contributed. This leads to noisy and uncertain gradient signals for early actions.
  • Poor causality:  The gradient estimator does not explicitly distinguish between actions genuinely contributing to a high return and those irrelevant to it.

\(=\sum_\tau P(\tau ; \theta) R(\tau)\)

\(\nabla_\theta U(\theta) \approx \hat{g} = \frac{1}{m}\sum_{i=1}^{m}\left(\sum_{t=0}\nabla_\theta \log \pi_\theta(a_t^{(i)}\mid s_t^{(i)})\right)R(\tau^{(i)})\)

This policy gradient estimator typically has high variance, due to:

• Limited Sample Size (\(m\) small)
  • Finite-sample estimation: Typically, only a limited number \(m\) of trajectories are sampled. Small sample sizes mean high sampling variability, thus high estimator variance.
  • Expensive sampling: Generating trajectories is computationally expensive, limiting practical trajectory counts and exacerbating variance.

Variance reduction:

• Getting more sample trajectories (sometimes infeasible)
• Temporal structure
• Subtracting a constant baseline \(b\)

\(\hat{g}=\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right)\left(R\left(\tau^{(i)}\right)\right)\)

\(=\frac{1}{m} \sum_{i=1}^m\left(\sum_{t=0}^{h-1} \nabla_\theta \log \pi_\theta\left(a_t^{(i)} \mid s_t^{(i)}\right)\right)\left(\sum_{t=0}^{h-1} R\left(s_t^{(i)}, a_t^{(i)}\right)\right)\)

\(=\frac{1}{m} \sum_{i=1}^m\left(\sum_{t=0}^{I I-1} \nabla_\theta \log \pi_\theta\left(a_t^{(i)} \mid s_t^{(i)}\right)\left[\left(\sum_{k=0}^{t-1} R\left(s_k^{(i)}, a_k^{(i)}\right)\right)+\left(\sum_{k=t}^{h-1} R\left(s_k^{(i)}, a_k^{(i)}\right)\right)\right]\right)\)

[Policy Gradient Theorem: Sutton et al 1999; GPOMDP: Bartlett & Baxter, 2001; Survey: Peters & Schaal, 2006]

Removing terms that don't depend on current action can lower variance:

\(\frac{1}{m} \sum_{i=1}^m \sum_{t=0}^{h-1} \nabla_\theta \log \pi_\theta\left(a_t^{(i)} \mid s_t^{(i)}\right)\left(\sum_{k=t}^{h-1} R\left(s_k^{(i)}, a_k^{(i)}\right)\right)\)

Temporal structure

Variance reduction:

• Subtracting a constant baseline \(b:\)

\(\nabla U(\theta) \approx \hat{g}=\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right)\left(R\left(\tau^{(i)}\right)-b\right)\)

[Williams, REINFORCE paper, 1992]

• Still unbiased, despite the additional term

\[\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right)(-b)\]

• with good choice of \(b,\) can reduce variance of \(\nabla U(\theta)\)

\(\nabla U(\theta) \approx \hat{g}=\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right)\left(R\left(\tau^{(i)}\right)-b\right)\)

\(\begin{aligned} & \mathbb{E}\left[\nabla_\theta \log P(\tau ; \theta) b\right] \\ & =\sum_\tau P(\tau ; \theta) \nabla_\theta \log P(\tau ; \theta) b \\ & =\sum_\tau P(\tau ; \theta) \frac{\nabla_\theta P(\tau ; \theta)}{P(\tau ; \theta)} b \\ & =\sum_\tau \nabla_\theta P(\tau ; \theta) b\end{aligned}\)

\(=\nabla_\theta\left(\sum_\tau P(\tau) b\right)=b \nabla_\theta\left(\sum_\tau P(\tau)\right)=b \times 0\)

[Williams, REINFORCE paper, 1992]

❓ Why still unbiased despite the additional term                                                                                                             

\[\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right)(-b)\]

Variance reduction:

• Getting more sample trajectories (sometimes infeasible)
• Subtracting a constant baseline \(b:\)

\(\nabla U(\theta) \approx \hat{g}=\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right)\left(R\left(\tau^{(i)}\right)-b\right)\)

[Williams, REINFORCE paper, 1992]

✅ Still unbiased, despite the additional term

\[\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right)(-b)\]

❓with good choice of \(b,\) can reduce variance of \(\nabla U(\theta)\)

Control Variates

• The main idea is to reduce variance in the estimate of an expectation.
• Suppose we want to estimate: \[\mu = \mathbb{E}[X]\] where \(X\) is some random variable.
• We introduce another random variable \(Y\) (the control variate), with a known expectation  \(\mathbb{E}[Y] = \nu\), and importantly, \(Y\) is correlated to \(X\).
• Estimator \(X-Y+\nu\) has variance \[\operatorname{Var}(X-Y)=\operatorname{Var}(X)+\operatorname{Var}(Y)-2 \operatorname{Cov}(X, Y)\]

We can also define a new estimator: \(X’ = X - \alpha(Y - \nu)\) where \(\alpha\) can be chosen optimally to minimize variance.

Control variates in RL

\(\nabla U(\theta) \approx \hat{g}=\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right)\left(R\left(\tau^{(i)}\right)-b\right)\)

• What's a good baseline \(b\) candidate?
• state-value function \( V^\pi(s) \)) from rewards
• \(b=\frac{1}{m} \sum_{i=1}^m R\left(\tau^{(i)}\right)\)
• Estimated state-dependent value functions: \(b\left(s_t\right)=\hat{V}^\pi\left(s_t\right)\)

\(\nabla U(\theta) \approx \hat{g}=\frac{1}{m} \sum_{i=1}^m \nabla_\theta \log P\left(\tau^{(i)} ; \theta\right)\left(R\left(\tau^{(i)}\right)-\hat{V}^\pi(s)\right)\)

[Greensmith, Bartlett, Baxter, JMLR 2004 for variance reduction techniques.]

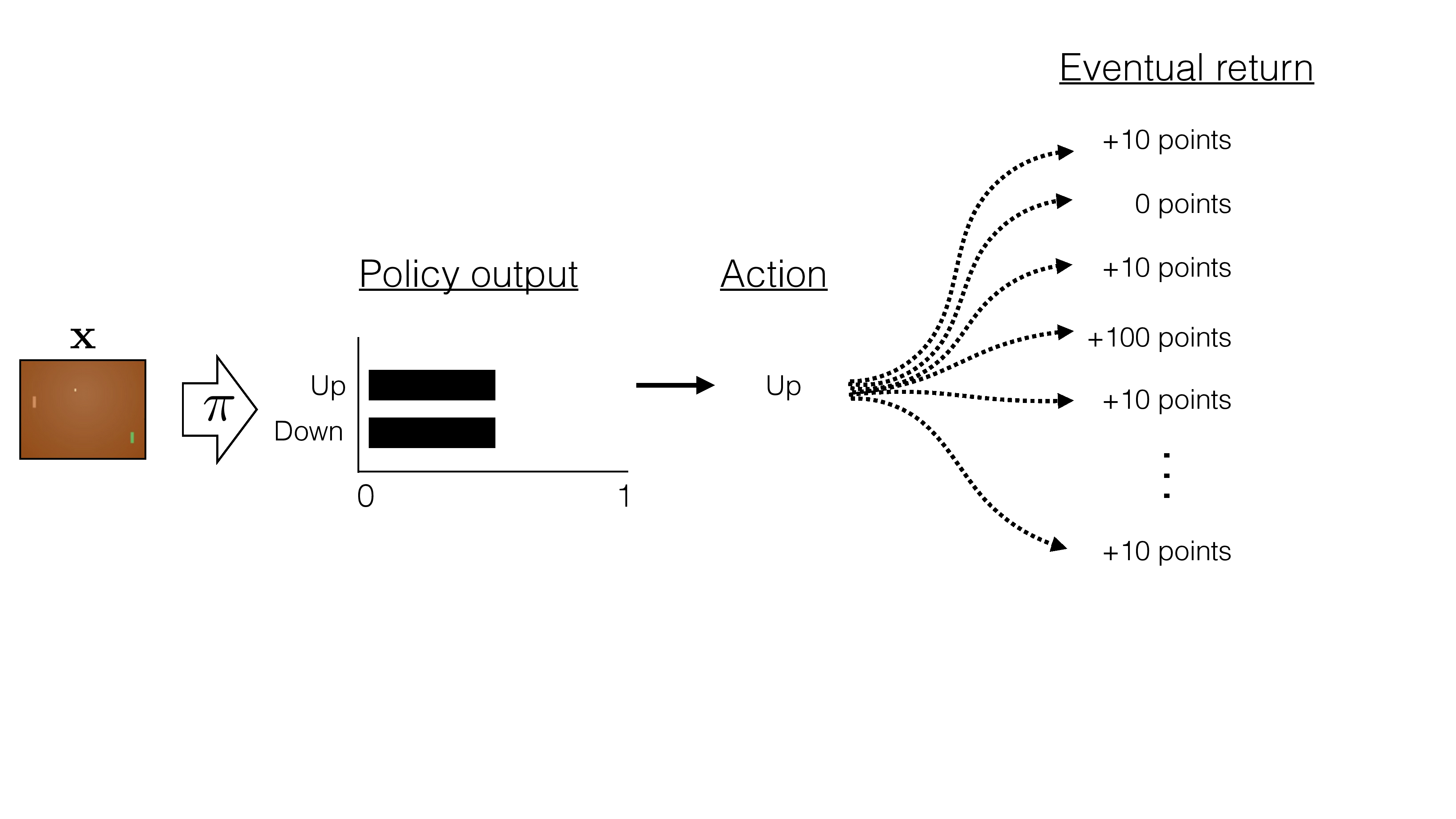
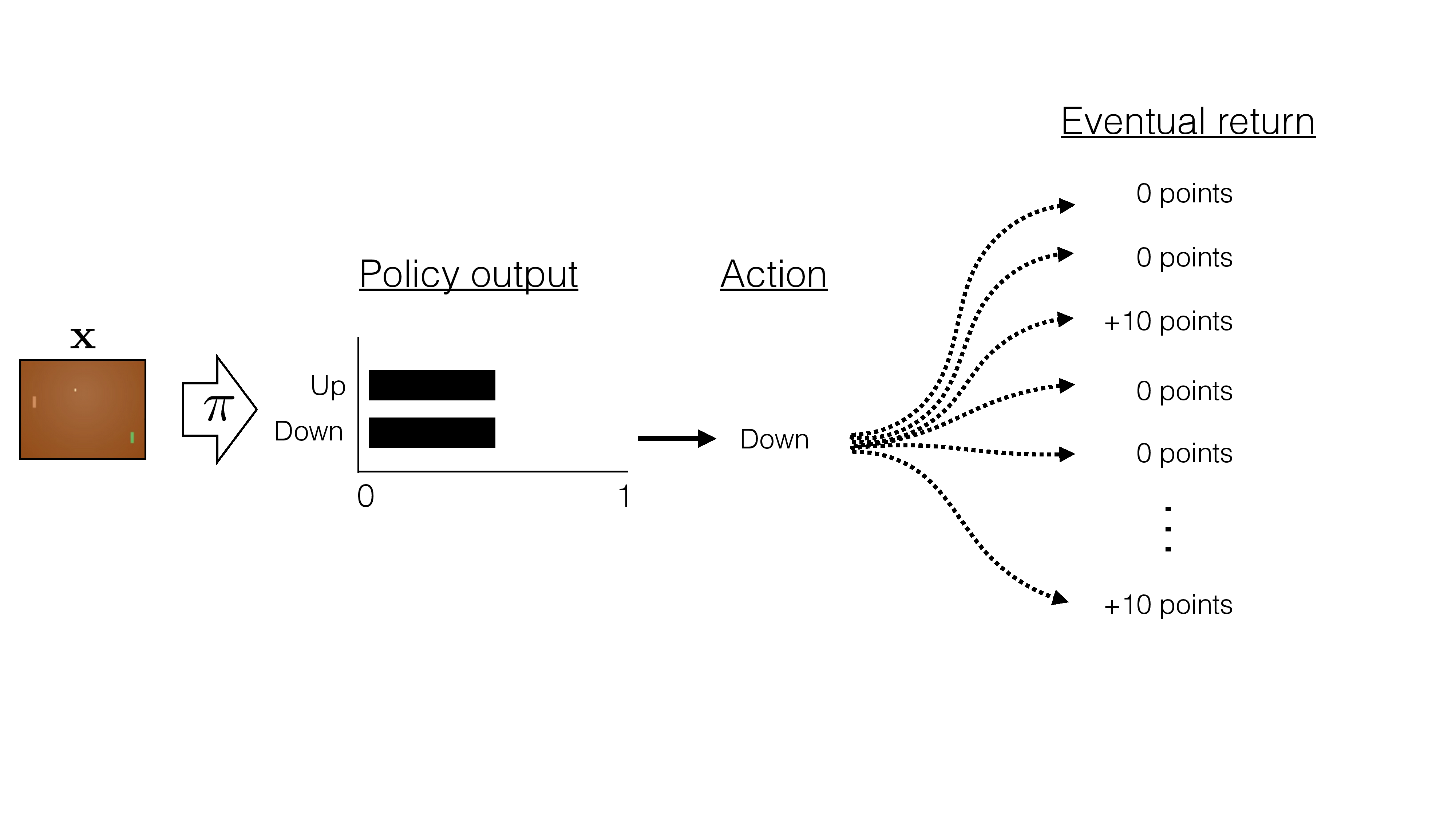
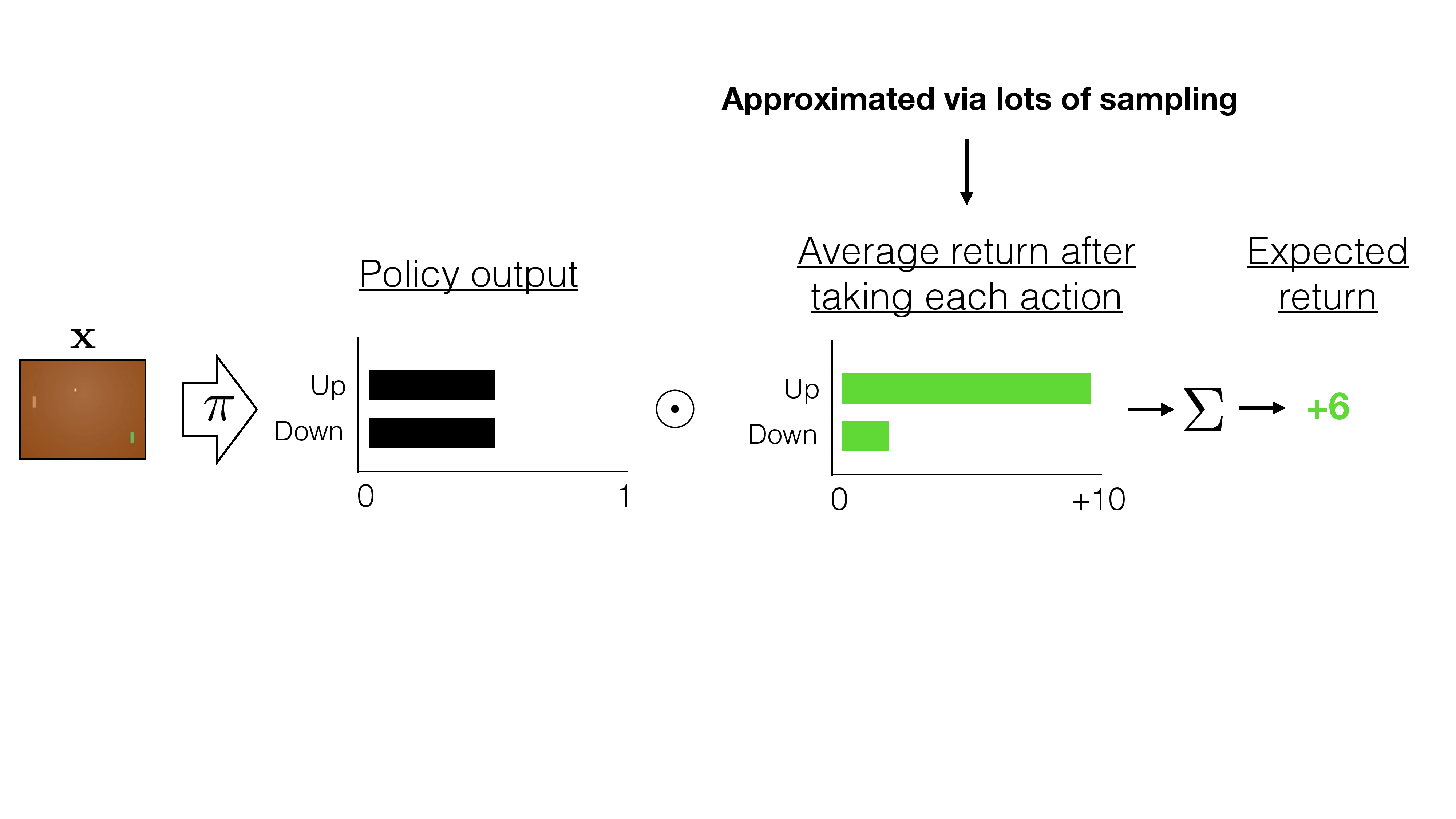
\(-b\)

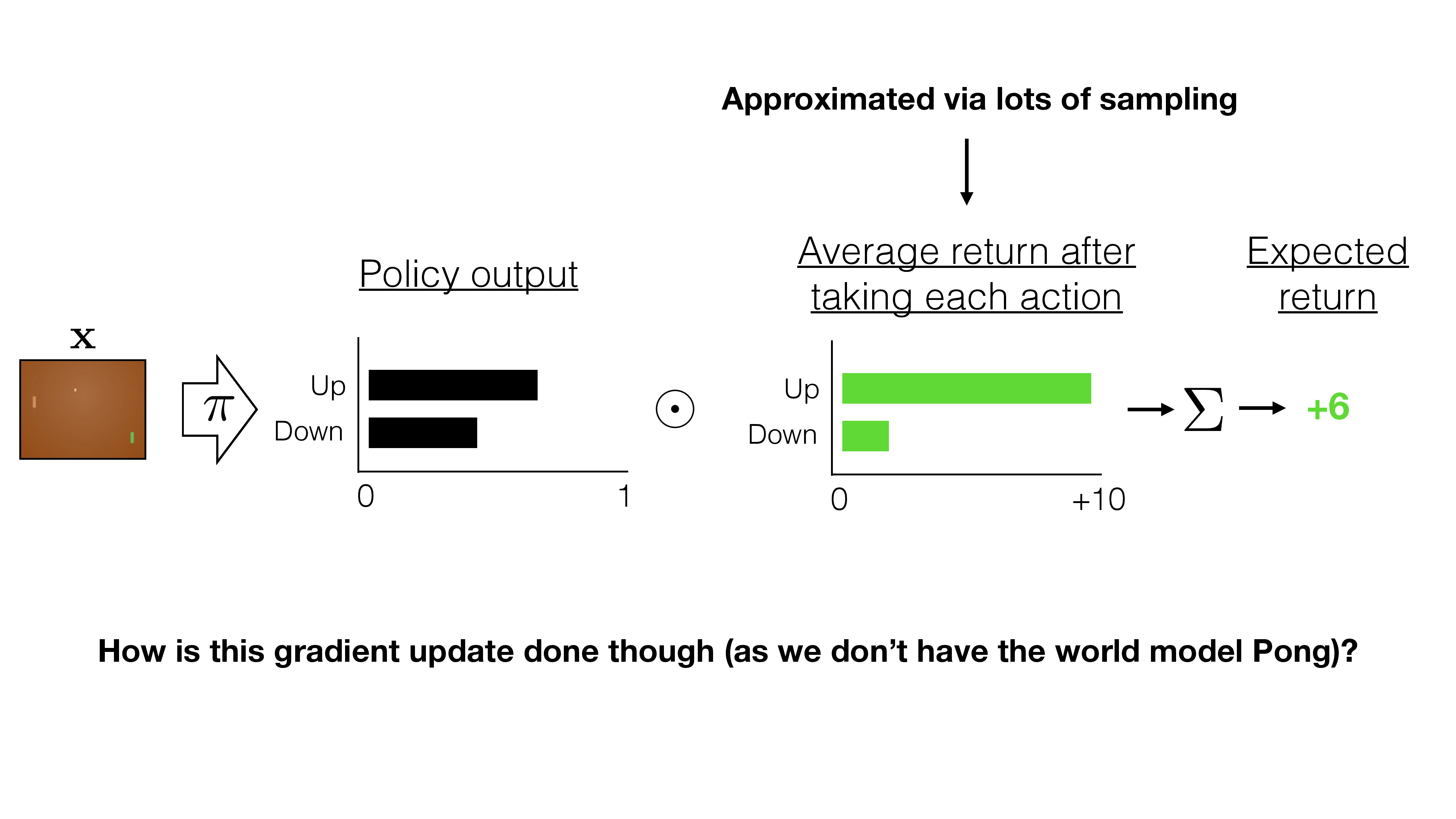
instead of increase the likelihood of all "winning" games, increase the likelihood of "better than average score" games

\(-b\)

How to estimate \(V^\pi\)?

• Again, Monte Carlo estimate \(b\left(s_t\right)=\mathbb{E}\left[r_t+r_{t+1}+r_{t+2}+\ldots+r_{H-1}\right]=V^\pi\left(s_t\right)\)

• Or, collect \(\tau_1, \ldots, \tau_m\), and regress against empirical return:  \(\phi_{i+1} \leftarrow \underset{\phi}{\arg \min } \frac{1}{m} \sum_{i=1}^m \sum_{t=0}^{H-1}\left(V_\phi^\pi\left(s_t^{(i)}\right)-\left(\sum_{k=t}^{H-1} R\left(s_k^{(i)}, u_k^{(i)}\right)\right)\right)^2\)

• Or, similar to fitted Q-learning, do fitted V-learning:                                                  \(\phi_{i+1} \leftarrow \min _\phi \sum_{\left(s, u, s^{\prime}, r\right)}\left\|r+V_{\phi_i}^\pi\left(s^{\prime}\right)-V_\phi(s)\right\|_2^2\)

[Greensmith, Bartlett, Baxter, JMLR 2004 for variance reduction techniques.]

How to estimate advatange?

(GAE) [Schulman et al, ICLR 2016]
TD(lambda) / eligibility traces [Sutton and Barto, 1990]

• \(\hat{Q}:\) lambda exponentially weighted average of all the above
• Advantage estimate then \(\hat{A}=\hat{Q}-\hat{V}\)

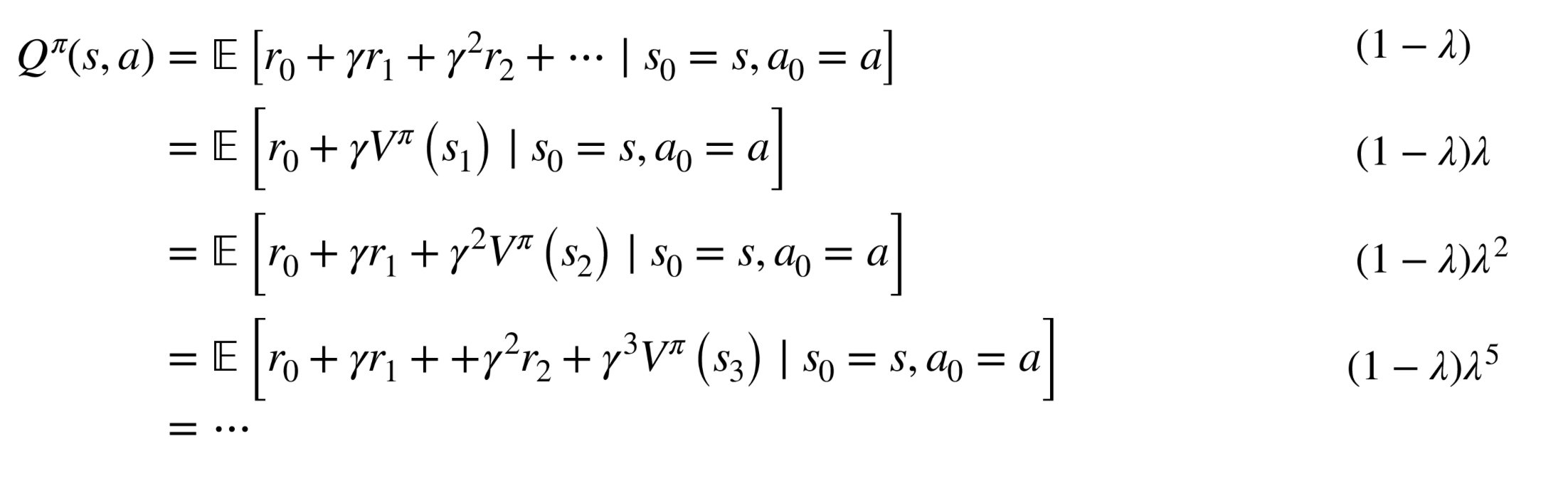
How to estimate advatange?

[Async Advantage Actor Critic (A3C) [Mnih et al, 2016]

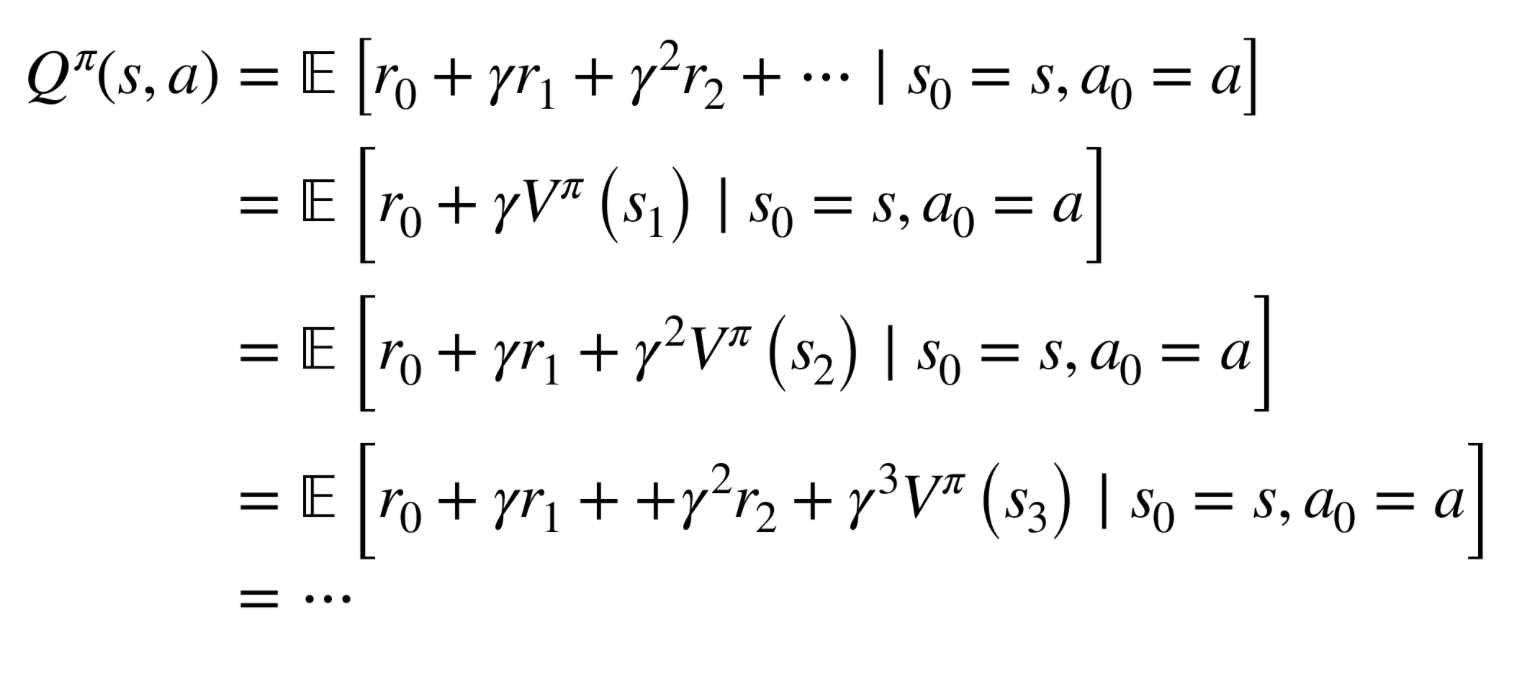
• \(\hat{Q}\) : one of the above choices (e.g. k=5 step lookahead)
• Advantage estimate then \(\hat{A}=\hat{Q}-\hat{V}\)

Actor-critic method

[Williams, REINFORCE paper, 1992]

actor

critic

Vanilla policy gradient/REINFORCE: step-sizing issue

• Step-sizes is worth tuning even in pure SGD under supervised learning.
• In policy gradient, bad step-sizes can have worse "chain effect":
  • Step too far, may lead to terrible policy
  • Next mini-batch: terrible data collected (with e.g. no reward signal; so no "correction")
  • Not clear how to recover
  • Intuitively, too big of a distributional shift
• Coupled with unknown dynamics/transition, good step-sizing is hard a-priori

Trust region policy optimization (TRPO)

• Interpretation of the objective via importance sampling (next slide)
• Interpretation of the constraint via distributional shift
• Can solve approximately via conjugate gradient method (using linear approx. of the objective and quadratic approx. of the KL)

\(\max L(\pi)=\mathbb{E}_{\pi \text { old }}\left[\frac{\pi(a \mid s)}{\pi_{\mathrm{old}}(a \mid s)} A^\pi_{old}\right.\)\(\left.(s, a)\right]\)

Constraint: \(\quad \mathbb{E}_{\pi_{\text {old }}}\left[K L\left(\pi \mid \pi_{\text {old }}\right)\right] \leq \epsilon\)

importance sampling

\(\mathbb{E}_{x \sim q}\left[\frac{p(x)}{q(x)} f(x)\right]=\mathbb{E}_{x \sim p}[f(x)]\)

\(U(\theta)=\mathbb{E}_{\tau \sim \theta} \mathrm{old}\left[\frac{P(\tau \mid \theta)}{P\left(\tau \mid \theta_{\mathrm{old}}\right)} R(\tau)\right]\)

\(=\mathbb{E}_{\tau \sim \theta_{\text {old }}}\left[\frac{\pi(\tau \mid \theta)}{\pi\left(\tau \mid \theta_{\text {old }}\right)} R(\tau)\right]\)

\(\nabla_\theta U(\theta)=\mathbb{E}_{\tau \sim \theta} \text { old }\left[\frac{\nabla_\theta P(\tau \mid \theta)}{P\left(\tau \mid \theta_{\text {old }}\right)} R(\tau)\right]\)

[Tang and Abbeel, On a Connection between Importance Sampling and the Likelihood Ratio Policy Gradient, 2011]

• Estimate both the utilities (objective) and policy gradient under new policy
• by using trajectories under old policy

• helps sample complexity, but increases variance actually (another tradeoff)

[Tang and Abbeel, On a Connection between Importance Sampling and the Likelihood Ratio Policy Gradient, 2011]

TRPO

\(\max L(\pi)=\mathbb{E}_{\pi \text { old }}\left[\frac{\pi(a \mid s)}{\pi_{\mathrm{old}}(a \mid s)} A^\pi_{old}\right.\)\(\left.(s, a)\right]\)

Constraint: \(\quad \mathbb{E}_{\pi_{\text {old }}}\left[K L\left(\pi \mid \pi_{\text {old }}\right)\right] \leq \epsilon\)

\(\max \mathbb{E}_{\pi \text { old }}\left[\frac{\pi(a \mid s)}{\pi_{\mathrm{old}}(a \mid s)} A^\pi_{old}\right.\)\(\left.(s, a)\right]\)

\(-\beta\left(\mathbb{E}_t\left[\operatorname{KL}\left(\pi_{o l d} \mid \pi\right)\right]-\delta\right)\)

Proximal Policy Optimization (PPO, v1)

Proximal Policy Optimization (PPO, v2)

Recall the objective:

\(\hat{\mathbb{E}}_t\left[\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_\theta \text { old }}{ }^{\left(a_t \mid s_t\right)} \hat{A}_t\right]\)

\(=\hat{\mathbb{E}}_t\left[\rho_t(\theta) \hat{A}_t\right]\)

A pwer bound of the above:

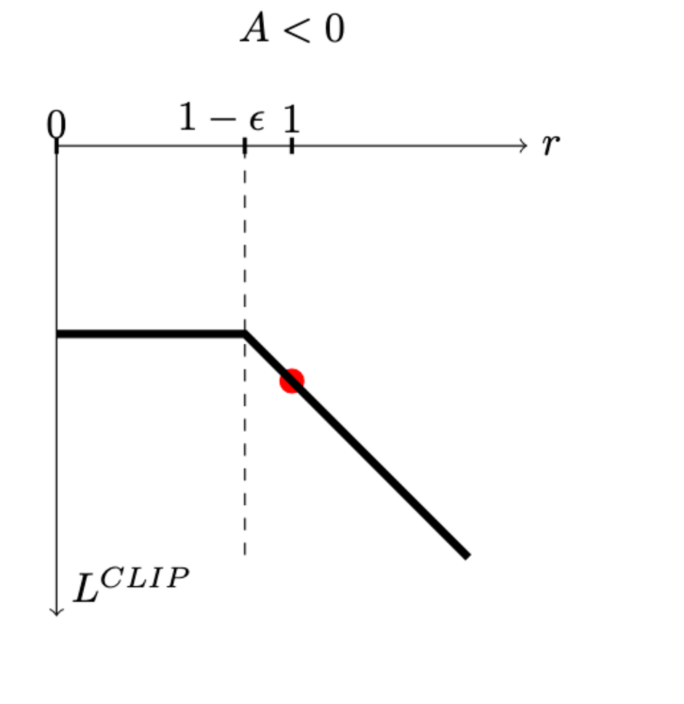
\(L^{C L I P}(\theta)=\hat{\mathbb{E}}_t\left[\min \left(\rho_t(\theta) \hat{A}_{t<0}, \operatorname{clip}\left(\rho_t(\theta), 1-\epsilon, 1+\epsilon\right) \hat{A}_t\right)\right]\)

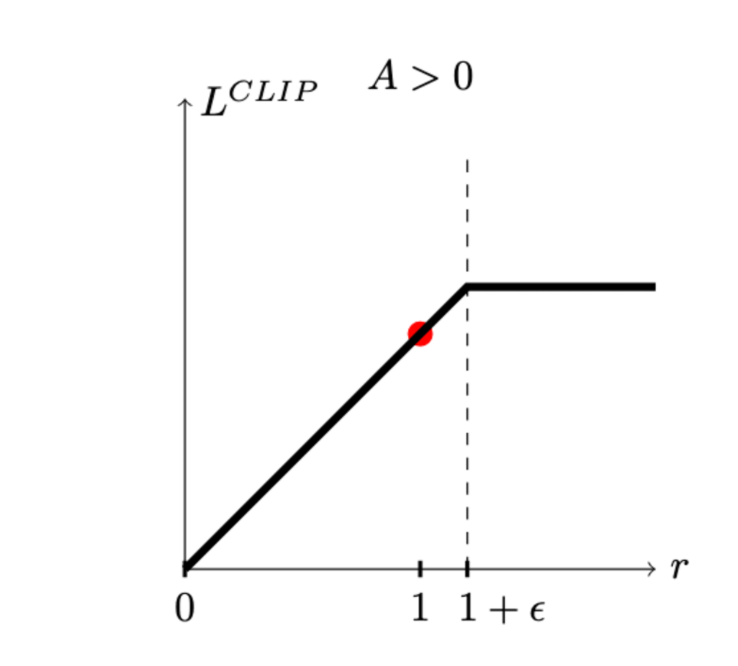
[table credit: Daniel Bick]

- The main loss \(L_t(\theta)=\min \left(r_t(\theta) \hat{A}_t, \operatorname{clip}\left(r_t(\theta)\right), 1-\epsilon, 1+\epsilon\right) \hat{A}_t\)
- Advantage estimate based on truncated GAE
- Adding an entropy term

Beyond what we covered

- POMDP
- Inverse RL
- Apprenticeship learning
- Behavioral cloning (Data Augmentation, a.k.a. DAgger)
- Transfer learning (sim to real)
- Domain randomization
- Multi-task learning
- Curriculum learning
- Hierarchical RL
- Safe/verifiable RL
- Multi-agent RL
- Offline RL
- Rewards shaping
- Fairness, ethical, explainable AI (value alignment)

Thanks!

We'd love to hear your thoughts.

Variance Reduction Achieved

• With the optimal control variate estimator \(X'\): \[\mathrm{Var}(X') = \mathrm{Var}(X - 0.8(Y - 1)).\]
• Expanding explicitly: \[\mathrm{Var}(X') = \mathrm{Var}(X - 0.8(X+\varepsilon - 1)) = \mathrm{Var}(0.2X - 0.8\varepsilon) = (0.2^2)\mathrm{Var}(X) + (-0.8^2)\mathrm{Var}(\varepsilon) = (0.04)(4) + (0.64)(1)= 0.16 + 0.64 = 0.8.\]
• Thus, we reduced the variance significantly: \( 4 \rightarrow 0.8 \) (5× improvement).