
Lecture 8: Domain Shift, Adaptation, and Robustness
Shen Shen
April 28, 2025
2:30pm, Room 32-144
Slides adapted from Tommi Jaakkola
Modeling with Machine Learning for Computer Science
- Project
- Method Document due today
- Sign up for presentation (sign-up form goes out after lecture today at 4pm)
- Nominal slot is 10min, so an ideal prep target would be 8min
- In-class exam next Monday (May 5)
- Reach out for conflict/accommodation
- Review session, stay tuned for time/room. (what would you like us to review?)
Logistics
- In the pre-training scenario, both data and task are typically different between the source (pre-training data/task) and the target (our actual task/data)
- For the rest of the lecture we focus on understanding and adjusting to “data shifts” while the prediction task remains the same
- The differences in the data arise for many reasons, and these reasons may be known or unknown
Domain Shift
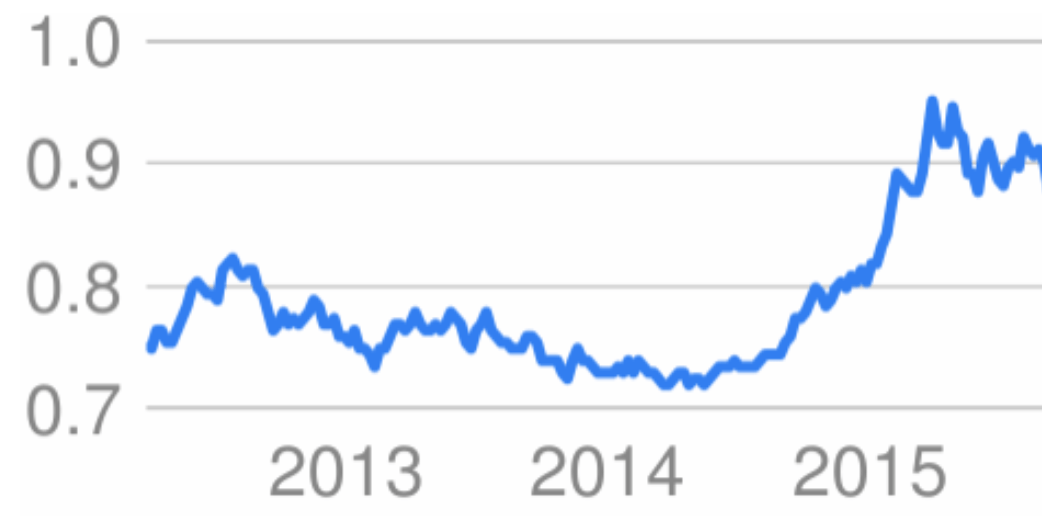
- E.g., temporal changes:
- predictors trained from older data, applied to new cases (such as customer behavior)
Domain Shift
Domain Shift
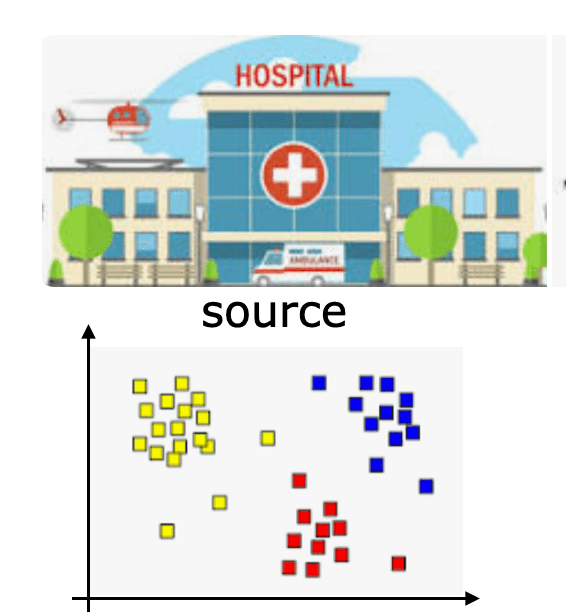
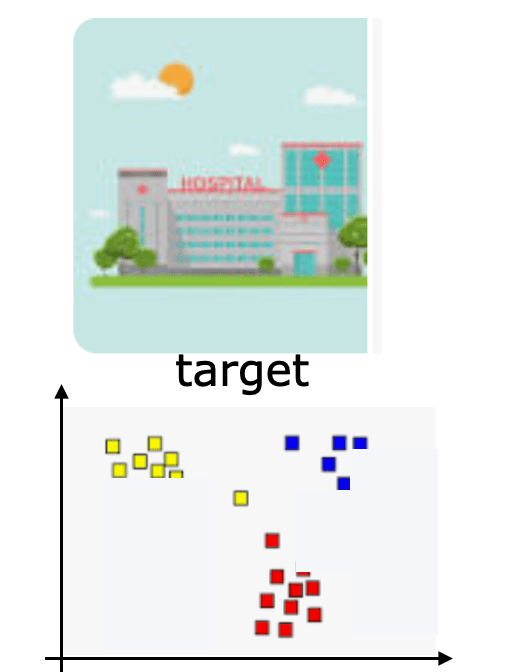
- E.g., demographic/context changes
- speech recognition system trained with one set of speakers, applied more broadly
- risk predictors that are based on patient data from one hospital but used in a different hospital with different demographics
Domain Shift
- E.g., actions we take
- predictors that are used in iterative experiment design (e.g., molecule optimization) where the current data comes from earlier rounds of selections
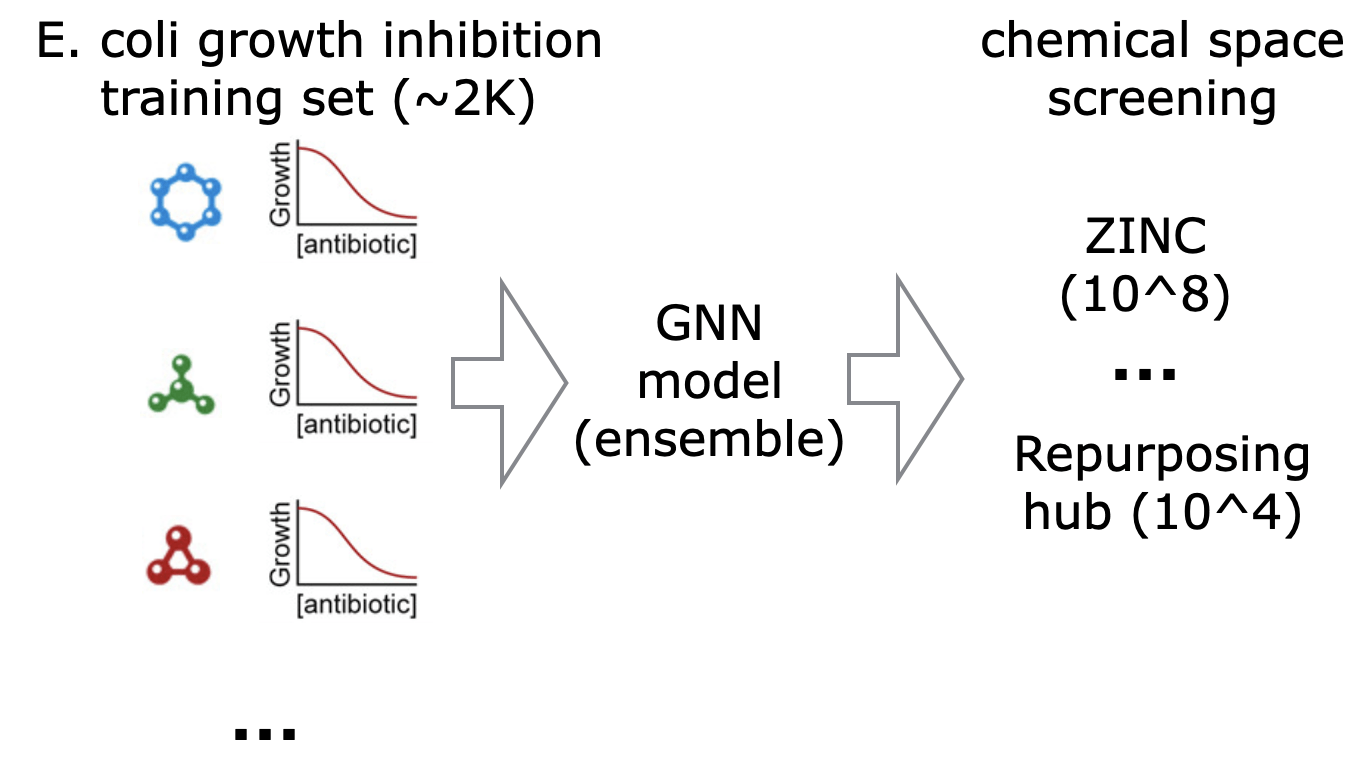
Domain Shift
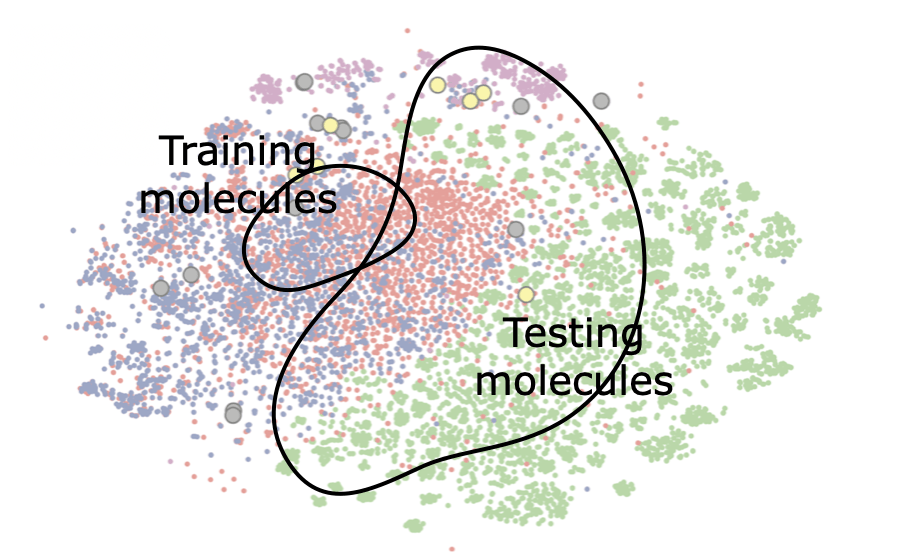
- E.g., wildlife species predictor, class distribution is different for each static sensor location

Domain Shift
- E.g., wildlife species predictor, class distribution is different for each static sensor location
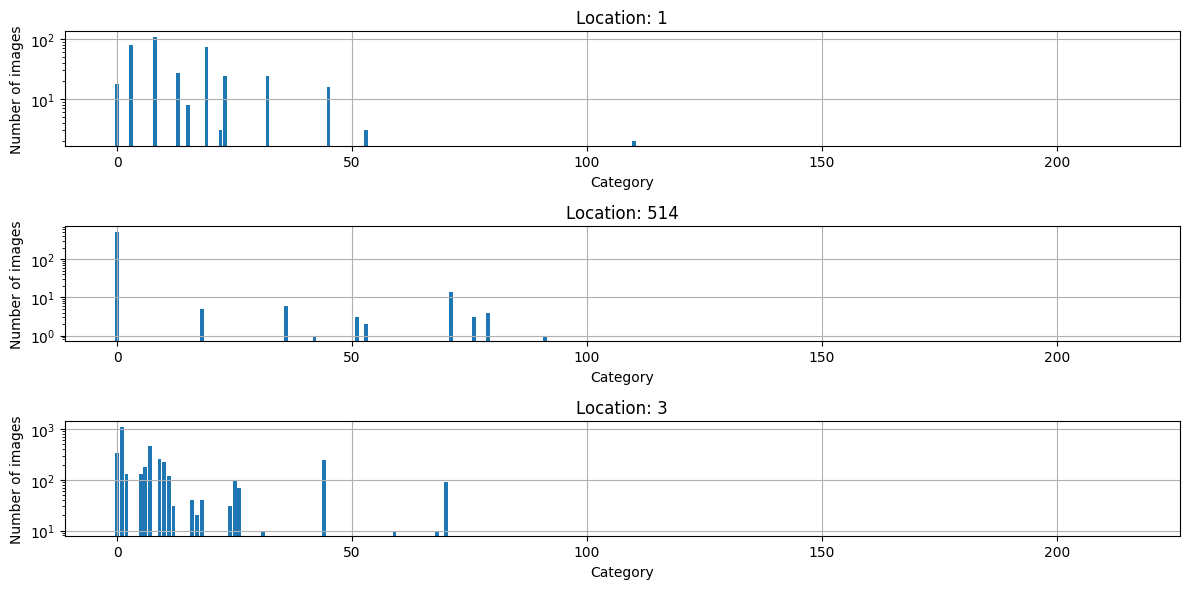
Domain Shift
- Performance can be substantially affected by “domain shift”… we need ways of dealing with such shifts
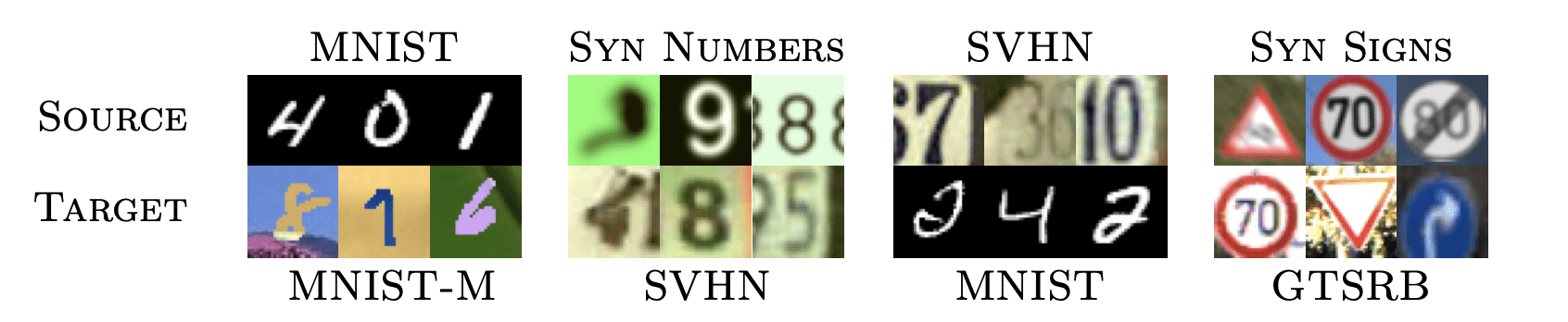
[Ganin et al. 2015]

Domain Shift
- Performance can be substantially affected by domain shift
[Koh et al. 2021]
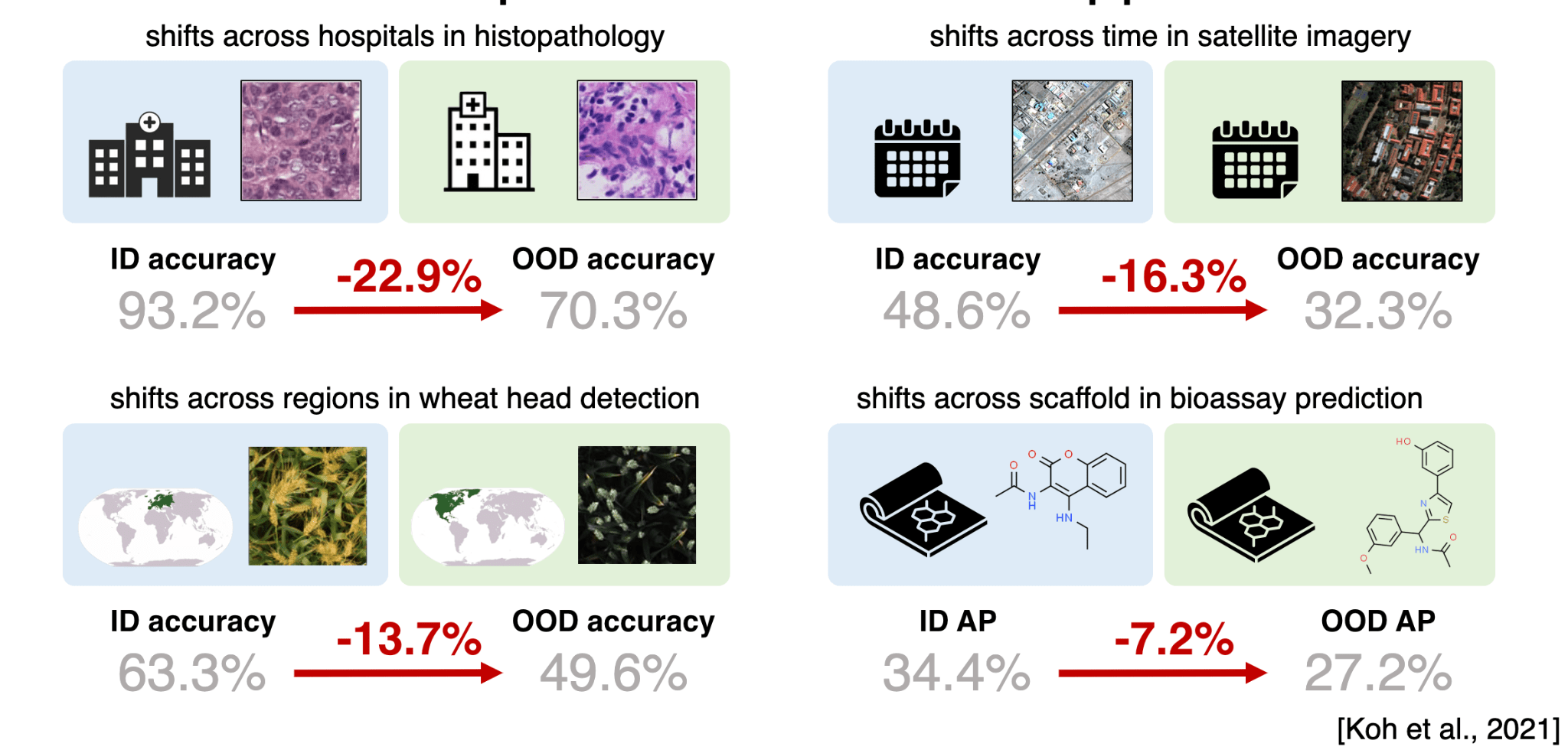
Domain Shift
- Performance can be substantially affected by domain shift
[Beery et al. 2020, Koh et al. 2021]

Domain adaptation possibilities
-
Goal is to learn from labeled/annotated training (source) examples and transfer this knowledge for use in a different (target) domain
-
For supervised learning: we have some annotated examples also from the target domain
-
For semi-supervised: we have lots of unlabeled target examples and just a few annotations
-
For unsupervised: we only have unlabeled examples from the target domain
-
For reinforcement learning: we have access to (source) environment, and aim to transfer policies to a (target) environment, possibly with limited or no interaction data from the target
Let’s consider two scenarios where we can adjust what we do
- Case #1 (label shift only): the proportions of labels differs from the source to the target domain, the data are otherwise generated the same
- Case #2 (co-variate shift only): the distribution of co-variates (distribution over x’s) differs from the source to target domain, the data are otherwise generated the same
(these are not mutually consistent, and do not cover all shifts)
Adjusting for two types of shifts
- One problem is how we can adjust an already trained classifier \(P_S(y \mid x)\) so that it is appropriate for the target domain where the label proportions are different
- E.g., a new specialized clinic appears next to a hospital. So patients with certain illnesses covered by the clinic are now less frequently coming to the hospital. But we can hypothesize that those who still come “look” the same as before, there are just fewer of them.
Label shift
Assumptions:
- Lots of source examples, can train an optimal source classifier \(P_S(y \mid x)\)
- Labeled examples look conditionally the same from source to target, i.e., \(P_S(x \mid y)=P_T(x \mid y)\), but proportions of different labels change
- We know the label proportions \(P_S(y)\) (observed) and \(P_T(y)\) (assumed)
We want:
- optimal target classifier \(P_T(y \mid x)\)
Label shift
- One problem is how we can adjust an already trained classifier \(P_S(y \mid x)\) so that it is appropriate for the target domain where the label proportions are different
- Let's consider any \(x\) (fixed, only y varies) and try to construct the target classifier based on the available information
Adjusting for label shift
\(P_T(y \mid x) \propto P_T(x \mid y) P_T(y)\)
\(=P_S(x \mid y) P_T(y)\)
\(=P_S(x \mid y) P_S(y) \frac{P_T(y)}{P_S(y)}\)
\(\propto \frac{P_S(x \mid y) P_S(y)}{P_S(x)} \frac{P_T(y)}{P_S(y)}\)
\(=P_S(y \mid x) \frac{P_T(y)}{P_S(y)}\)
class conditional distributions assumed to be the same
x is fixed, so we can include any x term
we have expressed the target classifier proportionally to the source classifier and the label ratios; normalizing this across y for any given x gives our target classifier
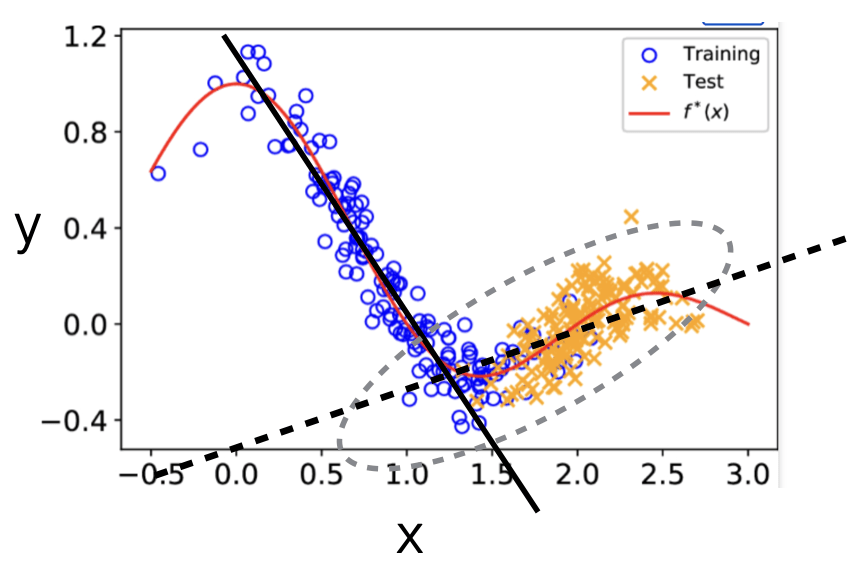
- The defining characteristic of co-variate shift, i.e., that the target \(P_T(x)\) differs from the source \(P_S(x)\), is present in almost any real prediction task
- There's an additional assumption that the relation between \(x\) and \(y\) remains the same; this assumption is less often true in reality (but enables us to do something)
- The effect is that, e.g., estimating a regression model from the source data may improperly emphasize the wrong examples (never seen in target domain)
Co-variate Shift
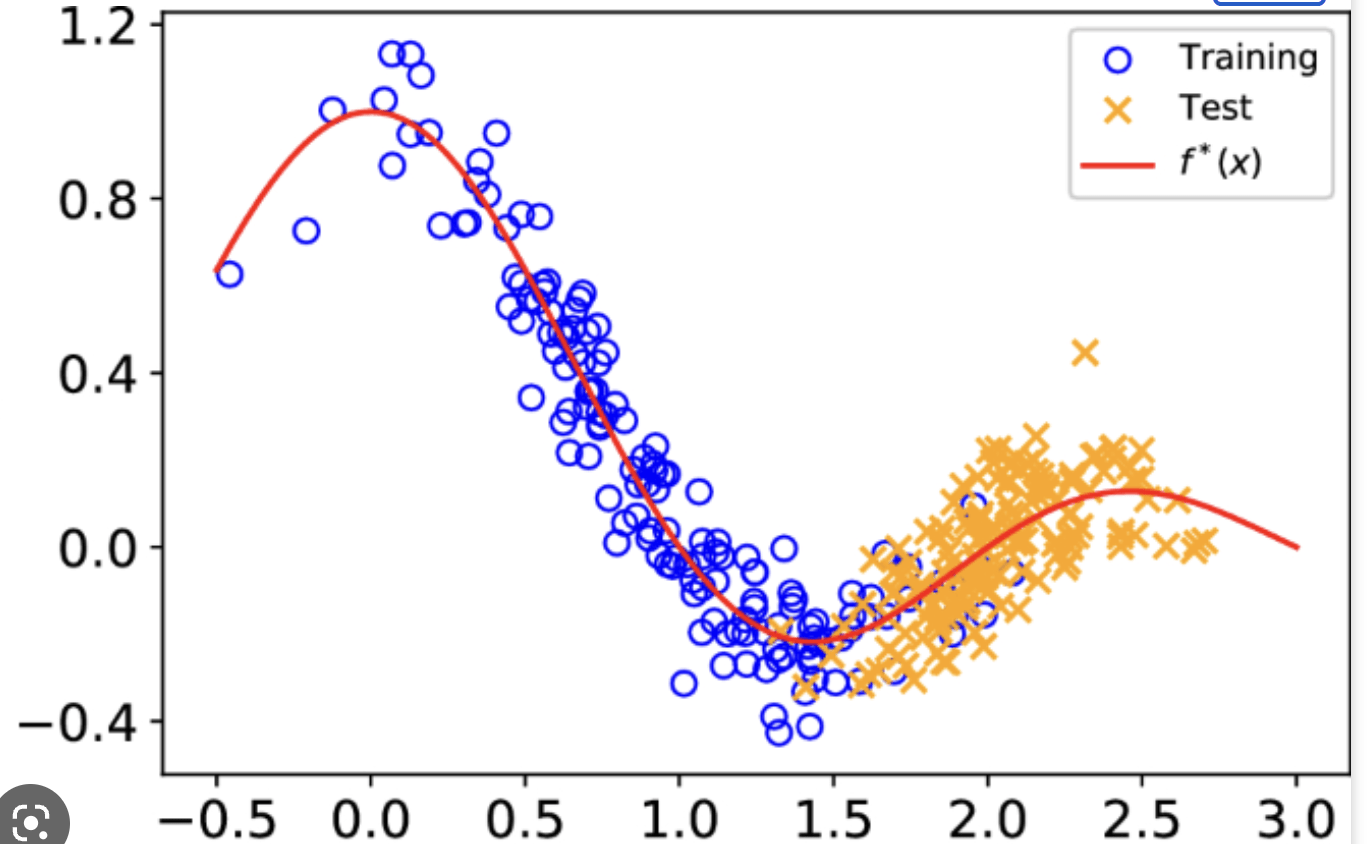
- The effect of co-variate shift is that, e.g., estimating a regression model from the source data may improperly emphasize the wrong examples
- Assumptions:
- common underlying function or \(P(y \mid x)\)
- lots of labeled examples from the source
- lots of unlabeled examples from the source and the target
- We want:
- a \(P(y \mid x)\) estimate that works well on the target samples
Co-variate Shift

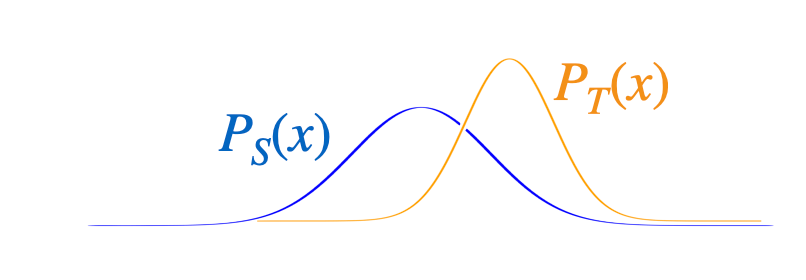
- When \(P_T(x)\) differs from \(P_S(x)\) we could still in principle use the same classifier or regression model \(P(y \mid x, \theta)\) trained from the source examples
- But estimating this regression model from the source data may improperly emphasize the wrong examples (e.g., x 's where \(P_S(x)\) is large but \(P_T(x)\) is small)
Co-variate Shift

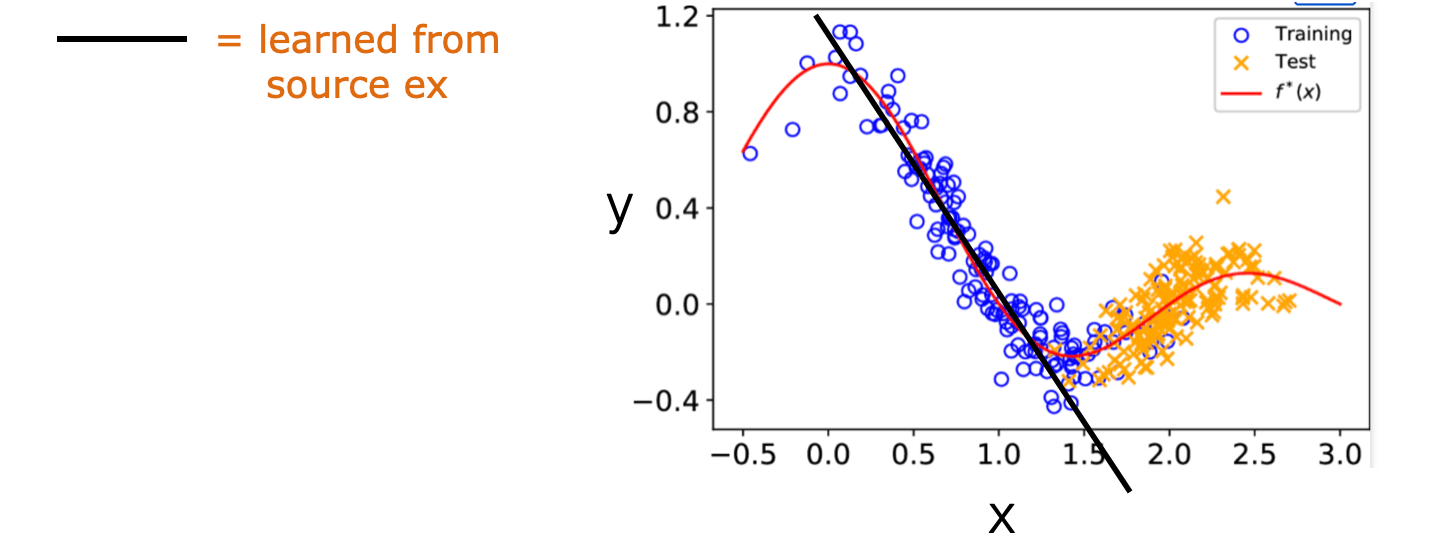

Co-variate Shift



We would like to estimate \(\theta\) that minimizes
\(\sum_{x, y} P_T(x, y) \operatorname{Loss}(x, y, \theta)\)
\(=\sum_{x, y} P_S(x, y) \frac{P_T(x, y)}{P_S(x, y)} \operatorname{Loss}(x, y, \theta)\)
\(=\sum_{x, y} P_S(x, y) \frac{P_T(x) P_T(y \mid x)}{P_S(x) P_S(y \mid x)} \operatorname{Loss}(x, y, \theta)\)
\(=\sum_{x, y} P_S(x, y) \frac{P_T(x)}{P_S(x)} \operatorname{Loss}(x, y, \theta)\)
average over the target distribution
weighted average over the source distribution
Co-variate Shift
- How do we get the ratio \(P_T(x) / P_S(x)\) used as weights in the new estimation criterion? If \(x\) is high dimensional, estimating such distributions is challenging.
- It turns out we can train a simple domain classifier to estimate this ratio
- only use unlabeled examples from the source and target
- label examples according to whether they come from the source S or target T
- estimate a domain classifier \(Q(S \mid x)\) from such labeled data -
If the domain classifier is "perfect" then
\(Q(S \mid x)=\frac{P_S(x)}{P_S(x)+P_T(x)} \quad \frac{Q(S \mid x)}{Q(T \mid x)}=\frac{P_S(x)}{P_T(x)}\)
-
So we can get the ratio weights required for estimation directly from the domain classifier
Co-variate Shift
- Since we can now get the required probability ratios from the domain classifier, we can estimate
- The labeled samples are now source training examples. The domain classifier itself is estimated from unlabeled source and target samples (co-variates only)
importance sampling
\(\mathbb{E}_{x \sim q}\left[\frac{p(x)}{q(x)} f(x)\right]=\mathbb{E}_{x \sim p}[f(x)]\)
\(U(\theta)=\mathbb{E}_{\tau \sim \theta} \mathrm{old}\left[\frac{P(\tau \mid \theta)}{P\left(\tau \mid \theta_{\mathrm{old}}\right)} R(\tau)\right]\)
\(=\mathbb{E}_{\tau \sim \theta_{\text {old }}}\left[\frac{\pi(\tau \mid \theta)}{\pi\left(\tau \mid \theta_{\text {old }}\right)} R(\tau)\right]\)
\(\nabla_\theta U(\theta)=\mathbb{E}_{\tau \sim \theta} \text { old }\left[\frac{\nabla_\theta P(\tau \mid \theta)}{P\left(\tau \mid \theta_{\text {old }}\right)} R(\tau)\right]\)
[Tang and Abbeel, On a Connection between Importance Sampling and the Likelihood Ratio Policy Gradient, 2011]
- Estimate both the utilities (objective) and policy gradient under new policy
- by using trajectories under old policy
Off-policy evaluation as dealing with co-variate shift
What's the conditional that remains the same? the unknown transitions.
Recall
Domain Adaptation Summary
| Shift Type | What Changes? | Typical Assumption | Need to Reweight? | Need to Relearn? |
|---|---|---|---|---|
| Covariate Shift | P(x) changes | P(y|x) stays the same | Yes (importance sampling on x) | No |
| Label Shift | P(y) changes | P(x|y) stays the same | Yes (importance sampling on y) | No |
| Concept Shift | P(y|x) changes | Neither P(x) nor P(y) necessarily stay the same | No (reweighting not enough) | Yes (new learning needed) |
Data augmentation


Data augmentation

Data augmentation
- Common problem: I collect all my data in Spring, but the model does not work anymore in Winter!
- Possible solutions:
- Add augmentation to account for distribution shift, e.g., color jittering
- Use pre-trained model that has been trained on all-season data, though not exactly your task
- Or… just wait for Winter and collect more data (most effective)!

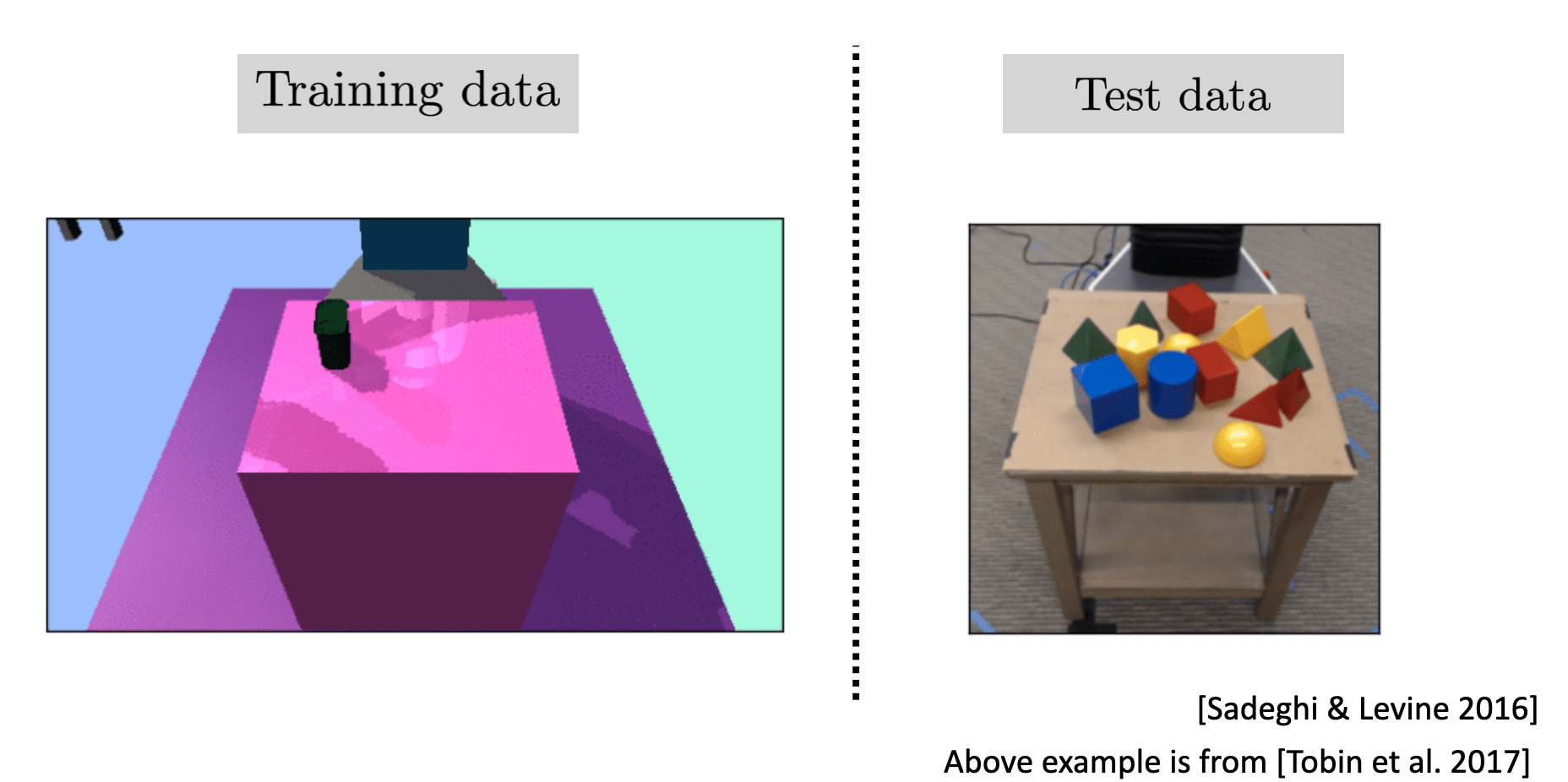
Domain randomization
Robustness









Thanks!
We'd love to hear your thoughts.
6.C011/C511 - ML for CS (Spring25) - Lecture 8 Domain Shift, Adaptation, and Robustness
By Shen Shen
6.C011/C511 - ML for CS (Spring25) - Lecture 8 Domain Shift, Adaptation, and Robustness
- 312



