Robotics and Generative AI
Some Slides forked from Russ Tedrake

Image credit: Boston Dynamics
Speaker: Shen Shen
May 8, 2025
MIT Undergraduate Math Association
DARPA Robotics Competition
2015
1. First-principle model
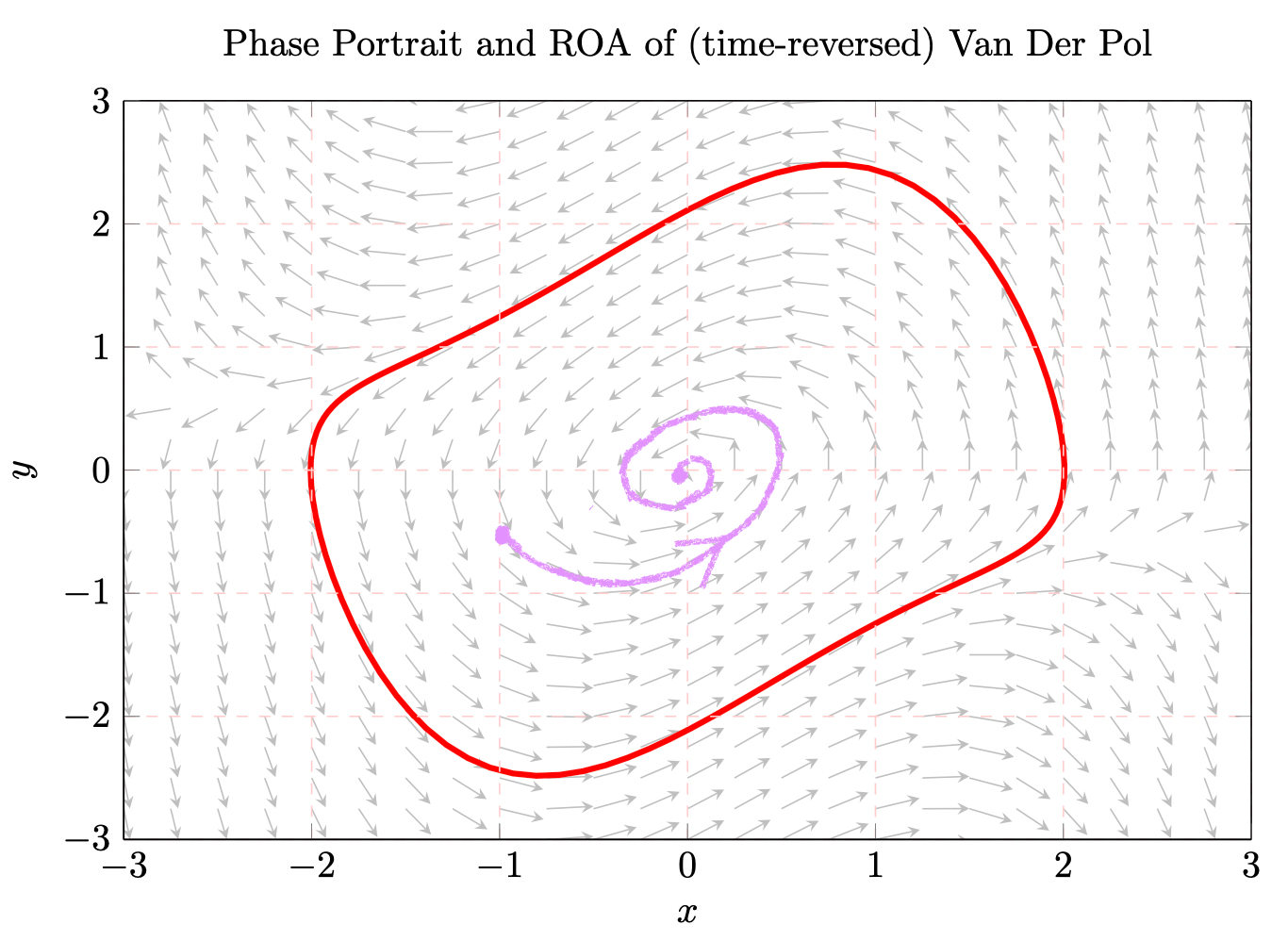
2. Lyapunov analysis
Search for a \(V\) such that:

(can be generalized for synthesis)
3. Optimization
Monomial basis \(m(x)\)
Gram matrix \(Q\)
- \(Q \succeq 0 \rightarrow \) \(f\geq 0\)
- Often see semi-definite programming (or other convex optimizations)
- Checking the sign of an arbitrary function is hard.
- Easier for polynomial functions.
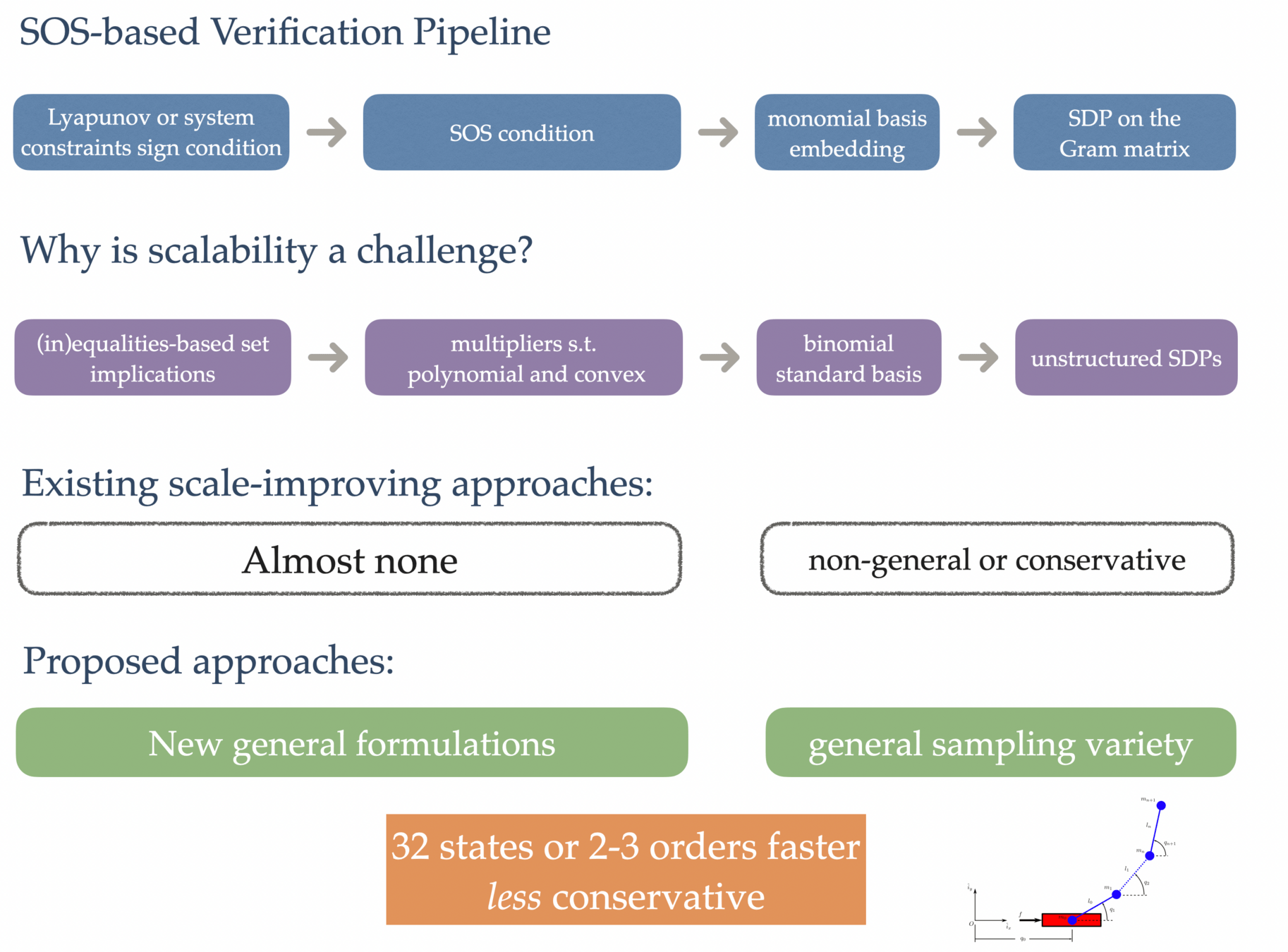
[Shen and Tedrake, "Sampling Quotient-Ring Sum-of-Squares Verification for Scalable Verification", CDC, 2020
Robots are dancing and starting to do parkour, but...
what about something more useful, like loading the dishwasher?


The Machine Learning Revolution
(for robotics; in a few slides)
What's my rule?
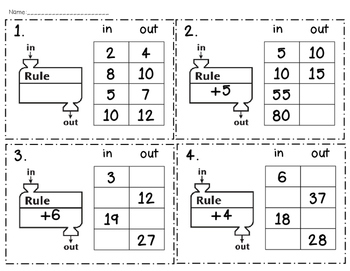
What's my rule?
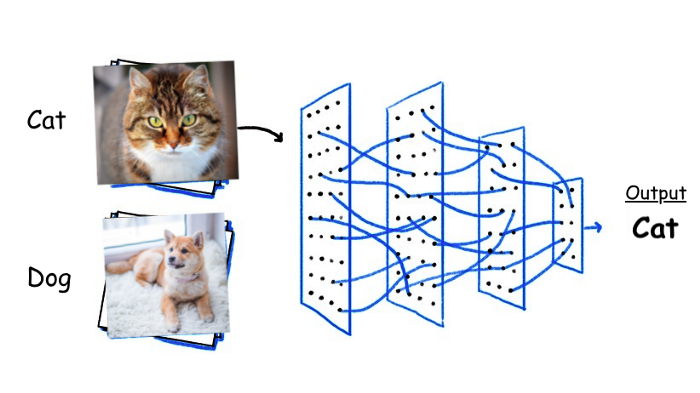
Input
Neural Network


ImageNet: 14 Million labeled images
Released in 2009
layer
linear combo
activations
layer
input
neuron
learnable weights
hidden
output
compositions of ReLU(s) can be quite expressive


in fact, asymptotically, can approximate any function!
[image credit: Phillip Isola]
Training data
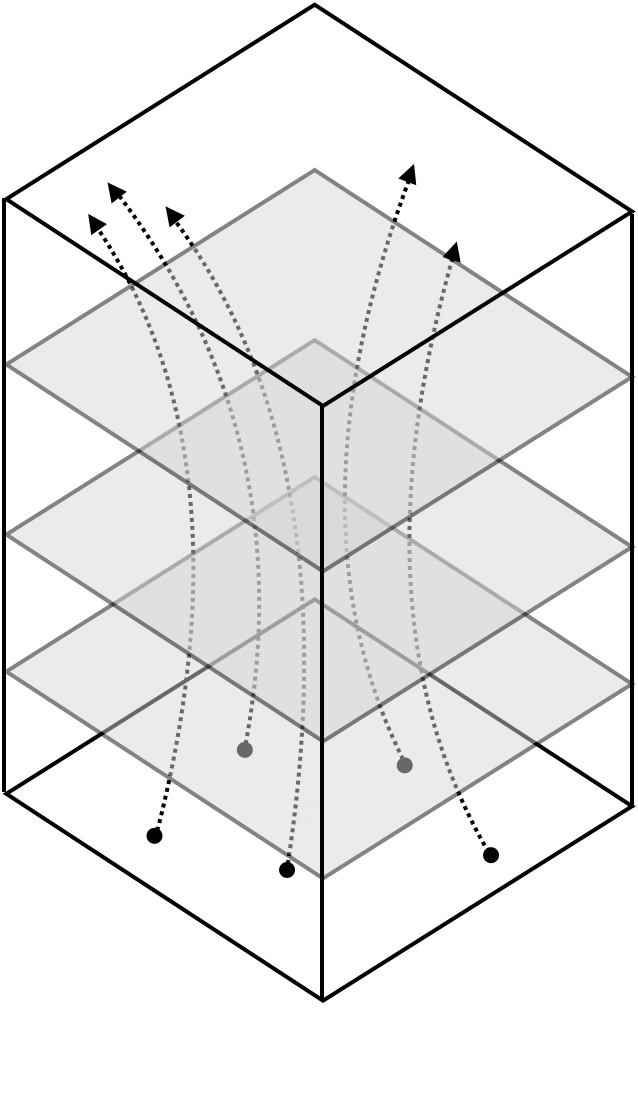
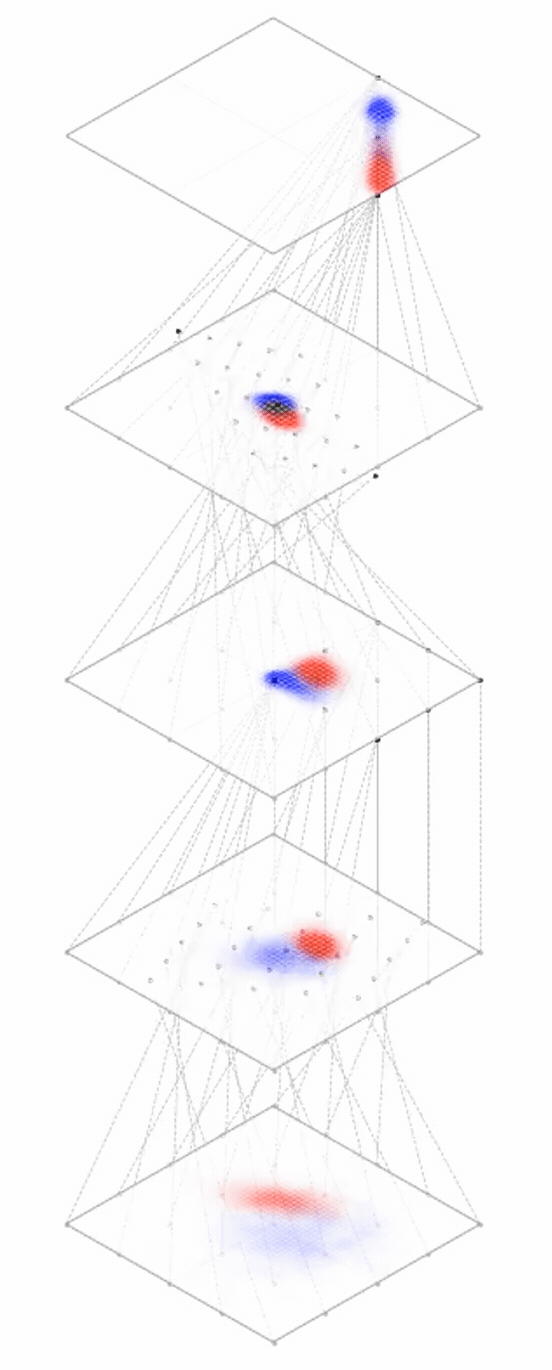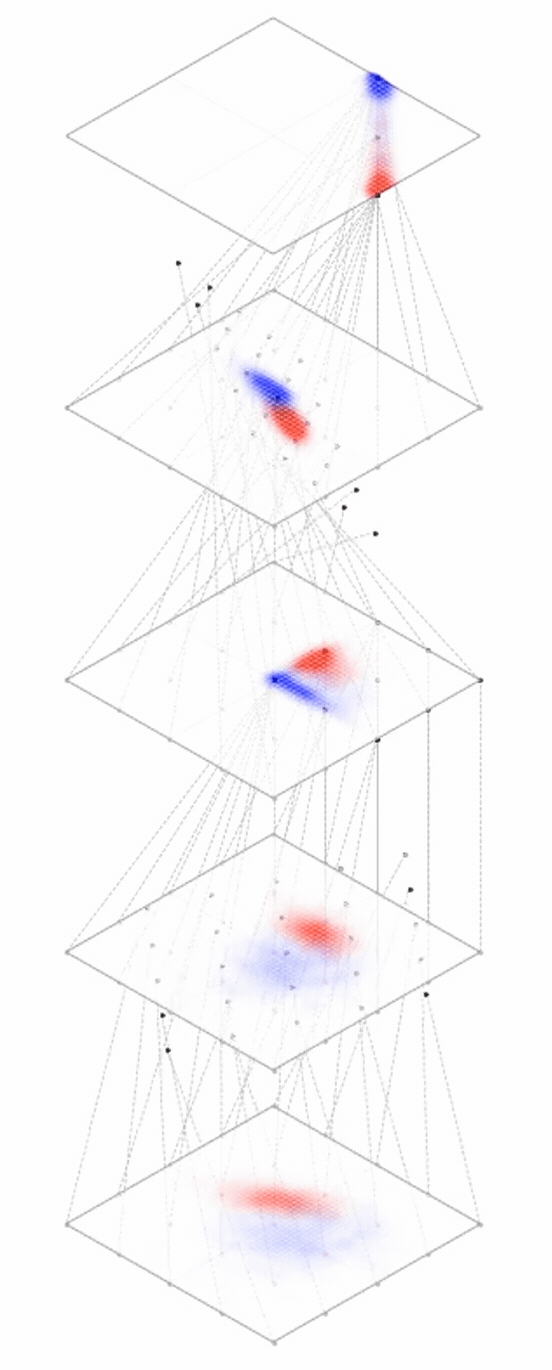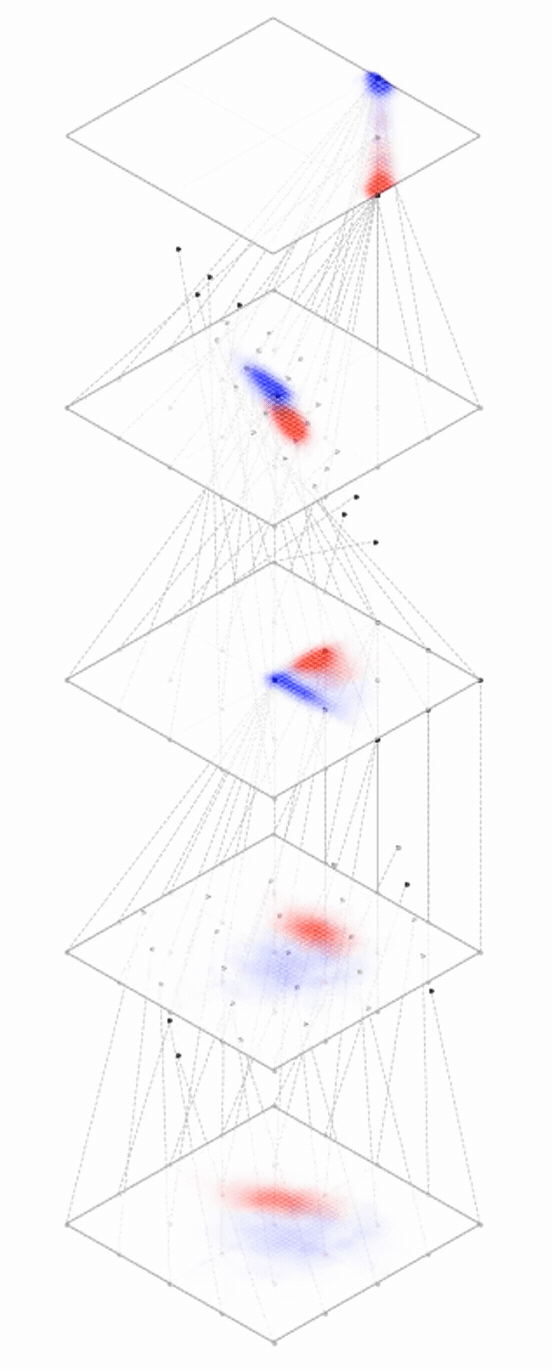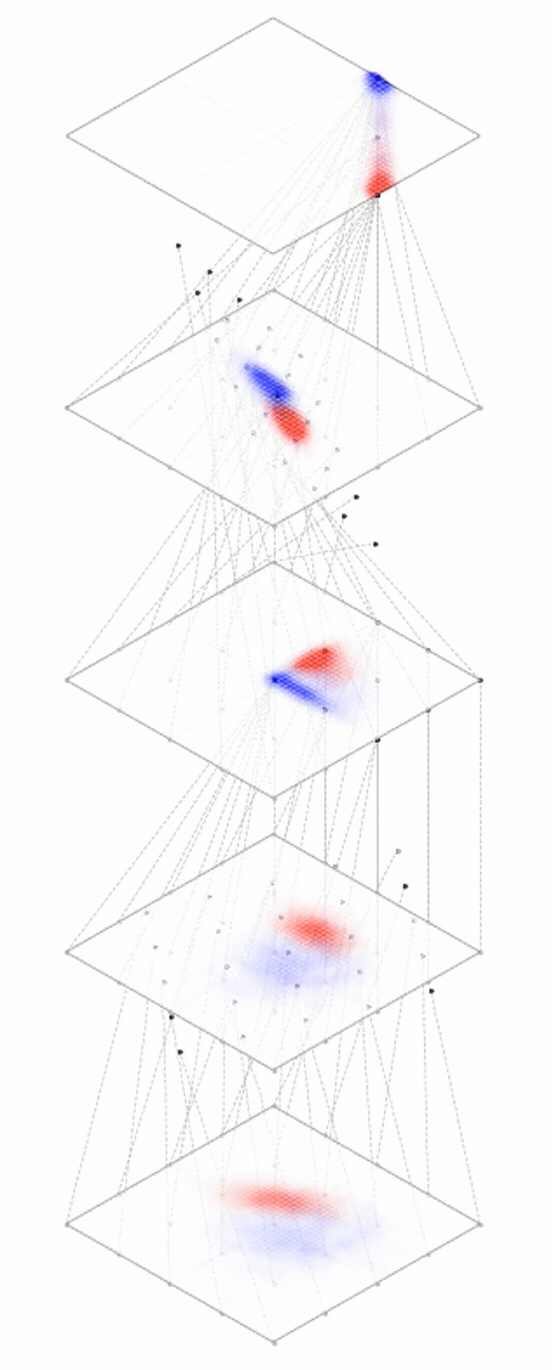


maps from complex data space to simple embedding space
[images credit: visionbook.mit.edu]
[video edited from 3b1b]
embedding

Large Language Models (LLMs) are trained in a self-supervised way

- Scrape the internet for unlabeled plain texts.
- Cook up “labels” (prediction targets) from the unlabeled texts.
- Convert “unsupervised” problem into “supervised” setup.
"To date, the cleverest thinker of all time was Issac. "
feature
label
To date, the
cleverest
To date, the cleverest
thinker
To date, the cleverest thinker
was
To date, the cleverest thinker of all time was
Issac
e.g., train to predict the next-word
Auto-regressive
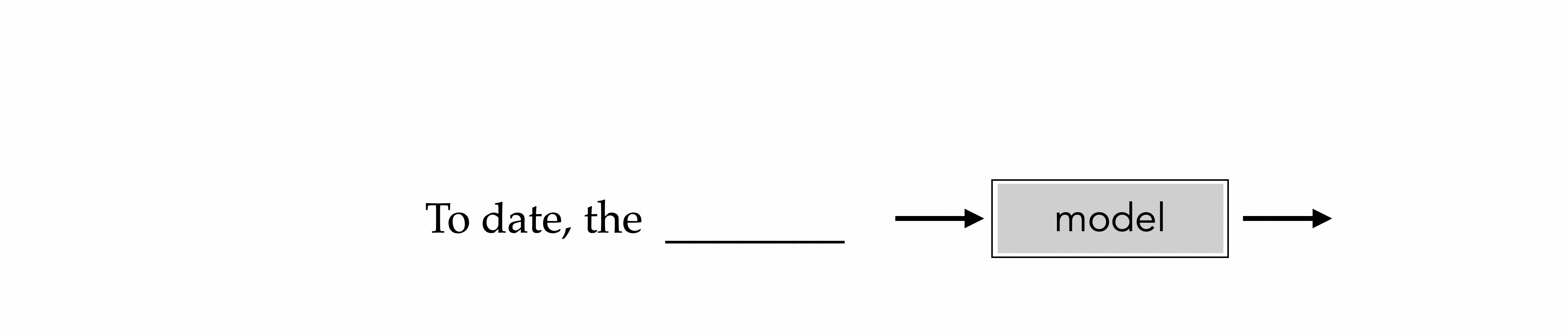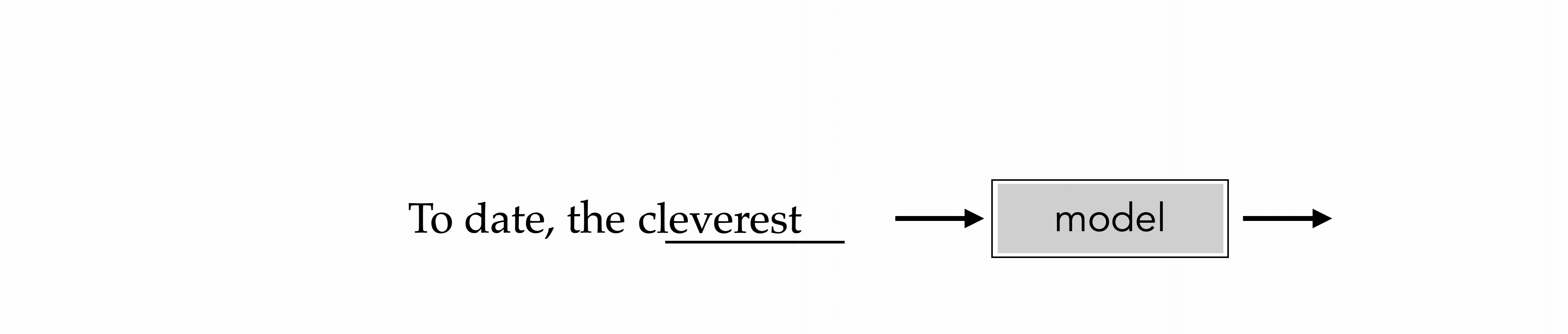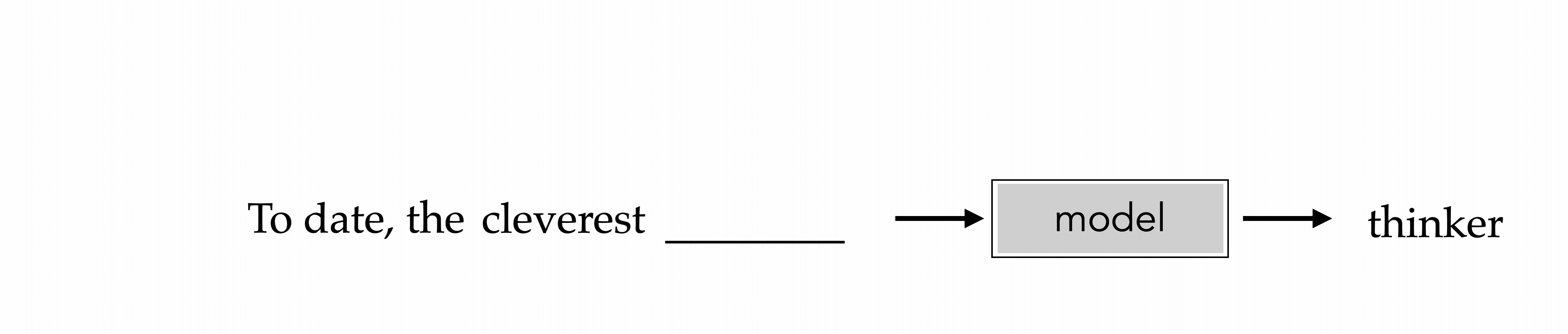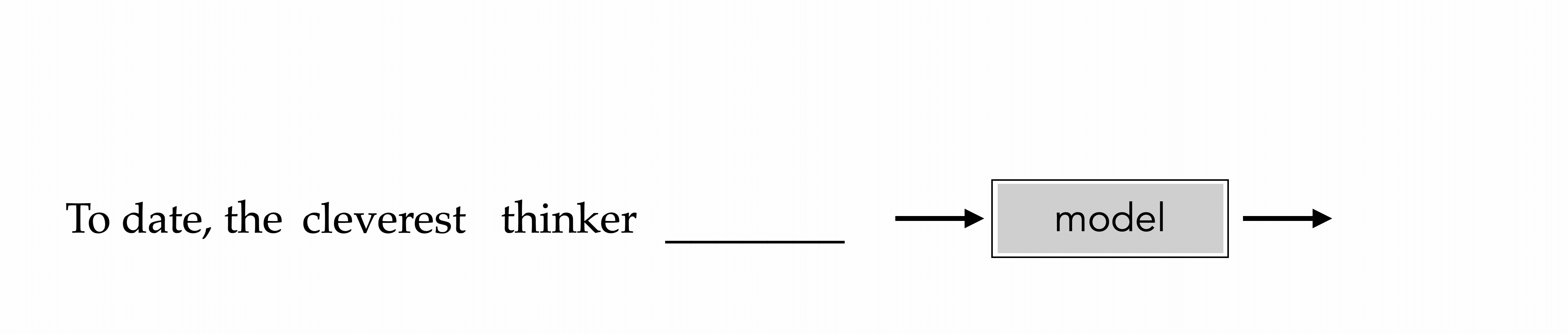
How to train? The same recipe:
- model has some learnable weights
- multi-class classification
[video edited from 3b1b]
[video edited from 3b1b]
[video edited from 3b1b]
[image edited from 3b1b]
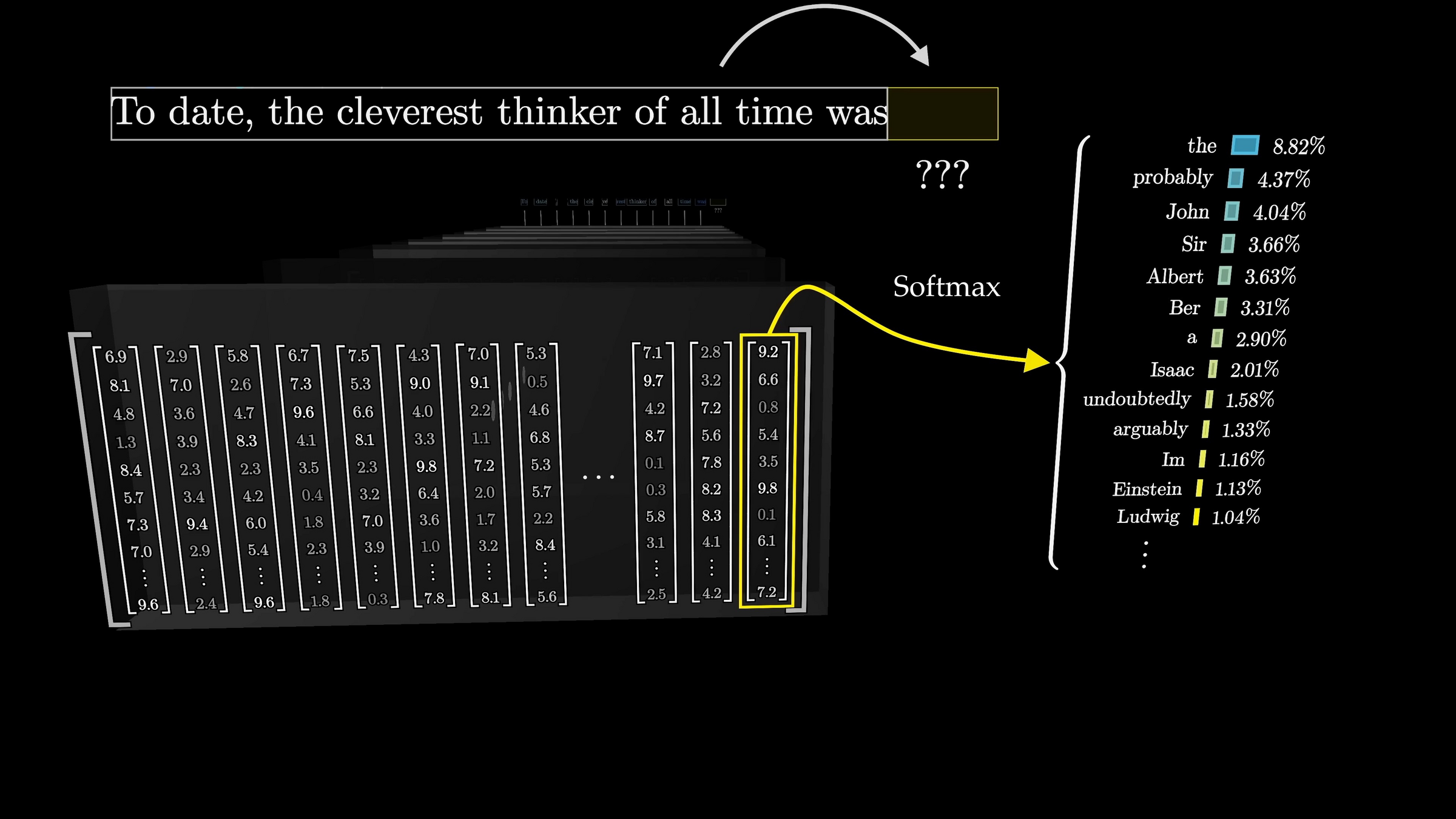
Cross-entropy loss encourages the internal weights update so as to make this probability higher
image credit: Nicholas Pfaff

Generative Boba by Boyuan Chen in Bldg 45
😉
😉
Image credit: Adding Conditional Control to Text-to-Image Diffusion Models https://arxiv.org/pdf/2302.05543
ControlNet: refined control

Text-to-audio generation
"Diffusion" models


Key Idea: denoising in many small steps is easier than attempting to remove all noise in a single step
1. Forward Process
- Encoder is a fixed noising procedure \( q(x_t \mid x_{t-1}) \) which gradually adds noise to the clean data \( x_0 \), producing gradually noisy latent variables \( x_1, \dots, x_T \).
2. Backward Process
- A learned decoder \( p_\theta(x_{t-1} \mid x_t) \) aims to reverse the forward process, and reconstruct step by step moving from \( x_T \) back to \( x_0 \).
- During training, we optimize \( \theta \) so each reverse step approximates the true posterior \( q(x_{t-1} \mid x_t) \).
- At inference time, we start from pure noise \( x_T \sim \mathcal{N}(0, I) \) and apply this backward chain to generate samples.

Forward process is easy: for fixed \( \{\beta_t\}_{t \in [T]} \in (0, 1) \), let \[ q(x_t \mid x_{t-1}) := \mathcal{N}(x_t \mid \sqrt{1 - \beta_t} \, x_{t-1}, \beta_t I) \]
Equivalently, \[ x_t = \sqrt{1 - \beta_t} \, x_{t-1} + \sqrt{\beta_t} \, \epsilon, \quad \epsilon \sim \mathcal{N}(0, I) \]
\[ \Rightarrow \quad x_t = \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon, \quad \epsilon \sim \mathcal{N}(0, I) \]
\(\alpha_t=1-\beta_t, \quad \bar{\alpha}_t=\prod_{s=1}^t \alpha_s\)
can think of \(\sqrt{\beta_t} \approx \sigma_t-\sigma_{t-1}\) noise schedule difference
Fact:
- for small \(\beta, \exists \mu\left(x_0, x_t\right)\), s.t. \(q\left(x_{t-1} \mid x_t\right) \approx \mathcal{N}\left(x_{t-1} ; \mu\left(x_0, x_t\right), \beta_t I\right)\)
- for large \(T, q\left(x_T\right) \approx \mathcal{N}(0,1)\)


Fact:
- for small \(\beta, \exists \mu\left(x_0, x_t\right)\), s.t. \(q\left(x_{t-1} \mid x_t\right) \approx \mathcal{N}\left(x_{t-1} ; \mu\left(x_0, x_t\right), \beta_t I\right)\)
- for large \(T, q\left(x_T\right) \approx \mathcal{N}(0,1)\)
\(q\left(x_{0: T}\right)=q\left(x_0\right) q\left(x_{1: T} \mid x_0\right)\)
\(=q\left(x_T\right) \prod_{t=1}^T q\left(x_{t-1} \mid x_t\right)\)
\(\approx \mathcal{N}(0, I) \prod_{t=1}^T \mathcal{N}\left(x_{t-1} ; \mu\left(x_0, x_t\right), \beta_t I\right)\)
by Markov
by the two facts
Choose to parameterize \(p_\theta\left(x_{t-1} \mid x_t\right)=\mathcal{N}\left(x_{t-1} ; \mu\left(x_0, x_t\right), \beta_t I\right)\), learn \(\hat{x}_0\left(x_t, t\right)\)
Reverse process key:
There are two important variations to this training procedure:
- How noise is added (variance preserving/exploding)
- What quantity to predict (noise, data, …)
Re-parameterize:
\(x_t=x_0+\sigma_t \epsilon, \epsilon \sim \mathcal{N}(0, I)\)
\(x_0=z_0, \quad x_t=z_t / \sqrt{\bar{\alpha}_t}, \quad \sigma_t=\sqrt{\frac{1-\bar{\alpha}_t}{\bar{\alpha}_t}}\)
Re-parameterize variation tends to perform better in practice, keeps model input constant norm

Denoising diffusion models estimate a noise vector \(\epsilon\) \(\in \mathbb{R}^n\) from a given noise level \(\sigma > 0\) and noisy input \(x_\sigma \in \mathbb{R}^n\) such that for some \(x_0\) in the data manifold \(\mathcal{K}\),
\[ {x_\sigma} \;\approx\; \textcolor{green}{x_0} \;+\; \textcolor{orange}{\sigma}\, \textcolor{red}{\epsilon}. \]
- \(x_0\) is sampled from training data
- \(\sigma\) is sampled from training noise schedule (known)
- \(\epsilon\) is sampled from \(\mathcal{N}(0, I_n)\) (i.i.d. Gaussian)
A denoiser \(\textcolor{red}{\epsilon_\theta} : \mathbb{R}^n \times \mathbb{R}_+ \to \mathbb{R}^n\) is learned by minimizing
\[ L(\theta) := \mathbb{E}_{\textcolor{green}{x_0},\textcolor{orange}{\sigma},\textcolor{red}{\epsilon}} \Biggl[\Biggl\|\textcolor{red}{\epsilon_\theta}\Biggl(\textcolor{green}{x_0} + \textcolor{orange}{\sigma}\,\textcolor{red}{\epsilon}, \textcolor{orange}{\sigma}\Biggr) - \textcolor{red}{\epsilon}\Biggr\|^2\Biggr]. \]
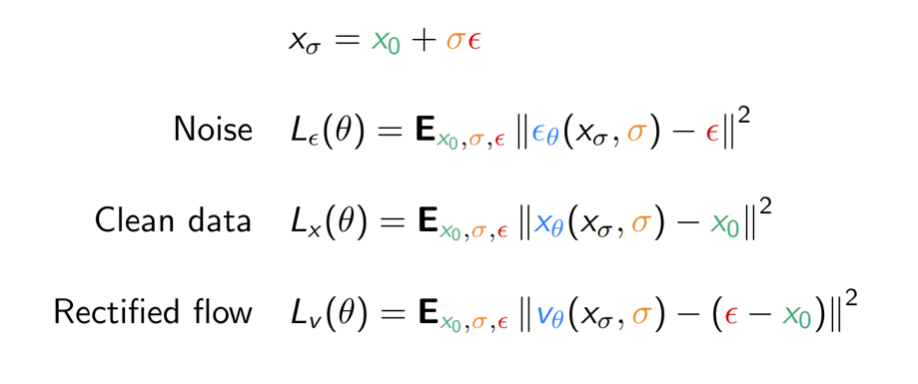
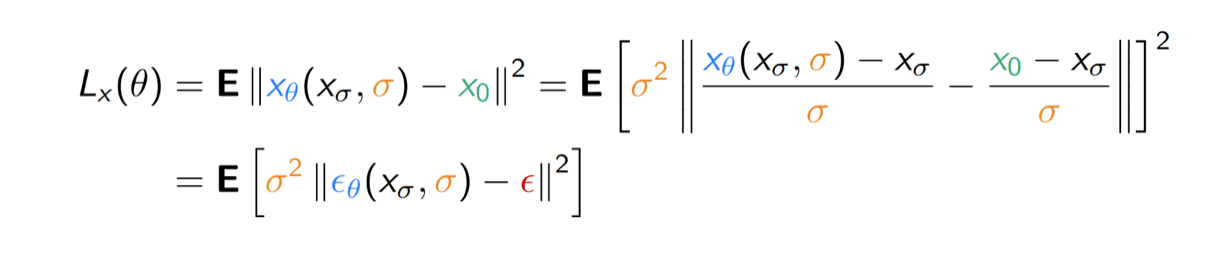
Mathematically equivalent for fixed \(\sigma\), but reweighs loss by a function of \(\sigma\) !
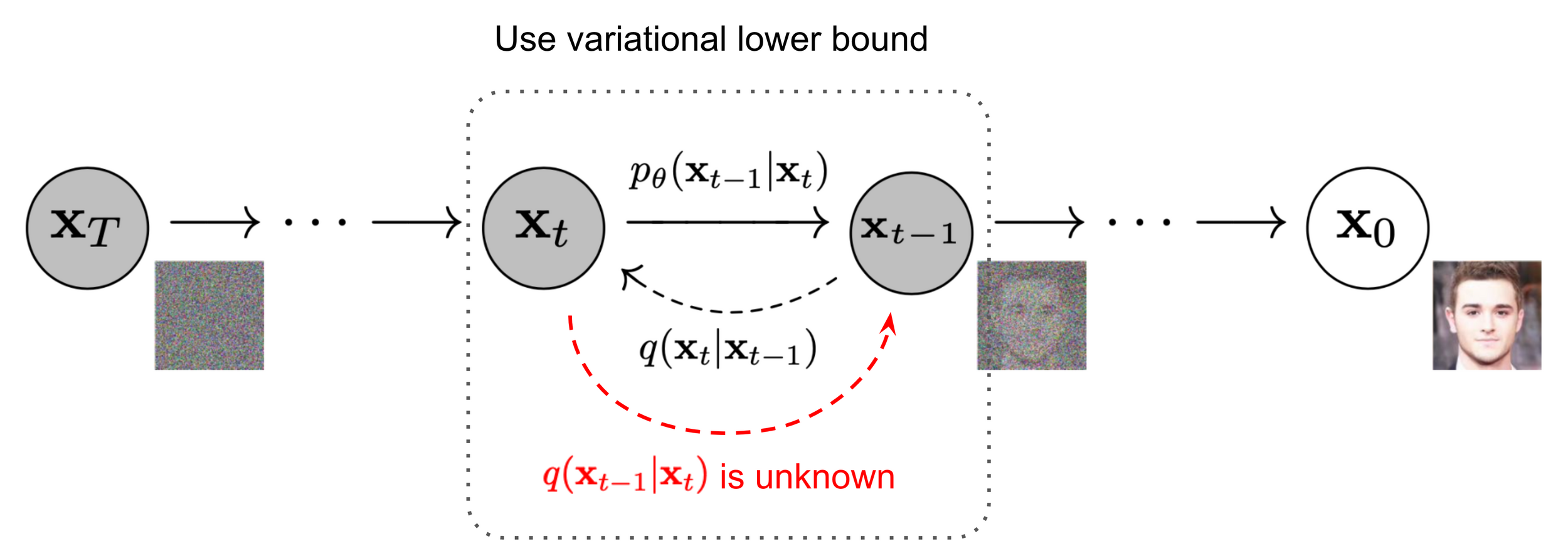
Denoising diffusion models
(for actions)
Image source: Ho et al. 2020
Denoiser can be conditioned on additional inputs, \(u\): \(p_\theta(x_{t-1} | x_t, u) \)
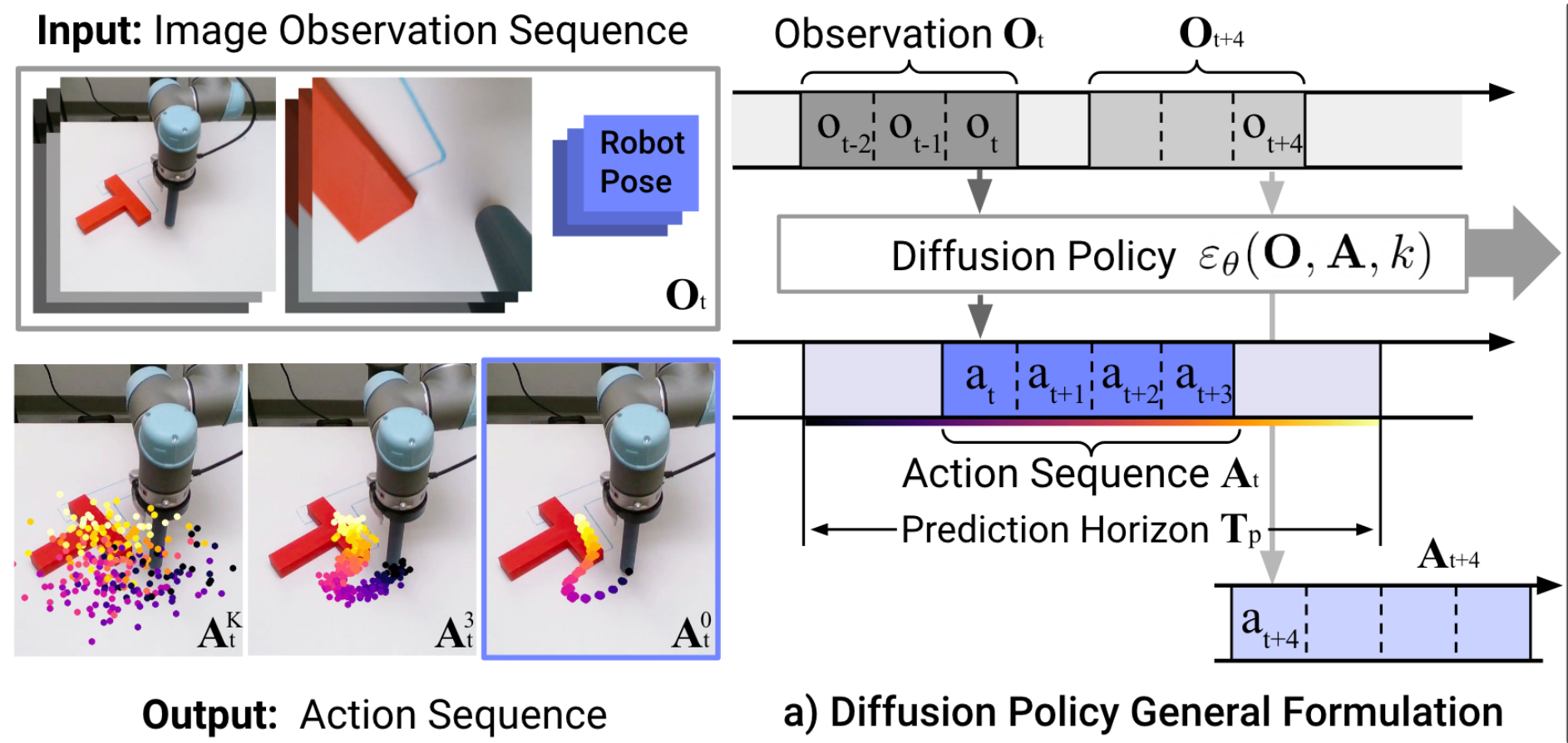
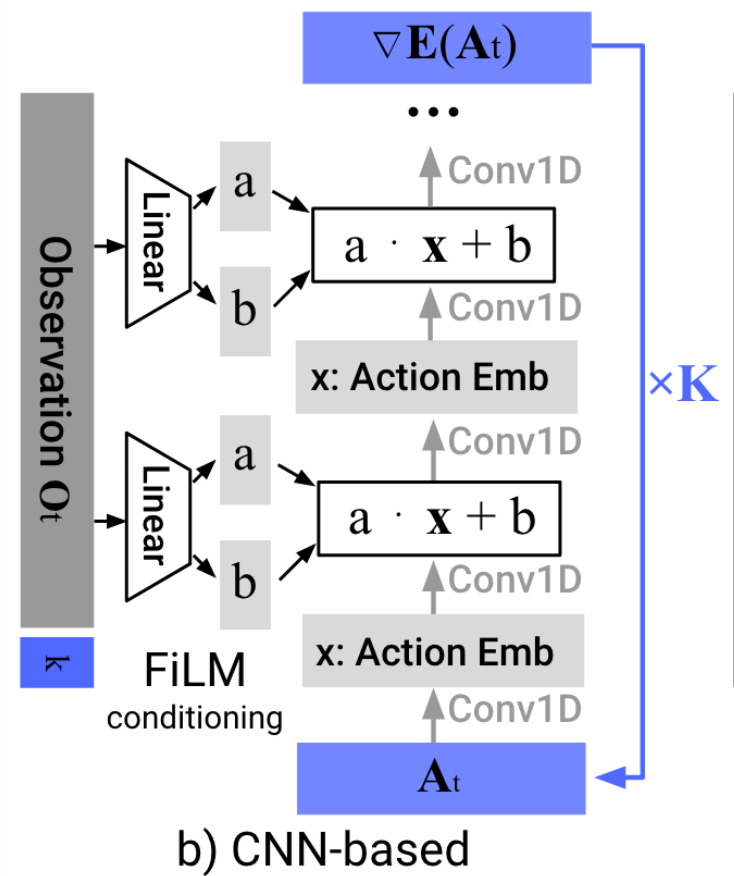
Image backbone: ResNet-18 (pretrained on ImageNet)
Total: 110M-150M Parameters
Training Time: 3-6 GPU Days ($150-$300)
LLMs for robotics
- Given a fixed list of options, can evaluate likelihood with LM
- Given all vocabularies, can sample with likelihood to generate
Ingredient 1
- Bind each executable skill to some text options
- Have a list of text options for LM to choose from
- Given instruction, choose the most likely one

Few-shot prompting of Large Language Models

LLMs can copy the logic and extrapolate it!
Prompt Large Language Models to do structured planning

LLMs for robotics
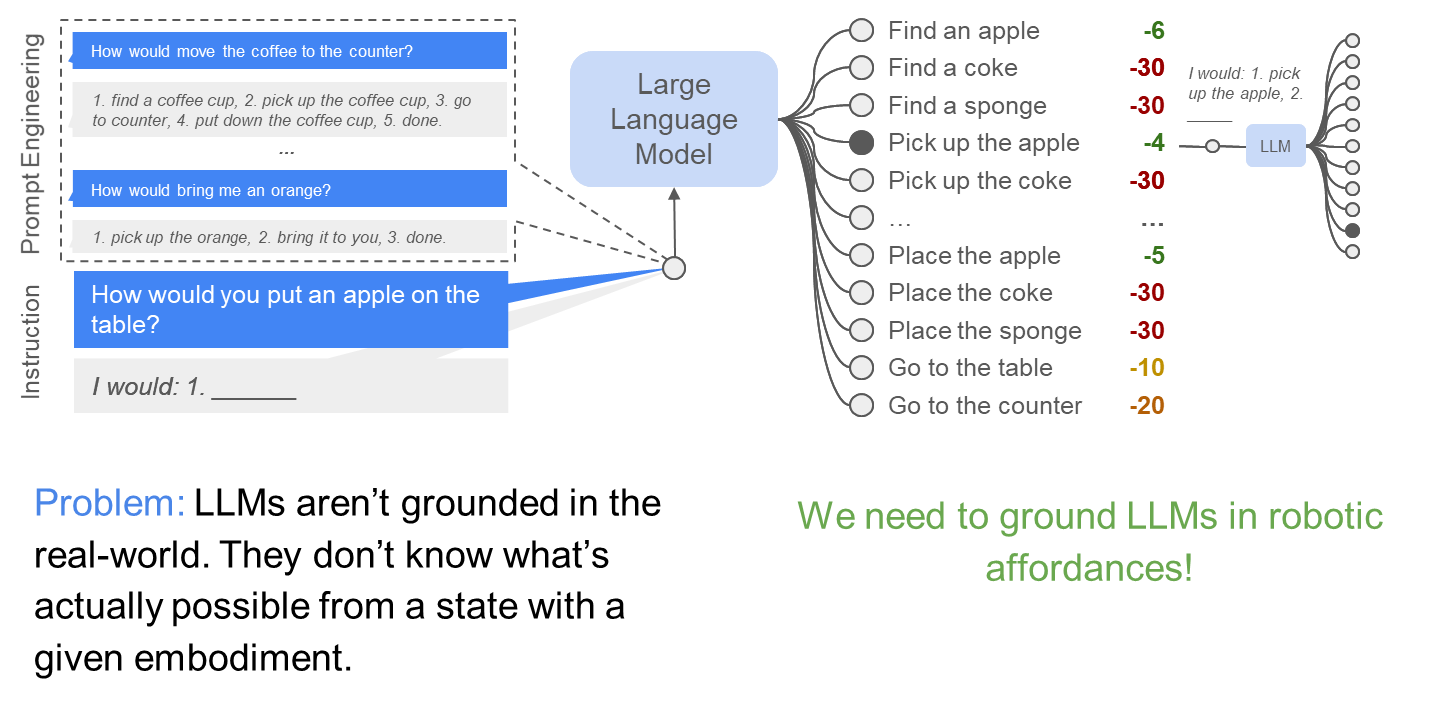
Do As I Can, Not As I Say: Grounding Language in Robotic Affordances, Ahn et al. , 2022
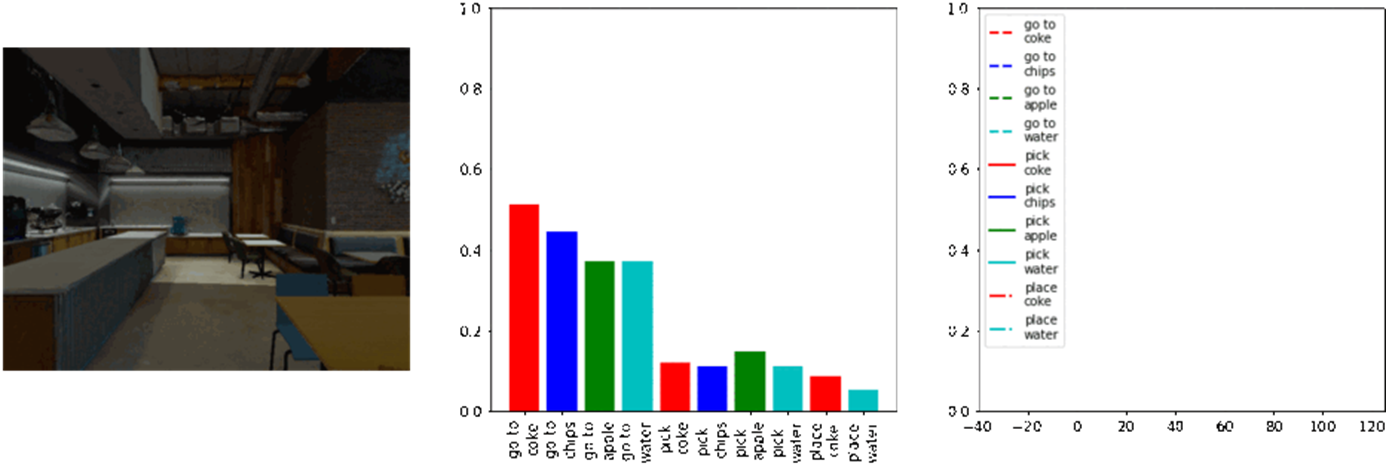
What task-based affordances reminds us of in MDP/RL?
Value functions!
[Value Function Spaces, Shah, Xu, Lu, Xiao, Toshev, Levine, Ichter, ICLR 2022]
Robotic affordances
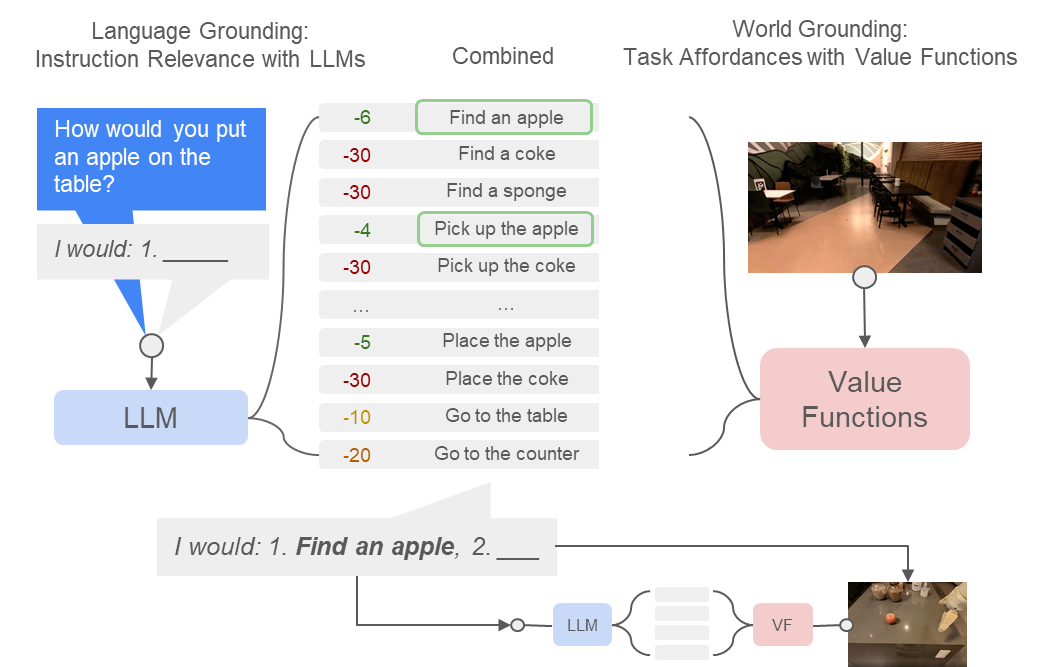
Do As I Can, Not As I Say: Grounding Language in Robotic Affordances, Ahn et al. , 2022


- Language Models as Zero-Shot Planners:
Extracting Actionable Knowledge for Embodied Agents - Inner Monologue: Embodied Reasoning through Planning with Language Models
- PaLM-E: An Embodied Multimodal Language Model
- Chain-of-thought prompting elicits reasoning in large language models
- Tree of Thoughts: Deliberate Problem Solving with Large Language Models
Extended readings in
LLM + Planning
Scaling Up
Haptic Teleop Interface
Excellent robot control
Towards grounding everything in language
Language
Control
Vision
Tactile
Socratic Models: Composing Zero-Shot Multimodal Reasoning with Language
https://socraticmodels.github.io
Lots of data
Less data
Less data

Roboticist
Vision
NLP
adapted from Tomás Lozano-Pérez
Why video
- Video is how human perceive the world (physics, 3D)
- Video is widely available on internet
- Internet videos contain human actions and tutorials
- Pre-train on entire youtube, first image + text -> video
- Finetune on some robot video
- Inference time, given observation image + text prompt -> video of robot doing the task -> back out actions
Video Prediction for Robots
Learning Universal Policies via Text-Guided Video Generation, Du et al. 2023

Video + Language
Video Language Planning, Du et al. 2023
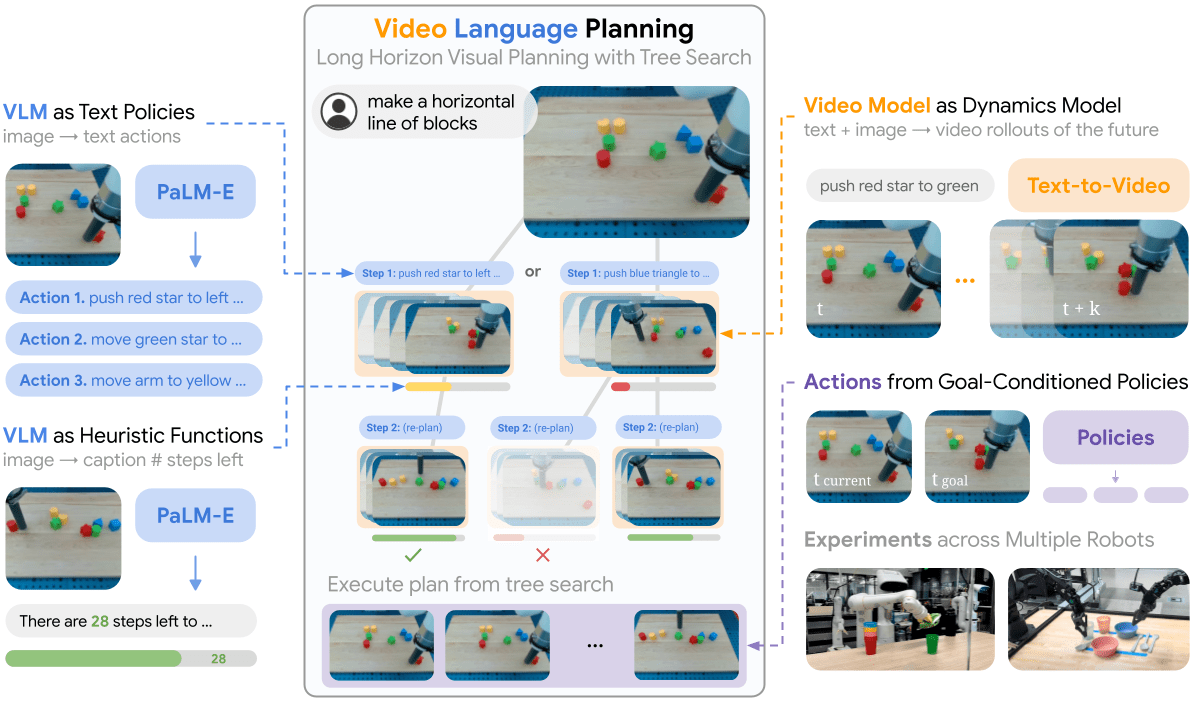
Video + Language
Video Language Planning, Du et al. 2023
Instruction: Make a Line
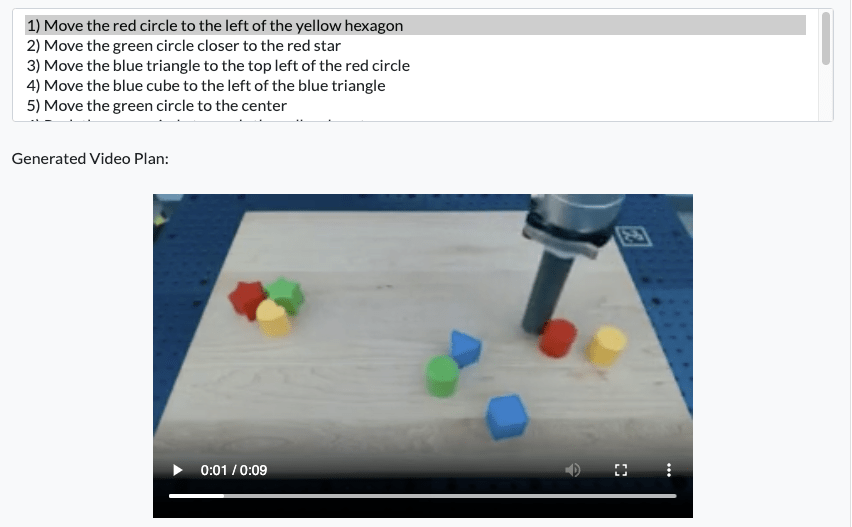
Video + RL
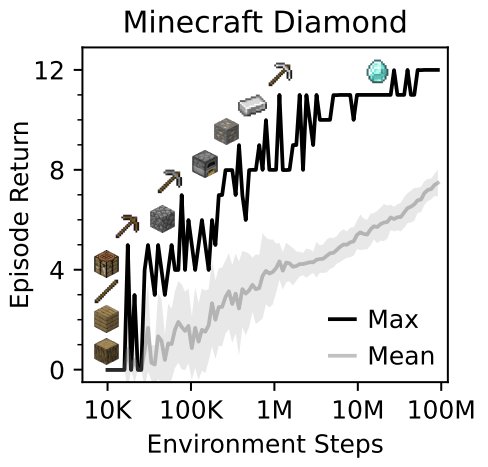
Mastering Diverse Domains through World Models, Hafner et al. 2023
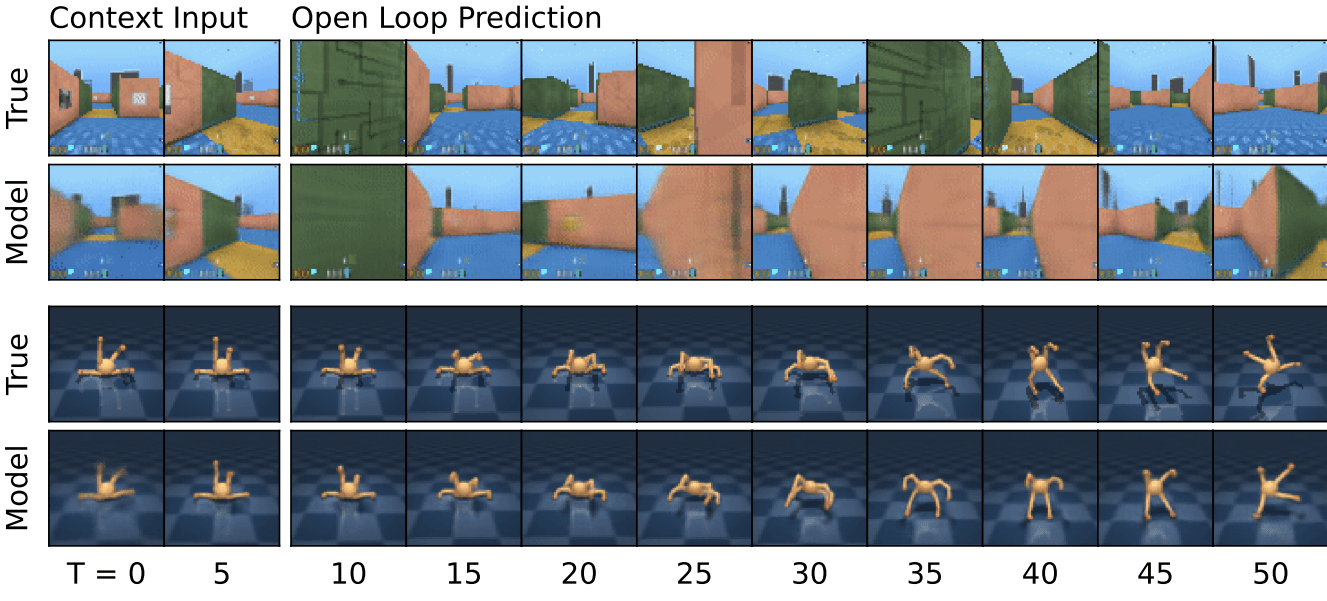
Do you love robotics?
What can you do right now?
- Programming => Software engineering
- Physics
- Math (it's extremely important!)
- Calculus
- Linear Algebra (the foundations of machine learning)
- Probability!
- Machine learning tutorials online are becoming very accessible
- Robotics club!
Online resources (notes, slides, demos)
https://introml.mit.edu/notes
https://slides.com/shensquared
Online resources (notes, slides, demos)
https://introml.mit.edu/notes
https://slides.com/shensquared
Online classes (video, notes, demo)
http://manipulation.mit.edu
http://underactuated.mit.edu
What do I do?
- Teaching (right now, mostly machine learning classes)
- Research (educational tech, optimization, control, robotics)
- Service (writing recommendation letters, reviewing papers, committee...)
- Hacking/coding for fun
What do I typically use genAI for?
- Documentation!
- Boilerplate code!
- Learning new programming languages -- syntax
- Writing scripts -- conjuring/hallucinating contrived story arc
- Brainstorming hack/project ideas
Robotics and Generative AI
By Shen Shen
Robotics and Generative AI
MIT Math Undergraduate Association Talk Series
- 341



