Uniform priors are not as uninformative as you might think
a
b
\(x\)
\(f_X(x)\)
Conditional Probability
\mathrm{P}(B \mid A) = \frac{\mathrm{P}(A \cap B)}{\mathrm{P}(A)}
Probability of observing \(B\) given \(A\) has been observed.
\(A\)
\(\bar{A}\)
\(\mathrm{P}(A)\)
\(\mathrm{P}(\bar{A})\)
\(\mathrm{P}(B\mid A)\)
\(\mathrm{P}(\bar{B}\mid A)\)
\(\mathrm{P}(B\mid \bar{A})\)
\(A \cap \bar{B}\)
\(A \cap B\)
\(\bar{A} \cap \bar{B}\)
\(\bar{A} \cap B\)
\(\mathrm{P}(\bar{B}\mid A)\)
\mathrm{P}(A \cap B) = \mathrm{P}(A) \cdot \mathrm{P}(B \mid A)
Bayes' Theorem
\mathrm{P}(B \mid A) = \frac{\mathrm{P}(A \cap B)}{\mathrm{P}(A)}
\mathrm{P}(A \mid B) = \frac{\mathrm{P}(A \cap B)}{\mathrm{P}(B)}
or
\mathrm{P}(B \mid A) = \frac{\mathrm{P}(B) \cdot \mathrm{P}(A \mid B)}{\mathrm{P}(A)}
Probability of observing \(B\) given \(A\) has been observed, in terms of the probability of observing \(A\) if \(B\) is observed.
Bayesian Inference
Probability as a measure of "degree of belief".
\mathrm{P}(\mathrm{Hypothesis}\mid\mathrm{Data}) = \frac{\mathrm{P}(\mathrm{Hypothesis}) \cdot \mathrm{P}(\mathrm{Data} \mid \mathrm{Hypothesis})}{\mathrm{P}(\mathrm{Data})}
\mathrm{posterior} = \frac{\mathrm{prior} \times \mathrm{likelihood}}{\mathrm{normalising\; constant}} \propto \mathrm{prior} \times \mathrm{likelihood}
p(\theta \mid y) \propto p(\theta) \times p(y\mid \theta)
Example 1
Y \sim \mathcal{N}(\mu,.)
\mu \sim \mathcal{N}(0, 2^2)
\begin{align*}
\bar{y} &= 3 \\
s &= 4 \\
n &= 10
\end{align*}
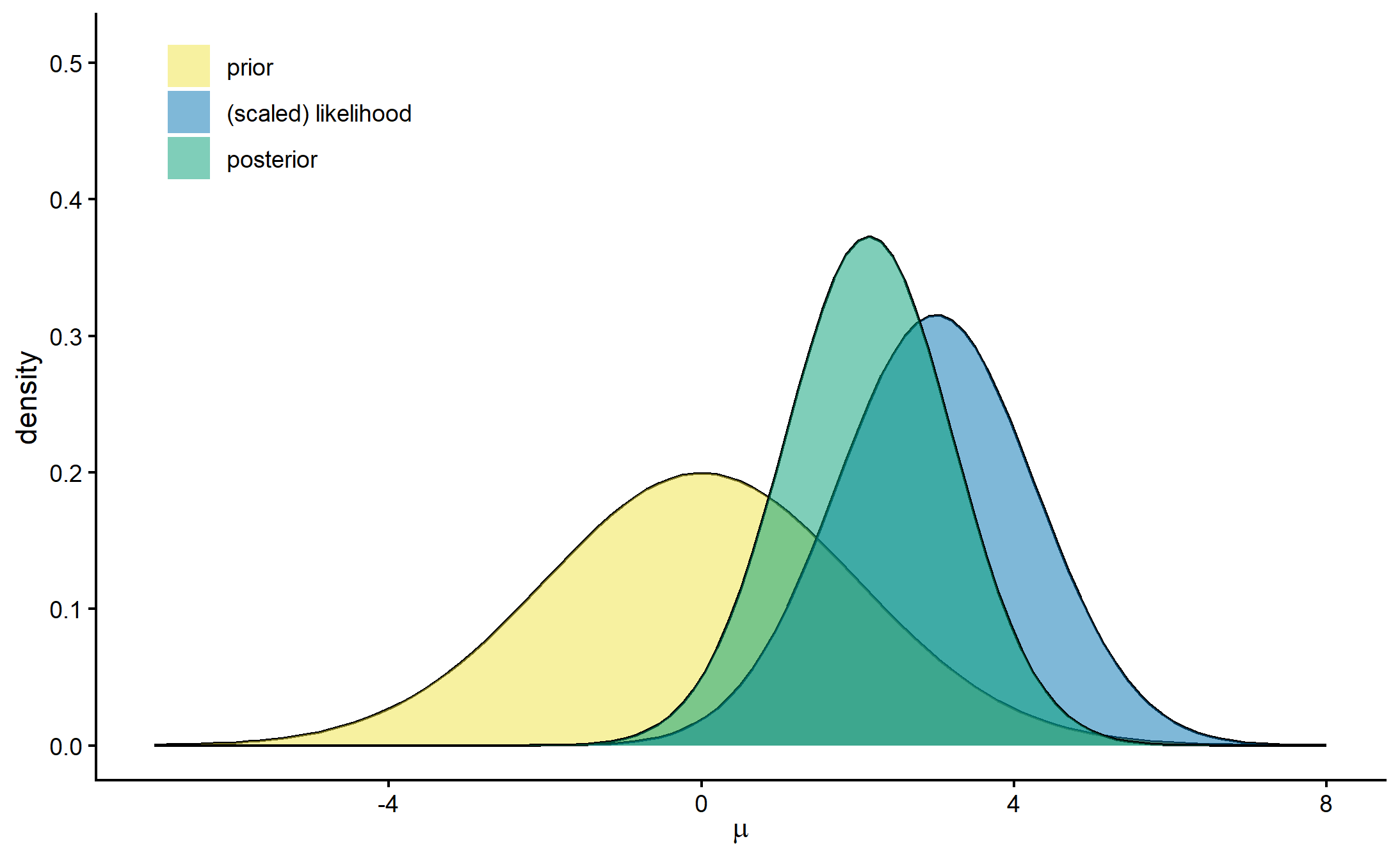
Likelihood
Prior
Observed data
Example 2
Y \sim \mathcal{N}(\mu,.)
\mu \sim \mathcal{N}(0, 1^2)
\begin{align*}
\bar{y} &= 3 \\
s &= 4 \\
n &= 10
\end{align*}
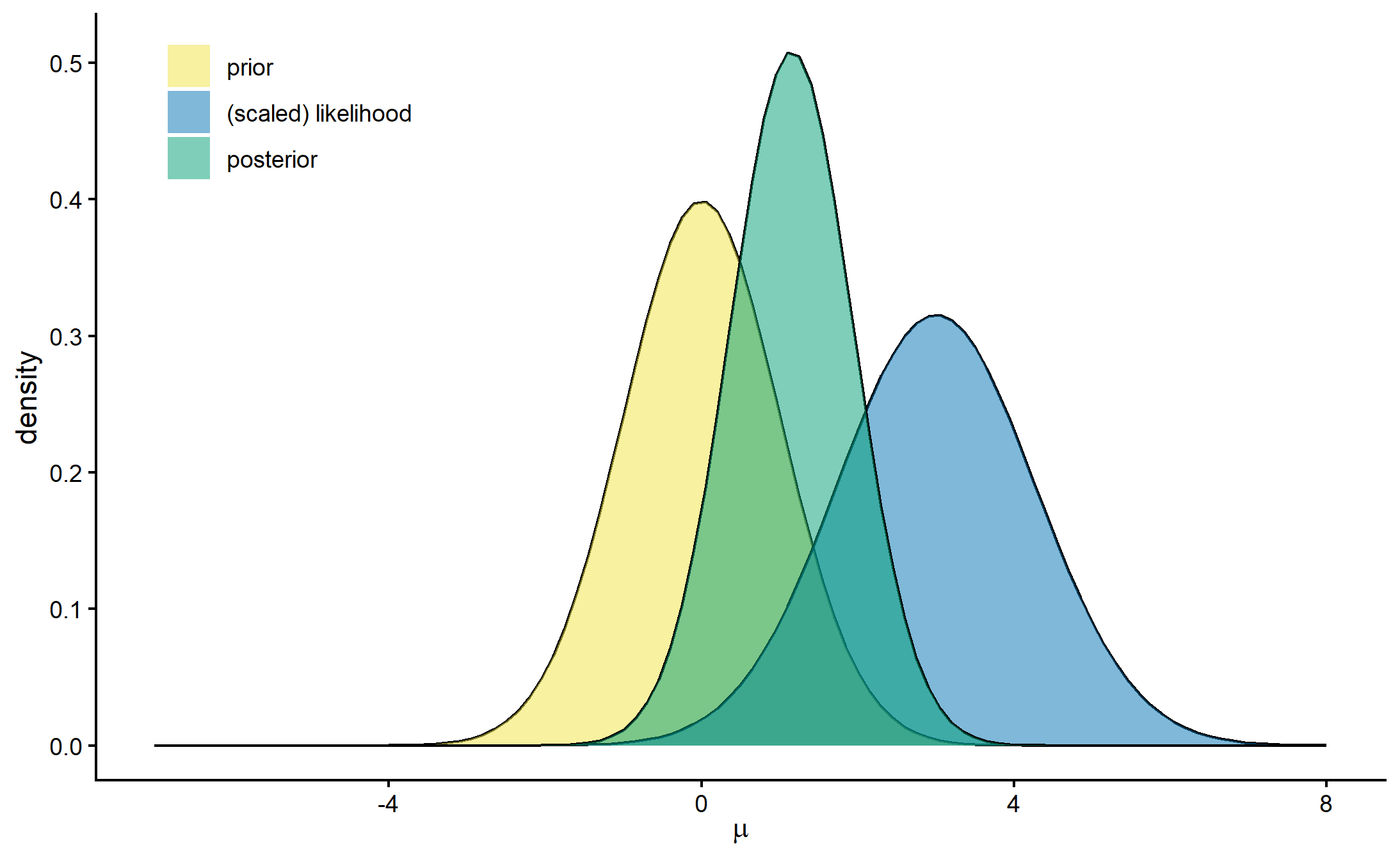
Likelihood
Prior
Observed data
The Prior Distribution
- The distribution of the parameter of interest before any data is observed.
- Can have a strong impact on the posterior estimate.
- Informative prior reflects having particular knowledge or information about the unknown parameter, e.g., typical range.
- Vague or diffuse prior reflects having little or uncertain information about the unknown parameter.
"Flat" Priors
A flat prior encodes the belief that all possible values of a parameter (perhaps within a range) are equally plausible.
a
b
\(x\)
\(f_X(x)\)
X \sim \mathrm{Uniform}[a,b]
Change of Coordinates
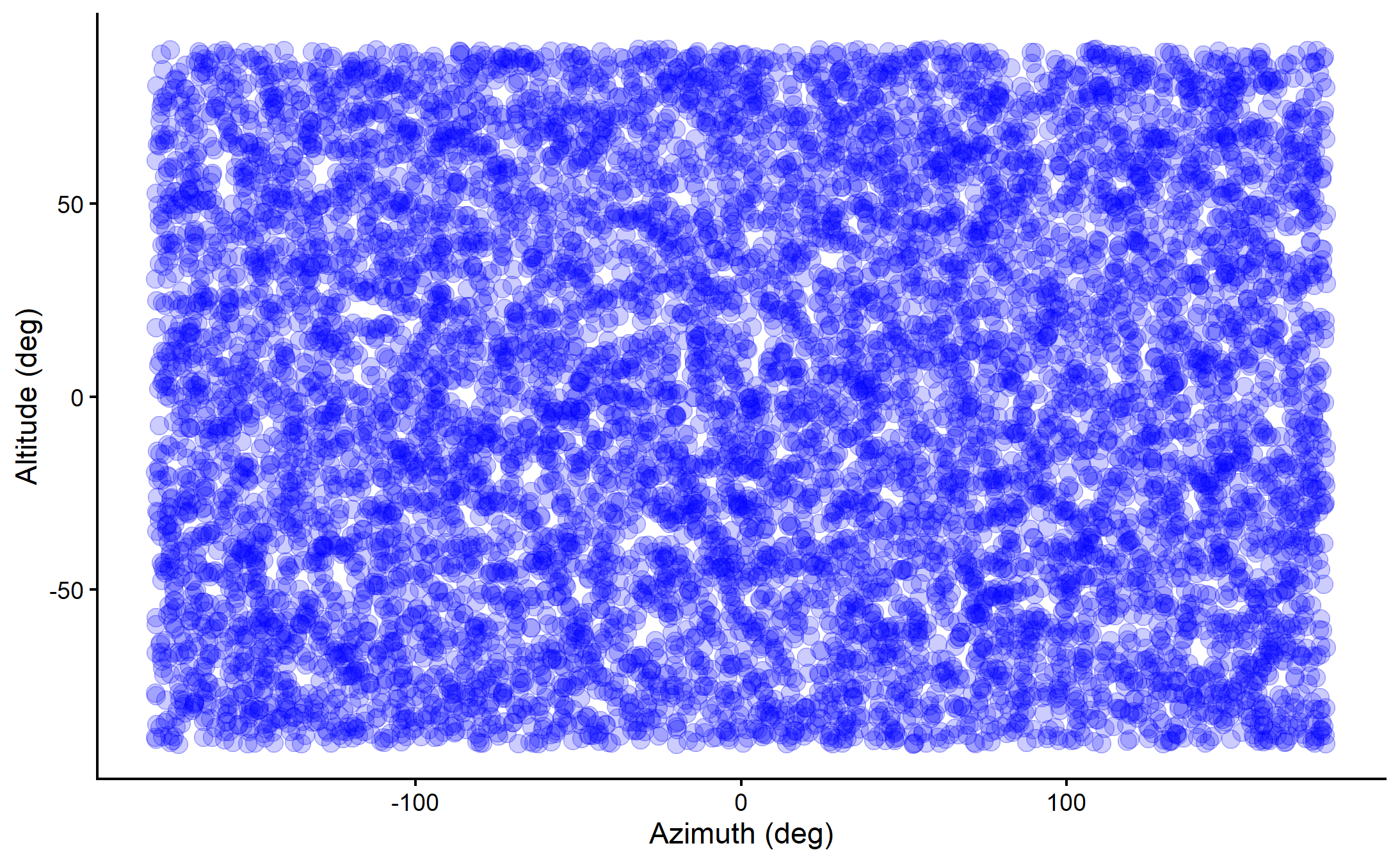
Altitude\(\quad\theta \sim \mathrm{Uniform}[-90^\circ, +90^\circ]\)
Azimuth\(\quad\phi \sim \mathrm{Uniform}[-180^\circ,+180^\circ]\)
Source: Wikimedia
Change of Coordinates
Altitude\(\quad\theta \sim \arccos(u),\quad u \sim \mathrm{Uniform}[-1, +1]\)
Azimuth\(\quad\phi \sim \mathrm{Uniform}[-180^\circ,+180^\circ]\)
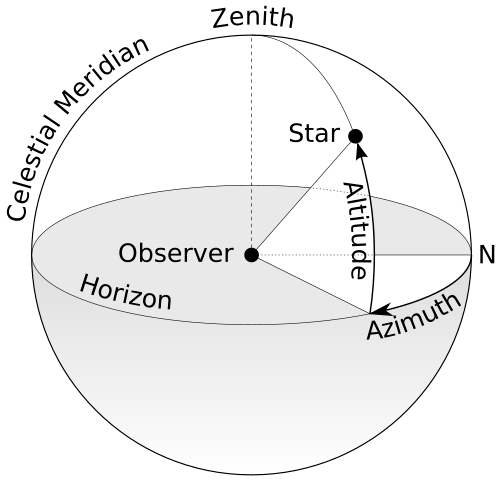
Source: Wikipedia
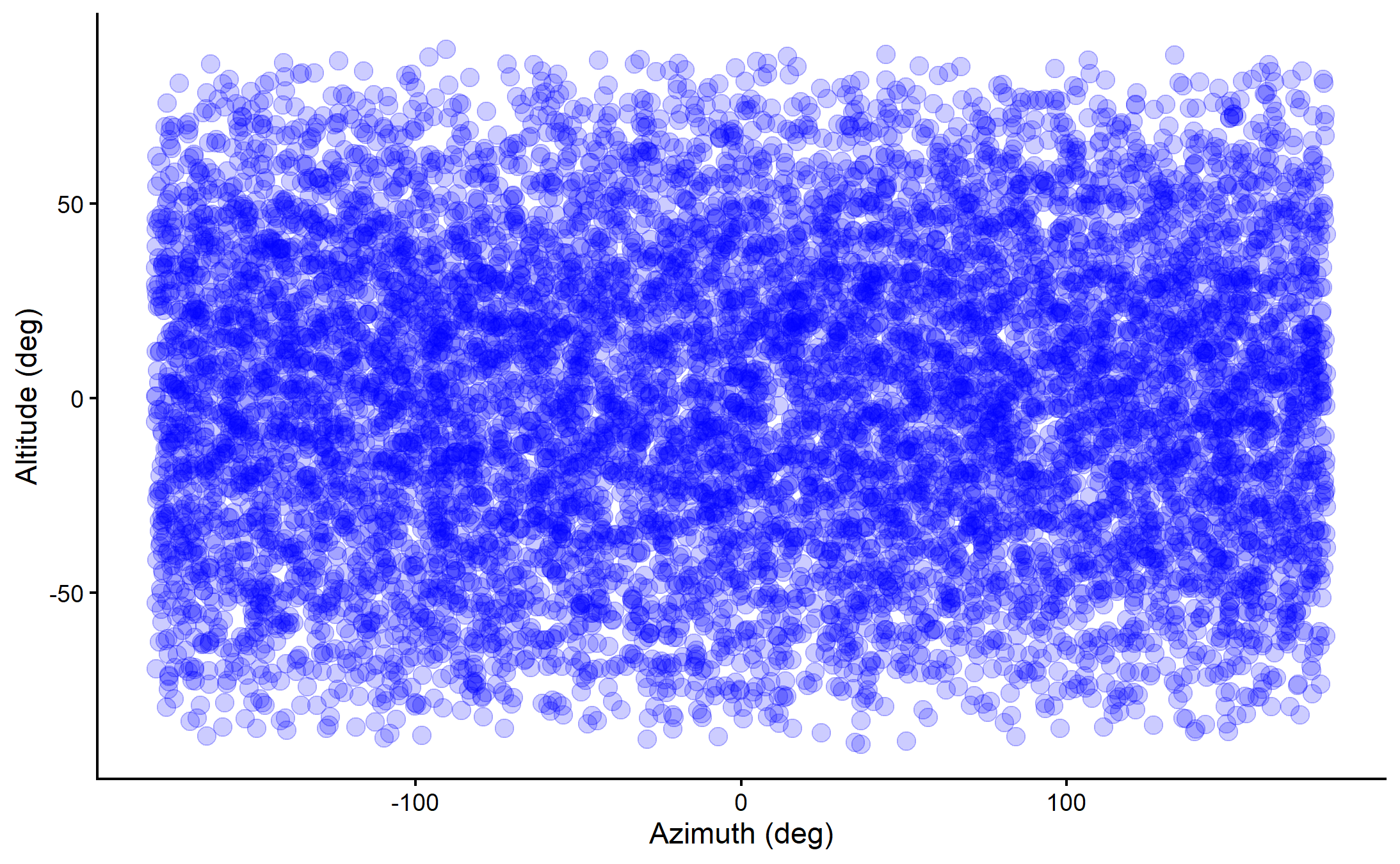
Source: Wikimedia
Hard Bounds
- Hard bounds will completely exclude portions of the parameter space!
- The support of the posterior distribution is inherited from the support of the prior distribution.
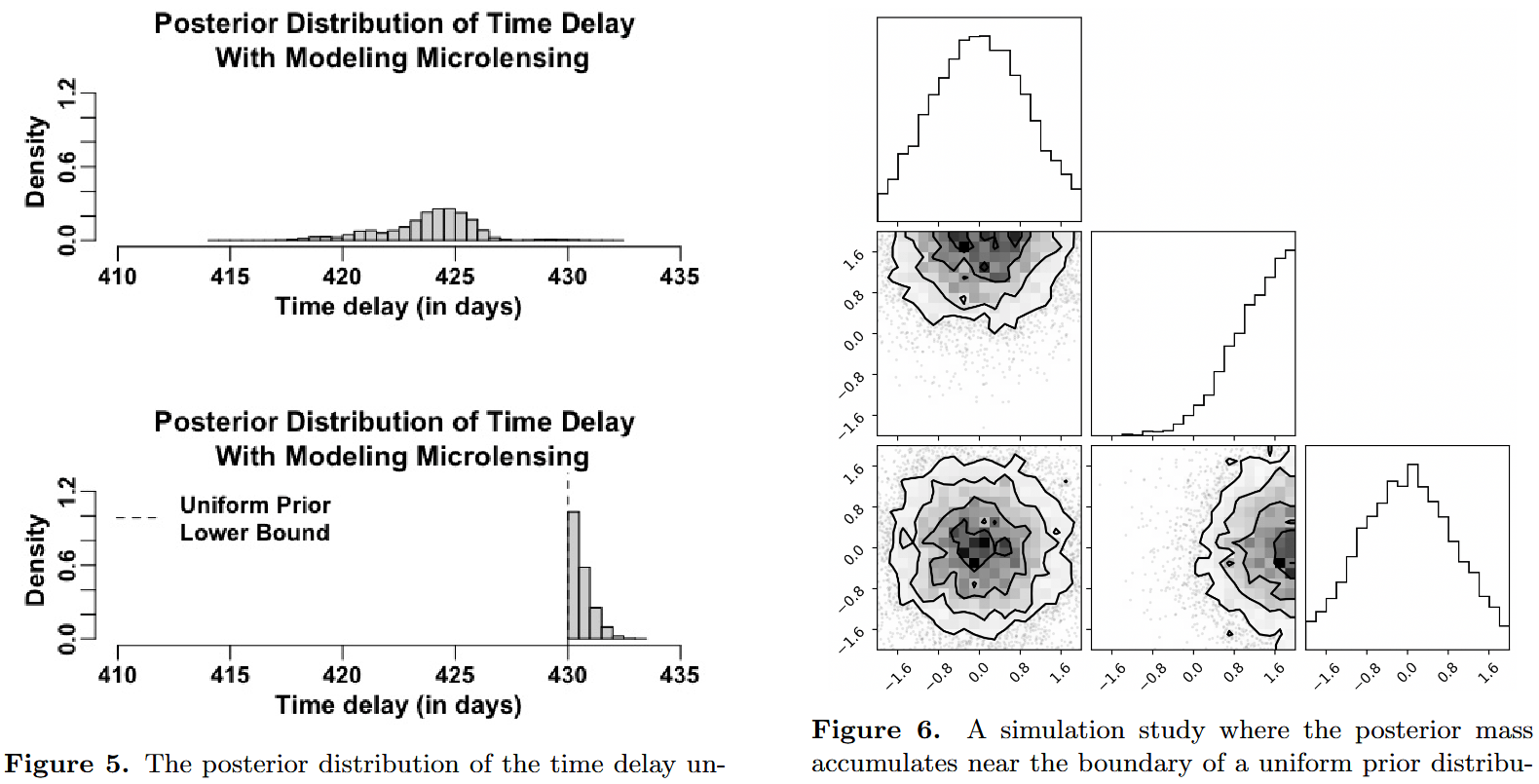
Source: Tak et al. (2024)
Change of Scale
\theta \sim \mathrm{Uniform}[10^{-3}, 10^1]
\log_{10}(\theta) \sim \mathrm{Uniform}[-3, 1]
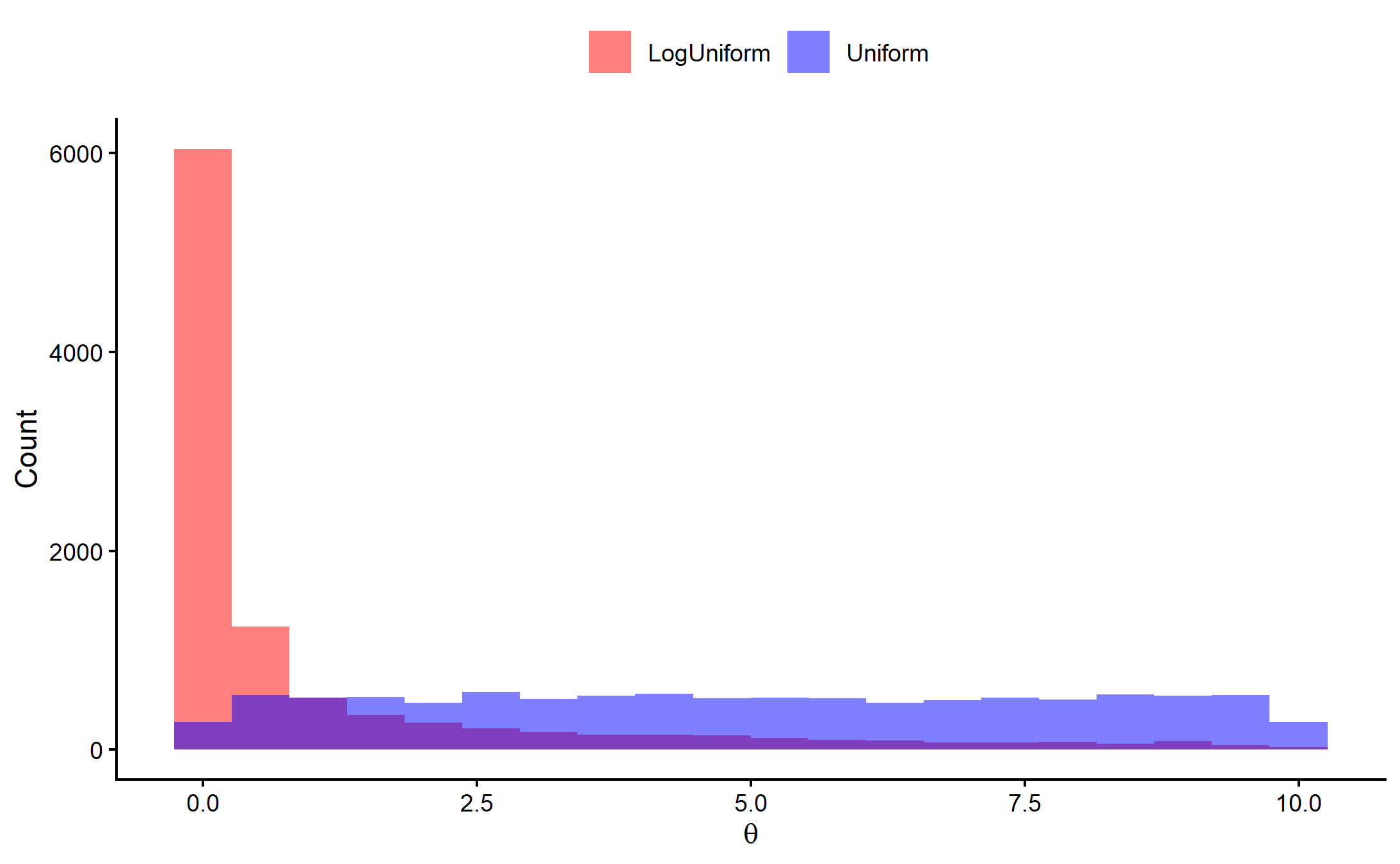
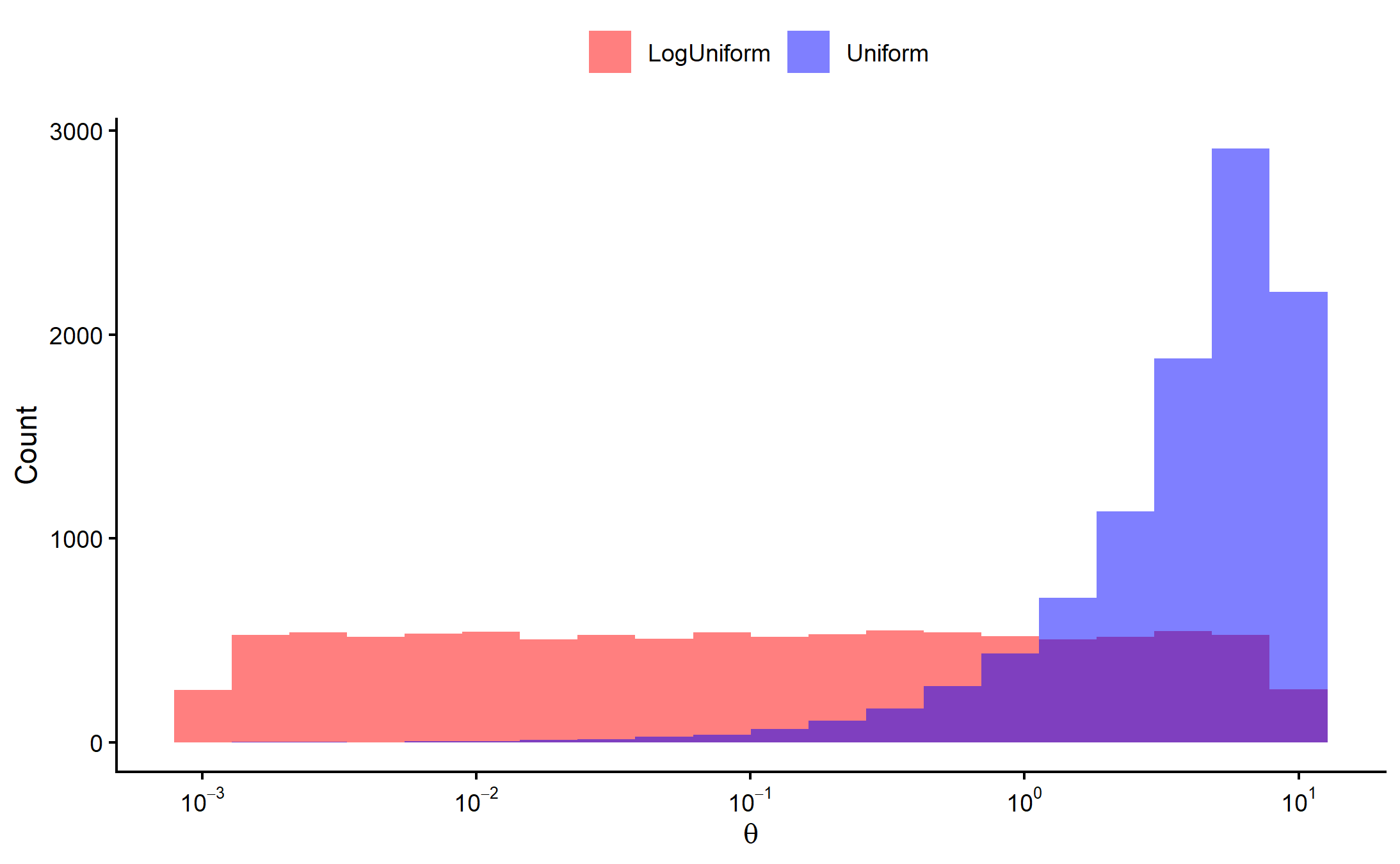
Text
Not the same!
General Advice
- Diagnostics
- Prior predictive checks can reveal if parts of the parameter space are being overlooked.
- Scatter plot matrix of posteriors.
- Remedies
- Apply an appropriate transformation to Uniform variates.
- Avoid hard boundaries, i.e., unbounded distributions with thin tails.
- Try Jeffreys Priors. These are non-informative prior distributions that are invariant under changes of coordinates for the parameter.
References
-
Tak, Hyungsuk, Yang Chen, Vinay L. Kashyap, et al. (2024) “Six Maxims of Statistical Acumen for Astronomical Data Analysis.” The Astrophysical Journal Supplement Series 275, no. 2 (2024): 30. https://doi.org/10.3847/1538-4365/ad8440.
-
Dogucu, Mine, Alicia A. Johnson, Miles Q. Ott (2021). Bayes Rules! An Introduction to Applied Bayesian Modeling. https://www.bayesrulesbook.com/.
-
Harold Jeffreys; An invariant form for the prior probability in estimation problems. Proc. A 1 September 1946; 186 (1007): 453–461. https://doi.org/10.1098/rspa.1946.0056
Uniform priors are not as uninformative as you might think
By Shih Ching Fu
