Study of maximum matching size on dynamic graph
Edge-Degree Constraint Subgraphs
(EDCS)
\text{Def. For any } \beta > \beta\_ \ge 1, \text{a subgraph } H \text{ of } G \text{ is a }(\beta, \beta\_)-\text{EDCS of } G \text { if} \\
\cdot deg_H(u) + deg_H(v) \le \beta~~~~\forall (u, v)\in E(H) \\
\cdot deg_H(u) + deg_H(v) \ge \beta\_~~~~\forall (u, v)\in E(G \setminus H)
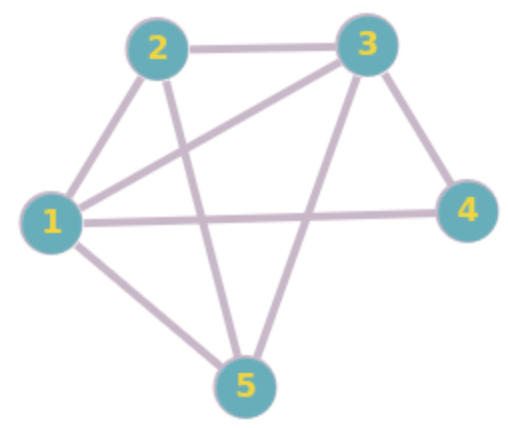
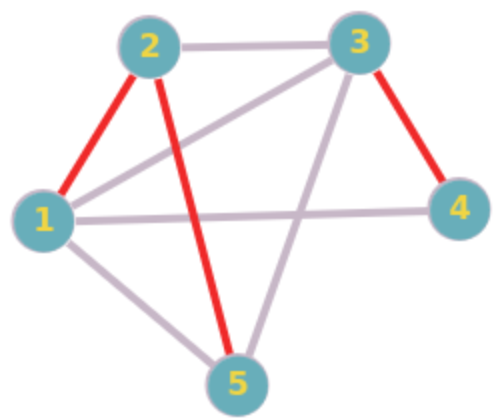
G
(3, 2)-\text{EDCS of } G
Main property of EDCS
\text{if }\beta \ge 1/\epsilon \text{ and } \beta\_ \ge (1 - \epsilon)\beta, \text{ then }\mu(H) \ge (\frac{2}{3} - O(\epsilon))\mu(G)
\text{That is, the size of maximum matching on EDCS will}\\
\text{be almost two-third of the original graph}
\text{But this is not enough to beating two-third}
On Tight Instance of EDCS in Bipartite Graph
\text{The author prove a stronger result, which says with right paramenters, }\\ \text{if } H ~\text{doesn't include a larger-than-two-third matching, then there exist an}\\ \text{almost 2/3 matching } M \text{ on }H ~s.t. ~ G ~\text{is far from maximal}
\text{We will make use of this property to beat two-third!}
On Tight Instance of EDCS in Bipartite Graph

\text{(P1): the subgraph }H' \text{ of }H \text{ have almost two-third matching}
\text{(P2): the graph consist of unmatched vertices is far from maximal}
\text{(P3): bound the size of }V_{mid}
On Tight Instance of EDCS in Bipartite Graph
\text{(P1): the subgraph }H' \text{ of }H \text{ have almost two-third matching}
\text{(P2): the graph consist of unmatched vertices is far from maximal}
\text{(P3): bound the size of }V_{mid}
(P1)
(P1)
(P2)
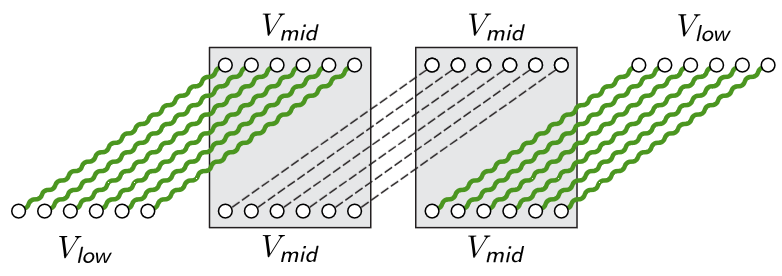
Some settings for the proves
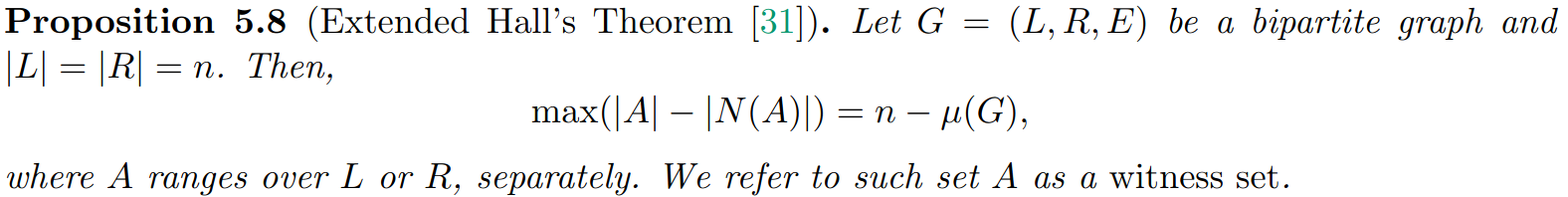
Some settings for the proves
\text{Let } A \text{ be the Hall's witness of }H, \text{ w.l.o.g. }A \subseteq L. \\
\text{Define } \bar A :=L \setminus A, ~B:=N_H(A), ~\bar B:= R \setminus B
\bar A
A
\bar B
B
H
H
Some settings for the proves
\text{Let } A \text{ be the Hall's witness of }H, \text{ w.l.o.g. }A \subseteq L. \\
\text{Define } \bar A :=L \setminus A, ~B:=N_H(A), ~\bar B:= R \setminus B
\bar A
A
\bar B
B
H
H
\text{Fix a maximum matching } M^* \text{ of graph }G, \\ \text{let }\bar M^* \text{be the edges in } M^* \text{ that connect }A \text{ and }\bar B, \\ \text{also define } S:=V(\bar M^*),~W:= V((A\cup\bar B)\setminus S),~T:= \bar A \cup B
S
S
W
W
T
T
\bar M^*
The characterizations
\text{If }\mu(H) < (2/3 + \delta)\mu(G), \text{we have the following characterization}
\bar A
A
\bar B
B
H
H
S(V_{mid})
W(V_{low})
T(V_{mid})
\bar M^*
\cdot |S\setminus V_{mid}| \le 199 \delta_{\mu}(G)~(\text{almost all vertices in }S \text{ belong to }V_{mid})
\cdot |T\setminus V_{mid}| \le 600 \delta_{\mu}(G) ~(\text{almost all vertices in }T \text{ belong to }V_{mid})
\cdot |W\setminus V_{low}| \le 33\sqrt{\delta}\mu(G)~(\text{almost all vertices in }W\text{ belong to } V_{low})
S(V_{mid})
W(V_{low})
T(V_{mid})
Some Auxiliary Claims
\text{Claim 5.9. } \mu(H) = |T|
\bar A
A
\bar B
B
H
H
S(V_{mid})
W(V_{low})
T(V_{mid})
\bar M^*
S(V_{mid})
W(V_{low})
T(V_{mid})
\text{Claim 5.15.} (\frac{2}{3} - 2\delta)\mu(G) \le |S| \le (\frac{2}{3} + 3\delta)\mu(G)
\text{That is, the size of }S \text{ is about two-third}
The proves
(P1) \mu(H') \ge ( \frac{2}{3}-120 \sqrt{\delta})\mu(G)
\bar A
A
\bar B
B
H
H
S(V_{mid})
W(V_{low})
T(V_{mid})
\bar M^*
S(V_{mid})
W(V_{low})
T(V_{mid})
\text{Define } \tilde M^* := M^* \setminus \bar M^*, \text{since } S:=V(\bar M^*), \text{edges in } \tilde M^* \\ \text{must connect } W \text{ and } T
\tilde M^*
\tilde M^*
The proves
(P1) \mu(H') \ge ( \frac{2}{3}-120 \sqrt{\delta})\mu(G)
\bar A
A
\bar B
B
H
H
S(V_{mid})
W(V_{low})
T(V_{mid})
\bar M^*
S(V_{mid})
W(V_{low})
T(V_{mid})
\text{Let call an edge "bad" if one of its endpoint is in }(W\setminus V_{low})\cup(T\setminus V_{mid})
\tilde M^*
\tilde M^*
\text{By the previous claims, such edges won't be too much}
\cdot |T\setminus V_{mid}| \le 600 \delta_{\mu}(G) ~(\text{almost all vertices in }T \text{ belong to }V_{mid})
\cdot |W\setminus V_{low}| \le 33\sqrt{\delta}\mu(G)~(\text{almost all vertices in }W\text{ belong to } V_{low})
The proves
(P1) \mu(H') \ge ( \frac{2}{3}-120 \sqrt{\delta})\mu(G)
\text{Let call an edge "bad" if one of its endpoint is in }(W\setminus V_{low})\cup(T\setminus V_{mid})
\text{By the previous claims, such edges won't be too much}
\cdot |T\setminus V_{mid}| \le 600 \delta_{\mu}(G) ~(\text{almost all vertices in }T \text{ belong to }V_{mid})
\cdot |W\setminus V_{low}| \le 33\sqrt{\delta}\mu(G)~(\text{almost all vertices in }W\text{ belong to } V_{low})
\text{\# of bad edges} \le |W\setminus V_{low}| + |T\setminus V_{mid}| \\ \le 33\sqrt{\delta}\mu(G)+600\delta \mu(G) \\ \le119 \sqrt{\delta}\mu(G)
(\text{since }\delta < \frac{1}{60})
The proves
(P1) \mu(H') \ge ( \frac{2}{3}-120 \sqrt{\delta})\mu(G)
\text{\# of bad edges} \le |W\setminus V_{low}| + |T\setminus V_{mid}| \\ \le 33\sqrt{\delta}\mu(G)+600\delta \mu(G) \\ \le119 \sqrt{\delta}\mu(G)
(\text{since }\delta < \frac{1}{60})
\text{Claim 5.15.} (\frac{2}{3} - 2\delta)\mu(G) \le |S| \le (\frac{2}{3} + 3\delta)\mu(G)
\text{\# of good edges} \ge |\tilde M^*| - 119\sqrt{\delta}\mu(G) \\
= (\mu(G) - |S|/2)-119\sqrt{\delta}\mu(G)\\
\ge\mu(G) - \frac{1}{2}(\frac{2}{3} + 3\delta)\mu(G)-119\sqrt{\delta}\mu(G)\\
>(\frac{2}{3}-120\sqrt{\delta})\mu(G)
(\text{since }|\bar M^*| = |S|/2)
(\text{since }\delta < \frac{1}{60})
The proves
(P1) \mu(H') \ge ( \frac{2}{3}-120 \sqrt{\delta})\mu(G)
\text{\# of good edges} >(\frac{2}{3}-120\sqrt{\delta})\mu(G)
\text{Since any good edge }(u, v) \text{ have one endpoint in }(W\cap V_{low}), \\
\text{another in }(T\cap V_{mid}), \text{we have } d_H(u) + d_H(v) \le .8\beta < (1 - \epsilon)\beta, \\
\text{it must belong to }H(\text{the EDCS}), \text{and belong to }H', \text{so we have }\\
\mu(H') \ge \text{\# of good edges} \ge (\frac{2}{3} - 120\sqrt{\delta})\mu(G)
The proves
(P1) \mu(H') \ge ( \frac{2}{3}-120 \sqrt{\delta})\mu(G)
\bar A
A
\bar B
B
H
H
S(V_{mid})
W(V_{low})
T(V_{mid})
\bar M^*
S(V_{mid})
W(V_{low})
T(V_{mid})
\text{Simply speaking, this part of the graph have almost }2/3 \text{ matching}
\tilde M^*
\tilde M^*
The proves
(P2) \text{For any matching } M \text{ in } H',~\mu(G[V_{mid}\setminus V(M)]) \ge (\frac{1}{3} - 800\delta)\mu(G)
\text{Let say an edge }(u, v) \in \bar M^* \text{ is wasted if at least one of its endpoint } u\\
\text{is matched in }M, \text{ and suppose it match to } w, \text{since }(u, w) \in M \subseteq H',\\
w \text{ should belong to }T, \text{ and either }u\in (S\cap V_{low}) \text{ or }w \in (T\cap V_{low}) \text{will hold}
\bar A
A
\bar B
B
H
H
S(V_{mid})
W(V_{low})
T(V_{mid})
\bar M^*
S(V_{mid})
W(V_{low})
T(V_{mid})
u
w
v
The proves
(P2) \text{For any matching } M \text{ in } H',~\mu(G[V_{mid}\setminus V(M)]) \ge (\frac{1}{3} - 800\delta)\mu(G)
\text{Let say an edge }(u, v) \in \bar M^* \text{ is wasted if at least one of its endpoint } u\\
\text{is matched in }M, \text{ and suppose it match to } w, \text{since }(u, w) \in M \subseteq H',\\
w \text{ should belong to }T, \text{ and either }u\in (S\cap V_{low}) \text{ or }w \in (T\cap V_{low}) \text{will hold}
\text{So for any wasted edge, there is one dedicated vertex in }S \cup T \text{ that}\\ \text{belong to }V_{low}, \text{and we have}
\text{\# of wasted edges } \le |S\cap V_{low}| + |T\cap V_{low}| \\
\le |S \setminus V_{mid}| + |T \setminus V_{mid}| \\
\le 199 \delta \mu(G) + 600 \delta \mu (G) = 799 \delta \mu (G)
\cdot |S\setminus V_{mid}| \le 199 \delta_{\mu}(G)~(\text{almost all vertices in }S \text{ belong to }V_{mid})
\cdot |T\setminus V_{mid}| \le 600 \delta_{\mu}(G) ~(\text{almost all vertices in }T \text{ belong to }V_{mid})
The proves
(P2) \text{For any matching } M \text{ in } H',~\mu(G[V_{mid}\setminus V(M)]) \ge (\frac{1}{3} - 800\delta)\mu(G)
\text{\# of wasted edges } \le |S\cap V_{low}| + |T\cap V_{low}| \\
\le |S \setminus V_{mid}| + |T \setminus V_{mid}| \\
\le 199 \delta \mu(G) + 600 \delta \mu (G) = 799 \delta \mu (G)
\text{Since any edge that is not wasted belongs to }G[V_{mid}\setminus V(M)], \text{we have}
\mu(G[V_{mid}\setminus V(M)] \ge |\bar M^*| - 799 \delta \mu (G) \\
=\frac{1}{2}|S| - 799 \delta\mu(G) \\
\ge \frac{1}{2}(\frac{2}{3}-2\delta)\mu (G) - 799 \delta \mu (G) \\
=(\frac{1}{3} - 800\delta)\mu(G)
(\text{Since } |\bar M^*| = \frac{1}{2}|S|)
\text{Claim 5.15.} (\frac{2}{3} - 2\delta)\mu(G) \le |S| \le (\frac{2}{3} + 3\delta)\mu(G)
(\text{By claim 5.15})
The proves
(P2) \text{For any matching } M \text{ in } H',~\mu(G[V_{mid}\setminus V(M)]) \ge (\frac{1}{3} - 800\delta)\mu(G)
\bar A
A
\bar B
B
H
H
S(V_{mid})
W(V_{low})
T(V_{mid})
\bar M^*
S(V_{mid})
W(V_{low})
T(V_{mid})
\text{Simply speaking, this part have almost }1/3 \text{ matching}
The proves
(P3) |V_{mid}| < 8 \mu(G)
|V_{mid}| = |V_{mid} \cap S| + |V_{mid} \cap T| + |V_{mid} \cap W| \\
\le |S| + |T| + |W\setminus V_{low}| \\
\le |S| + |T| + 33\sqrt{\delta}\mu (G) \\
< 8 \mu(G)
\cdot |W\setminus V_{low}| \le 33\sqrt{\delta}\mu(G)~(\text{almost all vertices in }W\text{ belong to } V_{low})
(\text{Since }|S| = 2|\bar M^*| \le 2 \mu (G) \text { and } |T| = \mu (H) \le \mu(G) \text{ and }\delta < \frac{1}{60})
\text{Claim 5.9. } \mu(H) = |T|
idea of the algorithm
\bar A
A
\bar B
B
H
H
S(V_{mid})
W(V_{low})
T(V_{mid})
\bar M^*
S(V_{mid})
W(V_{low})
T(V_{mid})
\tilde M^*
\tilde M^*
\text{If there is an greater-than-2/3 mataching on EDCS, then we are done,}\\
\text{otherwise, we try to find an almost 2/3 matching on }H', \\
\text{and find a greedy matching on the rest of the graph}
The black boxes
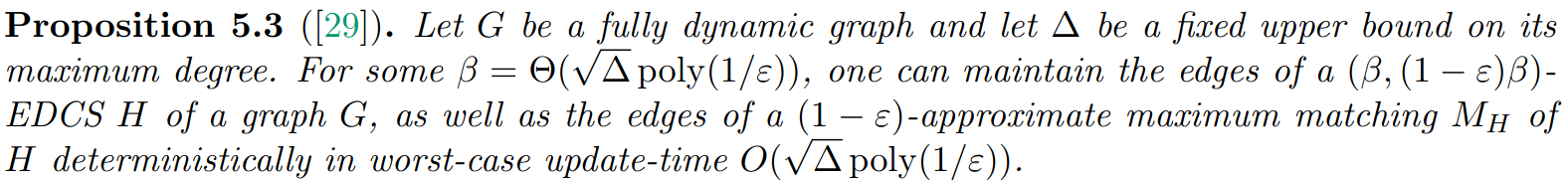
\text{That is, a black box that can maintain EDCS and a } (1 - \epsilon) \text{matching on it}\\ \text{dynamically with update-time }O(\sqrt{\Delta}poly(1/\epsilon))
The black boxes
\text{Hopcroft-Karp algorithm, which can find a } (1 - \epsilon) \text{matching of an}\\ \text{m-edge graph in }O(m/\epsilon )
The black boxes
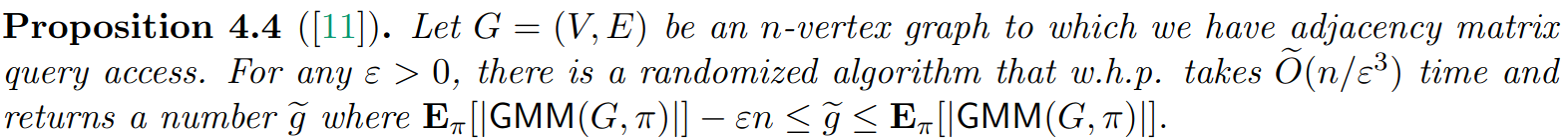
\text{That is, a black box that take the adjacency matrix query access and }\\
\text{estimate the size of a greedy matching in } \tilde O(n/\epsilon^3) \text{ time}, \\
\text{which will be a } (2, \epsilon) \text{ approximate matching}
The data structure
\text{We maintain the adjacency matrix of } G,\\
\text{and a }(\beta, (1-\epsilon)\beta)\text{-EDCS of } G \text{ where } \beta = \Theta (\sqrt{\Delta}poly(1/\epsilon)),\\
\text{ and a } (1-\epsilon) \text{ matching }M_H \text{ with }O(\sqrt{\Delta}poly(1/\epsilon)) \\
\text{ update time using EDCS maintainer}
The algorithm
\text{When being query, we run the following algorithm}

The algorithm
\text{The construction of } H' \text{ will takes } O(n\beta) \text{ since the degree of vertices} \\
\text{ in EDCS is at most } \beta

The algorithm

\text{To find a } (1 - \epsilon)-\text{approximate matching on } H' \text{, we use hopcroft-karp}
\text{Hopcroft-Karp algorithm, which can find a } (1 - \epsilon) \text{matching of an}\\ \text{m-edge graph in }O(m/\epsilon )
\text{Since the size of edge set of } H' \text{ is } O(n\beta),\\
\text{hopcroft-karp runs in } O(n\beta /\epsilon)
The algorithm

\text{Since the size of edge set of } F \text{ will be } O(|V_{mid}|^2) ,\\
\text{we don't construct it explicitly}
The algorithm

\text{Instead, we use the greedy matching estimator to compute a } \\
(2, \epsilon)\text{-matching of }F
\text{That is, a black box that take the adjacency matrix query access and }\\
\text{estimate the size of a greedy matching in } \tilde O(n/\epsilon^3) \text{ time}, \\
\text{which will be a } (2, \epsilon) \text{ approximate matching}
\text{Since we have adjacency matrix access of } G, \\
\text{we can also provide the access to }F
\text{So this part runs in } \tilde O(n/\epsilon^3)
The algorithm

\text{Finally, compare the size of } M_H ((1-\epsilon)\text{-matching on EDCS})\\
\text{with the size of } M_{H'} + g\text{, and output the larger one}
The algorithm

\text{Finally, compare the size of } M_H ((1-\epsilon)\text{-matching on EDCS})\\
\text{with the size of } M_{H'} + g\text{, and output the larger one}

\text{So if }M_H \text{ is over two-third we are done, }\\
\text{otherwise } |M_{H'}|+g \text{ will be over two-third by the tight instance lemma}
The algorithm

(O(n\beta/\epsilon) \text{time by hopcroft-karp})
(\tilde O(n/\epsilon^3) \text{ time by greedy matching estimator})
(O(n\beta) \text{time to construct }H')
\text{So the whole algorithm runs in } O(n\beta/\epsilon) + \tilde O(n/\epsilon^3), \\
\text{and we take }\beta = \sqrt{\Delta}poly(1/\epsilon),\\
\text{which leads to }O(n\sqrt{\Delta}poly(1/\epsilon)) + \tilde O(n poly(1/\epsilon))
The prove of approximate ratio
\text{Lemma 5.6. Let }\delta_0 = 1.8 \times 10^{-6}\text{, either }|M_H| \ge (\frac{2}{3}+\delta_0)\mu(G) \text{ or }\\
|M_{H'}| + g - \epsilon|V_{mid}| \ge(\frac{2}{3} +\delta_0)\mu(G) \text{ must hold}
\text{Let }\delta = 1.9\times 10^{-6} \text{and }\epsilon< \delta / 100 \text{, if }|M_H| \ge (1 - \epsilon)(\frac{2}{3} + \delta)\mu(G)\text{, then}
\text{Proof.}
|M_H| \ge (\frac{2}{3} + \delta - \epsilon)\mu(G) \ge (\frac{2}{3} + 0.99\delta)\mu(G) \ge (\frac{2}{3} + \delta_0)\mu(G)
The prove of approximate ratio
\text{Lemma 5.6. Let }\delta_0 = 1.8 \times 10^{-6}\text{, either }|M_H| \ge (\frac{2}{3}+\delta_0)\mu(G) \text{ or }\\
|M_{H'}| + g - \epsilon|V_{mid}| \ge(\frac{2}{3} +\delta_0)\mu(G) \text{ must hold}
\text{Otherwise }|M_H| < (1 - \epsilon)(\frac{2}{3} + \delta)\mu(G)\text{, since }|M_H| \text{ is a }(1 - \epsilon)\text{-matching,}\\
\text{we have }\mu(H) < (\frac{2}{3} + \delta_0)\mu(G)\text{, so we can use the tight instance lemma}
\text{Proof.}
The prove of approximate ratio
\text{Lemma 5.6. Let }\delta_0 = 1.8 \times 10^{-6}\text{, either }|M_H| \ge (\frac{2}{3}+\delta_0)\mu(G) \text{ or }\\
|M_{H'}| + g - \epsilon|V_{mid}| \ge(\frac{2}{3} +\delta_0)\mu(G) \text{ must hold}
\text{Otherwise }|M_H| < (1 - \epsilon)(\frac{2}{3} + \delta)\mu(G)\text{, since }|M_H| \text{ is a }(1 - \epsilon)\text{-matching,}\\
\text{we have }\mu(H) < (\frac{2}{3} + \delta_0)\mu(G)\text{, so we can use the tight instance lemma}
\text{Proof.}
\text{(P1)} \mu(H') \ge (\frac{2}{3} - 120\sqrt{\delta})\text{, which imply }|M_{H'}| \ge (1-\epsilon)(\frac{2}{3}-120\sqrt{\delta})\mu(G)
The prove of approximate ratio
\text{Lemma 5.6. Let }\delta_0 = 1.8 \times 10^{-6}\text{, either }|M_H| \ge (\frac{2}{3}+\delta_0)\mu(G) \text{ or }\\
|M_{H'}| + g - \epsilon|V_{mid}| \ge(\frac{2}{3} +\delta_0)\mu(G) \text{ must hold}
\text{Otherwise }|M_H| < (1 - \epsilon)(\frac{2}{3} + \delta)\mu(G)\text{, since }|M_H| \text{ is a }(1 - \epsilon)\text{-matching,}\\
\text{we have }\mu(H) < (\frac{2}{3} + \delta_0)\mu(G)\text{, so we can use the tight instance lemma}
\text{Proof.}
\text{(P1)} \mu(H') \ge (\frac{2}{3} - 120\sqrt{\delta})\text{, which imply }|M_{H'}| \ge (1-\epsilon)(\frac{2}{3}-120\sqrt{\delta})\mu(G)
\text{(P2) For any matching }M \text{ in }H', \mu(G[V_{mid}\setminus V(M)]) \ge (\frac{1}{3}-800\delta)\mu(G),\\
\text{which imply }\mu(F) \ge(\frac{1}{3}-800\delta)\mu(G)\text{, and since } g \text{ is the size of a maximal}\\
\text{matching, we have }g \ge\frac{1}{2}(\frac{1}{3} - 800\delta)\mu(G)
The prove of approximate ratio
\text{Lemma 5.6. Let }\delta_0 = 1.8 \times 10^{-6}\text{, either }|M_H| \ge (\frac{2}{3}+\delta_0)\mu(G) \text{ or }\\
|M_{H'}| + g - \epsilon|V_{mid}| \ge(\frac{2}{3} +\delta_0)\mu(G) \text{ must hold}
\text{Otherwise }|M_H| < (1 - \epsilon)(\frac{2}{3} + \delta)\mu(G)\text{, since }|M_H| \text{ is a }(1 - \epsilon)\text{-matching,}\\
\text{we have }\mu(H) < (\frac{2}{3} + \delta_0)\mu(G)\text{, so we can use the tight instance lemma}
\text{Proof.}
\text{(P1)} \mu(H') \ge (\frac{2}{3} - 120\sqrt{\delta})\text{, which imply }|M_{H'}| \ge (1-\epsilon)(\frac{2}{3}-120\sqrt{\delta})\mu(G)
\text{(P2) For any matching }M \text{ in }H', \mu(G[V_{mid}\setminus V(M)]) \ge (\frac{1}{3}-800\delta)\mu(G),\\
\text{which imply }\mu(F) \ge(\frac{1}{3}-800\delta)\mu(G)\text{, and since } g \text{ is the size of a maximal}\\
\text{matching, we have }g \ge\frac{1}{2}(\frac{1}{3} - 800\delta)\mu(G)
\text{(P3) } |V_{mid}| \le 8\mu(G)
The prove of approximate ratio
\text{Lemma 5.6. Let }\delta_0 = 1.8 \times 10^{-6}\text{, either }|M_H| \ge (\frac{2}{3}+\delta_0)\mu(G) \text{ or }\\
|M_{H'}| + g - \epsilon|V_{mid}| \ge(\frac{2}{3} +\delta_0)\mu(G) \text{ must hold}
\text{Proof.}
\text{(P1)} |M_{H'}| \ge (1-\epsilon)(\frac{2}{3}-120\sqrt{\delta})\mu(G)
\text{(P2) }g \ge\frac{1}{2}(\frac{1}{3} - 800\delta)\mu(G)
\text{(P3) } |V_{mid}| \le 8\mu(G)
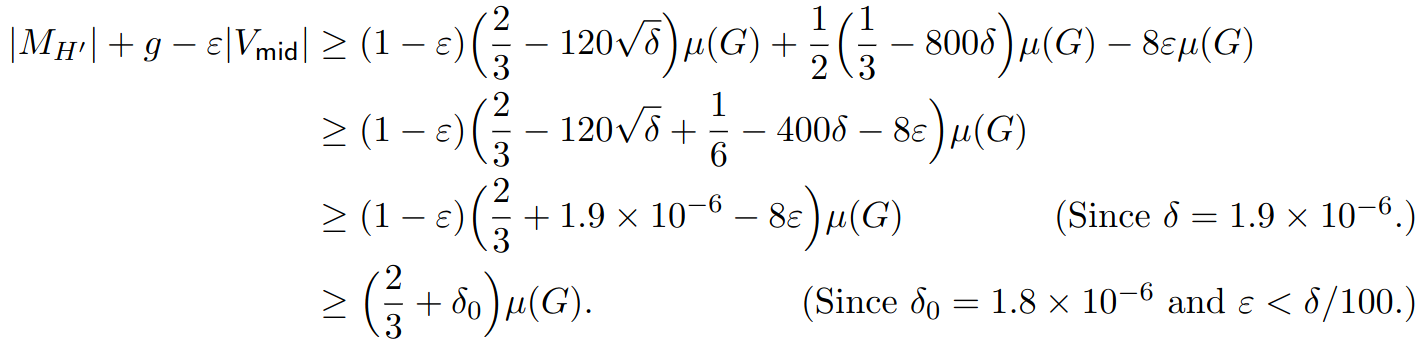
\text{Then just do some math using these property, and we are done}
The algorithm
\text{So the whole algorithm runs in } O(n\beta/\epsilon) + \tilde O(n/\epsilon^3), \\
\text{and we take }\beta = \sqrt{\Delta}poly(1/\epsilon),\\
\text{which leads to }O(n\sqrt{\Delta}poly(1/\epsilon)) + \tilde O(n poly(1/\epsilon))

\text{Finally, plug this algorithm into the "lazy update" lemma, }\\
\text{we get a fully dynamic algorithm maintain a }(\frac{2}{3}+\delta_0)\text{-apx matching size}\\
\text{with }O(\sqrt{n}) \text{ update time}
Final remark
\text{In conclusion, the algorithm first find a matching on EDCS, }\\
\text{if it is not over two-third, then we try to find a almost two-third}\\
\text{matching in the red part, and a greedy matching on the blue part,}\\
\text{then we can still get a over two-third matching under }\\
\text{the tight instance lemma}
\bar A
A
\bar B
B
H
H
S(V_{mid})
W(V_{low})
T(V_{mid})
\bar M^*
S(V_{mid})
W(V_{low})
T(V_{mid})
\tilde M^*
\tilde M^*
Copy of Dynamic Algorithm for Maximum Matching Size: Beating Two-Third For Bipartite Graph
By shioko
Copy of Dynamic Algorithm for Maximum Matching Size: Beating Two-Third For Bipartite Graph
- 12


